En gang for å vite alt om edelstenskrystallografi
En omfattende guidebok om krystallografiens former, typer, klassifikasjoner og forskjeller
Jorden består av utallige molekyler og atomer. Moderne vitenskapelig forskning har funnet ut at faste materialer i naturen består av ulike kjemiske grunnstoffer. Resultater fra røntgenanalyser viser at atomene i grunnstoffene i visse faste materialer er ordnet pent og regelmessig sammen. Disse materialene klassifiseres som krystallinske eller kalles krystaller, og det ordnede atomgitteret kalles krystallstruktur (figur 2-1-1).
De fleste edelstenematerialer som vokser i naturen og i laboratorier, er krystallinske. I dette kapittelet diskuterer vi begrepet krystaller, klassifiseringen av dem og forholdet mellom krystaller og grunnleggende terminologi i gemmologi.

Innholdsfortegnelse
Avsnitt ⅠBegrepet og beskrivelsen av krystaller
Når vi snakker om edelstener, tenker vi ofte på deres glitrende og gjennomskinnelige egenskaper (Figur 2-1-2). Sett fra geologers og gemmologers perspektiv tilhører de mest elskede edelstenene en geometrisk form av faste stoffer - krystaller. Essensen av krystallenes skjønnhet er faktisk geometriens skjønnhet.

1. Konseptet med krystaller
Krystaller er de lettest assosierbare og mest vanlige i naturen. Krystaller finnes på alle jordens syv kontinenter, og når de finnes i naturen, har de ofte form av geometriske polyedre (figur 2-1-3). De omtales vanligvis som krystaller. Senere ble dette begrepet utvidet til å referere til naturlig forekommende faste stoffer med geometriske polyedriske former, som for eksempel diamant- og akvamarin-krystaller (figur 2-1-4). Krystaller kan også beskrive faste stoffer med uregelmessige, ujevne, slitte, ødelagte eller kunstig bearbeidede overflater, men med et atomarrangement som likevel følger et regelmessig mønster. Krystallografer mener at alle krystaller har seks grunnleggende egenskaper: selvbegrensning, ensartethet, anisotropi, symmetri, stabilitet og fast smeltepunkt.
① Selvbegrensende refererer til grunnstoffers egenskap til spontant å danne geometriske polyedriske former. Denne egenskapen kan forklare hvorfor ulike grunnstoffer har forskjellige krystallgeometriske former.
② Ensartethet refererer til den egenskapen at alle krystalldelene har de samme fysiske og kjemiske egenskapene. Denne egenskapen kan hjelpe oss med å skille og identifisere ulike mineralkrystaller.
③ Anisotropi refererer til egenskapen der grunnstoffenes plassering varierer i ulike retninger, noe som fører til små forskjeller i fysiske egenskaper avhengig av retningen. Denne egenskapen kan forklare hvorfor diamanter med den høyeste hardheten kan slipes og poleres.
④ Symmetri refererer til egenskapen der identiske deler eller egenskaper i en krystall gjentas i et regelmessig mønster. Denne egenskapen er ekstremt viktig og spesiell for krystaller, og vil bli utdypet i den andre delen av dette kapittelet.
⑤ Stabilitet refererer til en krystalls stabilitet som følge av dens minimale indre energi. Hvis den indre energien i en krystall er høy og ujevn, er den utsatt for å sprekke av seg selv. Denne egenskapen kan forklare hvorfor rubinkrystaller syntetisert ved flammefusjonsteknikk alltid ser ut til å være halve i stedet for hele.
⑥ Fast smeltepunkt refererer til den egenskapen at en krystall har et fast smeltepunkt.

Figur 2-1-3 Granat (venstre side er krystallen, høyre side er den polerte granaten)

Figur 2-1-4 Akvamarin-krystall
2. Krystallers ideelle form
Krystallene som omtales i krystallografien, er hovedsakelig ideelle enkeltkrystaller. En ideell enkeltkrystall defineres som en krystall hvis indre struktur strengt følger reglene for romlige gitter, og hvis form er en regelmessig geometrisk kombinasjonsform. Formene til ideelle enkeltkrystaller deles inn i to typer: enkle former og kombinerte former.
(1) Enkel form
En enkel form refererer til en kombinasjon av en gruppe krystallflater som er forbundet med symmetrielementer, som kan forstås som en geometrisk kropp sammensatt av krystallflater med samme form og størrelse i en ideell tilstand (Figur 2-1-5). Det finnes 47 typer enkle former i krystaller.
De viktigste punktene for å identifisere enkle former er: Alle krystallflatene i krystallen har samme form og størrelse, og krystallflatene kan være orientert forskjellig.
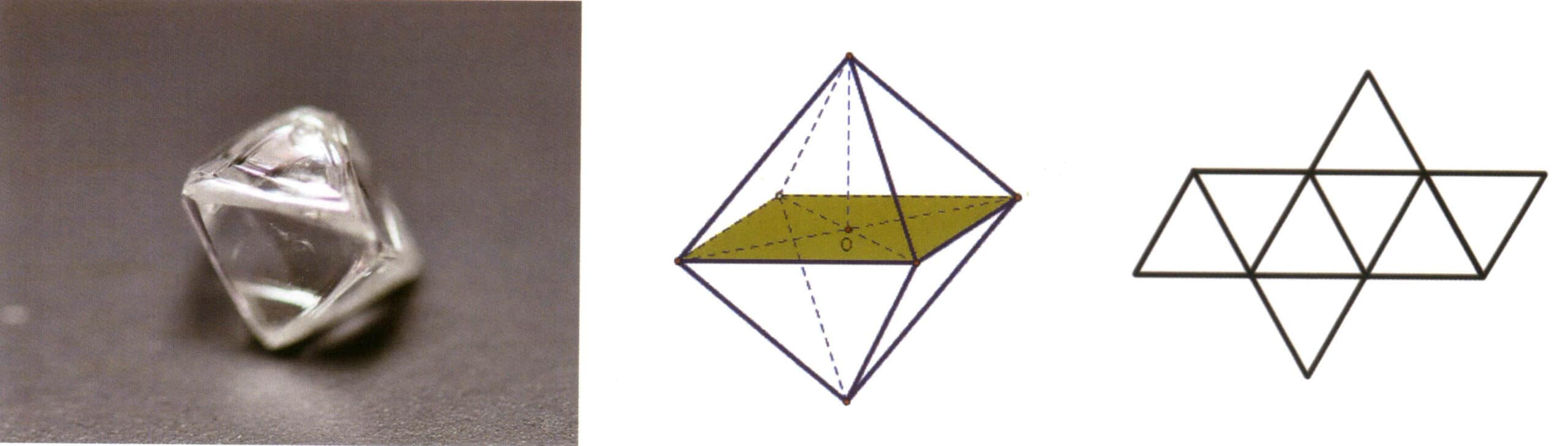
(2) Kombiner Skjema
Aggregeringen av enkle former kalles kombinatform, og består av to eller flere forskjellige enkle former. Ikke alle enkle former kan fritt kombineres til kombinatform; bare enkle former med samme punktgruppe kan aggregeres (figur 2-1-6 til 2-1-8).
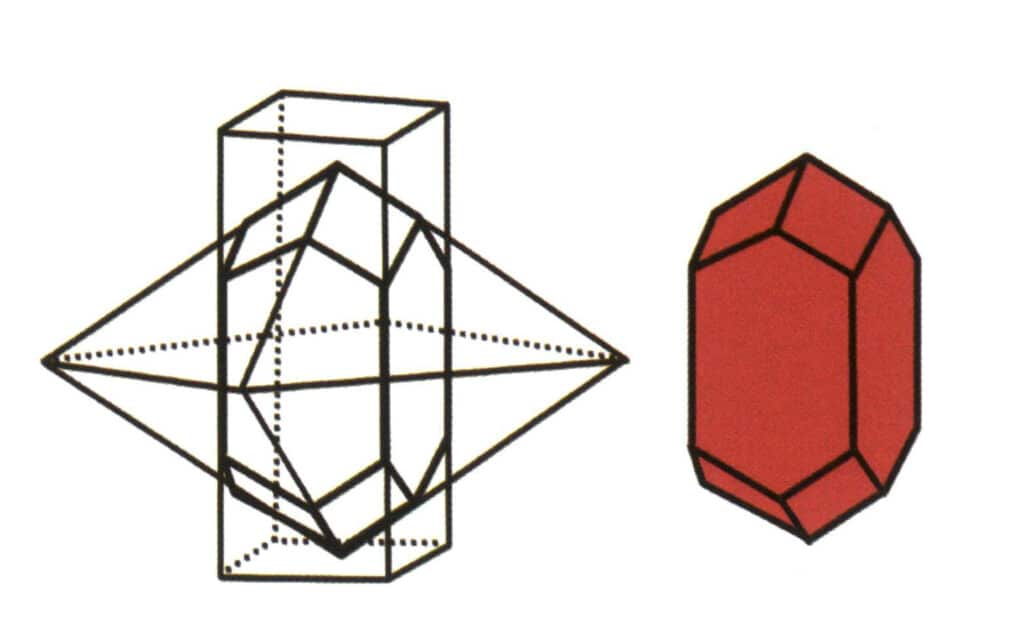
Figur 2-1-6 Kombinasjon av tetragonale prismer og tetragonale dipyramider
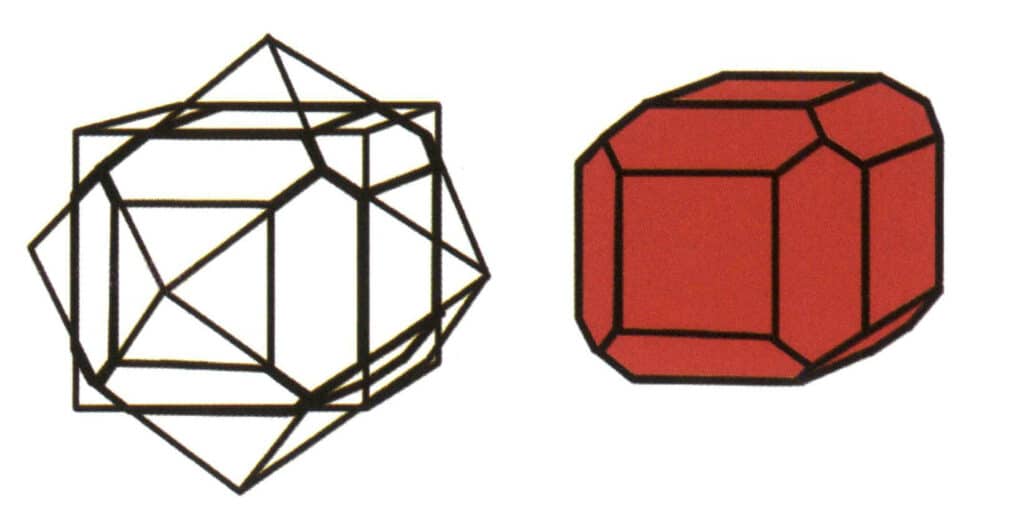
Figur 2-1-7 Kombinasjon av kuber og rombiske dodekaeder
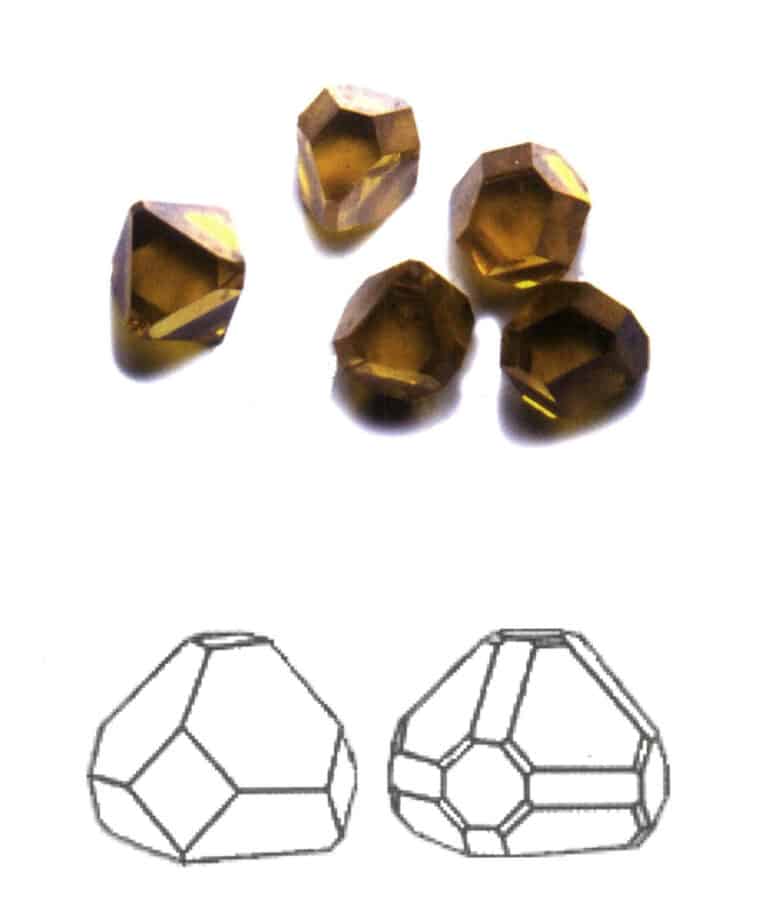
Det viktigste poenget med å identifisere kombinasjonsformer er tilstedeværelsen av to eller flere ulikt formede krystallflater i krystallen.
Når man finner enkeltkrystaller i naturen, har de alltid en betydelig forskjell fra den ideelle morfologien til enkeltkrystaller (Figur 2-1-9), for eksempel at en enkelt flate ikke nødvendigvis har samme form og størrelse, og at krystallflater forsvinner, noe som beskrives som forvrengte krystaller.

Forvrengte krystaller kan også beskrives som ekte krystaller som produseres i naturen, påvirket av vekstmiljøet. De mange krystallflatene som gjentar seg i faste vinkler i ideelle krystaller, har ikke nødvendigvis samme form og størrelse. For samme type krystall må likevel krystallflatene i samme monomorfe krystall ha samme mønster og fysiske egenskaper. Vinklene mellom tilsvarende krystallflater forblir uendret, noe som gjenspeiler krystallens iboende symmetri. Krystallene som finnes i virkeligheten, er forvrengt i varierende grad.
Tvinnede krystaller kan også beskrives som faktiske krystaller som produseres i naturen, påvirket av vekstmiljøet. De mange krystallflatene som gjentar seg i faste vinkler i ideelle krystaller, har ikke nødvendigvis samme form og størrelse. For samme type krystall må likevel flatene av samme form ha samme mønster og fysiske egenskaper. Vinklene mellom tilsvarende krystallflater forblir uendret, noe som gjenspeiler krystallens iboende symmetri. Krystallene som finnes i virkeligheten, er alle, i varierende grad, tvillede.
3. Krystalliseringsvanene til krystaller
Krystaller som dannes i naturen, kan aldri oppnå en perfekt form. Hvis de vokser i mellomrommene mellom steinlag, omgitt av stein, vil krystallens naturlige form bli forvrengt. Selv krystaller som dyrkes i et laboratorium, vil bli deformert på grunn av tyngdekraften. Det er bare i den internasjonale romstasjonens tyngdekraftsfrie omgivelser at forskerne kan dyrke frem de perfekt formede krystallene de er ute etter.
Selv om krystallene har ufullkomne former, har hver type mineralkrystall en tendens til å vokse eller gruppere seg sammen på ulike måter.
Hvert mineral dannes gjerne under spesifikke forhold, og dets egenskaper gjenspeiler forholdene under dannelsen. Noen mineraler, som kvarts, har komplekse og varierende dannelsesforhold. Derfor har kvarts også flere habitus.
Generelt refererer krystallvaner til egenskapene til en bestemt krystall som har en tendens til å danne en bestemt form under visse ytre forhold. Noen ganger refererer det til de vanlige typene av krystallens enkle form.
Basert på graden av utvikling av krystaller i tredimensjonalt rom, deles krystallvaner inn i tre grunnleggende typer.
(1) Uni-retningsbestemt forlengelse
Krystallene strekker seg i én retning, og opptrer i søyleformede, akikulære, fibrøse former osv. Mineraler som beryll, turmalin, hornblende og malakitt har ofte denne formen (figur 2-1-10 til figur 2-1-11).

Figur 2-1-10 Søyleformet akvamarin (øverst) og krystalldiagram (nederst)

Figur 2-1-11 Fibrøs malakitt (øverst) og dens krystallhabituttdiagram (nederst)
(2) Bi-retningsbestemt forlengelse
Krystallene strekker seg i et plan og opptrer i plateform, bladform, skjellform osv., slik mineraler som wolframit, glimmer, plumbago og tanzanitt ofte viser (figur 2-1-12).
(3) Tri-retningsbestemt isometrisk
Krystallene utvikler seg jevnt i tre retninger og har isometriske, kornformede former, slik som spinell, granat, diamant, pyritt og fluoritt, som ofte har denne habitusen (figur 2-1-13, 2-1-14).

Figur 2-1-12 Tanzanittens plateformede krystallform (øverst) og dens krystallformdiagram (nederst)

Figur 2-1-13 Den oktaedriske krystallformen til edelstenen spinell (øverst) og dens krystallformdiagram (nederst)
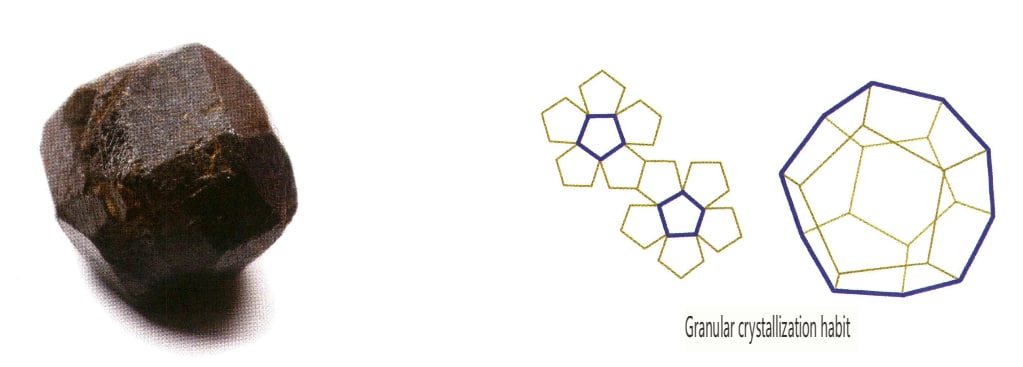
I tillegg finnes det overgangstyper som kort søyleformet, plateformet, stripelignende og tykk plateform.
Krystallens kjemiske sammensetning og struktur bestemmer hovedsakelig krystallvanen. Det er også nært knyttet til de ytre forholdene under krystalldannelsen (som temperatur, trykk, konsentrasjon, viskositet og urenheter), for eksempel forskjellene i krystallformer mellom diamanter og syntetiske diamantkrystaller.
4. Regelmessig aggregering av krystaller
I naturen kan vi finne enkeltkrystaller (figur 2-1-15) og to eller flere enkeltkrystaller som vokser sammen og danner en helhet. Dette fenomenet med flere krystaller som vokser sammen, kalles krystallaggregering. Krystallaggregering kan kategoriseres i irregulære og regulære typer. Uregelmessig krystallaggregering kan forstås som et kollektiv, noe som vil bli utdypet i kapittel tre. Det finnes fire vanlige typer regelmessig krystallaggregering: parallellaggregering, bikrystaller, overvekst og intervekst (figur 2-1-16 til 2-1-18). I dette avsnittet diskuteres hovedsakelig den typen regelmessig aggregering som kalles bikrystaller.

Figur 2-1-15 Enkrystall (turmalin)
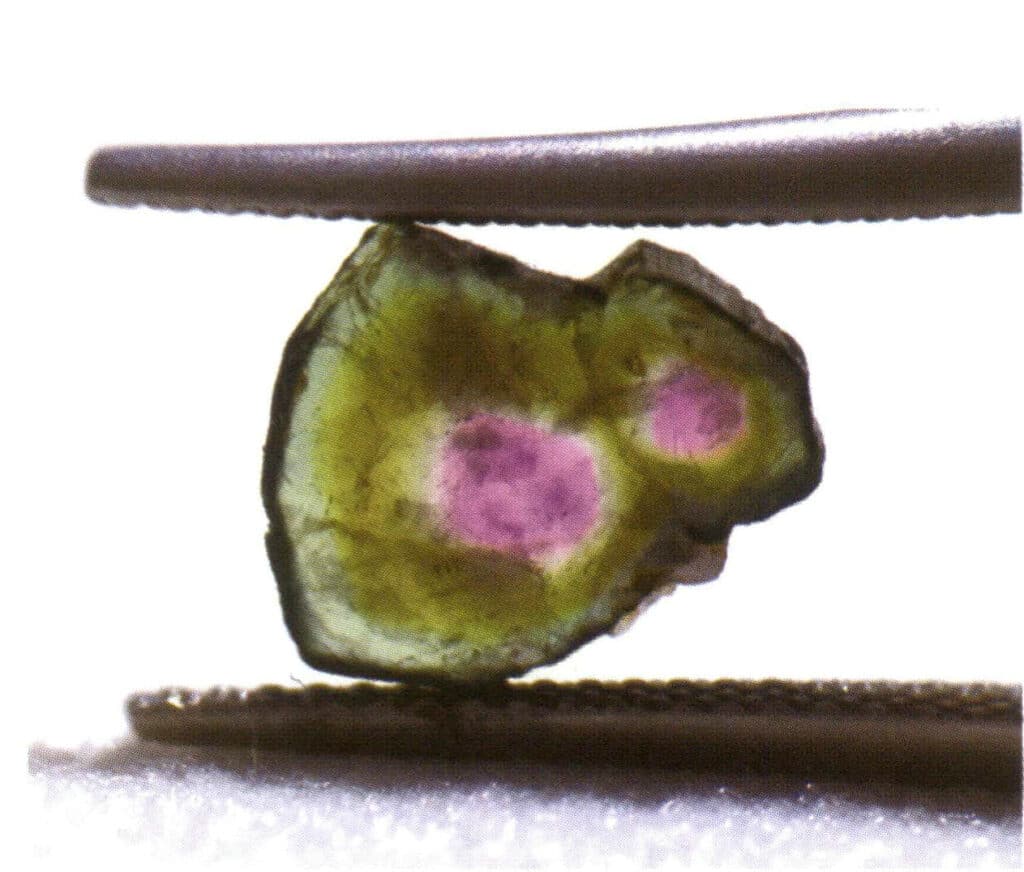
Figur 2-1-16 Parallell aggregering (Når flere krystaller av samme type vokser parallelt i rommet, kalles det parallell aggregering. På dette tidspunktet er de tilsvarende krystallflatene og kantene på de dyrkede krystallene alle parallelle med hverandre).

Figur 2-1-17 Tvillingkrystall (spinell)

Figur 2-1-18 Overvekst (en type krystall vokser på overflaten av en annen krystall i en bestemt krystallografisk retning, også kjent som epitaksial vekst)
Bikrystaller er en regelmessig sammenklumpning av to eller flere identiske krystaller i henhold til visse symmetriske regler. (Tvillingakse, tvillingplan) De to tilstøtende individenes tilsvarende flater, kanter og vinkler er ikke helt parallelle. Likevel kan de gjenspeile hverandre gjennom symmetriske operasjoner som rotasjon og rotasjonsinversjon, slik at de to individene kan sammenfalle eller justeres.
4.1 Nøkkelpunkter for identifisering av bikrystaller
① Konkave vinkler er synlige i tvinnede krystaller (Figur 2-1-19).
② Stylolitt: Mikromorfologien og andre egenskaper ved krystalloverflatene på begge sider av stylolitten er diskontinuerlig (Figur 2-1-20).
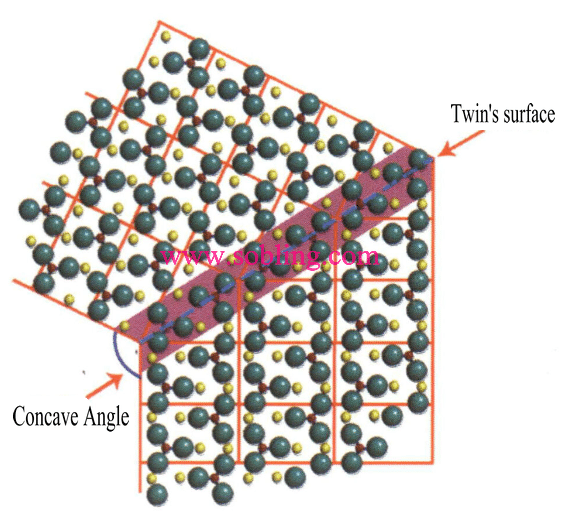
Figur 2 - 1-19 Tvillingens konkave vinkel
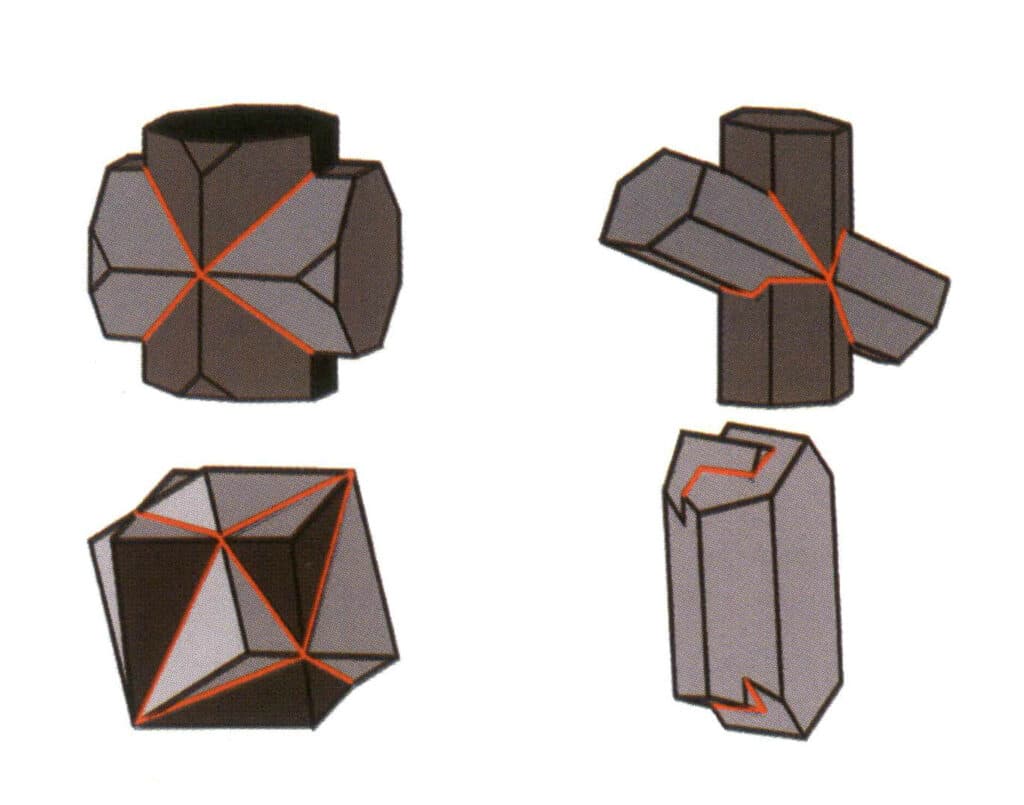
Figur 2-1-20 Stylolitt (ulike farger i figuren representerer ulike krystaller; de røde linjene indikerer tvillingstylolitt)
③ Tvillingstriper: Krystallflater eller spaltningsplan viser fine tvillingstriper (figur 2-1-21)
④ Etsningsfigur: Utseendet til etsefiguren indikerer tilstedeværelsen av twinning (Figur 2-1-22)

Figur 2-1-21 Skjematisk fremstilling av polysyntetiske tvillinger

Figur 2-1-22 Overflate av spinell med omvendte trekantede groper.
⑤ Opptreden av pseudosymmetri: fremveksten av symmetriforhold som ikke stemmer overens med den iboende punktgruppen til enkeltkrystallen (Figur 2-1-23 til Figur 2-1-24).

Figur 2-1-23 Enkeltkrystall av krysoberyl

Figur 2-1-24 Kneformet tvilling av krysoberyll
Tvillingdannelse deles inn i fem typer basert på stablingsegenskapene: kontakttvillinger (Figur 2-1-25 til Figur 2-1-26), polysyntetiske tvillinger (Figur 2-1-27), interpenetrerende tvillinger (Figur 2-1-28), triplettkrystaller (Figur 2-1-29) og komplekse tvillinger, der de fire første typene er vanlige.


Figur 2-1-26 Kontakttvilling av spinell (øverst) og skjematisk fremstilling (nederst)

Figur 2-1-27 Polysyntetisk tvilling av labradoritt (øverst) og skjematisk fremstilling (nederst)
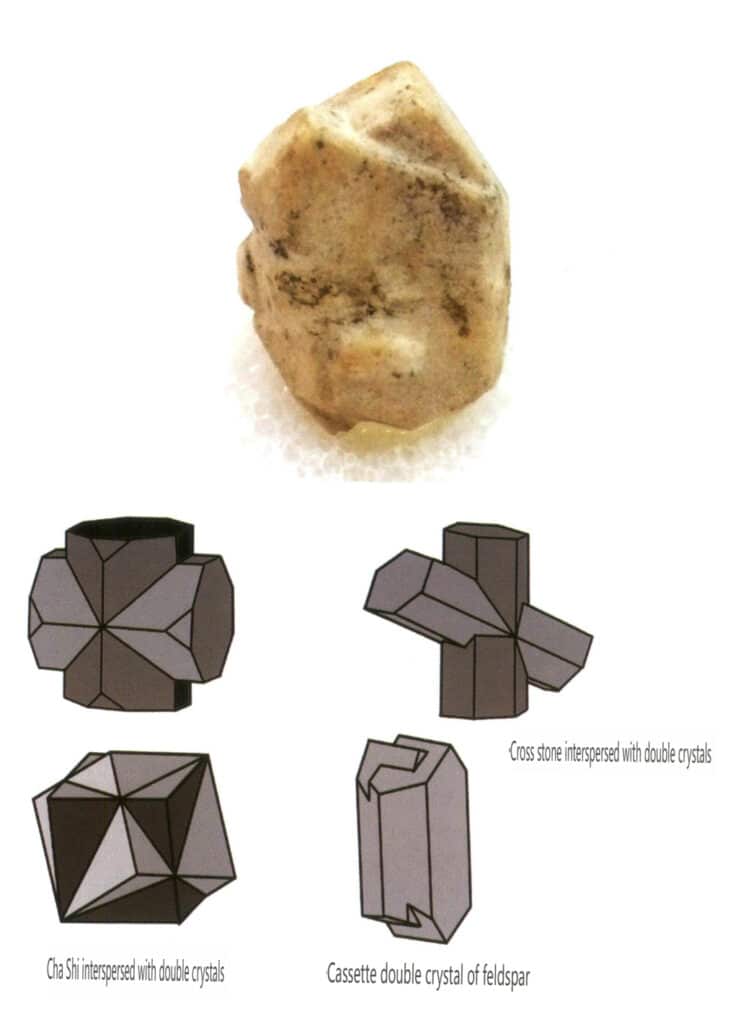
Figur 2-1-28 Tvillinkrystaller av feltspat (øverst) og skjematisk fremstilling av interpenetrerende tvillingkrystaller av andre typer (nederst)

Figur 2-1-29 Trigonal tvillingdannelse i krysoberyl (øverst) og skjematisk fremstilling (nederst)
4.2 Dannelsen av bikrystaller
① Den dannes under krystallveksten og kan utvikle seg fra tvillingkrystaller eller små krystaller som vokser avhengig av tvillingens posisjon.
② Dannes under heteromorfismeomdannelsesprosessen, for eksempel når α-kvarts omdannes til β-kvarts og danner tvillinger.
③ Dannet ved mekanisk påvirkning, der en del av krystallen glir langs et bestemt retningsplan for å danne deformasjonstvillinger, som for eksempel tvillingene i kalsitt.
5.Crystal Face-mønstre
Når krystaller oppdages i naturen, har de ofte ufullstendige former (figur 2-1-30) og spesielle overflatemønstre. Noen ganger vokser de sammen i klynger (figur 2-1-31), som ofte viser betydelige forskjeller fra de geometriske standardpolyedrene vi er kjent med, som kuber og sekskantede prismer. Dette fenomenet kalles krystallenes virkelige form. Den virkelige krystallformen har en detaljert klassifisering i krystallografien, som forvrengte krystaller, konvekse krystaller, krumme krystaller, flytende krystaller, striper på krystallflaten, etsningsfigurer, tvillingstriper osv.

Figur 2-1-30 Rubinkrystall

Figur 2-1-31 Pyrittkrystaller (til venstre flere pyrittkrystaller som vokser sammen, og til høyre en enkelt pyrittkrystall)
Denne delen tar hovedsakelig for seg krystallflatemønstrene i den virkelige krystallformen.
Teoretisk sett er krystallplanene glatte og flate. Under selve veksten eller oppløsningen av krystaller etterlater overflaten seg likevel ofte litt ujevne, regelmessige mønstre, ofte kalt krystallflatemønstre. Krystalloverflatemønstre inkluderer vekststriper, vekstlag, spiralmønstre, vekstbakker og etsefigurer. Krystalloverflatemønstrene som omtales i denne boken, refererer hovedsakelig til krystalloverflatestriper og etsefigurer som kan observeres med det blotte øye eller under lave forstørrelsesforhold.
Krystallflatestriper er en serie parallelle, rette linjer på krystalloverflaten som skyldes gjentatt konvergens og vekslende vekst av ulike enkeltformer. Disse er også kjent som "kombinasjonsstriper", og ses bare på krystalloverflater, også kalt vekststriper. For eksempel har kvarts' heksagonale prismatiske krystallflate ofte heksagonale prismatiske og rombeformede dodekaedriske finkrystallflater som vekselvis er utviklet til aggregerte tverrgående striper (figur 2-1-32).

Etsfigurer refererer til de spesifikt formede gropene (dvs. etsegroper) som blir igjen på krystallflaten på grunn av korrosjon etter at krystallen er dannet. Etsningsfigurene styres av plasseringen av grunnstoffpartiklene i krystallflaten. Etsningsfigurenes form og orientering varierer derfor mellom ulike mineraler og enkeltformer av samme krystall. For eksempel varierer etsefigurene på ulike enkeltformer av diamantkrystaller; trekantede groper kan sees på oktaedriske krystaller (Figur 2-1-33), firsidige groper på kubiske flater, overlappende firsidige groper danner et gitterlignende mønster, og linjemønstre eller mikroskopiske skivelignende mønstre kan sees på rombiske dodekaeder (Figur 2-1-34).

Figur 2-1-33 Synlige omvendte trekantede groper på den oktaederformede diamantkrystallen

Figur 2-1-34 Lineært mønstret tekstur synlig på diamantformede dodekaedriske krystaller
Bare etsefigurene på samme krystallflate av samme form kan være like, så etsefigurer brukes ofte til å identifisere mineraler og avgjøre om krystallflatene tilhører samme enkeltform (Figur 2-1-35 til Figur 2-1-42).

Figur 2-1-35 Innlagte striper av fluorittkrystaller på tregulv

Figur 2-1-36 Naturlig triangulær etsefigur i rubin (vanlige horisontale striper i rubiner, vekstlinjer parallelle med rombohedral retning, naturlige etsninger i triangulære eller sekskantede former)

Figur 2-1-37 Langsgående striper på overflaten av turmalin

Figur 2-1-38 horisontale striper på overflaten av krystallen

Figur 2-1-39 Etsfigurer på overflaten av krystallen

Figur 2-1-40 Langsgående striper på overflaten av topas

Figur 2-1-41 Topografisk bilde av en topasskrystall

Figur 2-1-42 Etsningsfigurer av spinell
Del II 47 Typer krystallformer
Det finnes 146 forskjellige enkeltformer i krystallografi, som kan klassifiseres i 47 geometriske former basert på deres geometriske former når de eksisterer uavhengig av hverandre. Disse geometriske formene er navngitt på følgende måter:
① Navngitt i henhold til egenskapene til tverrsnittsformen, for eksempel trigonalt prisme, tetragonalt prisme, sekskantet prisme, romboedrisk bipyramide osv.
② Navngitt i henhold til formen på enkeltformen, for eksempel sylinder, dobbel kjegle, kube osv.
③ Oppkalt etter antall geometriske flater, for eksempel enkeltflate, oktaeder osv.
④ Oppkalt etter formen på de geometriske flatene, for eksempel romboeder, pentakontaeder osv.
I krystallografi deles enkeltformer inn i fire kategorier: generelle former og spesielle former, lukkede former og åpne former, regulære former og irregulære former, venstrehåndsformer og høyrehåndsformer. I dette kapittelet vil vi kort diskutere lukkede og åpne former.
Lukkede former refererer til de som har krystallflater som kan omslutte et lukket rom, inndelt i tre hovedkategorier: polyedriske klasser, skjeve polyedriske klasser og bipyramidale klasser, totalt 30 typer. Hver kategori har mer detaljerte klassifikasjoner; for eksempel er den polyedriske klassen inndelt i tetraedrisk klasse, oktaedrisk klasse, kubisk klasse, etc. (figur 2-1-43 til 2-1-48).

Figur 2-1-43 Tetraederklassen
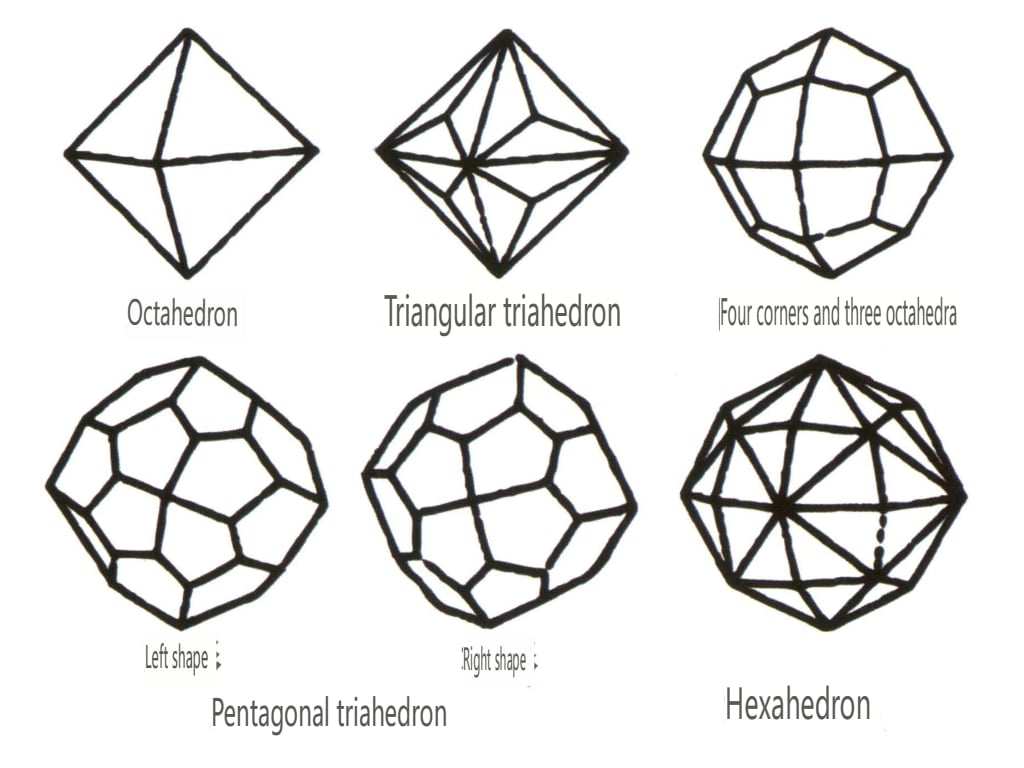
Figur 2-1-44 Oktaedral klasse
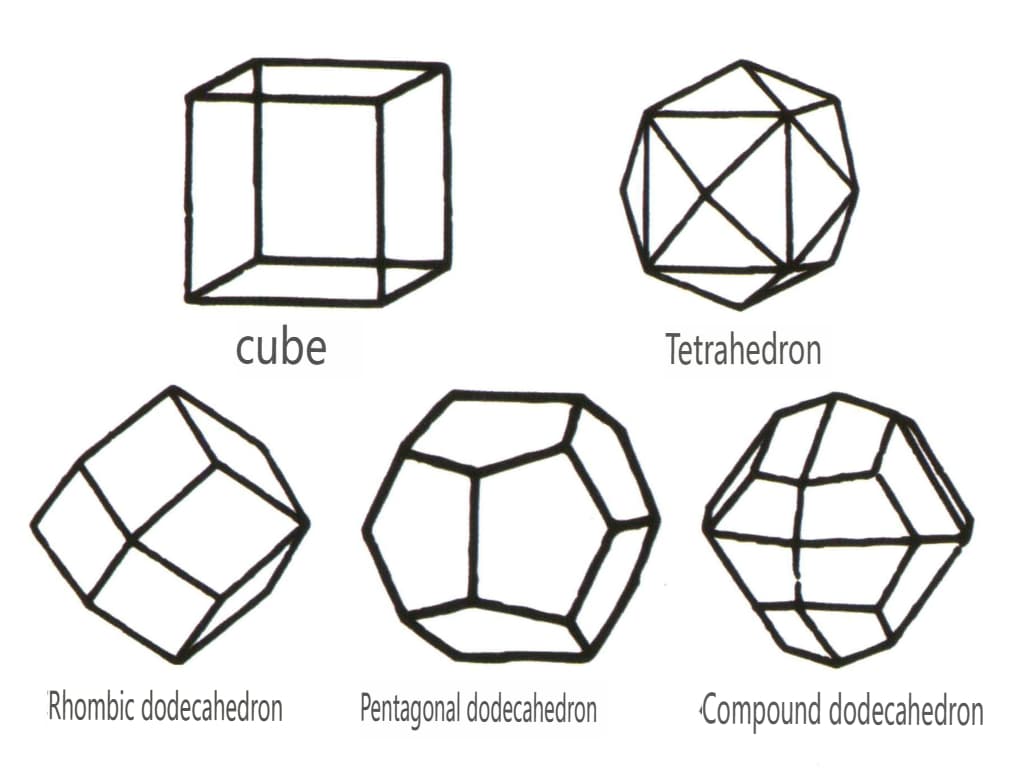
Figur 2-1-45 Kubiske og dodekaedriske klasser
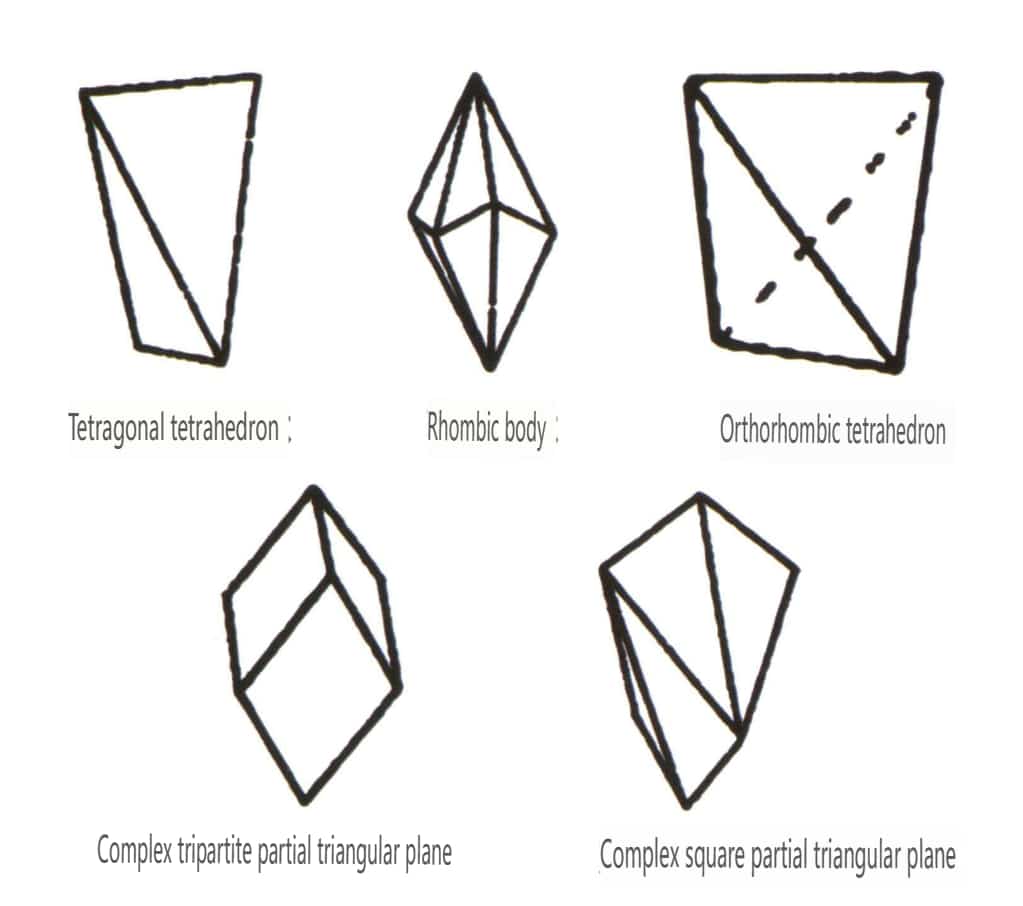
Figur 2-1-46 Andre polyedertyper
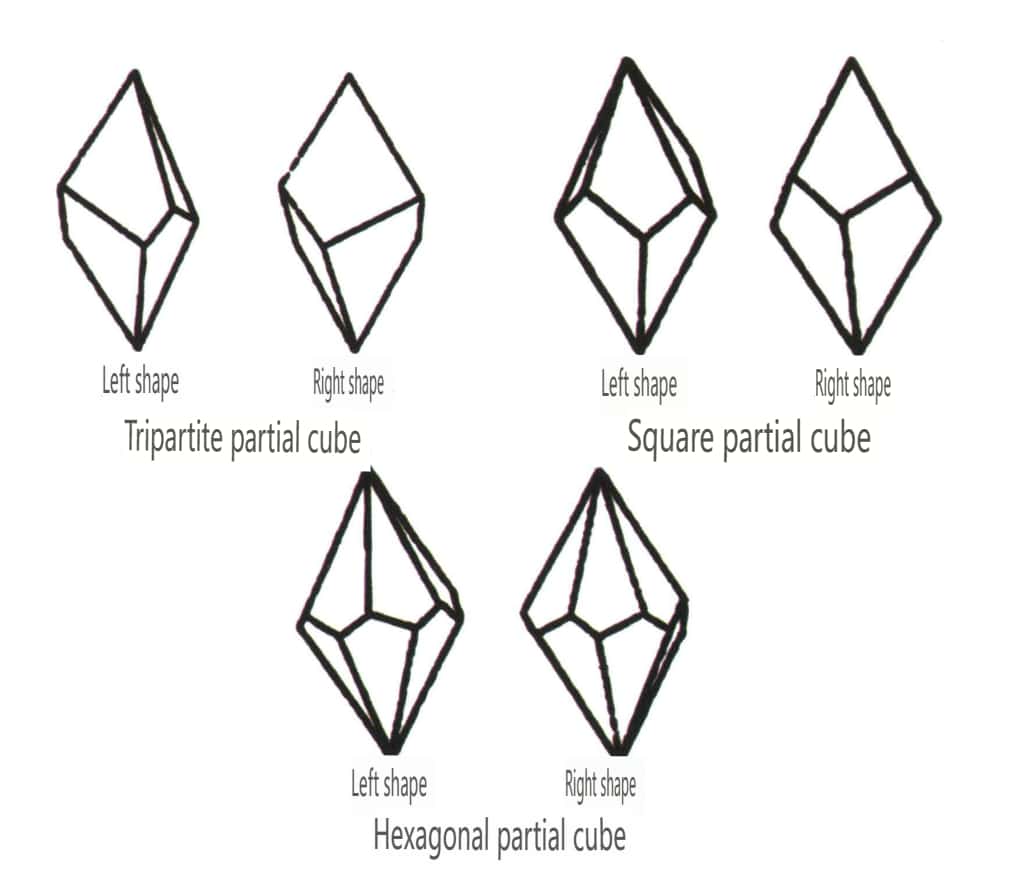
Figur 2-1-47 Skrå kombinasjonsform Klasse
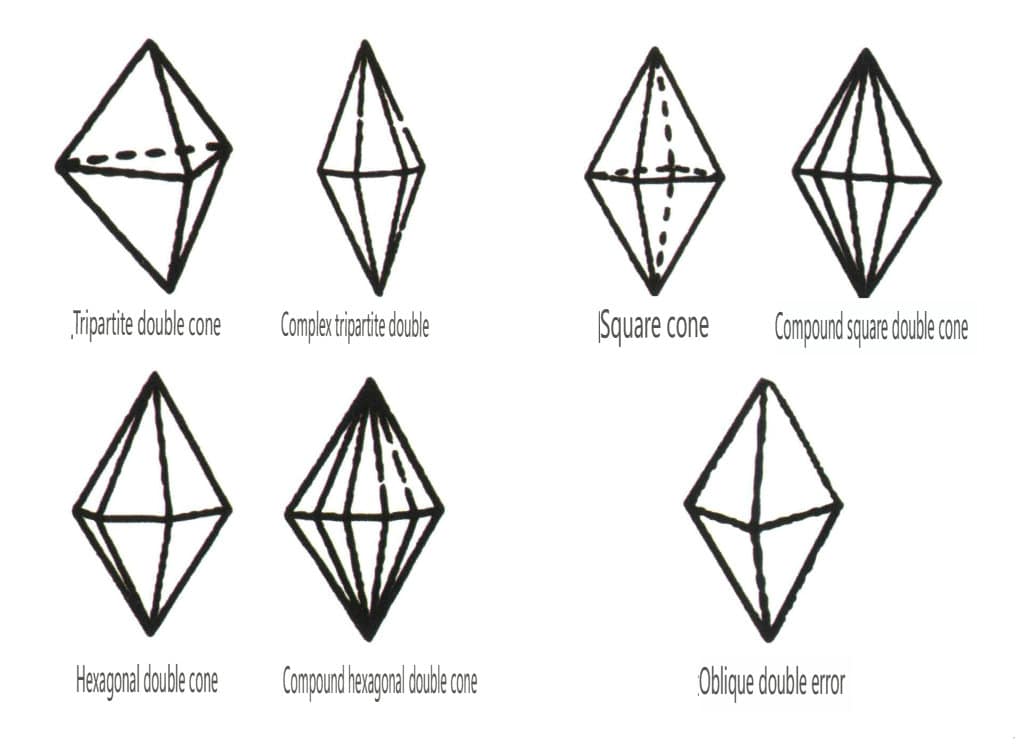
Figur 2-1-48 Dobbel pyramideklasse
Åpne former refererer til de som har krystallflater som ikke kan omslutte et lukket rom, inndelt i fire hovedkategorier: enkeltflater, dobbeltflater, søyleklasser og enkeltpyramideklasser, til sammen 17 typer (figur 2-1-49 og 2-1-51).
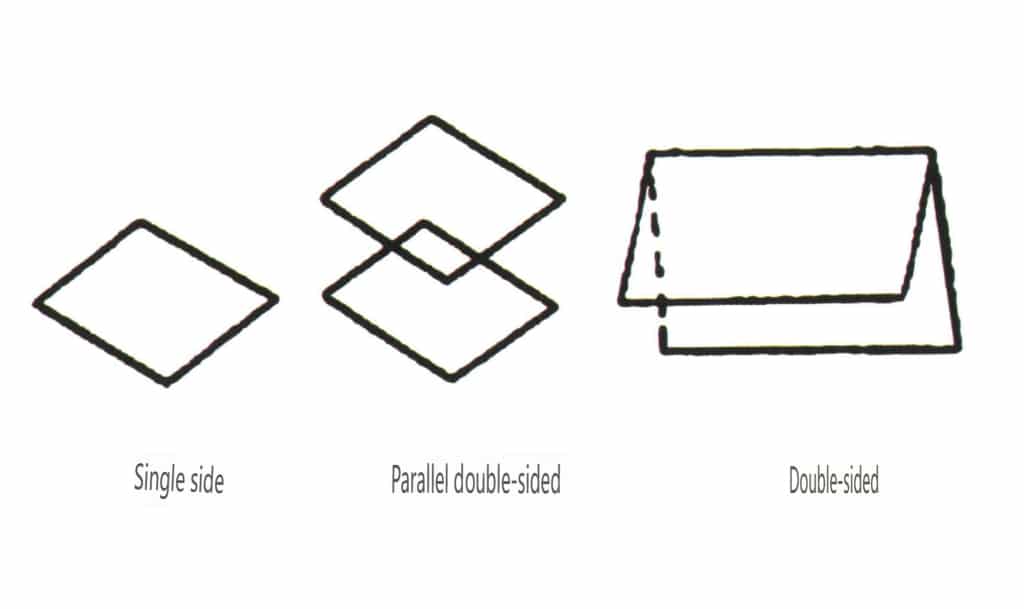
Figur 2-1-49 Enkeltsidig og dobbeltsidig
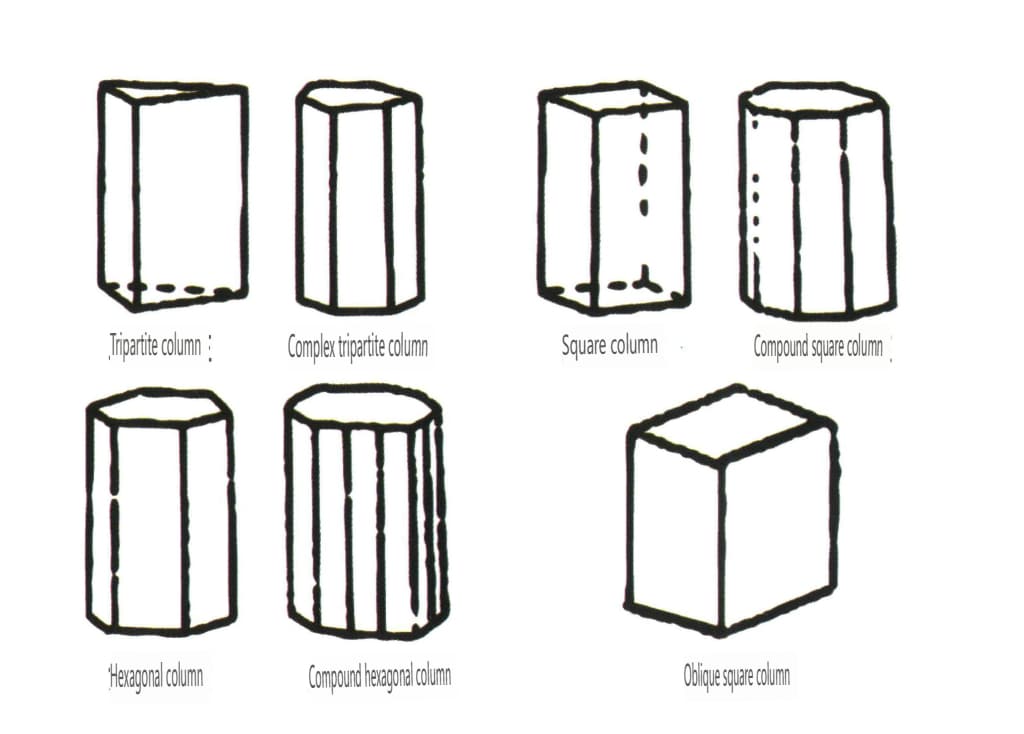
Figur 2-1-50 Kolonner

Del III Klassifisering av krystaller
1. Krystallers symmetri
Symmetri er et abstrakt begrep som brukes når man studerer ekte krystaller og ubearbeidede edelsteinsmaterialer. Det beskriver repetisjonen som vises når krystallstrukturen refereres til av en retning eller et plan som går gjennom den. Dette er grunnlaget for klassifiseringen av krystaller.
Symmetrien i en krystall kan forstås fra et mikroskopisk perspektiv som en metode for å beskrive repetisjonen i krystallstrukturen, og fra et makroskopisk perspektiv som repetisjonen av to eller flere geometriske flater som har samme form og størrelse, men som kan variere i retning, i henhold til visse regler. Dette repetisjonsmønsteret kan beskrives ved hjelp av symmetriakser og symmetriplan, der hver symmetriakse eller hvert symmetriplan omtales som et symmetrielement. Når man observerer eller utleder symmetrien til et objekt, kalles det å utføre symmetrioperasjoner.
2. Symmetrielementer i krystaller
I krystallografi finnes det fire symmetrielementer: symmetriakse, symmetriplan, rotasjonsomvendingssymmetriakser og symmetrisentrum. Dette vil involvere de to symmetrielementene symmetriakse og symmetriplan.
2.1 Symmetriens akse
(1) Begrepet symmetriakse og notasjon av disse.
Symmetriaksen er en tenkt rett linje som angir hvor mange ganger basisnivået (figur 2-2-1 til figur 2-2-2) vises i samme posisjon når gitterstrukturen roteres 360° rundt denne tenkte linjen. Dette tallet kan bare være 2, 3, 4 eller 6 ganger i 4 tilfeller. Det kan også forstås som en tenkt linje som går gjennom midten av det geometriske legemet, og som roterer det geometriske legemet 360° langs denne linjen. Anta at formen på det geometriske legemet etter å ha rotert en viss vinkel stemmer overens med formen på det geometriske legemet ved de opprinnelige nullgradene. I så fall kalles denne imaginære linjen symmetriaksen.
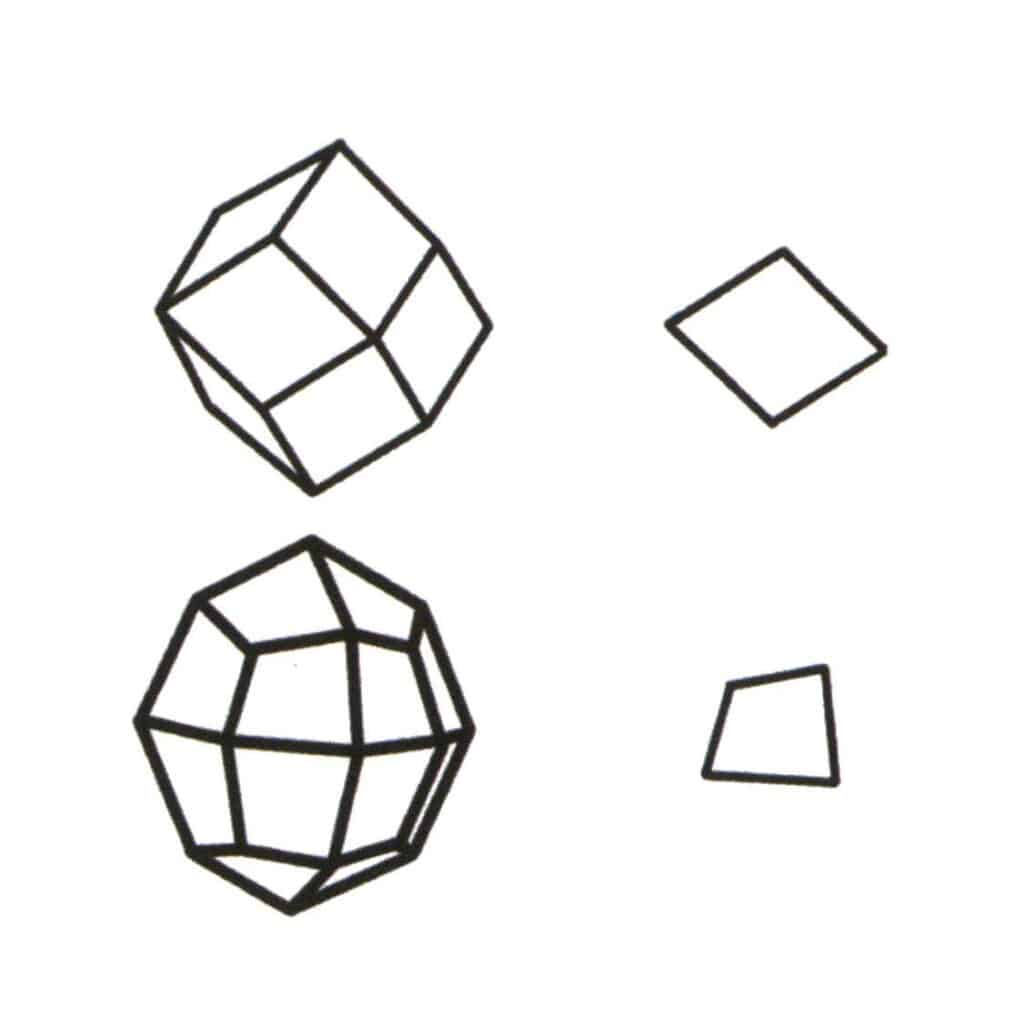
Figur 2-2-1 Valg av basisnivå for enkeltskjemaet.
Basisnivået til en enkelt form er det minste repeterende planet som utgjør simplexet. Øverst til venstre i figuren ser du et rombisk dodekaeder, som er en lukket form som består av én type flater. Det minste repeterende planet er romben som er vist øverst til høyre, så basisnivået for det rombiske dodekaederet er romben. Nederst til venstre i figuren ser du et firsidig oktaeder, som er en lukket form som består av én type flater. Det minste gjentagende planet er firflaten som vises nederst til høyre, så basisnivået for det firsidige oktaederet er firflaten.
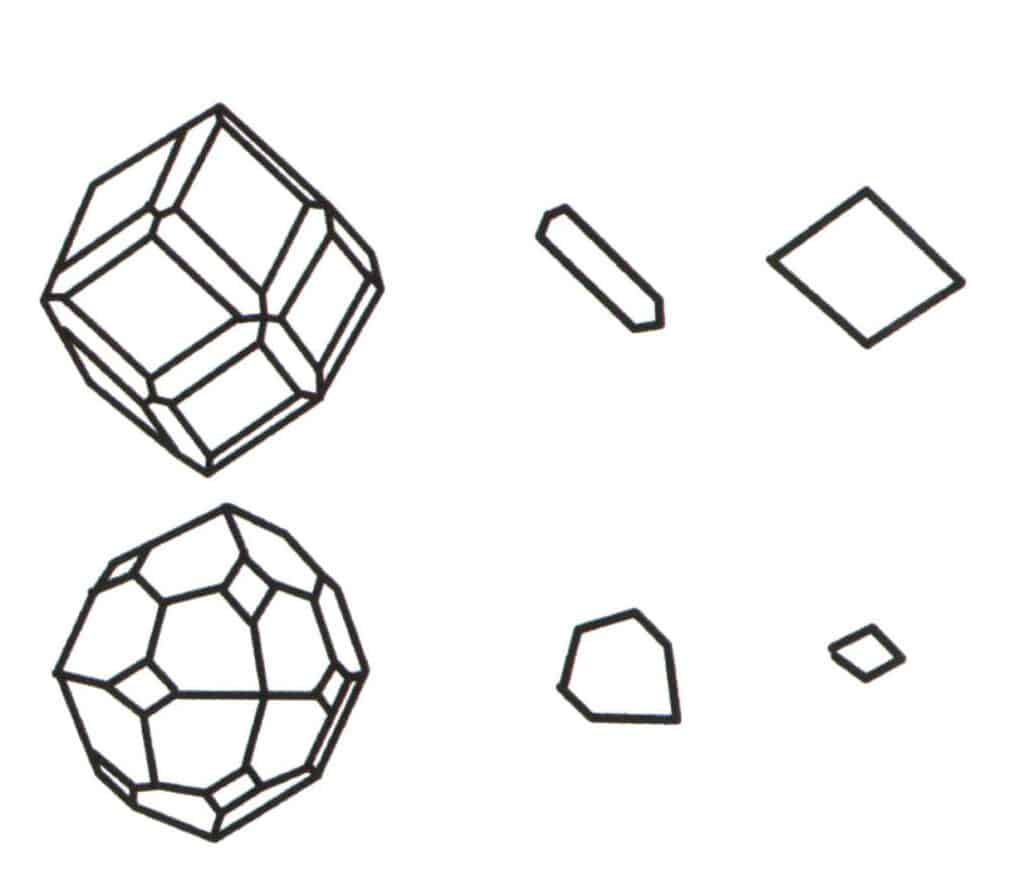
Figur 2-2-2 Valg av basisnivå for polytopen.
Aggregeringen av flere enkle former danner en kombinert form, og valget av basisnivå for den kombinerte formen er en vurdering av de enkle formene som kombineres for å danne den kombinerte formen. Den første søylen fra venstre i figuren representerer en kombinatform (dannet ved aggregering av enkeltformer av et dodekaeder og et tetraeder), og dette geometriske legemet er en lukket figur som består av to typer flater. Sekskanten representerer det minste gjentagende planet i den andre kolonnen og romben til høyre i den tredje kolonnen. Basisnivået for den kombinerte formen i den første kolonnen er derfor enten sekskanten eller romben. Ved beregning av symmetriaksen kan bare én form velges som basisnivå for symmetriregistreringen.
Symmetriaksen representeres av den store bokstaven L, med rekkefølgen på aksen n skrevet i øvre høyre hjørne av L, skrevet som Lⁿ. En 2-foldig akse representeres for eksempel som L², en 3-foldig akse som L³, en 4-foldig akse som L⁴ og en 6-foldig akse som L⁶. L⁶, L⁴, L³ blir vanligvis referert til som en akse av høyere orden.
Krystaller kan ha symmetriakser i forskjellige retninger, og antallet av disse ikke-sammenfallende symmetriaksene skrives vanligvis til venstre for L. For eksempel er seks sekundærakser representert som 6L² (figur 2-2-3 til figur 2-2-9), tre tertiærakser er representert som 3L³ (figur 2-2-10 til figur 2-2-14), fire tertiærakser er representert som 4L³ (figur 2-2-15 til figur 2-2-18), og én sekskantet akse er representert som L⁶ (figur 2-2-19).
Når en krystall har flere symmetriakser, ordner den registrerte metoden dem fra venstre mot høyre i synkende rekkefølge, med antall symmetriakser skrevet på venstre side av den tilsvarende aksen, for eksempel L⁶6L², 3L⁴4L³6L².
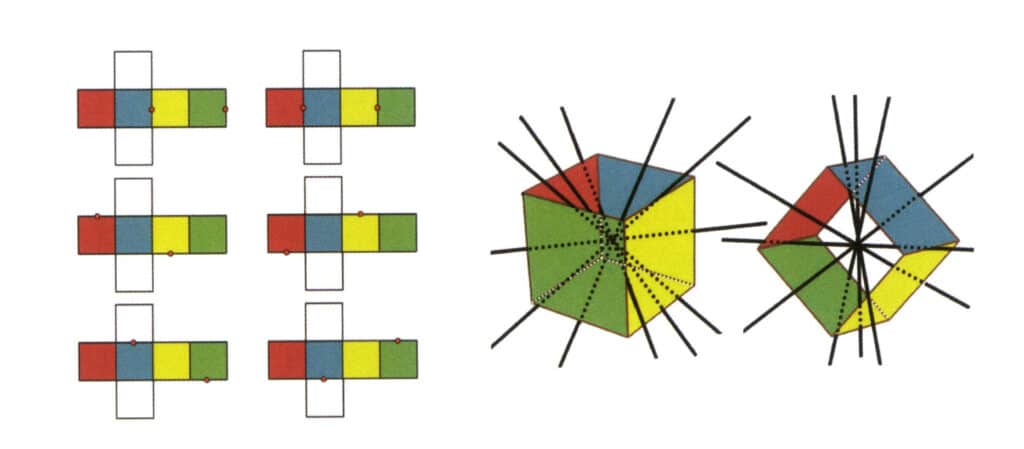
Figur 2-2-3 Kubens sekundære akse
Venstre side av figuren viser en utbrettet kube, med røde prikker som angir skjæringspunktene mellom den imaginære linjen og kantene. Den høyre siden av figuren viser en lukket kube, der sekundæraksen kan ligge i midtpunktet av parallelle kantlinjer, midtpunktet av parallelle rektangulære flater eller skjæringspunktene mellom tre eller flere parallelle flater som ligner et rektangel. eller flere parallelle flater som ligner et rektangel.
Copywrite @ Sobling.jewelry - Tilpasset smykkeprodusent, OEM og ODM smykkefabrikk
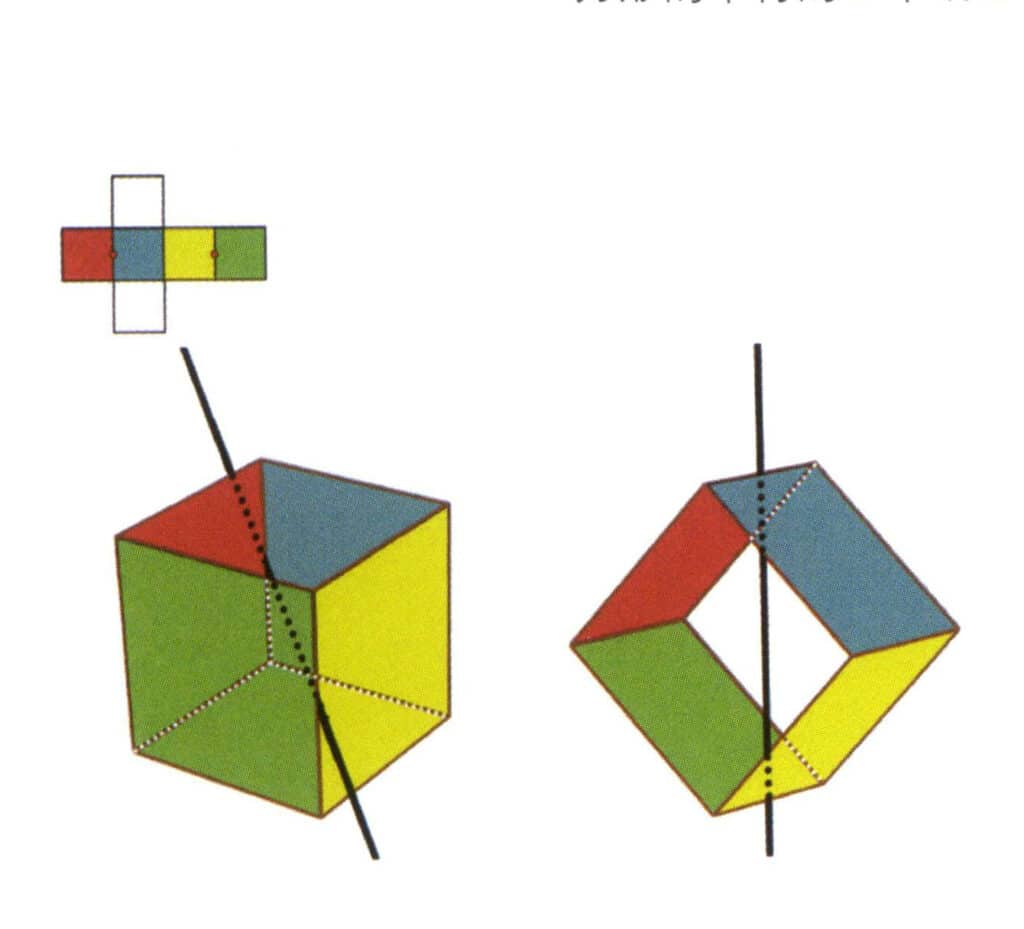
Figur 2-2-4 Den første sekundæraksen i kuben
Velg midtpunktet på de parallelle linjene, som vist i figuren. Forestill deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. Basenivåene med forskjellige farger, men samme form, vil gjenta seg to ganger i samme posisjon (de røde og blå flatene, de gule og grønne flatene, de to fargeløse flatene og tre sett med gjentatte flater. Selv om tre sett med gjentatte flater vil vises siden den imaginære linjen ikke har endret posisjon og vinkel, registreres sekundæraksen bare én gang). Denne imaginære linjen registreres som sekundæraksen.
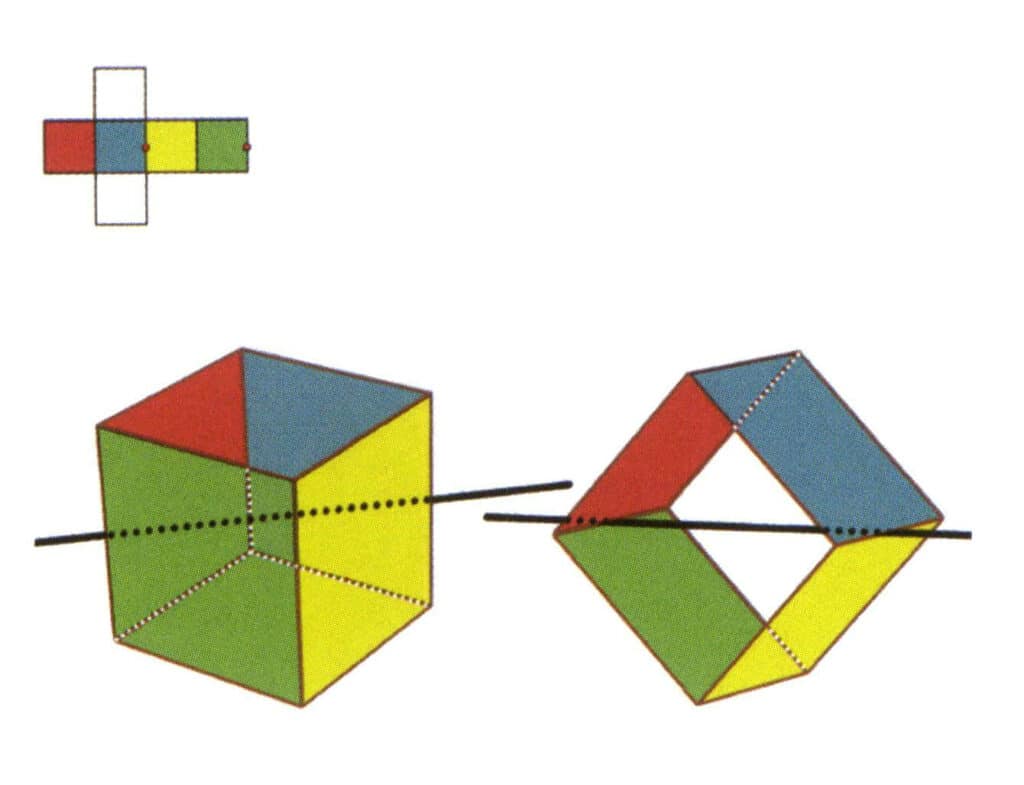
Figur 2-2-5 Den andre sekundæraksen i kuben
Velg midtpunktet på de parallelle linjene, som vist i figuren. Forestill deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. Basisnivåene med forskjellige farger, men samme form, vil gjenta seg to ganger i samme posisjon (de røde og grønne flatene, de gule og blå flatene, de to fargeløse flatene og tre sett med gjentatte flater). Denne imaginære linjen registreres som den andre sekundæraksen.
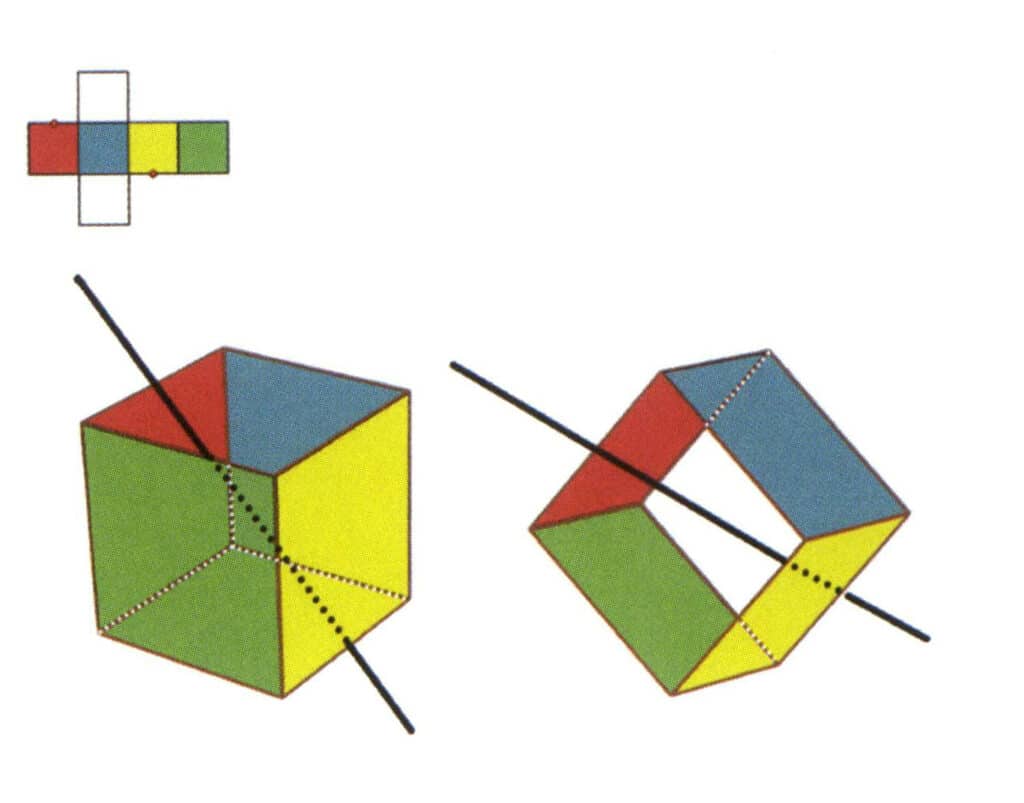
Figur 2-2-6 Den tredje sekundæraksen i kuben.
Velg midtpunktet på de parallelle linjene, som vist i figuren. Tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. Basenivåene med forskjellige farger, men samme form vil gjenta seg to ganger i samme posisjon (de røde og fargeløse flatene, de grønne og blå flatene, de fargeløse og gule flatene, tre sett med gjentatte flater). Denne imaginære linjen registreres som den tredje sekundæraksen
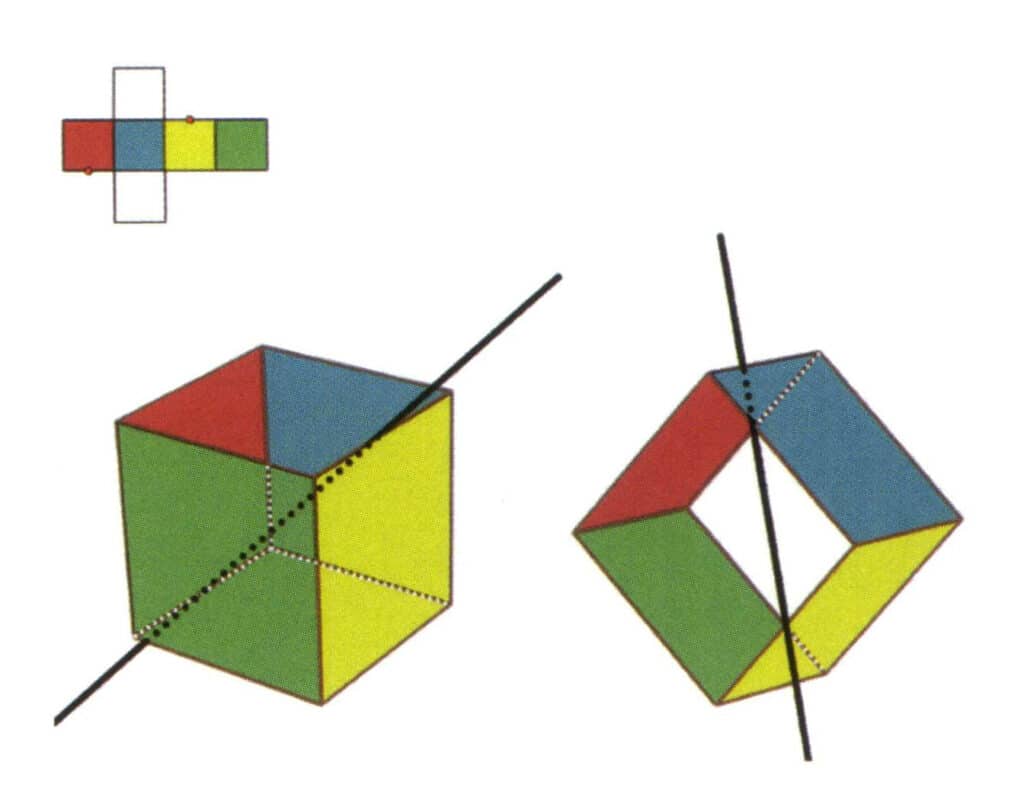
Figur 2-2-7 Den fjerde sekundæraksen i kuben
Velg midtpunktet på de parallelle linjene som vist i figuren, tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°; de ulikt fargede, men identisk formede referanseflatene vil gjenta seg i samme posisjon to ganger (de røde og fargeløse flatene, de grønne og blå flatene, de fargeløse og gule flatene, tre sett med gjentatte flater), og denne imaginære rette linjen registreres som den fjerde sekundæraksen.
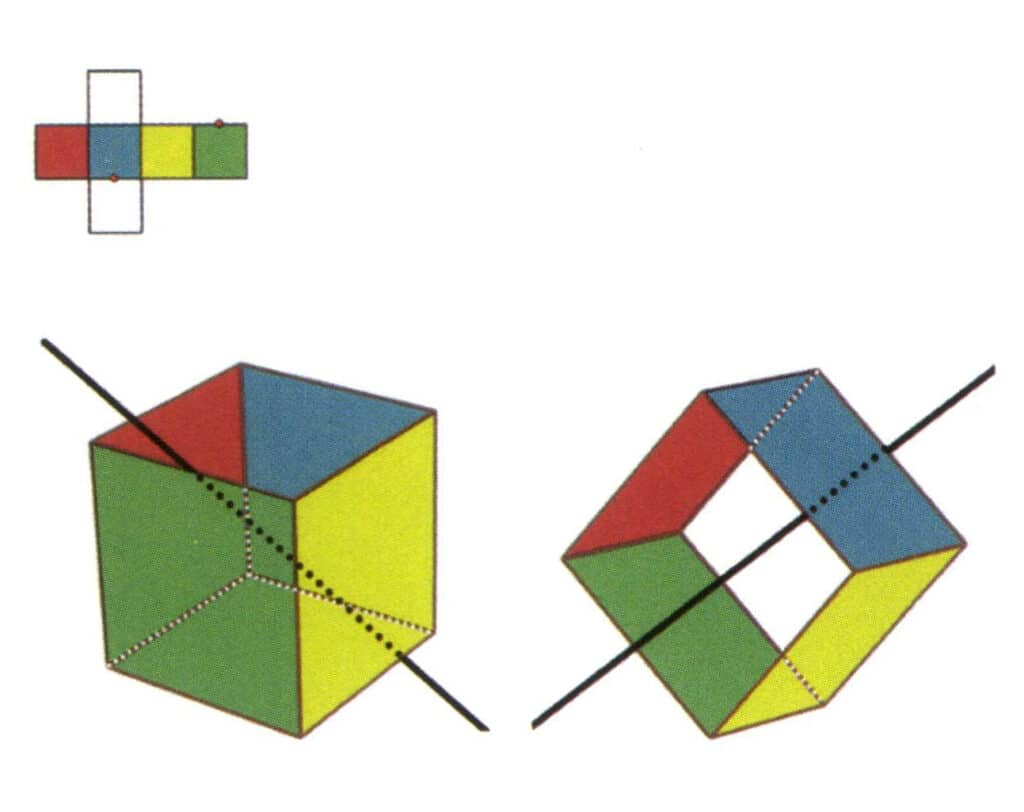
Figur 2-2-8 Den femte sekundæraksen i kuben.
Velg midtpunktene på de parallelle linjene som vist i figuren, tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, roter kuben 360°, de ulikt fargede, men identisk formede referanseflatene vil gjenta seg i samme posisjon to ganger (røde og fargeløse flater, grønne og blå flater, fargeløse og gule flater, tre sett med gjentatte flater), denne tenkte rette linjen registreres som den femte sekundæraksen.
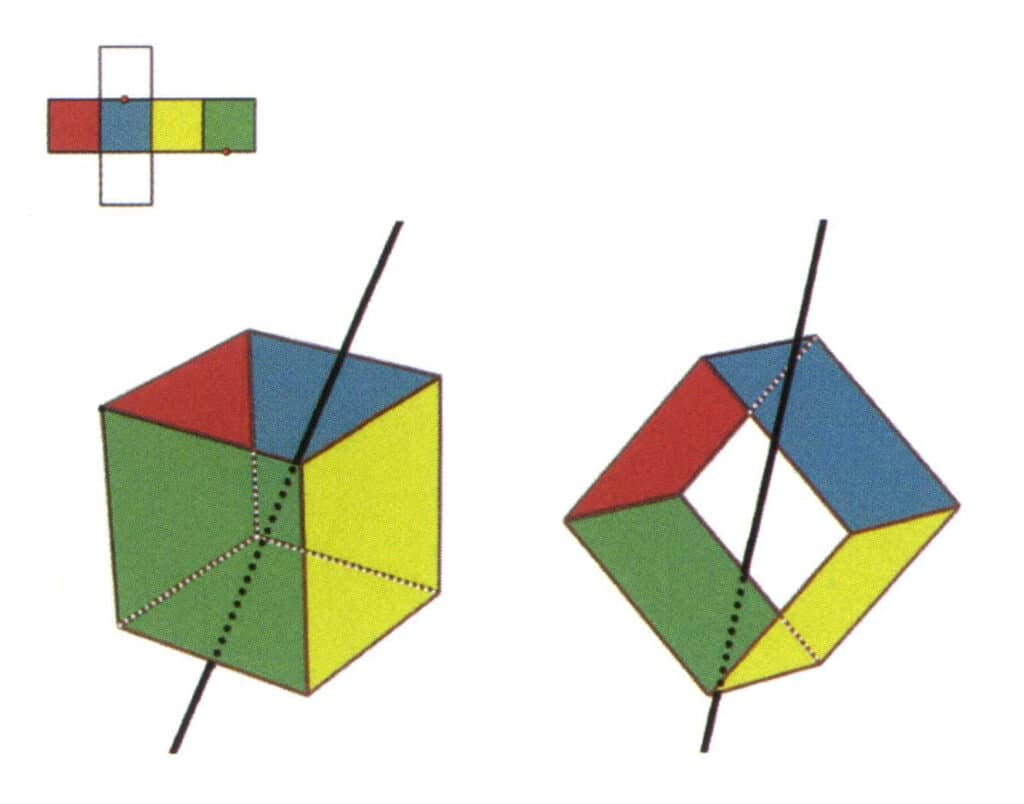
Figur 2-2-9 Den sjette sekundæraksen i kuben
Velg midtpunktet på de parallelle linjene, som vist i figuren. Tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. De ulikt fargede, men identisk formede basisnivåene vil gjenta seg i samme posisjon to ganger (grønne og fargeløse flater, røde og gule flater, fargeløse og blå flater, tre sett med gjentatte flater). Denne imaginære linjen registreres som den sjette sekundæraksen.
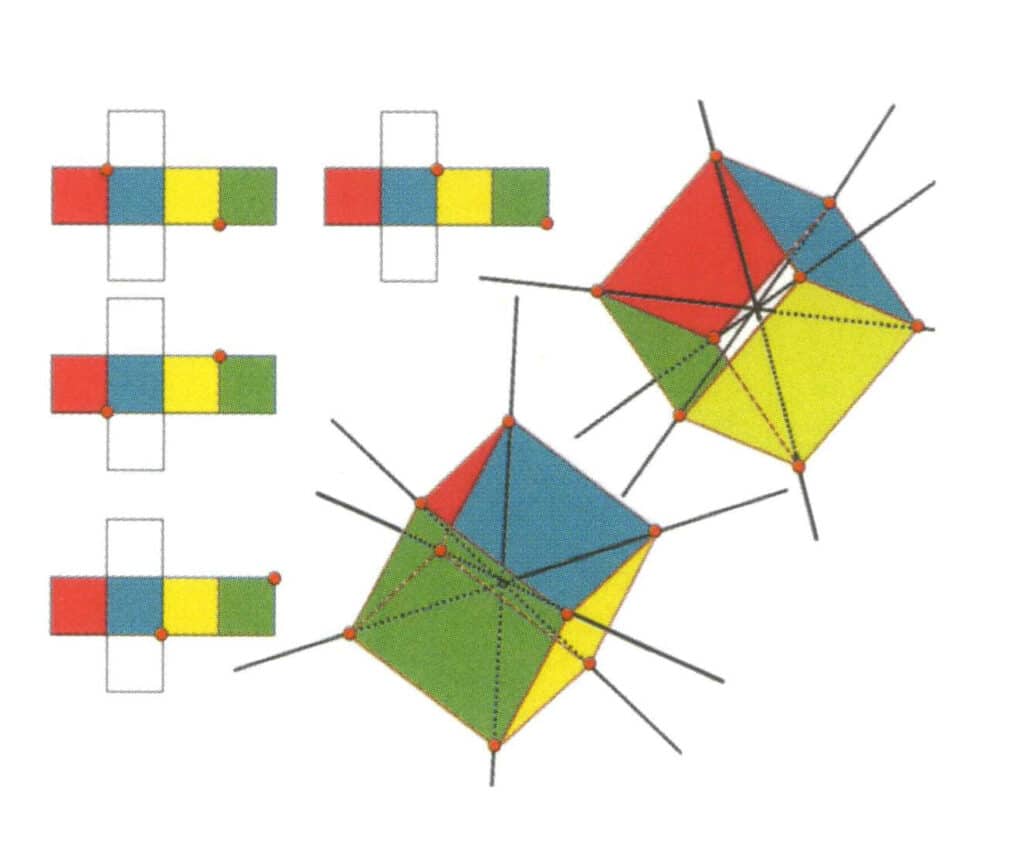
Figur 2-2-10 Tertiæraksen til kuben
Venstre side av figuren viser kuben utbrettet, og den røde prikken angir skjæringspunktet mellom den imaginære linjen og kantlinjen. Høyre side av figuren viser den lukkede kuben; de røde punktene angir skjæringspunktet mellom den imaginære rette linjen og kantene. Tertiæraksen kan oppstå i midtpunktet av flatene i en parallell likesidet trekant, i skjæringspunktet mellom tre eller flere parallelle flater som ligner en likesidet trekant.
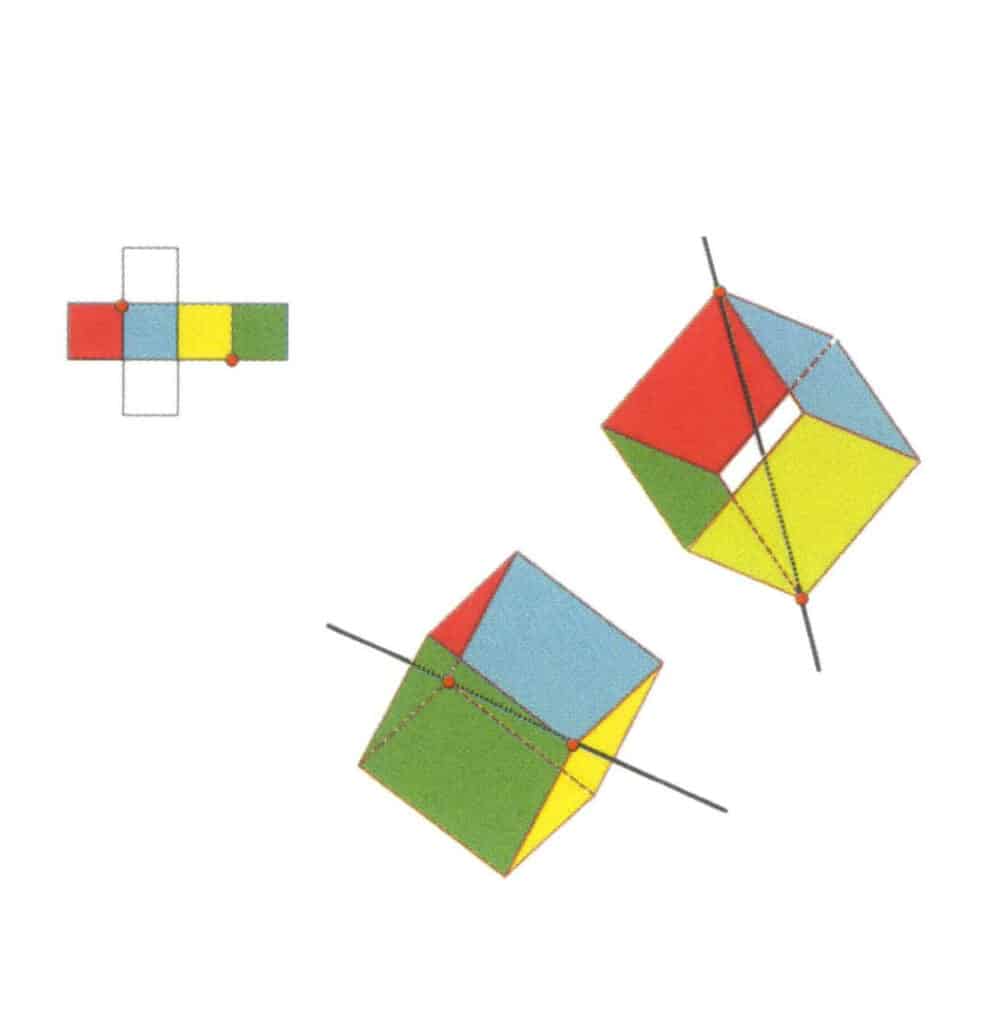
Figur 2-2-11 Kubens første tertiære akse.
Velg skjæringspunktene mellom de tre flatene som vist i figuren, tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, roter kuben 360°, de ulikt fargede, men identisk formede referanseplanene vil gjenta seg i samme posisjon tre ganger (røde, fargeløse og blå flater, grønne, fargeløse og gule flater, to sett med gjentatte flater), denne tenkte rette linjen registreres som den første tertiæraksen
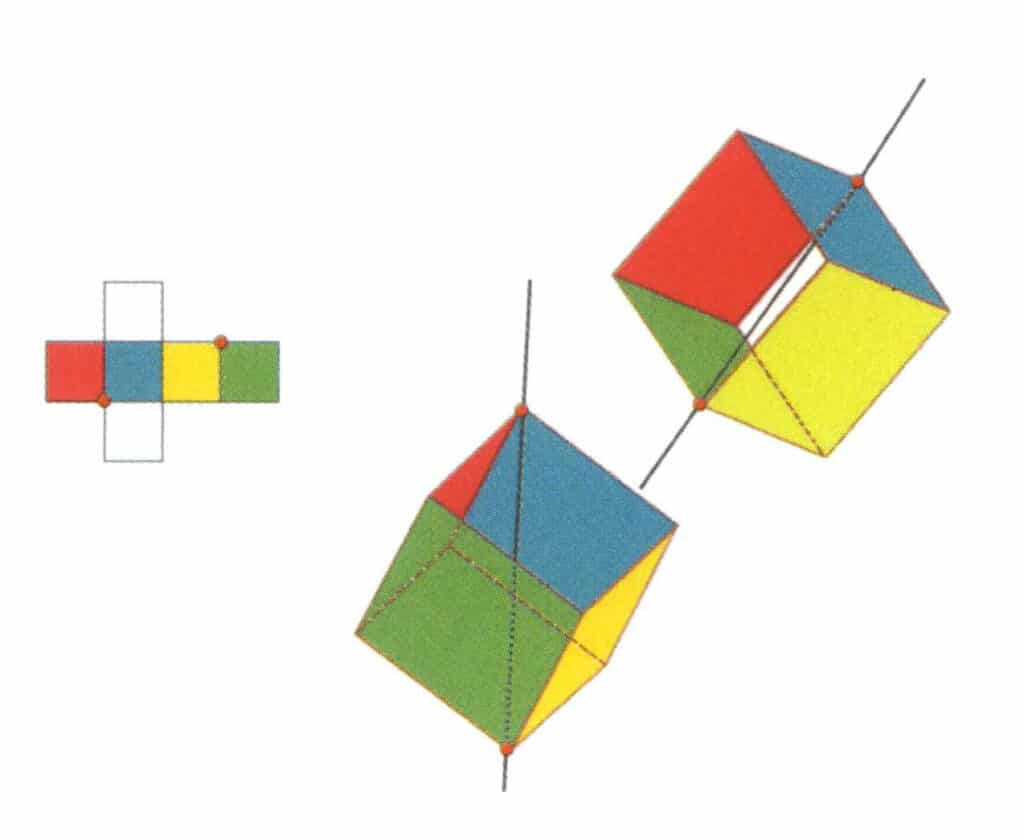
Figur 2-2-12 Kubens andre tertiære akse.
Velg skjæringspunktene mellom de tre flatene, som vist i figuren. Tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. De ulikt fargede, men identisk formede basisnivåene vil gjenta seg i samme posisjon tre ganger (røde, fargeløse og blå flater; grønne, fargeløse og gule flater, to sett med gjentatte flater). Denne imaginære linjen registreres som den andre tertiære aksen.
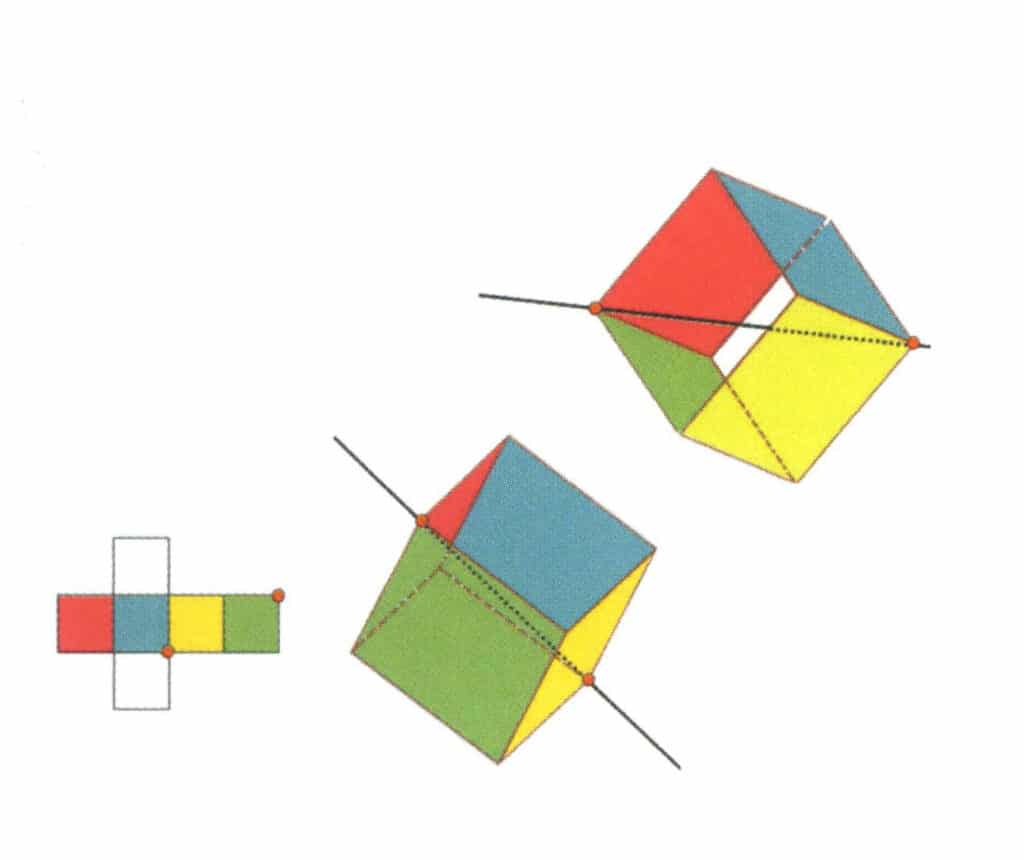
Figur 2-2-13 Kubens tredje tertiære akse
Velg skjæringspunktene mellom de tre flatene, som vist i figuren. Tenk deg en rett linje som går gjennom midtpunktene på disse to kantene, og roter kuben 360°. De ulikt fargede, men identisk formede basisnivåene vil gjenta seg i samme posisjon tre ganger (røde, fargeløse og grønne flater; blå, fargeløse og gule flater, to sett med gjentatte flater). Denne imaginære linjen registreres som den tredje tertiære aksen.
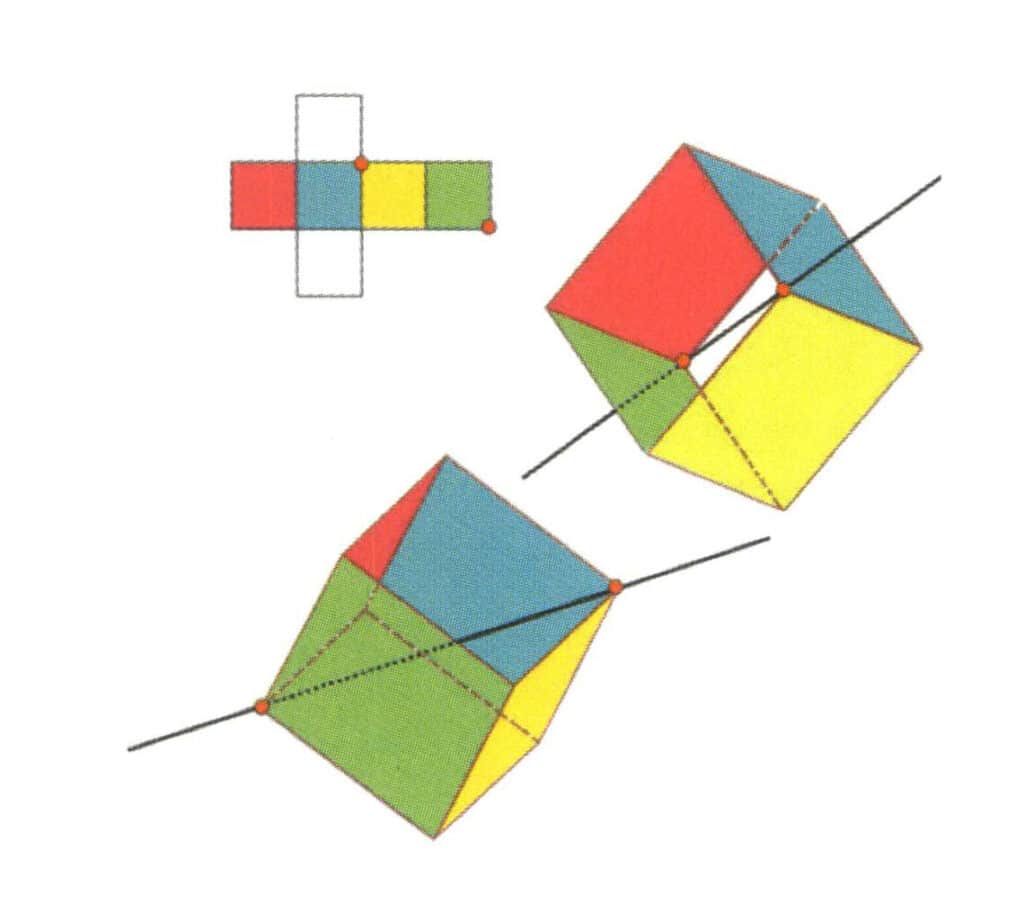
Figur 2-2-14 Kubens fjerde kubikkakse.
Velg skjæringspunktet mellom de tre flatene som vist i figuren, forutsatt at det går en rett linje gjennom midtpunktet av de to kantene, roterer kuben 360°, forskjellige farger, men samme form basisnivået vil være det samme. Gjenta posisjonen tre ganger (rød, fargeløs, grønn flate, blå, fargeløs og gul flate, to sett med gjentatte flater). Denne imaginære linjen registreres som den fjerde kubikkaksen.
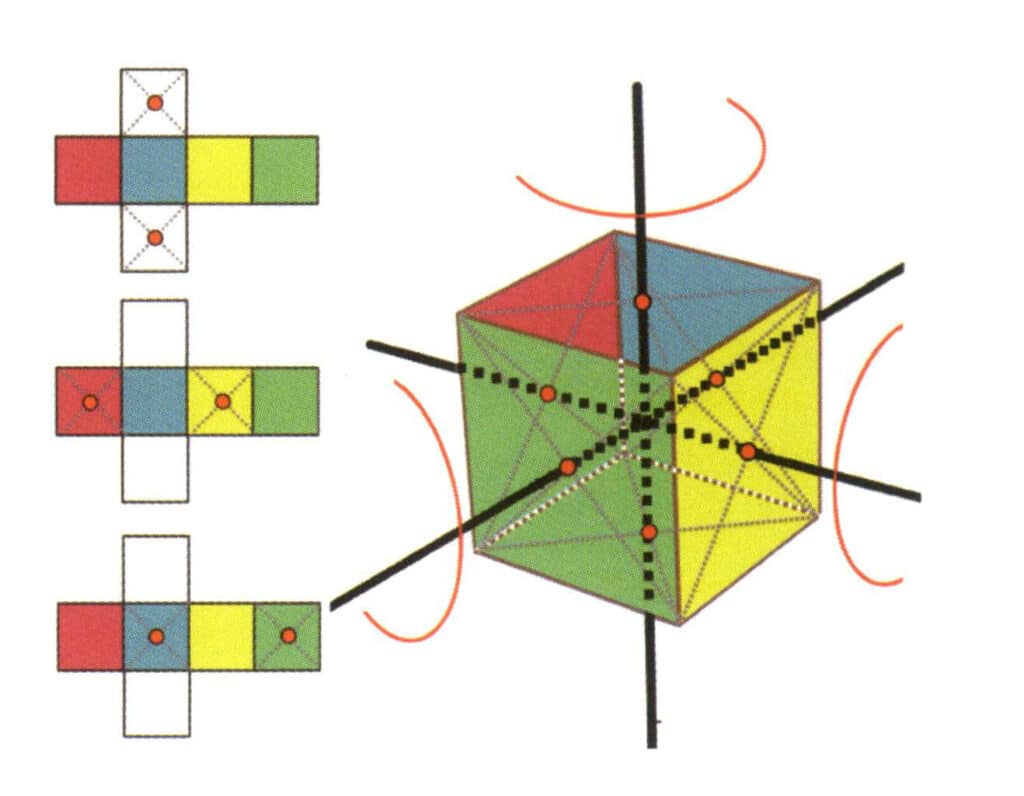
Figur 2-2-15 Terningens fjerde akse
Venstre side av figuren viser en utbrettet kube, med de røde prikkene som angir skjæringspunktene mellom den imaginære linjen og kantene. Den høyre siden av figuren viser en lukket kube, der de røde prikkene angir skjæringspunktene mellom den imaginære linjen og planet. Den fjerde aksen kan oppstå i midtpunktet av parallelle kvadratiske flater, i skjæringspunktet mellom tre eller flere parallelle flater som ligner på et kvadrat.
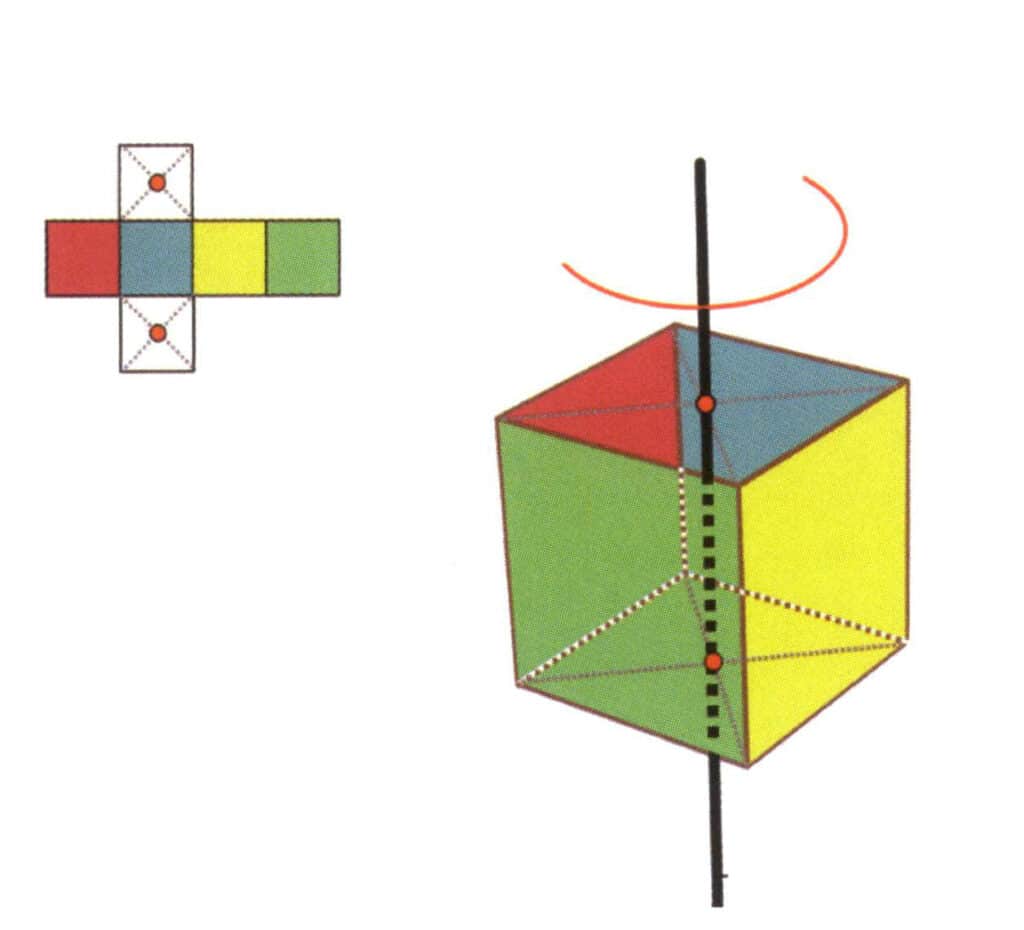
Figur 2-2-16 Den første kvartilsaksen i kuben
Velg midtpunktene til planene som er vist i figuren, anta at det går en rett linje gjennom midtpunktene til de to planene, og roter kuben 360°. De ulike fargede, men likeformede flatene på grunnflaten vil bli gjentatt i samme posisjon fire ganger (rød, blå, grønn og gul flate), og denne hypotetiske rette linjen registreres som en firedobbelt aksial.
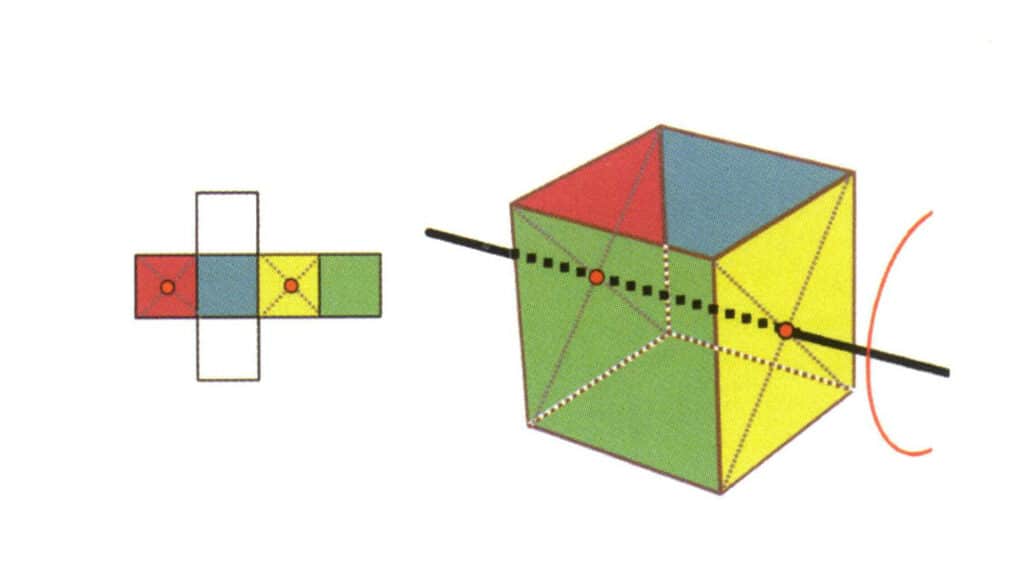
Figur 2-2-17 Kubens andre kvartiske akse
Velg midtpunktet i planet som vist i figuren, tenk deg en rett linje gjennom kuben, og roter kuben 360°; grunnflaten med forskjellige farger, men samme form, vil bli gjentatt fire ganger i samme posisjon (fargeløs, blå flate øverst, fargeløs, grønn flate nederst), og denne imaginære linjen vil bli registrert som den andre kvadratiske aksen.
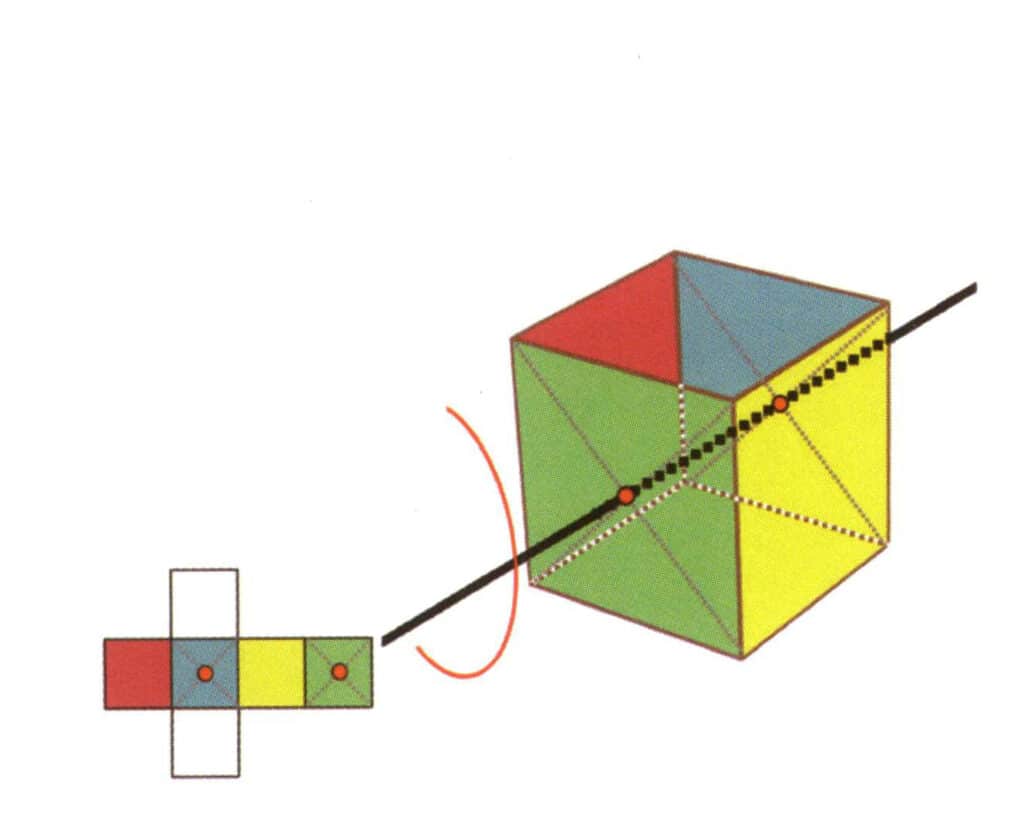
Figur 2-2-18 Terningens tredje kvartiske akse
Velg midtpunktet i planet som vist i figuren, forestill deg en rett linje gjennom kuben, og roter kuben 360°. Basenivået med forskjellige farger, men samme form, vil bli gjentatt fire ganger i samme posisjon (fargeløs, rød flate øverst, fargeløs, gul flate nederst), og denne imaginære linjen vil bli registrert som den tredje, fjerde aksen
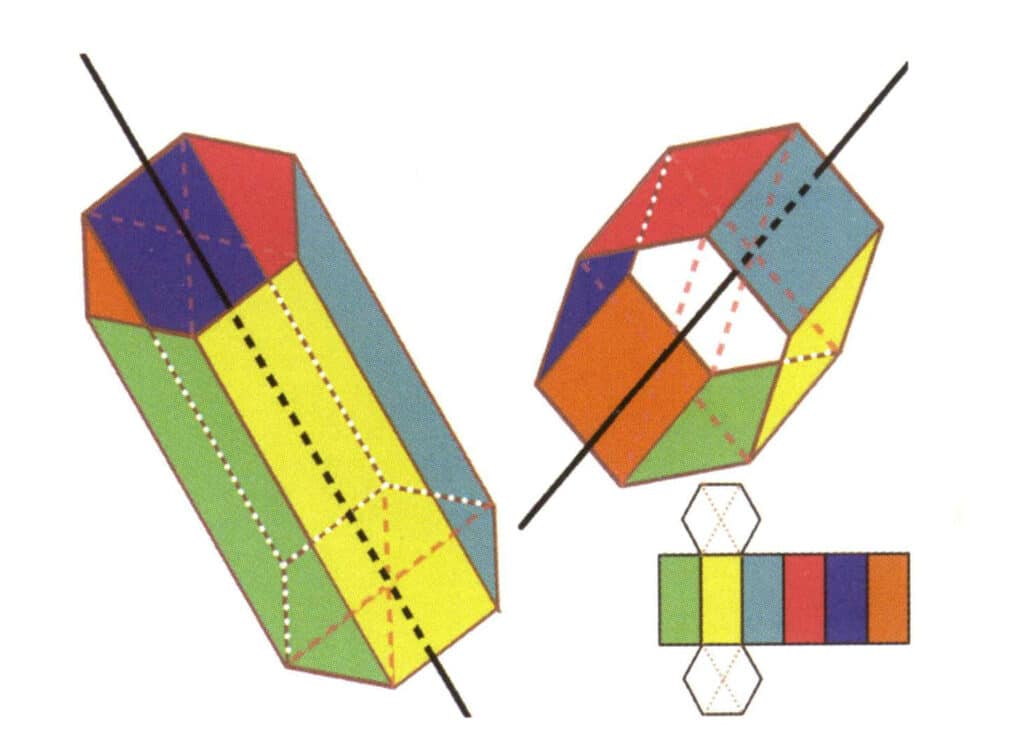
Figur 2-2-19 Seks akser i et sekskantet prisme
De svarte linjene til venstre og øverst til høyre representerer de seks aksene i det sekskantede prismet. Nederst til høyre er en utvidelse av det sekskantede prismet Den sekskantede aksen kan ligge i midtpunktet av flatene i en parallell sekskant eller i skjæringspunktet mellom de seks flatene i en sekskant.
(2) Overveielser for å finne symmetriaksen.
① Det finnes fem typer posisjoner for symmetriaksen.
Midtpunktet mellom to parallelle kanter, for eksempel posisjonen til sekundæraksen i en kube.
Midtpunktet mellom to parallelle plan, for eksempel posisjonen til den kvadratiske aksen i en kube.
Mellom to hjørner (skjæringspunktene mellom flere flater), for eksempel posisjonen til tertiæraksen i en kube.
Midtpunktet mellom et toppunkt og et parallelt plan, for eksempel posisjonen til tertiæraksen i et tetraeder.
Midtpunktet mellom kantlinjen og midtpunktet i det parallelle planet, for eksempel posisjonen til sekundæraksen i et trekantet prisme.
Valget av symmetriaksen i samme retning følger prinsippet om det laveste nummeret. Hvis for eksempel en retning finner seks symmetriakser og tre symmetriakser, vil den til slutt bli registrert som L³ i henhold til laveste tall-prinsippet. Symmetriaksene i forskjellige retninger skal registreres i henhold til antallet som er funnet.
Det er verdt å merke seg at bortsett fra den seksdelte symmetriaksen og den firedelte symmetriaksen, som ikke kan opptre samtidig, og bare én seksdelt symmetriakse kan opptre, kan andre symmetriakser eksistere samtidig i ulike former eller flere forekomster.
③ Basisnivået må velges som det minste enhetsplanet; to eller flere kryssende plan kan ikke velges som basisnivå. I motsatt fall vil det påvirke nøyaktigheten av symmetriaksevurderingen.
④ Når du registrerer antall symmetriakser, er det viktig å bestemme hvor mange ganger samme form og størrelse på planet gjentas i samme posisjon.
⑤ Hvis det finnes en sekundærakse med vertikal symmetri Lⁿ(n = 3, 4 eller 6), må det være n sekundærakser som er vertikale i forhold til Lⁿ.
2.2 Fly av symmetri
(1) Konsept og registreringsmetode for plan av symmetri
Et symmetriplan er et tenkt plan som, når krystallen skjæres langs dette planet, gjør at hver halvdel av krystallen kan være et speilbilde av den andre halvdelen (figur 2-2-20). I en og samme krystallstruktur kan et slikt plan opptre maksimalt 9 ganger (figur 2-2-21), noe som betyr at det kan deles på 9 forskjellige måter, og de to halvdelene kan falle helt sammen. Det er selvfølgelig ikke alle krystallstrukturer som har symmetriplan.
Den store bokstaven P representerer symmetriplanet. Noen krystaller har flere symmetriplan som ikke sammenfaller, og antallet av disse symmetriplanene skrives vanligvis til venstre for P; for eksempel representeres fire symmetriplan som 4P, og ett symmetriplan representeres som P.
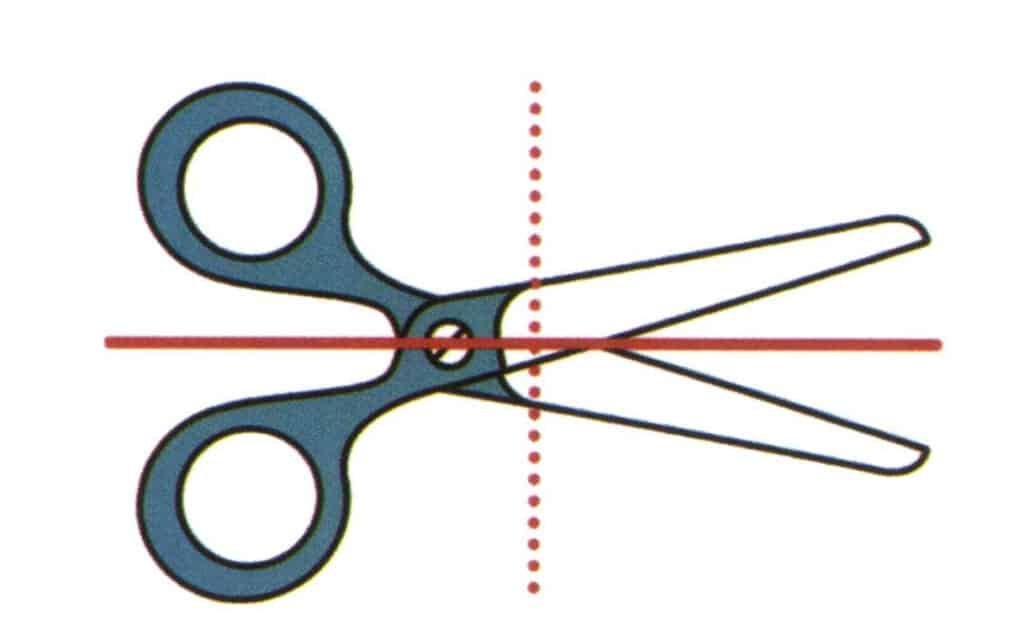
Figur 2-2-20 Forestill deg et loddrett papirplan og et plan som strekker seg langs retningen til den røde heltrukne linjen, som deler saksen i en øvre og en nedre del. Den øvre og den nedre delen er speilsymmetriske. Dette tenkte planet kalles symmetriplanet. Tenk deg et annet plan som står vinkelrett på papirflaten og strekker seg langs den røde stiplede linjen, som deler saksen i en venstre og en høyre del, men saksens form på venstre og høyre side er ikke symmetrisk.
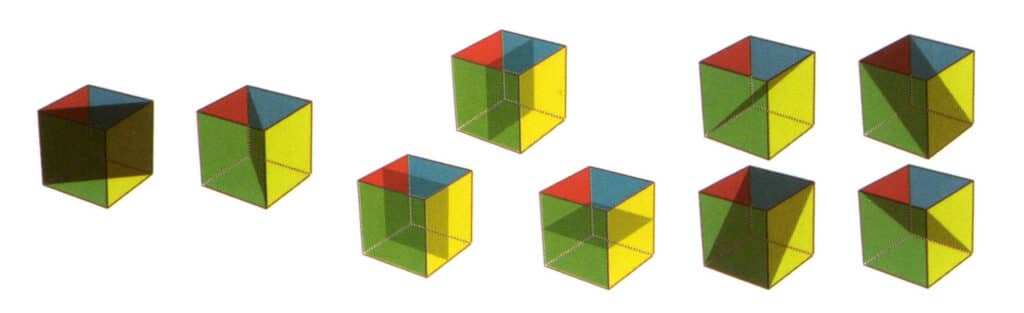
Figur 2-2-21 De ni symmetriplanene i en kube
(2) Tips for å finne Symmetriens plan.
① Symmetriplanet er ofte parallelt med og sammenfallende med symmetriaksen.
② Symmetriplanet er et imaginært plan som deler den krystallinske geometrien, som er forskjellig fra det parallelle dobbeltplanet i geometrien.
③ Hvis et symmetriplan inneholder symmetriaksen Lⁿ, må det finnes n symmetriplan som inneholder Lⁿ.
(3) Punkt Gruppe.
Punktgruppen er summen av alle symmetrielementene i en krystall. Rekkefølgen for å skrive punktgruppen er symmetriakse + symmetriplan, for eksempel 3L²3P (Figur 2-2-22). Hvis en krystall har flere symmetriakser, er det vanlig å skrive dem fra venstre mot høyre, fra akse av høyere orden til akse av lavere orden, og rekkefølgen av symmetriplanene, for eksempel L⁴4L²5P (figur 2-2-23). Det finnes 32 typer symmetri i krystaller.
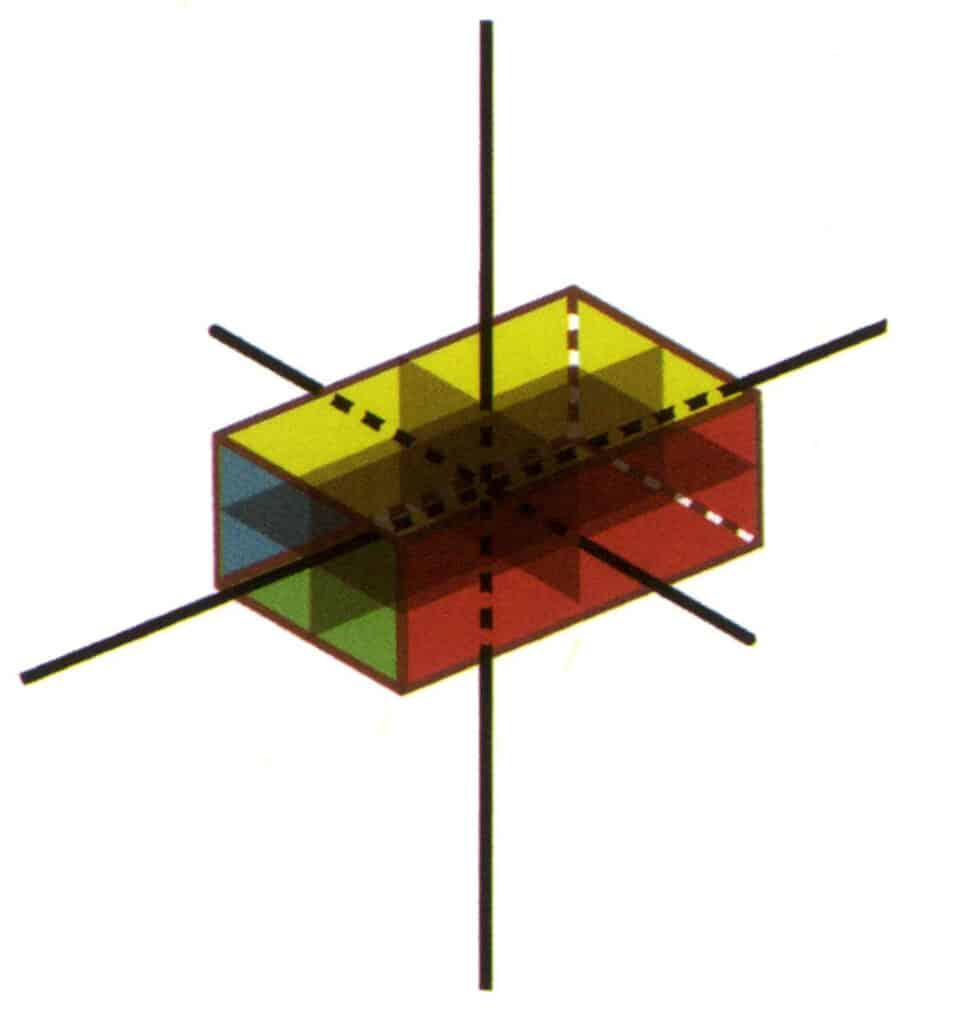
Figur 2-2-22 3L²3P punktgruppe (rektangulær kuboid med rektangulært tverrsnitt)
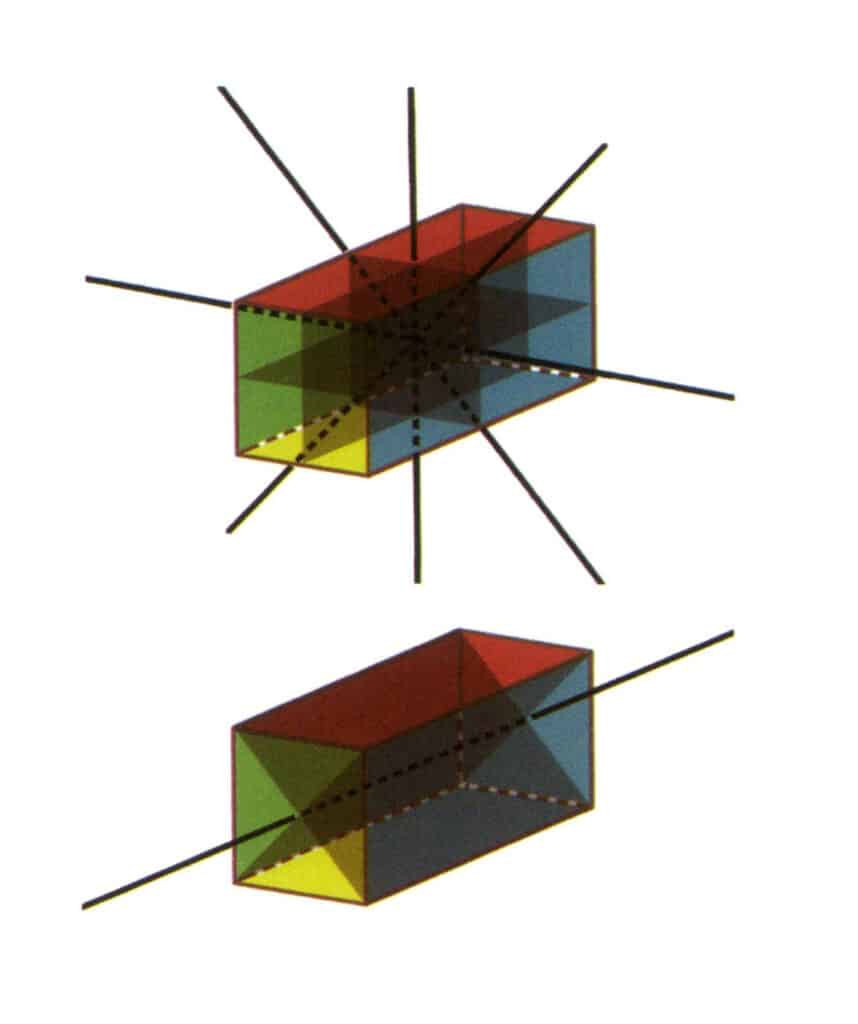
Figur 2-2-23 L⁴4L²5P punktgruppe (et rektangulært prisme med kvadratisk tverrsnitt), med fire andre akser og tre symmetriske flater på toppen, og en fjerde akse og to symmetriske flater på bunnen.
3. Klassifisering av krystaller
Symmetri er en del av krystallklassifiseringen. Et annet begrep - krystallakse - må introduseres for å beskrive krystallstrukturen til helt naturlige og kunstige krystaller i et krystallklassifiseringssystem. Krystallaksen er en tenkt linje gjennom krystallstrukturen, som angir retningen som gitterknutene gjentar seg i og den relative avstanden som knutene gjentar seg i langs denne retningen. Krystallaksen sammenfaller med normalen til symmetriaksen eller symmetriplanet. Hvis det ikke finnes noen symmetriakse eller noe symmetriplan, kan krystallaksen velges parallelt med krystallkantens retning.
Basert på symmetrielementer og krystallakser klassifiserer det akademiske systemet krystaller i tre krystallfamilier og sju krystallsystemer (tabell 1).
Tabell 1: Nøkkelpunkter for å bestemme krystallfamilier og -systemer
| Krystallfamilien | Krystall | Viktige punkter for bestemmelse | Vanlige edelsteinsvarianter |
|---|---|---|---|
| Krystallsystem på lavt nivå | Triklinisk system | Ingen andre akse eller symmetriplan | Amazonitt, rhodonitt, turkis |
| Monoklinisk krystallsystem | Ingen høyere ordens akser, ikke mer enn én sekundærakse og symmetriplan | Jadeitt, diopsid, spodumen, epidot | |
| Ortorhombisk krystallsystem | Ingen høyere ordens akser, mer enn én sekundærakse eller symmetriplan | Olivin, topas, saualpit (inkludert tanzanitt), cordieritt, krysoberyl, enstatitt | |
| Mellomliggende krystallfamilie | Tetragonalt krystallsystem | 1 firedobbel akse (kan representeres av L4) | Diamant |
| Trigonalt krystallsystem | 1 trigonale akser (kan representeres av L3) | Korund, rubin, safir, turmalin , krystaller i kvartsfamilien (som krystall, ametyst, sitrin osv.), rhodokrositt | |
| Sekskantet krystallsystem | 1 sekskantet akse (kan representeres av L6) | Akvamarin, smaragd og andre edelstener i beryllittfamilien, apatitt | |
| Avansert krystallfamilie | Isometrisk krystallsystem | 4 trigonale akser (kan representeres av 4L3) | Diamant, granat, spinell, flusspat |
4. Vanlige kjennetegn ved edelstenskrystaller
Vanlige edelstener inkluderer diamant, spinell, flusspat, granat, beryllitt, zirkon, korund, turmalin, krystall, krysoberyl, topas osv. Hver type edelsten har sine egne faste krystallkarakteristikker.
Edelstener i høykrystallfamilien har for det meste en kornet krystallform, og vanlige varianter opptrer ofte i faste krystallformer (tabell 2).
Krystallhabitatet til krystallfamilier på middels og lavt nivå er søyleformet (tabell 3).
Tabell 2: Felles krystallegenskaper for krystallfamilier på høyt nivå
| Gems tone Navn | Krystallklassifisering | Viktige krystallkarakteristikker | |||
|---|---|---|---|---|---|
| Gems tone Navn | Krystallklassifisering | Crystal Habit | Vanlige krystallformer | Vanlige tvillingformer | Vanlige mønstre for krystalloverflater |
| Diamant | Isometrisk krystallsystem | Granulær krystallform (Figur 2-2-24), ofte sett i oktaedriske granuler | Oktaederet er en vanlig krystallform, og mer komplekse krystallformer, inkludert rombiske dodekaeder, kan også forekomme, ofte med avrundede krystallflater, som kan oppvise trefoldig symmetri | Trekantet, flat tvilling, noen ganger uten synlige konkave vinkler (Figur 2-2-25) | Overflaten viser omvendte trekantede etsegroper (figur 2-2-26, 2-2-27) og andre krystallflatemønstre (figur 2-2-28, 2-2-29) |
| Spinell | Granulært krystallinsk utseende (Figur 2-2-30), ofte sett i oktaedriske granuler | Krystallflatene er ofte oktaedriske og kan være svært flate og se ut som om de er polerte (Figur 2-2-31). | Tvillingkrystallene er svært flate, og ligner en trekantet form med avkuttede hjørner (figur 2¬2-32) | Overflatesynlige etsningsgroper, noen ligner diamanter i en omvendt trekantform (Figur 2-2-33) | |
| Fluoritt | Granulær krystallform (Figur 2-2-34) | Oktaedriske og kubiske krystallformer (Figur 2-2-35) | Interpenetrerende twinning | Firkantede trinnvekstmerker, for det meste med spaltningshull, fargebånd parallelle med retningene til kubens seks flater | |
| Granat | Granulær krystallinsk habitus, ofte sett i rombiske, dodekaederformede korn (Figur 2-2-36) | Rhombisk dodekaeder eller kvadratisk trapetsoeder | Sjelden | Konsentriske ringbånd synlige med samme form som krystallflatene (Figur2-2-37) | |
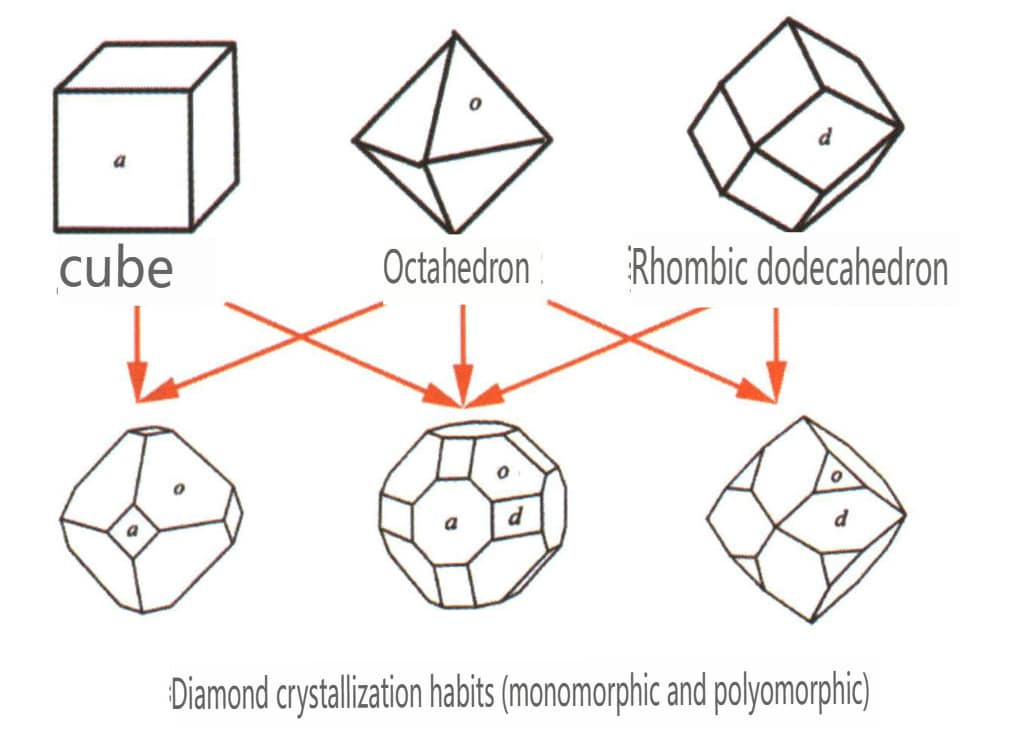
Figur 2-2-24 Diamantkrystallens vaner
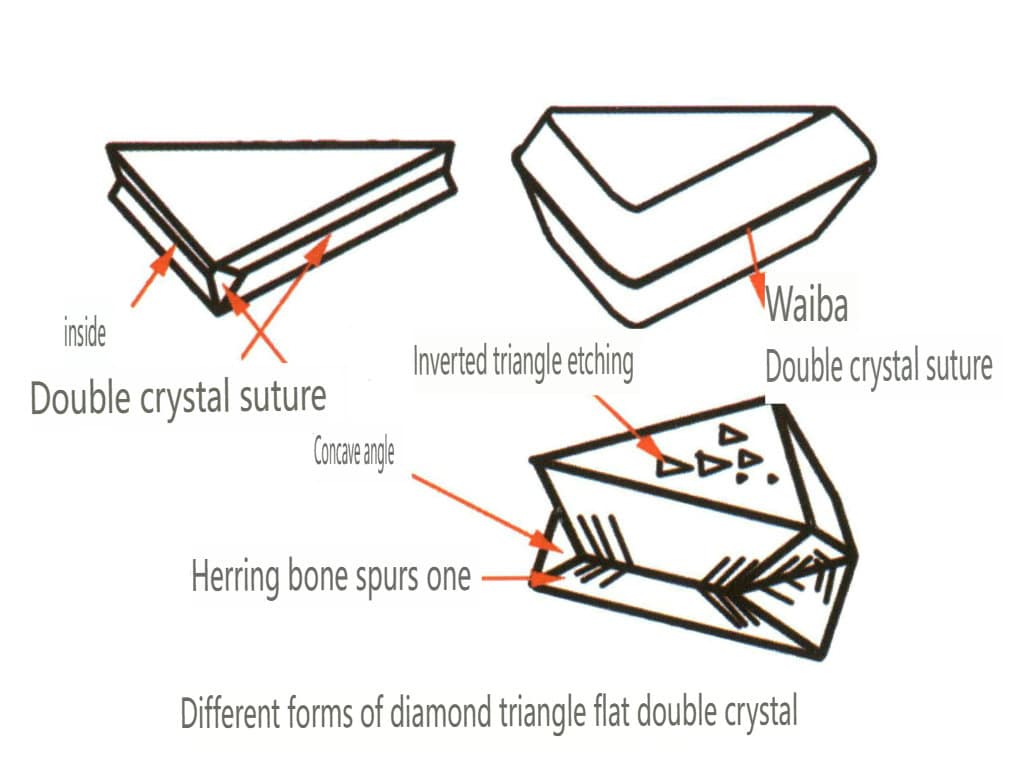
Figur 2-2-25 Diamant tvillinghabit
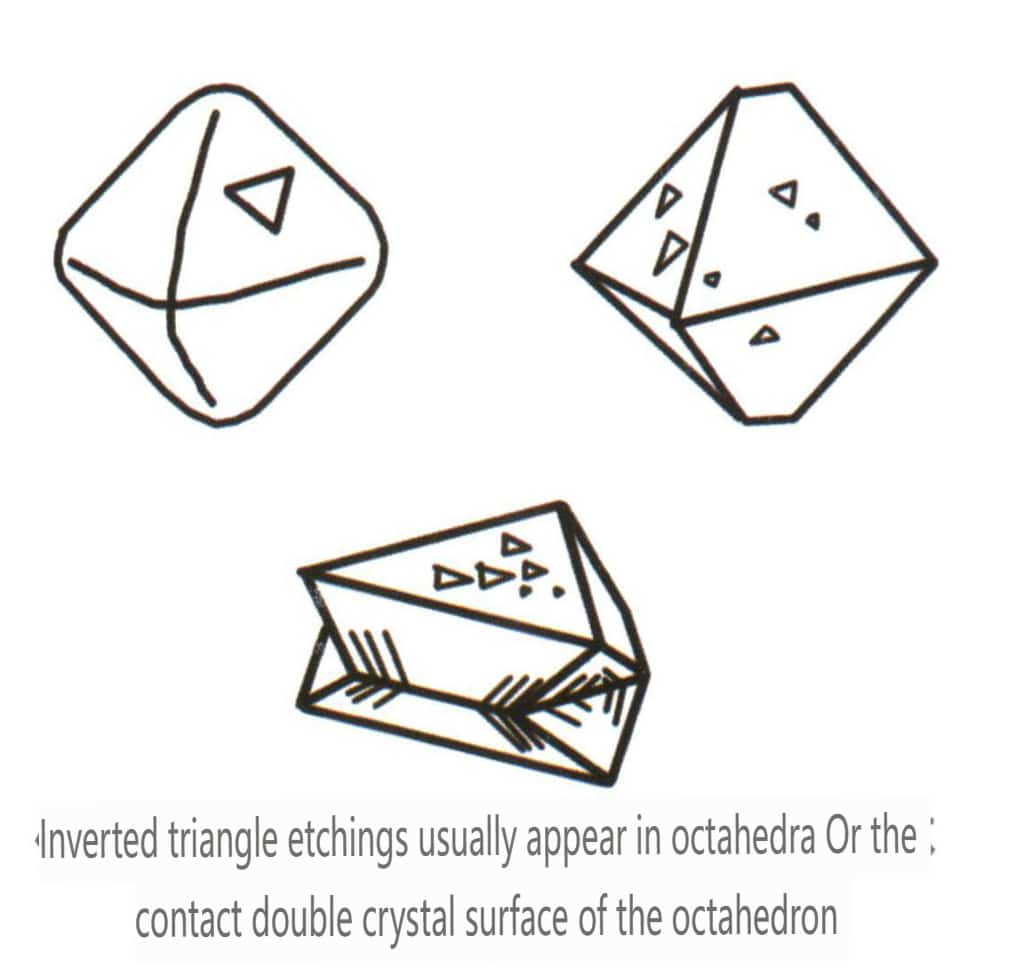
Figur 2-2-26 Etset figur av diamant-oktaedriske krystallflater i omvendt trekant

Figur 2-2-27 Invertert trekantet etsefigur på overflaten av en oktaederformet diamantkrystall
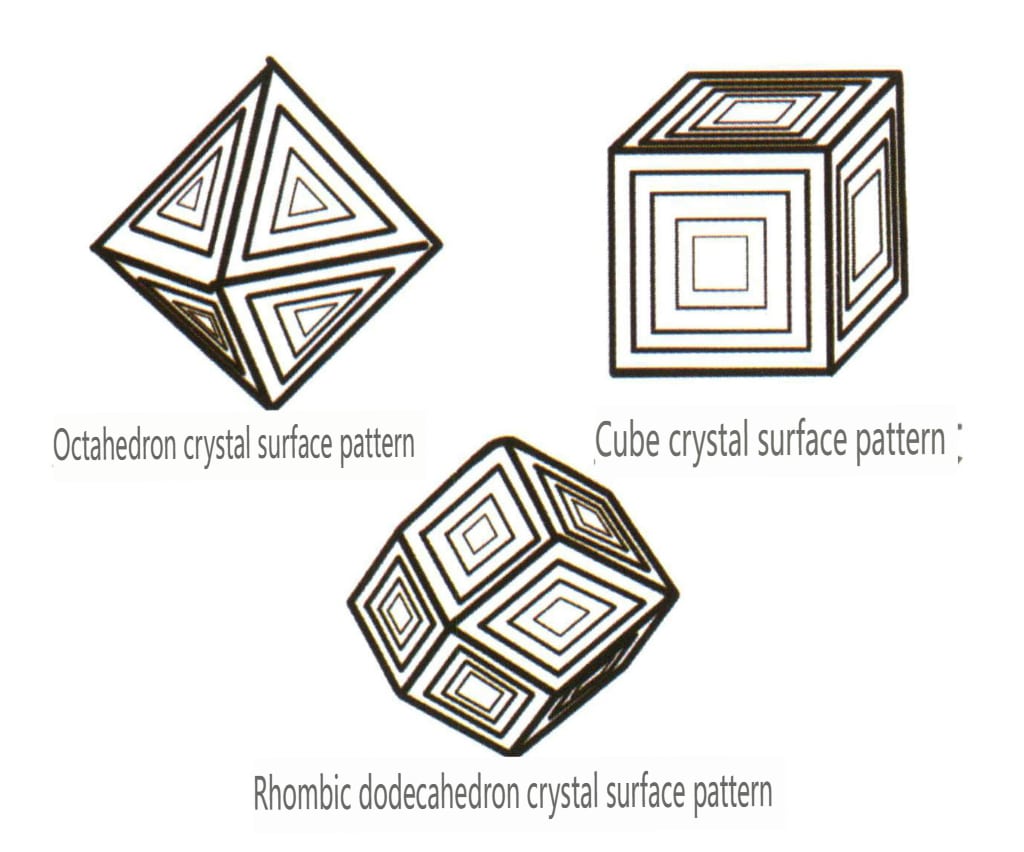
Figur 2-2-28 Etset figur av diamant-oktaedriske krystallflater i omvendt trekant

Figur 2-2-29 Invertert trekantet etsefigur på overflaten av en oktaederformet diamantkrystall
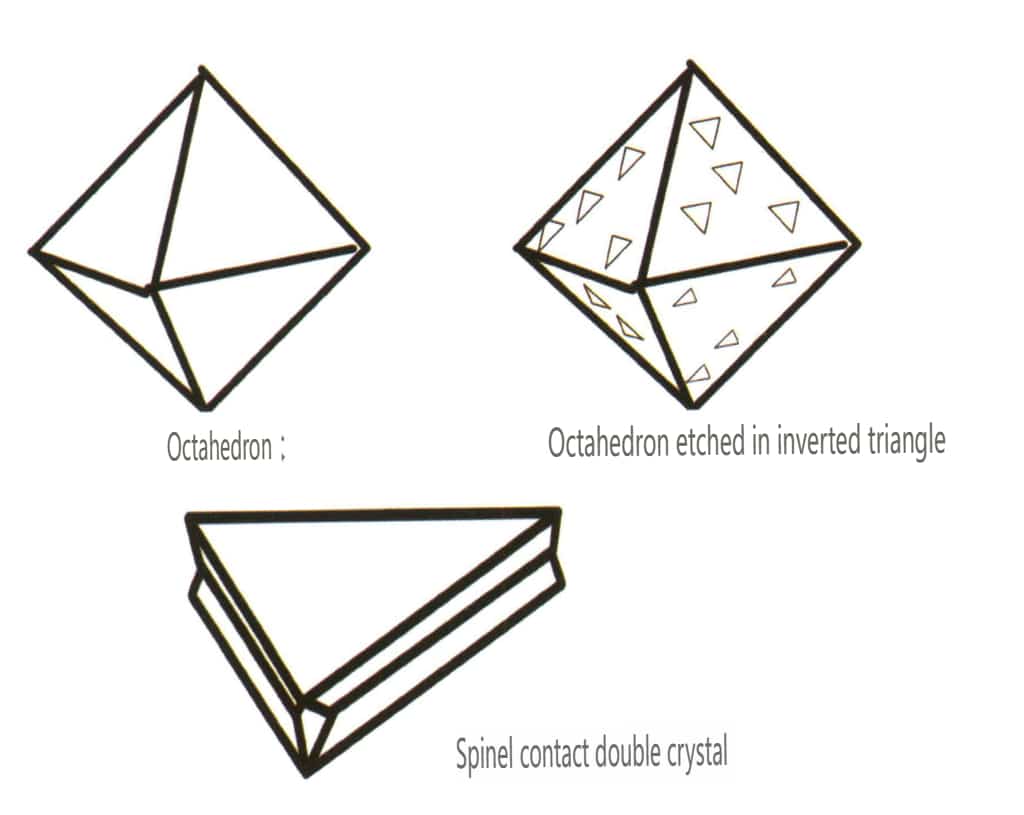
Figur 2-2-30 Spinellens krystallform

Figur 2-2-31 Vanlige former av spinellkrystaller

Figur 2-2-32 Kontakttvilling av spinell
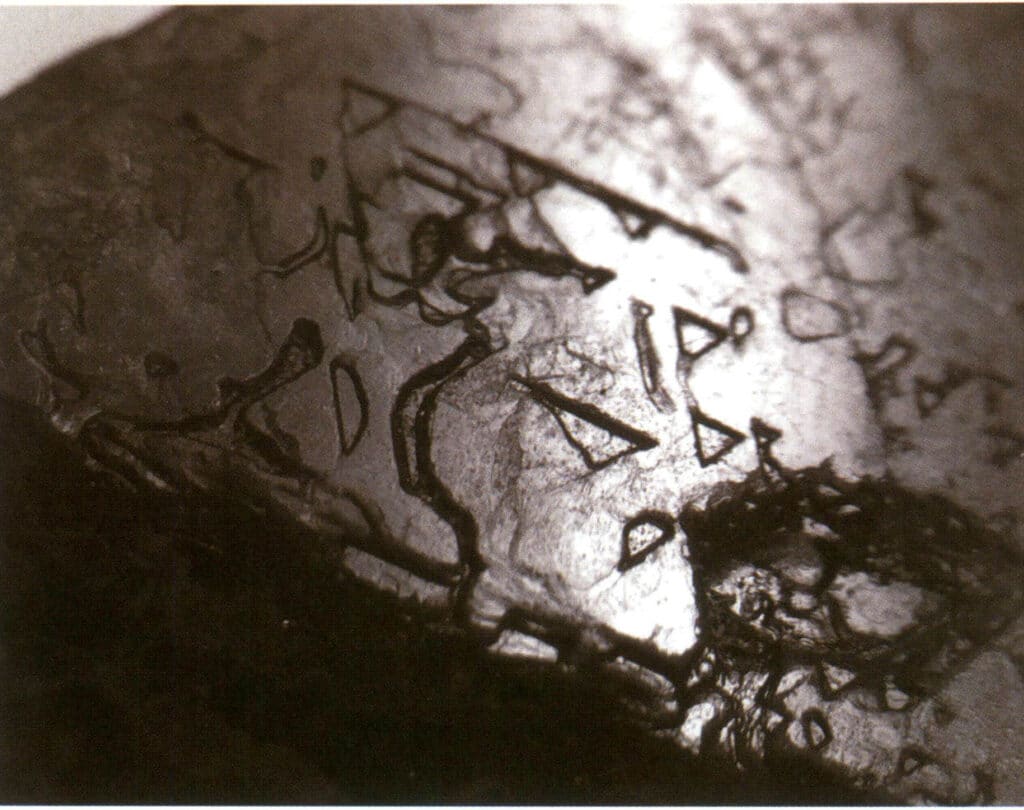
Figur 2-2-33 Invertert trekantet etsemønster på overflaten av spinell
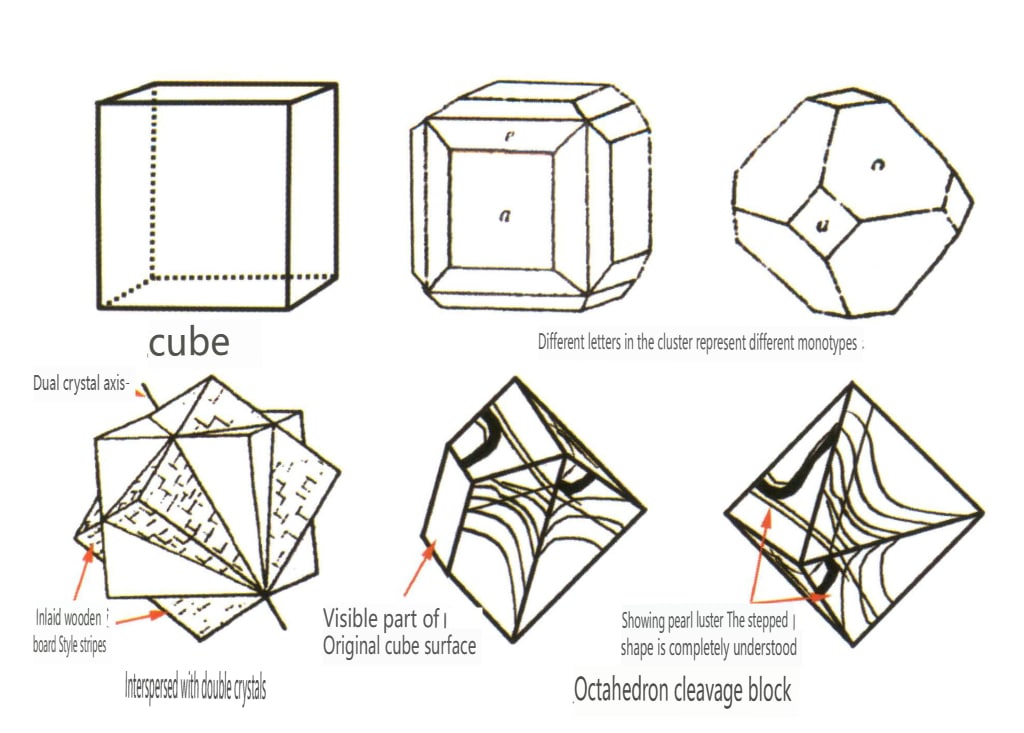
Figur 2-2-34 Fluoritt-krystallvaner

Figur 2-2-35 Fluorittkrystall
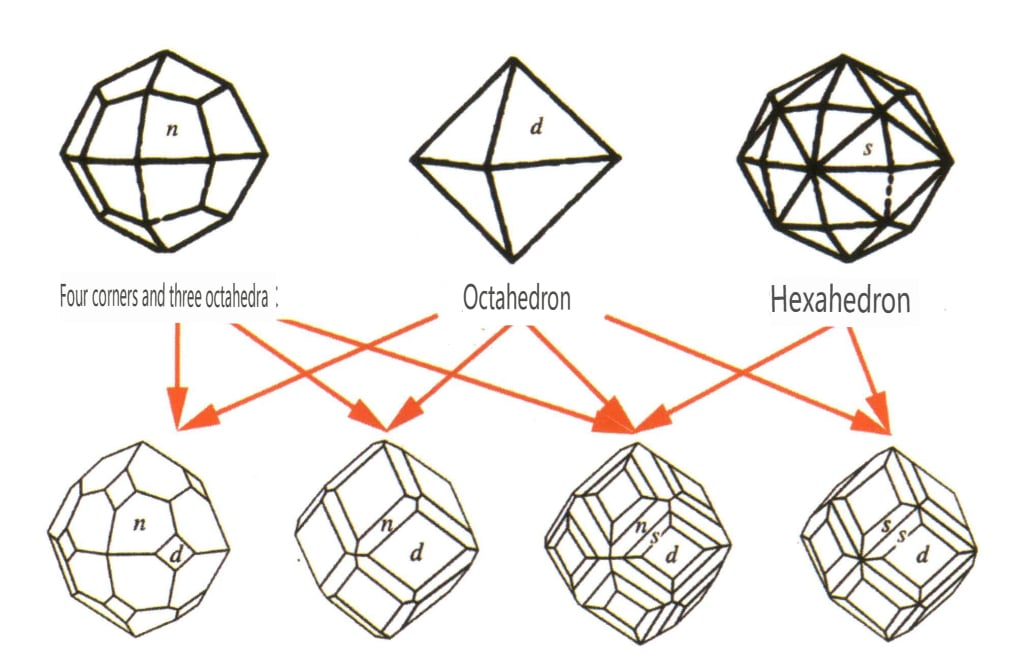
Figur 2-2-36 Granatens krystallform

Figur 2-2-37 Konsentriske ringbånd på overflaten av granatkrystaller som har samme form som krystallflatene
Tabell 3: Vanlige edelstenkrystallkarakteristikker for mellom- og lavkrystallfamilier
| Gems tone Navn | Krystallklassifisering | Viktige krystallkarakteristikker | |||
|---|---|---|---|---|---|
| Gems tone Navn | Krystallklassifisering | Crystal Habit | Vanlige krystallformer | Vanlige tvillingformer | Vanlige mønstre for krystalloverflater |
| Beryl | Sekskantet krystallsystem | Søyleformet krystallform (figur 2-2-38) | Sekskantet, søyleformet krystallform (figur 2-2-39, 2-2-40) | Sjelden | Synlige langsgående striper |
| Blystein | Tetragonalt krystallsystem | Søyleformet krystallform (Figur 2-2-41) | En firkantet søyle med kvadratisk tverrsnitt, som opptrer sammen med en kvadratisk dobbeltkonus (figur 2-2-42) | Synlige kneformede tvillingkrystaller | Ingen spesielle mønstre |
| Korund | Trigonalt krystallsystem | Platelignende krystallform, søyleformet krystallform (Figur 2-2-43) | Rubiner har ofte en sekskantet prismeform (Figur 2-2-44), mens safirer ofte har en sekskantet bipyramidal tønneformet krystallform (Figur 2-2-45). | Vanlig forekommende bi-krystaller. | Synlige striper. |
| Turmalin . | Søyleformet krystallform (Figur 2-2-46) | Krystallflatene i begge ender er forskjellige, og tverrsnittet er en sfærisk trekant (Figur 2-2-47) | Sjelden | Synlige langsgående striper (Figur 2-2-48) | |
| Kvarts (krystallkvarts) | Søyleformet krystallform (Figur 2-2-49) | Tverrsnittet er sekskantet, sekskantede bipyramider er sjeldne (figur 2-2-50, 2-2-51), sekskantede monopyramider er vanlige | Vanlig kontakt med bikrystaller (også kjent som japanske bikrystaller) | Vanlige horisontale striper på krystalloverflater | |
| Chrysoberyl | Trigonalt krystallsystem | Søyleformede krystalliseringsegenskaper (figur 2-¬2-52) | Monokrystallinsk er sjelden | Tri-krystallinsk er vanlig (Figur 2-2-53), sekskantede og konkave vinkler kan brukes som identifikasjonskriterier | Stripene av tri-krystallinsk kan brukes som identifikasjonskriterier |
| Topas | Søyleformet krystallform (Figur 2-2-54) | Tverrsnittet er diamantformet, og toppen ser ofte ut som en konvolutt (Figur2-2-55) | Bi-krystaller er sjeldne | Synlige langsgående striper | |
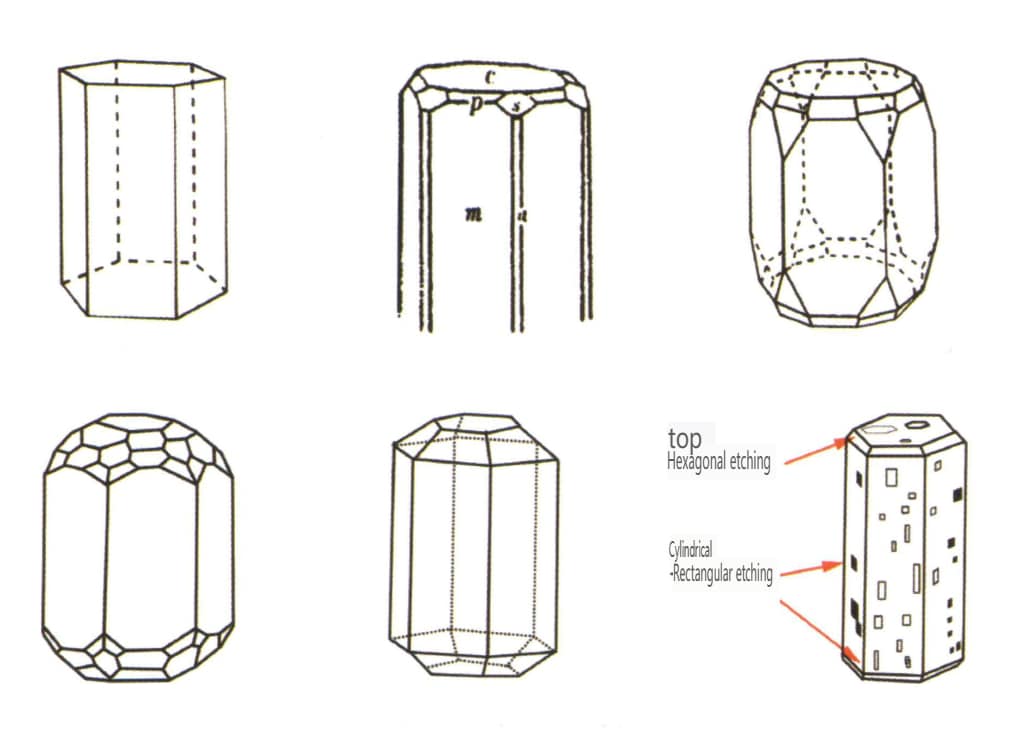
Figur 2-2-38 Berylls krystallform

Figur 2-2-39 Vanlige former av smaragdkrystaller

Figur 2-2-40 Vanlige former av akvamarin-krystaller
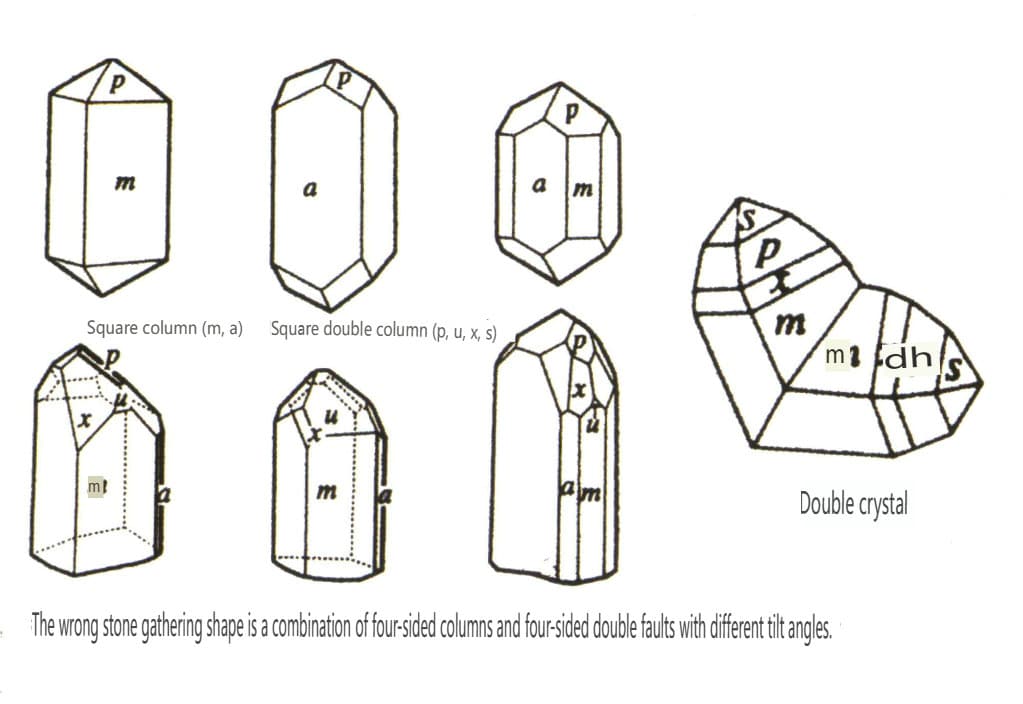
Figur 2-2-41 Zirkon-krystallens form

Figur 2-2-42 Zirkonkrystall
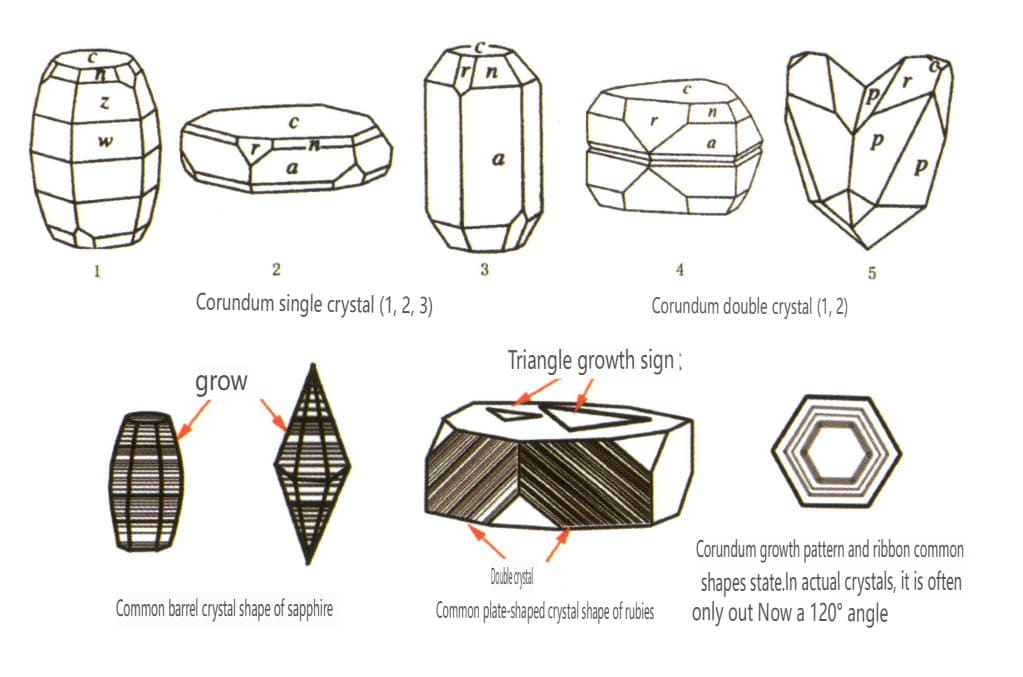
Figur 2-2-43 Korund krystallform

Figur 2-2-44 Rubinkrystall

Figur 2-2-45 Mekanisk tvilling av rubin
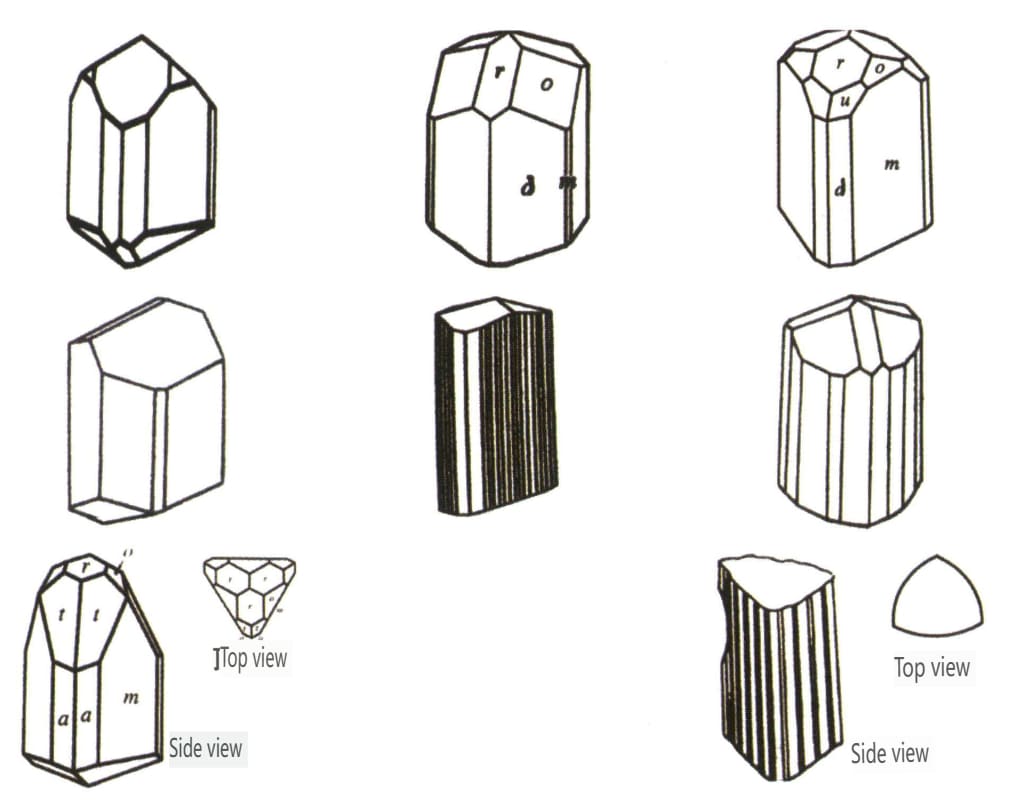
Figur 2-2-46 Turmalins krystallvaner

Figur 2-2-47 Turmalinkrystall

Figur 2-2-48 Langsgående striper på overflaten av turmalinkrystall
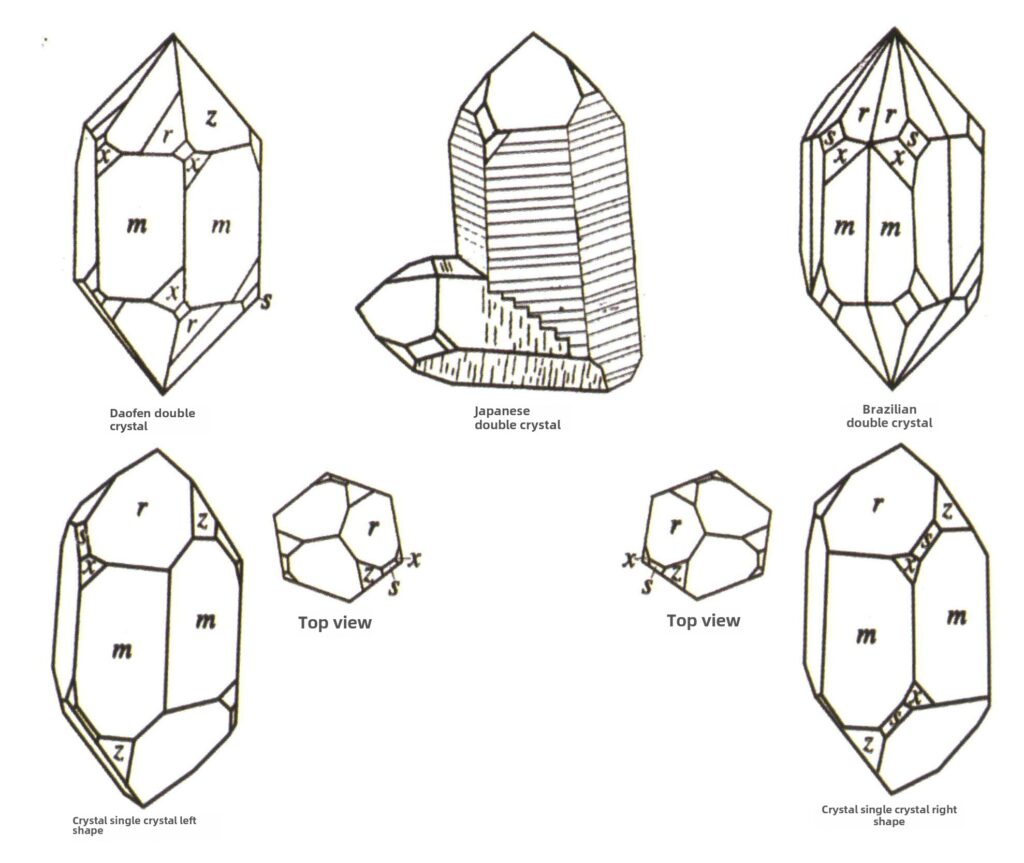
Figur 2-2-49 Krystallens krystalliseringsvaner

Figur 2-2-50 Krystallhus

Figur 2-2-51 Krystallhus
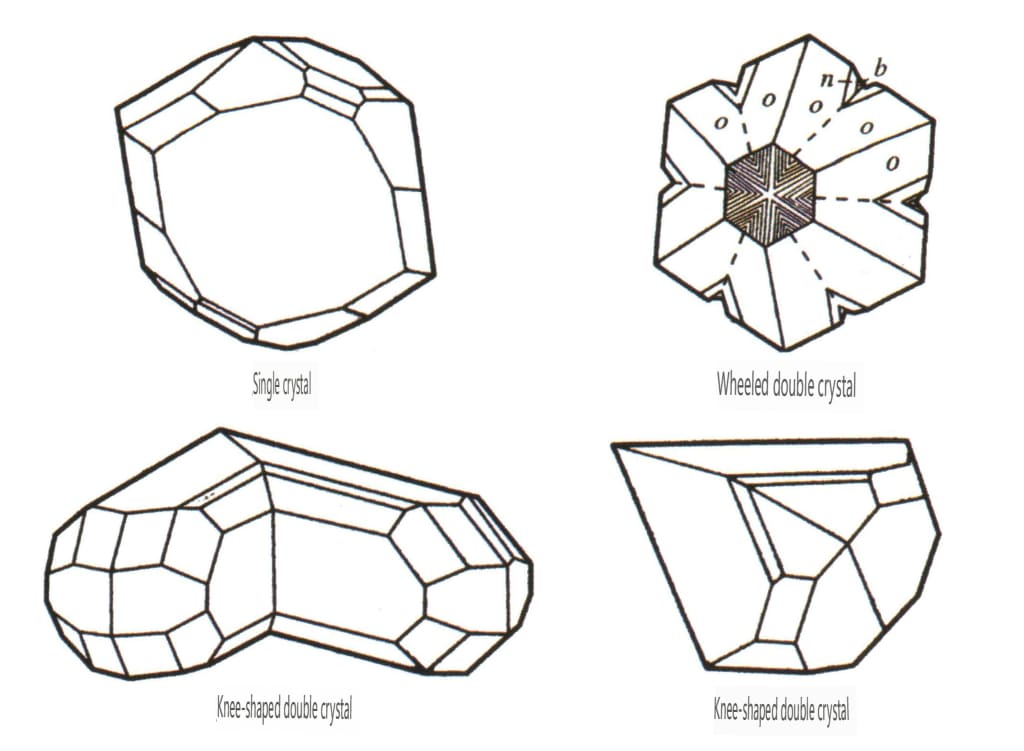
Figur 2-2-52 Krystallform av Chrysoberyl

Figur 2-2-53 Krystall av Chrysoberyl
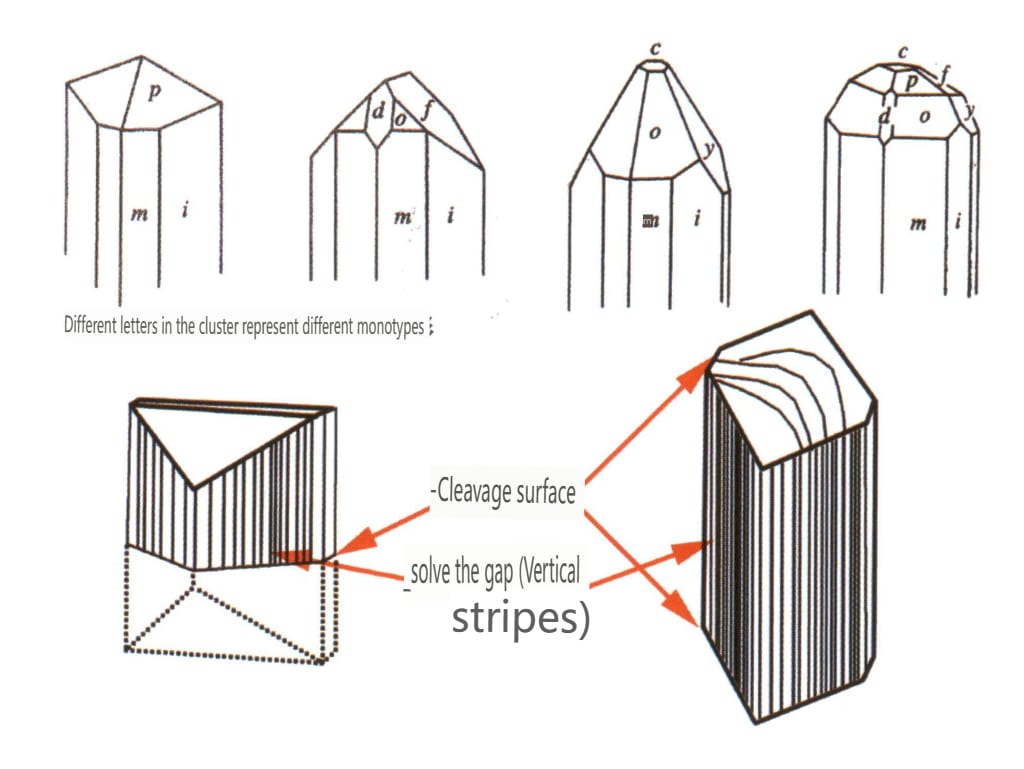
Figur 2-2-54 Krystallvaner for topas

Figur 2-2-55 Topasskrystall
Seksjon IV Hvorfor vokser edelstenskrystaller forskjellig?
Fra et mikroskopisk synspunkt er en edelstenkrystall et fast stoff som består av grunnstoffer av ulik størrelse som er ordnet etter ulike regler. Fra et makroskopisk synspunkt har mange edelstener krystallformegenskaper på grunn av deres forskjellige sammensetninger. Det finnes imidlertid noen spesielle tilfeller, for eksempel heteromorfe. For å bedre forstå hvorfor edelstenkrystaller ser forskjellige ut, vil vi her introdusere fem aspekter: heteromorf, isomorfisme, molekylær mekanisk blanding, vann i edelstenmineraler og kjemisk sammensetning av edelstener.
1. Heteromorf
Selv om noen mineraler har samme kjemiske sammensetning, har de svært forskjellige krystallstrukturer (grunnstoffenes plassering i det tredimensjonale rommet) og utviser betydelige forskjeller i fysiske og kjemiske egenskaper (tabell 4). Vi kaller dette fenomenet heteromorfisme, for eksempel diamant og grafitt (figur 2-2-56).
Vanlig kvarts har fenomenet heteromorfisme. Sillimanitt, andalusitt og kyanitt er en gruppe av heteromorfismevarianter.
Transformasjonen av heteromorfisme skjer under faststoffforhold. Under den strukturelle transformasjonsprosessen kan det utvikles trykk i krystallen, noe som ofte fører til tvillingdannelse inne i krystallen.

Tabell 4: Sammenligning av egenskapene til diamant og grafitt
| Mineral | Diamant | Grafitt |
|---|---|---|
| Komponenter | Karbon (C) | Karbon (C) |
| Formasjonsforhold | Høy temperatur og høyt trykk | Høy temperatur |
| Krystallsystem, vane | Isometrisk krystallsystem, oktaeder, rombisk dodekaeder | Sekskantet krystallsystem, lagdelt |
| Farge | Fargeløs, gul, blå, rosa, grønn osv. | Svart |
| Glans | Adamantinsk glans | Metallisk glans |
| Åpenhet | Gjennomsiktig til ugjennomsiktig | Ugjennomsiktig |
| Brytningsindeks | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Mekaniske egenskaper | Moderat oktaedrisk spaltning, hardhet 10, tetthet 3,52 | Et sett med perfekt spalting, hardhet 1, tetthet 2,10 |
| Andre eiendommer | Utmerket varmeledningsevne; med unntak av naturlige blå diamanter som er halvledere, er diamanter i andre farger isolatorer. | Moderat varmeledningsevne, god elektrisk ledningsevne |
2. Isomorfisme
Isomorfisme refererer til fenomenet der noen partikler i gitterstrukturen erstattes av andre partikler med lignende egenskaper, noe som resulterer i små endringer i gitterparametere og fysiske og kjemiske egenskaper. Derimot forblir krystallstrukturen fundamentalt uendret. Det kan forstås som at grunnstoffene i edelstenkrystallen blir erstattet av andre grunnstoffer. Derimot forblir det repeterende mønsteret av grunnstoffene i edelstenkrystallen det samme, med små avvik i avstandene mellom atomene. De fysisk-kjemiske egenskapene til edelstenskrystallen gjennomgår likevel små endringer (Figur 2-2-57 til Figur 2-2-58).
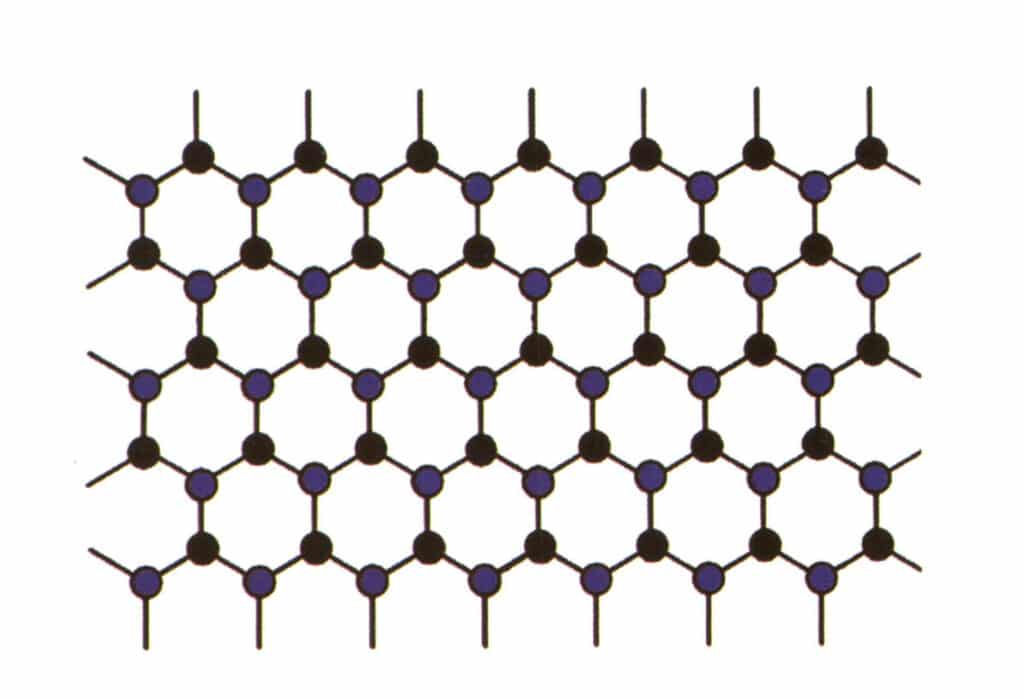
Figur 2-2-57 Simuleringsdiagram for krystallstruktur (blått og svart indikerer elementpartikler)
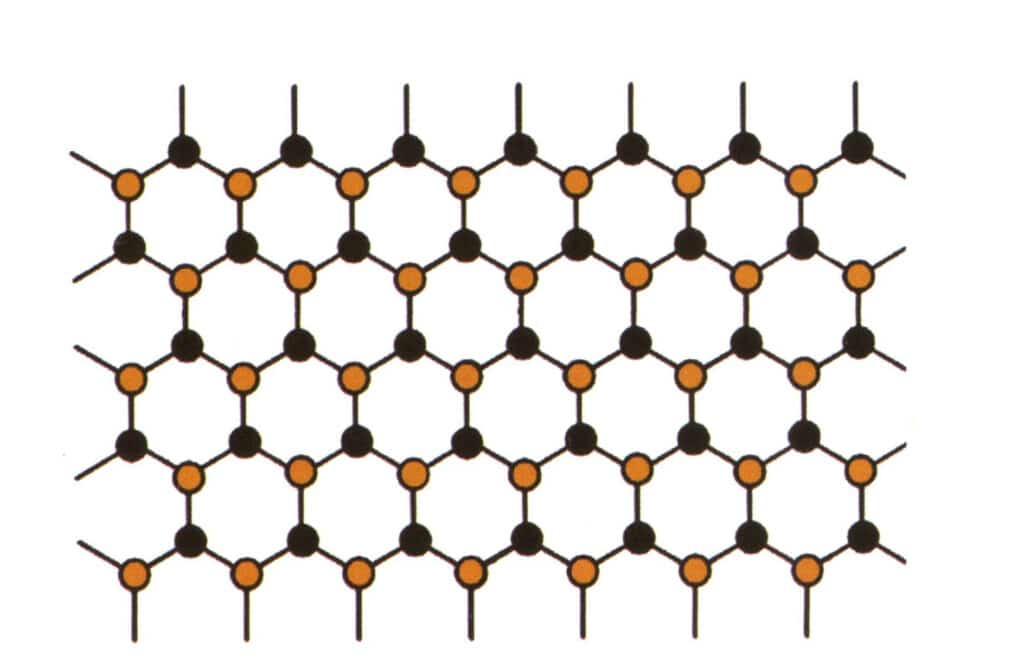
Figur 2-2-58 Simuleringsdiagram for krystallstruktur (svart representerer grunnstoffpartikler, gult representerer nye grunnstoffpartikler som delvis erstatter de blå grunnstoffpartiklene, gult erstatter kanskje ikke alle de blå partiklene helt)
Begrepet isomorfisme kan forklare hvorfor edelstener fra samme familie kan ha så mange farger, og hvorfor det er variasjoner i brytningsindeks og tetthet blant edelstener fra samme familie.
En familie kan forstås som en type edelstener der de repeterende mønstrene av krystallelementer er de samme, men de fysiske og kjemiske formene er litt forskjellige. Korundfamilien består for eksempel av rubin og safir, mens beryllfamilien omfatter smaragd, akvamarin og morganitt.
(1) Olivin
Den kjemiske sammensetningen av olivin er (Mg,Fe)₂SiO₄. Den komplette isomorfe substitusjonen av Fe- og Mg-elementer forekommer i sammensetningen. Når Fe-innholdet i olivin øker, blir fargen på olivin mørkere, brytningsindeksen øker, og tettheten øker også.
(2) Korund
Ren korund uten urenheter (Al₂O₃) er fargeløs, og når Cr erstatter Al, får edelstenen en rosarød til rød fargetone, kjent som rubin. De resterende fargene kalles safir, for eksempel oransjegul safir eller fargeløs safir. Den mest omtalte safiren er den blå safiren, der Fe og Ti erstatter Al. Jo høyere innhold av fargestoffene i erstatningsperlen, desto dypere blir fargen på perlen; omvendt, jo lavere innhold, desto lysere blir fargen.
(3) Turmalin
Turmalin refererer til samme type edelsten som turmalin, der turmalin er det mineralogiske navnet, og turmalin er det gemmologiske navnet. Den kjemiske sammensetningen av beryll er (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), der R hovedsakelig er Mg , Fe , Cr , Li, Al , Mn, og elementene i R kan helt eller delvis erstatte hverandre, noe som resulterer i et ekstremt bredt utvalg av farger for turmalin. For eksempel, når R hovedsakelig er Fe, beryl presenterer en dypblå eller til og med svart farge; når R hovedsakelig er Mg, beryl presenterer gul til brun; når R hovedsakelig er Li eller Mn, er beryll rosa eller lyseblå; når R hovedsakelig er Cr, er turmalin dypgrønn.
Av det ovennevnte kan man se at utskifting av elementer med lignende egenskaper fører til vakrere og mer strålende farger i edelstener.
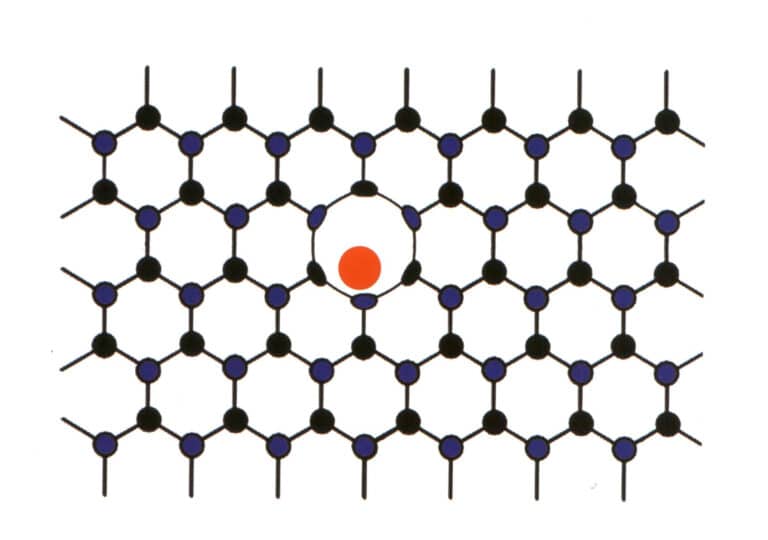
3. Molekylær mekanisk sammenblanding
Noen ganger kommer visse elementer med makt inn mellom hovedelementene i regelmessig ordnede edelstener. Den lave andelen av de innkommende elementene forstyrrer imidlertid ikke det repeterende mønsteret til de viktigste edelstenelementene, men forårsaker bare deformasjon (Figur 2-2-59). Denne situasjonen kalles molekylær mekanisk blanding, som for eksempel molekylær mekanisk blanding av nitrogen og bor i diamanter, som gir blå, rosa og gule diamanter, som er svært verdifulle.
4. Vann i edelstenmineraler
Noen edelstener inneholder vann, som er en viktig bestanddel av edelstenmineraler og er nært knyttet til edelstenenes egenskaper. Basert på hvilken form for vann som finnes i edelstenmineraler og dets rolle i krystallstrukturen, kan vannet i edelstener deles inn i to kategorier: den ene er absorpsjonsvann, som ikke er relatert til krystallstrukturen, og den andre er vann som deltar i mineralkrystallstrukturen, inkludert krystalliseringsvann, zeolittisk vann, vann mellom lagene og konstitusjonsvann. Vannet som er nært knyttet til edelstener, omfatter absorpsjonsvann, krystalliseringsvann og konstitusjonsvann.
Den ene er å absorbere vann, for eksempel Opal (kjemisk sammensetning er SiO₂ - nH₂O, n representerer antall H₂O, innholdet er variabelt) i vannmolekylet, som er et nøytralt vannmolekyl som mekanisk adsorberes for mineralpartikler eller bruddflater. Når temperaturen når 100 ~ 110 ° grader under normalt trykk, kan vannmolekylene alle unnslippe og ikke skade krystallgitterstrukturen, så for å unngå Opal i disken i lang tid med sterk lyseksponering tørr sprekk, bør du sette en kopp vann i disken.
Det andre er krystallisasjonsvannet, som krystallisasjonsvannet i turkis [kjemisk sammensetning er CuAl₆(PO₄)₄(OH)₈-4H₂O, der innholdet av H₂O kan nå 19,47%]. Dette nøytrale vannmolekylet finnes i faste posisjoner i gitteret og fungerer som en strukturell enhet, og er en del av mineralets kjemiske sammensetning. Temperaturen der krystalliseringsvannet slipper ut, overstiger vanligvis ikke 600 °C og slipper vanligvis ut ved 100-200 °C. Når en edelsten mister krystallisasjonsvannet, blir krystallstrukturen skadet og danner en ny struktur.
Det tredje er konstitusjonsvann, også kjent som kombinert vann, som inngår i mineralgitteret i form av OH-, H⁺, H₃O⁺ plasma, der OH- er det vanligste. Konstitusjonsvann er en del av mineralets kjemiske sammensetning, og inntar faste posisjoner i gitterstrukturen med en definert andel i sammensetningen. Strukturelt vann krever en høyere temperatur for å slippe ut og skade strukturen, vanligvis rundt 600 -1000 °C. Når en edelsten mister strukturelt vann, ødelegges krystallstrukturen. Mange edelstener inneholder strukturelt vann, for eksempel turmalin [kjemisk sammensetning er ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), der R hovedsakelig inkluderer Mg, Fe, Cr, Li, Al, Mn, osv, og elementene i R kan helt eller delvis erstatte hverandre], og topas [kjemisk sammensetning er Al₂SiO₄( F, OH) ₂ ].
5. Den kjemiske sammensetningen av edelstener
Edelstener, som andre stoffer, er sammensatt av kjemiske elementer. Hver type edelsten har sin spesifikke kjemiske sammensetning og et visst variasjonsområde, som bestemmer edelstenens ulike egenskaper og karakteristika. Edelstener tilhører mineralene og bergartene, og klassifiseringen av edelstenens kjemiske sammensetning kan spores tilbake til den kjemiske sammensetningen av mineralene.
De viktigste klassifiseringsmetodene for mineraler i dag omfatter klassifisering etter kjemisk sammensetning (Dana-systemet), geokjemisk klassifisering, genetisk klassifisering, anvendelsesklassifisering og krystallkjemisk klassifisering. Den mest utbredte metoden er kjemisk klassifisering basert på kjemisk sammensetning og krystallstruktur (Hugo Strunz-systemet) (tabell 5).
Tabell 5: Kjemisk klassifiseringssystem for mineralkrystaller
| Nivåsekvens | Grunnlag for inndeling | Eksempel |
|---|---|---|
| Hovedkategori | Sammensatt type | Oksygenholdig salt Hovedkategori |
| Klasse | Anion- eller komplekse anion-typer | Silikatklasse |
| (Underkategori) | Anionisk kompleksstruktur | Underklasse av rammesilikat |
| Gruppe | Krystallstrukturtyper og ioniske egenskaper | Korundgruppen, beryllgruppen, granatgruppen |
| (Undergruppe) | Kationtyper | Alkalisk feltspat-undergruppe |
| Art | Visse krystallstrukturer og kjemisk sammensetning | Ortoklas KAlSi3O8 |
| (Underart) | Samme krystallstruktur, forskjellig sammensetning eller egenskaper, morfologi | Adularia KAlSi3O8 |