Um momento para saber tudo sobre a cristalografia de pedras preciosas
Um guia completo sobre as formas, tipos, classificações e diferenças da Cristalografia
A Terra é composta por inúmeras moléculas e átomos. A investigação científica moderna descobriu que os materiais sólidos na natureza são constituídos por diferentes elementos químicos. Os resultados da análise de raios X mostram que os átomos dos elementos de certos materiais sólidos estão dispostos de forma ordenada e regular. Estes materiais são classificados como cristalinos ou designados por cristais, e a sua estrutura atómica ordenada é designada por estrutura cristalina (Figura 2-1-1).
A maioria dos materiais de gema que crescem na natureza e nos laboratórios são cristalinos. Este capítulo abordará o conceito de cristais, a sua classificação e a relação entre os cristais e a terminologia básica em gemologia.

Índice
Secção ⅠO conceito e a descrição dos cristais
Quando falamos de gemas, pensamos frequentemente nas suas caraterísticas cintilantes e translúcidas (Figura 2-1-2). Na perspetiva dos geólogos e gemólogos, as gemas mais apreciadas pertencem a uma forma geométrica de sólidos - os cristais. A essência da beleza dos cristais é, de facto, a beleza da geometria.

1. O conceito de cristais
Os cristais são os mais facilmente associados e mais comummente encontrados na natureza. Os cristais encontram-se em todos os sete continentes da Terra e, quando encontrados na natureza, assumem frequentemente a forma de poliedros geométricos (Figura 2-1-3). Eles são comumente chamados de cristais. Mais tarde, este termo foi alargado para se referir a substâncias sólidas que ocorrem naturalmente com formas geométricas poliédricas, como os cristais de diamante e água-marinha (Figura 2-1-4). Os cristais também podem descrever materiais sólidos com superfícies irregulares, desiguais, desgastadas, partidas ou processadas artificialmente, mas com um arranjo atómico que ainda segue um padrão regular. Os cristalógrafos acreditam que todos os cristais possuem seis caraterísticas básicas: auto-limitação, uniformidade, anisotropia, simetria, estabilidade e ponto de fusão fixo.
① A autolimitação refere-se à propriedade dos elementos químicos de formarem espontaneamente formas geométricas poliédricas. Esta propriedade pode explicar porque é que diferentes elementos têm diferentes formas geométricas de cristal.
② Uniformidade refere-se à propriedade de que as propriedades físicas e químicas de todas as partes do cristal são as mesmas. Esta propriedade pode ajudar-nos a distinguir e identificar diferentes cristais minerais.
③ A anisotropia refere-se à propriedade em que a disposição dos elementos varia em diferentes direcções, conduzindo a ligeiras diferenças nas propriedades físicas, dependendo da direção. Esta propriedade pode explicar porque é que os diamantes com a maior dureza podem ser cortados e polidos.
④ A simetria refere-se à propriedade em que partes ou propriedades idênticas num cristal são repetidas num padrão regular. Esta propriedade é extremamente importante e especial para os cristais e será desenvolvida na segunda secção deste capítulo.
⑤ A estabilidade refere-se à estabilidade de um cristal resultante da sua energia interna mínima. Se a energia interna de um cristal é alta e irregular, ele é propenso a rachar por si só. Essa propriedade pode explicar por que os cristais de rubi sintetizados pela técnica de fusão por chama sempre parecem estar pela metade em vez de completos.
⑥ O ponto de fusão fixo refere-se à propriedade de um cristal ter um ponto de fusão fixo.

Figura 2-1-3 Granada (o lado esquerdo é o cristal, o lado direito é a granada polida)

Figura 2-1-4 Cristal de água-marinha
2. A forma ideal dos cristais
Os cristais discutidos em cristalografia são principalmente monocristais ideais. Um monocristal ideal é definido como aquele cuja estrutura interna segue estritamente as regras das redes espaciais e cuja forma é uma combinação geométrica regular. As formas dos monocristais ideais dividem-se em dois tipos: formas simples e formas combinadas.
(1) Formulário simples
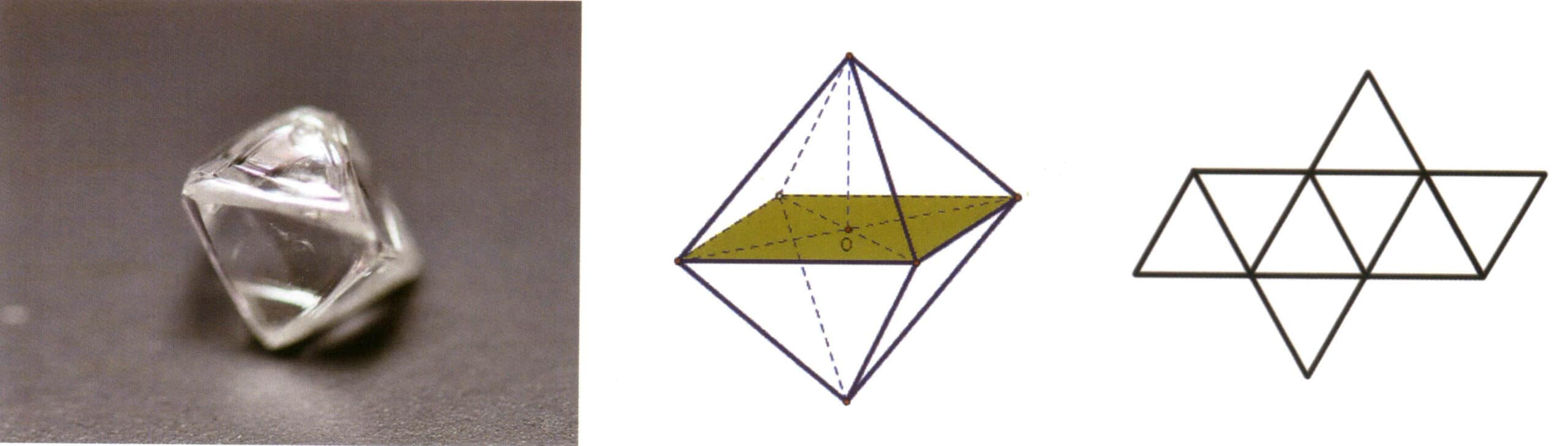
Uma forma simples refere-se a uma combinação de um grupo de faces de cristal ligadas por elementos de simetria, que pode ser entendida como um corpo geométrico composto por faces de cristal com a mesma forma e tamanho num estado ideal (Figura 2-1-5). Existem 47 tipos de formas simples em cristais.
Os pontos-chave para a identificação de formas simples são: todas as faces cristalinas do cristal têm a mesma forma e tamanho e as faces cristalinas podem ser orientadas de forma diferente.
(2) Combinar Formulário
A agregação de formas simples é chamada de forma combinada, composta de duas ou mais formas simples diferentes. Nem todas as formas simples podem ser livremente combinadas numa forma combinada; apenas as formas simples com o mesmo grupo de pontos podem ser agregadas (Figuras 2-1-6 a 2-1-8).
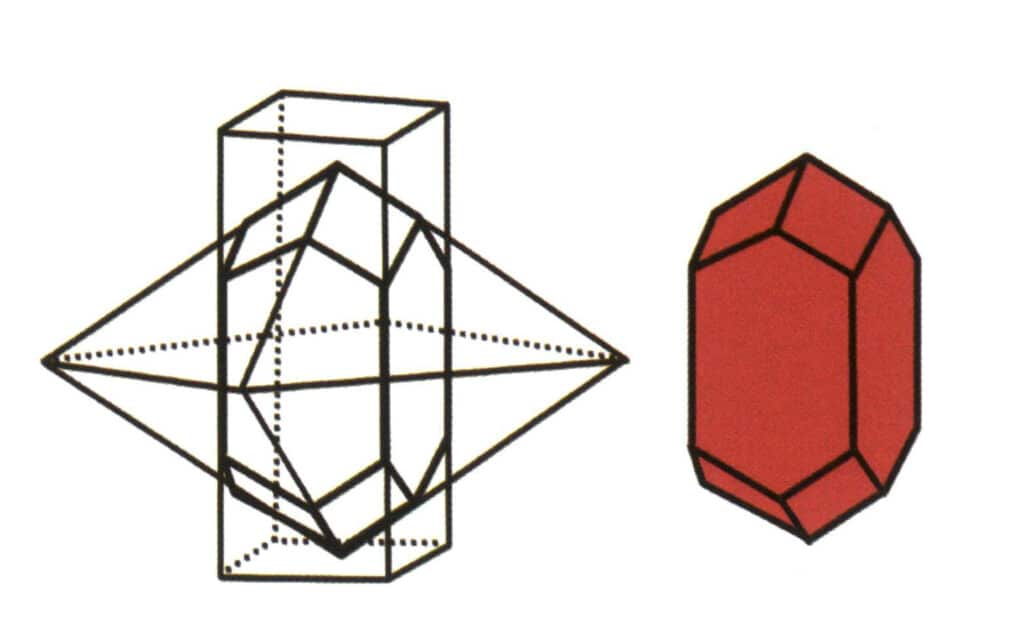
Figura 2-1-6 Combinação de prismas tetragonais e dipiramidais tetragonais
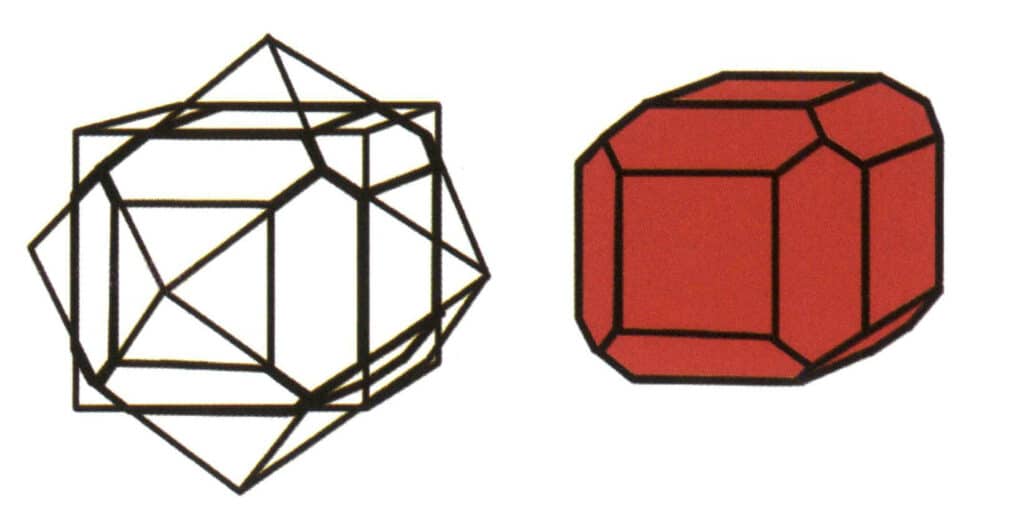
Figura 2-1-7 Combinação de cubos e dodecaedros rômbicos
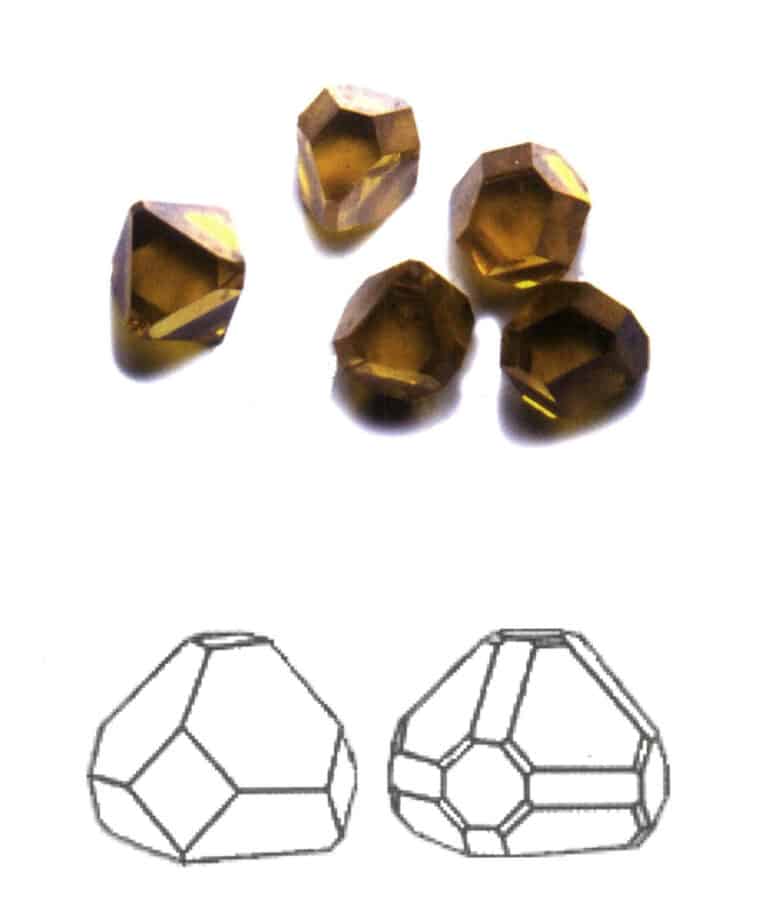
O ponto-chave da identificação da forma combinada é a presença de duas ou mais faces cristalinas com formas diferentes no cristal.
Quando os monocristais são encontrados na natureza, apresentam sempre uma diferença significativa em relação à morfologia ideal dos monocristais (Figura 2-1-9), como o facto de uma única face não ter necessariamente a mesma forma e tamanho e o desaparecimento de faces cristalinas, o que é descrito como cristais distorcidos.

Os cristais distorcidos também podem ser descritos como cristais reais produzidos na natureza, influenciados pelo ambiente de crescimento. As múltiplas faces cristalinas que se repetem em ângulos fixos nos cristais ideais podem não ter necessariamente a mesma forma e tamanho. Ainda assim, para o mesmo tipo de cristal, as faces cristalinas do mesmo monomorfo devem ter o mesmo padrão e propriedades físicas. Os ângulos entre as faces cristalinas correspondentes permanecem inalterados, reflectindo a simetria inerente ao próprio cristal. Os cristais encontrados na realidade são distorcidos em graus variados.
Os cristais geminados também podem ser descritos como cristais reais produzidos na natureza, influenciados pelo ambiente de crescimento. As múltiplas faces do cristal que se repetem em ângulos fixos nos cristais ideais podem não ter necessariamente a mesma forma e tamanho. Ainda assim, para o mesmo tipo de cristal, as faces da mesma forma devem ter os mesmos padrões e propriedades físicas. Os ângulos entre as faces correspondentes do cristal permanecem inalterados, reflectindo a simetria inerente ao próprio cristal. Os cristais encontrados na realidade são todos, em graus variados, geminados.
3. Os hábitos de cristalização dos cristais
Os cristais formados na natureza nunca podem atingir uma forma perfeita. Se crescerem nos intervalos das camadas rochosas, rodeados de rocha, a forma natural do cristal será distorcida. Mesmo os cristais cultivados em laboratório serão deformados devido à influência da gravidade. Só nas condições de gravidade zero da Estação Espacial Internacional é que os cientistas podem cultivar os cristais de forma perfeita que procuram.
Embora as formas dos cristais sejam imperfeitas, cada tipo de cristal mineral tende a crescer ou a agrupar-se de formas ou hábitos diferentes.
Cada mineral tende a formar-se em condições específicas, e os seus hábitos reflectem as condições da sua formação. Alguns minerais, como o quartzo, têm condições de formação complexas e variáveis. Assim, o quartzo também possui múltiplos hábitos.
Em geral, os hábitos dos cristais referem-se às caraterísticas de um determinado cristal que tende a formar uma forma específica sob certas condições externas. Por vezes, refere-se aos tipos comuns da forma simples desse cristal.
Com base no grau de desenvolvimento dos cristais no espaço tridimensional, os hábitos cristalinos são divididos em três tipos básicos.
(1) Uni-extensão direcional
Os cristais se estendem em uma direção, aparecendo em formas colunares, aciculares, fibrosas, etc. Minerais como o berilo, a turmalina, a hornblenda e a malaquite apresentam frequentemente este hábito (Figuras 2-1-10 a 2-1-11).

Figura 2-1-10 Água-marinha colunar (em cima) e seu diagrama de hábito cristalino (embaixo)

Figura 2-1-11 Malaquita fibrosa (em cima) e seu diagrama de hábito cristalino (em baixo)
(2) Bi-extensão direcional
Os cristais estendem-se num plano, aparecendo em forma de placa, folha, escamas, etc., uma vez que minerais como a volframite, a mica, o plumbago e a tanzanite apresentam frequentemente este hábito (Figura 2-1-12).
(3) Tri-isométrico direcional
Os cristais desenvolvem-se uniformemente em três direcções, apresentando formas isométricas e granulares, tais como espinélio, granada, diamante, pirite e fluorite, que exibem frequentemente este hábito (Figuras 2-1-13, 2-1-14).

Figura 2-1-12 O hábito cristalino tipo placa da tanzanite (em cima) e o seu diagrama de hábito cristalino (em baixo)

Figura 2-1-13 O hábito cristalino octaédrico da pedra preciosa espinélio (em cima) e o seu diagrama de hábito cristalino (em baixo)
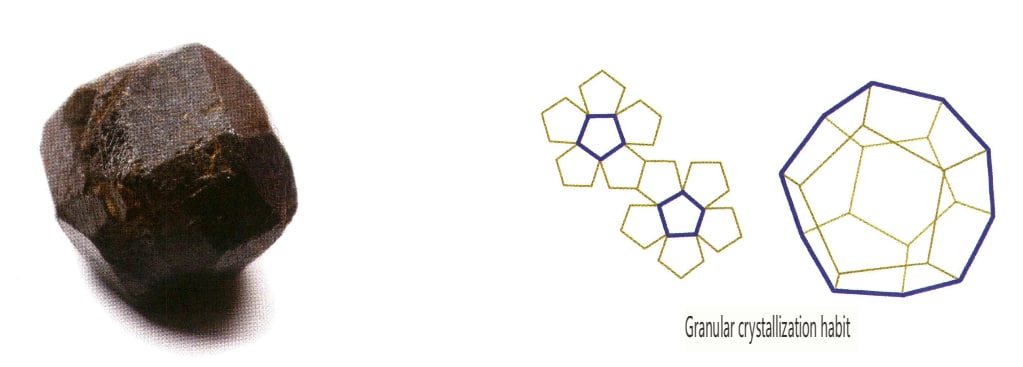
Além disso, existem tipos de transição, tais como formas colunares curtas, colunares em placa, em faixa e em placa espessa.
A composição química e a estrutura do cristal determinam principalmente o hábito do cristal. Também está intimamente relacionado com as condições externas durante a formação do cristal (como temperatura, pressão, concentração, viscosidade e impurezas), como as diferenças nas formas de cristal entre diamantes e cristais de diamante sintético.
4. Agregação regular de cristais
Na natureza, podemos encontrar cristais individuais (Figura 2-1-15) e dois ou mais cristais individuais crescendo juntos para formar um todo. Este fenómeno de crescimento conjunto de vários cristais é designado por agregação de cristais. A agregação de cristais pode ser classificada em tipos irregulares e regulares. A agregação irregular de cristais pode ser entendida como um coletivo, sobre o qual o Capítulo Três se debruçará. Na agregação regular de cristais, existem quatro tipos comuns: agregação paralela, bicristais, sobrecrescimento e intercrescimento (Figuras 2-1-16 a 2-1-18). Esta secção discute principalmente o tipo de agregação regular conhecido como bicristais.

Figura 2-1-15 Monocristal (Turmalina)
Figura 2-1-16 Agregação paralela (Quando vários cristais do mesmo tipo crescem paralelamente no espaço, chama-se agregação paralela. Nesta altura, as faces e arestas correspondentes dos cristais crescidos são todas paralelas entre si).

Figura 2-1-17 Cristal gémeo (espinélio)

Figura 2-1-18 Crescimento excessivo (um tipo de cristal cresce na superfície de outro cristal numa direção cristalográfica específica, também conhecido como crescimento epitaxial)
Os bicristais são a agregação regular de dois ou mais cristais idênticos de acordo com certas regras de simetria. (Eixo gémeo, plano gémeo) As faces, arestas e ângulos correspondentes dos dois indivíduos adjacentes não são completamente paralelos. No entanto, podem refletir-se mutuamente através de operações de simetria como a rotação e a inversão da rotação, permitindo que os dois indivíduos coincidam ou se alinhem.
4.1 Pontos-chave para a identificação de bicristais
① Ângulos côncavos visíveis em cristais geminados (Figura 2-1-19).
② Estilolito: A micro-morfologia e outras caraterísticas das superfícies cristalinas em ambos os lados do estilolito são descontínuas (Figura 2-1-20).
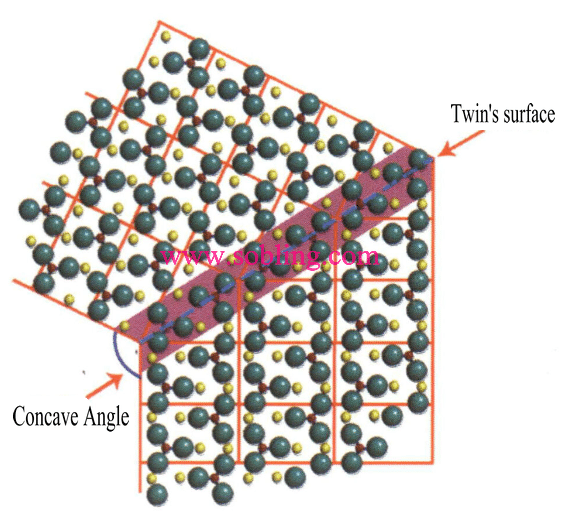
Figura 2 - 1-19 Ângulo côncavo do gémeo
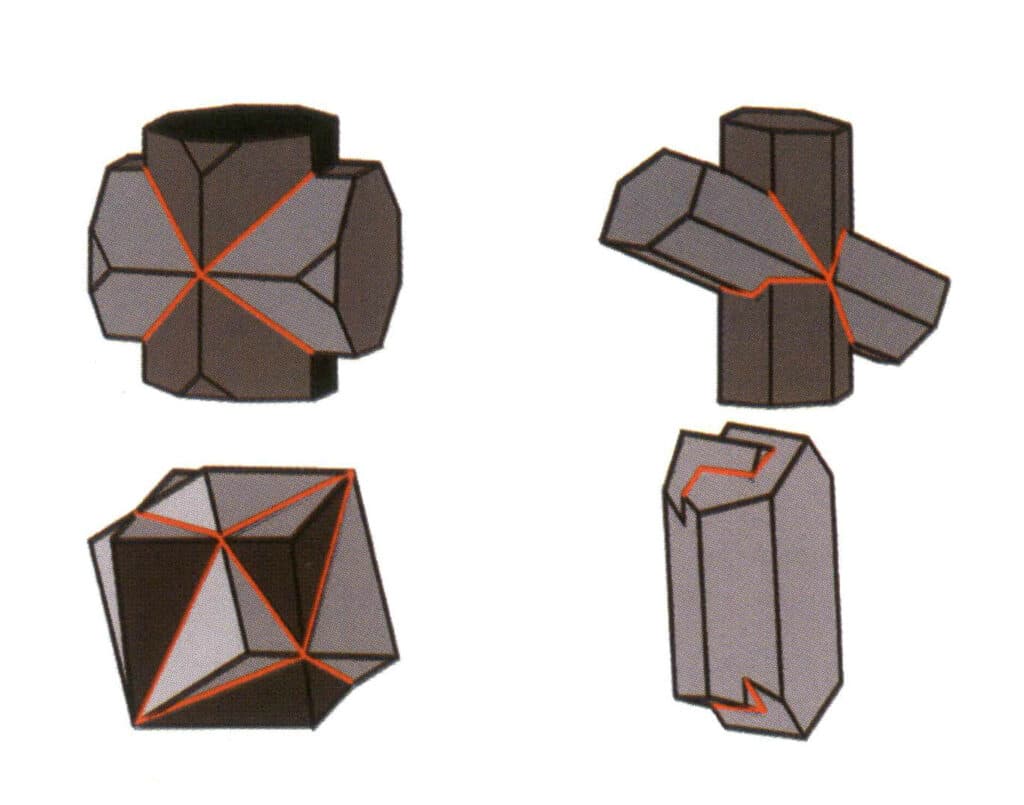
Figura 2-1-20 Estilolito (cores diferentes na figura representam cristais diferentes; as linhas vermelhas indicam o estilolito gémeo)
③ Estriação de geminação: As faces cristalinas ou os planos de clivagem apresentam estrias finas de geminação (Figura 2-1-21)
④ Figura de corrosão: O aparecimento da figura de corrosão indica a presença de geminação (Figura 2-1-22)

Figura 2-1-21 Diagrama esquemático de gémeos polissintéticos

Figura 2-1-22 Superfície de espinélio com pontuações triangulares invertidas.
⑤ O aparecimento de pseudo-simetria: o surgimento de relações de simetria inconsistentes com o grupo de pontos inerente do cristal único (Figura 2-1-23 a Figura 2-1-24).

Figura 2-1-23 Cristal único de crisoberilo

Figura 2-1-24 Gémeo do crisoberilo em forma de joelho
A geminação é dividida em cinco tipos com base nas suas caraterísticas de empilhamento: gémeos de contacto (Figura 2-1-25 a Figura 2-1-26), gémeos polissintéticos (Figura 2-1-27), gémeos interpenetrantes (Figura 2-1-28), cristal tripleto (Figura 2-1-29) e gémeos complexos, entre os quais os primeiros quatro tipos são comuns.


Figura 2-1-26 Geminação por contacto de espinélio (em cima) e respetivo esquema (em baixo)

Figura 2-1-27 Gémeo polissintético da labradorite (em cima) e respetivo esquema (em baixo)
Figura 2-1-28 Cristais gémeos de feldspato (em cima) e esquema de cristais gémeos interpenetrantes de outros tipos (em baixo)

Figura 2-1-29 Geminação trigonal do crisoberilo (em cima) e respetivo esquema (em baixo)
4.2 A formação de bicristais
① Formado durante o crescimento do cristal, pode desenvolver-se a partir de germes cristalinos gémeos ou pequenos cristais que crescem de forma dependente de acordo com a posição do gémeo.
② Formado durante o processo de transformação de heteromorfismo, como quando o quartzo α se transforma em quartzo β, formando gémeos.
③ Formado por ação mecânica, em que uma parte do cristal desliza ao longo de um determinado plano direcional para formar gémeos de deformação, como os gémeos da calcite.
5.Padrões de faces de cristal
Quando os cristais são descobertos na natureza, têm frequentemente formas incompletas (Figura 2-1-30) e padrões de superfície especiais. Por vezes, crescem juntos em grupos (Figura 2-1-31), que frequentemente apresentam diferenças significativas em relação aos poliedros geométricos padrão que conhecemos, como os cubos e os prismas hexagonais. Este fenómeno é designado por forma real dos cristais. A forma real dos cristais tem uma classificação pormenorizada em cristalografia, como cristais distorcidos, cristais convexos, cristais curvos, cristais flutuantes, riscas nas faces dos cristais, figuras gravadas, estrias de geminação, etc.

Figura 2-1-30 Cristal de rubi

Figura 2-1-31 Cristais de pirita (a esquerda mostra múltiplos cristais de pirita crescendo juntos, e a direita mostra um único cristal de pirita)
Esta secção aborda principalmente os padrões de faces de cristais na forma real de cristais.
Teoricamente, os planos cristalinos são lisos e planos. No entanto, durante o crescimento ou dissolução real dos cristais, a superfície deixa frequentemente para trás padrões regulares ligeiramente irregulares, normalmente designados por padrões da face do cristal. Os padrões da face do cristal incluem estrias de crescimento, camadas de crescimento, padrões em espiral, colinas de crescimento e figuras de gravura. Os padrões da face do cristal discutidos neste livro referem-se principalmente às riscas da face do cristal e às figuras de corrosão que podem ser observadas a olho nu ou em condições de baixa ampliação.
As riscas da face do cristal referem-se a uma série de linhas rectas paralelas na superfície do cristal devido à convergência repetida e ao crescimento alternado de diferentes formas individuais. Também conhecidas como "riscas combinadas", estas são vistas apenas nas superfícies dos cristais, também chamadas riscas de crescimento. Por exemplo, a face cristalina prismática hexagonal do quartzo frequentemente tem faces cristalinas finas prismáticas hexagonais e dodecaédricas rômbicas desenvolvidas alternadamente em faixas transversais agregadas (Figura 2-1-32).

As figuras de corrosão referem-se aos buracos de forma específica (ou seja, buracos de corrosão) deixados na face do cristal devido à corrosão após a formação do cristal. As figuras de corrosão são controladas pela disposição das partículas elementares na face do cristal. Assim, as formas e orientações das figuras de corrosão variam entre diferentes minerais e formas individuais do mesmo cristal. Por exemplo, as figuras de corrosão em diferentes formas individuais de cristais de diamante variam; poços triangulares podem ser vistos em cristais octaédricos (Figura 2-1-33), poços quadrilaterais em faces cúbicas, poços quadrilaterais sobrepostos formam um padrão semelhante a uma grade, e padrões de linha ou padrões microscópicos semelhantes a discos podem ser vistos em dodecaedros rômbicos (Figura 2-1-34).

Figura 2-1-33 Pontos triangulares invertidos visíveis no cristal octaédrico de diamante

Figura 2-1-34 Textura com padrão linear visível em cristais dodecaédricos em forma de diamante
Somente as figuras de gravura na mesma face de cristal da mesma forma podem ser as mesmas, de modo que as figuras de gravura são freqüentemente usadas para identificar minerais e determinar se as faces de cristal pertencem à mesma forma única (Figura 2-1-35 a Figura 2-1-42).

Figura 2-1-35 Riscas em estilo de pavimento de madeira incrustado com cristais de fluorite

Figura 2-1-36 Gravura triangular natural em rubi (riscas horizontais comuns em rubis, linhas de crescimento paralelas à direção romboédrica, gravuras naturais em formas triangulares ou hexagonais)

Figura 2-1-37 Riscas longitudinais na superfície da turmalina

Figura 2-1-38 Riscas horizontais na superfície do cristal

Figura 2-1-39 Figuras de gravura na superfície do cristal

Figura 2-1-40 Estrias longitudinais superficiais do topázio

Figura 2-1-41 Imagem topográfica de um cristal de topázio

Figura 2-1-42 Figuras de gravura de espinélio
Secção II 47 Tipos de formas cristalinas
Existem 146 formas individuais diferentes em cristalografia, que podem ser classificadas em 47 formas geométricas com base nas suas formas geométricas quando existem independentemente. Estas formas geométricas são designadas da seguinte forma:
① Nomeado de acordo com as caraterísticas da forma da secção transversal, como prisma trigonal, prisma tetragonal, prisma hexagonal, bipirâmide romboédrica, etc.
② Nomeado de acordo com a forma da forma única, como cilindro, cone duplo, cubo, etc.
③ Nomeado de acordo com o número de faces geométricas, como face única, octaedro, etc.
④ Nomeados de acordo com a forma das faces geométricas, tais como romboedro, pentacontaedro, etc.
Em cristalografia, as formas simples são divididas em quatro categorias: formas gerais e formas especiais, formas fechadas e formas abertas, formas regulares e formas irregulares, formas canhotas e formas destras. Este capítulo abordará brevemente as formas fechadas e as formas abertas.
As formas fechadas referem-se àquelas cujas faces cristalinas podem encerrar um espaço fechado, divididas em três categorias principais: classes poliédricas, classes poliédricas enviesadas e classes bipiramidais, totalizando 30 tipos. Cada categoria tem classificações mais detalhadas; por exemplo, a classe poliédrica é subdividida em classe tetraédrica, classe octaédrica, classe cúbica, etc. (Figuras 2-1-43 a 2-1-48)

Figura 2-1-43 Classe de tetraedro
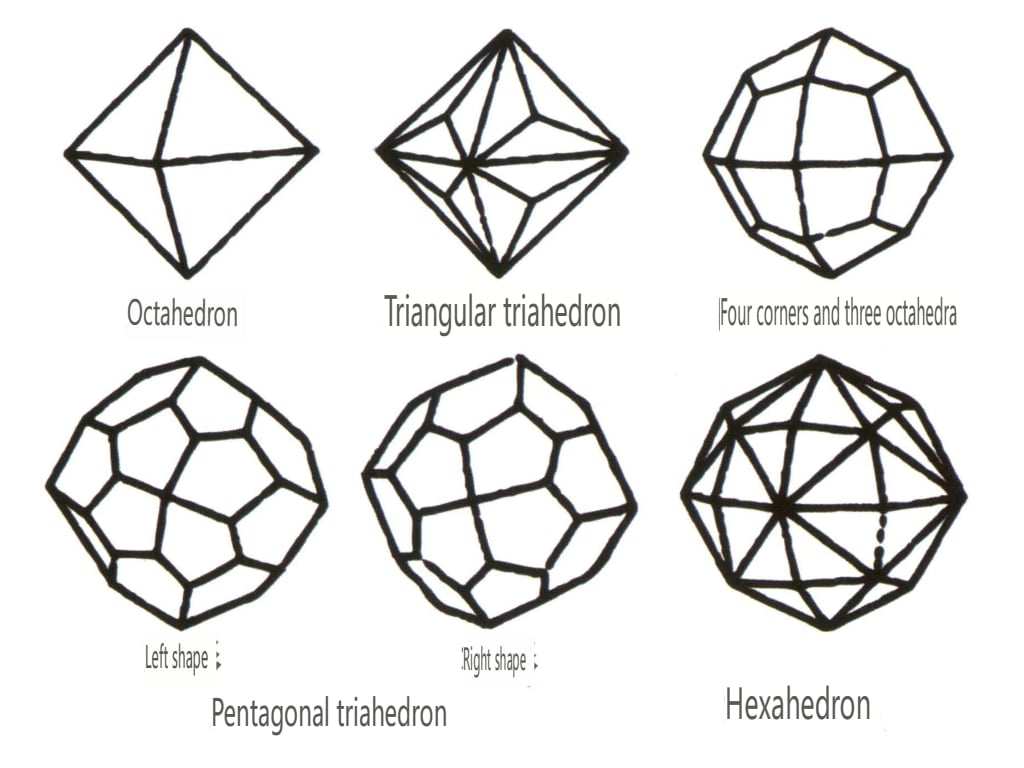
Figura 2-1-44 Classe 0ctaédrica
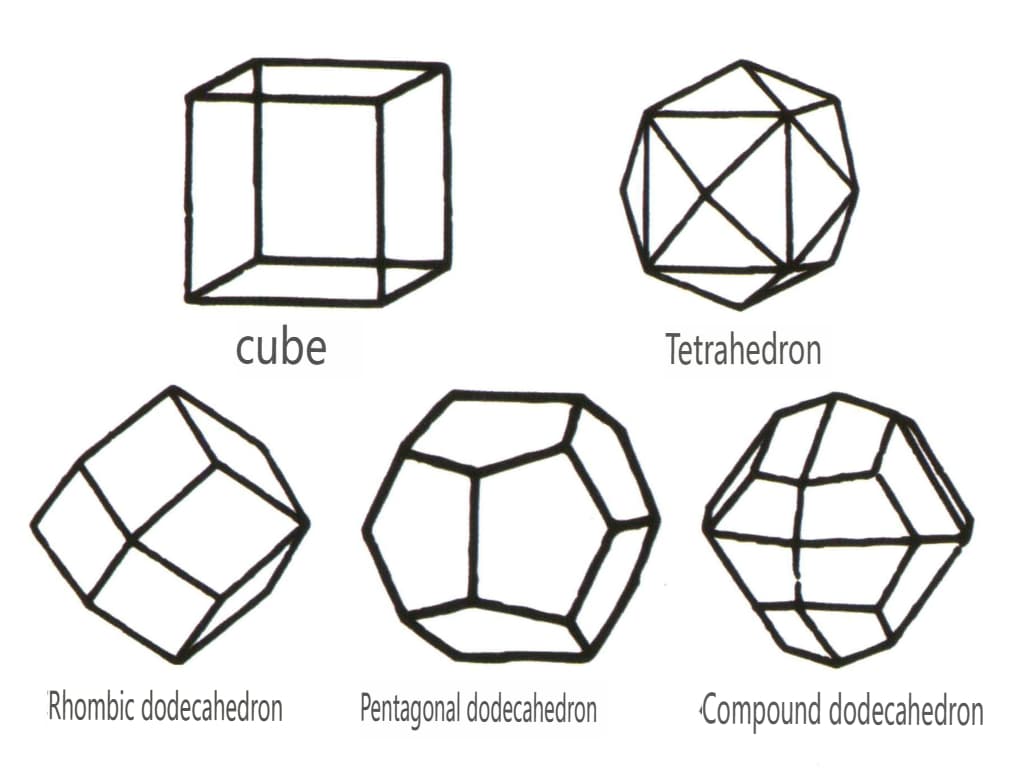
Figura 2-1-45 Classes cúbicas e dodecaédricas
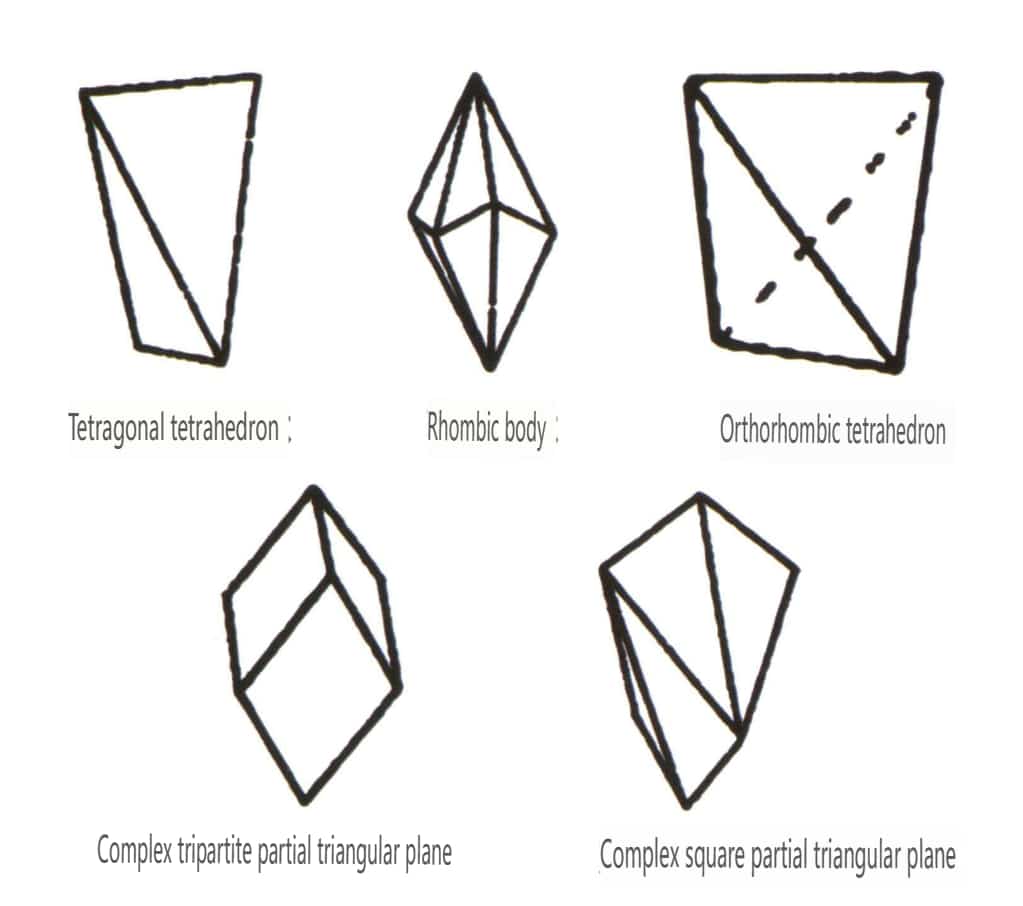
Figura 2-1-46 Outros tipos poliédricos
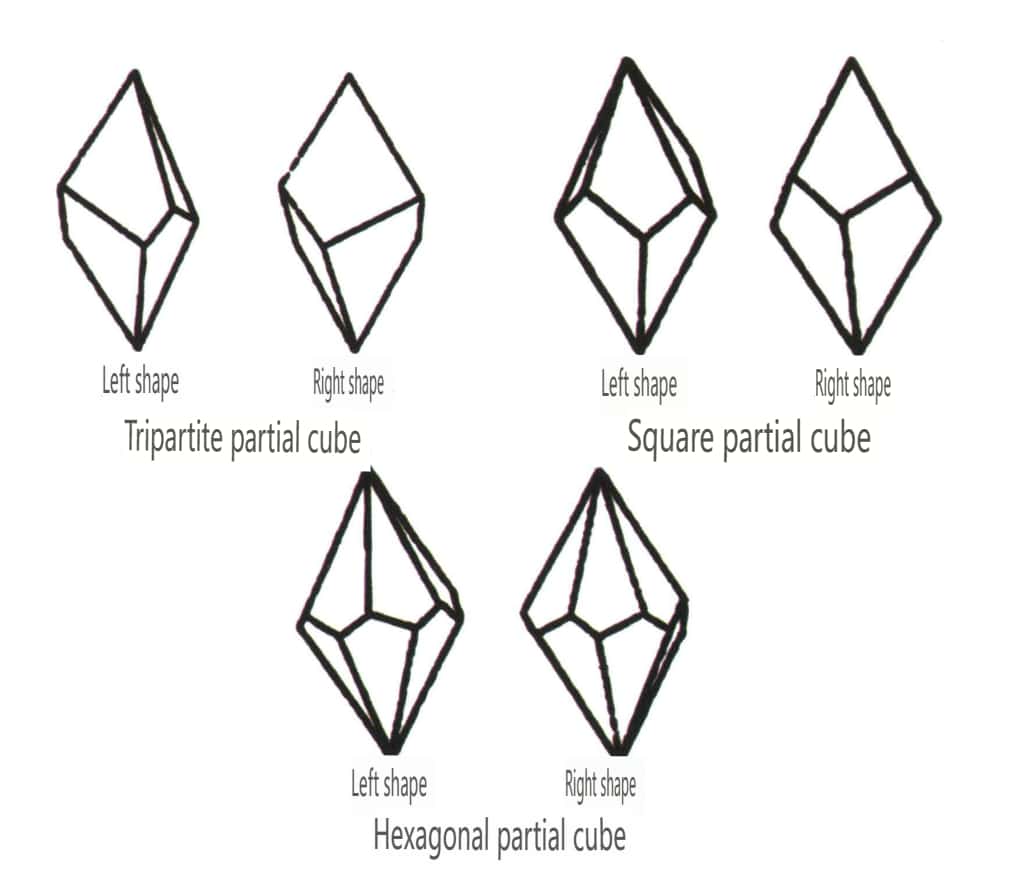
Figura 2-1-47 Forma combinada oblíqua Classe
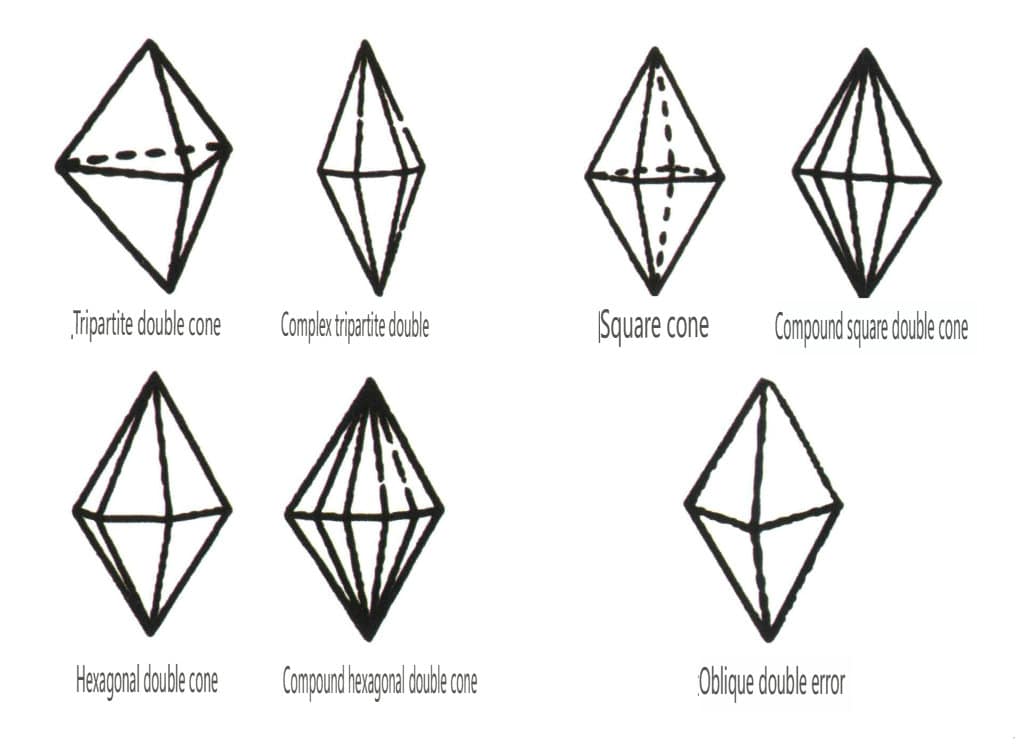
Figura 2-1-48 Classe piramidal dupla
As formas abertas referem-se àquelas cujas faces cristalinas não podem encerrar um espaço fechado, divididas em quatro categorias principais: face simples, face dupla, classes colunares e classes piramidais simples, totalizando 17 tipos (Figuras 2-1-49 e 2-1-51)
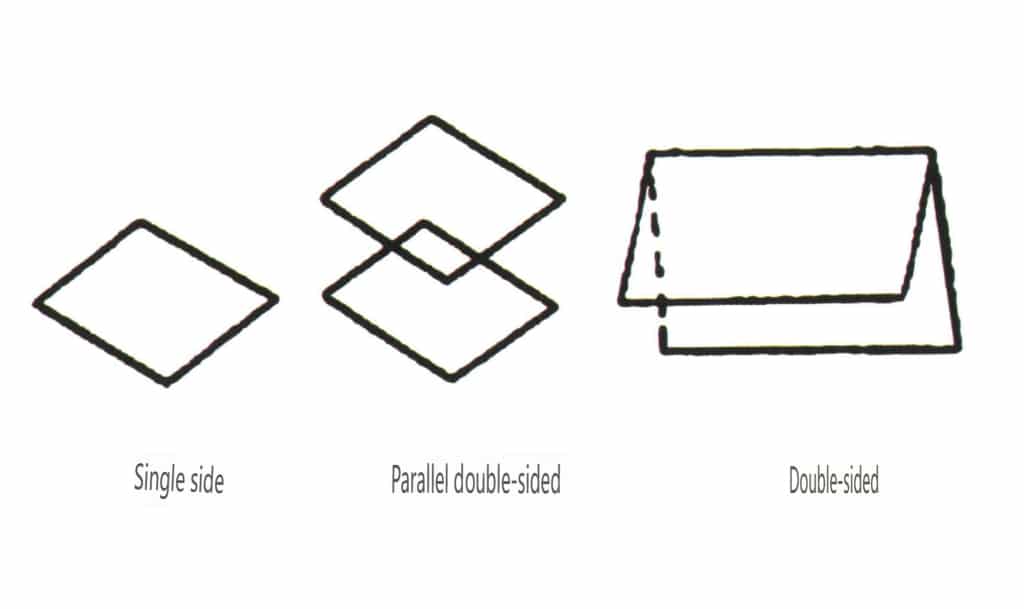
Figura 2-1-49 Face simples e face dupla
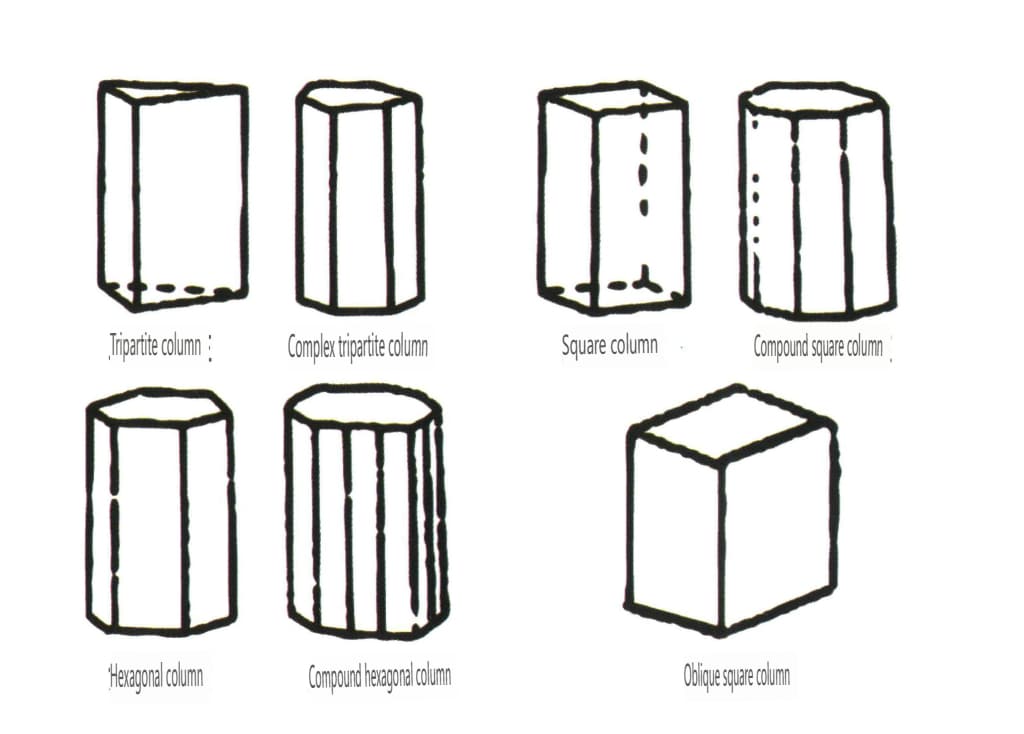
Figura 2-1-50 Colunas

Secção III Classificação dos cristais
1. Simetria dos cristais
A simetria é um conceito abstrato envolvido no estudo de cristais reais e materiais de pedras preciosas não processados. Descreve a repetição exibida quando a estrutura cristalina é referenciada por uma direção ou plano que a atravessa. Esta é a base para a classificação dos cristais.
A simetria de um cristal pode ser entendida, de uma perspetiva microscópica, como um método para descrever a repetitividade da estrutura cristalina e, de uma perspetiva macroscópica, como a repetição de duas ou mais faces geométricas que têm a mesma forma e tamanho, mas que podem diferir em direção, de acordo com determinadas regras. Este padrão de repetição pode ser descrito utilizando eixos de simetria e planos de simetria, sendo cada eixo de simetria ou plano de simetria referido como um elemento de simetria. Ao observar ou inferir a simetria de um objeto, esta ação é descrita como a realização de operações sobre a simetria.
2. Elementos de simetria dos cristais
Em cristalografia, existem quatro elementos de simetria: eixo de simetria, plano de simetria, eixos de simetria de rotoinversão e centro de simetria. Este trabalho envolverá os dois elementos de simetria: eixo de simetria e plano de simetria.
2.1 Eixo de simetria
(1) O conceito de eixo de simetria e a sua notação.
O eixo de simetria é uma linha reta imaginária que indica o número de vezes que o nível de base (Figuras 2-2-1 a Figura 2-2-2) aparece na mesma posição quando a estrutura da grelha é rodada 360° em torno desta linha imaginária. Este número só pode ser 2, 3, 4 ou 6 vezes em 4 casos. Também pode ser entendido como uma linha imaginária que passa pelo centro do corpo geométrico, rodando o corpo geométrico ao longo desta linha 360°. Suponhamos que a forma do corpo geométrico depois de rodar um certo ângulo é consistente com a forma do corpo geométrico nos zero graus iniciais. Nesse caso, esta linha imaginária é designada por eixo de simetria.
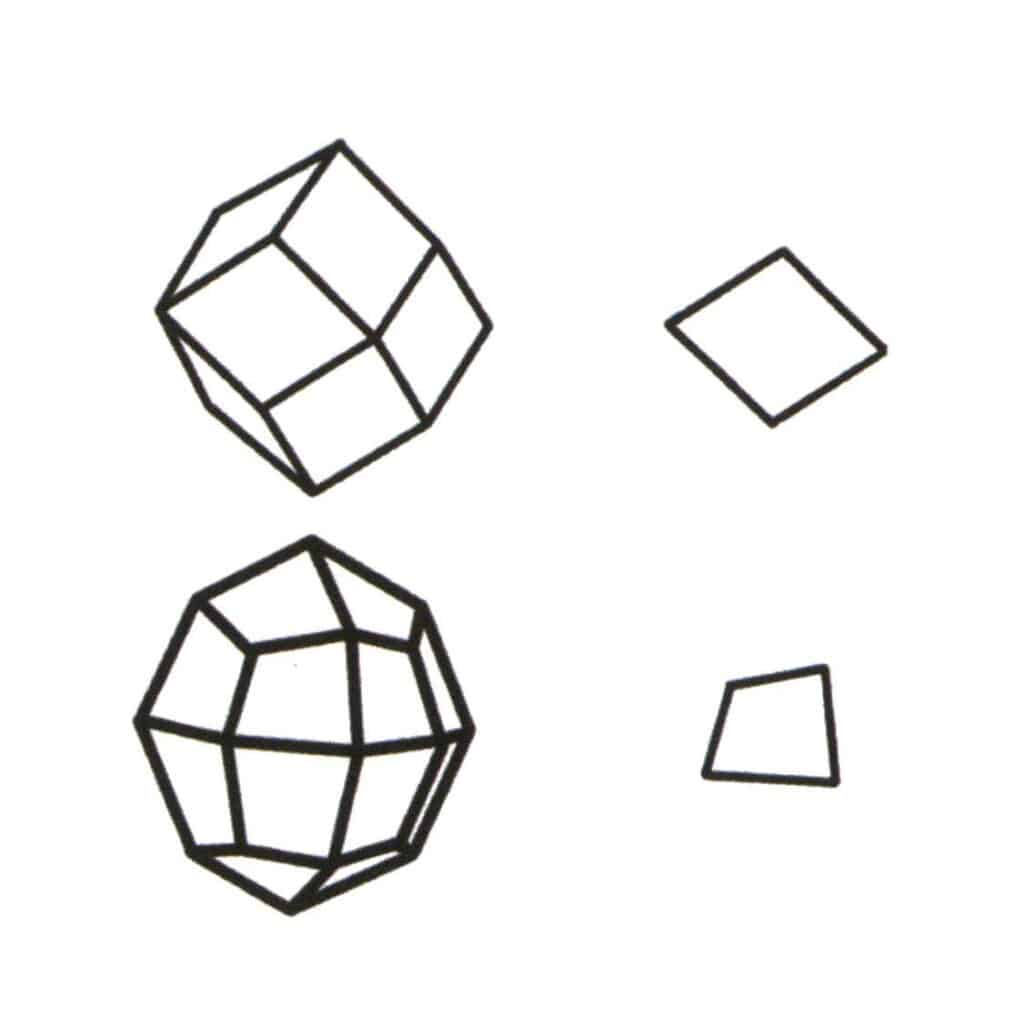
Figura 2-2-1 Seleção do nível de base para o formulário único.
O nível de base de uma forma simples é o plano de repetição mais pequeno que compõe o simplex. O canto superior esquerdo da figura mostra um dodecaedro rômbico, que é uma forma fechada composta por um tipo de face. O plano de repetição mais pequeno é o losango mostrado no canto superior direito, pelo que o nível de base do dodecaedro rômbico é o losango. O canto inferior esquerdo da figura mostra um octaedro quadrilátero, que é uma forma fechada composta por um tipo de face. O plano de repetição mais pequeno é o quadrilátero representado no canto inferior direito, pelo que o nível de base do octaedro quadrilátero é o quadrilátero.
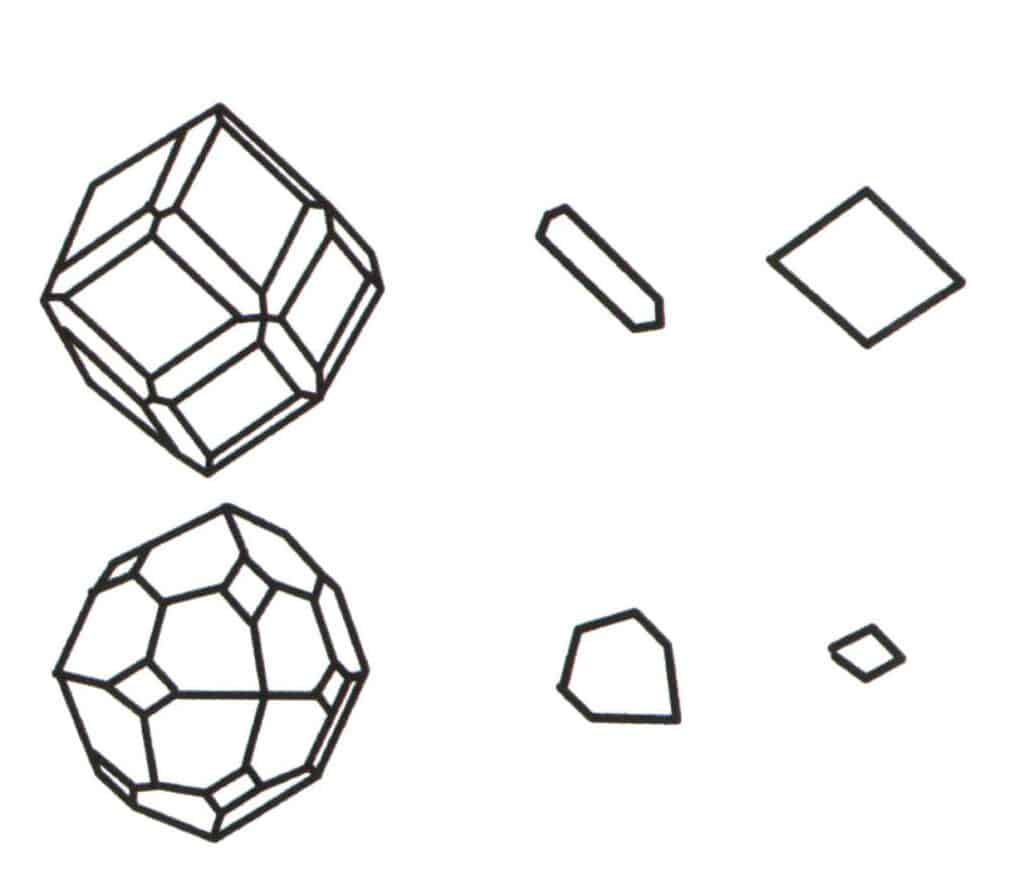
Figura 2-2-2 Seleção do nível de base para o polítopo.
A agregação de múltiplas formas simples forma uma forma combinada, e a escolha do nível de base para a forma combinada é o julgamento da forma simples que se combina para formar a forma combinada. A primeira coluna a contar da esquerda na figura representa uma forma combinada (formada pela agregação de formas simples de um dodecaedro e de um tetraedro), e este corpo geométrico é uma figura fechada composta por dois tipos de faces. O hexágono representa o plano mínimo de repetição na segunda coluna e o losango à direita na terceira coluna. Assim, o nível de base da forma combinada da primeira coluna é o hexágono ou o losango. Ao calcular o eixo de simetria, apenas uma forma pode ser selecionada como nível de base para o registo da simetria.
O eixo de simetria é representado pela letra L maiúscula, com a ordem do eixo n escrito no canto superior direito de L, escrito como Lⁿ. Por exemplo, um eixo de 2 dobras é representado por L², um eixo de 3 dobras por L³, um eixo de 4 dobras por L⁴ e um eixo de 6 dobras por L⁶. L⁶, L⁴, L³ é habitualmente referido como um eixo de ordem superior.
Os cristais podem ter eixos de simetria em diferentes direcções, e o número desses eixos de simetria não coincidentes é convencionalmente escrito à esquerda de L. Por exemplo, seis eixos secundários são representados como 6L² (Figura 2-2-3 a Figura 2-2-9), três eixos terciários são representados como 3L³ (Figura 2-2-10 a Figura 2-2-14), quatro eixos terciários são representados como 4L³ (Figura 2-2-15 a Figura 2-2-18), e um eixo hexagonal é representado como L⁶ (Figura 2-2-19).
Quando um cristal tem múltiplos eixos de simetria, o método registado organiza-os da esquerda para a direita por ordem decrescente, com o número de eixos de simetria escrito no lado esquerdo do eixo correspondente, por exemplo, L⁶6L², 3L⁴4L³6L².
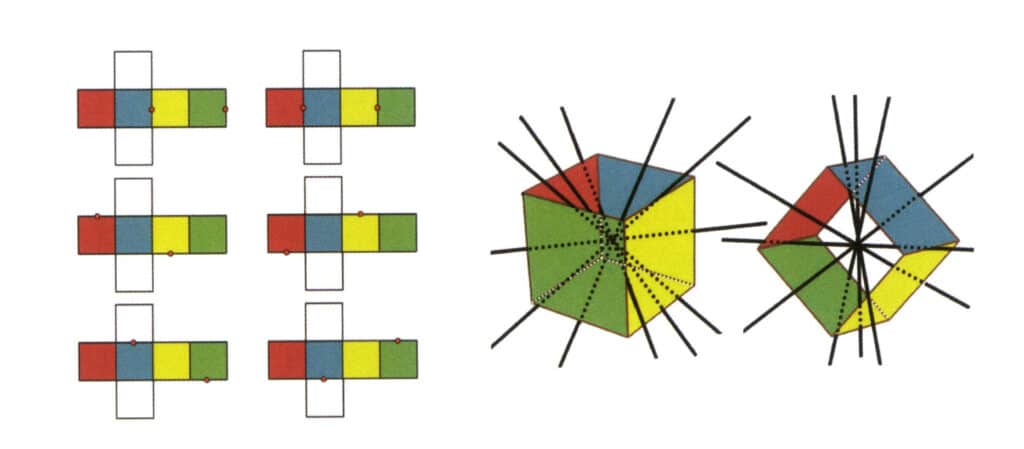
Figura 2-2-3 Eixo secundário do cubo
O lado esquerdo da figura mostra a vista desdobrada de um cubo, com pontos vermelhos indicando os pontos de intersecção da linha imaginária com as arestas. O lado direito da figura mostra um cubo fechado, onde o eixo secundário pode aparecer no ponto médio de linhas de aresta paralelas, no ponto médio de faces rectangulares paralelas, ou nos pontos de intersecção de três ou mais faces paralelas que se assemelham a um retângulo. ou mais faces paralelas que se assemelham a um retângulo.
Copywrite @ Sobling.Jewelry - Fabricante de jóias personalizadas, fábrica de jóias OEM e ODM
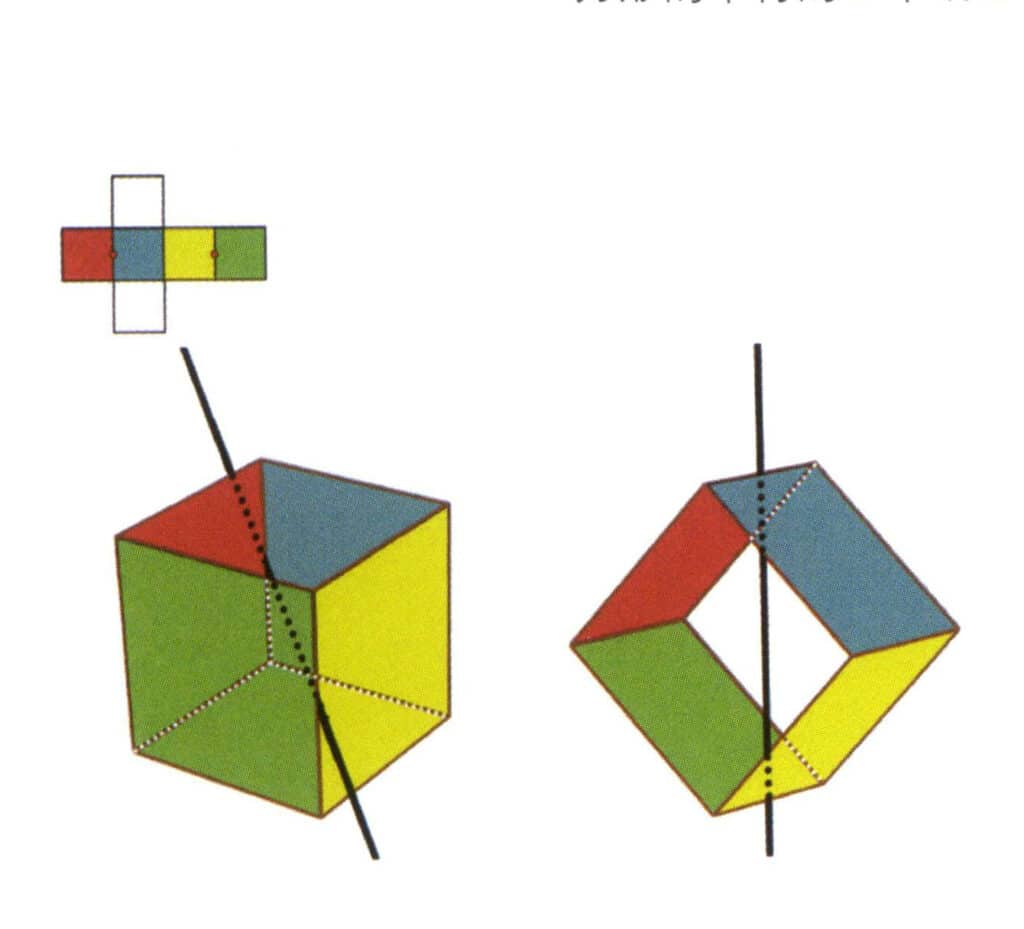
Figura 2-2-4 O primeiro eixo secundário do cubo
Selecione o ponto médio das rectas paralelas, como mostra a figura. Imagine uma reta a passar pelos pontos médios destas duas arestas, rodando o cubo em 360°. Os níveis de base com cores diferentes mas com a mesma forma repetir-se-ão duas vezes na mesma posição (as faces vermelha e azul, as faces amarela e verde, as duas faces incolores e três conjuntos de faces repetidas. Embora apareçam três conjuntos de faces repetidas, uma vez que a linha imaginária não mudou de posição nem de ângulo, o eixo secundário é registado apenas uma vez). Esta linha imaginária é registada como eixo secundário.
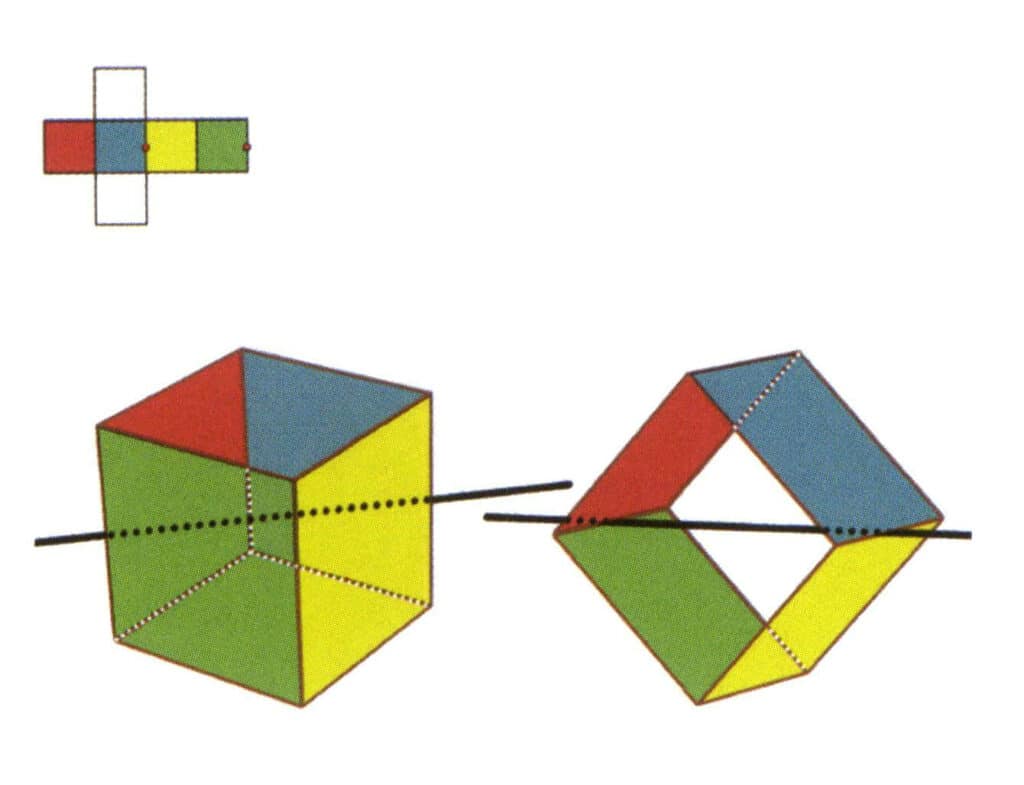
Figura 2-2-5 O segundo eixo secundário do cubo
Selecione o ponto médio das rectas paralelas, como mostra a figura. Imagine uma reta a passar pelos pontos médios destas duas arestas, rodando o cubo em 360°. Os níveis de base com cores diferentes mas com a mesma forma repetir-se-ão duas vezes na mesma posição (as faces vermelha e verde, as faces amarela e azul, as duas faces incolores e três conjuntos de faces repetidas). Esta linha imaginária é registada como o segundo eixo secundário.
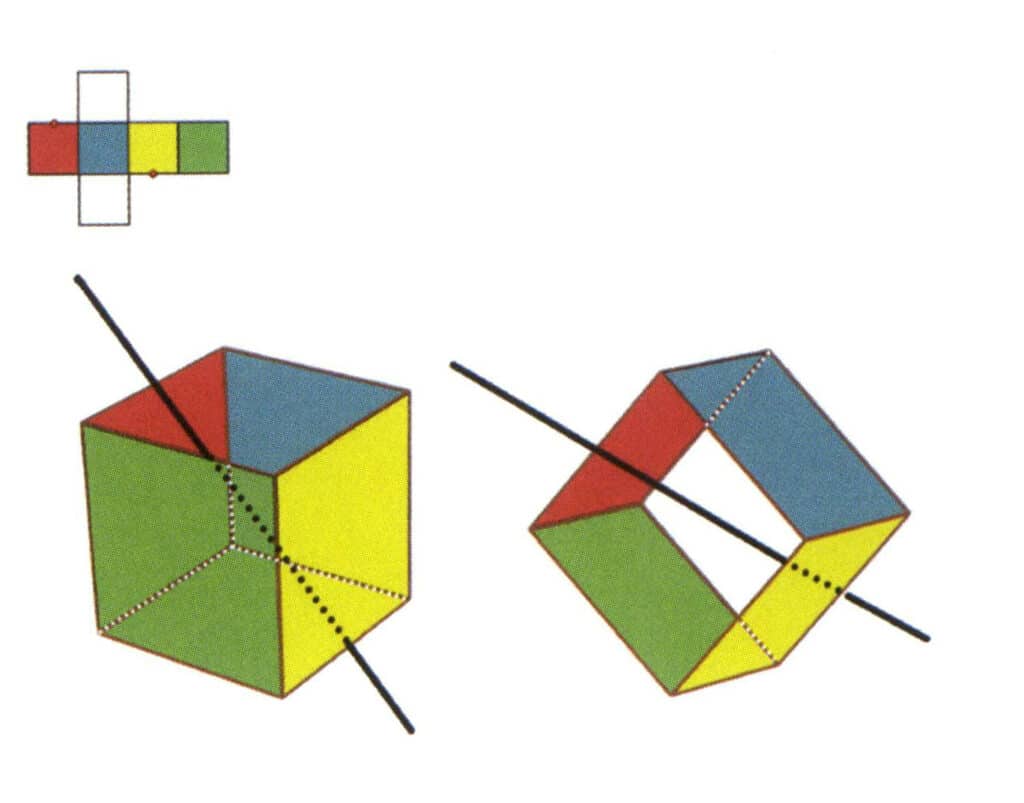
Figura 2-2-6 O terceiro eixo secundário do cubo.
Selecione o ponto médio das rectas paralelas, como mostra a figura. Imagine uma reta a passar pelos pontos médios destas duas arestas, rodando o cubo em 360°. Os níveis de base com cores diferentes, mas com a mesma forma, repetir-se-ão duas vezes na mesma posição (as faces vermelha e incolor, as faces verde e azul, as faces incolor e amarela, três conjuntos de faces repetidas). Esta linha imaginária é registada como o terceiro eixo secundário
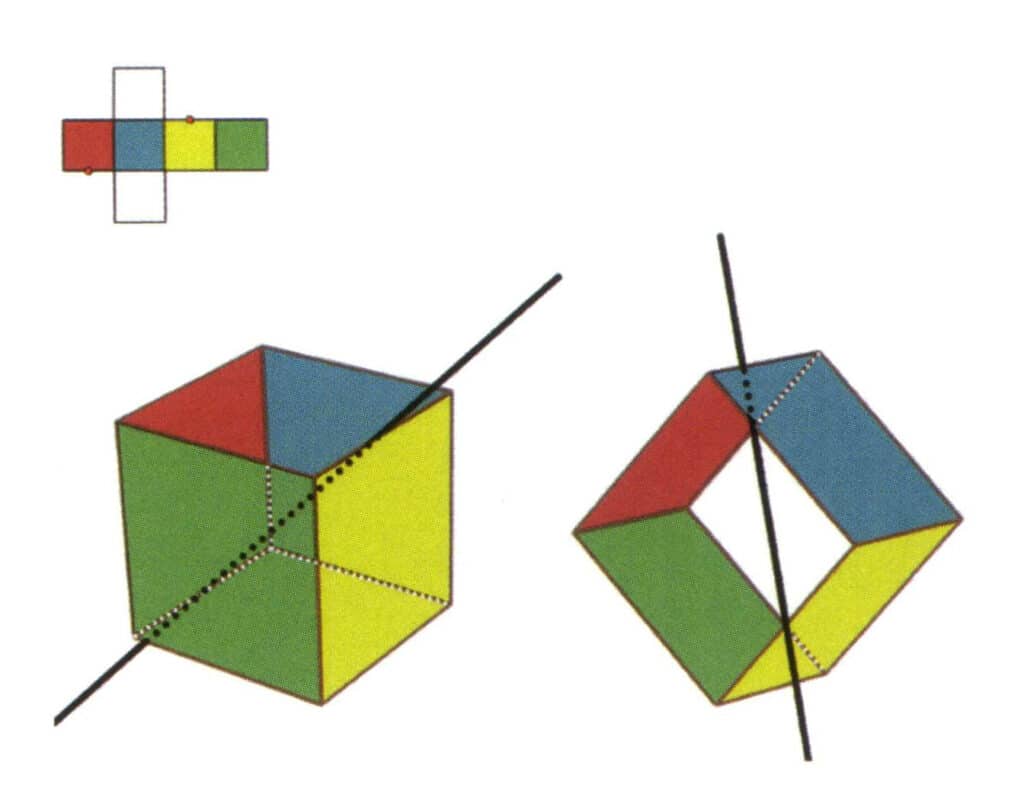
Figura 2-2-7 O quarto eixo secundário do cubo
Selecione o ponto médio das linhas paralelas, como mostra a figura, imagine uma reta a passar pelos pontos médios destas duas arestas e rode o cubo 360°; os planos de referência de cores diferentes, mas de forma idêntica, repetir-se-ão duas vezes na mesma posição (as faces vermelha e incolor, verde e azul, incolor e amarela, três conjuntos de faces repetidas), esta reta imaginária é registada como o quarto eixo secundário.
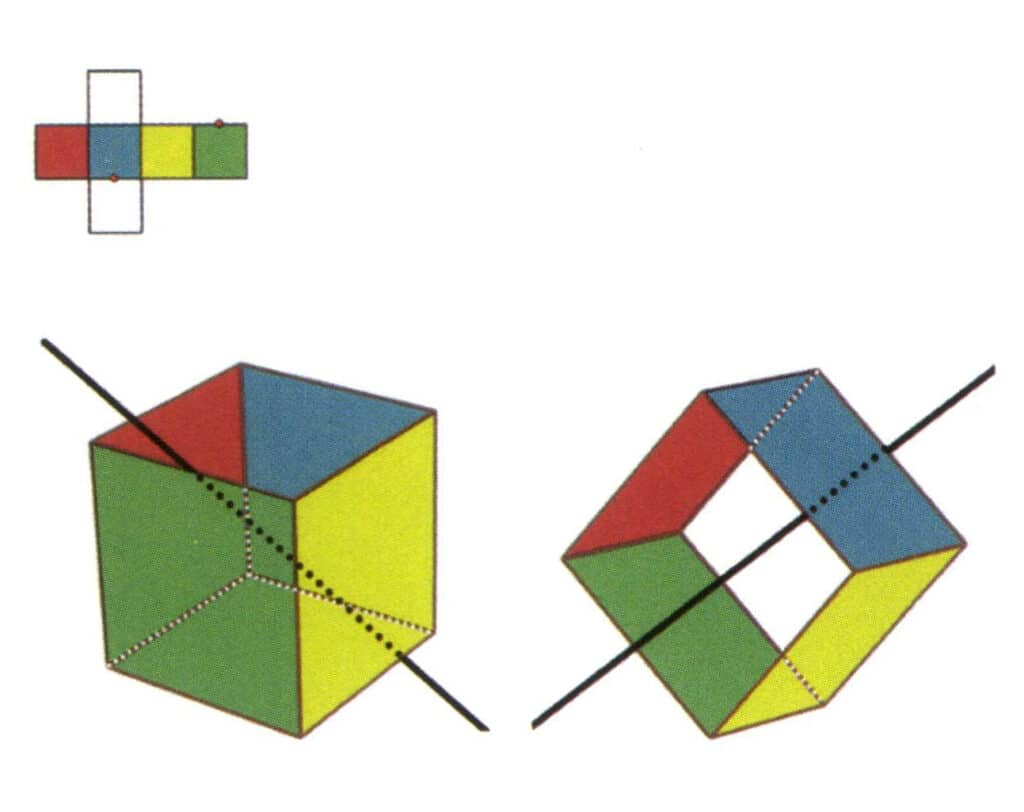
Figura 2-2-8 O quinto eixo secundário do cubo.
Selecione os pontos médios das linhas paralelas, como mostra a figura, imagine uma linha reta a passar pelos pontos médios destas duas arestas, rode o cubo 360°, os planos de referência de cores diferentes mas com formas idênticas irão repetir-se na mesma posição duas vezes (faces vermelhas e incolores, faces verdes e azuis, faces incolores e amarelas, três conjuntos de faces repetidas), esta linha reta imaginada é registada como o quinto eixo secundário.
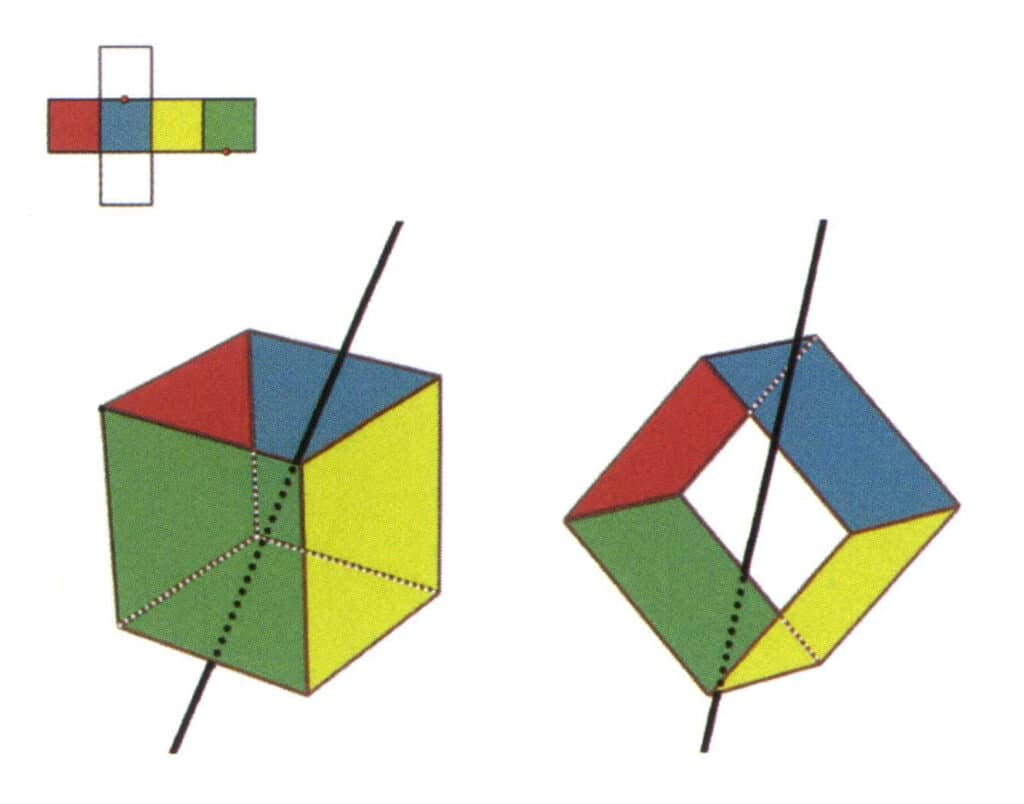
Figura 2-2-9 O sexto eixo secundário do cubo
Selecione o ponto médio das rectas paralelas, como mostra a figura. Imagine uma linha reta a passar pelos pontos médios destas duas arestas, fazendo rodar o cubo 360°. Os níveis da base, de cores diferentes mas de forma idêntica, repetir-se-ão duas vezes na mesma posição (faces verdes e incolores, faces vermelhas e amarelas, faces incolores e azuis, três conjuntos de faces repetidas). Esta linha imaginária é registada como o sexto eixo secundário.
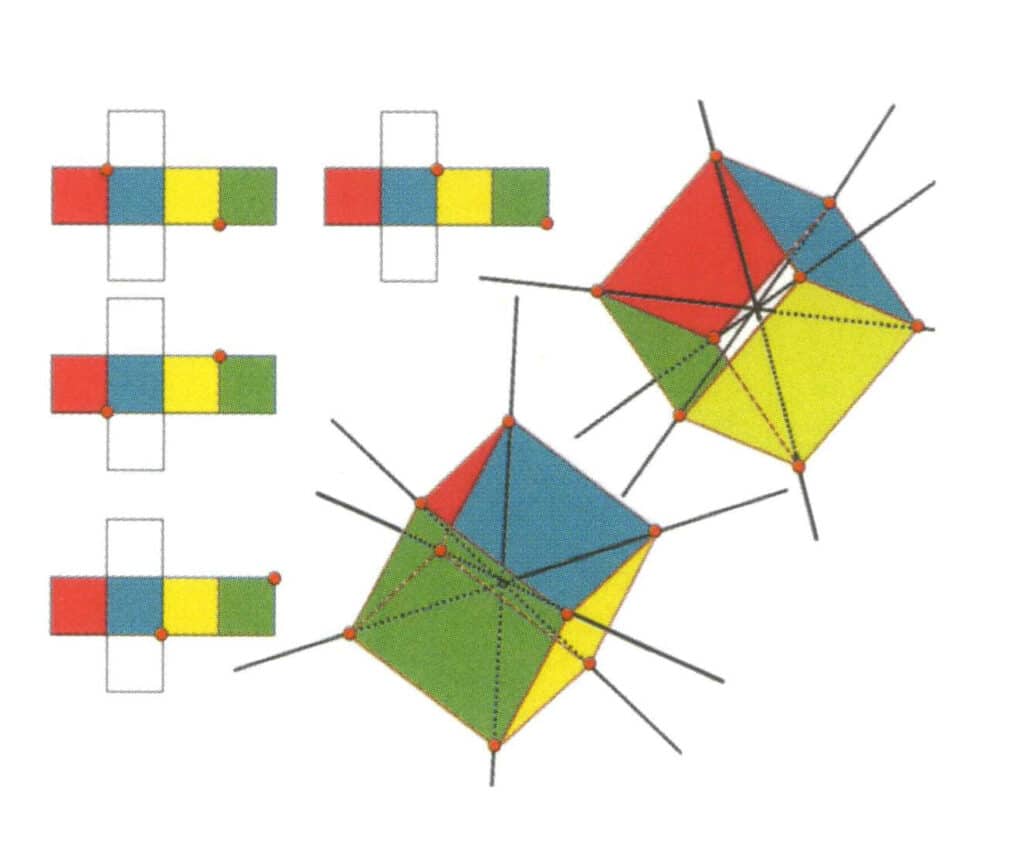
Figura 2-2-10 O eixo terciário do cubo
O lado esquerdo da figura mostra a vista desdobrada do cubo, com o ponto vermelho a indicar o ponto de intersecção da reta imaginária com a linha de aresta. O lado direito da figura mostra o cubo fechado; os pontos vermelhos indicam a intersecção da reta imaginária com as arestas. O eixo terciário pode aparecer no ponto médio das faces de um triângulo equilátero paralelo, na intersecção de três ou mais faces paralelas que se assemelham a um triângulo equilátero.
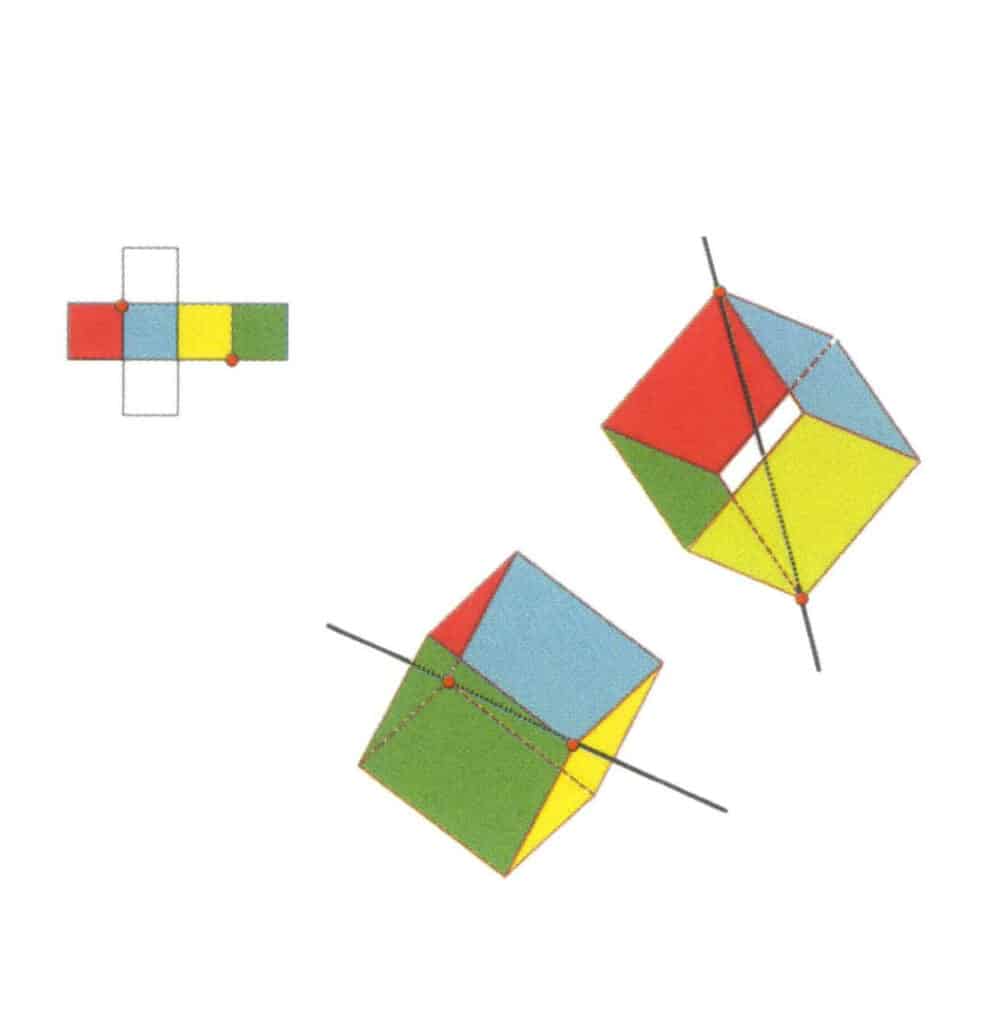
Figura 2-2-11 O primeiro eixo terciário do cubo.
Selecione os pontos de intersecção das três faces, como mostra a figura, imagine uma linha reta a passar pelos pontos médios destas duas arestas, rode o cubo 360°, os planos de referência de cores diferentes, mas de forma idêntica, repetir-se-ão na mesma posição três vezes (faces vermelha, incolor e azul, faces verde, incolor e amarela, dois conjuntos de faces repetidas), esta linha reta imaginada é registada como o primeiro eixo terciário
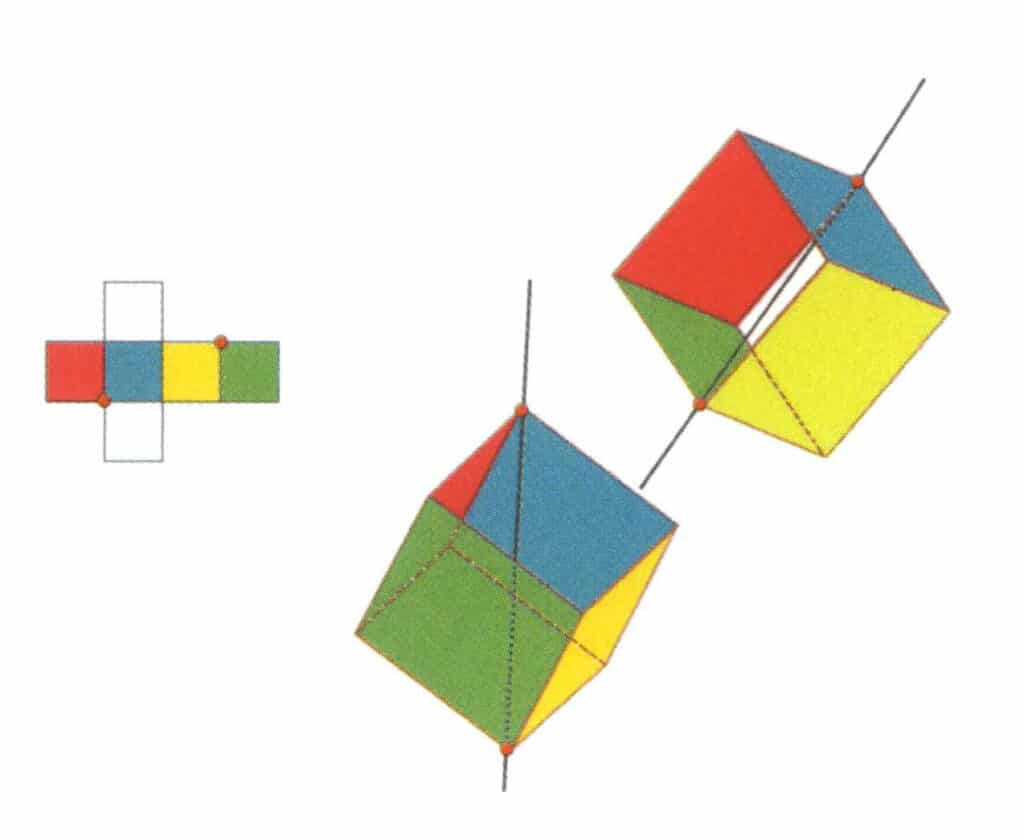
Figura 2-2-12 O segundo eixo terciário do cubo.
Selecione os pontos de intersecção das três faces, como mostra a figura. Imagine uma linha reta a passar pelos pontos médios destas duas arestas, fazendo rodar o cubo 360°. Os níveis de base, de cores diferentes mas de forma idêntica, repetir-se-ão três vezes na mesma posição (faces vermelha, incolor e azul; faces verde, incolor e amarela, dois conjuntos de faces repetidas). Esta linha imaginária é registada como o segundo eixo terciário.
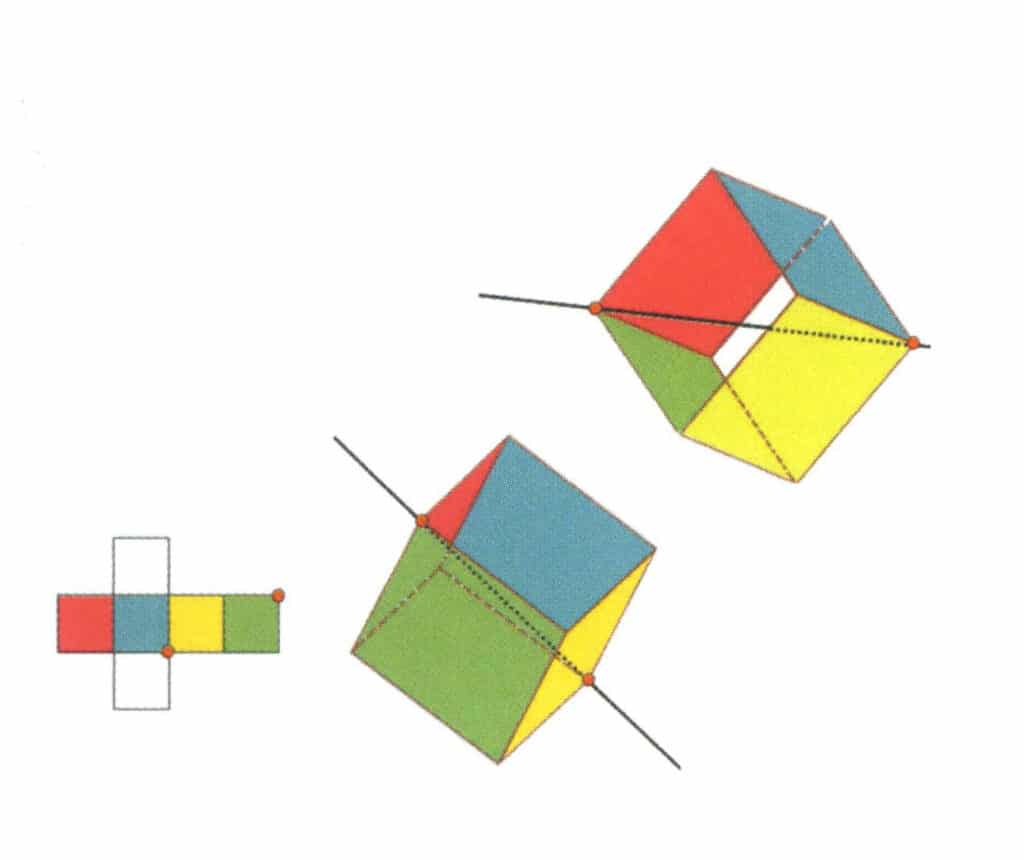
Figura 2-2-13 O terceiro eixo terciário do cubo
Selecione os pontos de intersecção das três faces, como mostra a figura. Imagine uma linha reta a passar pelos pontos médios destas duas arestas, fazendo rodar o cubo 360°. Os níveis de base, de cores diferentes mas de forma idêntica, repetir-se-ão três vezes na mesma posição (faces vermelha, incolor e verde; faces azul, incolor e amarela, dois conjuntos de faces repetidas). Esta linha imaginária é registada como o terceiro eixo terciário.
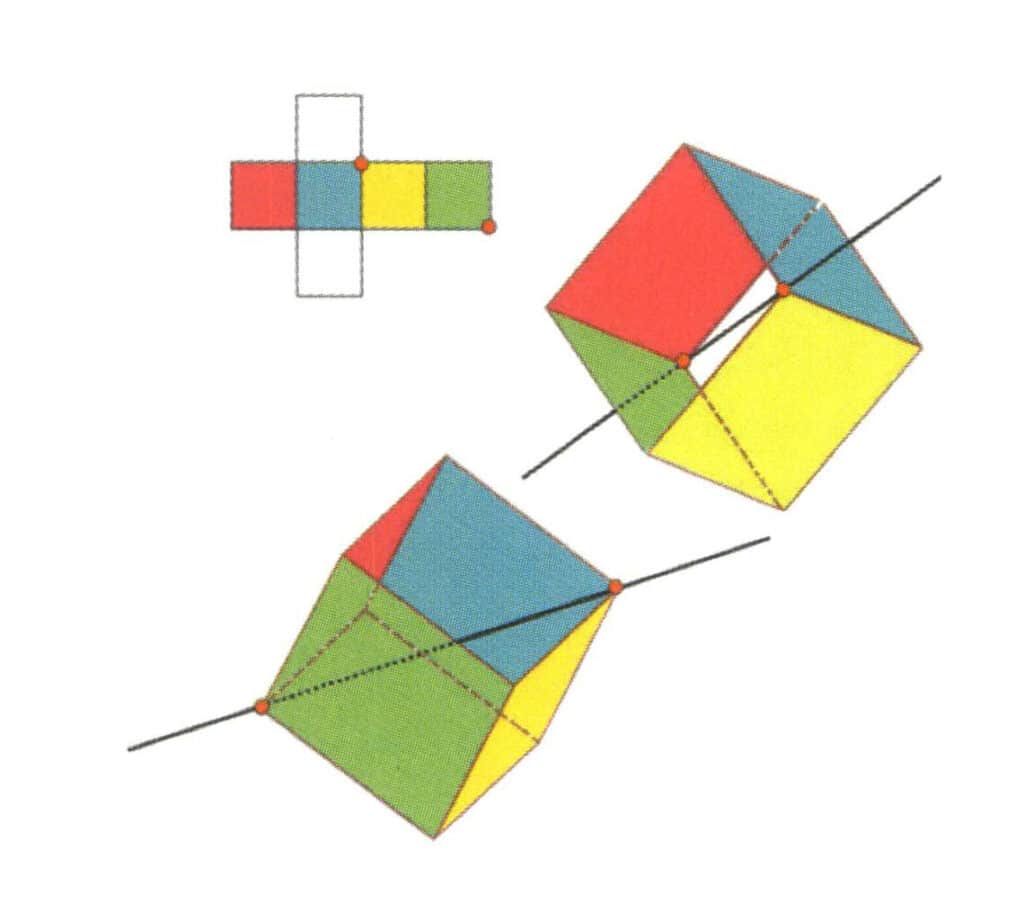
Figura 2-2-14 Quarto eixo cúbico do cubo.
Selecione a intersecção das três faces, como mostra a figura, assumindo que existe uma linha reta que passa pelo ponto médio das duas arestas, rode o cubo 360°, cores diferentes mas a mesma forma, o nível de base será o mesmo. Repita a posição três vezes (faces vermelha, incolor, verde, azul, incolor e amarela, dois conjuntos de faces repetidas). Esta linha imaginária é registada como o quarto eixo cúbico.
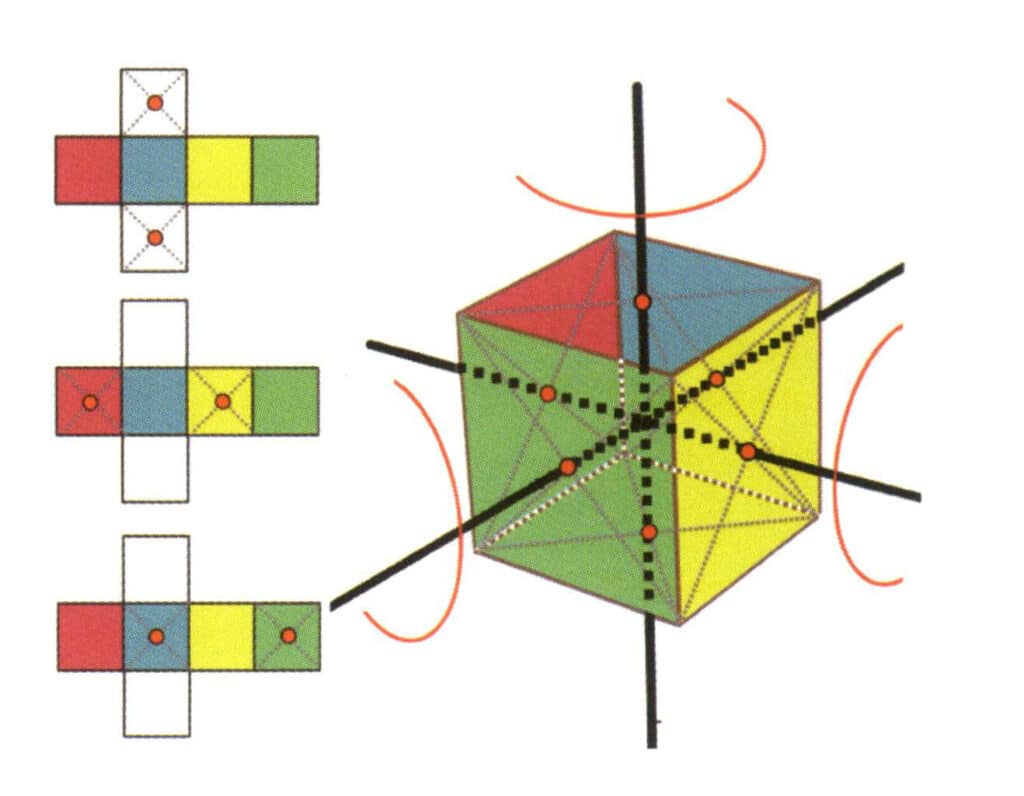
Figura 2-2-15 Quarto eixo do cubo
O lado esquerdo da figura mostra a vista desdobrada do cubo, com os pontos vermelhos a indicar os pontos de intersecção da linha imaginária com as arestas. O lado direito da figura mostra um cubo fechado, com os pontos vermelhos a indicar os pontos de intersecção da linha imaginária com o plano. O quarto eixo pode aparecer no ponto médio de faces paralelas de um quadrado, na intersecção de três ou mais faces paralelas que se assemelham a um quadrado.
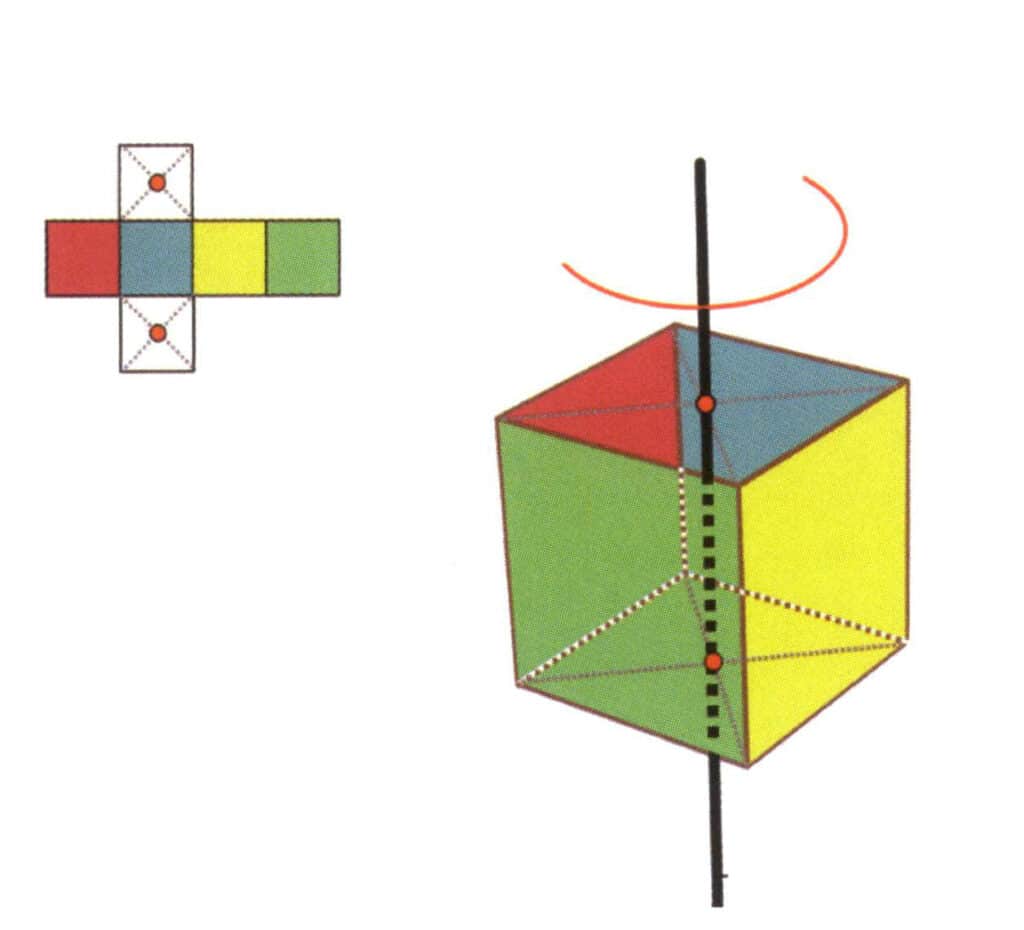
Figura 2-2-16 O primeiro eixo quártico do cubo
Escolha os pontos médios dos planos apresentados na figura, assuma que existe uma reta que passa pelos pontos médios dos dois planos e rode o cubo 360°. As faces de cores diferentes, mas com a mesma forma, da base do cubo repetem-se na mesma posição quatro vezes (faces vermelha, azul, verde e amarela), e esta hipotética reta é registada como uma axial quádrupla.
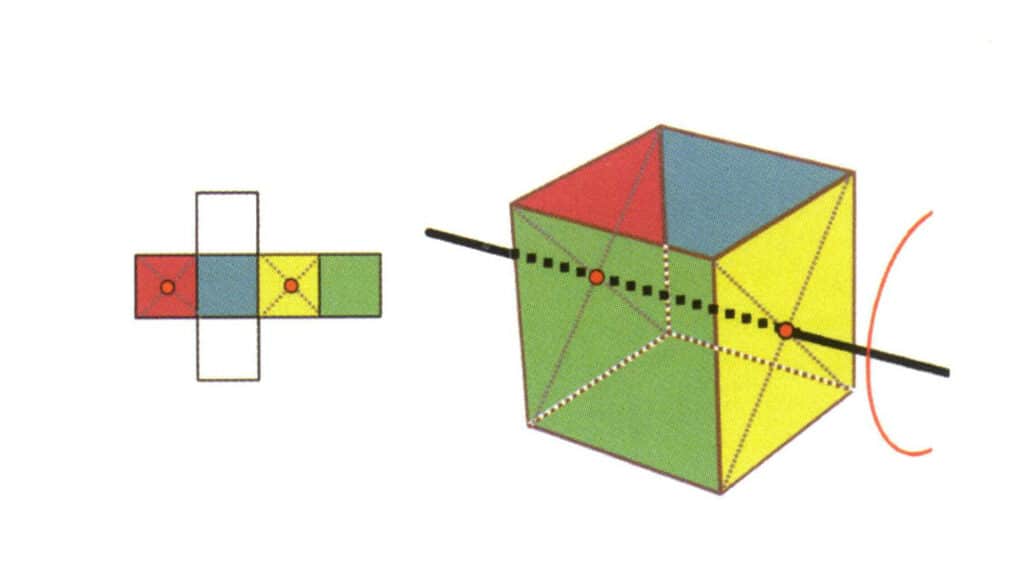
Figura 2-2-17 O segundo eixo quártico do cubo
Selecione o ponto médio do plano como mostra a figura, imagine uma linha reta a atravessar o cubo e rode o cubo 360°; a superfície do nível de base de cores diferentes mas com a mesma forma será repetida quatro vezes na mesma posição (incolor, face azul em cima, incolor, face verde em baixo), e esta linha imaginária será registada como o segundo eixo quádruplo.
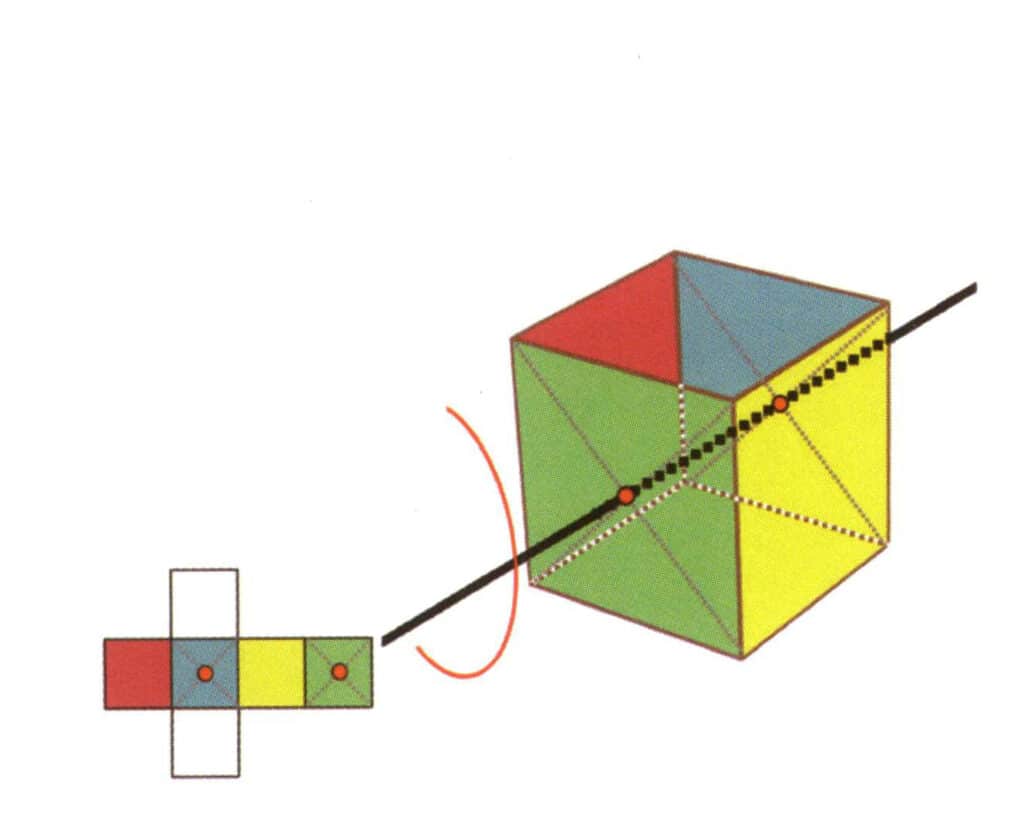
Figura 2-2-18 Terceiro eixo quártico do cubo
Selecione o ponto médio do plano, como mostra a figura, imagine uma linha reta a atravessar o cubo e rode o cubo 360°. O nível de base de cores diferentes mas com a mesma forma será repetido quatro vezes na mesma posição (incolor, face vermelha em cima, incolor, face amarela em baixo), e esta linha imaginária será registada como o terceiro, quarto eixo
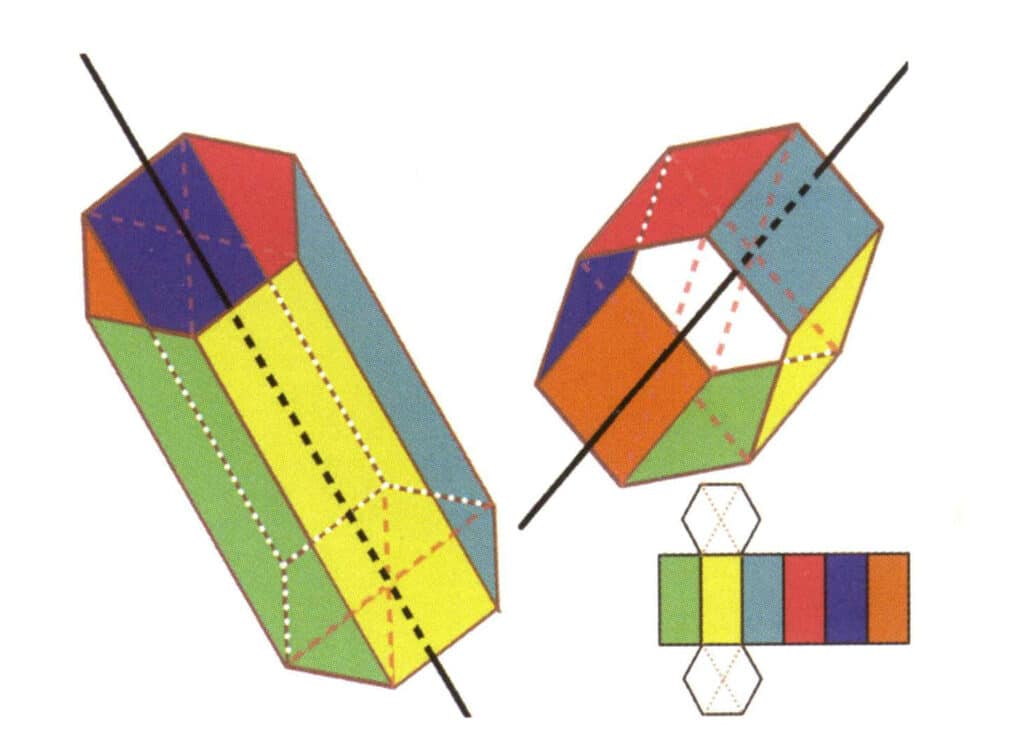
Figura 2-2-19 Seis eixos de um prisma hexagonal
As linhas pretas à esquerda e no canto superior direito representam os seis eixos do prisma hexagonal. A parte inferior direita é uma expansão do prisma hexagonal O eixo sextante pode aparecer no ponto médio das faces de um hexágono paralelo ou na intersecção das seis faces de um hexágono.
(2) Considerações para encontrar o eixo de simetria.
① Existem cinco tipos de posições para o eixo de simetria.
O ponto médio de duas arestas paralelas, como a posição do eixo secundário de um cubo.
O ponto médio de dois planos paralelos, como a posição do eixo quártico de um cubo.
Entre dois vértices (os pontos de intersecção de várias faces), como a posição do eixo terciário de um cubo.
O ponto médio entre um vértice e um plano paralelo, como a posição do eixo terciário de um tetraedro.
O ponto médio da linha de aresta e o ponto médio do plano paralelo, como a posição do eixo secundário de um prisma triangular.
② A seleção do eixo de simetria na mesma direção segue o princípio do número mais baixo. Por exemplo, de acordo com o princípio do menor número, se numa direção se encontrarem seis eixos de simetria e três eixos de simetria, será finalmente registado como L³. Os eixos de simetria em diferentes direcções devem ser registados de acordo com o número encontrado.
É de notar que, com exceção do eixo de simetria sêxtuplo e do eixo de simetria quádruplo, que não podem aparecer simultaneamente, e que só pode aparecer um eixo sêxtuplo, os outros eixos de simetria podem coexistir sob várias formas ou em múltiplas instâncias.
③ O nível de base deve ser selecionado como o plano unitário mais pequeno; dois ou mais planos que se intersectem não podem ser selecionados como nível de base. Caso contrário, isso afectará a precisão do julgamento do eixo de simetria.
④ Ao registar o número de eixos de simetria, é essencial determinar o número de vezes que a mesma forma e tamanho do plano se repete na mesma posição.
⑤ Se houver um eixo secundário de simetria vertical Lⁿ(n = 3, 4 ou 6), deve haver n eixos secundários verticais a Lⁿ.
2.2 Plano de Simetria
(1) Conceito e método de registo do plano de Simetria
Um plano de simetria é um plano imaginário que, quando o cristal é cortado ao longo desse plano, permite que cada metade do cristal seja uma imagem espelhada da outra metade (Figura 2-2-20). Na mesma estrutura cristalina, esse plano pode aparecer no máximo 9 vezes (Figura 2-2-21), o que significa que pode ser bissectado de 9 maneiras diferentes, e as duas metades podem coincidir completamente. Naturalmente, nem todas as estruturas cristalinas têm planos de simetria.
A letra maiúscula P representa o plano de simetria. Alguns cristais têm múltiplos planos de simetria não coincidentes, e o número desses planos de simetria é convencionalmente escrito à esquerda de P; por exemplo, quatro planos de simetria são representados como 4P, e um plano de simetria é representado como P.
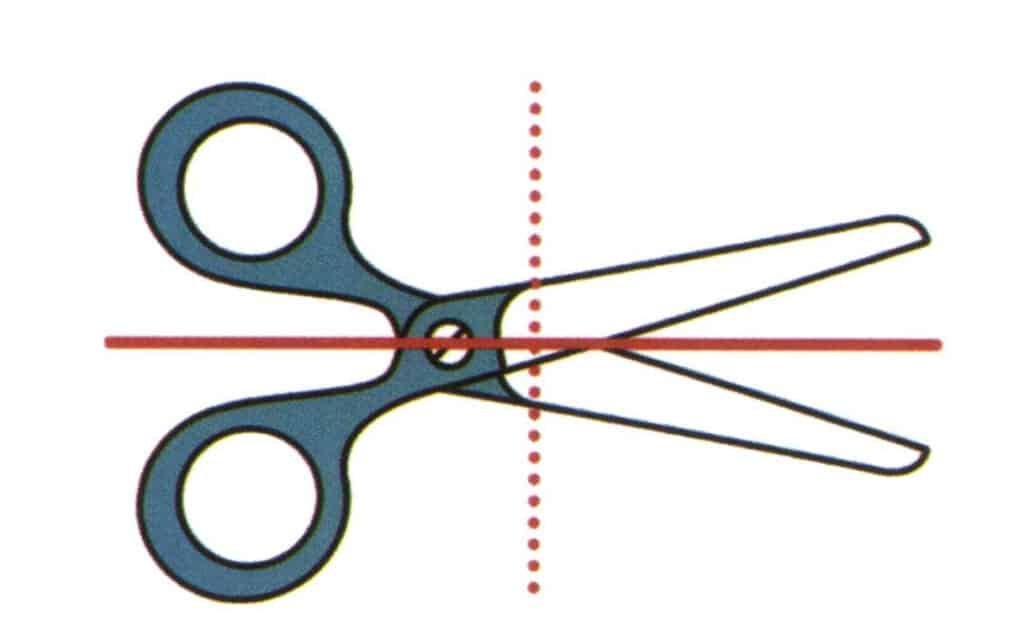
Figura 2-2-20 Imagine um plano vertical de papel e um plano que se estende ao longo da direção da linha sólida vermelha, que divide a tesoura em partes superior e inferior, e as partes superior e inferior são simétricas em espelho. Este plano imaginado é designado por plano de simetria. Imagine outro plano perpendicular à superfície do papel e que se estende ao longo da direção da linha tracejada vermelha, que divide a tesoura em partes esquerda e direita, mas as formas da tesoura do lado esquerdo e do lado direito não são simétricas.
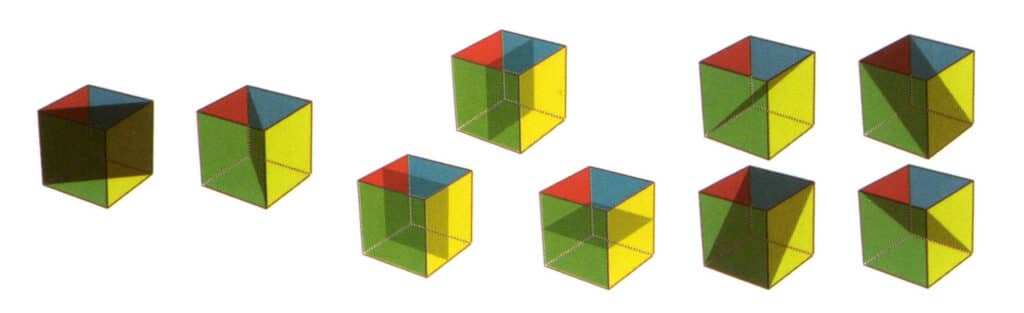
Figura 2-2-21 Nove planos de simetria de um cubo
(2) Dicas para encontrar Planos de simetria.
① O plano de simetria é frequentemente paralelo e coincidente com o eixo de simetria.
② O plano de simetria é um plano imaginário que divide a geometria cristalina, que é diferente do plano duplo paralelo em geometria.
③ Se um plano de simetria contém o eixo de simetria Lⁿ, então deve haver n planos de simetria que contêm Lⁿ.
(3) Ponto Grupo.
O grupo de pontos é a soma de todos os elementos de simetria de um cristal. A ordem de escrever o grupo de pontos é eixo de simetria + plano de simetria, por exemplo, 3L²3P (Figura 2-2-22). Se um cristal tem múltiplos eixos de simetria, é costume registá-los da esquerda para a direita, do eixo de maior ordem para o eixo de menor ordem, e a ordem dos planos de simetria, por exemplo, L⁴4L²5P (Figura 2-2-23). Existem 32 tipos de simetria nos cristais.
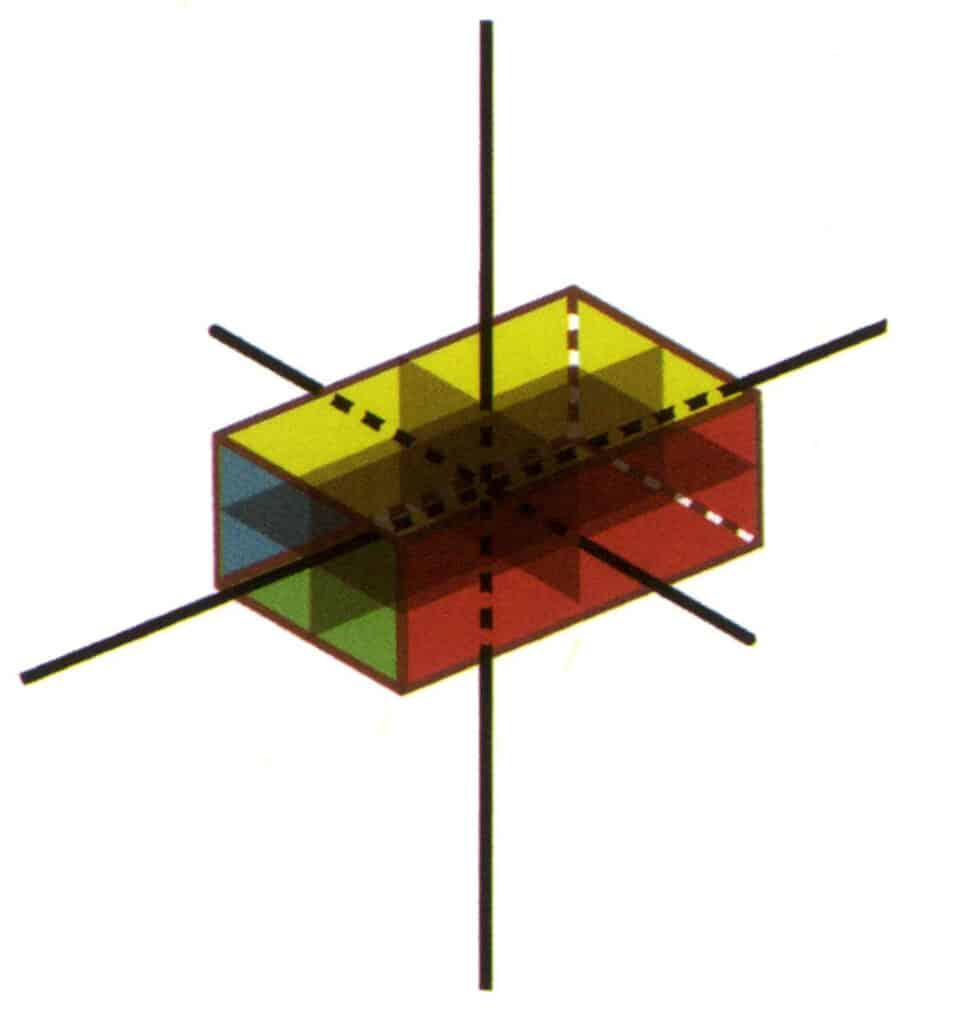
Figura 2-2-22 Grupo de pontos 3L²3P (cuboide retangular com secção transversal retangular)
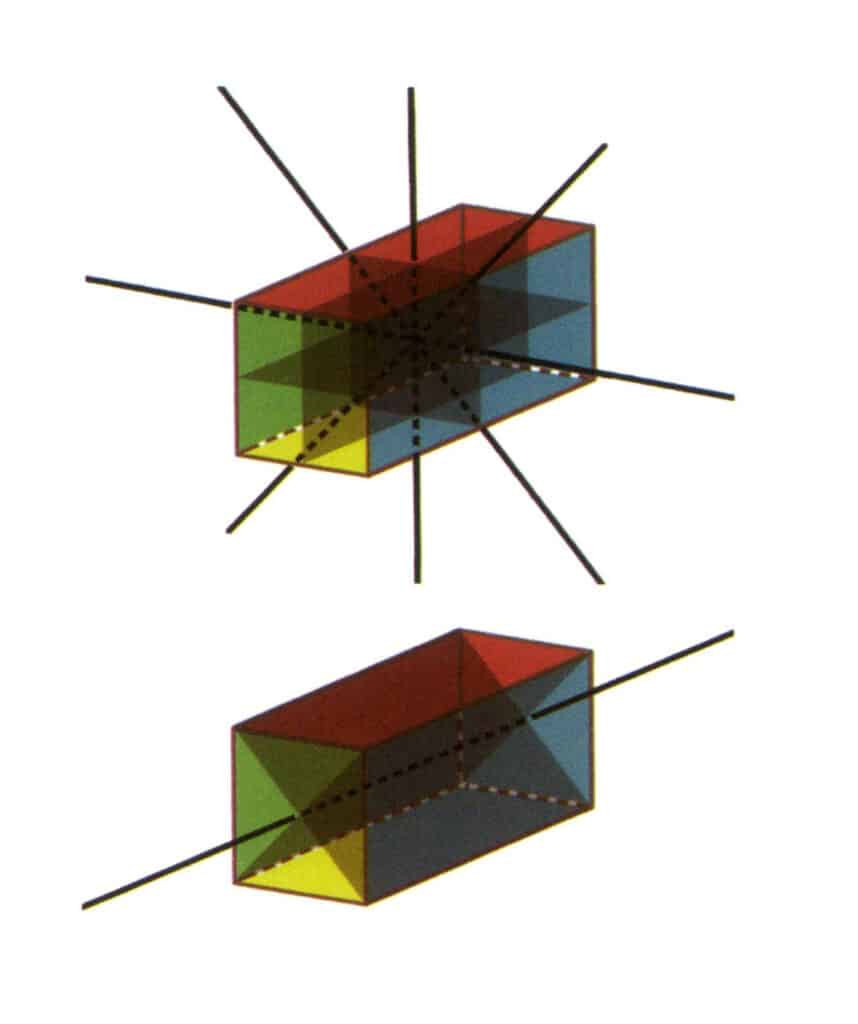
Figura 2-2-23 Grupo de pontos L⁴4L²5P (um prisma retangular com secção transversal quadrada), com quatro segundos eixos e três faces simétricas na parte superior, e um quarto eixo e duas faces simétricas na parte inferior.
3. Classificação dos cristais
A simetria é uma parte da classificação dos cristais. É necessário introduzir outro conceito - eixo cristalino - para descrever a estrutura cristalina das pedras preciosas naturais e artificiais num esquema de classificação de cristais. O eixo cristalino é uma linha imaginária que atravessa a estrutura cristalina, indicando a direção em que os nós da rede se repetem e a distância relativa em que os nós se repetem ao longo dessa direção. O eixo cristalino coincide com a normal do eixo de simetria ou com o plano de simetria. Se não existir um eixo de simetria ou um plano de simetria, o eixo do cristal pode ser selecionado em paralelo com a direção da aresta do cristal.
Com base nos elementos de simetria e nos eixos cristalinos, o sistema académico classifica os cristais em três famílias de cristais e sete sistemas cristalinos (Tabela 1).
Tabela 1: Pontos-chave para a determinação de famílias e sistemas de cristais
| Família Crystal | Cristal | Pontos-chave para a determinação | Variedades comuns de pedras preciosas |
|---|---|---|---|
| Sistema de cristais de baixo nível | Sistema triclínico | Sem segundo eixo ou plano de simetria | Amazonite, rodonite, Turquesa |
| Sistema cristalino monoclínico | Sem eixos de ordem superior, sem mais do que um eixo secundário e plano de simetria | Jadeíte, diopsídio, espodumena, epidoto | |
| Sistema cristalino ortorrômbico | Sem eixos de ordem superior, mais do que um eixo secundário ou plano de simetria | Olivina, topázio, saualpite (incluindo tanzanite), cordierite, crisoberilo, enstatite | |
| Família de cristais intermédios | Sistema cristalino tetragonal | 1 eixo quádruplo (pode ser representado por L4) | Diamante |
| Sistema de Cristal Trigonal | 1 eixos trigonais (podem ser representados por L3) | Corindo, rubi, safira, turmalina, cristais da família do quartzo (como o cristal, a ametista, o citrino, etc.), rodocrosite | |
| Sistema cristalino hexagonal | 1 eixo hexagonal (pode ser representado por L6) | Água-marinha, esmeralda e outras pedras preciosas da família da berilite, apatite | |
| Família de cristais avançados | Sistema isométrico de cristais | 4 eixos trigonais (podem ser representados por 4L3) | Diamante, granada, espinélio, espatoflúor |
4. Caraterísticas comuns dos cristais de pedras preciosas
As pedras preciosas comuns incluem o diamante, o espinélio, o espatoflúor, a granada, a berilite, o zircão, o corindo, a turmalina, o cristal, o crisoberilo, o topázio, etc. Cada tipo de pedra preciosa tem as suas próprias caraterísticas cristalinas fixas.
As pedras preciosas da família dos cristais de alto nível são maioritariamente granulares no hábito cristalino, e as variedades comuns aparecem frequentemente em formas cristalinas fixas (Tabela 2).
O hábito cristalino das famílias de cristais de nível intermédio e baixo é colunar (Tabela 3).
Tabela 2: Caraterísticas comuns dos cristais das famílias de cristais de alto nível
| Nome do tom das gemas | Classificação de cristais | Caraterísticas importantes dos cristais | |||
|---|---|---|---|---|---|
| Nome do tom das gemas | Classificação de cristais | Hábito do cristal | Formas cristalinas comuns | Formas gémeas comuns | Padrões comuns de faces de cristais |
| Diamante | Sistema isométrico de cristais | Hábito cristalino granular (Figura 2-2-24), normalmente observado em grânulos octaédricos | O octaedro é uma forma cristalina comum, podendo também surgir formas cristalinas mais complexas, incluindo dodecaedros rômbicos, muitas vezes com faces cristalinas arredondadas, que podem apresentar uma simetria tripla | Gémeo plano triangular, por vezes sem ângulos côncavos visíveis (Figura 2-2-25) | A superfície mostra poços de corrosão triangulares invertidos (Figuras 2-2-26, 2-2-27) e outros padrões de faces cristalinas (Figuras 2-2-28, 2-2-29) |
| Espinélio | Hábito cristalino granular (Figura 2-2-30), normalmente observado em grânulos octaédricos | Frequentemente produzido na forma octaédrica, as faces cristalinas podem ser muito planas, parecendo polidas (Figura 2-2-31) | Os cristais gémeos são muito planos, assemelhando-se a uma forma triangular com os cantos cortados (Figura 2¬2-32) | Furos de gravura visíveis à superfície, alguns semelhantes a diamantes em forma de triângulo invertido (Figura 2-2-33) | |
| Fluorite | Hábito cristalino granular (Figura 2-2-34) | Formas cristalinas octaédricas e cúbicas (Figura 2-2-35) | Geminação interpenetrante | Marcas de crescimento em degraus quadrados, na sua maioria com lacunas de clivagem, bandas de cor paralelas às direcções das seis faces do cubo | |
| Granada | Hábito cristalino granular, normalmente observado em grãos dodecaédricos rômbicos (Figura 2-2-36) | Dodecaedro rômbico ou quadrado-trapezoidal | Raro | Bandas anulares concêntricas visíveis com a mesma forma das faces cristalinas (Figura 2-2-37) | |
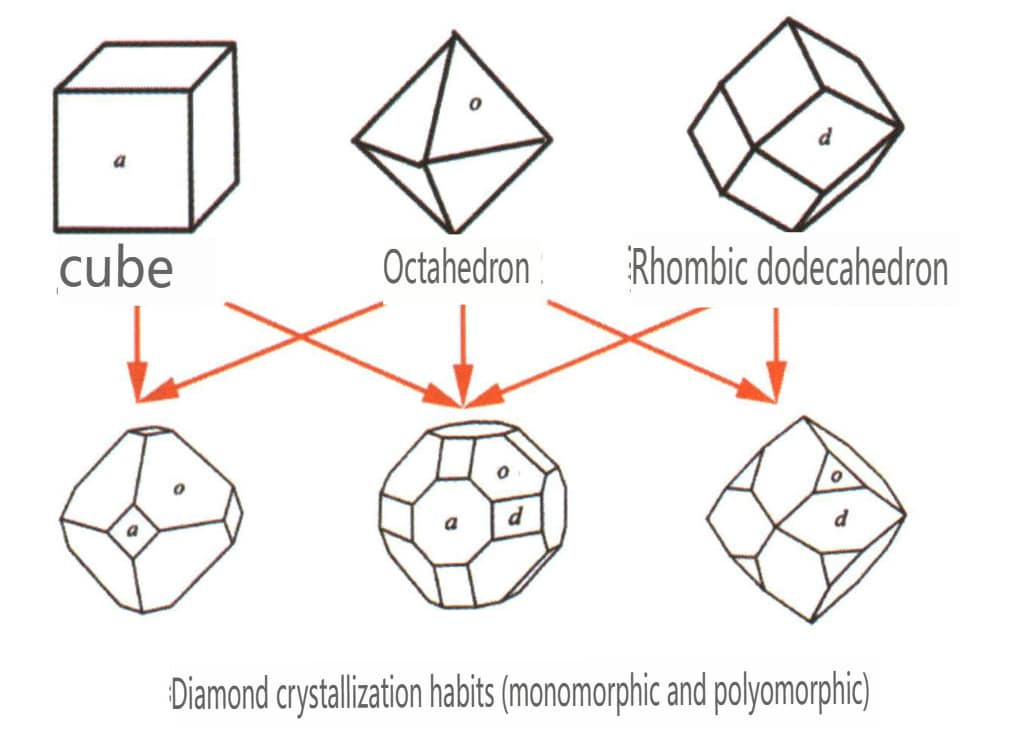
Figura 2-2-24 Hábitos do cristal de diamante
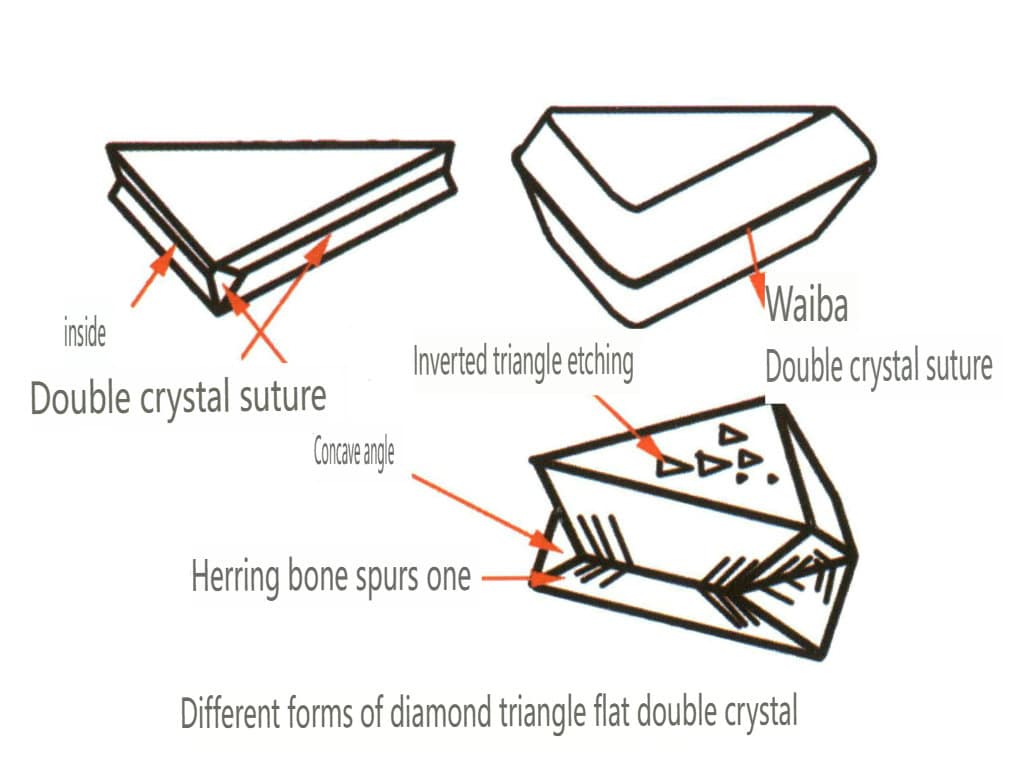
Figura 2-2-25 Hábito duplo de diamante
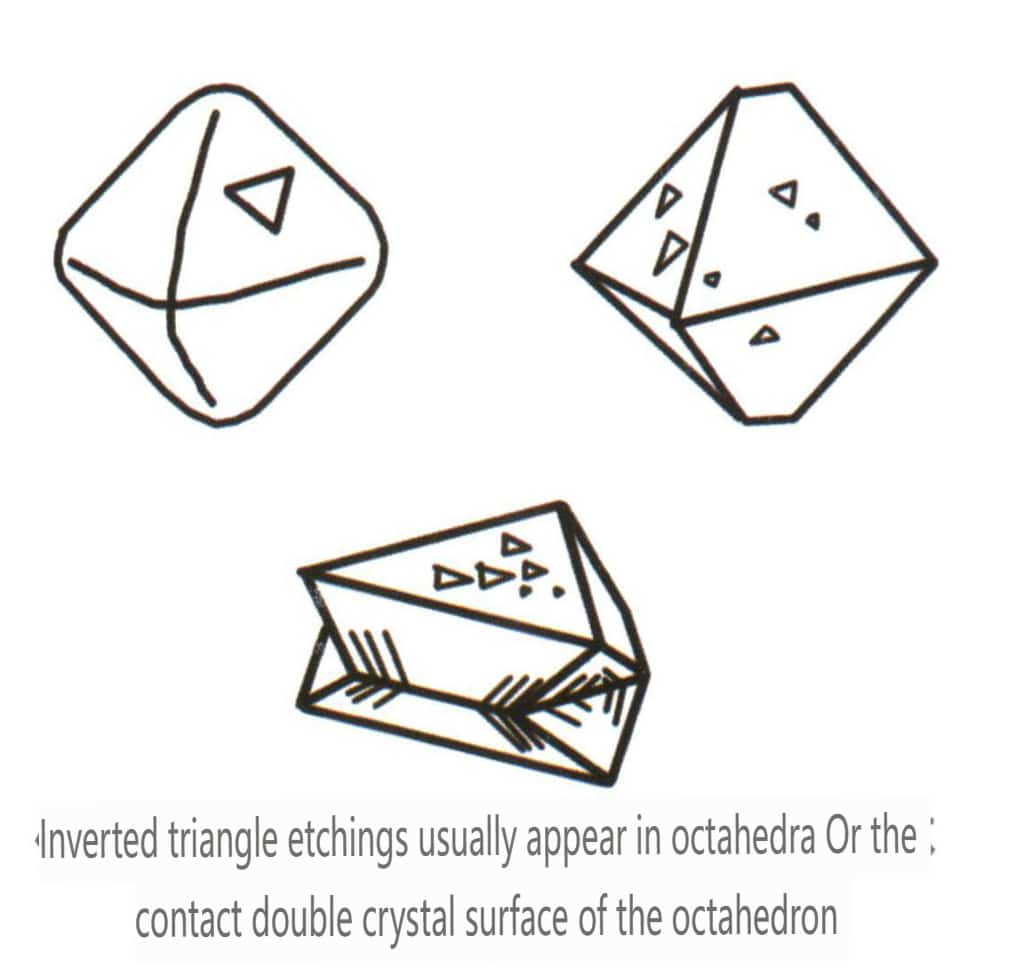
Figura 2-2-26 Figura de gravação em triângulo invertido das faces octaédricas do cristal de diamante

Figura 2-2-27 Figura de gravura triangular invertida na superfície de um cristal octaédrico de diamante
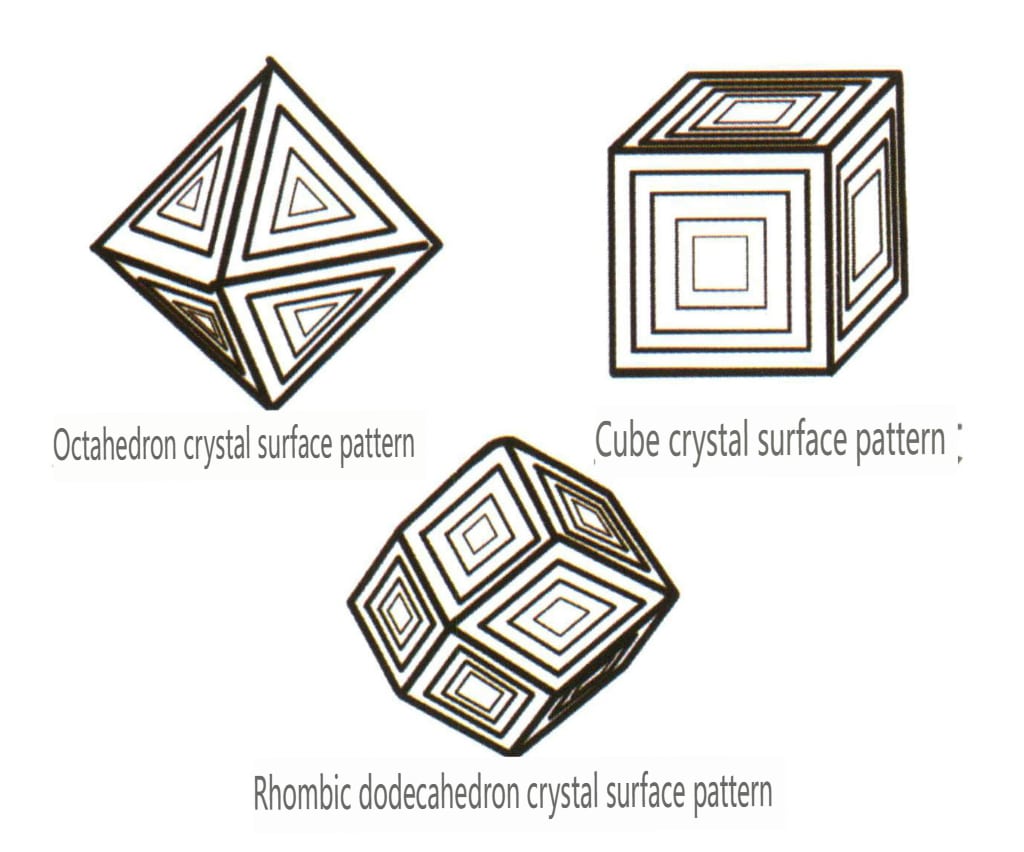
Figura 2-2-28 Figura de gravação em triângulo invertido das faces octaédricas do cristal de diamante

Figura 2-2-29 Figura de gravura triangular invertida na superfície de um cristal octaédrico de diamante
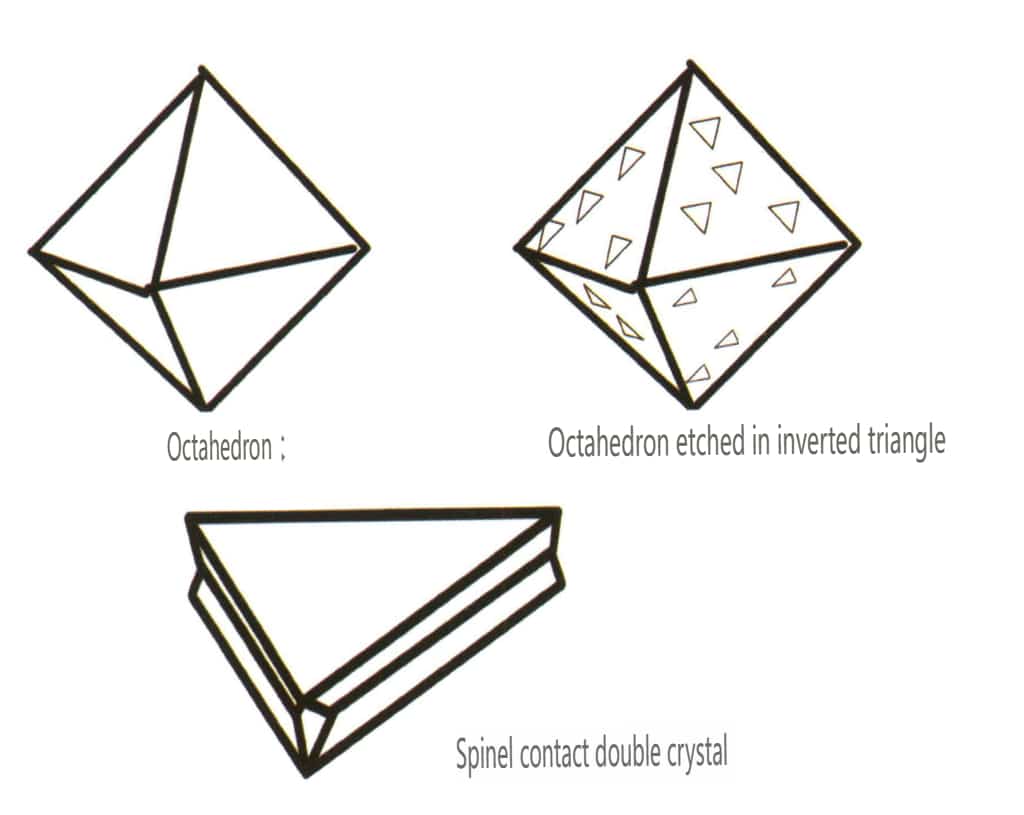
Figura 2-2-30 Hábito cristalino do espinélio

Figura 2-2-31 Formas comuns de cristais de espinélio

Figura 2-2-32 Geminação de contacto do espinélio
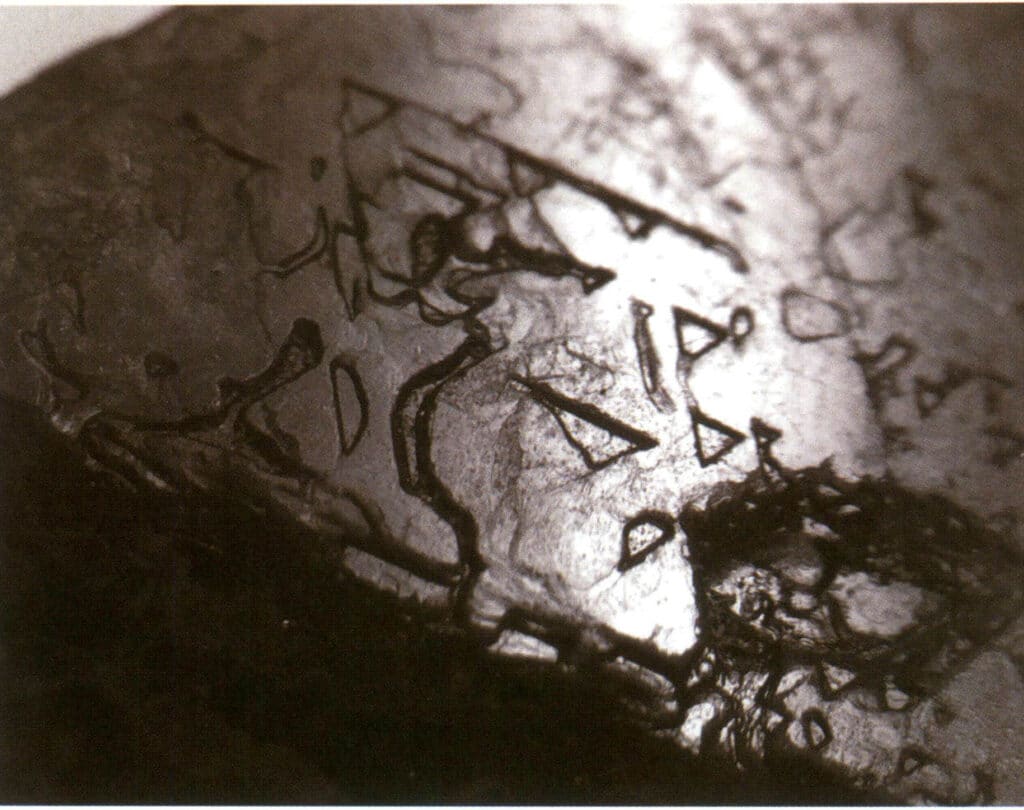
Figura 2-2-33 Padrão triangular invertido na superfície do espinélio
Figura 2-2-34 Hábitos cristalinos da fluorite

Figura 2-2-35 Cristal de fluorite
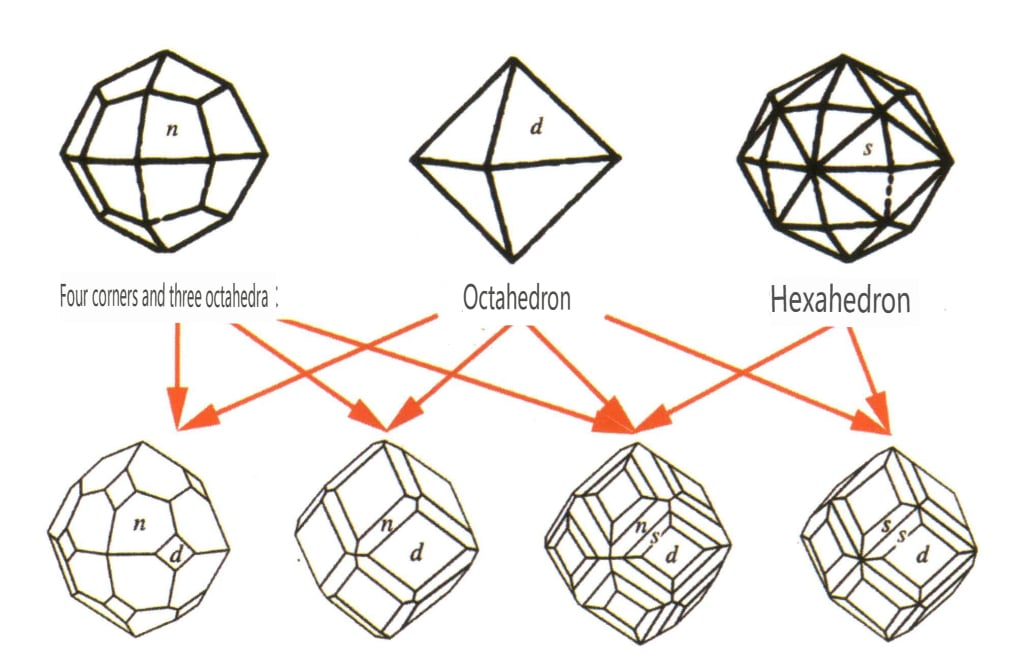
Figura 2-2-36 Hábito cristalino da granada

Figura 2-2-37 Bandas de anéis concêntricos na superfície de cristais de granada que têm a mesma forma que as faces do cristal
Tabela 3: Caraterísticas comuns dos cristais de gema das famílias de cristais intermédios e baixos
| Nome do tom das gemas | Classificação de cristais | Caraterísticas importantes dos cristais | |||
|---|---|---|---|---|---|
| Nome do tom das gemas | Classificação de cristais | Hábito do cristal | Formas cristalinas comuns | Formas gémeas comuns | Padrões comuns de faces de cristais |
| Berilo | Sistema cristalino hexagonal | Hábito cristalino colunar (Figura 2-2-38) | Forma cristalina colunar hexagonal (Figuras 2-2-39, 2-2-40) | Raro | Riscas longitudinais visíveis |
| Pedra de chumbo | Sistema cristalino tetragonal | Hábito cristalino colunar (Figura 2-2-41) | Um pilar quadrado com uma secção transversal quadrada, que aparece juntamente com um cone duplo quadrado (Figura 2-2-42) | Cristais gémeos visíveis em forma de joelho | Sem padrões especiais |
| Corindo | Sistema cristalino trigonal | Hábito cristalino tipo placa, hábito cristalino colunar (Figura 2-2-43) | Os rubis apresentam frequentemente uma forma de prisma hexagonal (Figura 2-2-44), enquanto as safiras exibem frequentemente uma forma cristalina hexagonal bipiramidal em forma de barril (Figura 2-2-45) | É frequente ver bi-cristais. | Estrias visíveis. |
| Turmalina . | Hábito cristalino colunar (Figura 2-2-46) | As faces do cristal em ambas as extremidades são diferentes, e a secção transversal é um triângulo esférico (Figura 2-2-47) | Raro | Riscas longitudinais visíveis (Figura 2-2-48) | |
| Quartzo (quartzo cristal) | Hábito cristalino colunar (Figura 2-2-49) | A secção transversal é hexagonal, as bipirâmides hexagonais são raras (Figuras 2-2-50, 2-2-51), as monopirâmides hexagonais são comuns | Contacto comum com bicristais (também conhecidos como bicristais japoneses) | Riscas horizontais comuns em superfícies de cristal | |
| Crisoberilo | Sistema cristalino trigonal | Caraterísticas da cristalização colunar (Figura 2-¬2-52) | A monocristalina é rara | A forma tri-cristalina é comum (Figura 2-2-53), os ângulos hexagonais e côncavos podem ser utilizados como critérios de identificação | As riscas do tri-cristalino podem ser utilizadas como critério de identificação |
| Topázio | Hábito cristalino colunar (Figura 2-2-54) | A secção transversal tem a forma de um diamante e a parte superior parece frequentemente um envelope (Figura 2-2-55) | Os bi-cristais são raros | Riscas longitudinais visíveis | |
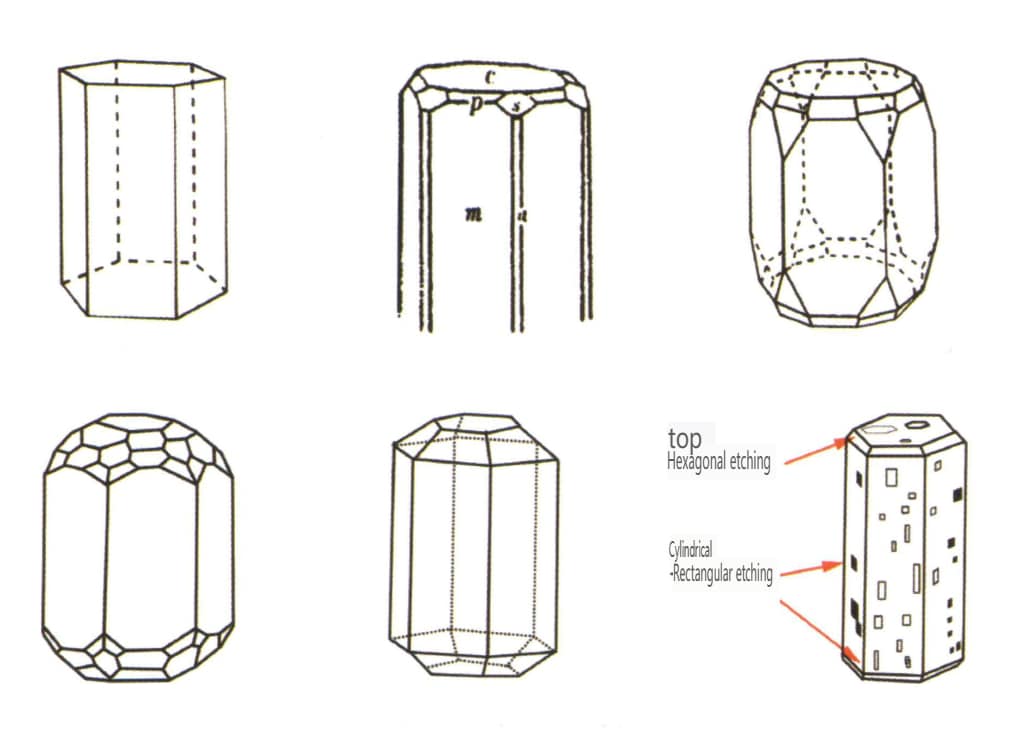
Figura 2-2-38 Hábito cristalino do berilo

Figura 2-2-39 Formas comuns de cristais de esmeralda

Figura 2-2-40 Formas comuns de cristais de água-marinha
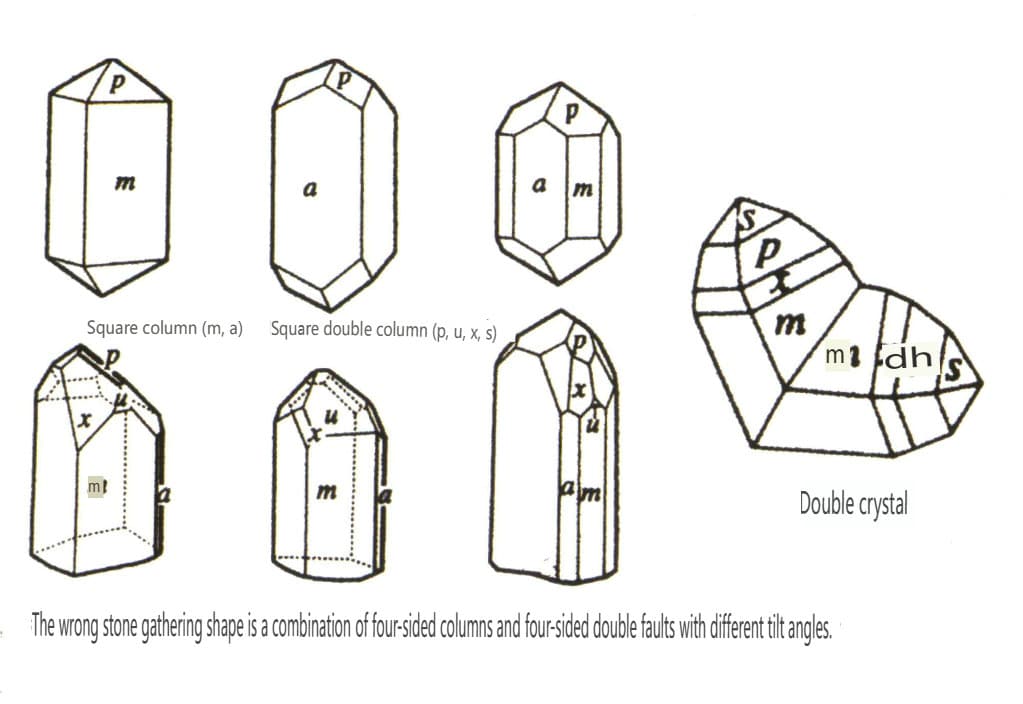
Figura 2-2-41 Hábitos dos Cristais de Zircão

Figura 2-2-42 Cristal de zircão
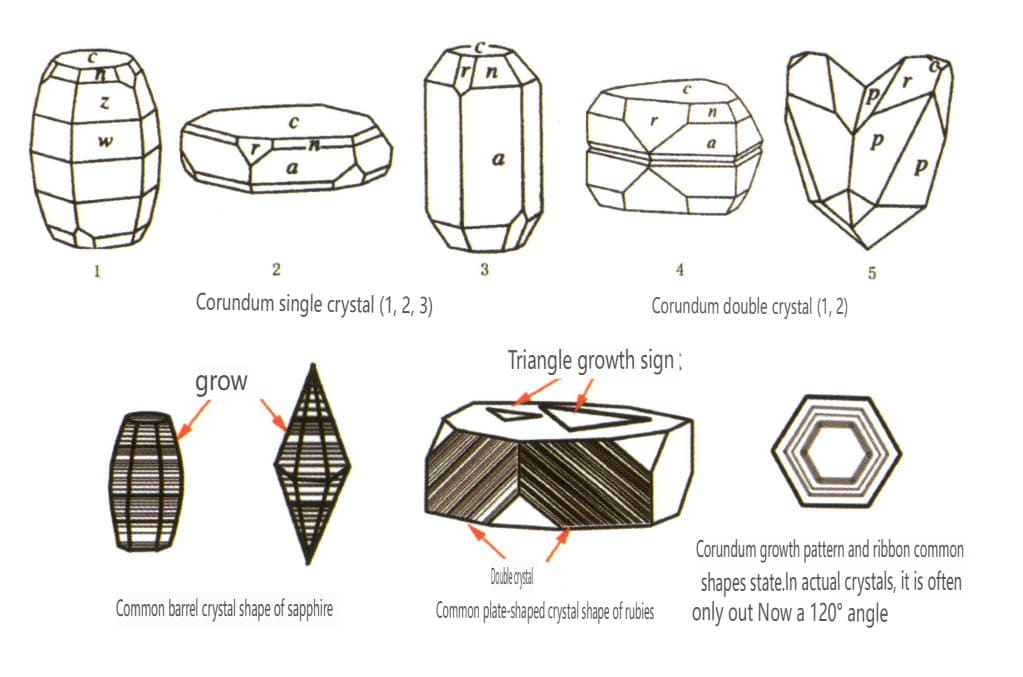
Figura 2-2-43 Hábito cristalino do corindo

Figura 2-2-44 Cristal de rubi

Figura 2-2-45 Gémeo mecânico do rubi
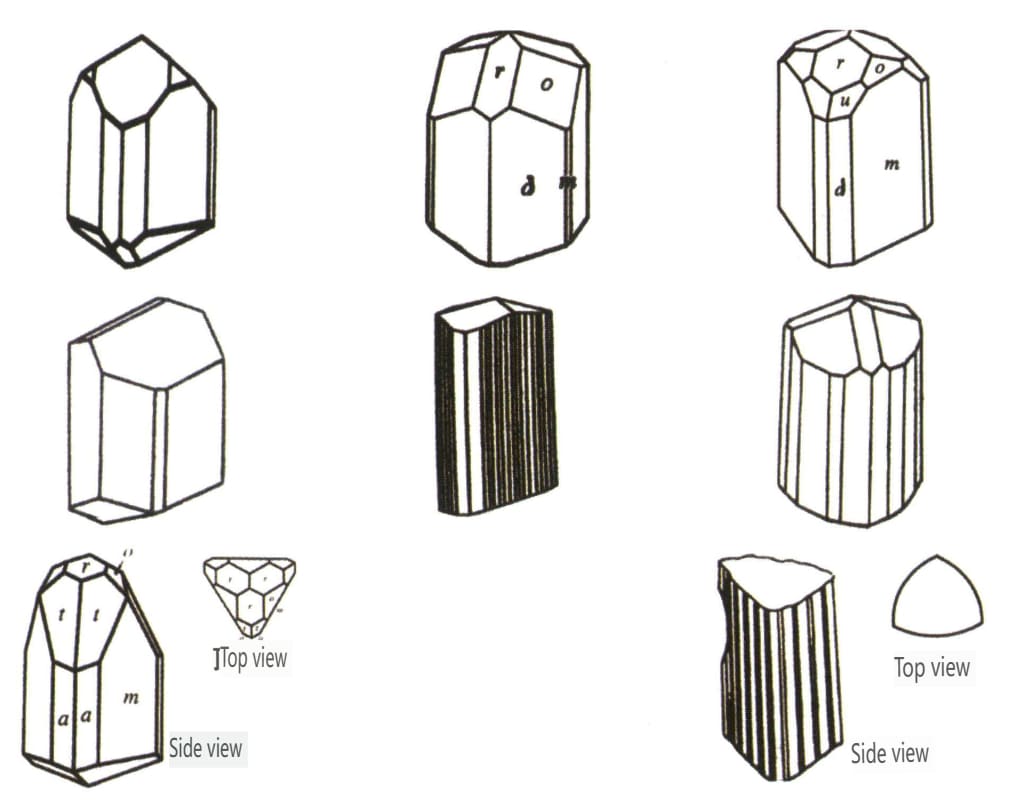
Figura 2-2-46 Hábitos dos Cristais de Turmalina

Figura 2-2-47 Cristal de turmalina

Figura 2-2-48 Listras longitudinais na superfície do cristal de turmalina
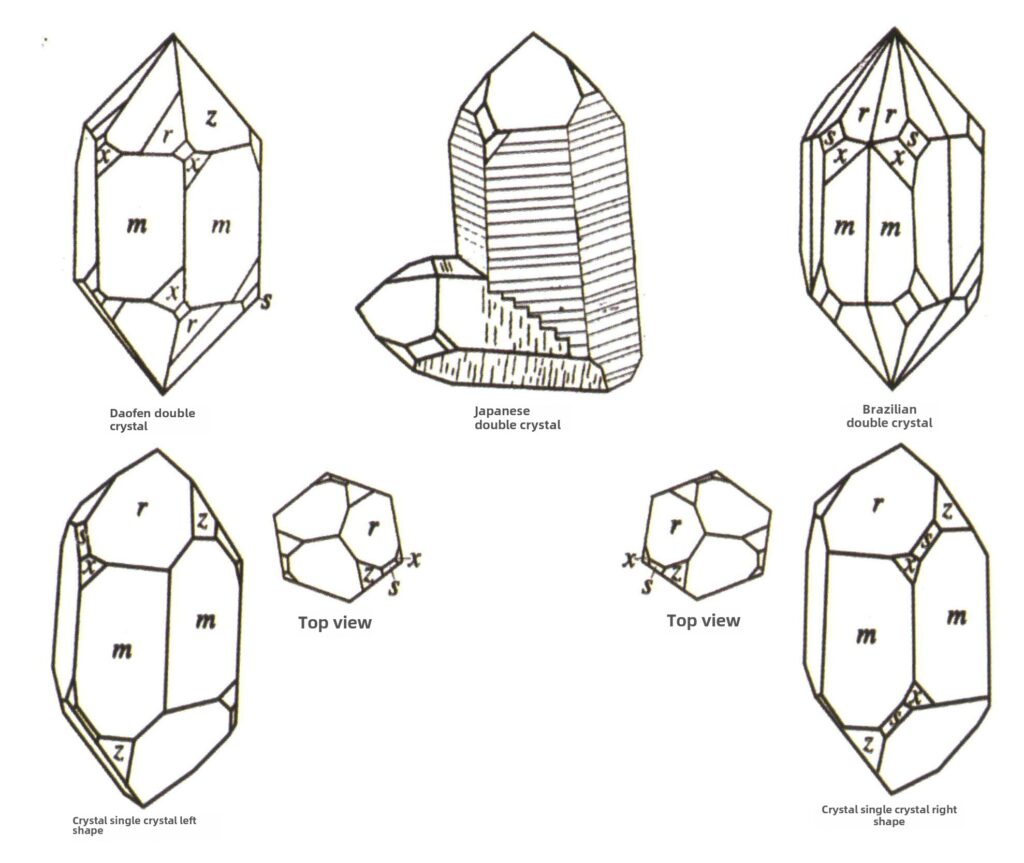
Figura 2-2-49 Hábitos de cristalização de cristais

Figura 2-2-50 Corpo do cristal

Figura 2-2-51 Corpo do cristal
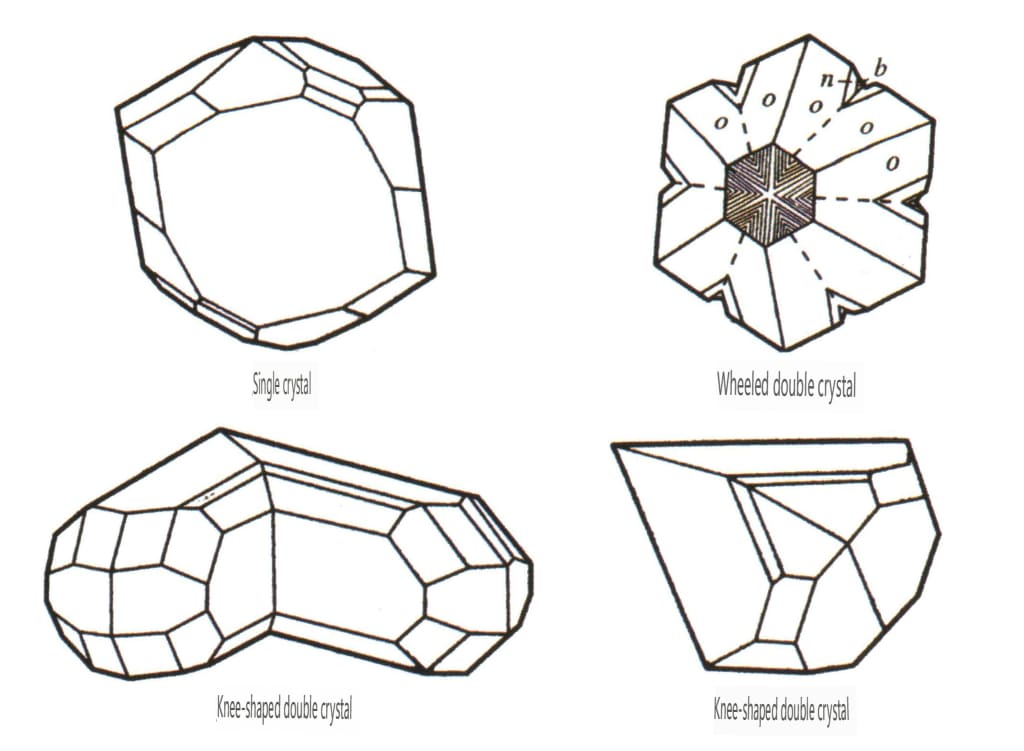
Figura 2-2-52 Hábito Cristalino do Crisoberilo

Figura 2-2-53 Cristal de Crisoberilo
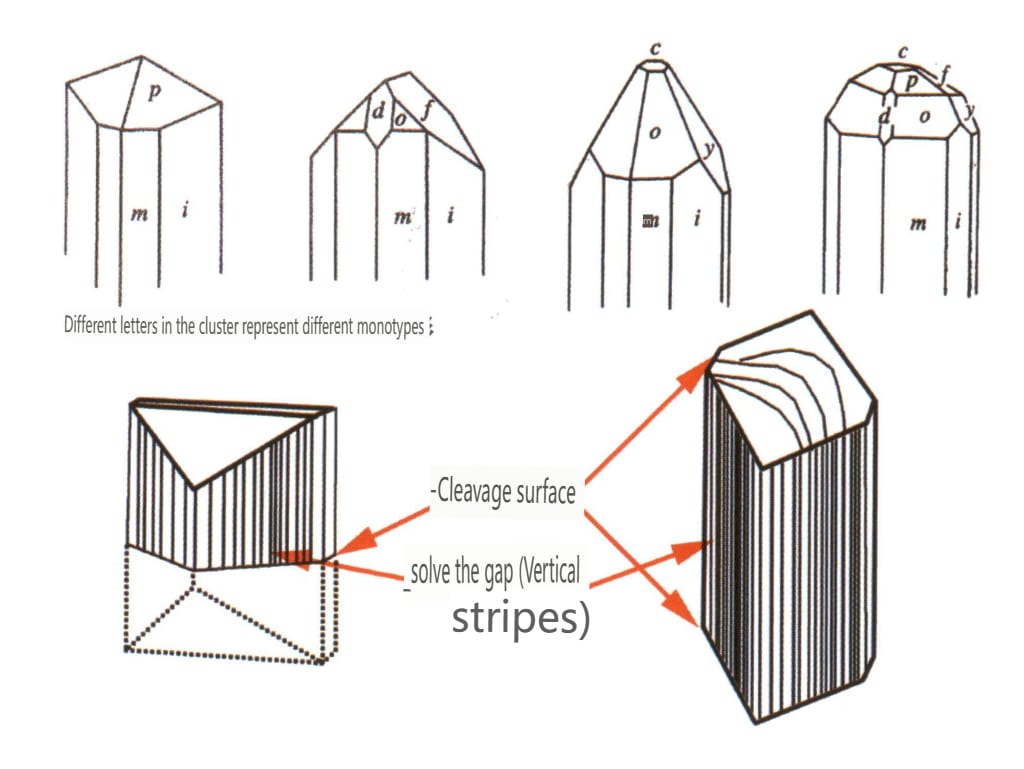
Figura 2-2-54 Hábitos cristalinos do topázio

Figura 2-2-55 Cristal de topázio
Secção IV Porque é que os cristais de pedras preciosas crescem de forma diferente
De um ponto de vista microscópico, o cristal de gema é um sólido composto por elementos de diferentes tamanhos dispostos segundo regras diferentes. De um ponto de vista macroscópico, muitas gemas têm caraterísticas de forma cristalina devido às suas diferentes composições. No entanto, existem alguns casos especiais, como o heteromorfo. Para compreender melhor porque é que os cristais de gema têm um aspeto diferente, vamos apresentar cinco aspectos: heteromorfia, isomorfismo, mistura mecânica molecular, água nos minerais de gema e composição química das gemas.
1. Heteromorfo
Embora alguns minerais tenham a mesma composição química, têm estruturas cristalinas muito diferentes (a disposição dos elementos no espaço tridimensional) e exibem diferenças significativas nas propriedades físicas e químicas (Tabela 4). Chamamos a este fenómeno heteromorfismo, por exemplo, o diamante e a grafite (Figura 2-2-56).
O quartzo comum apresenta o fenómeno do heteromorfismo. A sillimanite, a andaluzite e a cianite são um grupo de variantes do heteromorfismo.
A transformação do heteromorfismo ocorre em condições de estado sólido. Durante o processo de transformação estrutural, a pressão pode desenvolver-se no interior do cristal, levando frequentemente à formação de geminações no interior do cristal.

Tabela 4: Comparação das propriedades do diamante e da grafite
| Mineral | Diamante | Grafite |
|---|---|---|
| Componentes | Carbono (C) | Carbono (C) |
| Condições de formação | Alta temperatura e alta pressão | Alta temperatura |
| Sistema cristalino, hábito | Sistema cristalino isométrico, octaedro, dodecaedro rômbico | Sistema cristalino hexagonal, em camadas |
| Cor | Incolor, amarelo, azul, cor-de-rosa, verde, etc. | Preto |
| Brilho | Brilho adamantino | Brilho metálico |
| Transparência | Transparente a opaco | Opaco |
| Índice de refração | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Propriedades mecânicas | Clivagem octaédrica moderada, dureza 10, densidade 3,52 | Um conjunto de clivagem perfeita, dureza 1, densidade 2,10 |
| Outras propriedades | Excelente condutividade térmica; com exceção dos diamantes azuis naturais que são semicondutores, os diamantes de outras cores são isolantes. | Condutividade térmica moderada, boa condutividade eléctrica |
2. Isomorfismo
O isomorfismo refere-se ao fenómeno em que algumas partículas na estrutura da rede são substituídas por outras partículas com propriedades semelhantes, resultando em ligeiras alterações no parâmetro da rede e nas propriedades físicas e químicas. Em contrapartida, a estrutura cristalina permanece fundamentalmente inalterada. Pode ser entendido como os elementos no cristal de pedra preciosa sendo substituídos por outros elementos. Em contrapartida, o padrão de repetição dos elementos do cristal de gema permanece o mesmo, com ligeiros desvios nas distâncias entre os átomos. Ainda assim, as propriedades físico-químicas do cristal de gema sofrem ligeiras alterações (Figura 2-2-57 a Figura 2-2-58).
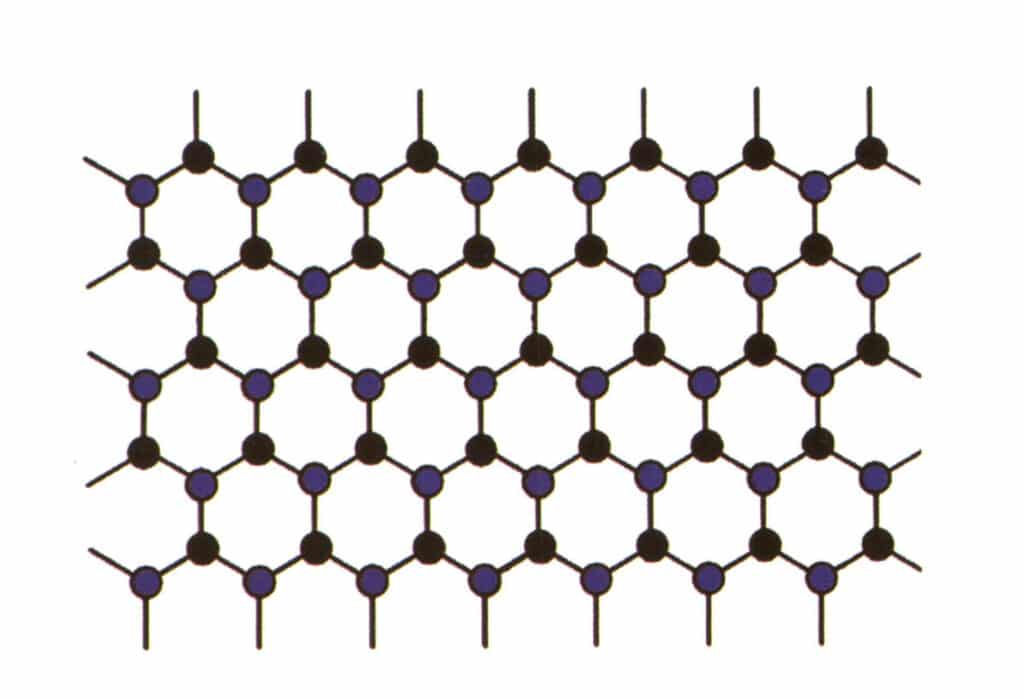
Figura 2-2-57 Diagrama de simulação da estrutura cristalina (azul e preto indicam partículas de elementos)
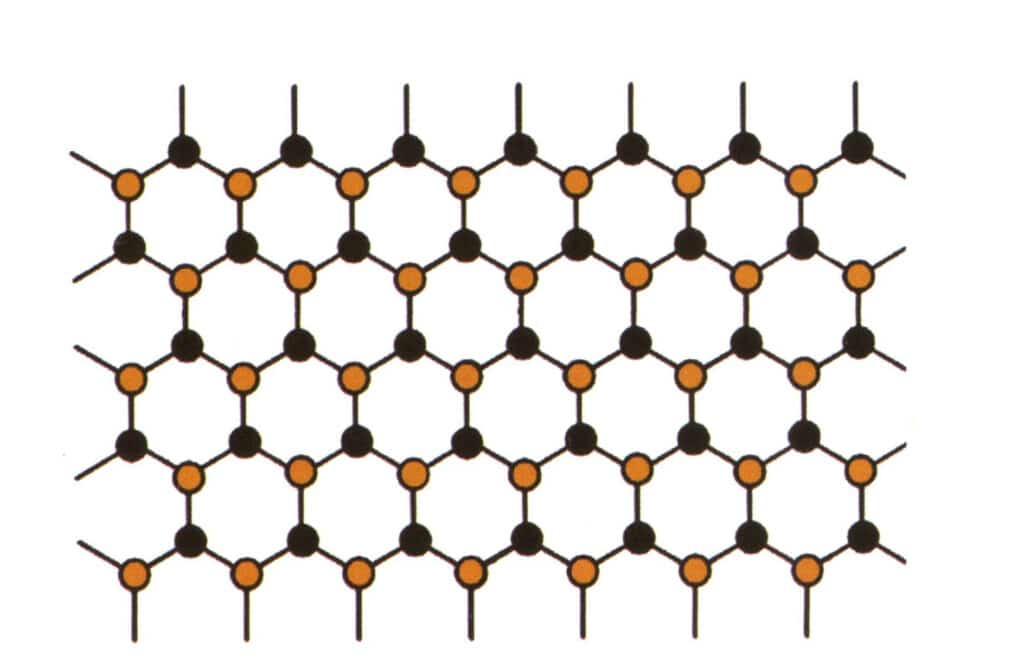
Figura 2-2-58 Diagrama de simulação da estrutura cristalina (o preto representa as partículas elementares, o amarelo representa as novas partículas elementares que substituem parcialmente as partículas elementares azuis, o amarelo pode não substituir completamente todas as partículas azuis)
O conceito de isomorfismo pode explicar porque é que as pedras preciosas da mesma família podem ter tantas cores e porque é que existem variações no índice de refração e na densidade entre pedras preciosas da mesma família.
Uma família pode ser entendida como um tipo de pedra preciosa em que os padrões de repetição dos elementos cristalinos são os mesmos, mas as formas físicas e químicas são ligeiramente diferentes. Por exemplo, a família do corindo inclui dois membros, o rubi e a safira, enquanto a família do berilo inclui as variedades esmeralda, água-marinha e morganite.
(1) Olivina
A composição química da olivina é (Mg,Fe)₂SiO₄. A substituição isomórfica completa dos elementos Fe e Mg ocorre em sua composição. À medida que o teor de Fe na olivina aumenta, a cor da olivina torna-se mais escura, o índice de refração aumenta e a densidade também aumenta.
(2) Corindo
O corindo puro e sem impurezas (Al₂O₃) é incolor, e quando o Cr substitui o Al, a gema apresenta uma tonalidade rosa-avermelhada a vermelha, conhecida como rubi. As restantes cores são designadas por safira, como a safira amarelo-alaranjada ou a safira incolor. A safira comummente designada por safira é especificamente a safira azul, onde o Fe e o Ti substituem o Al. Quanto mais elevado for o teor dos elementos corantes na gema de substituição, mais profunda será a cor da gema; inversamente, quanto mais baixo for o teor, mais clara será a cor.
(3) Turmalina
Turmalina refere-se ao mesmo tipo de gema como turmalina, onde turmalina é o seu nome mineralógico, e turmalina é o seu nome gemológico. A composição química do berilo é (Na, Ca) R₃Al₃Si₆O₁₈ (O, OH, F), onde R é principalmente Mg, Fe, Cr, Li, Al, Mn, e os elementos em R podem substituir-se total ou parcialmente, resultando em uma variedade extremamente ampla de cores para turmalina. Por exemplo, quando R é principalmente Fe, o berilo apresenta uma cor azul profunda ou mesmo preta; quando R é principalmente Mg, o berilo apresenta-se amarelo a castanho; quando R é principalmente Li ou Mn, o berilo apresenta-se rosa ou azul claro; quando R é principalmente Cr, a turmalina apresenta um verde profundo.
A partir do exposto, pode-se ver que a substituição de elementos com propriedades semelhantes leva a cores mais bonitas e brilhantes nas gemas.
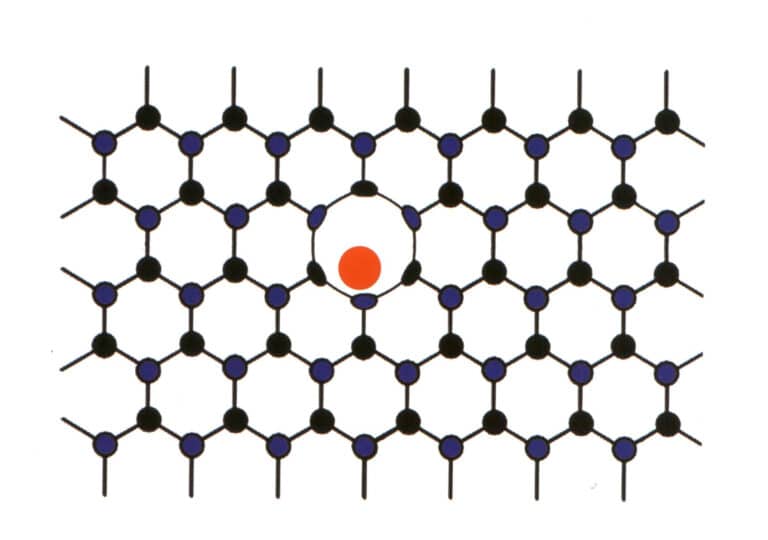
3. Intermistura mecânica molecular
Por vezes, certos elementos entram à força entre os elementos principais de pedras preciosas dispostas regularmente. No entanto, a baixa proporção dos elementos que entram não perturba o padrão repetitivo dos elementos principais da pedra preciosa, causando apenas deformação (Figura 2-2-59). Esta situação é referida como mistura mecânica molecular, tal como a mistura mecânica molecular de azoto e boro nos diamantes, que produz diamantes azuis, rosa e amarelos, que são altamente valiosos.
4. Água em minerais de gema
Algumas pedras preciosas contêm água, que é um componente importante dos minerais de gema e está intimamente relacionado com as propriedades das pedras preciosas. Com base na forma de água presente nos minerais de gema e no seu papel na estrutura cristalina, a água nas pedras preciosas pode ser dividida em duas categorias: uma é a água de absorção, que não está relacionada com a estrutura cristalina, e a outra é a água que participa na estrutura cristalina mineral, incluindo a água de cristalização, água zeolítica, água entre camadas e água de constituição. A água intimamente relacionada com as pedras preciosas inclui a água de absorção, a água de cristalização e a água de constituição.
Uma é a absorção de água, como a Opala (a composição química é SiO₂ - nH₂O, n representa o número de H₂O, o conteúdo é variável) na molécula de água, que é uma molécula de água neutra adsorvida mecanicamente para partículas minerais ou superfícies de fratura. Quando a temperatura atinge 100 ~ 110 ° graus sob pressão normal, as moléculas de água podem escapar e não danificar a estrutura da estrutura cristalina, de modo a evitar a Opala no balcão em um longo tempo de exposição à luz forte rachadura seca, deve colocar um copo de água no balcão.
Em segundo lugar está a água de cristalização, como a água de cristalização da turquesa [a composição química é CuAl₆(PO₄)₄(OH)₈-4H₂O, onde o conteúdo de H₂O pode chegar a 19,47% ]. Esta molécula de água neutra existe em posições fixas dentro da rede e serve como uma unidade estrutural, fazendo parte da composição química do mineral. A temperatura na qual a água de cristalização escapa geralmente não excede 600 ℃ e geralmente escapa a 100 -200 ℃. Quando uma pedra preciosa perde sua água de cristalização, sua estrutura cristalina é danificada, formando uma nova estrutura.
Em terceiro lugar está a água de constituição, também conhecida como água combinada, que participa da rede mineral na forma de plasma OH-, H⁺, H₃O⁺, sendo o OH- o mais comum. A água de constituição faz parte da composição química do mineral, ocupando posições fixas na estrutura da rede com uma proporção definida na sua composição. A água estrutural requer uma temperatura mais alta para escapar e danificar sua estrutura, geralmente em torno de 600 -1000 ℃. Quando uma pedra preciosa perde água estrutural, sua estrutura cristalina é destruída. Muitas pedras preciosas contêm água de constituição, como a turmalina [a composição química é ( Na, Ca) R₃Al₃Si₆O₁₈ (O, OH, F), onde R inclui principalmente Mg, Fe, Cr, Li, Al, Mn, etc., e os elementos em R podem substituir-se total ou parcialmente], e topázio [composição química é Al₂SiO₄( F, OH) ₂ ].
5. A composição química das pedras preciosas
As gemas, tal como outras substâncias, são compostas por elementos químicos. Cada tipo de gema tem a sua composição química específica e uma certa gama de variação, que determina as várias caraterísticas e propriedades da gema. As gemas pertencem aos minerais e às rochas, e a classificação da composição química de uma gema pode ser rastreada até à composição química dos minerais.
Atualmente, os principais métodos de classificação dos minerais incluem a classificação pela composição química (sistema Dana), a classificação geoquímica, a classificação genética, a classificação de aplicação e a classificação cristais-química. O método amplamente adotado é a classificação química baseada na composição química e na estrutura cristalina (sistema Hugo Strunz) (Quadro 5).
Tabela 5: Sistema de classificação química de cristais minerais
| Sequência de níveis | Base da divisão | Exemplo |
|---|---|---|
| Categoria principal | Tipo de composto | Sal que contém oxigénio Categoria principal |
| Classe | Tipos de aniões ou aniões complexos | Classe de silicatos |
| (Subcategoria) | Estrutura do complexo aniónico | Subclasse de silicato de estrutura |
| Grupo | Tipos de estruturas cristalinas e propriedades iónicas | Grupo do corindo, grupo do berilo, grupo da granada |
| (Subgrupo) | Tipos de catiões | Subgrupo dos feldspatos alcalinos |
| Espécie | Determinada estrutura cristalina e composição química | Ortoclásio KAlSi3O8 |
| (Subespécie) | Mesma estrutura cristalina, composição ou propriedades diferentes, morfologia | Adularia KAlSi3O8 |