Один раз, чтобы узнать все о кристаллографии драгоценных камней
Исчерпывающий справочник о формах, видах, классификациях и различиях кристаллографии
Земля состоит из бесчисленных молекул и атомов. Современные научные исследования показали, что твердые материалы в природе состоят из различных химических элементов. Результаты рентгеновского анализа показывают, что атомы в элементах некоторых твердых материалов расположены аккуратно и регулярно друг к другу. Такие материалы классифицируются как кристаллические или называются кристаллами, а их упорядоченная атомная решетка называется кристаллической структурой (рис. 2-1-1).
Большинство драгоценных материалов, которые растут в природе и в лабораториях, являются кристаллическими. В этой главе мы рассмотрим понятие кристаллов, их классификацию, связь между кристаллами и основной терминологией в геммологии.

Оглавление
Раздел Ⅰ Понятие и описание кристаллов
Когда мы упоминаем драгоценные камни, мы часто думаем об их сверкающих и полупрозрачных свойствах (рис. 2-1-2). С точки зрения геологов и геммологов, большинство любимых драгоценных камней относятся к геометрической форме твердого тела - кристаллам. Суть красоты кристаллов, по сути, заключается в красоте геометрии.

1. Понятие о кристаллах
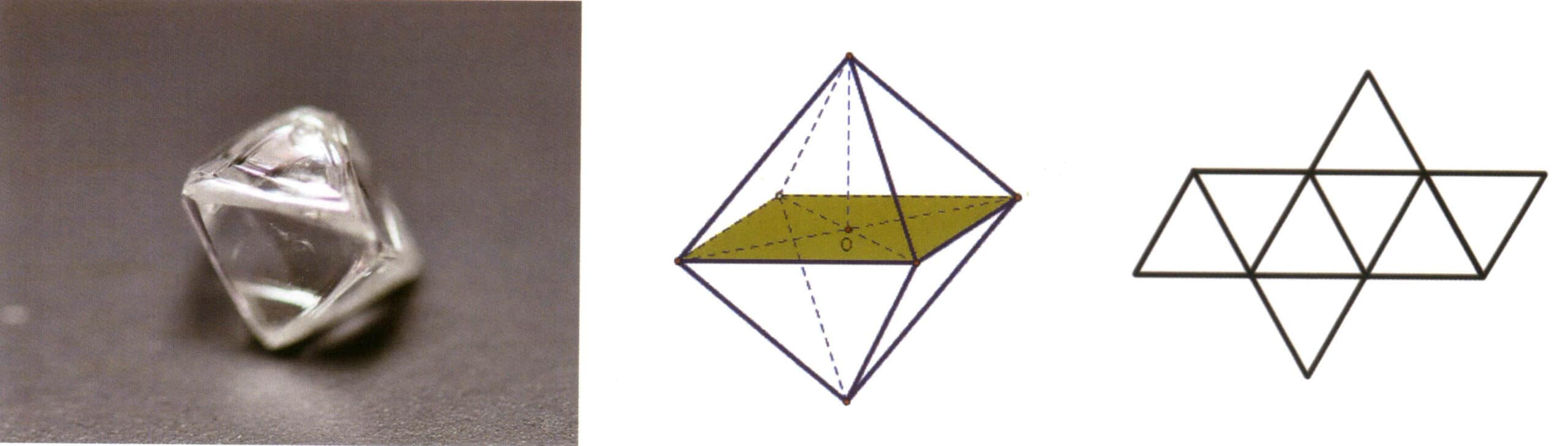
Кристаллы - самые легко ассоциируемые и наиболее часто встречающиеся в природе. Кристаллы встречаются на всех семи континентах Земли, а в природе они часто имеют форму геометрических многогранников (рис. 2-1-3). Их принято называть кристаллами. Позже этот термин был расширен для обозначения встречающихся в природе твердых веществ с геометрическими многогранными формами, таких как кристаллы алмаза и аквамарина (Рисунок 2-1-4). Кристаллами также называют твердые материалы с неровной, неоднородной, изношенной, изломанной или искусственно обработанной поверхностью, но с атомарным расположением, которое все еще следует регулярному образцу. Кристаллографы считают, что все кристаллы обладают шестью основными характеристиками: самоограничением, однородностью, анизотропией, симметрией, стабильностью и фиксированной температурой плавления.
① Самоограничение относится к свойству химических элементов спонтанно образовывать геометрические многогранные формы. Это свойство может объяснить, почему различные элементы имеют разные геометрические формы кристаллов.
② Однородность - это свойство, при котором физические и химические свойства всех частей кристалла одинаковы. Это свойство помогает нам различать и идентифицировать различные минеральные кристаллы.
③ Анизотропия - это свойство, при котором расположение элементов изменяется в разных направлениях, что приводит к незначительным различиям в физических свойствах в зависимости от направления. Это свойство объясняет, почему алмазы с самой высокой твердостью можно резать и полировать.
④ Симметрия - это свойство, при котором идентичные части или свойства в кристалле повторяются в регулярном порядке. Это свойство является чрезвычайно важным и особенным для кристаллов и будет подробно рассмотрено во втором разделе этой главы.
⑤ Стабильность - это устойчивость кристалла, обусловленная его минимальной внутренней энергией. Если внутренняя энергия кристалла высока и неоднородна, он склонен к самостоятельному растрескиванию. Это свойство объясняет, почему кристаллы рубина, синтезированные методом плавления, всегда кажутся не полными, а половинчатыми.
⑥ Фиксированная температура плавления означает свойство кристалла иметь фиксированную температуру плавления.

Рисунок 2-1-3 Гранат (слева - кристалл, справа - полированный гранат)

Рисунок 2-1-4 Кристалл аквамарина
2. Идеальная форма кристаллов
Кристаллы, рассматриваемые в кристаллографии, в основном являются идеальными монокристаллами. Идеальный монокристалл - это кристалл, внутренняя структура которого строго подчиняется правилам пространственных решеток, а форма представляет собой правильную геометрическую комбинацию. Формы идеальных монокристаллов делятся на два типа: простые формы и комбинационные формы.
(1) Простая форма
Под простой формой понимается сочетание группы кристаллических граней, соединенных элементами симметрии, которое в идеальном состоянии можно понимать как геометрическое тело, состоящее из кристаллических граней одинаковой формы и размера (рис. 2-1-5). В кристаллах существует 47 типов простых форм.
Ключевыми моментами для определения простых форм являются: все грани кристалла имеют одинаковую форму и размер, а грани кристалла могут быть ориентированы по-разному.
(2) Комбинезон Форма
Совокупность простых форм называется комбинированной формой, состоящей из двух или более различных простых форм. Не все простые формы могут свободно объединяться в комбинированную форму; объединяться могут только простые формы с одинаковой группой точек (рис. 2-1-6 - 2-1-8).
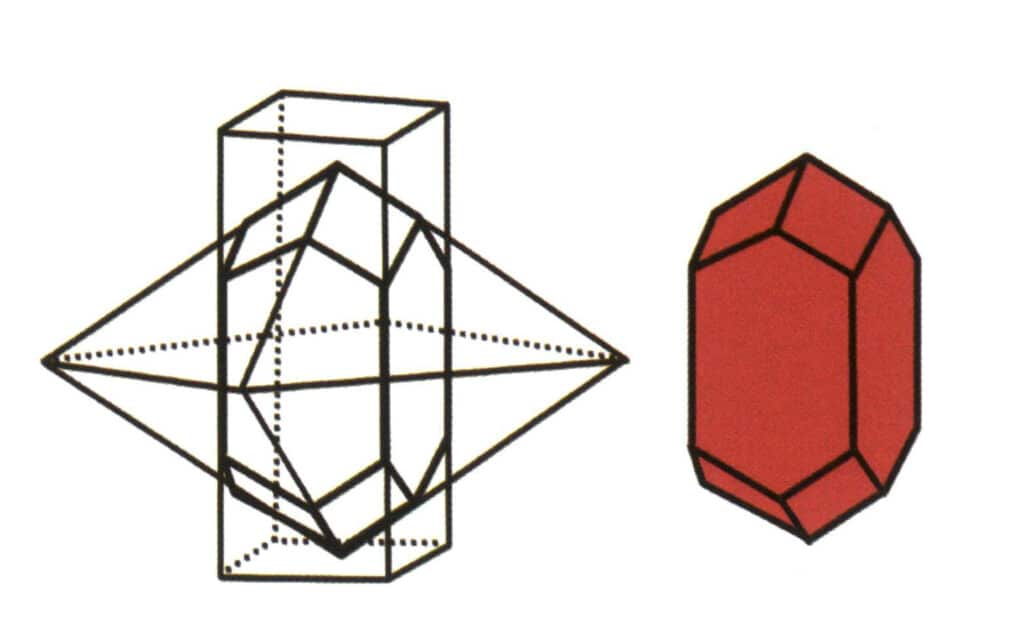
Рисунок 2-1-6 Комбинация из тетрагональной призмы и тетрагональной дипирамиды
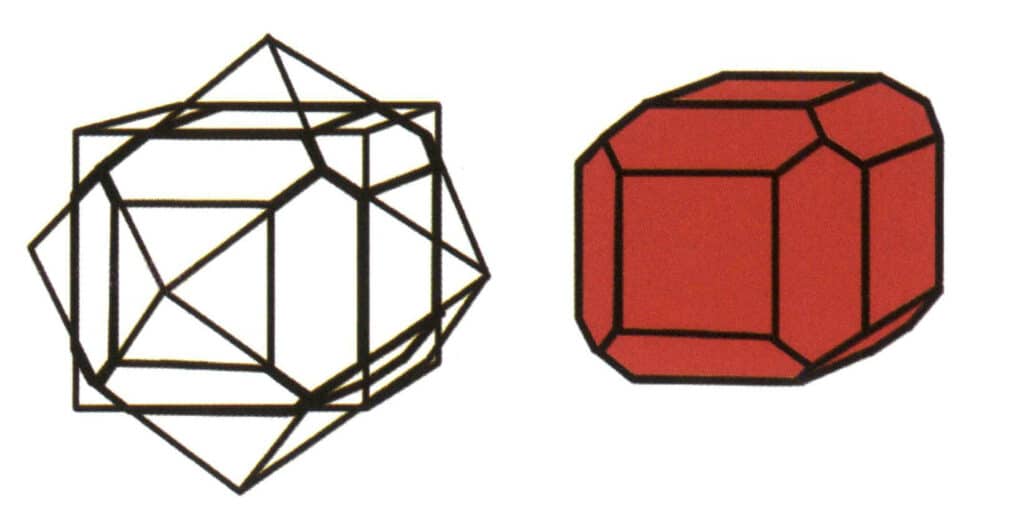
Рисунок 2-1-7 Комбинация из кубов и ромбических додекаэдров
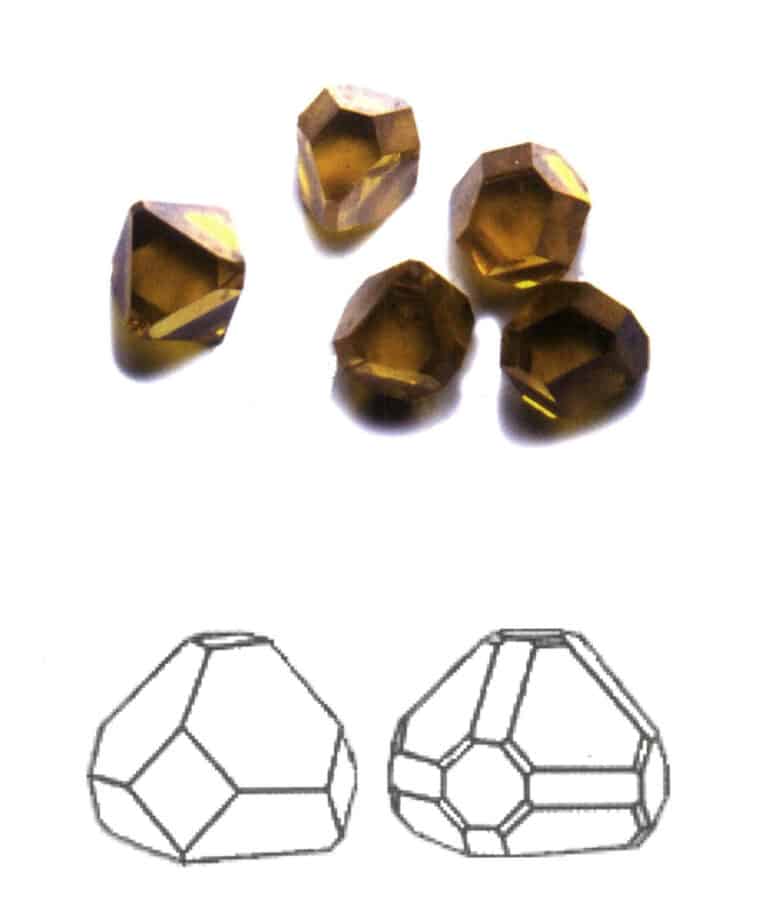
Ключевым моментом идентификации комбинированной формы является наличие в кристалле двух или более граней разной формы.
Когда монокристаллы встречаются в природе, они всегда значительно отличаются от идеальной морфологии монокристаллов (рис. 2-1-9), например, одна грань не обязательно имеет одинаковую форму и размер, а также наблюдается исчезновение граней кристалла, что называется искажением кристаллов.

Искаженные кристаллы также можно назвать настоящими кристаллами, образующимися в природе под влиянием среды роста. Множество кристаллических граней, повторяющихся под фиксированными углами в идеальных кристаллах, не обязательно должны быть одинаковой формы и размера. Тем не менее, для одного и того же типа кристаллов грани одного и того же мономорфного кристалла должны иметь одинаковый рисунок и физические свойства. Углы между соответствующими гранями кристалла остаются неизменными, отражая симметрию, присущую самому кристаллу. Кристаллы, встречающиеся в реальности, искажены в разной степени.
Двойниковые кристаллы также можно описать как реальные кристаллы, образующиеся в природе под влиянием среды роста. Множество граней кристалла, повторяющихся под фиксированными углами в идеальных кристаллах, не обязательно должны быть одинаковой формы и размера. Тем не менее, для одного и того же типа кристаллов грани одной формы должны иметь одинаковые рисунки и физические свойства. Углы между соответствующими гранями кристалла остаются неизменными, отражая симметрию, присущую самому кристаллу. Все кристаллы, встречающиеся в реальности, в той или иной степени являются двойниками.
3. Привычки кристаллизации кристаллов
Кристаллы, образующиеся в природе, никогда не могут иметь идеальную форму. Если они растут в промежутках между слоями горных пород, окруженные породой, естественная форма кристалла будет искажена. Даже выращенные в лаборатории кристаллы будут деформироваться под воздействием гравитации. Только в условиях нулевой гравитации на Международной космической станции ученые могут вырастить кристаллы идеальной формы, к которой они стремятся.
Хотя формы кристаллов несовершенны, каждый тип минеральных кристаллов имеет тенденцию расти или группироваться вместе различными способами или привычками.
Каждый минерал формируется в определенных условиях, и его повадки отражают условия его формирования. Некоторые минералы, такие как кварц, имеют сложные и изменчивые условия образования. Таким образом, кварц также обладает множеством привычек.
В общем случае под привычками кристаллов понимаются характеристики определенного кристалла, склонные к формированию определенной формы при определенных внешних условиях. Иногда речь идет о распространенных типах простой формы этого кристалла.
Исходя из степени развития кристаллов в трехмерном пространстве, кристаллические габитусы делятся на три основных типа.
(1) Уни-направленное расширение
Кристаллы вытянуты в одном направлении, имеют столбчатую, ациклическую, волокнистую форму и т. д. Минералы, такие как берилл, турмалин, горнбленд и малахит, часто демонстрируют эту форму (рис. 2-1-10 - рис. 2-1-11).

Рисунок 2-1-10 Столбчатый аквамарин (вверху) и диаграмма его кристаллической габитуса (внизу)

Рисунок 2-1-11 Волокнистый малахит (вверху) и диаграмма его кристаллических габитусов (внизу)
(2) Би-направленное расширение
Кристаллы вытянуты в плоскости, имеют пластинчатую, листовидную, чешуйчатую и т. д. формы, что часто наблюдается у таких минералов, как вольфрамит, слюда, плюмбаго и танзанит (рис. 2-1-12).
(3) Три-направленная изометрия
Кристаллы развиваются равномерно в трех направлениях, представляя собой изометричные, зернистые формы, такие как шпинель, гранат, алмаз, пирит и флюорит, часто демонстрирующие эту привычку (рис. 2-1-13, 2-1-14).

Рисунок 2-1-12 Пластинчатый габитус танзанита (вверху) и диаграмма его габитуса (внизу)

Рисунок 2-1-13 Октаэдрический габитус драгоценного камня шпинель (вверху) и диаграмма его габитуса (внизу)
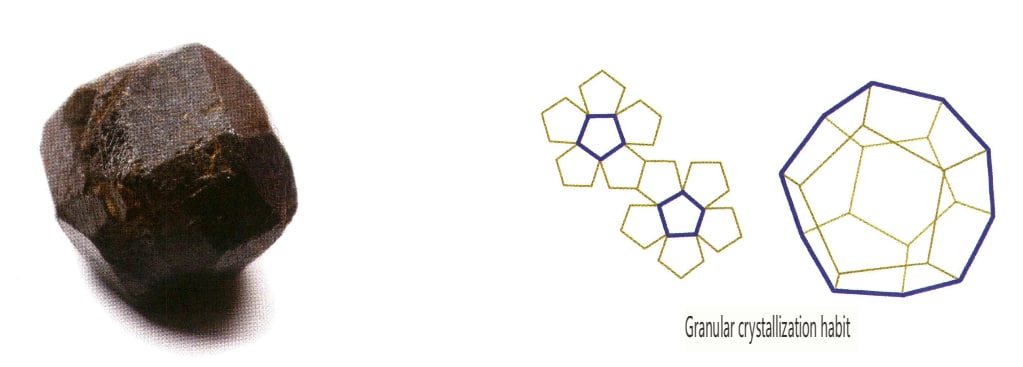
Кроме того, существуют переходные типы, такие как короткостолбчатые, пластинчатостолбчатые, полосчатые и толстостолистные формы.
Химический состав и структура кристалла в основном определяют его форму. Она также тесно связана с внешними условиями при формировании кристалла (такими как температура, давление, концентрация, вязкость и примеси), например, различия в форме кристаллов между алмазами и синтетическими кристаллами алмазов.
4. Регулярная агрегация кристаллов
В природе можно встретить как отдельные кристаллы (рис. 2-1-15), так и два или более отдельных кристаллов, растущих вместе и образующих единое целое. Это явление, когда несколько кристаллов растут вместе, называется агрегацией кристаллов. Агрегацию кристаллов можно разделить на нерегулярную и регулярную. Нерегулярную агрегацию кристаллов можно понимать как коллективную, о чем подробнее будет рассказано в третьей главе. Регулярная агрегация кристаллов имеет четыре распространенных типа: параллельная агрегация, бикристаллы, зарастание и взаимозарастание (рис. 2-1-16 - 2-1-18). В этом разделе в основном рассматривается тип регулярной агрегации, известный как бикристаллы.

Рисунок 2-1-15 Монокристалл (турмалин)
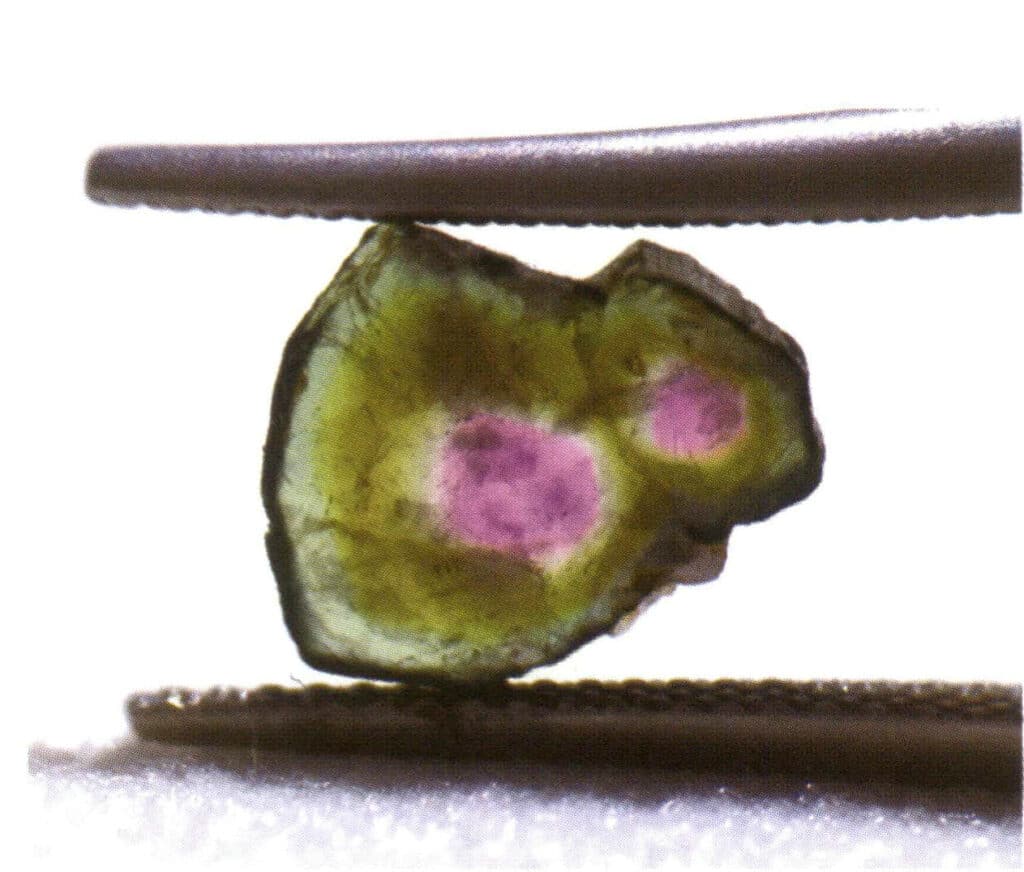
Рисунок 2-1-16 Параллельная агрегация (Когда несколько кристаллов одного типа растут параллельно в пространстве, это называется параллельной агрегацией. В это время соответствующие грани и ребра выросших кристаллов параллельны друг другу).

Рисунок 2-1-17 Двойной кристалл (шпинель)

Рисунок 2-1-18 Наращивание (один тип кристалла растет на поверхности другого кристалла в определенном кристаллографическом направлении, также известен как эпитаксиальный рост)
Бикристаллы - это регулярное объединение двух или более одинаковых кристаллов в соответствии с определенными правилами симметрии. (Двойная ось, двойная плоскость) Соответствующие грани, ребра и углы двух соседних кристаллов не являются полностью параллельными. Тем не менее, они могут отражать друг друга с помощью таких симметричных операций, как вращение и инверсия вращения, что позволяет им совпадать или выравниваться.
4.1 Ключевые моменты для идентификации бикристаллов
① Вогнутые углы видны в двойниковых кристаллах (рис. 2-1-19).
② Стилолит: Микроморфология и другие характеристики кристаллических поверхностей с обеих сторон стилолита прерывисты (рис. 2-1-20).
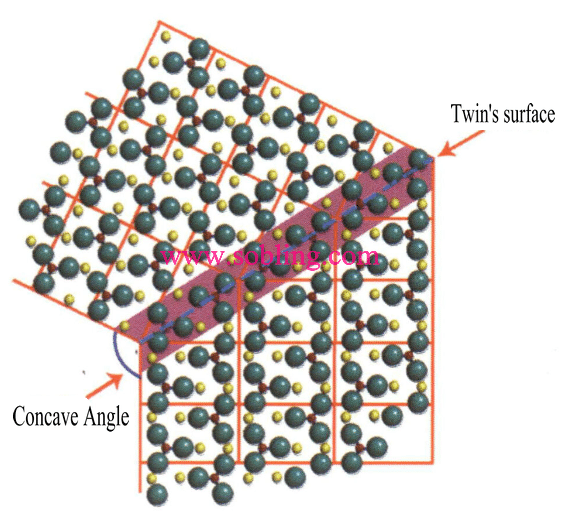
Рисунок 2 - 1-19 Вогнутый угол близнеца
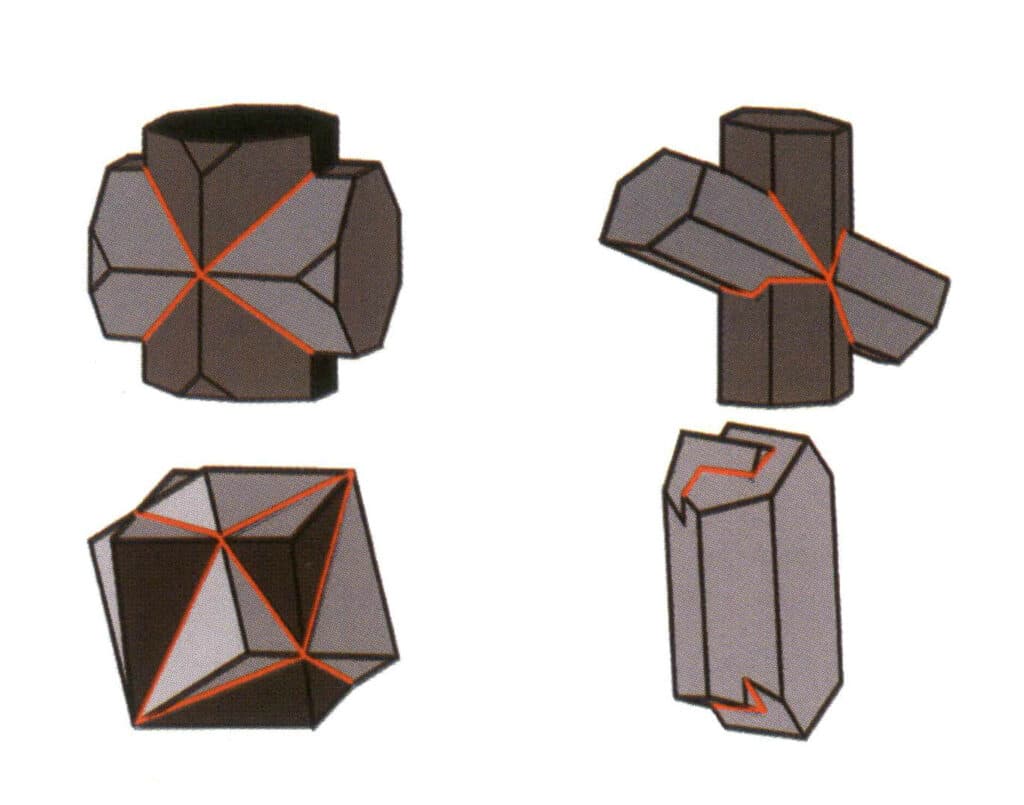
Рисунок 2-1-20 Стилолит (разные цвета на рисунке обозначают разные кристаллы; красные линии указывают на сдвоенный стилолит)
③ Полоса двойникования: На гранях кристаллов или плоскостях спайности видны тонкие полосы двойникования (рис. 2-1-21).
④ Фигура травления: Появление рисунка травления указывает на наличие двойникования (рис. 2-1-22)

Рисунок 2-1-21 Схематическая диаграмма полисинтетических близнецов

Рисунок 2-1-22 Поверхность шпинели с перевернутыми треугольными ямками.
⑤ Появление псевдосимметрии: возникновение отношений симметрии, не согласующихся с присущей монокристаллу точечной группой (рис. 2-1-23 - рис. 2-1-24).

Рисунок 2-1-23 Монокристалл хризоберилла

Рисунок 2-1-24 Коленчатый двойник хризоберилла
Двойникование подразделяется на пять типов по характеристикам укладки: контактные двойники (Рисунок 2-1-25 - Рисунок 2-1-26), полисинтетические двойники (Рисунок 2-1-27), взаимопроникающие двойники (Рисунок 2-1-28), триплетный кристалл (Рисунок 2-1-29) и сложные двойники, среди которых распространены первые четыре типа.


Рисунок 2-1-26 Контактное двойникование шпинели (вверху) и его схема (внизу)

Рисунок 2-1-27 Полисинтетический двойник лабрадорита (вверху) и его схема (внизу)
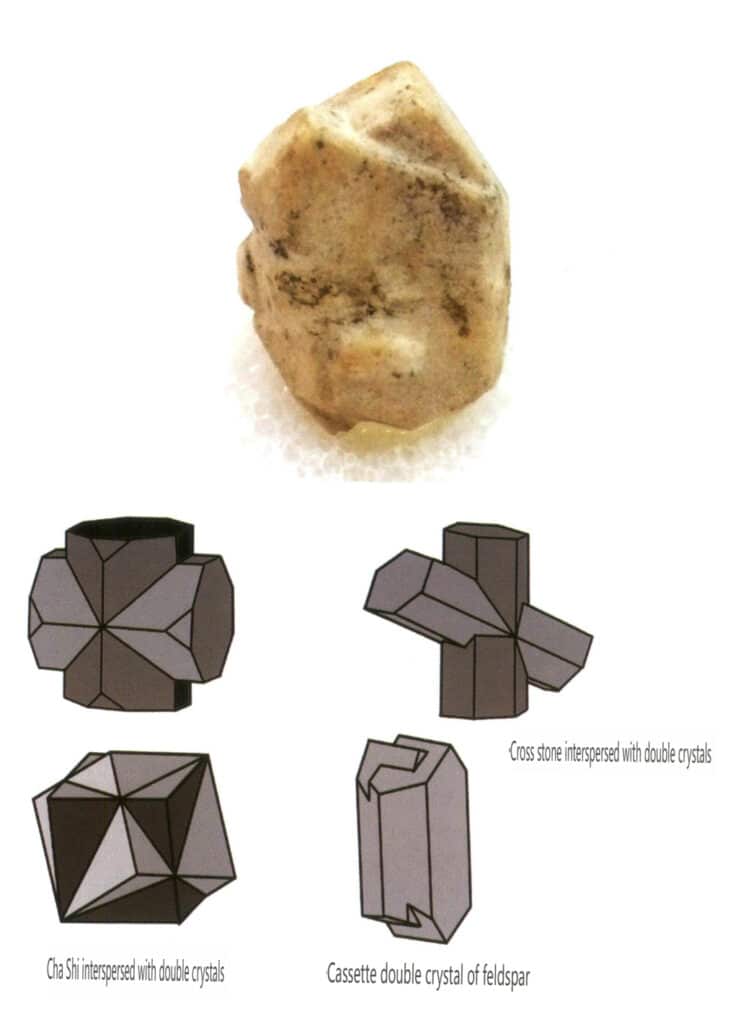
Рисунок 2-1-28 Двойные кристаллы полевого шпата (вверху) и схема взаимопроникающих двойных кристаллов других типов (внизу)

Рисунок 2-1-29 Тригональное двойникование хризоберилла (вверху) и его схема (внизу)
4.2 Образование бикристаллов
① Образуется в процессе роста кристалла, может развиваться из сдвоенных кристаллических зародышей или маленьких кристаллов, растущих в зависимости от положения сдвоенного кристалла.
② Образуется в процессе трансформации гетероморфизма, например, когда α-кварц превращается в β-кварц, образуя двойники.
③ Образуется в результате механического воздействия, когда часть кристалла скользит вдоль определенной направленной плоскости, образуя деформационные двойники, например, двойники кальцита.
5.Кристаллические узоры для лица
Когда в природе обнаруживаются кристаллы, они часто имеют незавершенную форму (рис. 2-1-30) и особый рисунок поверхности. Иногда они растут вместе в кластеры (рис. 2-1-31), которые часто значительно отличаются от знакомых нам стандартных геометрических многогранников, таких как кубы и шестигранные призмы. Это явление называется реальной формой кристаллов. Реальная форма кристаллов имеет подробную классификацию в кристаллографии, например, искаженные кристаллы, выпуклые кристаллы, изогнутые кристаллы, плавающие кристаллы, полосы на гранях кристаллов, фигуры травления, полосы двойникования и т.д.

Рисунок 2-1-30 Рубиновый кристалл

Рисунок 2-1-31 Кристаллы пирита (слева показаны несколько кристаллов пирита, растущих вместе, а справа - один кристалл пирита)
В этом разделе рассматриваются в основном узоры кристаллических граней в реальной форме кристаллов.
Теоретически плоскости кристаллов гладкие и плоские. Однако в процессе роста или растворения кристаллов на их поверхности часто остаются неровные регулярные узоры, которые обычно называют узорами кристаллических граней. К таким узорам относятся полосы роста, слои роста, спиральные узоры, бугры роста и фигуры травления. Узоры кристаллической грани, обсуждаемые в этой книге, в основном относятся к полосам кристаллической грани и фигурам травления, которые можно наблюдать невооруженным глазом или при малом увеличении.
Полосы на гранях кристаллов представляют собой серию параллельных прямых линий на поверхности кристалла, возникающих в результате многократного сближения и попеременного роста различных одиночных форм. Их также называют "комбинационными полосами", они видны только на поверхности кристаллов, которые также называют полосами роста. Например, гексагонально-призматическая кристаллическая грань кварца часто имеет гексагонально-призматические и ромбически-додекаэдрические мелкокристаллические грани, попеременно развитые в совокупность поперечных полос (рис. 2-1-32).

Под фигурами травления понимаются ямки специфической формы (т.е. ямки травления), остающиеся на грани кристалла в результате коррозии после его формирования. Фигуры травления контролируются расположением элементарных частиц внутри грани кристалла. Таким образом, формы и ориентация фигур травления варьируются среди различных минералов и отдельных форм одного и того же кристалла. Например, фигуры травления на различных монокристаллах алмаза различаются; треугольные ямки видны на октаэдрических кристаллах (Рисунок 2-1-33), четырехугольные ямки - на кубических гранях, перекрывающиеся четырехугольные ямки образуют решеткоподобный узор, а линейные узоры или микроскопические дископодобные узоры видны на ромбических додекаэдрах (Рисунок 2-1-34).

Рисунок 2-1-33 Видимые перевернутые треугольные ямки на октаэдрическом кристалле алмаза

Рисунок 2-1-34 Линейно-узорчатая текстура, видимая на ромбовидных додекаэдрических кристаллах
Только фигуры травления на одной грани кристалла одной формы могут быть одинаковыми, поэтому фигуры травления часто используются для идентификации минералов и определения принадлежности граней кристалла к одной и той же форме (рис. 2-1-35 - рис. 2-1-42).

Рисунок 2-1-35 Полосы на деревянном полу с инкрустацией кристаллами флюорита

Рисунок 2-1-36 Природная треугольная фигура травления в рубине (обычные горизонтальные полосы в рубинах, линии роста параллельны ромбоэдрическому направлению, природные травления в треугольной или шестиугольной форме)

Рисунок 2-1-37 Поверхностные продольные полосы турмалина

Рисунок 2-1-38 горизонтальные полосы на поверхности кристалла

Рисунок 2-1-39 Травление фигур на поверхности кристалла

Рисунок 2-1-40 Поверхностные продольные полосы топаза

Рисунок 2-1-41 Топографическое изображение кристалла топаза

Рисунок 2-1-42 Фигуры травления шпинели
Раздел II 47 Типы кристаллических форм
В кристаллографии существует 146 различных одиночных форм, которые можно разделить на 47 геометрических форм, исходя из их геометрических форм, существующих независимо друг от друга. Эти геометрические формы названы следующим образом:
① Называются в зависимости от характеристик формы поперечного сечения, например, тригональная призма, тетрагональная призма, гексагональная призма, ромбоэдрическая бипирамида и т.д.
② Названы в соответствии с формой одиночной формы, например, цилиндр, двойной конус, куб и т.д.
③ Называются в зависимости от количества геометрических граней, например, одногранник, октаэдр и т.д.
④ Названы в соответствии с формой геометрических граней, например, ромбоэдр, пентаконтаэдр и т.д.
В кристаллографии одиночные формы делятся на четыре категории: общие формы и специальные формы, закрытые формы и открытые формы, регулярные формы и нерегулярные формы, левосторонние формы и правосторонние формы. В этой главе мы кратко рассмотрим закрытые и открытые формы.
Закрытые формы относятся к тем, чьи кристаллические грани могут заключать в себе замкнутое пространство. Они делятся на три основные категории: полиэдрические, косоугольные и бипирамидальные, всего 30 типов. Каждая категория имеет более подробную классификацию; например, полиэдрический класс подразделяется на тетраэдрический, октаэдрический, кубический и т. д. (рис. 2-1-43 - 2-1-48).

Рисунок 2-1-43 Класс тетраэдра
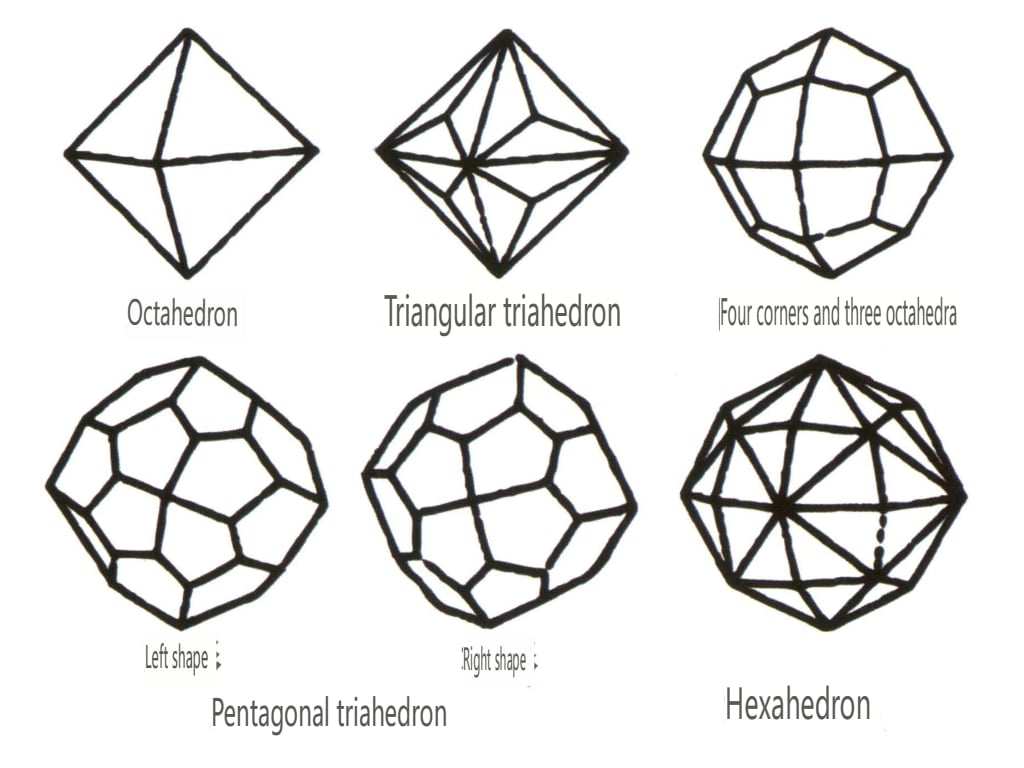
Рисунок 2-1-44 0ктаэдрический класс
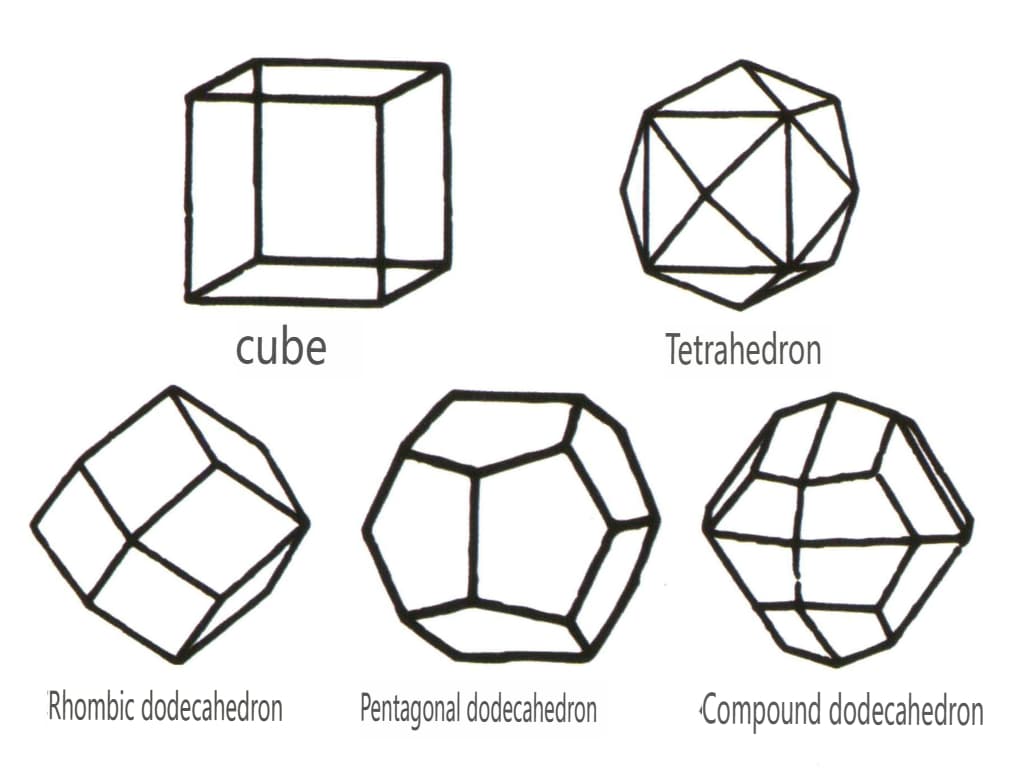
Рисунок 2-1-45 Кубические и додекаэдрические классы
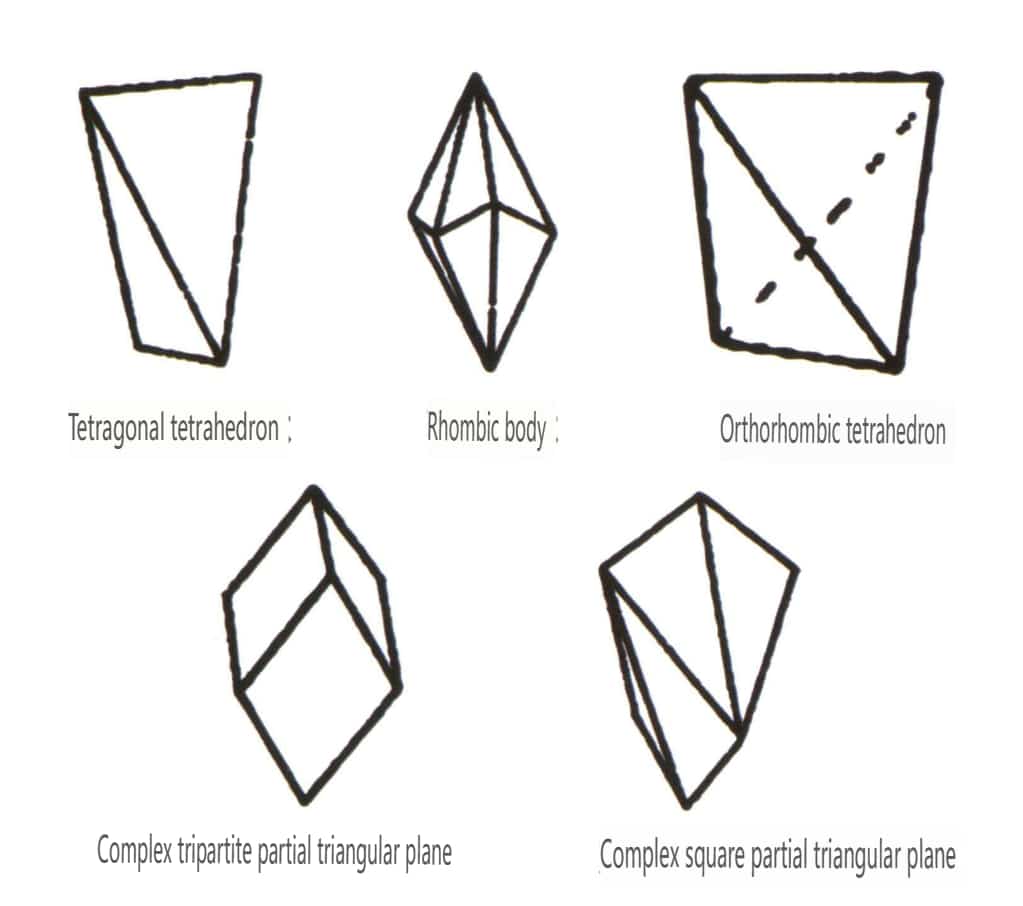
Рисунок 2-1-46 Другие многогранные типы
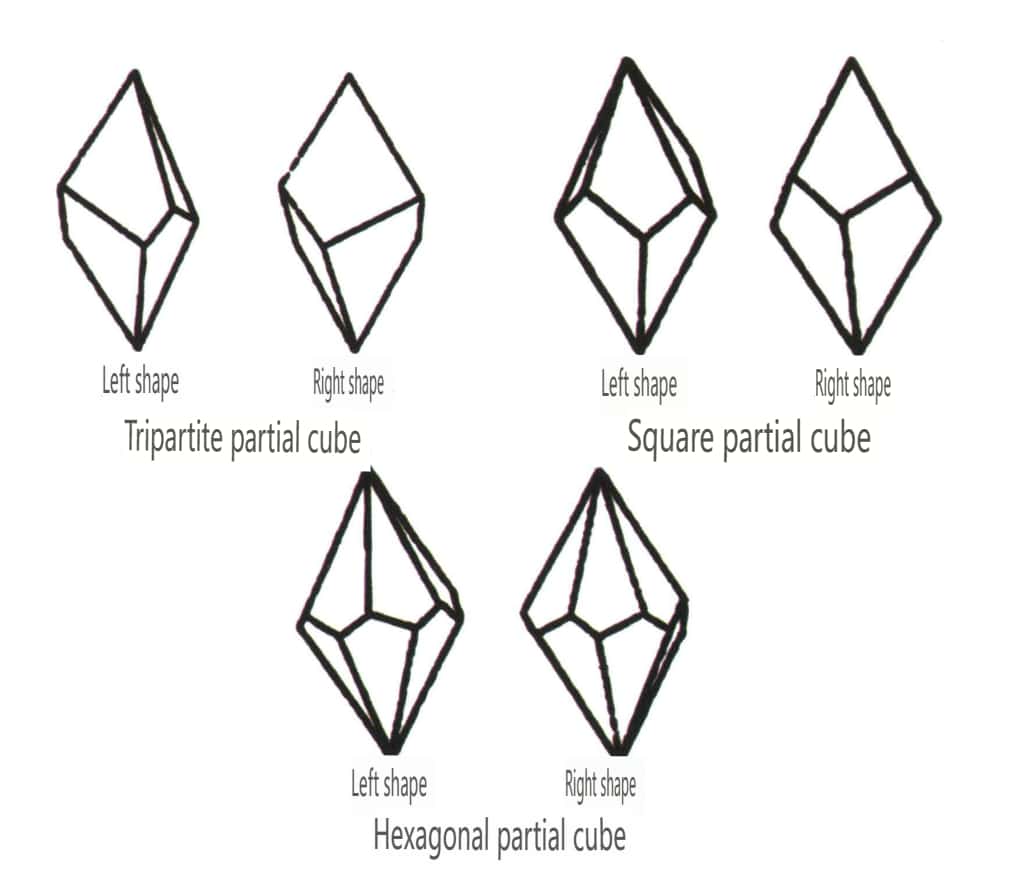
Рисунок 2-1-47 Косая комбинированная форма Класс
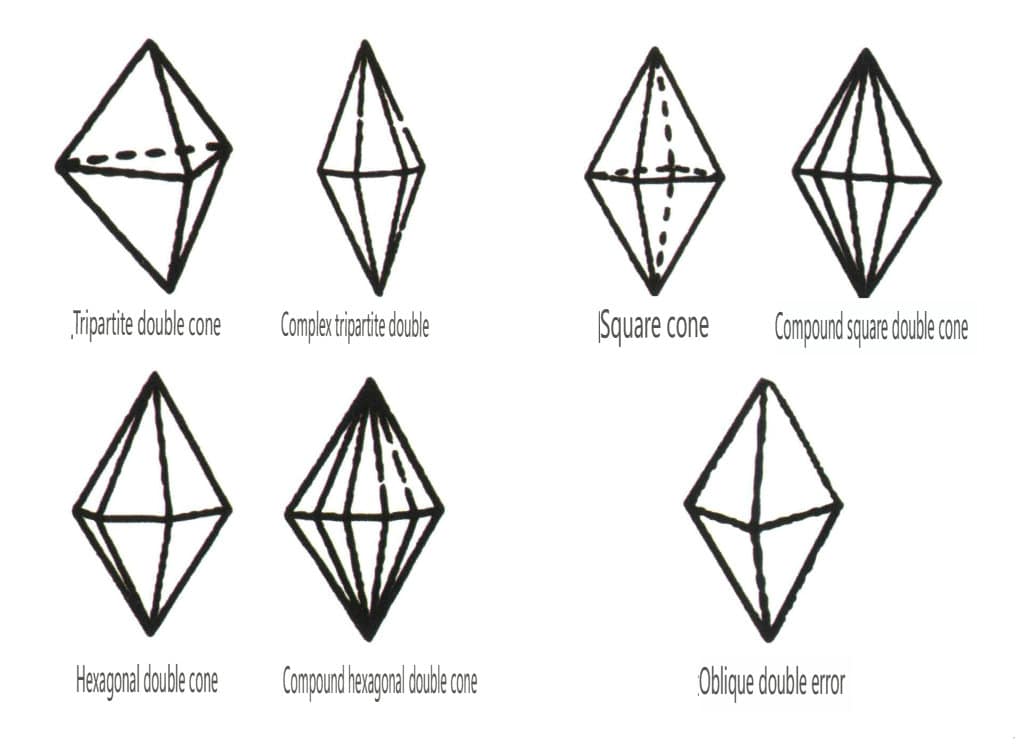
Рисунок 2-1-48 Класс двойной пирамиды
К открытым формам относятся те, грани кристаллов которых не могут заключать в себе замкнутое пространство; они делятся на четыре основные категории: одногранные, двухгранные, столбчатые и однопирамидальные, всего 17 типов (рис. 2-1-49 и 2-1-51).
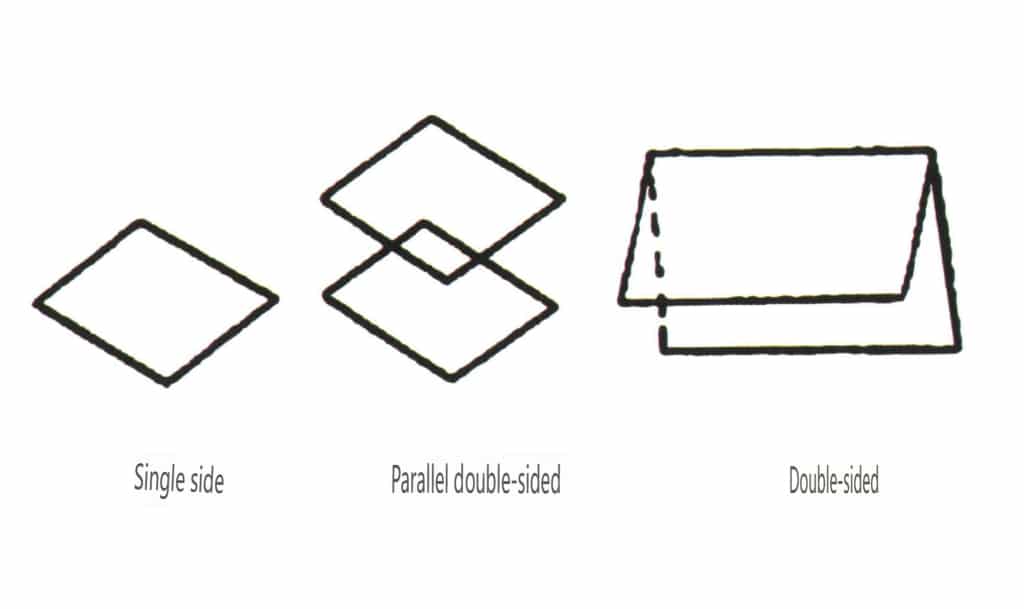
Рисунок 2-1-49 Односторонний и двусторонний
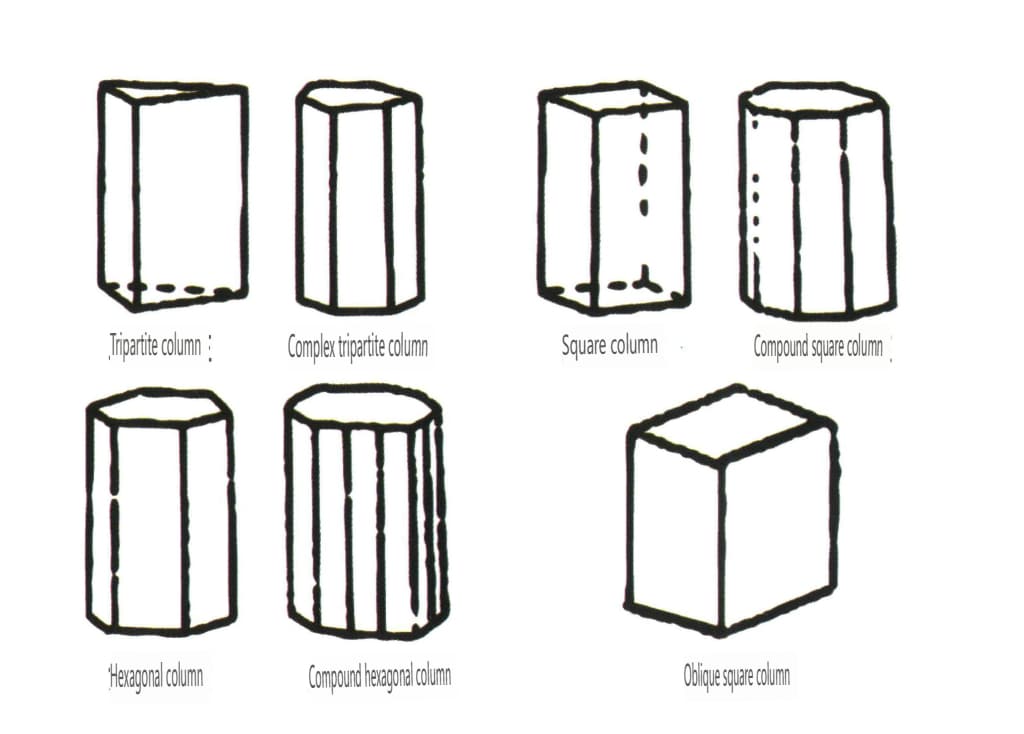
Рисунок 2-1-50 Колонки

Раздел III Классификация кристаллов
1. Симметрия кристаллов
Симметрия - это абстрактное понятие, связанное с изучением настоящих кристаллов и необработанных материалов драгоценных камней. Она описывает повторение, которое наблюдается, когда кристаллическая структура связана с направлением или плоскостью, проходящей через нее. На этом основана классификация кристаллов.
Симметрию кристалла можно понимать с микроскопической точки зрения как метод описания повторяемости кристаллической структуры, а с макроскопической - как повторение двух или более геометрических граней, одинаковых по форме и размеру, но отличающихся по направлению, в соответствии с определенными правилами. Этот шаблон повторения можно описать с помощью осей симметрии и плоскостей симметрии, причем каждая ось симметрии или плоскость симметрии называется элементом симметрии. При наблюдении или выводе о симметрии объекта это действие называется выполнением операций над симметрией.
2. Элементы симметрии кристаллов
В кристаллографии существует четыре элемента симметрии: ось симметрии, плоскость симметрии, ротоинверсионные оси симметрии и симметричный центр. В данном случае речь пойдет о двух элементах симметрии - оси симметрии и плоскости симметрии.
2.1 Ось симметрии
(1) Понятие оси симметрии и их обозначение.
Ось симметрии - это воображаемая прямая линия, которая показывает, сколько раз базовый уровень (рис. 2-2-1 - рис. 2-2-2) оказывается в одном и том же положении, когда решетчатая структура поворачивается на 360° вокруг этой воображаемой линии. Это число может быть только 2, 3, 4 или 6 раз в 4 случаях. Его также можно понимать как воображаемую линию, проходящую через центр геометрического тела, и вращать геометрическое тело вдоль этой линии на 360°. Предположим, что форма геометрического тела после поворота на определенный угол совпадает с формой геометрического тела в исходном нуле градусов. В таком случае эта воображаемая линия называется осью симметрии.
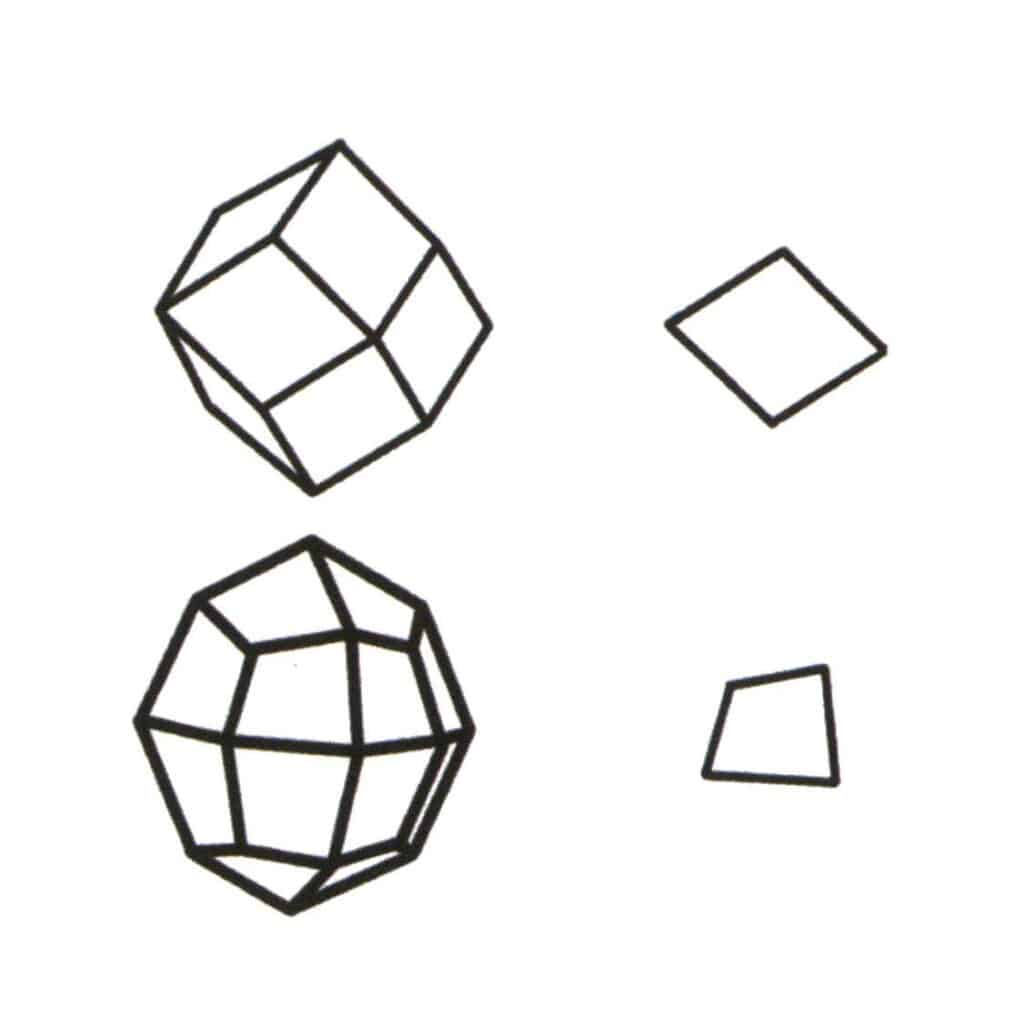
Рисунок 2-2-1 Выбор базового уровня для одиночной формы.
Базовый уровень одиночной формы - это наименьшая повторяющаяся плоскость, составляющая симплекс. В левом верхнем углу рисунка показан ромбический додекаэдр - замкнутая форма, состоящая из одного типа граней. Наименьшей повторяющейся плоскостью является ромб, показанный в правом верхнем углу, поэтому базовым уровнем для ромбического додекаэдра является ромб. Слева внизу на рисунке показан четырехугольный октаэдр - замкнутая фигура, состоящая из одного типа граней. Наименьшей повторяющейся плоскостью является четырехугольник, показанный в правом нижнем углу, поэтому базовым уровнем для четырехугольного октаэдра является четырехугольник.
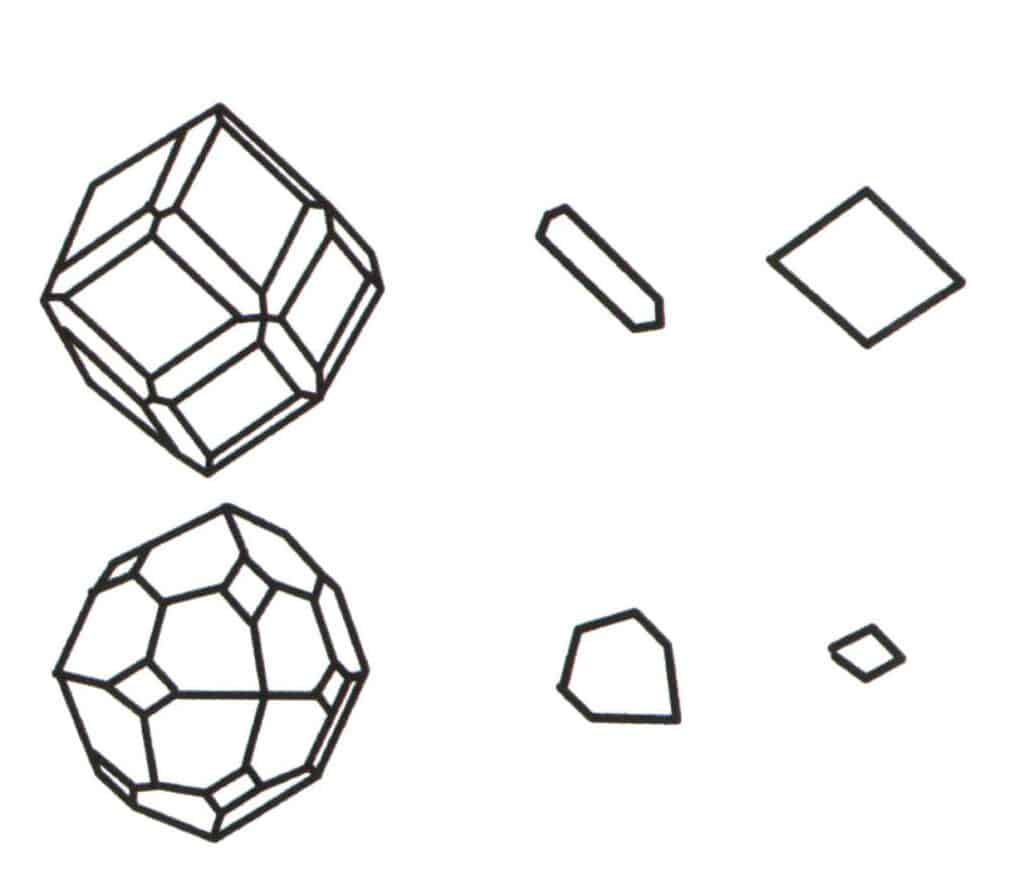
Рисунок 2-2-2 Выбор базового уровня для политопа.
Объединение множества простых форм образует комбинаторную форму, а выбор базового уровня для комбинаторной формы - это суждение о единичных формах, которые объединяются в комбинаторную форму. Первый столбец слева на рисунке представляет собой комбинаторную форму (образованную объединением одиночных форм додекаэдра и тетраэдра), и это геометрическое тело является замкнутой фигурой, состоящей из двух типов граней. Шестиугольник представляет собой минимальную повторяющуюся плоскость во втором столбце, а ромб - справа в третьем столбце. Следовательно, базовым уровнем для комбинаторной формы в первом столбце является либо шестиугольник, либо ромб. При расчете оси симметрии в качестве базового уровня для записи симметрии может быть выбрана только одна форма.
Ось симметрии обозначается заглавной буквой L, а порядок расположения осей n написанная в правом верхнем углу L, записывается как Lⁿ. Например, 2-кратная ось изображается как L², 3-кратная - как L³, 4-кратная - как L⁴, а 6-кратная - как L⁶. L⁶, L⁴, L³ принято называть осью высшего порядка.
Кристаллы могут иметь оси симметрии в разных направлениях, и количество этих несовпадающих осей симметрии условно записывается слева от L. Например, шесть вторичных осей обозначаются как 6L² (Рисунок 2-2-3 - Рисунок 2-2-9), три третичные оси обозначаются как 3L³ (Рисунок 2-2-10 - Рисунок 2-2-14), четыре третичные оси обозначаются как 4L³ (Рисунок 2-2-15 - Рисунок 2-2-18), а одна гексагональная ось обозначается как L⁶ (Рисунок 2-2-19).
Если кристалл имеет несколько осей симметрии, записанный метод упорядочивает их слева направо в порядке убывания, при этом номер оси симметрии записывается слева от соответствующей оси, например, L⁶6L², 3L⁴4L³6L².
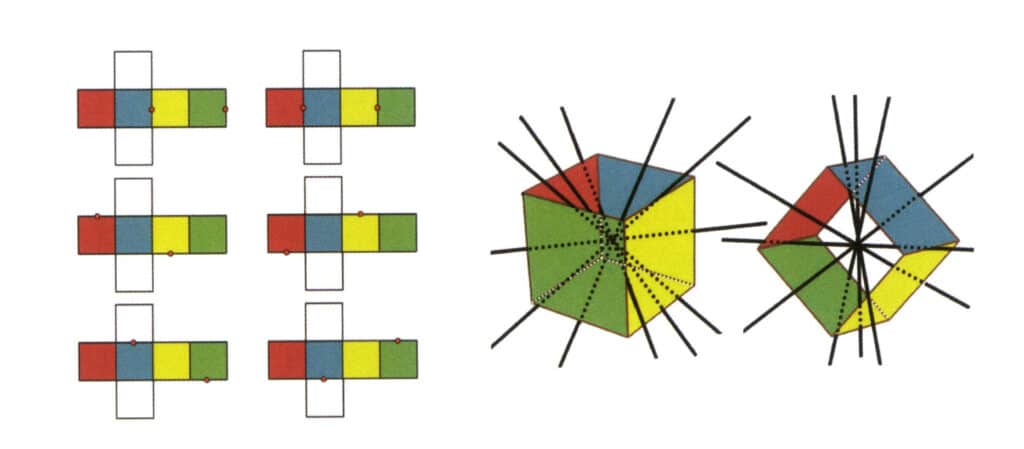
Рисунок 2-2-3 Вторичная ось куба
В левой части рисунка показан развернутый вид куба, красными точками обозначены точки пересечения воображаемой линии и граней. В правой части рисунка показан замкнутый куб, где вторичная ось может находиться в средней точке параллельных линий граней, в средней точке параллельных прямоугольных граней или в точках пересечения трех или более параллельных граней, напоминающих прямоугольник. или более параллельных граней, напоминающих прямоугольник.
Копирайт @ Sobling.Jewelry - Пользовательские ювелирные изделия производителя, OEM и ODM ювелирный завод
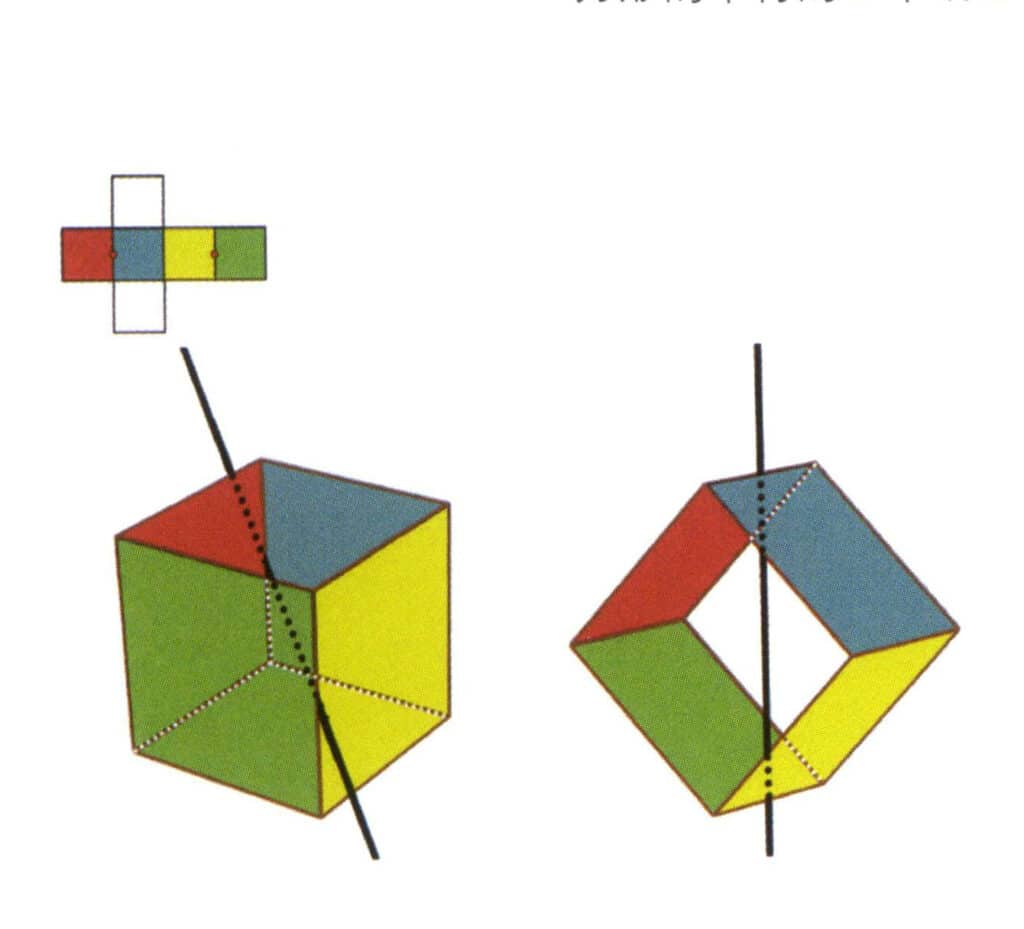
Рисунок 2-2-4 Первая вторичная ось куба
Выберите середину параллельных линий, как показано на рисунке. Представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°. Базовые уровни разных цветов, но одинаковой формы будут повторяться дважды в одном и том же положении (красная и синяя грани, желтая и зеленая грани, две бесцветные грани и три набора повторяющихся граней. Хотя три набора повторяющихся граней появятся, поскольку воображаемая линия не изменила своего положения и угла, вторичная ось записывается только один раз). Эта воображаемая линия записывается как вторичная ось.
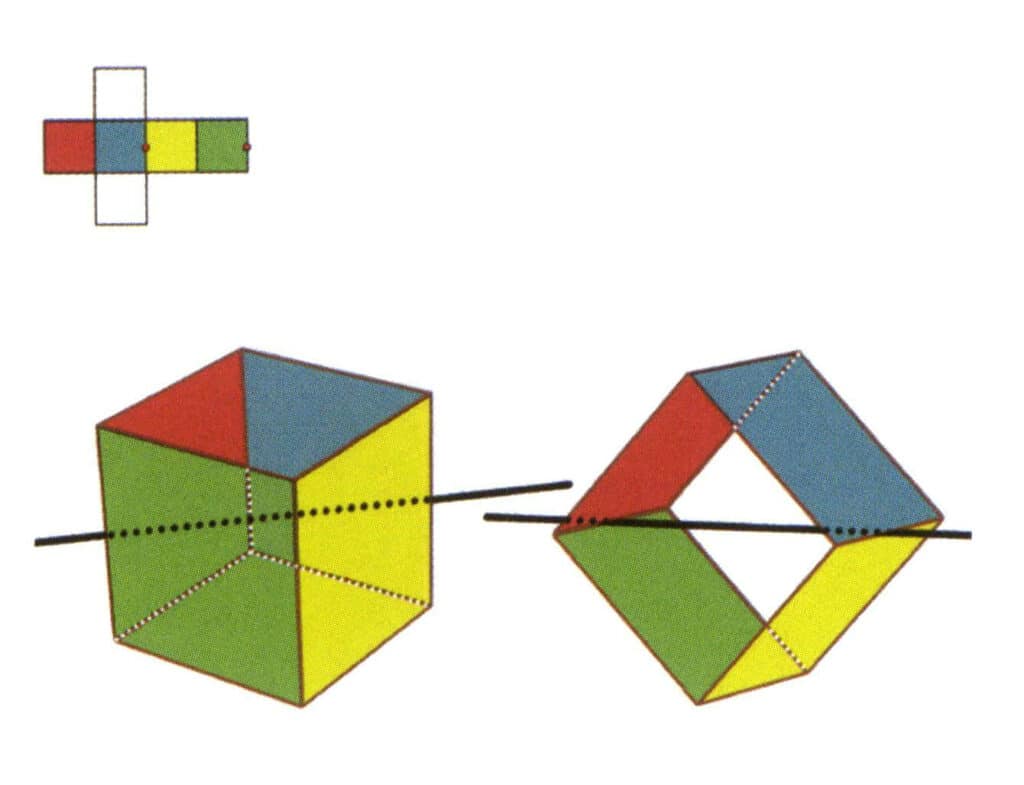
Рисунок 2-2-5 Вторая вторичная ось куба
Выберите середину параллельных линий, как показано на рисунке. Представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°. Базовые уровни с разными цветами, но одинаковой формой будут повторяться дважды в одном и том же положении (красная и зеленая грани, желтая и синяя грани, две бесцветные грани и три набора повторяющихся граней). Эта воображаемая линия записывается как вторая вторичная ось.
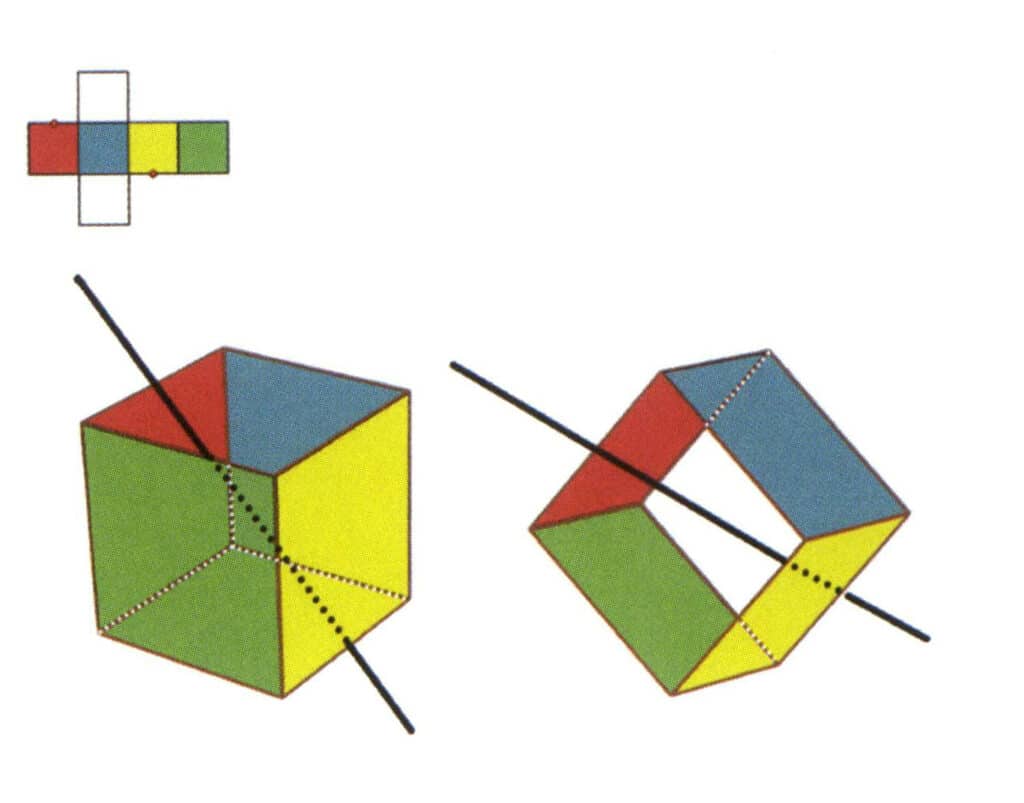
Рисунок 2-2-6 Третья вторичная ось куба.
Выберите середину параллельных линий, как показано на рисунке. Представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°. Базовые уровни разных цветов, но одной и той же формы будут повторяться дважды в одном и том же положении (красная и бесцветная грани, зеленая и синяя грани, бесцветная и желтая грани, три набора повторяющихся граней). Эта воображаемая линия записывается как третья вторичная ось
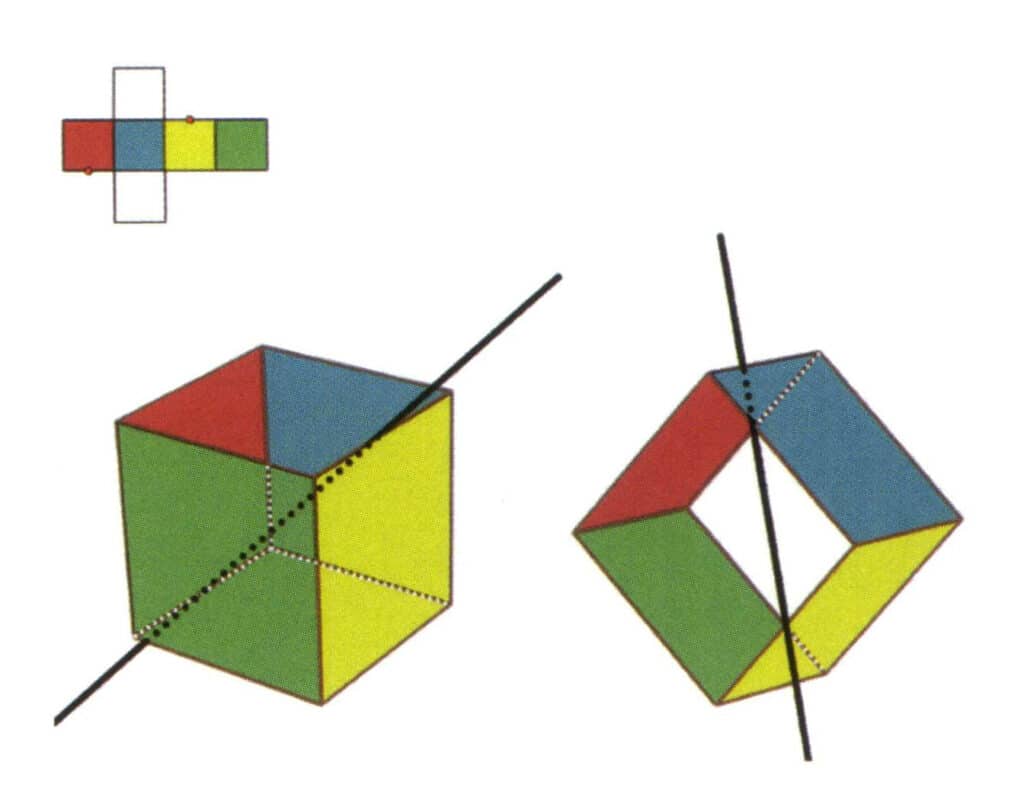
Рисунок 2-2-7 Четвертая вторичная ось куба
Выберите середину параллельных линий, как показано на рисунке, представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°; разноцветные, но одинаковые по форме опорные плоскости будут повторяться в одном и том же положении дважды (красная и бесцветная грани, зеленая и синяя грани, бесцветная и желтая грани - три набора повторяющихся граней); эта воображаемая прямая линия записывается как четвертая вторичная ось.
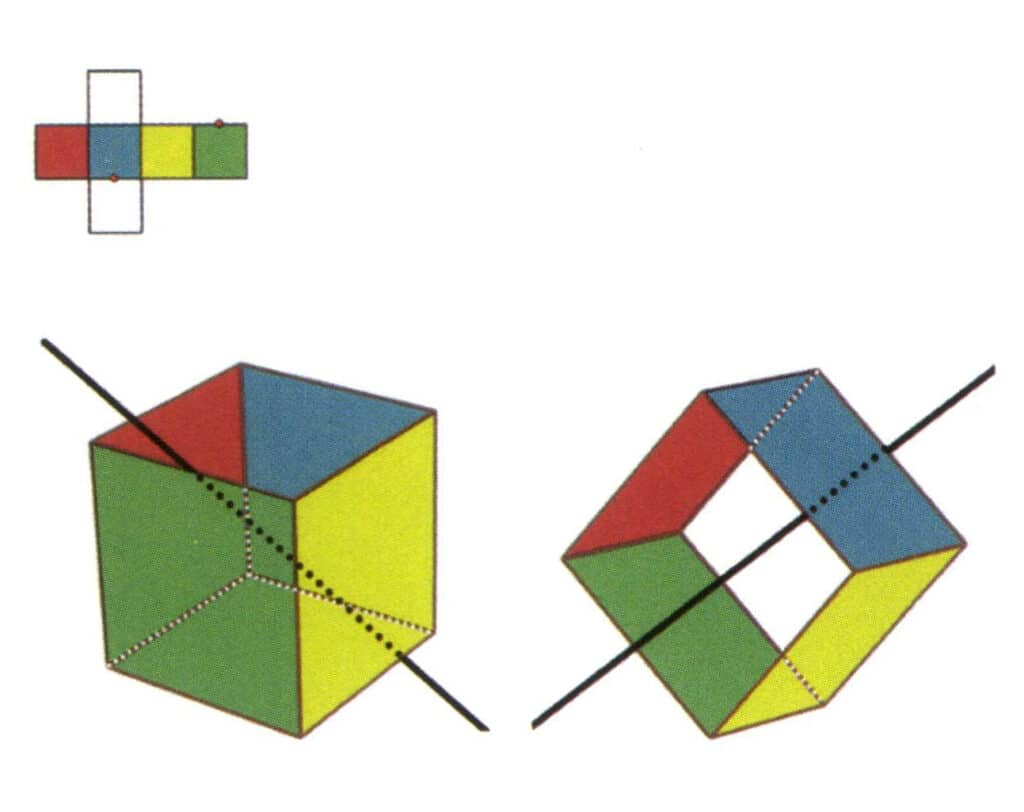
Рисунок 2-2-8 Пятая вторичная ось куба.
Выберите середины параллельных линий, как показано на рисунке, представьте прямую линию, проходящую через середины этих двух граней, поверните куб на 360°, разноцветные, но одинаковые по форме опорные плоскости повторятся в одном и том же положении дважды (красные и бесцветные грани, зеленые и синие грани, бесцветные и желтые грани, три набора повторяющихся граней), эта воображаемая прямая линия записывается как пятая вторичная ось.
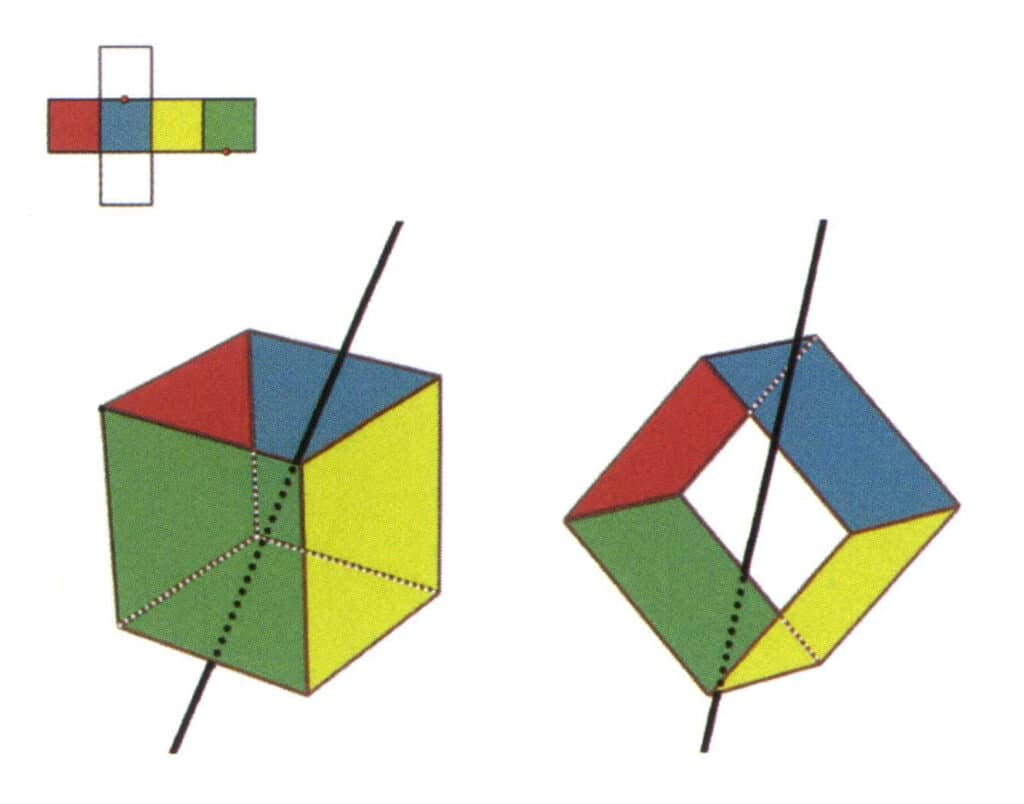
Рисунок 2-2-9 Шестая вторичная ось куба
Выберите середину параллельных линий, как показано на рисунке. Представьте, что через середины этих двух граней проходит прямая линия, поворачивающая куб на 360°. Разноцветные, но одинаковые по форме базовые уровни дважды повторятся в одном и том же положении (зеленые и бесцветные грани, красные и желтые грани, бесцветные и синие грани, три набора повторяющихся граней). Эта воображаемая линия записывается как шестая вторичная ось.
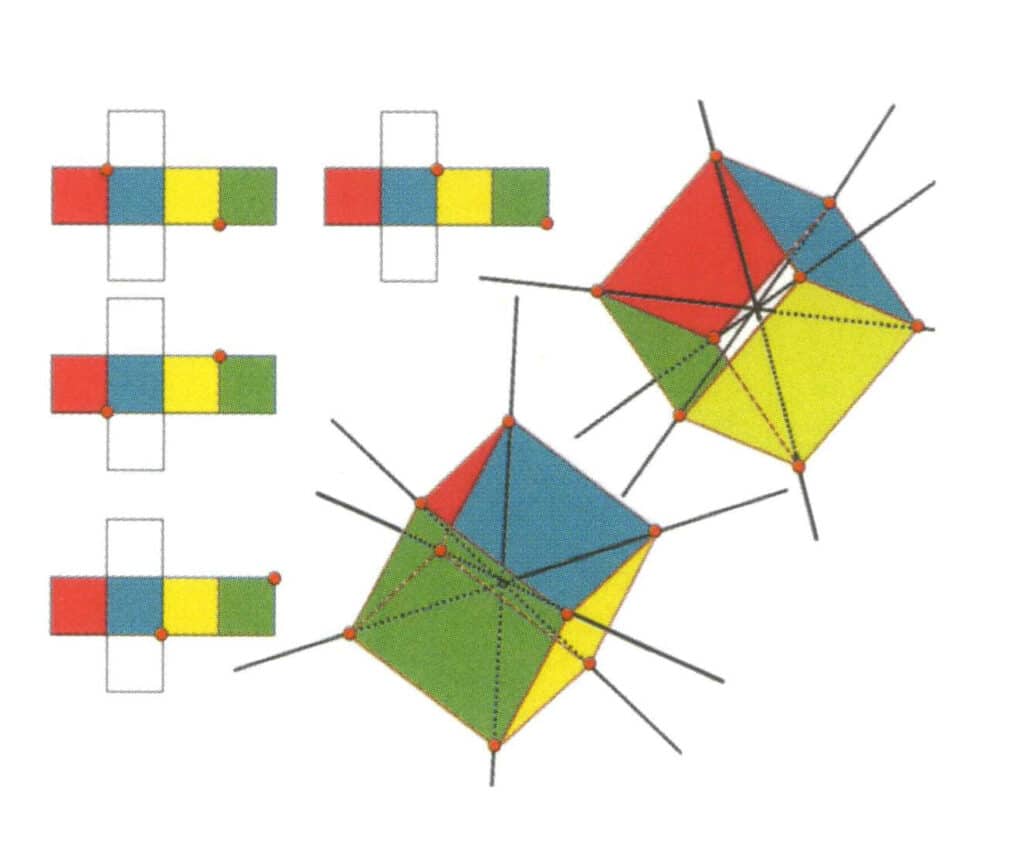
Рисунок 2-2-10 Третичная ось куба
В левой части рисунка показан развернутый вид куба, красной точкой отмечена точка пересечения воображаемой прямой и линии ребра. В правой части рисунка показан закрытый куб; красные точки обозначают точки пересечения воображаемой прямой и граней. Третичная ось может находиться в середине граней параллельного равностороннего треугольника, в точке пересечения трех или более параллельных граней, напоминающих равносторонний треугольник.
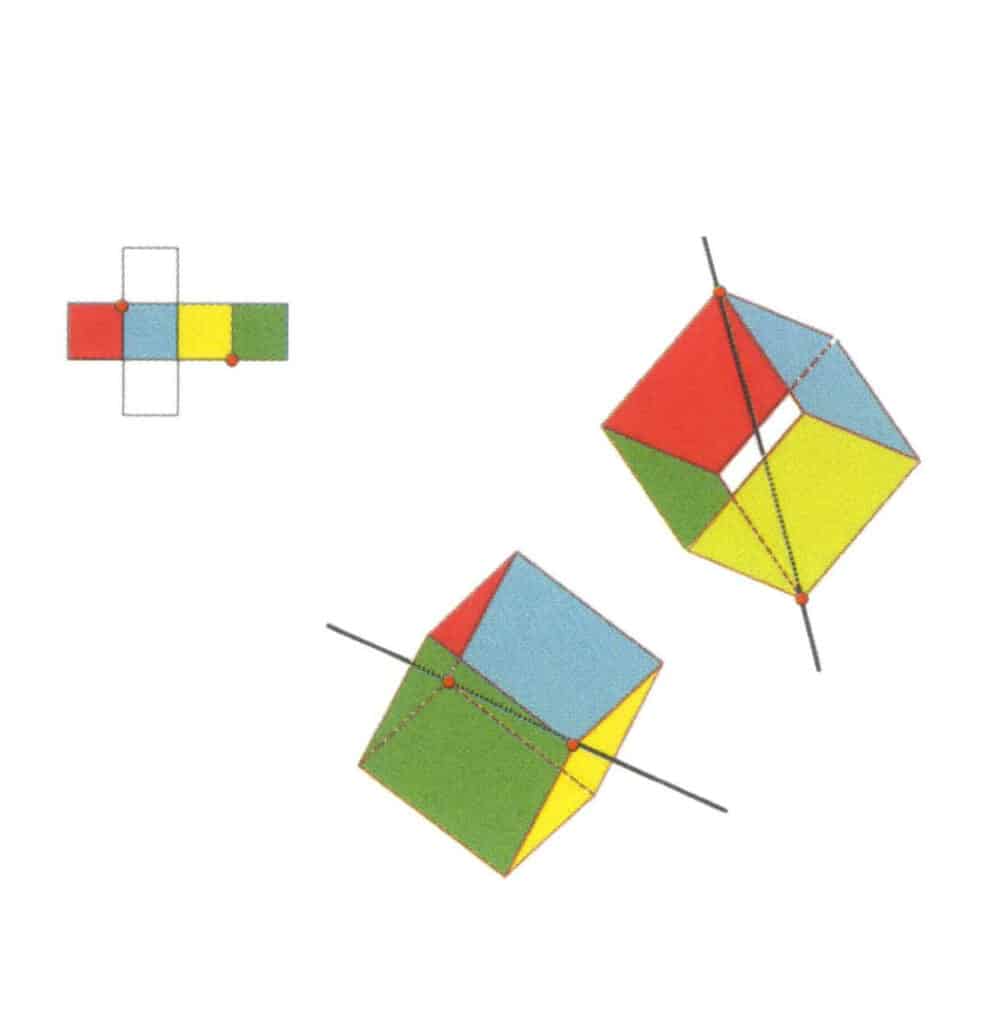
Рисунок 2-2-11 Первая третичная ось куба.
Выберите точки пересечения трех граней, как показано на рисунке, представьте прямую линию, проходящую через середины этих двух граней, поверните куб на 360°, разноцветные, но одинаковые по форме опорные плоскости повторятся в одном и том же положении три раза (красная, бесцветная и синяя грани, зеленая, бесцветная и желтая грани, два набора повторяющихся граней), эта воображаемая прямая линия записывается как первая третичная ось
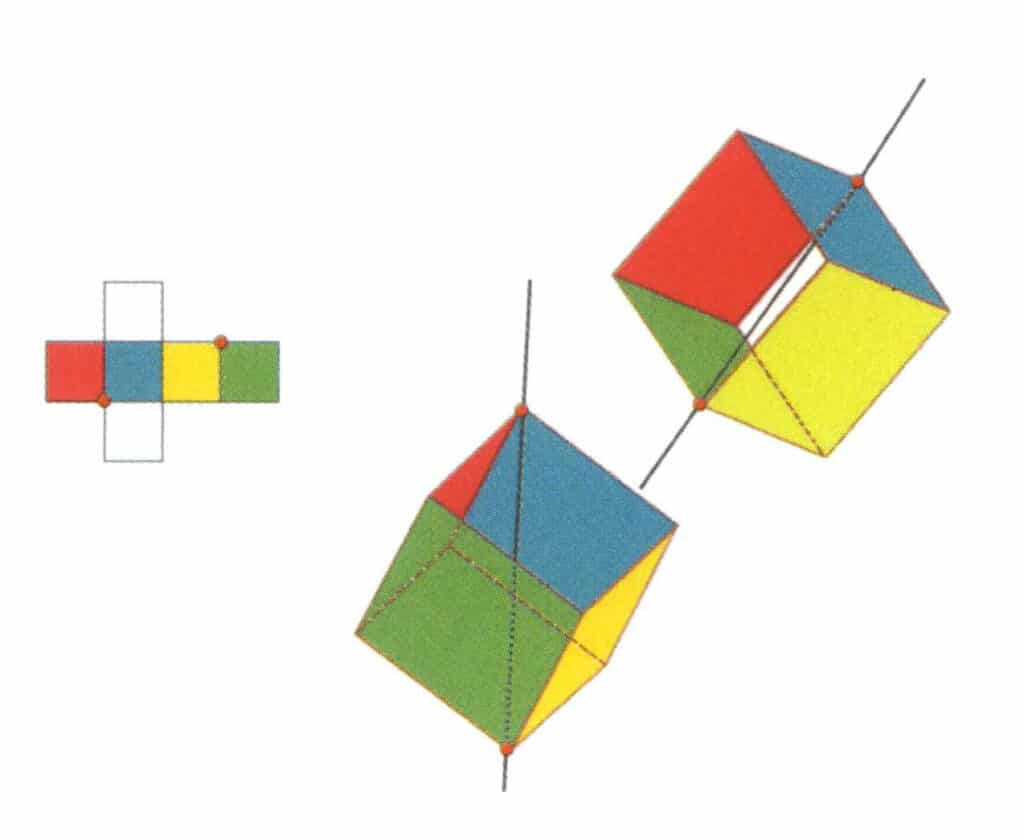
Рисунок 2-2-12 Вторая третичная ось куба.
Выберите точки пересечения трех граней, как показано на рисунке. Представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°. Разноцветные, но одинаковые по форме базовые уровни будут повторяться в одном и том же положении три раза (красная, бесцветная и синяя грани; зеленая, бесцветная и желтая грани - два набора повторяющихся граней). Эта воображаемая линия записывается как вторая третичная ось.
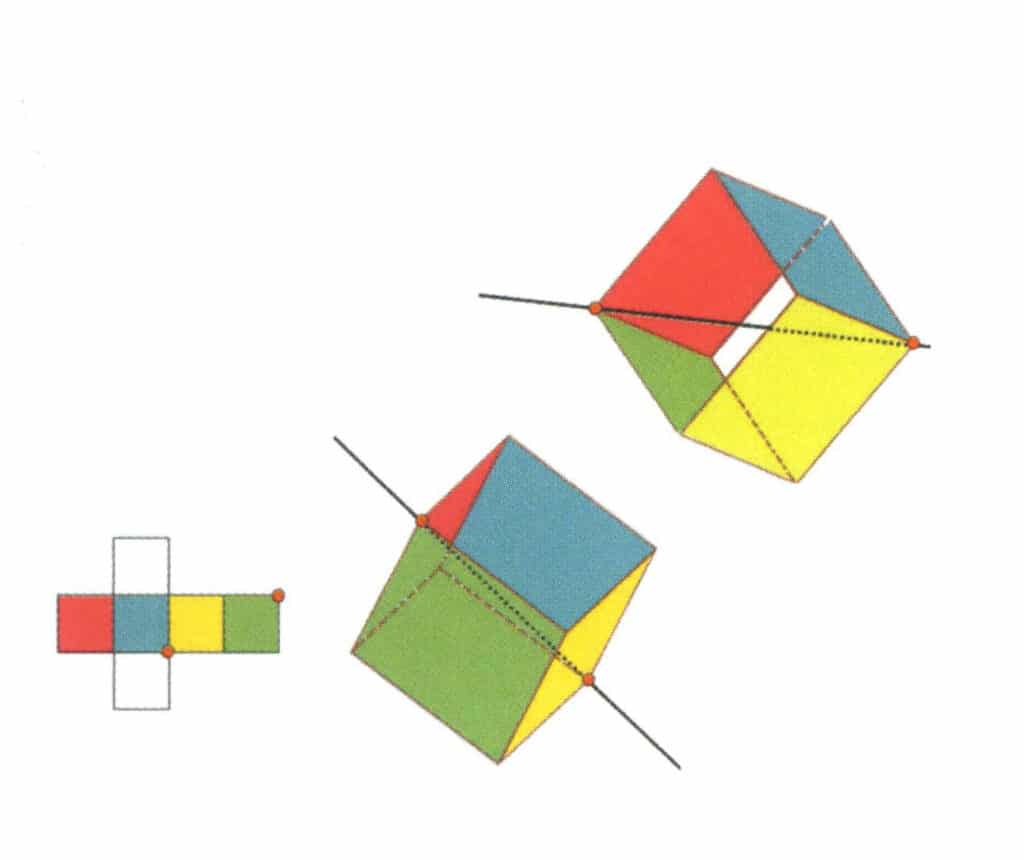
Рисунок 2-2-13 Третья третичная ось куба
Выберите точки пересечения трех граней, как показано на рисунке. Представьте прямую линию, проходящую через середины этих двух граней, и поверните куб на 360°. Разноцветные, но одинаковые по форме базовые уровни будут повторяться в одном и том же положении три раза (красная, бесцветная и зеленая грани; синяя, бесцветная и желтая грани - два набора повторяющихся граней). Эта воображаемая линия записывается как третья третичная ось.
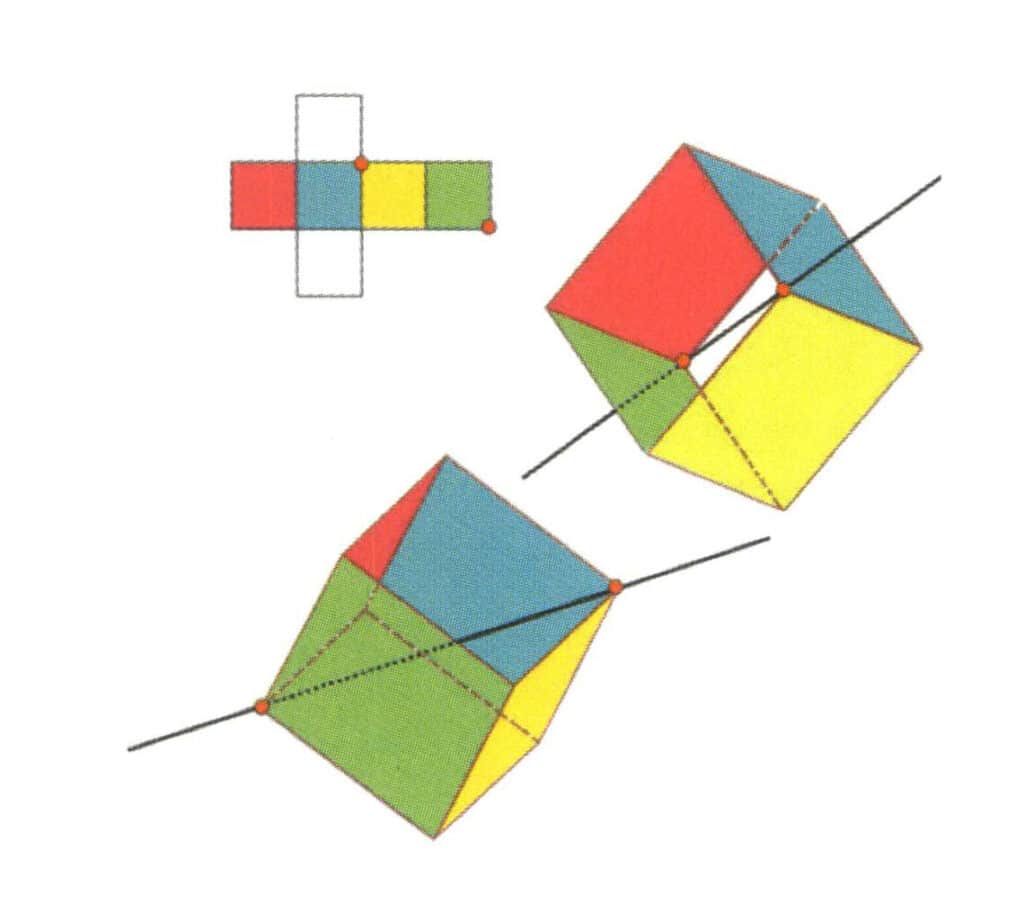
Рисунок 2-2-14 Четвертая кубическая ось куба.
Выберите точку пересечения трех граней, как показано на рисунке, предполагая, что через середину двух граней проходит одна прямая линия, поверните куб на 360°, разные цвета, но одинаковая форма базового уровня будет одинаковой. Повторите это положение три раза (красная, бесцветная, зеленая грани, синяя, бесцветная и желтая грани, два набора повторяющихся граней). Эта воображаемая линия записывается как четвертая кубическая ось.
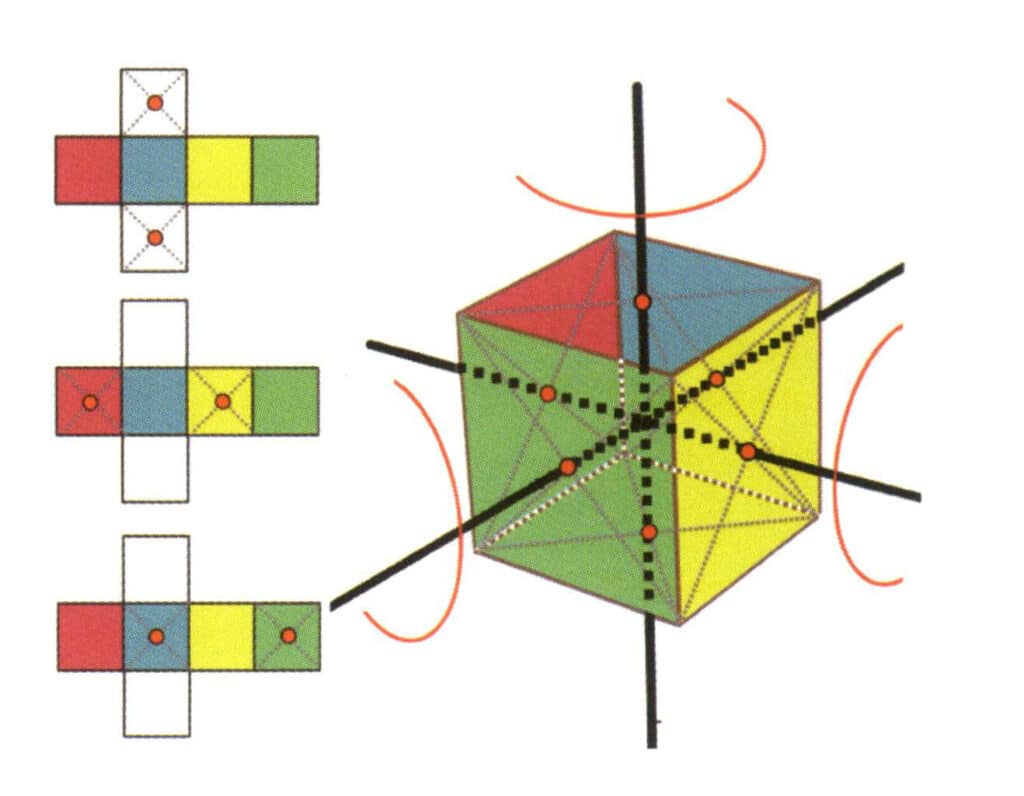
Рисунок 2-2-15 Четвертая ось куба
В левой части рисунка показан развернутый вид куба, красными точками отмечены точки пересечения воображаемой прямой и граней. В правой части рисунка показан закрытый куб, красными точками обозначены точки пересечения воображаемой линии и плоскости. Четвертая ось может появиться в средней точке параллельных граней квадрата, на пересечении трех или более параллельных граней, напоминающих квадрат.
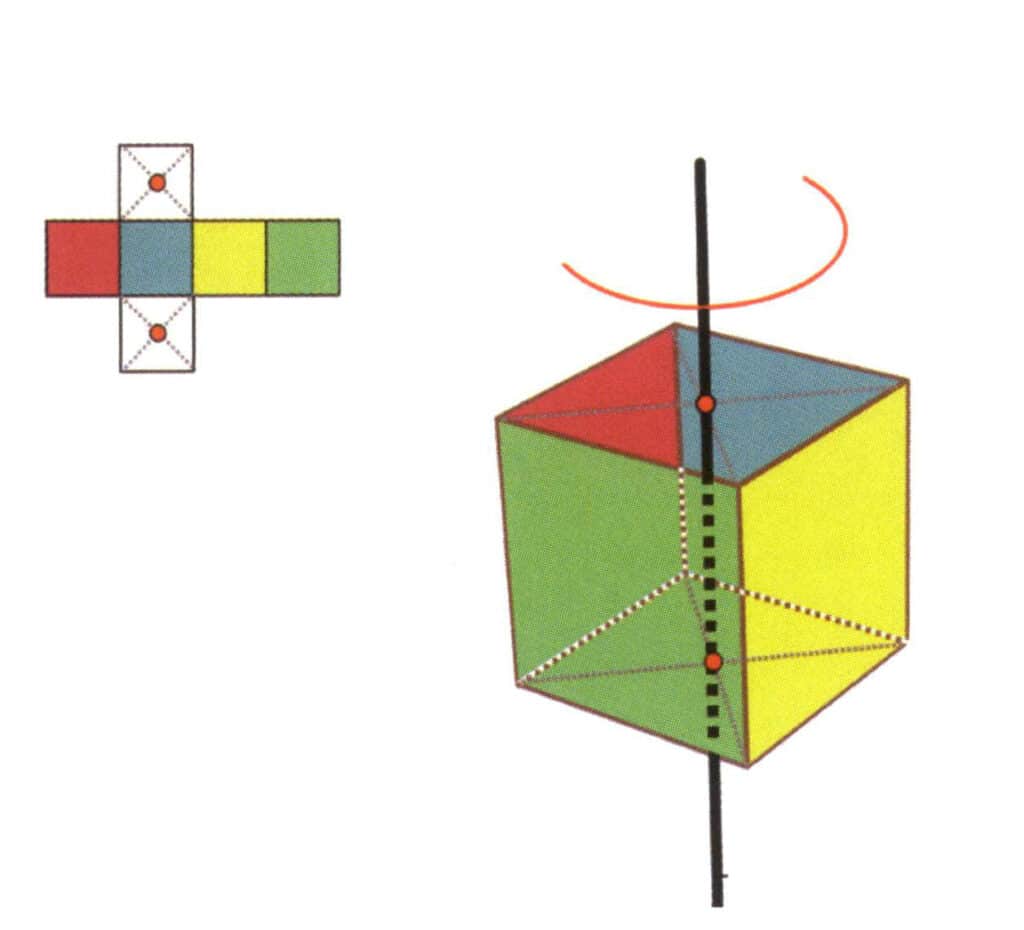
Рисунок 2-2-16 Первая кваритическая ось куба
Выберите средние точки плоскостей, показанных на рисунке, предположите, что через средние точки двух плоскостей проходит прямая линия, и поверните куб на 360°. Разноцветные, но одинаковые по форме грани базового уровня будут повторяться в одном и том же положении четыре раза (красная, синяя, зеленая и желтая грани), и эта гипотетическая прямая линия записывается как четверная ось.
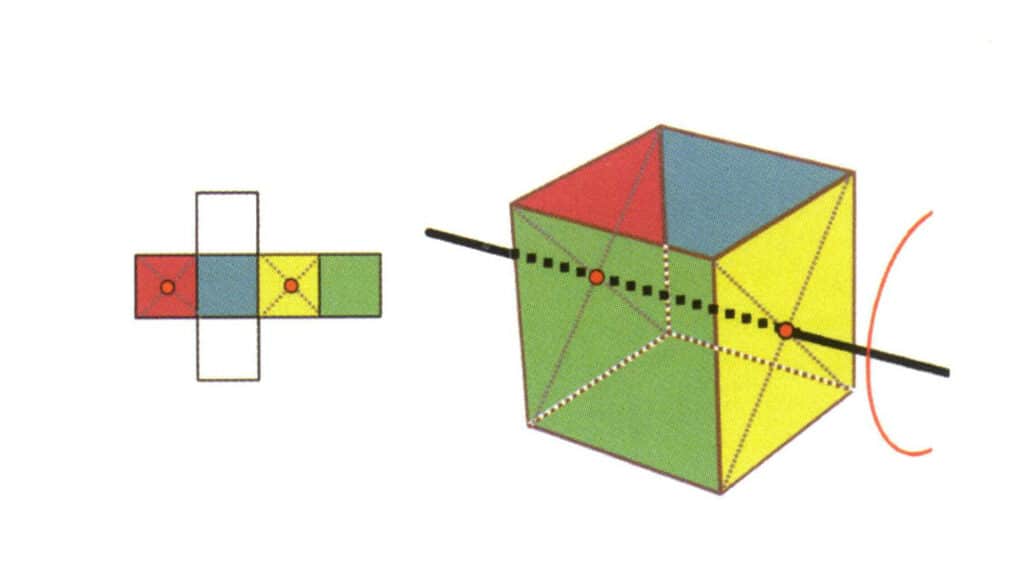
Рисунок 2-2-17 Вторая кваритическая ось куба
Выберите среднюю точку плоскости, как показано на рисунке, проведите прямую линию через куб и поверните куб на 360°; поверхность базового уровня разного цвета, но одинаковой формы будет повторяться четыре раза в одном и том же положении (бесцветная синяя грань сверху, бесцветная зеленая грань снизу), и эта воображаемая линия будет записана как вторая квадрическая ось.
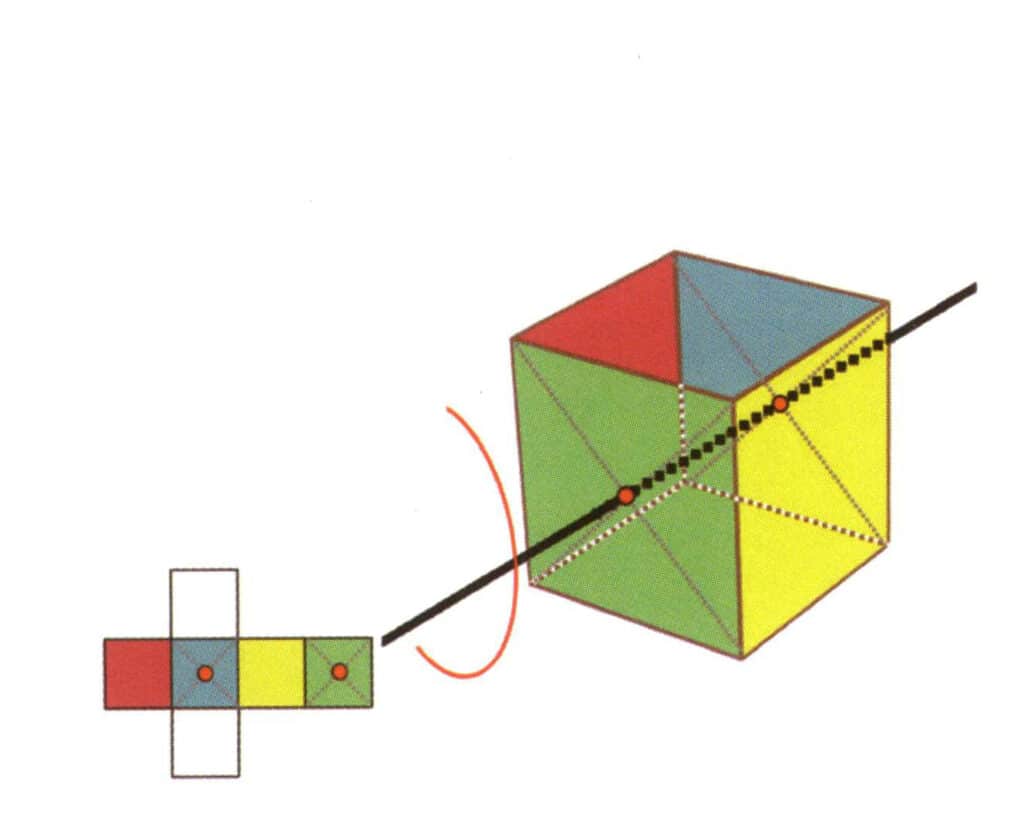
Рисунок 2-2-18 Третья кваритическая ось куба
Выберите среднюю точку плоскости, как показано на рисунке, проведите через куб прямую линию и поверните куб на 360°. Базовый уровень разного цвета, но одинаковой формы повторится четыре раза в одном и том же положении (бесцветная, красная грань сверху, бесцветная, желтая грань снизу), и эта воображаемая линия будет записана как третья, четвертая оси
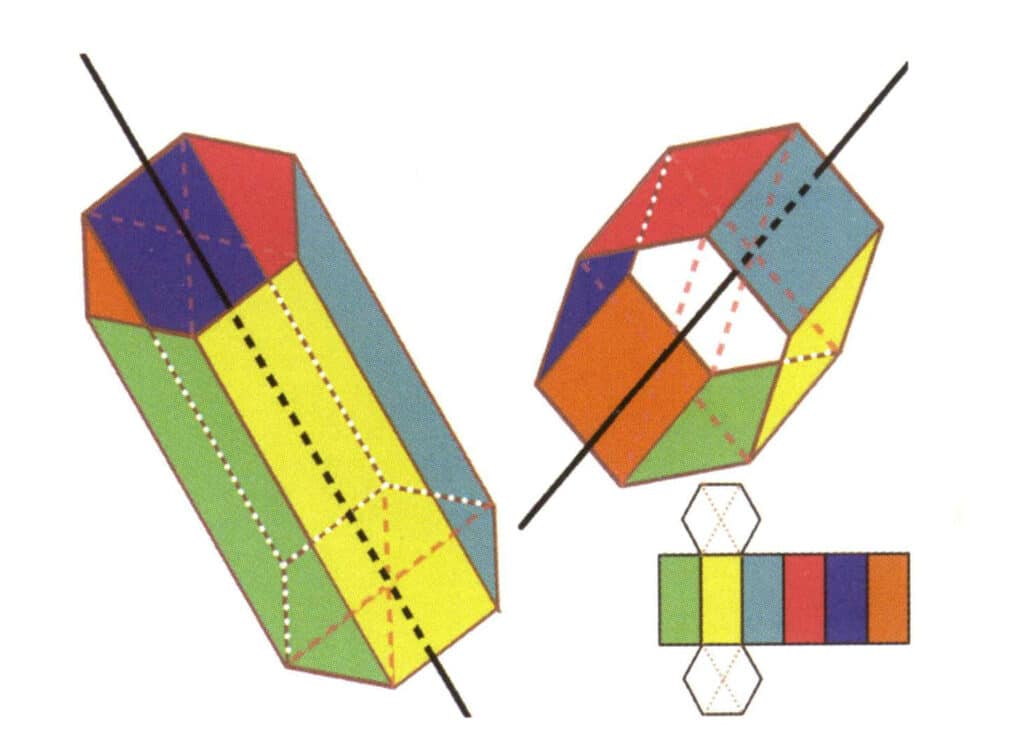
Рисунок 2-2-19 Шесть осей шестигранной призмы
Черные линии слева и справа вверху представляют собой шесть осей шестиугольной призмы. Справа внизу - расширение гексагональной призмы. Секстическая ось может находиться в средней точке граней параллельного шестиугольника или в точке пересечения шести граней шестиугольника.
(2) Соображения для нахождения оси симметрии.
① Существует пять типов положения оси симметрии.
Средняя точка двух параллельных граней, например, положение вторичной оси куба.
Средняя точка двух параллельных плоскостей, например, положение оси куба.
Между двумя вершинами (точками пересечения нескольких граней), например, положение третичной оси куба.
Средняя точка между вершиной и параллельной плоскостью, например, положение третичной оси тетраэдра.
Средняя точка краевой линии и средняя точка параллельной плоскости, например, положение вторичной оси треугольной призмы.
② Выбор оси симметрии в одном направлении происходит по принципу наименьшего числа. Например, согласно принципу наименьшего числа, если в одном направлении найдено шесть осей симметрии и три оси симметрии, то в конечном итоге это будет записано как L³. Оси симметрии в разных направлениях должны быть записаны в соответствии с найденным числом.
Следует отметить, что за исключением шестикратной оси симметрии и четырехкратной оси симметрии, которые не могут проявляться одновременно, и только одна шестикратная ось может проявляться, другие оси симметрии могут сосуществовать в различных формах или в нескольких экземплярах.
③ Базовый уровень должен быть выбран как наименьшая единичная плоскость; две или более пересекающихся плоскостей не могут быть выбраны в качестве базового уровня. В противном случае это повлияет на точность определения оси симметрии.
④ При записи количества осей симметрии необходимо определить, сколько раз одна и та же форма и размер плоскости повторяется в одном и том же положении.
⑤ Если существует вторичная ось вертикальной симметрии Lⁿ(n = 3, 4 или 6), то должно существовать n вторичных осей, вертикальных по отношению к Lⁿ.
2.2 Самолет Симметрия
(1) Понятие и метод записи плоскости Симметрия
Плоскость симметрии - это воображаемая плоскость, которая при разрезании кристалла вдоль этой плоскости позволяет каждой половине кристалла быть зеркальным отражением другой половины (рис. 2-2-20). В одной и той же кристаллической структуре такая плоскость может появляться максимум 9 раз (Рисунок 2-2-21), то есть она может быть разрезана 9 различными способами, и две половинки могут полностью совпадать. Конечно, не все кристаллические структуры имеют плоскости симметрии.
Заглавная буква P обозначает плоскость симметрии. Некоторые кристаллы имеют несколько несовпадающих плоскостей симметрии, и количество этих плоскостей симметрии условно пишется слева от P; например, четыре плоскости симметрии обозначаются как 4P, а одна плоскость симметрии - как P.
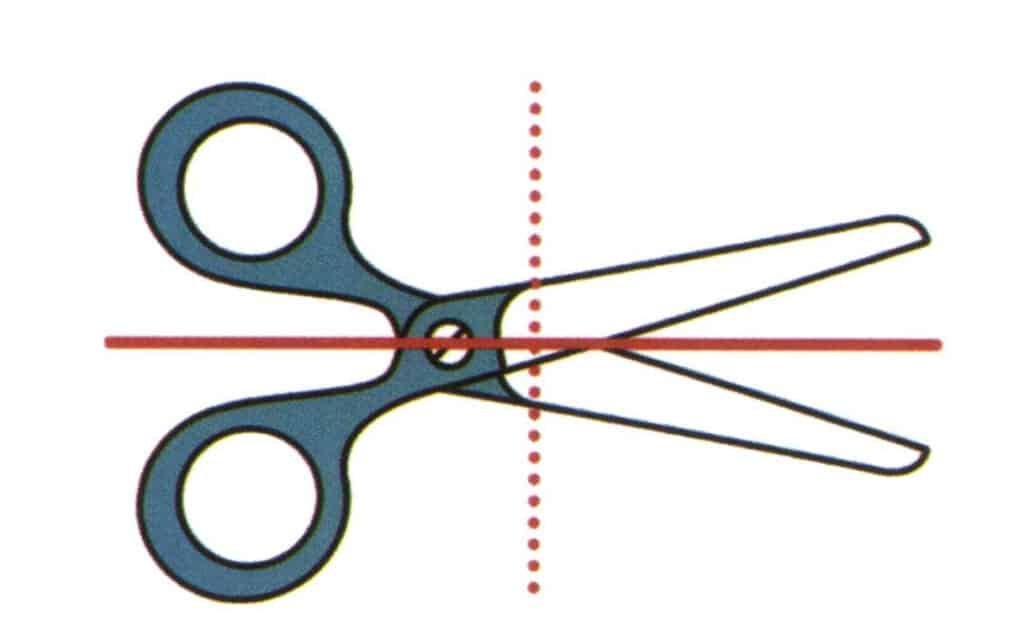
Рисунок 2-2-20 Представьте себе вертикальную плоскость бумаги и плоскость, простирающуюся вдоль направления красной сплошной линии, которая делит ножницы на верхнюю и нижнюю части, причем верхняя и нижняя части зеркально симметричны. Эта воображаемая плоскость называется плоскостью симметрии. Представьте себе другую плоскость, перпендикулярную поверхности бумаги и продолжающуюся вдоль направления красной пунктирной линии, которая делит ножницы на левую и правую части, но формы ножниц с левой и правой стороны не симметричны.
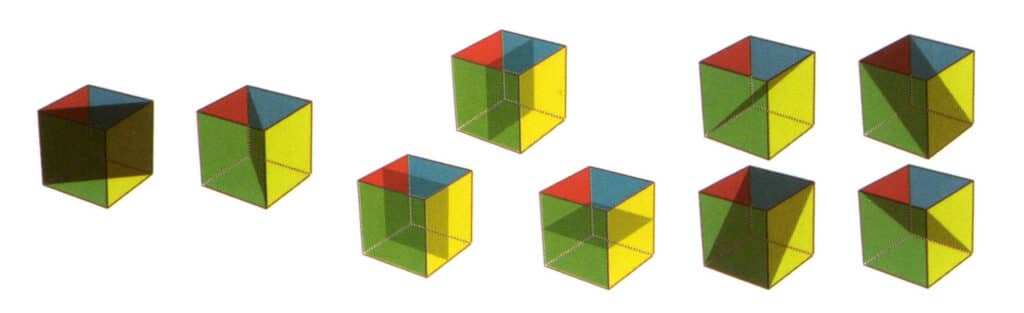
Рисунок 2-2-21 Девять плоскостей симметрии куба
(2) Советы по поиску Плоскости симметрии.
① Плоскость симметрии часто параллельна и совпадает с осью симметрии.
② Плоскость симметрии - это воображаемая плоскость, разделяющая кристаллическую геометрию, которая отличается от параллельной двойной плоскости в геометрии.
③ Если плоскость симметрии содержит ось симметрии Lⁿ, то должно существовать n плоскостей симметрии, содержащих Lⁿ.
(3) Пункт Группа.
Точечная группа - это сумма всех элементов симметрии в кристалле. Порядок записи группы точек - ось симметрии + плоскость симметрии, например, 3L²3P (рис. 2-2-22). Если кристалл имеет несколько осей симметрии, то принято записывать их слева направо, от оси высшего порядка к оси низшего порядка, и в порядке плоскостей симметрии, например, L⁴4L²5P (рис. 2-2-23). В кристаллах существует 32 типа симметрии.
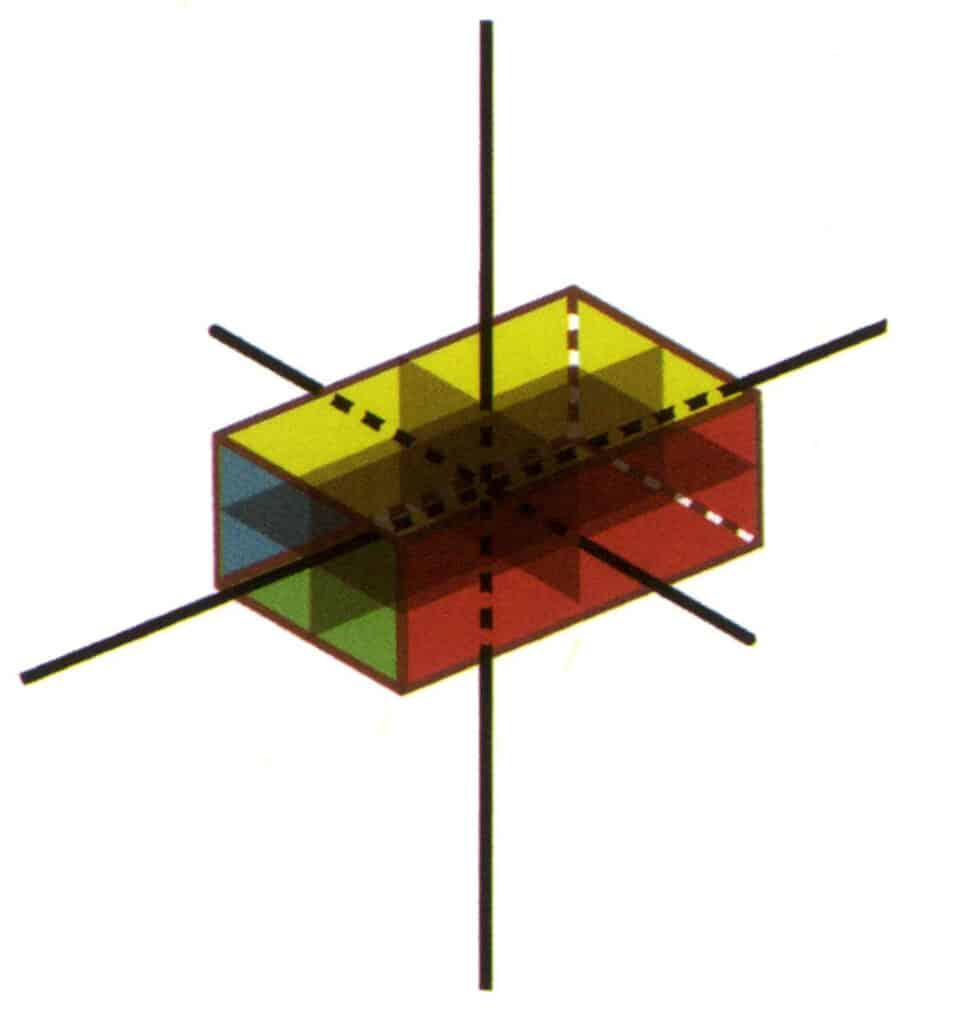
Рисунок 2-2-22 Группа точек 3L²3P (прямоугольный кубоид с прямоугольным сечением)
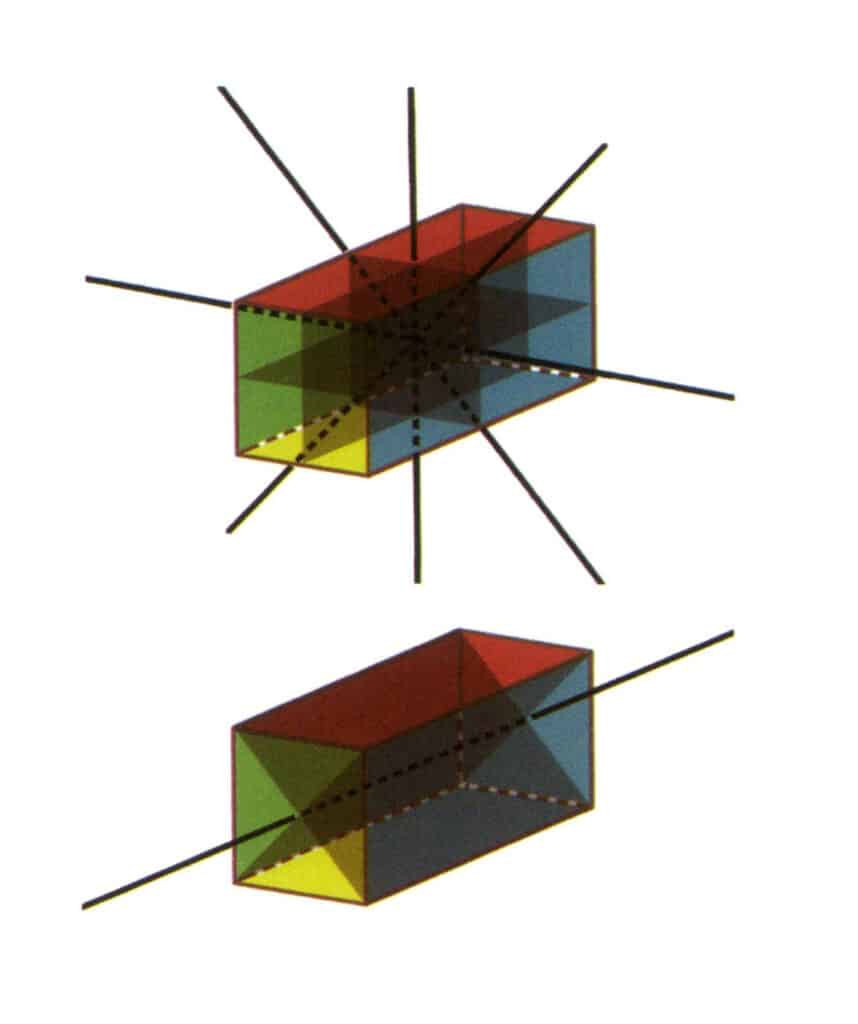
Рисунок 2-2-23 Группа точек L⁴4L²5P (прямоугольная призма с квадратным сечением) с четырьмя вторыми осями и тремя симметричными гранями сверху, и одной четвертой осью и двумя симметричными гранями снизу.
3. Классификация кристаллов
Симметрия является частью классификации кристаллов. Для описания кристаллической структуры натуральных и искусственных драгоценных камней в схеме классификации кристаллов необходимо ввести еще одно понятие - кристаллическая ось. Кристаллическая ось - это воображаемая линия, проходящая через кристаллическую структуру и указывающая направление, в котором повторяются узлы решетки, и относительное расстояние, на котором узлы повторяются вдоль этого направления. Ось кристалла совпадает с нормалью к оси симметрии или плоскостью симметрии. Если ось симметрии или плоскость симметрии отсутствуют, ось кристалла может быть выбрана параллельно направлению ребра кристалла.
На основании элементов симметрии и кристаллических осей академическая система классифицирует кристаллы на три кристаллических семейства и семь кристаллических систем (табл. 1).
Таблица 1: Ключевые моменты для определения семейств и систем кристаллов
| Кристальная семья | Кристалл | Ключевые моменты для определения | Распространенные разновидности драгоценных камней |
|---|---|---|---|
| Низкоуровневая кристаллическая система | Триклиническая система | Отсутствие второй оси или плоскости симметрии | Амазонит, родонит, бирюза |
| Моноклинная кристаллическая система | Отсутствие осей высшего порядка, не более одной вторичной оси и плоскости симметрии | Жадеит, диопсид, сподумен, эпидот | |
| Орторомбическая кристаллическая система | Отсутствие осей высшего порядка, более одной вторичной оси или плоскости симметрии | Оливин, топаз, сауальпит (включая танзанит), кордиерит, хризоберилл, энстатит | |
| Семейство промежуточных кристаллов | Тетрагональная кристаллическая система | 1 четырехкратная ось (может быть представлена L4) | Алмаз |
| Тригональная кристаллическая система | 1 тригональные оси (могут быть представлены L3) | Корунд, рубин, сапфир, турмалин, кристаллы семейства кварца (такие как хрусталь, аметист, цитрин и др.), родохрозит | |
| Гексагональная кристаллическая система | 1 гексагональная ось (может быть представлена L6) | Аквамарин, изумруд и другие драгоценные камни семейства берилитов, апатит | |
| Усовершенствованное семейство кристаллов | Изометрическая система кристаллов | 4 тригональные оси (могут быть представлены 4L3) | Алмаз, гранат, шпинель, плавиковый шпат |
4. Общие характеристики кристаллов драгоценных камней
К распространенным драгоценным камням относятся алмаз, шпинель, плавиковый шпат, гранат, берилит, циркон, корунд, турмалин, хрусталь, хризоберилл, топаз и др. Каждый вид драгоценных камней имеет свои фиксированные кристаллические характеристики.
Драгоценные камни семейства высококристаллических в основном имеют зернистую структуру, а распространенные разновидности часто встречаются в фиксированных кристаллических формах (табл. 2).
Кристаллический габитус семейств промежуточных и низких кристаллов - столбчатый (табл. 3).
Таблица 2: Общие характеристики кристаллов семейств кристаллов высокого уровня
| Название тона драгоценных камней | Классификация кристаллов | Важные характеристики кристаллов | |||
|---|---|---|---|---|---|
| Название тона драгоценных камней | Классификация кристаллов | Привычка к кристаллам | Распространенные формы кристаллов | Распространенные формы близнецов | Распространенные рисунки граней кристаллов |
| Алмаз | Изометрическая система кристаллов | Зернистый кристалл (рис. 2-2-24), обычно встречается в октаэдрических гранулах | Октаэдр - распространенная форма кристаллов, но могут появляться и более сложные формы кристаллов, в том числе ромбические додекаэдры, часто с округлыми гранями, которые могут обладать тройной симметрией | Треугольная плоская двойка, иногда без видимых вогнутых углов (рис. 2-2-25) | На поверхности видны перевернутые треугольные ямки травления (рис. 2-2-26, 2-2-27) и другие узоры на гранях кристаллов (рис. 2-2-28, 2-2-29). |
| Шпинель | Зернисто-кристаллический (рис. 2-2-30), обычно встречается в октаэдрических гранулах | Кристаллические грани часто имеют октаэдрическую форму и могут быть очень плоскими, как будто отполированными (рис. 2-2-31). | Двойные кристаллы очень плоские, напоминают треугольную форму со срезанными углами (рис. 2¬2-32). | Видимые на поверхности ямки травления, некоторые из которых напоминают бриллианты в форме перевернутого треугольника (рис. 2-2-33) | |
| Флюорит | Зернистый кристалл (рисунок 2-2-34) | Октаэдрическая и кубическая формы кристаллов (рис. 2-2-35) | Взаимопроникающее двойникование | Квадратные ступенчатые знаки роста, в основном с расщепленными щелями, цветные полосы параллельны направлениям шести граней куба | |
| Гранат | Зернистый кристалл, обычно представленный ромбическими додекаэдрическими зернами (рис. 2-2-36). | Ромбический додекаэдр или квадратный трапецоэдр | Редкие | Видны концентрические кольцевые полосы той же формы, что и грани кристаллов (рис. 2-2-37) | |
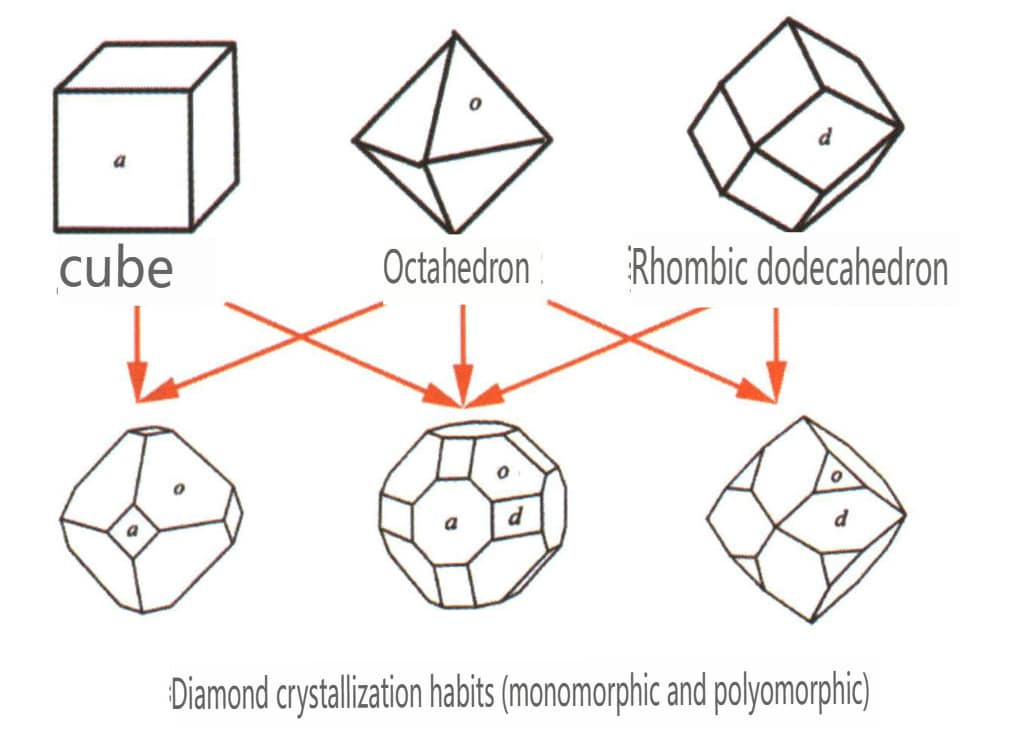
Рис. 2-2-24 Повадки алмазного кристалла
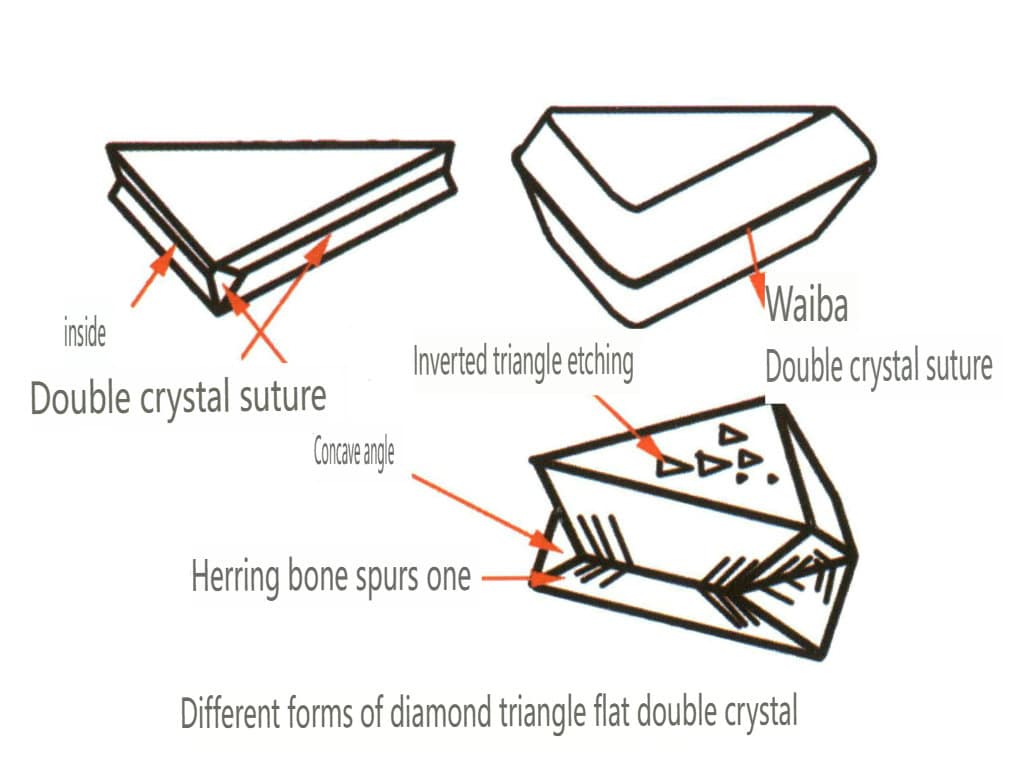
Рисунок 2-2-25 Алмазная сдвоенная габитус
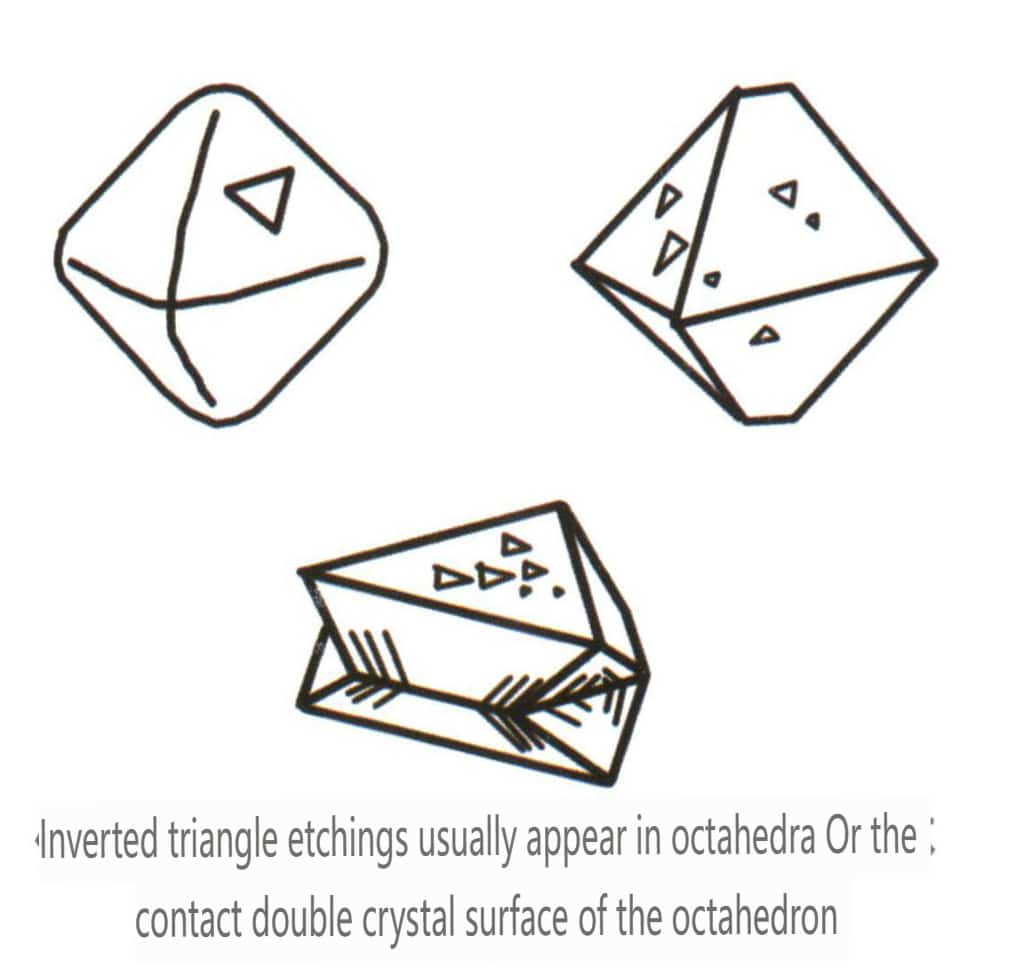
Рисунок 2-2-26 Фигура травления "Перевернутый треугольник" граней октаэдрического кристалла алмаза

Рисунок 2-2-27 Перевернутая треугольная фигура травления на поверхности октаэдрического кристалла алмаза
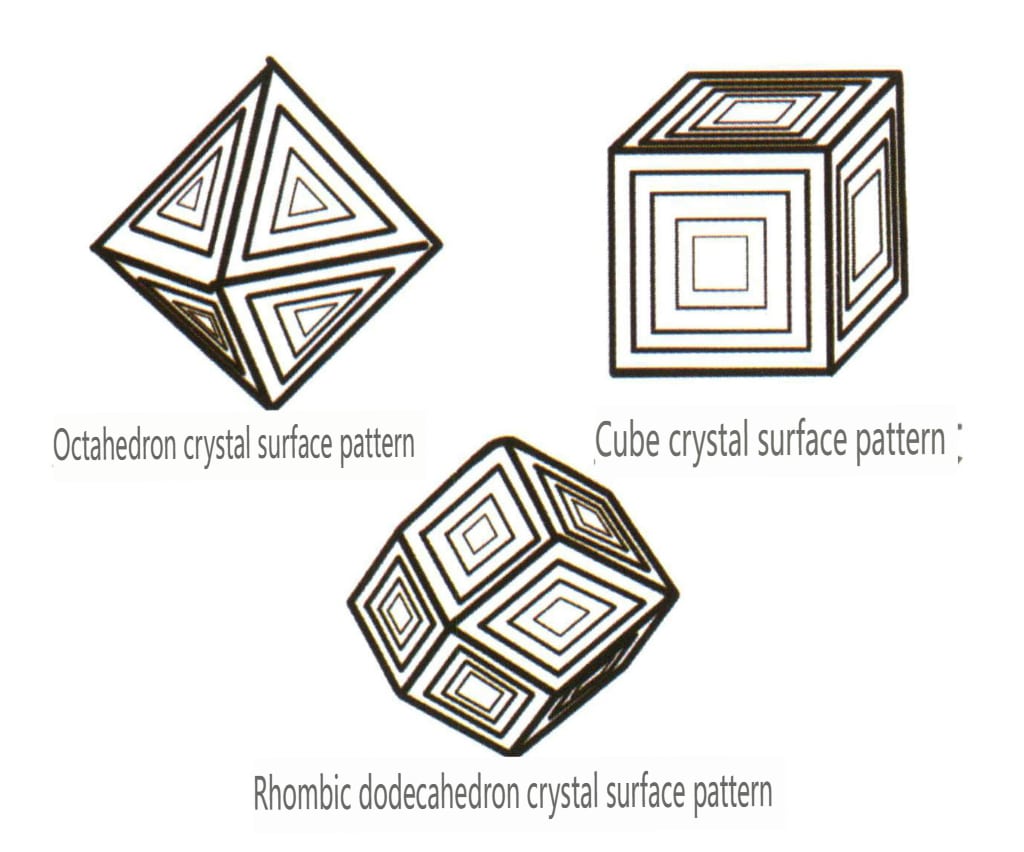
Рисунок 2-2-28 Фигура травления "Перевернутый треугольник" граней октаэдрического кристалла алмаза

Рисунок 2-2-29 Перевернутая треугольная фигура травления на поверхности октаэдрического кристалла алмаза
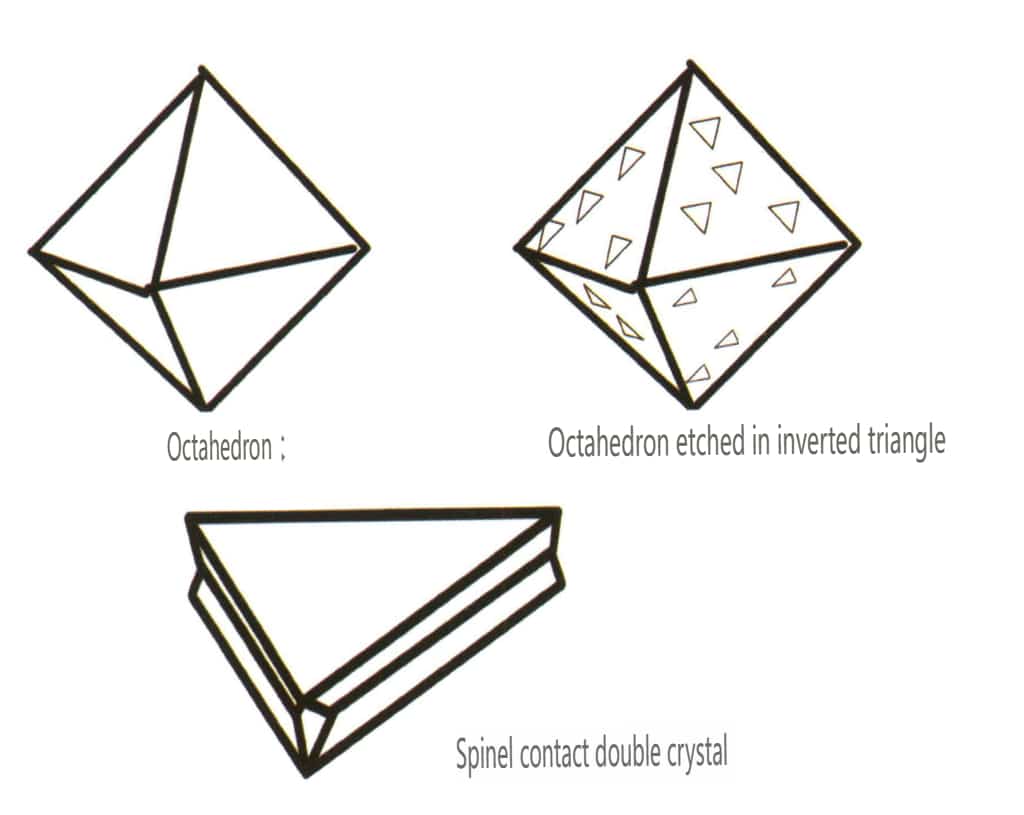
Рис. 2-2-30 Структура кристалла шпинели

Рисунок 2-2-31 Распространенные формы кристаллов шпинели

Рисунок 2-2-32 Контактное двойникование шпинели
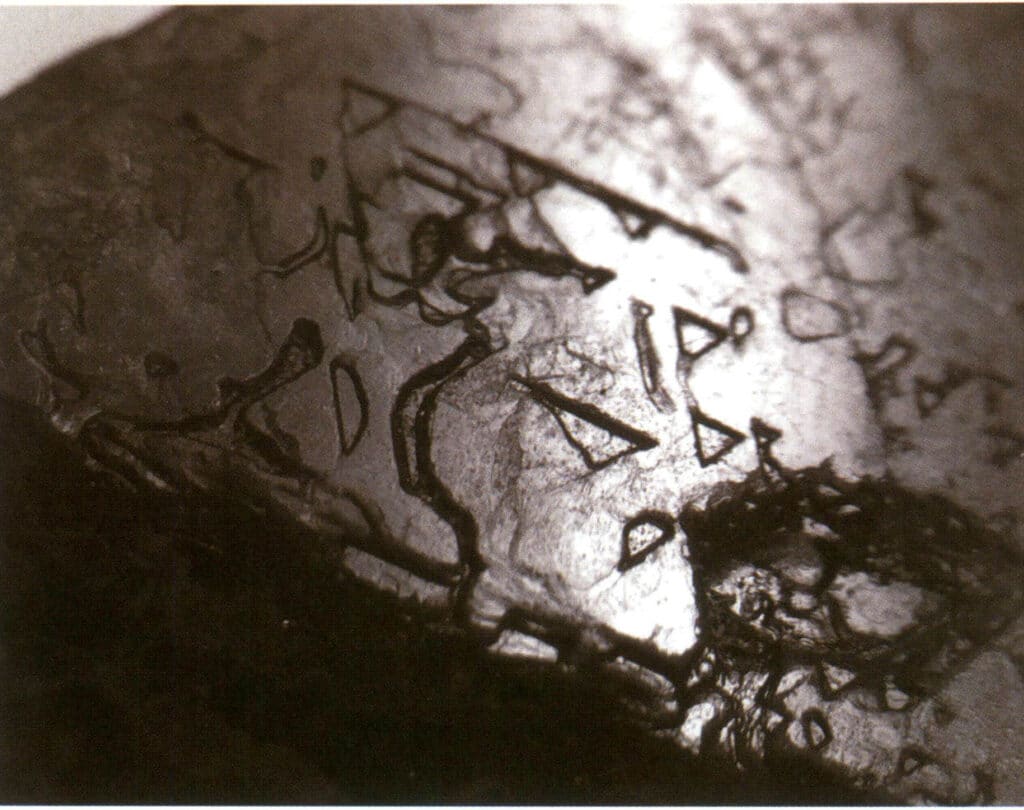
Рисунок 2-2-33 Перевернутый треугольный рисунок травления на поверхности шпинели
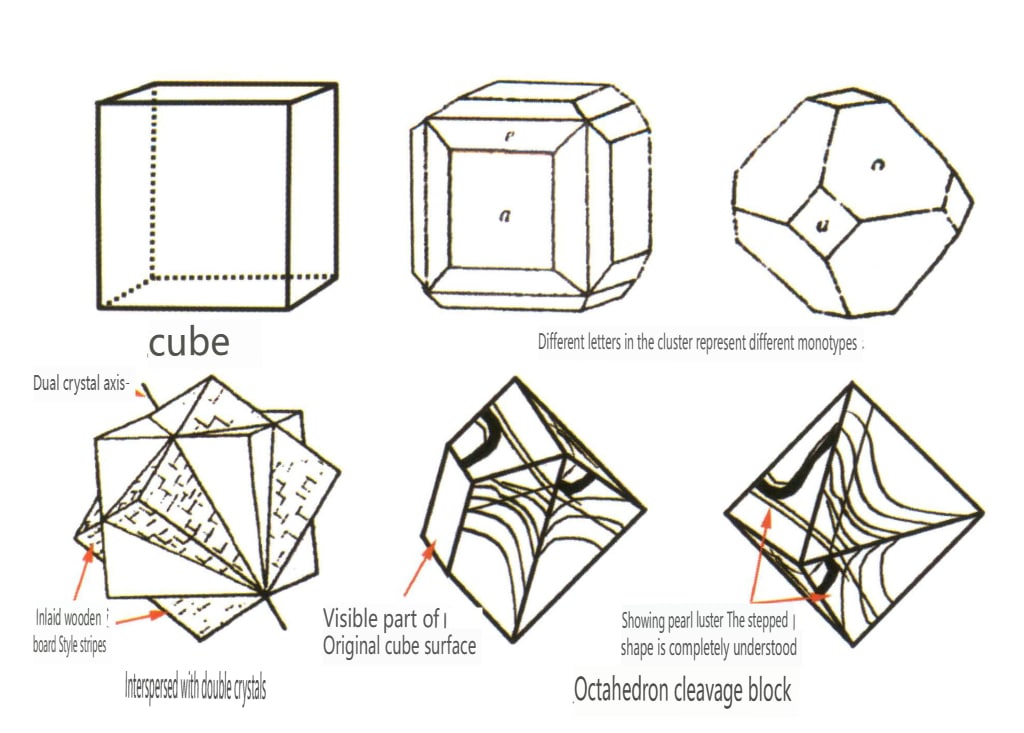
Рис. 2-2-34 Повадки кристаллов флюорита

Рисунок 2-2-35 Кристалл флюорита
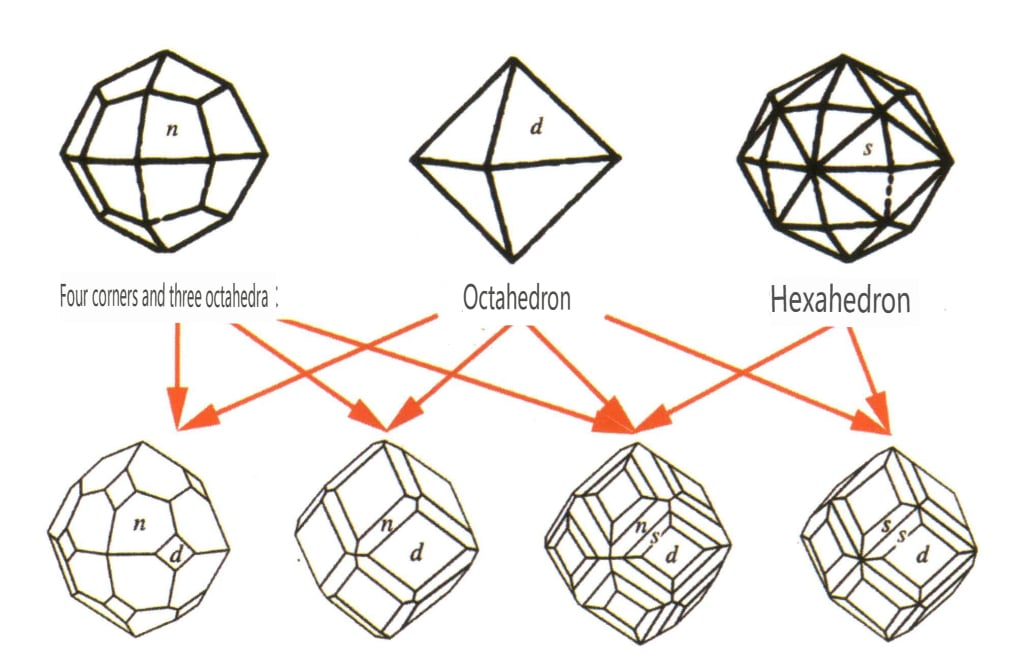
Рисунок 2-2-36 Характер кристалла граната

Рисунок 2-2-37 Концентрические кольцевые полосы на поверхности кристаллов граната, имеющие ту же форму, что и грани кристалла
Таблица 3: Общие характеристики кристаллов драгоценных камней семейств со средним и низким содержанием кристаллов
| Название тона драгоценных камней | Классификация кристаллов | Важные характеристики кристаллов | |||
|---|---|---|---|---|---|
| Название тона драгоценных камней | Классификация кристаллов | Привычка к кристаллам | Распространенные формы кристаллов | Распространенные формы близнецов | Распространенные рисунки граней кристаллов |
| Берил | Гексагональная кристаллическая система | Столбчатая форма кристаллов (Рисунок 2-2-38) | Гексагональная столбчатая форма кристаллов (рис. 2-2-39, 2-2-40) | Редкие | Видимые продольные полосы |
| Свинцовый камень | Тетрагональная кристаллическая система | Столбчатая форма кристаллов (Рисунок 2-2-41) | Квадратная колонна с квадратным сечением, появляющаяся вместе с квадратным двойным конусом (рис. 2-2-42) | Видимые коленообразные двойные кристаллы | Никаких особых узоров |
| Корунд | Тригональная кристаллическая система | Пластинчатый кристалл, столбчатый кристалл (Рисунок 2-2-43) | Рубины часто имеют форму гексагональной призмы (рис. 2-2-44), а сапфиры - гексагональную бипирамидальную бочкообразную форму кристаллов (рис. 2-2-45). | Часто встречаются бикристаллы. | Видимые полосы. |
| Турмалин . | Столбчатая форма кристаллов (Рисунок 2-2-46) | Грани кристалла на обоих концах различны, а поперечное сечение представляет собой сферический треугольник (рис. 2-2-47). | Редкие | Видимые продольные полосы (Рисунок 2-2-48) | |
| Кварц (кристаллический кварц) | Столбчатая форма кристаллов (Рисунок 2-2-49) | Сечение гексагональное, редко встречаются гексагональные бипирамиды (рис. 2-2-50, 2-2-51), часто встречаются гексагональные монопирамиды | Общий контакт с бикристаллами (также известными как японские бикристаллы) | Обычные горизонтальные полосы на поверхности кристаллов | |
| Хризоберилл | Тригональная кристаллическая система | Характеристики столбчатой кристаллизации (Рисунок 2-¬2-52) | Монокристаллические встречаются редко | Часто встречается трехкристаллический (рис. 2-2-53), в качестве критериев идентификации можно использовать гексагональные и вогнутые углы. | Полосы трикристалла могут быть использованы в качестве критериев идентификации |
| Топаз | Столбчатая форма кристаллов (Рисунок 2-2-54) | Поперечное сечение ромбовидное, а верхняя часть часто кажется конвертообразной (рис. 2-2-55). | Би-кристаллы встречаются редко | Видимые продольные полосы | |
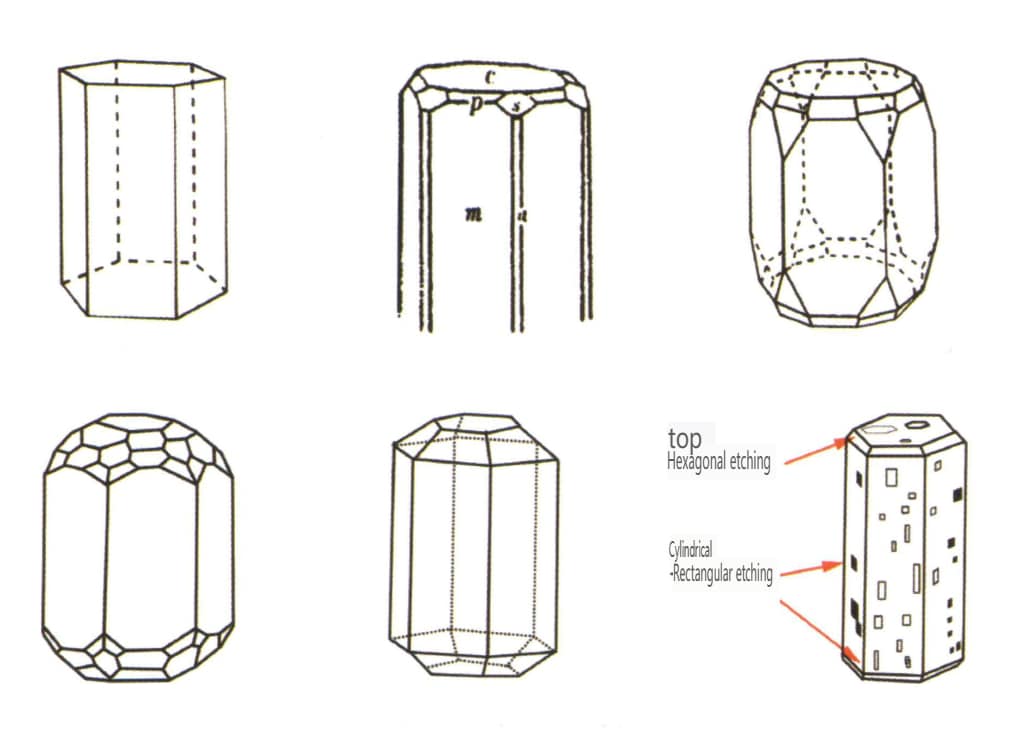
Рис. 2-2-38 Габитус кристалла берилла

Рисунок 2-2-39 Распространенные формы кристаллов изумруда

Рисунок 2-2-40 Распространенные формы кристаллов аквамарина
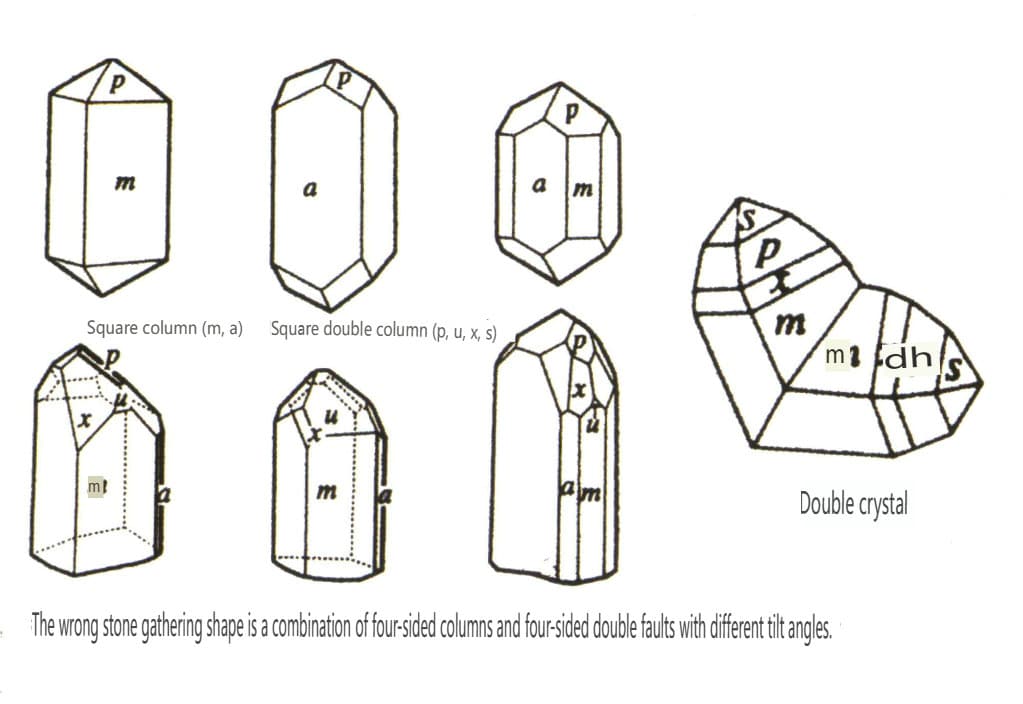
Рисунок 2-2-41 Кристаллическая структура циркона

Рисунок 2-2-42 Кристалл циркона
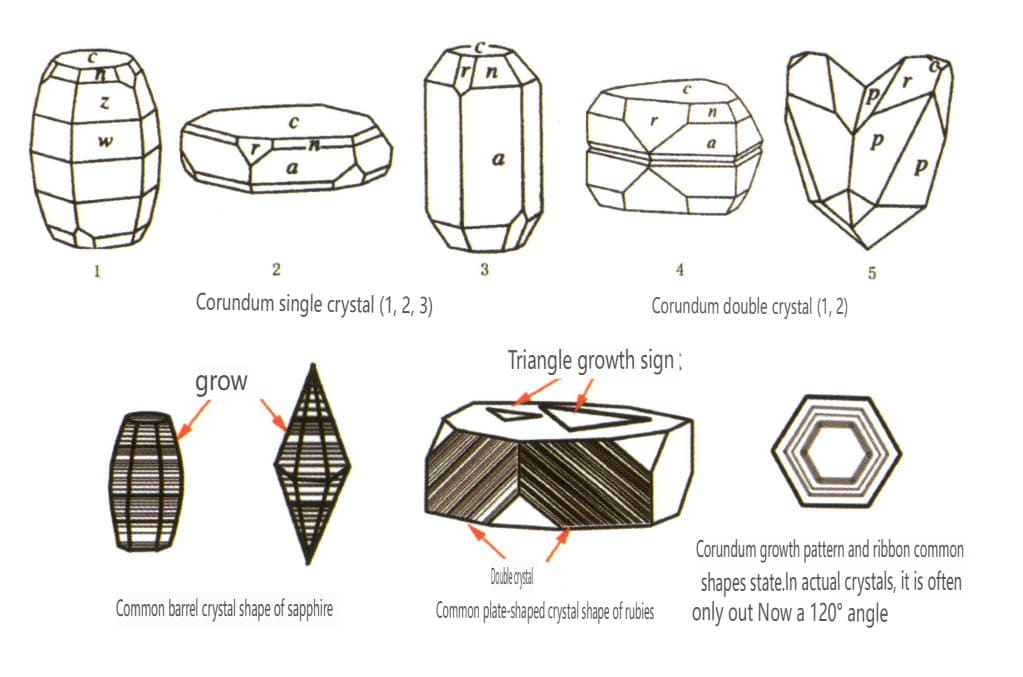
Рисунок 2-2-43 Характер кристаллов корунда

Рисунок 2-2-44 Рубиновый кристалл

Рисунок 2-2-45 Механический двойник рубина
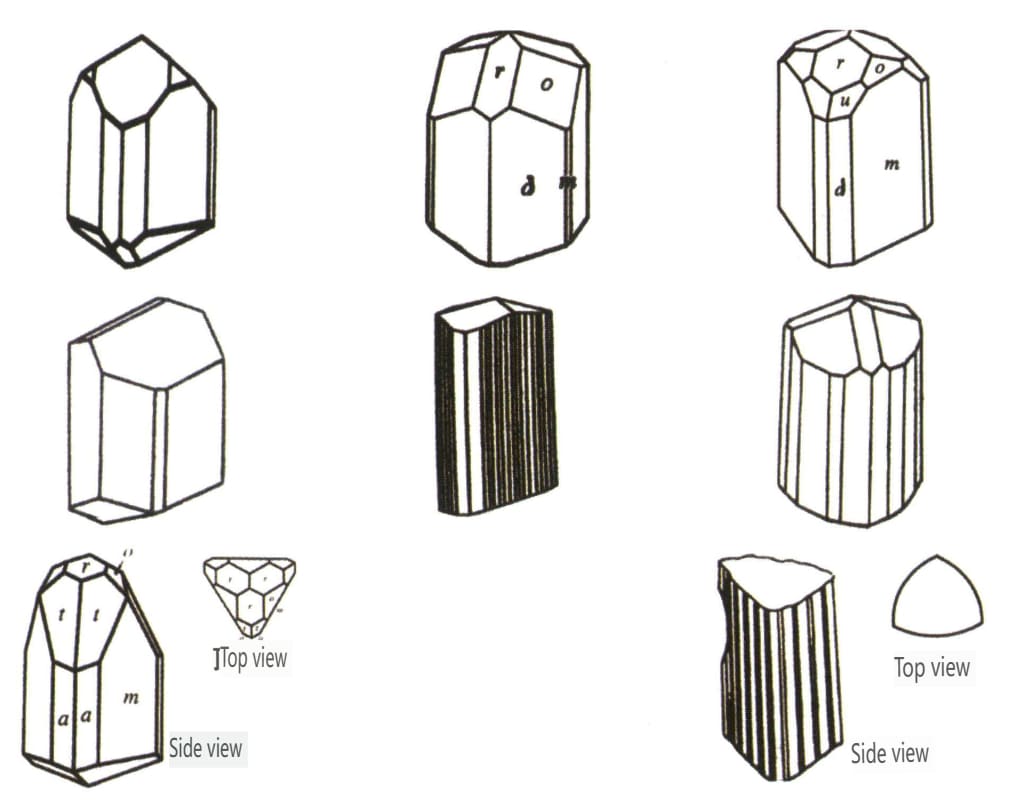
Рисунок 2-2-46 Облик кристаллов турмалина

Рисунок 2-2-47 Кристалл турмалина

Рисунок 2-2-48 Поверхностные продольные полосы кристалла турмалина
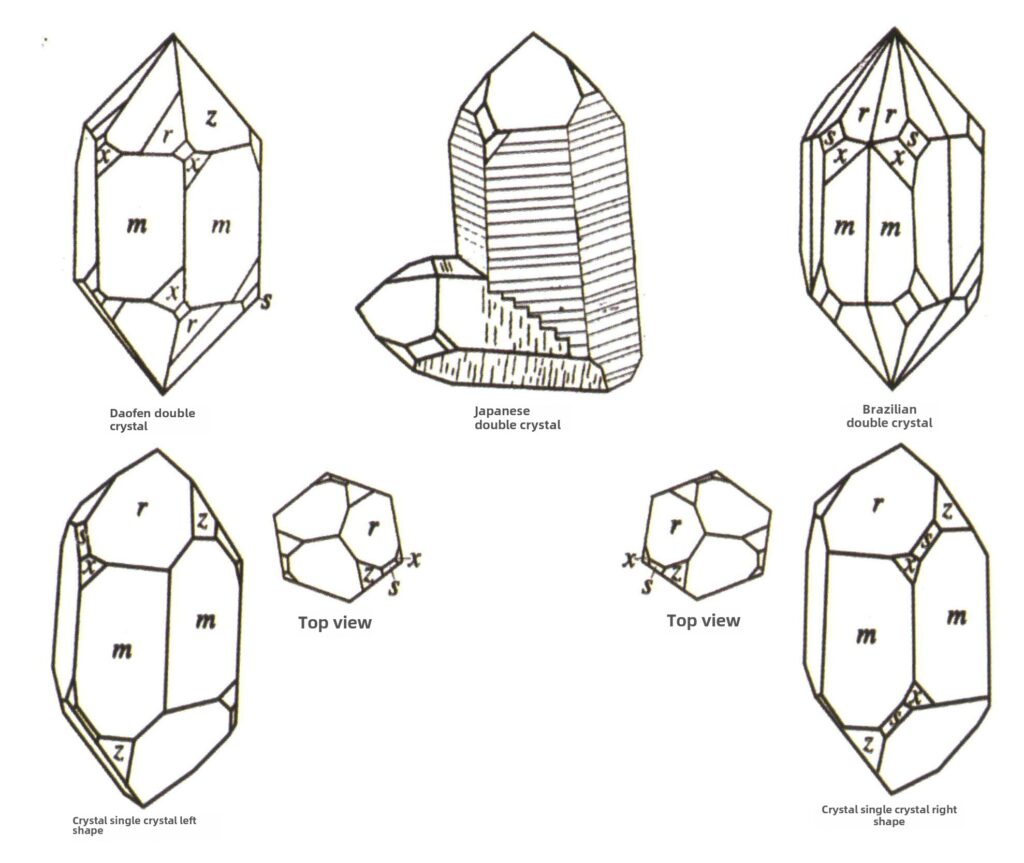
Рисунок 2-2-49 Привычки кристаллизации

Рисунок 2-2-50 Корпус кристалла

Рисунок 2-2-51 Корпус кристалла
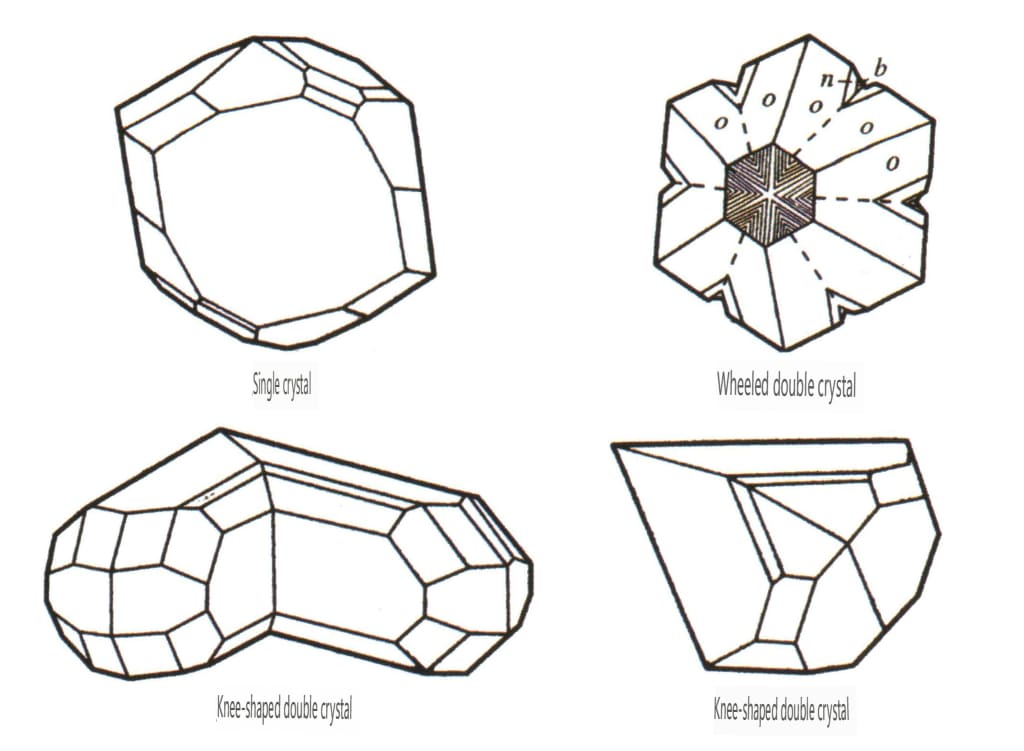
Рисунок 2-2-52 Кристаллическая габитус хризоберилла

Рисунок 2-2-53 Кристалл хризоберилла
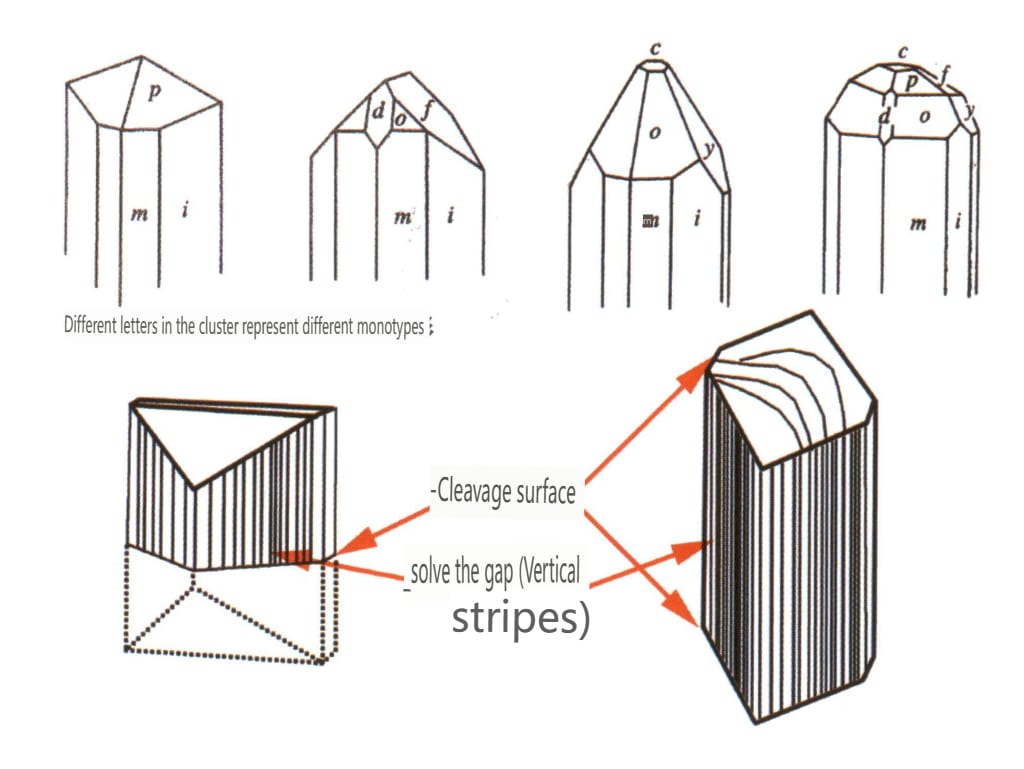
Рисунок 2-2-54 Кристаллические привычки топаза

Рисунок 2-2-55 Кристалл топаза
Раздел IV Почему кристаллы драгоценных камней растут по-разному
С микроскопической точки зрения, кристалл драгоценного камня - это твердое тело, состоящее из элементов разного размера, расположенных по разным правилам. С макроскопической точки зрения, многие драгоценные камни имеют кристаллическую форму из-за их различного состава. Однако существуют и особые случаи, например, гетероморфные. Чтобы лучше понять, почему кристаллы драгоценных камней выглядят по-разному, мы рассмотрим пять аспектов: гетероморфность, изоморфизм, молекулярно-механическое перемешивание, вода в минералах драгоценных камней и химический состав драгоценных камней.
1. Гетероморфный
Хотя некоторые минералы имеют одинаковый химический состав, они обладают совершенно разными кристаллическими структурами (расположение элементов в трехмерном пространстве) и демонстрируют значительные различия в физических и химических свойствах (Таблица 4). Мы называем это явление гетероморфизмом, например, алмаз и графит (рис. 2-2-56).
Обыкновенному кварцу свойственно явление гетероморфизма. Силлиманит, андалузит и кианит относятся к группе гетероморфных разновидностей.
Преобразование гетероморфизма происходит в твердотельных условиях. В процессе структурной трансформации внутри кристалла может возникать давление, что часто приводит к образованию двойникования внутри кристалла.

Таблица 4: Сравнение свойств алмаза и графита
| Минерал | Алмаз | Графит |
|---|---|---|
| Компоненты | Углерод (C) | Углерод (C) |
| Условия формирования | Высокая температура и высокое давление | Высокая температура |
| Кристаллическая система, привычка | Изометрическая кристаллическая система, октаэдр, ромбический додекаэдр | Гексагональная кристаллическая система, слоистая |
| Цвет | Бесцветный, желтый, голубой, розовый, зеленый и т.д. | Черный |
| Блеск | Адамантиновый блеск | Металлический блеск |
| Прозрачность | От прозрачного до непрозрачного | Непрозрачный |
| Показатель преломления | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Механические свойства | Умеренная октаэдрическая спайность, твердость 10, плотность 3.52 | Набор с идеальным расщеплением, твердость 1, плотность 2.10 |
| Другие свойства | Отличная теплопроводность; за исключением природных голубых бриллиантов, которые являются полупроводниками, бриллианты других цветов - изоляторы. | Умеренная теплопроводность, хорошая электропроводность |
2. Изоморфизм
Изоморфизм - это явление, при котором одни частицы в структуре решетки заменяются другими с аналогичными свойствами, что приводит к незначительным изменениям параметров решетки и физико-химических свойств. В отличие от этого, кристаллическая структура остается принципиально неизменной. Это можно понимать так, что элементы в кристалле драгоценного камня заменяются другими элементами. Напротив, повторяющаяся схема расположения элементов кристалла драгоценного камня остается прежней, с небольшими отклонениями в расстояниях между атомами. Тем не менее физико-химические свойства кристалла драгоценного камня претерпевают незначительные изменения (рис. 2-2-57 - рис. 2-2-58).
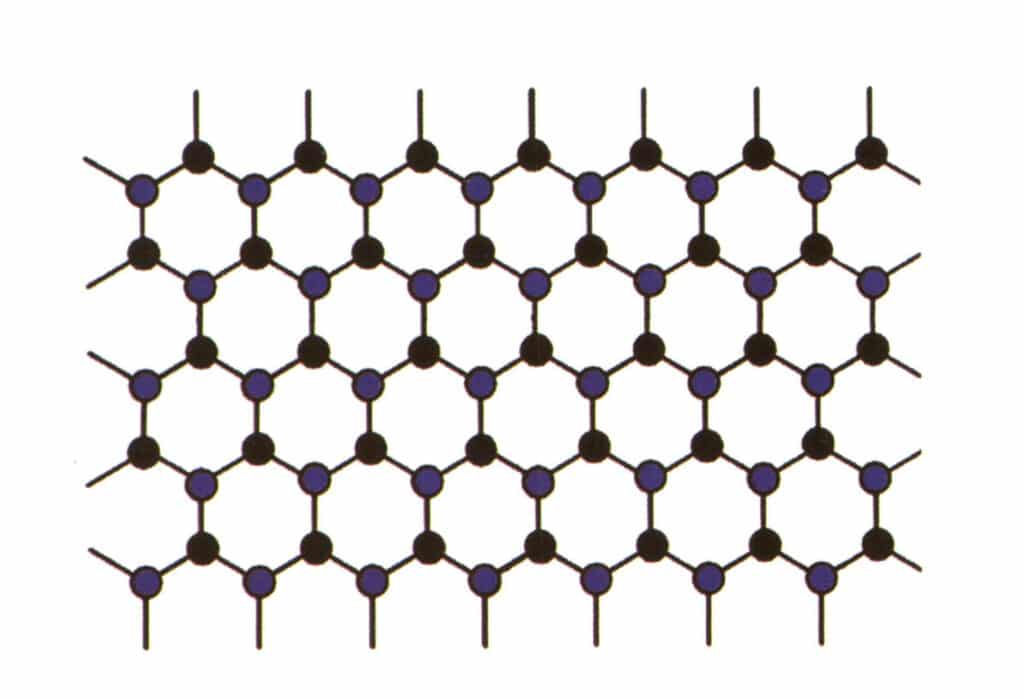
Рисунок 2-2-57 Схема моделирования кристаллической структуры (синим и черным обозначены частицы элементов)
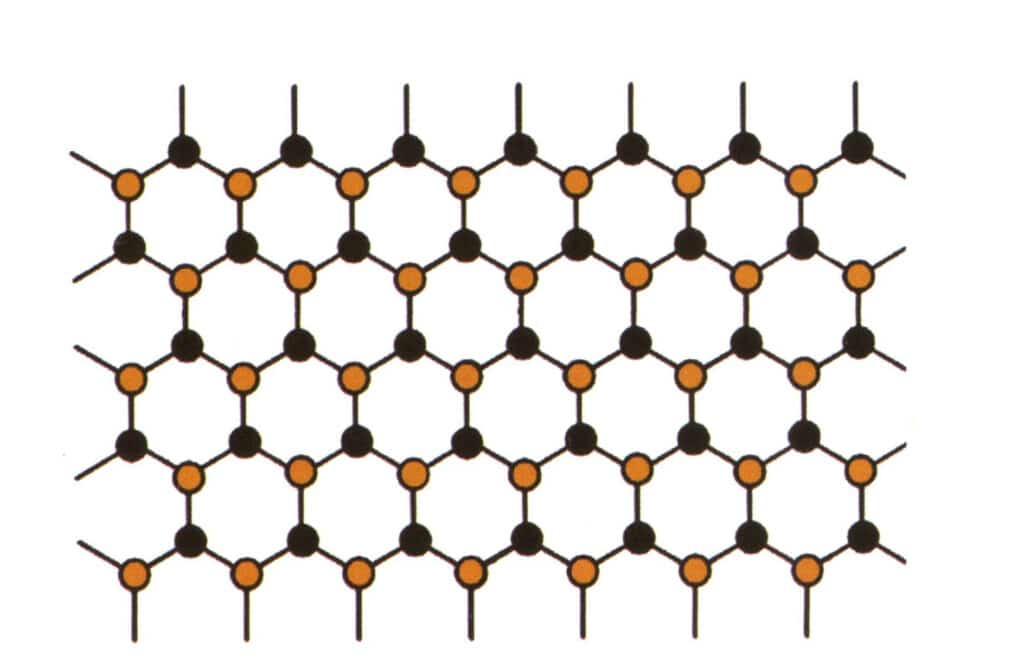
Рисунок 2-2-58 Диаграмма моделирования кристаллической структуры (черным цветом представлены элементарные частицы, желтым - новые элементарные частицы, частично замещающие синие элементарные частицы, желтый цвет может не полностью замещать все синие частицы)
Концепция изоморфизма объясняет, почему драгоценные камни одного семейства могут иметь так много цветов и почему существуют различия в показателе преломления и плотности между драгоценными камнями одного семейства.
Под семейством можно понимать тип драгоценного камня, в котором повторяющиеся узоры кристаллических элементов одинаковы, но физические и химические формы несколько отличаются. Например, семейство корундов включает два представителя - рубин и сапфир, а семейство бериллов - изумруд, аквамарин и морганит.
(1) Оливин
Химический состав оливина - (Mg,Fe)₂SiO₄. В его составе происходит полное изоморфное замещение элементов Fe и Mg. При увеличении содержания Fe в оливине цвет оливина становится темнее, показатель преломления увеличивается, плотность также возрастает.
(2) Корунд
Чистый корунд без примесей (Al₂O₃) бесцветен, а когда Cr заменяет Al, драгоценный камень приобретает розово-красный или красный оттенок, называемый рубином. Остальные цвета называются сапфировыми, например оранжево-желтый сапфир или бесцветный сапфир. Сапфиром принято называть именно синий сапфир, в котором Fe и Ti заменяют Al. Чем выше содержание красящих элементов в камне-заменителе, тем глубже цвет камня; и наоборот, чем ниже содержание, тем светлее цвет.
(3) Турмалин
Турмалин относится к тому же типу драгоценных камней, что и турмалин, где турмалин - минералогическое название, а турмалин - геммологическое. Химический состав берилла - (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), где R в основном Mg, Fe, Cr, Li, Al, Mn, причем элементы в R могут полностью или частично замещать друг друга, что приводит к чрезвычайно широкому разнообразию цветов турмалина. Например, когда R состоит в основном из Fe, берилл имеет глубокий синий или даже черный цвет; когда R состоит в основном из Mg, берилл имеет цвет от желтого до коричневого; когда R в основном Li или Mn, берилл имеет розовый или светло-голубой цвет; когда R в основном Cr, турмалин имеет темно-зеленый цвет.
Из вышесказанного видно, что замена элементов со схожими свойствами приводит к получению более красивых и ярких цветов в драгоценных камнях.
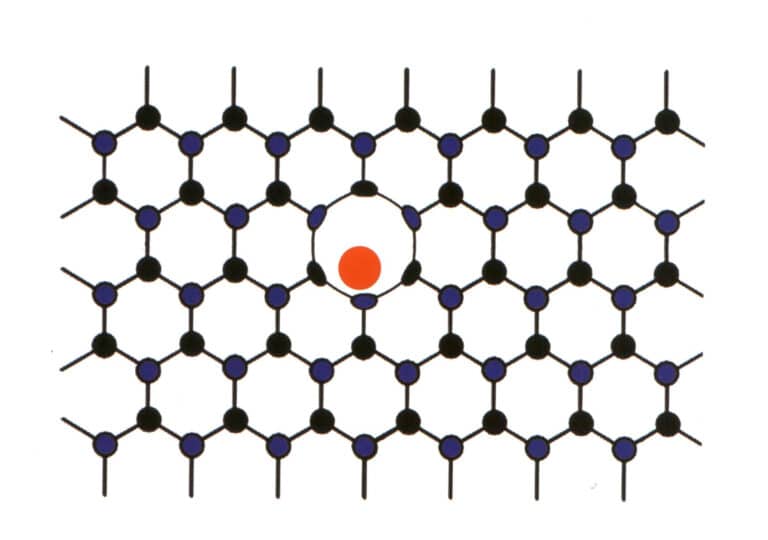
3. Молекулярно-механическое перемешивание
Иногда некоторые элементы насильственно проникают между основными элементами правильно расположенных драгоценных камней. Однако малая доля входящих элементов не нарушает повторяющийся рисунок основных элементов драгоценного камня, вызывая лишь деформацию (рис. 2-2-59). Такая ситуация называется молекулярно-механическим смешением, например молекулярно-механическое смешение азота и бора в алмазах, в результате которого образуются голубые, розовые и желтые бриллианты, имеющие высокую ценность.
4. Вода в драгоценных минералах
Некоторые драгоценные камни содержат воду, которая является важным компонентом минералов и тесно связана со свойствами драгоценных камней. В зависимости от формы воды, присутствующей в минералах, и ее роли в кристаллической структуре, воду в драгоценных камнях можно разделить на две категории: абсорбционная вода, которая не связана с кристаллической структурой, и вода, участвующая в кристаллической структуре минерала, включая кристаллизационную воду, цеолитовую воду, межслоевую воду и конституционную воду. Вода, тесно связанная с драгоценными камнями, включает абсорбционную, кристаллизационную и конституционную воду.
Одним из них является поглощение воды, таких как Opal (химический состав SiO₂ - nH₂O, n представляет собой количество H₂O, содержание переменной) в молекуле воды, которая является нейтральной молекулы воды механически адсорбируются на минеральные частицы или поверхности излома. Когда температура достигает 100 ~ 110° градусов при нормальном давлении, молекулы воды могут все уйти и не повредить структуру кристаллической решетки, поэтому, чтобы избежать опал в прилавке в течение длительного времени сильного воздействия света сухой трещины, следует поставить чашку с водой в прилавке.
Вторая - кристаллизационная вода, например, кристаллизационная вода в бирюзе [химический состав: CuAl₆(PO₄)₄(OH)₈-4H₂O, где содержание H₂O может достигать 19,47% ]. Эта нейтральная молекула воды существует в фиксированных позициях в решетке и служит структурной единицей, являясь частью химического состава минерала. Температура, при которой кристаллизационная вода уходит, обычно не превышает 600℃ и обычно уходит при 100 -200℃. Когда драгоценный камень теряет кристаллизационную воду, его кристаллическая структура повреждается, образуя новую структуру.
Третья - конституционная вода, также известная как комбинированная вода, которая участвует в минеральной решетке в виде OH-, H⁺, H₃O⁺ плазмы, причем OH- является наиболее распространенной. Конституционная вода является частью химического состава минерала, занимая фиксированные позиции в структуре решетки с определенной долей в ее составе. Структурная вода требует более высокой температуры для выхода и повреждения своей структуры, обычно около 600-1000℃. Когда драгоценный камень теряет структурную воду, его кристаллическая структура разрушается. Многие драгоценные камни содержат структурную воду, например, турмалин [химический состав: ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), где R в основном включает Mg, Fe, Cr, Li, Al, Mn и т.д., и элементы в R могут полностью или частично заменять друг друга], и топаз [химический состав Al₂SiO₄( F, OH) ₂ ].
5. Химический состав драгоценных камней
Драгоценные камни, как и другие вещества, состоят из химических элементов. Каждый вид драгоценных камней имеет свой специфический химический состав и определенный диапазон изменения, который определяет различные характеристики и свойства драгоценного камня. Драгоценные камни относятся к минералам и горным породам, и классификация химического состава драгоценных камней может быть прослежена на основе химического состава минералов.
В настоящее время основными методами классификации минералов являются классификация по химическому составу (система Дана), геохимическая классификация, генетическая классификация, классификация по применению и кристаллохимическая классификация. Широко распространенной является химическая классификация, основанная на химическом составе и кристаллической структуре (система Хьюго Штрунца) (табл. 5).
Таблица 5: Система химической классификации минеральных кристаллов
| Последовательность уровней | Основание для разделения | Пример |
|---|---|---|
| Основная категория | Тип соединения | Кислородсодержащая соль Основная категория |
| Класс | Типы анионов или комплексных анионов | Класс силикатов |
| (Подкатегория) | Структура анионного комплекса | Подкласс каркасных силикатов |
| Группа | Типы кристаллических структур и ионные свойства | Группа корунда, группа берилла, группа граната |
| (Подгруппа) | Типы катионов | Подгруппа щелочных полевых шпатов |
| Specie | Определенная кристаллическая структура и химический состав | Ортоклаз KAlSi3O8 |
| (подвид) | Одинаковая кристаллическая структура, разный состав или свойства, морфология | Адулярия KAlSi3O8 |