Una sola volta per sapere tutto sulla cristallografia delle pietre preziose
Una guida completa sulle forme, i tipi, le classificazioni e le differenze della cristallografia.
La Terra è composta da innumerevoli molecole e atomi. La ricerca scientifica moderna ha scoperto che i materiali solidi in natura sono composti da diversi elementi chimici. I risultati delle analisi a raggi X mostrano che gli atomi degli elementi di alcuni materiali solidi sono disposti in modo ordinato e regolare. Questi materiali sono classificati come cristallini o denominati cristalli e il loro reticolo atomico ordinato è chiamato struttura cristallina (Figura 2-1-1).
La maggior parte dei materiali gemmologici che crescono in natura e nei laboratori sono cristallini. In questo capitolo si parlerà del concetto di cristalli, della loro classificazione e della relazione tra i cristalli e la terminologia di base in gemmologia.

Indice dei contenuti
Sezione ⅠIl concetto e la descrizione dei cristalli
Quando si parla di gemme, spesso si pensa alle loro caratteristiche di scintillio e traslucenza (Figura 2-1-2). Dal punto di vista dei geologi e dei gemmologi, le gemme più amate appartengono a una forma geometrica di solido: i cristalli. L'essenza della bellezza dei cristalli è, infatti, la bellezza della geometria.

1. Il concetto di cristalli
I cristalli sono le forme più facilmente associabili e più comunemente presenti in natura. I cristalli sono presenti in tutti i sette continenti della Terra e, quando si trovano in natura, assumono spesso la forma di poliedri geometrici (Figura 2-1-3). Vengono comunemente chiamati cristalli. In seguito, questo termine è stato esteso per indicare le sostanze solide presenti in natura con forme geometriche poliedriche, come i cristalli di diamante e di acquamarina (Figura 2-1-4). I cristalli possono anche descrivere materiali solidi con superfici irregolari, irregolari, usurate, rotte o lavorate artificialmente, ma con una disposizione atomica che segue comunque uno schema regolare. I cristallografi ritengono che tutti i cristalli possiedano sei caratteristiche fondamentali: autolimitazione, uniformità, anisotropia, simmetria, stabilità e punto di fusione fisso.
L'autolimitazione si riferisce alla proprietà degli elementi chimici di formare spontaneamente forme geometriche poliedriche. Questa proprietà può spiegare perché elementi diversi hanno forme geometriche cristalline diverse.
② L'uniformità si riferisce alla proprietà che tutte le proprietà fisiche e chimiche delle parti del cristallo sono uguali. Questa proprietà può aiutarci a distinguere e identificare i diversi cristalli minerali.
③ L'anisotropia si riferisce alla proprietà per cui la disposizione degli elementi varia in diverse direzioni, determinando leggere differenze nelle proprietà fisiche a seconda della direzione. Questa proprietà può spiegare perché i diamanti con la più alta durezza possono essere tagliati e lucidati.
④ La simmetria si riferisce alla proprietà per cui parti o proprietà identiche in un cristallo si ripetono in uno schema regolare. Questa proprietà è estremamente importante e speciale per i cristalli e verrà approfondita nella seconda sezione di questo capitolo.
La stabilità si riferisce alla stabilità di un cristallo derivante dalla sua energia interna minima. Se l'energia interna di un cristallo è elevata e irregolare, esso è incline a rompersi da solo. Questa proprietà può spiegare perché i cristalli di rubino sintetizzati con la tecnica della flamefusion appaiono sempre a metà piuttosto che completi.
Il punto di fusione fisso si riferisce alla proprietà di un cristallo di avere un punto di fusione fisso.

Figura 2-1-3 Granato (a sinistra il cristallo, a destra il granato lucidato)

Figura 2-1-4 Cristallo di acquamarina
2. La forma ideale dei cristalli
I cristalli discussi in cristallografia sono principalmente cristalli singoli ideali. Si definisce cristallo singolo ideale quello la cui struttura interna segue rigorosamente le regole dei reticoli spaziali e la cui forma è una forma geometrica regolare combinata. Le forme dei cristalli singoli ideali si dividono in due tipi: forme semplici e forme combinate.
(1) Forma semplice
Una forma semplice si riferisce a una combinazione di un gruppo di facce cristalline collegate da elementi di simmetria, che può essere intesa come un corpo geometrico composto da facce cristalline della stessa forma e dimensione in uno stato ideale (Figura 2-1-5). Esistono 47 tipi di forme semplici nei cristalli.
I punti chiave per identificare le forme semplici sono: tutte le facce del cristallo hanno la stessa forma e dimensione e le facce del cristallo possono essere orientate in modo diverso.
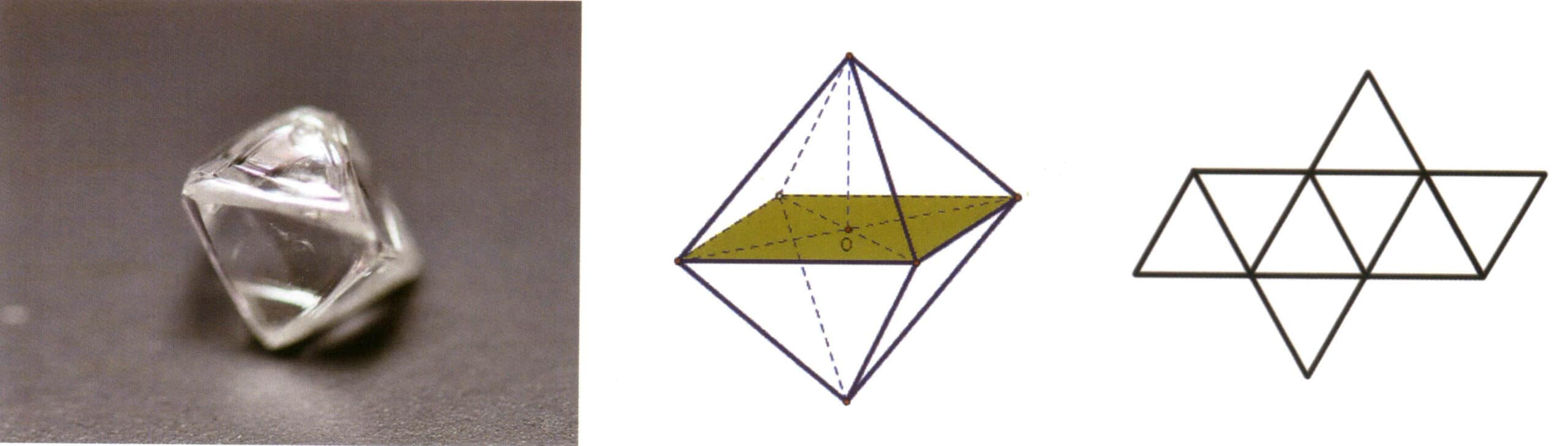
(2) Combinare Forma
L'aggregazione di forme semplici è chiamata forma combinata, composta da due o più forme semplici diverse. Non tutte le forme semplici possono essere liberamente combinate in forma combinata; solo le forme semplici con lo stesso gruppo di punti possono aggregarsi (Figure da 2-1-6 a 2-1-8).
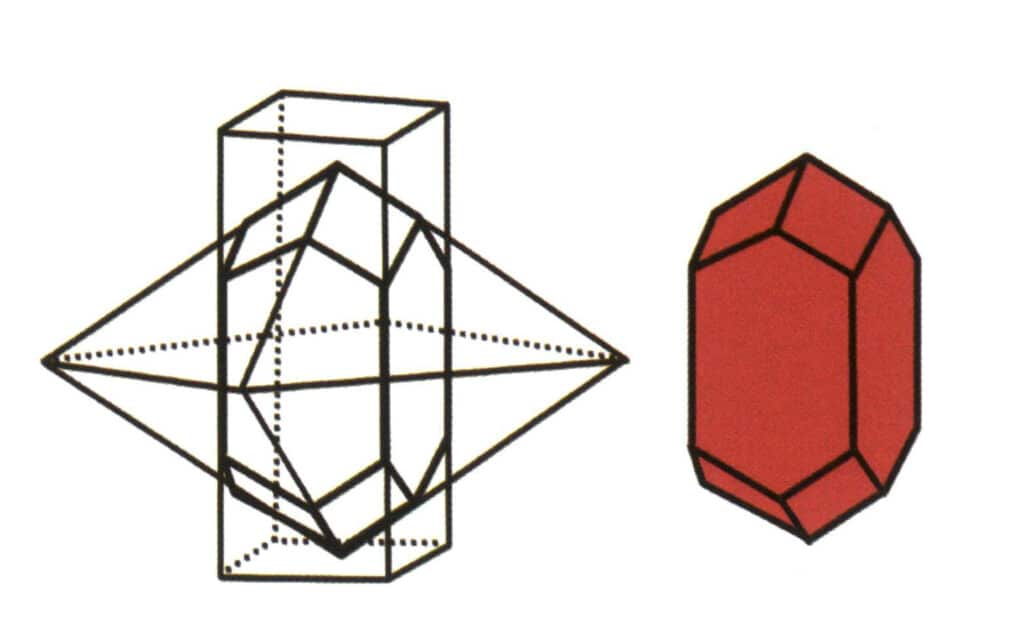
Figura 2-1-6 Combinazione di prismi tetragonali e di piramidi tetragonali
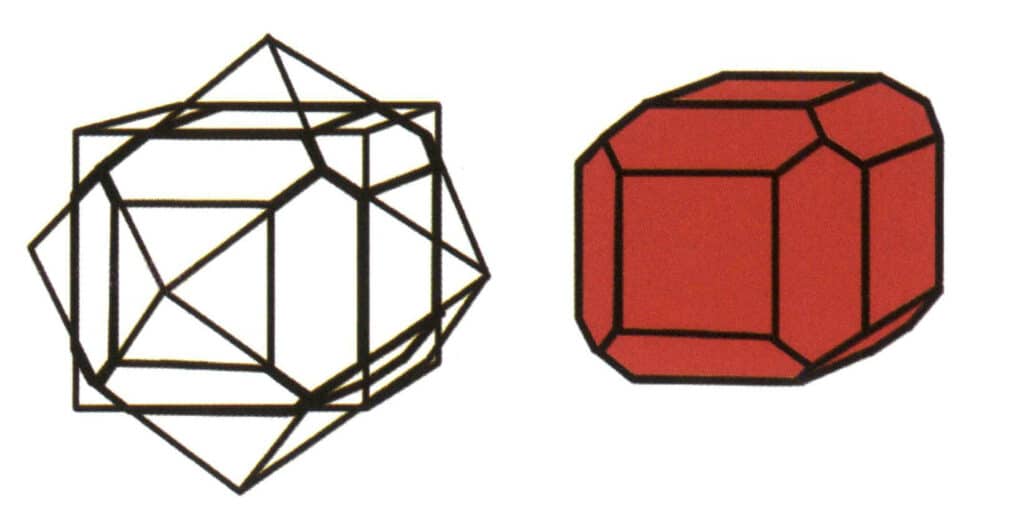
Figura 2-1-7 Combinazione di Cubi e Dodecaedri rombici
Il punto chiave dell'identificazione della forma combinata è la presenza di due o più facce cristalline di forma diversa nel cristallo.
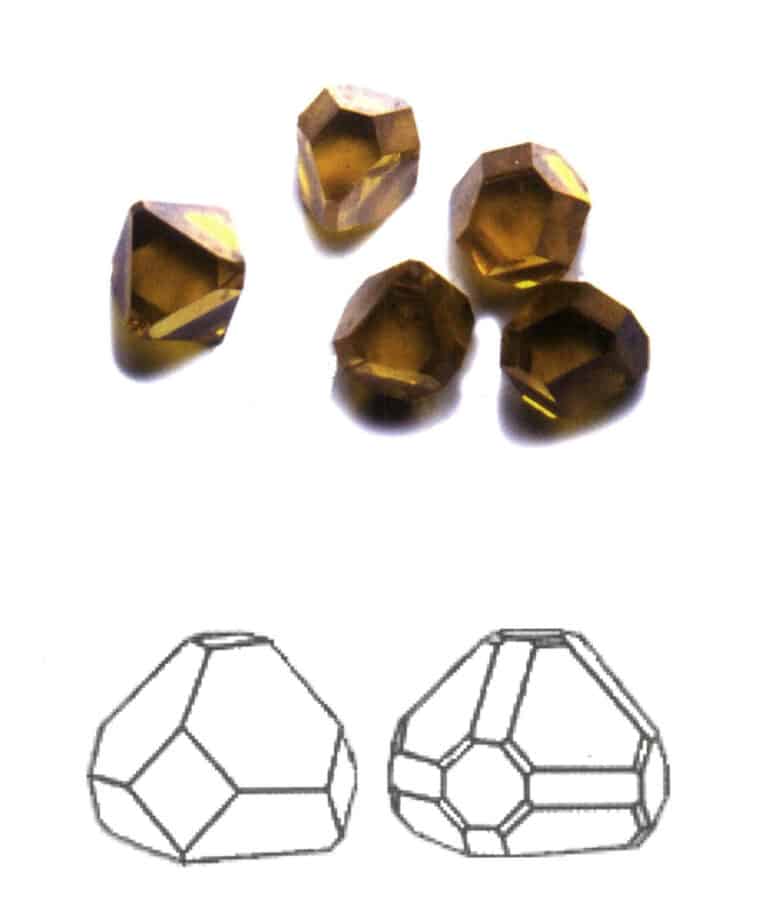
Quando si trovano cristalli singoli in natura, presentano sempre una differenza significativa rispetto alla morfologia ideale dei cristalli singoli (Figura 2-1-9), come ad esempio una singola faccia che non ha necessariamente la stessa forma e dimensione e la scomparsa delle facce del cristallo, che viene descritta come cristalli distorti.

I cristalli distorti possono anche essere descritti come cristalli reali prodotti in natura, influenzati dall'ambiente di crescita. Le facce multiple del cristallo che si ripetono ad angoli fissi nei cristalli ideali possono non essere necessariamente della stessa forma e dimensione. Tuttavia, per lo stesso tipo di cristallo, le facce dello stesso monomorfo devono avere lo stesso modello e le stesse proprietà fisiche. Gli angoli tra le facce del cristallo corrispondenti rimangono invariati, riflettendo la simmetria intrinseca del cristallo stesso. I cristalli che si trovano nella realtà sono distorti in misura variabile.
I cristalli geminati possono anche essere descritti come cristalli reali prodotti in natura, influenzati dall'ambiente di crescita. Le facce multiple del cristallo che si ripetono ad angoli fissi nei cristalli ideali possono non essere necessariamente della stessa forma e dimensione. Tuttavia, per lo stesso tipo di cristallo, le facce della stessa forma devono avere gli stessi schemi e le stesse proprietà fisiche. Gli angoli tra le facce corrispondenti del cristallo rimangono invariati, riflettendo la simmetria intrinseca del cristallo stesso. I cristalli che si trovano nella realtà sono tutti, in varia misura, geminati.
3. Le abitudini di cristallizzazione dei cristalli
I cristalli formati in natura non possono mai raggiungere una forma perfetta. Se crescono negli interstizi degli strati rocciosi, circondati dalla roccia, la forma naturale del cristallo sarà distorta. Anche i cristalli coltivati in laboratorio si deformano a causa dell'influenza della gravità. Solo nelle condizioni di gravità zero della Stazione Spaziale Internazionale gli scienziati possono coltivare i cristalli di forma perfetta che cercano.
Sebbene le forme dei cristalli siano imperfette, ogni tipo di cristallo minerale tende a crescere o a raggrupparsi in modi o abitudini diverse.
Ogni minerale tende a formarsi in condizioni specifiche e le sue abitudini riflettono le condizioni di formazione. Alcuni minerali, come il quarzo, presentano condizioni di formazione complesse e variabili. Pertanto, anche il quarzo possiede molteplici abitudini.
In generale, le abitudini dei cristalli si riferiscono alle caratteristiche di un certo cristallo che tende a formare una forma specifica in determinate condizioni esterne. A volte, si riferisce ai tipi comuni di forma semplice di quel cristallo.
In base al grado di sviluppo dei cristalli nello spazio tridimensionale, le abitudini dei cristalli si dividono in tre tipi fondamentali.
(1) Uni-Estensione direzionale
I cristalli si estendono in un'unica direzione, presentandosi in forme colonnari, aciculari, fibrose, ecc. Minerali come il berillo, la tormalina, l'orneblenda e la malachite presentano spesso questo aspetto (Figure da 2-1-10 a 2-1-11).

Figura 2-1-10 Acquamarina colonnare (in alto) e diagramma delle caratteristiche del cristallo (in basso)

Figura 2-1-11 Malachite fibrosa (in alto) e diagramma delle sue abitudini cristalline (in basso)
(2) Bi-Estensione direzionale
I cristalli si estendono su un piano, apparendo in forme simili a lastre, fogli, scaglie, ecc.
(3) Tri-isometrico direzionale
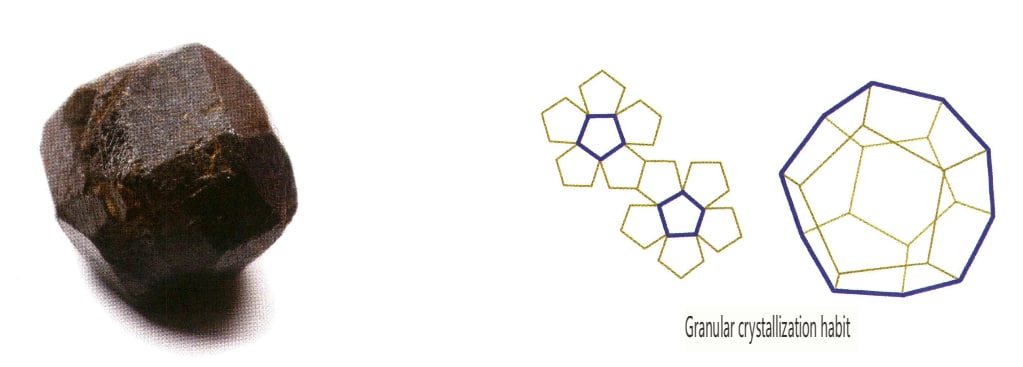
I cristalli si sviluppano uniformemente in tre direzioni, presentando forme isometriche e granulari, come lo spinello, il granato, il diamante, la pirite e la fluorite, che spesso presentano questo aspetto (Figure 2-1-13, 2-1-14).

Figura 2-1-12 L'abito cristallino a placca della tanzanite (in alto) e il suo diagramma di abito cristallino (in basso)

Figura 2-1-13 L'abito cristallino ottaedrico della gemma spinello (in alto) e il suo diagramma di abito cristallino (in basso)
Inoltre, esistono tipi di transizione come le forme colonnari corte, colonnari a placche, a strisce e a placche spesse.
La composizione chimica e la struttura del cristallo determinano principalmente l'aspetto del cristallo. È anche strettamente correlata alle condizioni esterne durante la formazione del cristallo (come la temperatura, la pressione, la concentrazione, la viscosità e le impurità), come le differenze di forma del cristallo tra diamanti e cristalli di diamante sintetici.
4. Aggregazione regolare dei cristalli
In natura, possiamo trovare cristalli singoli (Figura 2-1-15) e due o più cristalli singoli che crescono insieme per formare un insieme. Questo fenomeno di crescita di più cristalli insieme è chiamato aggregazione cristallina. L'aggregazione cristallina può essere classificata in irregolare e regolare. L'aggregazione cristallina irregolare può essere intesa come un collettivo, di cui si parlerà nel capitolo terzo. Nell'aggregazione cristallina regolare, esistono quattro tipi comuni: aggregazione parallela, bicristalli, sovracrescita e intercrescita (Figure da 2-1-16 a 2-1-18). Questa sezione tratta principalmente il tipo di aggregazione regolare nota come bicristalli.

Figura 2-1-15 Monocristallo (tormalina)
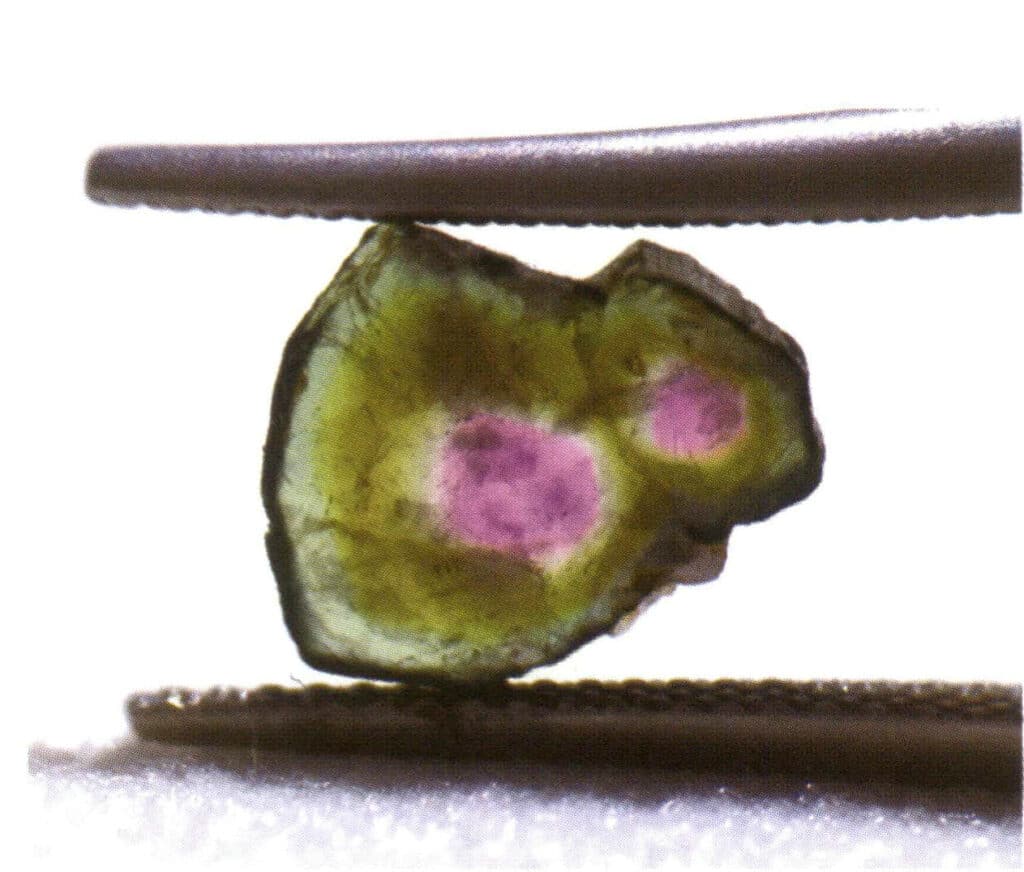
Figura 2-1-16 Aggregazione parallela (Quando più cristalli dello stesso tipo crescono parallelamente nello spazio, si parla di aggregazione parallela. In questo caso, le facce e gli spigoli corrispondenti dei cristalli cresciuti sono tutti paralleli tra loro).

Figura 2-1-17 Cristallo gemello (Spinello)

Figura 2-1-18 Sovracrescita (un tipo di cristallo cresce sulla superficie di un altro cristallo in una specifica direzione cristallografica, nota anche come crescita epitassiale)
Il bicristallo è l'aggregazione regolare di due o più cristalli identici secondo determinate regole di simmetria. (Le facce, gli spigoli e gli angoli corrispondenti dei due individui adiacenti non sono completamente paralleli. Tuttavia, possono riflettersi l'un l'altro attraverso operazioni simmetriche come la rotazione e l'inversione della rotazione, permettendo ai due individui di coincidere o allinearsi.
4.1 Punti chiave per l'identificazione dei bicristalli
① Angoli concavi visibili nei cristalli geminati (Figura 2-1-19).
② Stylolite: La micromorfologia e altre caratteristiche delle superfici cristalline su entrambi i lati della stilolite sono discontinue (Figura 2-1-20).
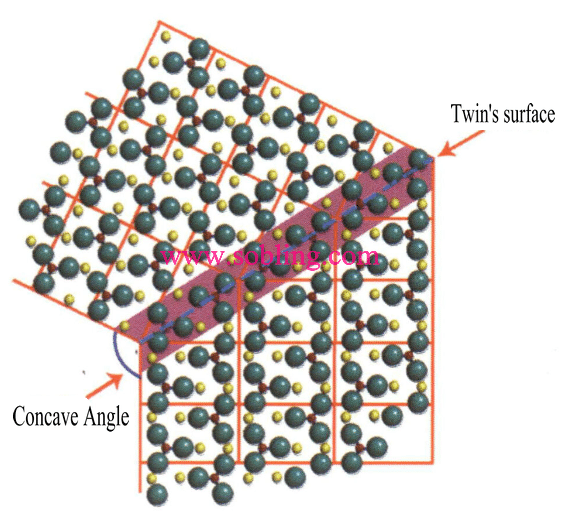
Figura 2 - 1-19 Angolo di concavità del gemello
Figura 2-1-20 Stilolite (i diversi colori della figura rappresentano i diversi cristalli; le linee rosse indicano la stilolite gemella)
③ Striature di geminazione: Le facce dei cristalli o i piani di clivaggio mostrano sottili striature di geminazione (Figura 2-1-21).
④ Figura di mordenzatura: L'aspetto della figura di mordenzatura indica la presenza di gemellatura (Figura 2-1-22).

Figura 2-1-21 Schema dei gemelli polisintetici

Figura 2-1-22 Superficie di spinello con fosse triangolari invertite.
⑤ Comparsa di pseudo-simmetria: comparsa di relazioni di simmetria non coerenti con il gruppo di punti intrinseco del cristallo singolo (da Figura 2-1-23 a Figura 2-1-24).

Figura 2-1-23 Cristallo singolo di crisoberillo

Figura 2-1-24 Gemello a forma di ginocchio di crisoberillo
La gemellarità è suddivisa in cinque tipi in base alle loro caratteristiche di impilamento: gemelli di contatto (Figura 2-1-25 a Figura 2-1-26), gemelli polisintetici (Figura 2-1-27), gemelli compenetrati (Figura 2-1-28), cristallo tripletto (Figura 2-1-29) e gemelli complessi, tra cui i primi quattro tipi sono comuni.


Figura 2-1-26 Gemellaggio di contatto dello spinello (in alto) e sua schematizzazione (in basso)

Figura 2-1-27 Gemello polisintetico di labradorite (in alto) e sua schematizzazione (in basso)
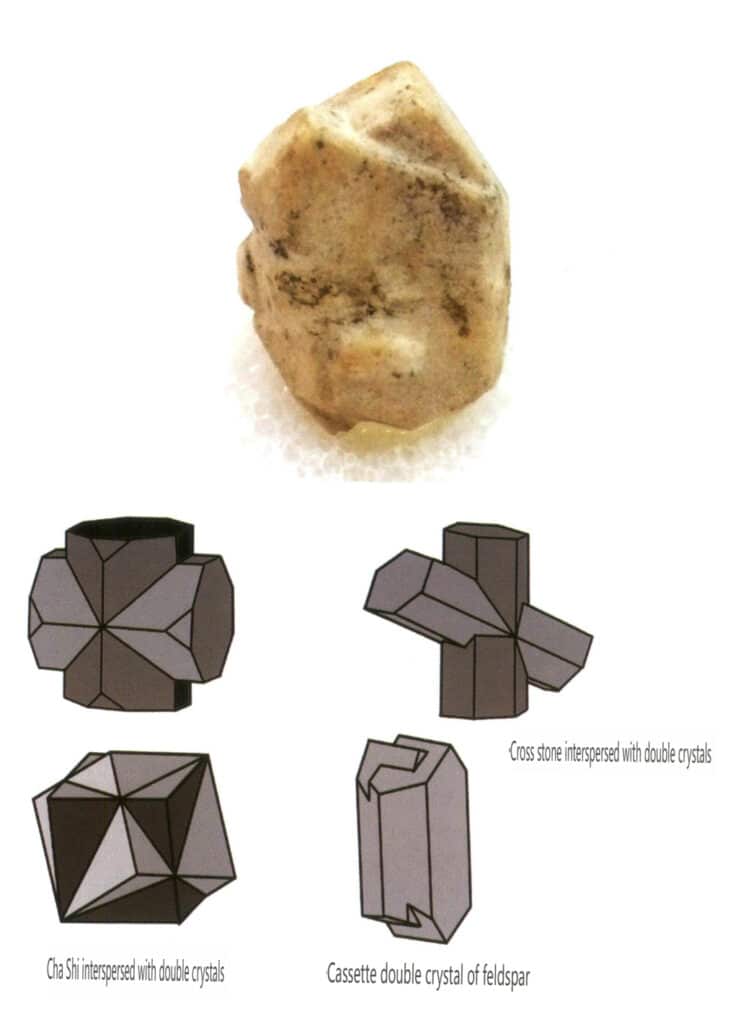
Figura 2-1-28 Cristalli gemelli di feldspato (in alto) e schema di cristalli gemelli compenetrati di altri tipi (in basso)

Figura 2-1-29 Gemellaggio trigonale del crisoberillo (in alto) e sua schematizzazione (in basso)
4.2 La formazione di bicristalli
① Formata durante la crescita del cristallo, può svilupparsi da germi cristallini gemelli o da piccoli cristalli che crescono in modo dipendente dalla posizione del gemello.
② Si forma durante il processo di trasformazione eteromorfa, come quando il quarzo α si trasforma in quarzo β, formando dei gemelli.
③ Formati per azione meccanica, dove una parte del cristallo scivola lungo un certo piano direzionale per formare gemelli di deformazione, come i gemelli della calcite.
5.Modelli di facce di cristallo
Quando vengono scoperti in natura, i cristalli hanno spesso forme incomplete (Figura 2-1-30) e particolari motivi superficiali. A volte crescono insieme in ammassi (Figura 2-1-31), che spesso mostrano differenze significative rispetto ai poliedri geometrici standard che conosciamo, come i cubi e i prismi esagonali. Questo fenomeno è chiamato forma reale dei cristalli. La forma reale dei cristalli ha una classificazione dettagliata in cristallografia, come i cristalli distorti, i cristalli convessi, i cristalli curvi, i cristalli fluttuanti, le striature delle facce dei cristalli, le figure di incisione, le striature di geminazione, ecc.

Figura 2-1-30 Cristallo di rubino

Figura 2-1-31 Cristalli di pirite (a sinistra si vedono più cristalli di pirite che crescono insieme, a destra un singolo cristallo di pirite)
Questa sezione tratta principalmente i modelli di facce di cristallo nella forma reale dei cristalli.
In teoria, i piani cristallini sono lisci e piatti. Tuttavia, durante l'effettiva crescita o dissoluzione dei cristalli, la superficie spesso lascia dietro di sé schemi regolari leggermente irregolari, comunemente chiamati schemi delle facce dei cristalli. I modelli delle facce dei cristalli includono striature di crescita, strati di crescita, modelli a spirale, collinette di crescita e figure di incisione. I modelli delle facce dei cristalli discussi in questo libro si riferiscono principalmente alle striature delle facce dei cristalli e alle figure di incisione che possono essere osservate a occhio nudo o in condizioni di basso ingrandimento.
Le striature della faccia del cristallo si riferiscono a una serie di linee rette parallele sulla superficie del cristallo dovute alla convergenza ripetuta e alla crescita alternata di diverse forme singole. Conosciute anche come "strisce combinate", sono visibili solo sulle superfici dei cristalli, chiamate anche strisce di crescita. Ad esempio, la faccia prismatica esagonale del quarzo presenta spesso facce prismatiche esagonali e dodecaedriche rombiche di cristallo fine sviluppate alternativamente in strisce trasversali aggregate (Figura 2-1-32).

Le figure di mordenzatura si riferiscono alle fosse di forma specifica (cioè le fosse di mordenzatura) lasciate sulla superficie del cristallo a causa della corrosione dopo la formazione del cristallo. Le figure di mordenzatura sono controllate dalla disposizione delle particelle elementari all'interno della superficie del cristallo. Pertanto, le forme e gli orientamenti delle figure di incisione variano tra i diversi minerali e le singole forme dello stesso cristallo. Per esempio, le figure di mordenzatura su diverse forme singole di cristalli di diamante variano; si possono osservare pozzetti triangolari su cristalli ottaedrici (Figura 2-1-33), pozzetti quadrilateri su facce cubiche, pozzetti quadrilateri sovrapposti che formano un motivo a griglia e motivi a linea o microscopici a disco su dodecaedri rombici (Figura 2-1-34).

Figura 2-1-33 Fosse triangolari invertite visibili sul cristallo ottaedrico di diamante

Figura 2-1-34 Struttura a motivi lineari visibile su cristalli dodecaedrici a forma di diamante
Solo le figure mordenzate sulla stessa faccia cristallina della stessa forma possono essere uguali, quindi le figure mordenzate sono spesso utilizzate per identificare i minerali e determinare se le facce cristalline appartengono alla stessa forma singola (da Figura 2-1-35 a Figura 2-1-42).

Figura 2-1-35 Strisce in stile pavimento in legno intarsiato con cristallo di fluorite

Figura 2-1-36 Figura di incisione triangolare naturale nel rubino (strisce orizzontali comuni nei rubini, linee di crescita parallele alla direzione romboedrica, incisioni naturali in forma triangolare o esagonale)

Figura 2-1-37 Strisce longitudinali superficiali di tormalina

Figura 2-1-38 strisce orizzontali sulla superficie del cristallo

Figura 2-1-39 Figure di mordenzatura sulla superficie del cristallo

Figura 2-1-40 Striature longitudinali superficiali del topazio

Figura 2-1-41 Immagine topografica di un cristallo di topazio

Figura 2-1-42 Figure di mordenzatura dello spinello
Sezione II 47 Tipi di forme cristalline
In cristallografia esistono 146 forme singole diverse, che possono essere classificate in 47 forme geometriche in base alle loro forme geometriche quando esistono indipendentemente. Queste forme geometriche sono denominate nei seguenti modi:
Denominato in base alle caratteristiche della forma della sezione trasversale, come prisma trigonale, prisma tetragonale, prisma esagonale, bipiramide romboedrica, ecc.
② Denominazione in base alla forma della singola forma, come cilindro, doppio cono, cubo, ecc.
③ Il nome dipende dal numero di facce geometriche, come ad esempio faccia singola, ottaedro, ecc.
④ Chiamati in base alla forma delle facce geometriche, come romboedro, pentacontaedro, ecc.
In cristallografia, le forme singole si dividono in quattro categorie: forme generali e forme speciali, forme chiuse e forme aperte, forme regolari e forme irregolari, forme sinistre e forme destre. In questo capitolo si parlerà brevemente delle forme chiuse e delle forme aperte.
Le forme chiuse si riferiscono a quelle le cui facce cristalline possono racchiudere uno spazio chiuso, suddivise in tre categorie principali: classi poliedriche, classi poliedriche oblique e classi bipiramidali, per un totale di 30 tipi. Ogni categoria ha classificazioni più dettagliate; ad esempio, la classe poliedrica è suddivisa in classe tetraedrica, classe ottaedrica, classe cubica, ecc.

Figura 2-1-43 Classe tetraedro
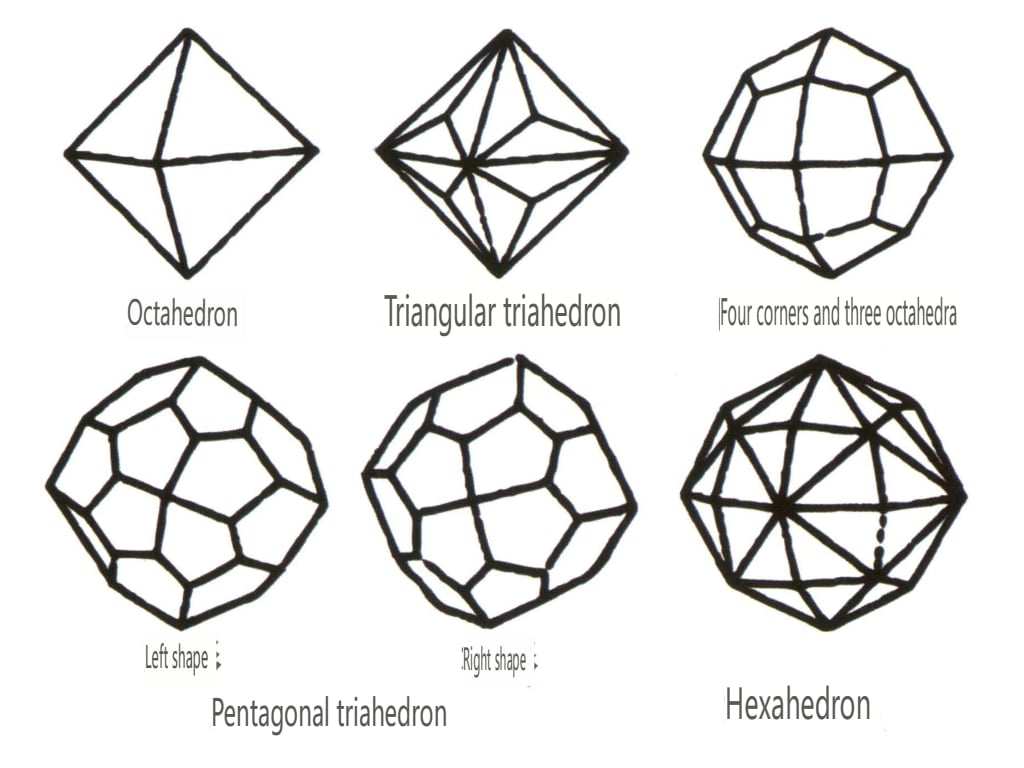
Figura 2-1-44 Classe 0ctaedrica
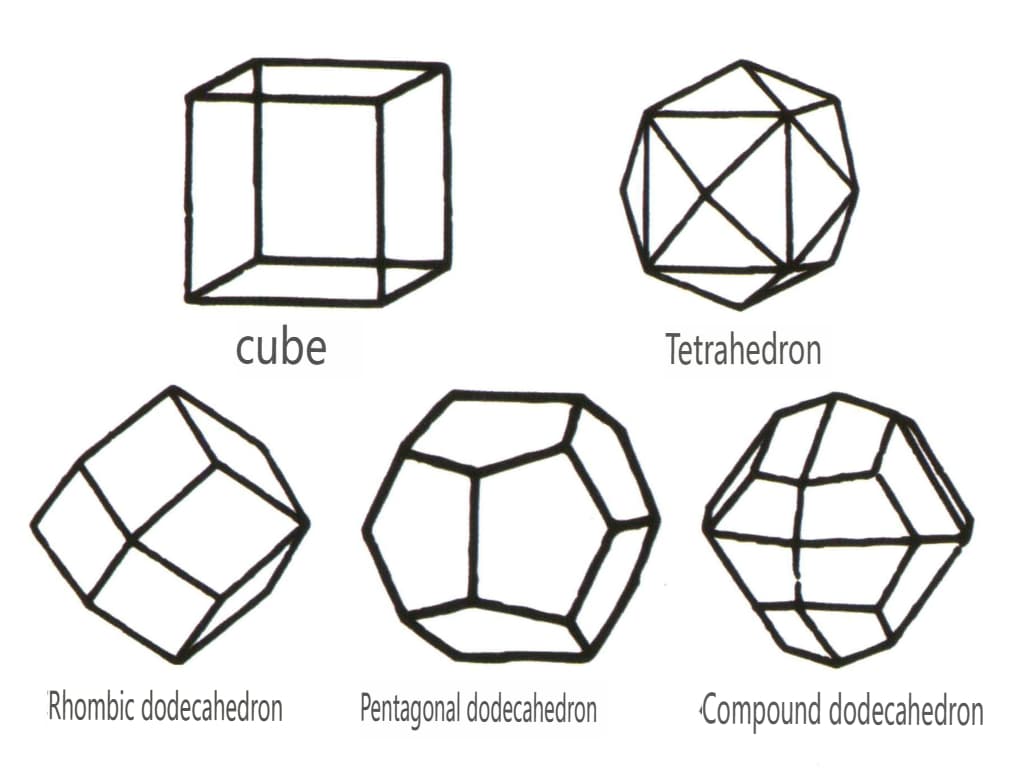
Figura 2-1-45 Classi cubiche e dodecaedriche
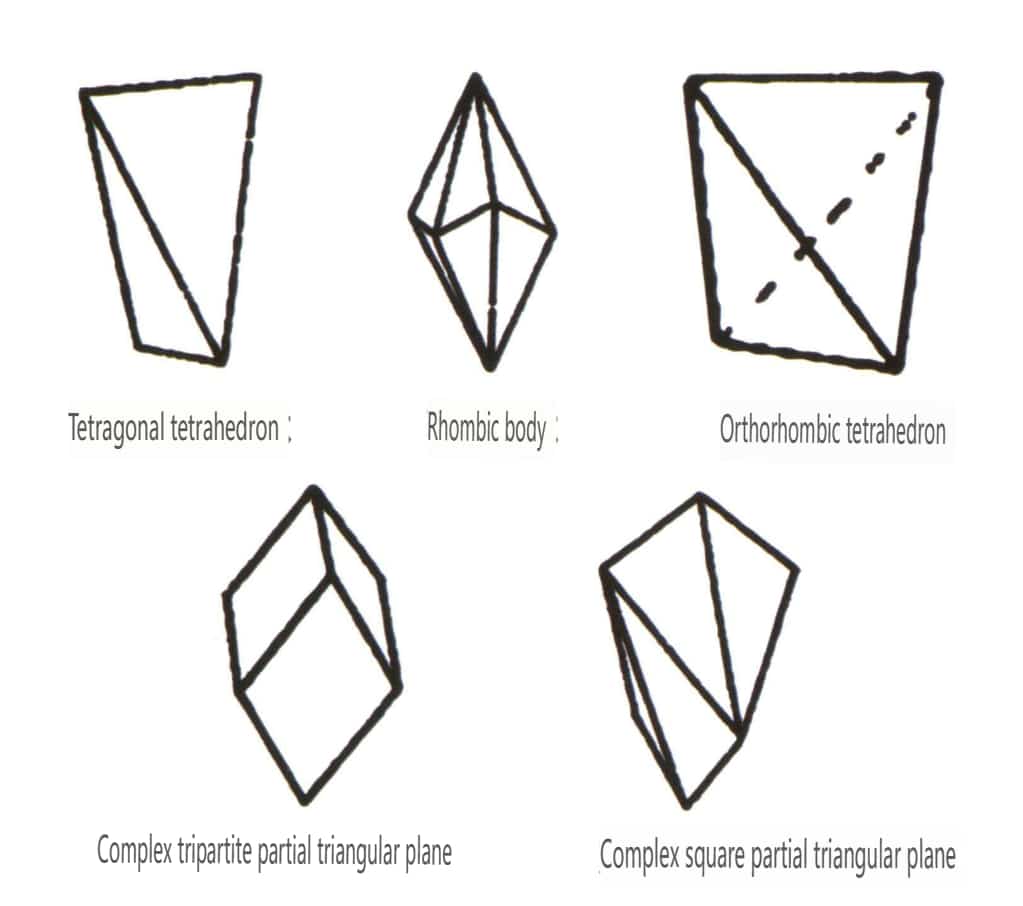
Figura 2-1-46 Altri tipi di poliedri
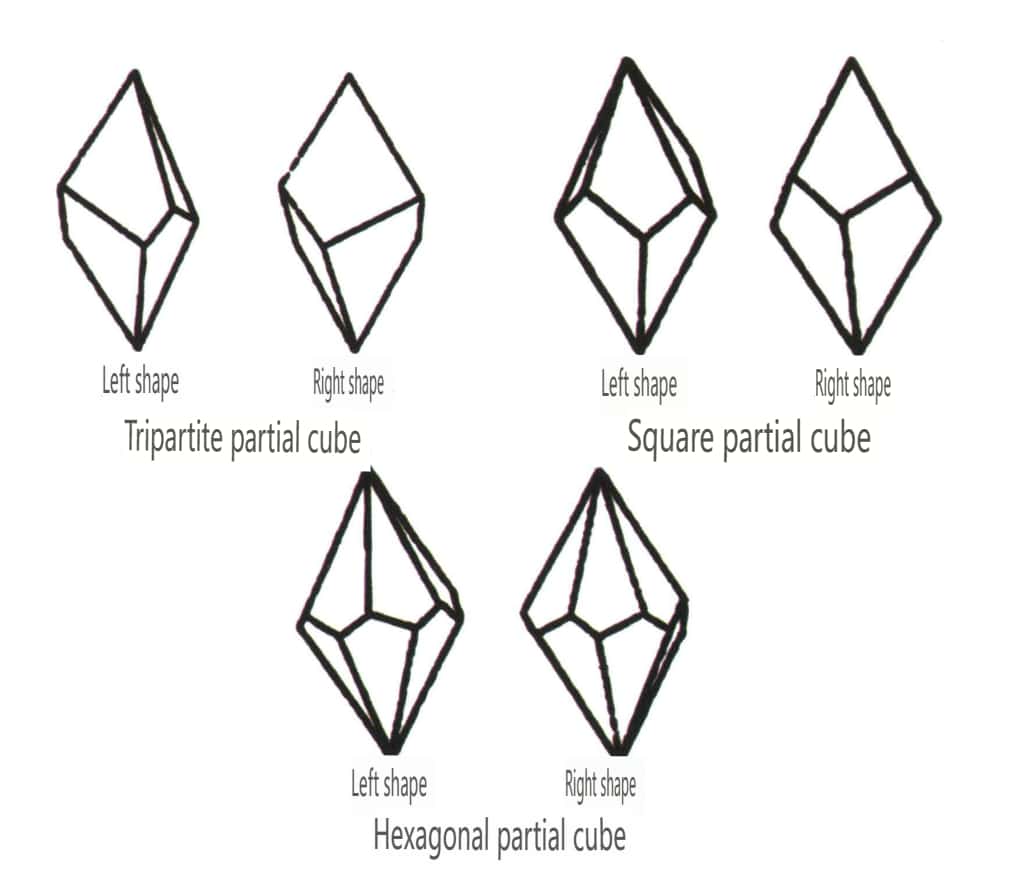
Figura 2-1-47 Forma combinata obliqua Classe
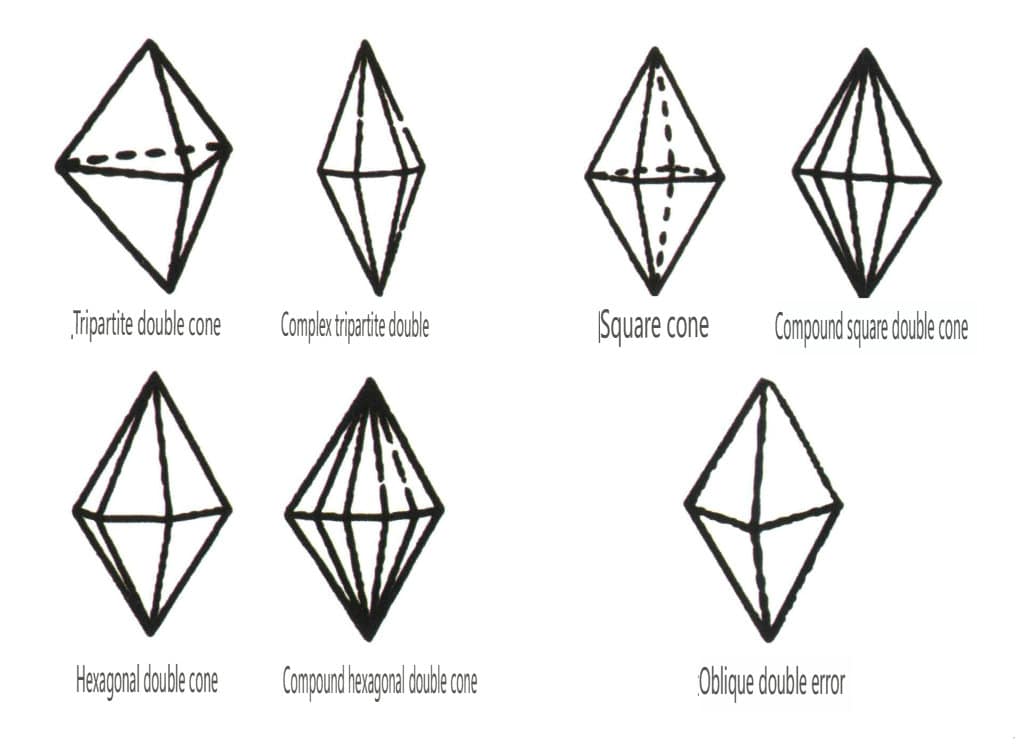
Figura 2-1-48 Classe piramidale doppia
Le forme aperte si riferiscono a quelle le cui facce cristalline non possono racchiudere uno spazio chiuso, suddivise in quattro categorie principali: monofaccia, bifaccia, classi colonnari e classi piramidali singole, per un totale di 17 tipi (Figure 2-1-49 e 2-1-51).
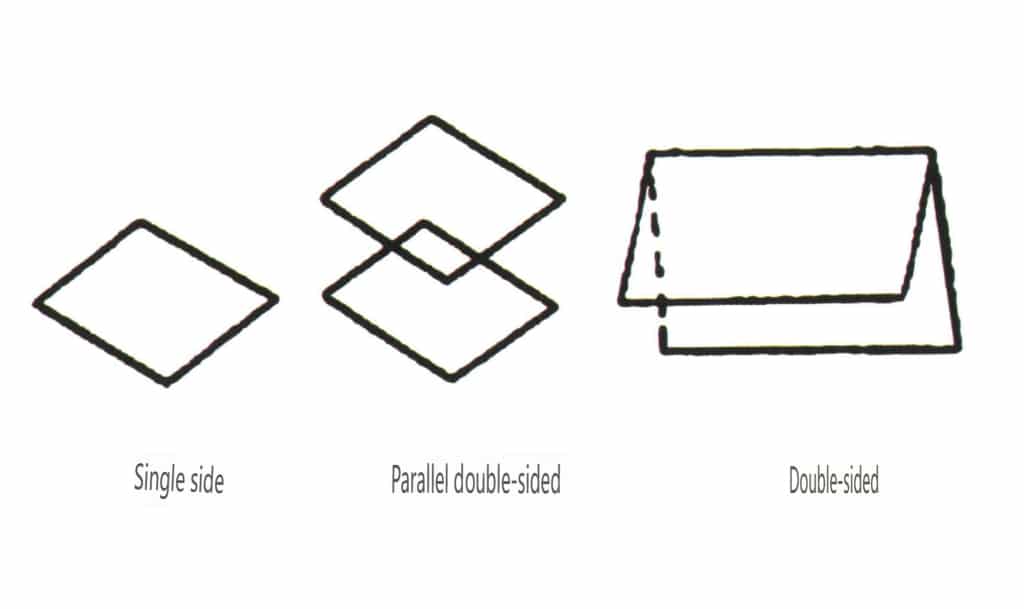
Figura 2-1-49 Lato singolo e lato doppio
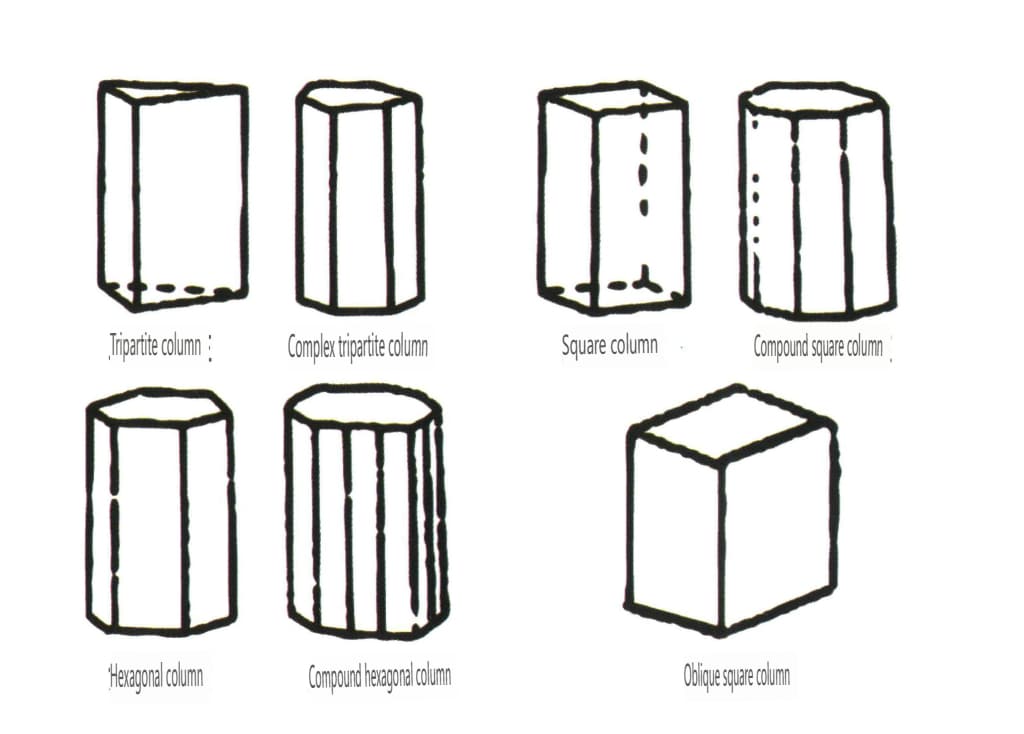
Figura 2-1-50 Colonne

Sezione III Classificazione dei cristalli
1. Simmetria dei cristalli
La simmetria è un concetto astratto coinvolto nello studio dei cristalli reali e dei materiali gemmologici non lavorati. Descrive la ripetizione esibita quando la struttura cristallina è riferita a una direzione o a un piano che la attraversa. È la base per la classificazione dei cristalli.
La simmetria di un cristallo può essere intesa, da un punto di vista microscopico, come un metodo per descrivere la ripetitività della struttura cristallina e, da un punto di vista macroscopico, come la ripetizione di due o più facce geometriche che hanno la stessa forma e dimensione ma possono differire nella direzione, secondo determinate regole. Questo schema di ripetizione può essere descritto utilizzando assi di simmetria e piani di simmetria, e ogni asse di simmetria o piano di simmetria viene definito elemento di simmetria. Quando si osserva o si deduce la simmetria di un oggetto, si parla di operazioni sulla simmetria.
2. Elementi di simmetria dei cristalli
In cristallografia, gli elementi di simmetria sono quattro: asse di simmetria, piano di simmetria, assi di simmetria di rotoinversione e centro di simmetria. In questo caso, si tratta di due elementi di simmetria: l'asse di simmetria e il piano di simmetria.
2.1 Asse di simmetria
(1) Il concetto di asse di simmetria e la sua notazione.
L'asse di simmetria è una linea retta immaginaria che indica il numero di volte in cui il livello di base (Figure da 2-2-1 a 2-2-2) appare nella stessa posizione quando la struttura reticolare viene ruotata di 360° intorno a questa linea immaginaria. Questo numero può essere solo 2, 3, 4 o 6 volte in 4 casi. Si può anche intendere come una linea immaginaria che passa per il centro del corpo geometrico, ruotando il corpo geometrico lungo questa linea di 360°. Supponiamo che la forma del corpo geometrico dopo la rotazione di un certo angolo sia coerente con la forma del corpo geometrico a zero gradi iniziale. In tal caso, questa linea immaginaria è chiamata asse di simmetria.
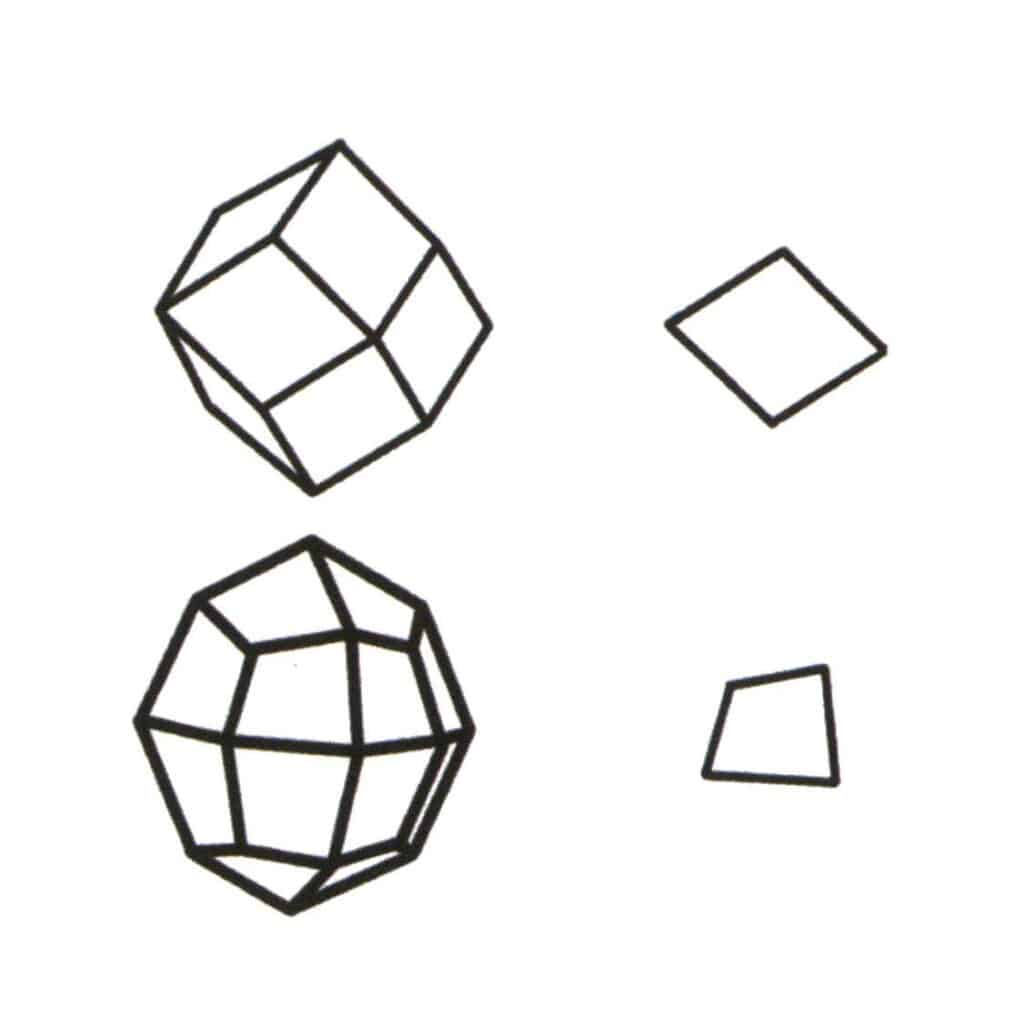
Figura 2-2-1 Selezione del livello di base per il modulo singolo.
Il livello di base di una singola forma è il piano di ripetizione più piccolo che compone il simplex. La figura in alto a sinistra mostra un dodecaedro rombico, che è una forma chiusa composta da un solo tipo di facce. Il piano ripetitivo più piccolo è il rombo mostrato in alto a destra, quindi il livello di base del dodecaedro rombico è il rombo. La figura in basso a sinistra mostra un ottaedro quadrilatero, che è una forma chiusa composta da un solo tipo di facce. Il piano di ripetizione più piccolo è il quadrilatero mostrato in basso a destra, quindi il livello di base dell'ottaedro quadrilatero è il quadrilatero.
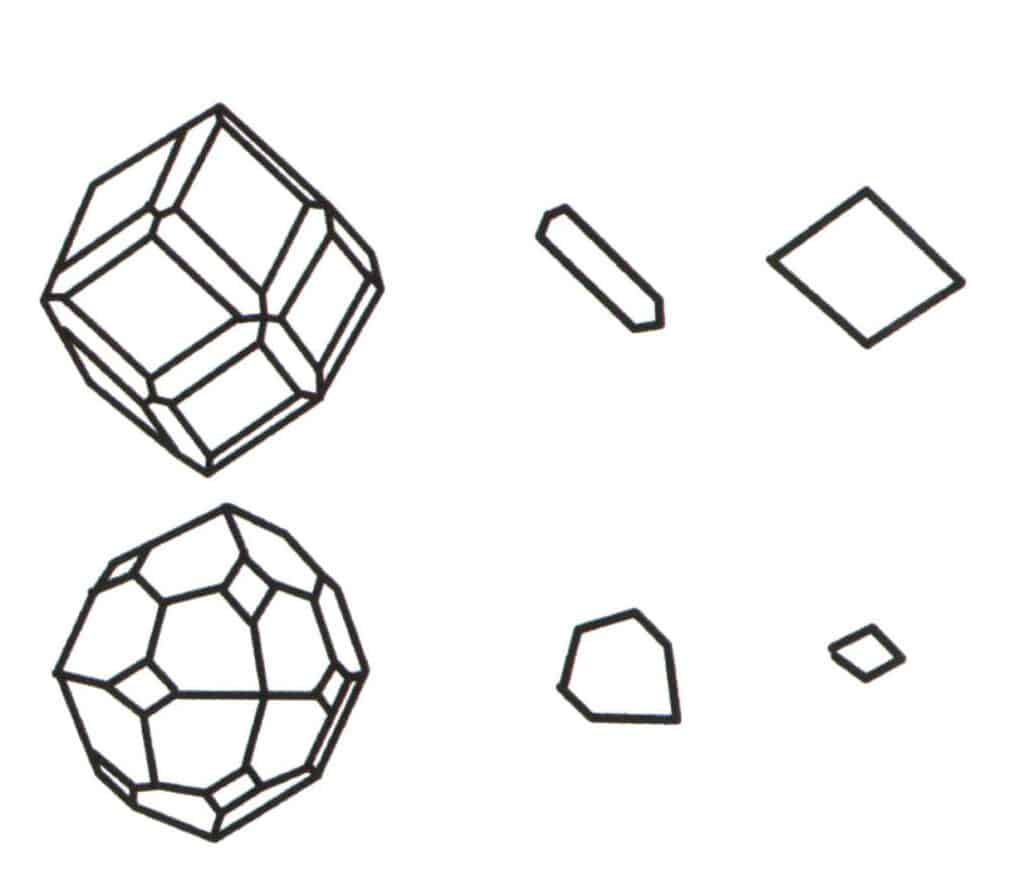
Figura 2-2-2 Selezione del livello di base del politopo.
L'aggregazione di più forme semplici forma una forma combinata, e la scelta del livello di base per la forma combinata è il giudizio sulle singole forme che si combinano per formare la forma combinata. La prima colonna da sinistra nella figura rappresenta una forma combinata (formata dall'aggregazione delle singole forme di un dodecaedro e di un tetraedro), e questo corpo geometrico è una figura chiusa composta da due tipi di facce. L'esagono rappresenta il piano minimo di ripetizione nella seconda colonna e il rombo a destra nella terza colonna. Pertanto, il livello di base della forma combinata nella prima colonna è l'esagono o il rombo. Quando si calcola l'asse di simmetria, è possibile selezionare una sola forma come livello di base per la registrazione della simmetria.
L'asse di simmetria è rappresentato dalla lettera maiuscola L, con l'ordine degli assi n scritto nell'angolo superiore destro di L, scritto come Lⁿ. Ad esempio, un asse a 2 pieghe è rappresentato come L², un asse a 3 pieghe come L³, un asse a 4 pieghe come L⁴ e un asse a 6 pieghe come L⁶. L⁶, L⁴, L³ sono abitualmente indicati come assi di ordine superiore.
I cristalli possono avere assi di simmetria in diverse direzioni e il numero di questi assi di simmetria non coincidenti viene convenzionalmente scritto a sinistra di L. Ad esempio, sei assi secondari sono rappresentati come 6L² (da Figura 2-2-3 a Figura 2-2-9), tre assi terziari sono rappresentati come 3L³ (da Figura 2-2-10 a Figura 2-2-14), quattro assi terziari sono rappresentati come 4L³ (da Figura 2-2-15 a Figura 2-2-18) e un asse esagonale è rappresentato come L⁶ (Figura 2-2-19).
Quando un cristallo ha più assi di simmetria, il metodo registrato li dispone da sinistra a destra in ordine decrescente, con il numero di assi di simmetria scritto a sinistra dell'asse corrispondente, ad esempio, L⁶6L², 3L⁴4L³6L².
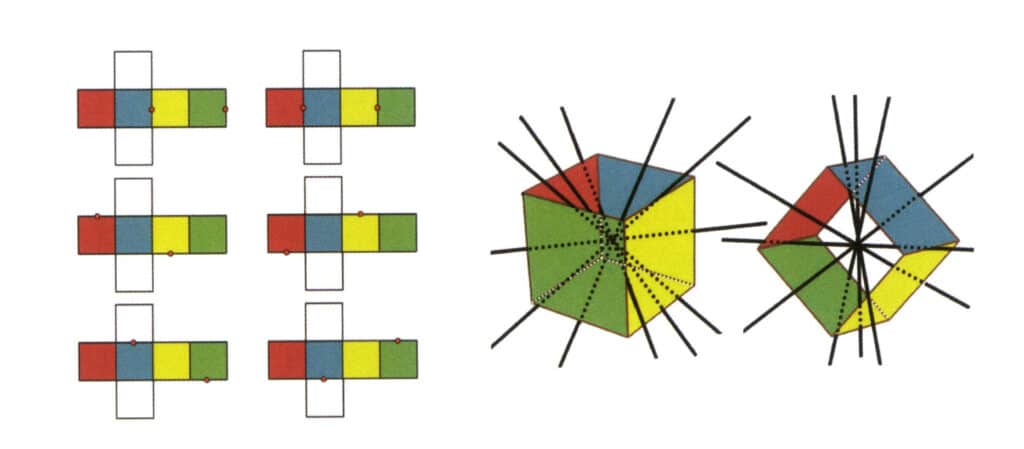
Figura 2-2-3 Asse secondario del cubo
Il lato sinistro della figura mostra la vista dispiegata di un cubo, con punti rossi che indicano i punti di intersezione della linea immaginaria e degli spigoli. Il lato destro della figura mostra un cubo chiuso, in cui l'asse secondario può apparire nel punto medio di linee di bordo parallele, nel punto medio di facce rettangolari parallele o nei punti di intersezione di tre o più facce parallele che assomigliano a un rettangolo. o più facce parallele che assomigliano a un rettangolo.
Copywrite @ Sobling.Jewelry - Produttore di gioielli personalizzati, fabbrica di gioielli OEM e ODM
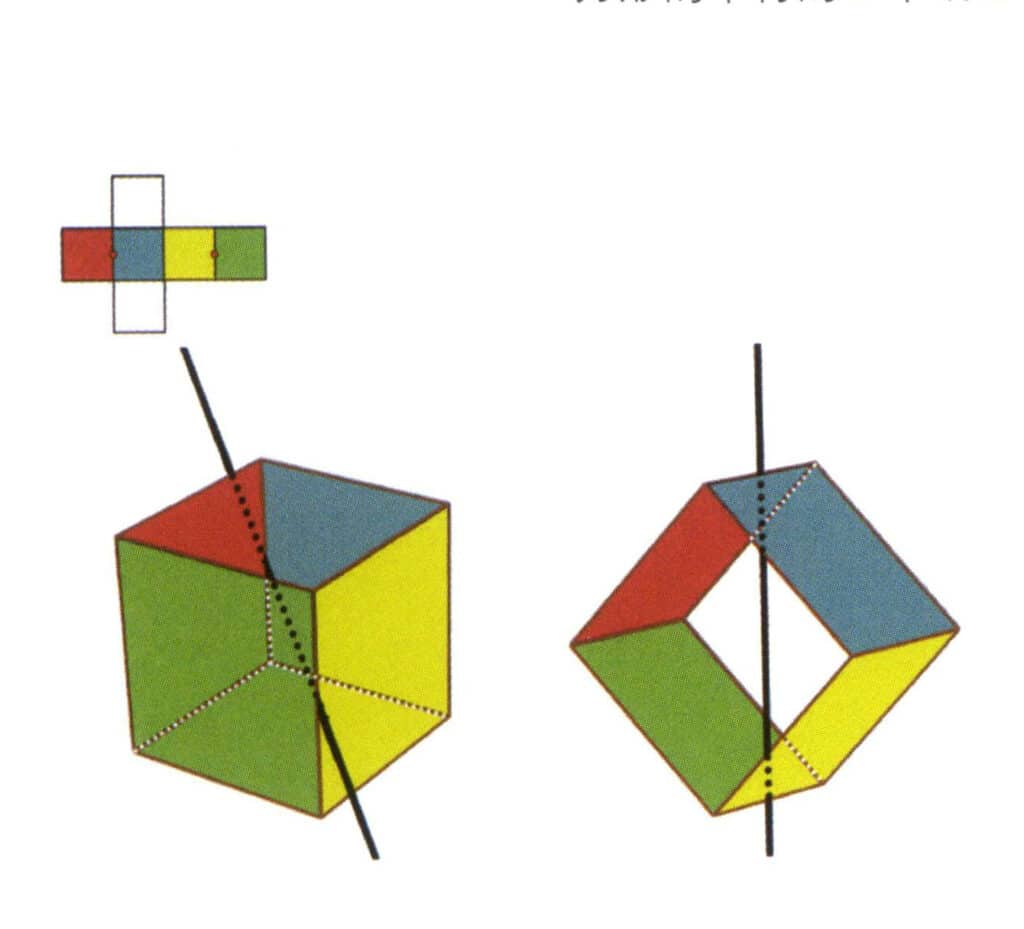
Figura 2-2-4 Il primo asse secondario del cubo
Selezionate il punto medio delle linee parallele, come mostrato nella figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base con colori diversi ma con la stessa forma si ripeteranno due volte nella stessa posizione (le facce rosse e blu, le facce gialle e verdi, le due facce incolori e tre serie di facce ripetute. Anche se appariranno tre serie di facce ripetute, poiché la linea immaginaria non è cambiata in posizione e angolo, l'asse secondario viene registrato solo una volta). Questa linea immaginaria viene registrata come asse secondario.
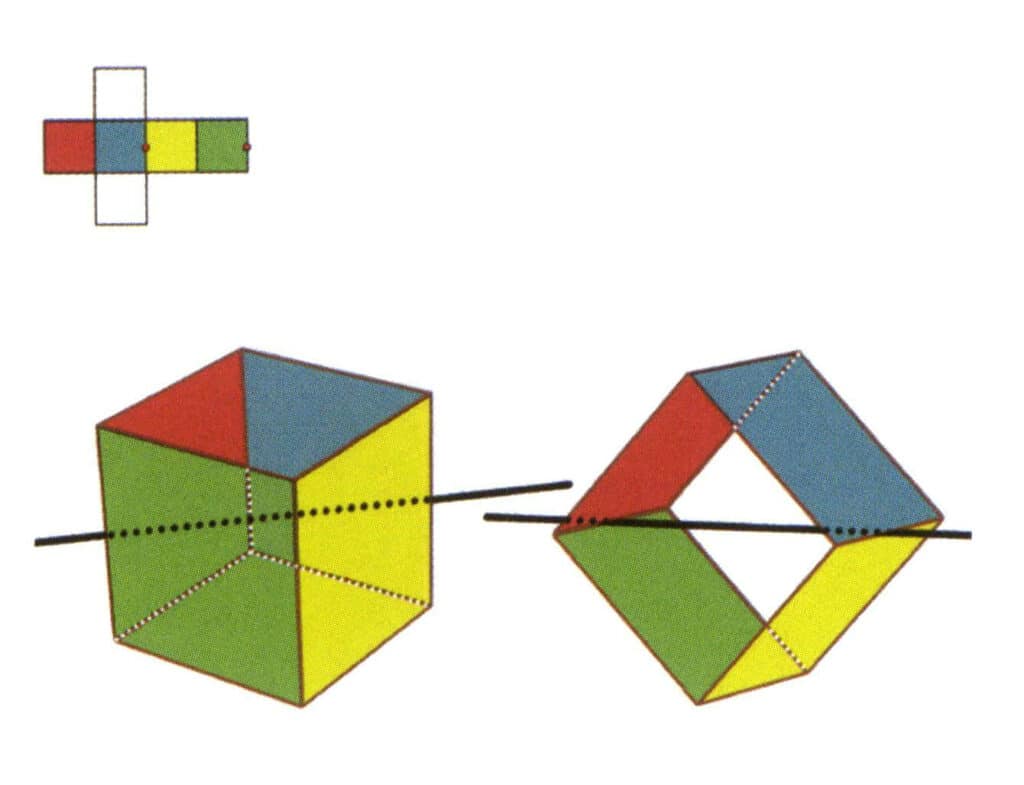
Figura 2-2-5 Il secondo asse secondario del cubo
Selezionate il punto medio delle linee parallele, come mostrato nella figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base con colori diversi ma con la stessa forma si ripeteranno due volte nella stessa posizione (le facce rosse e verdi, le facce gialle e blu, le due facce incolori e tre serie di facce ripetute). Questa linea immaginaria viene registrata come secondo asse secondario.
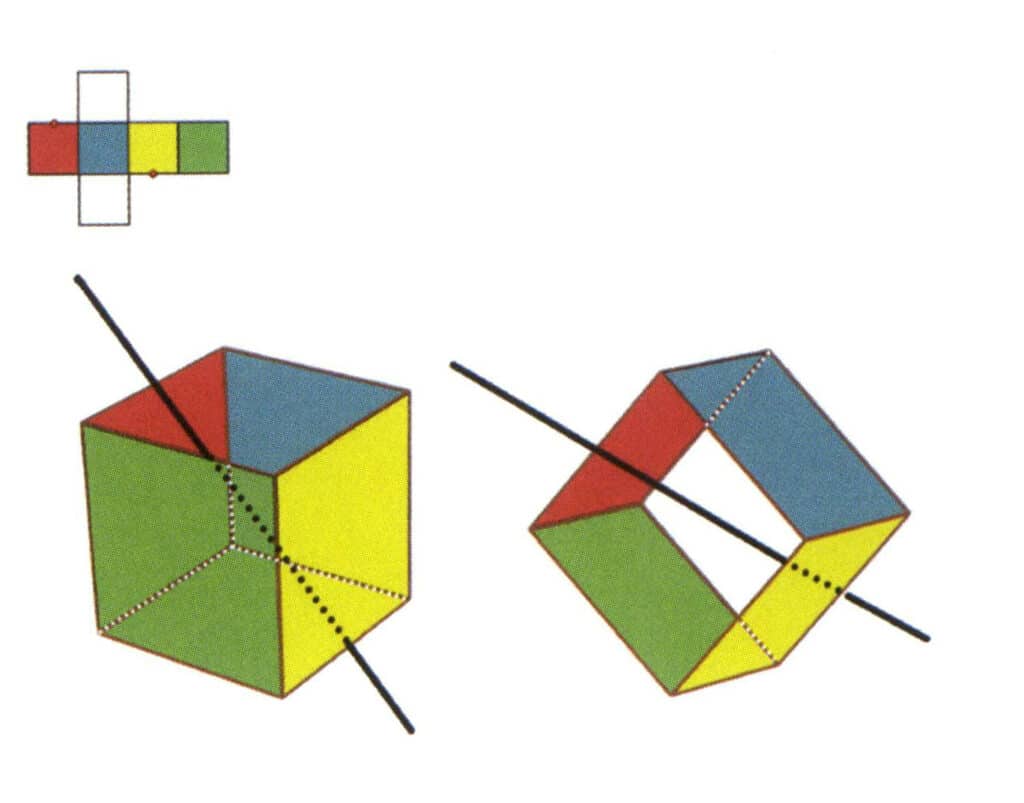
Figura 2-2-6 Il terzo asse secondario del cubo.
Selezionate il punto medio delle linee parallele, come mostrato nella figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base con colori diversi, ma la stessa forma, si ripeteranno due volte nella stessa posizione (le facce rosse e incolori, le facce verdi e blu, le facce incolori e gialle, tre serie di facce ripetute). Questa linea immaginaria viene registrata come terzo asse secondario.
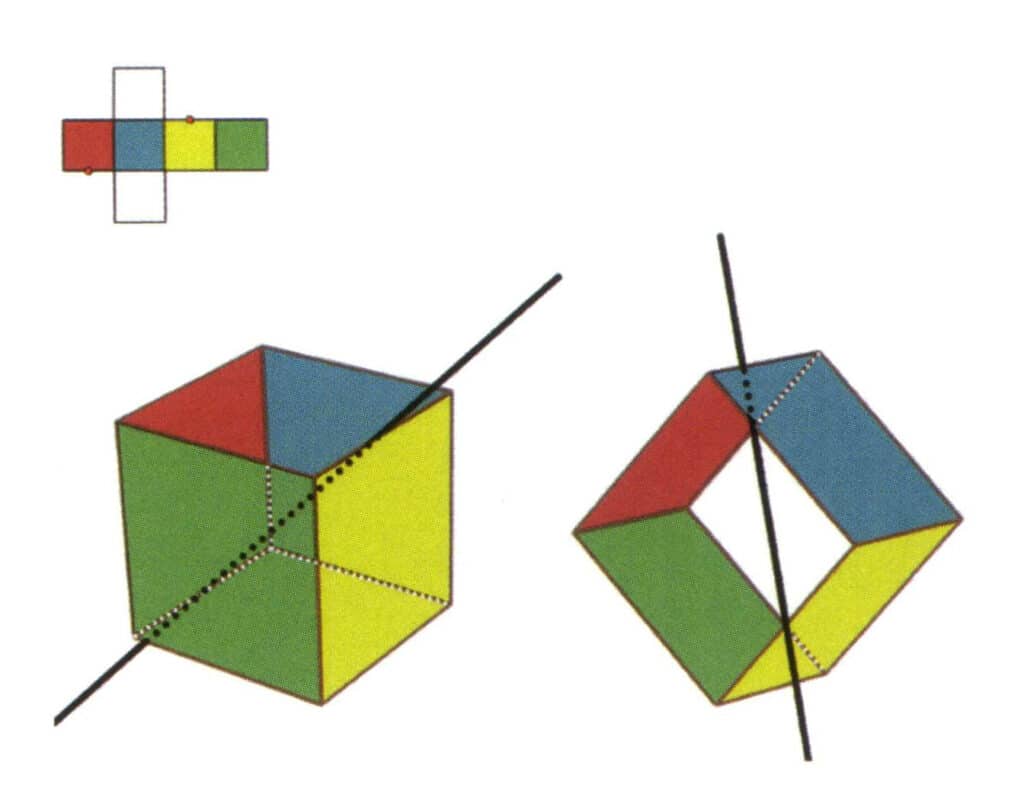
Figura 2-2-7 Il quarto asse secondario del cubo
Selezionare il punto medio delle linee parallele come mostrato in figura, immaginare una linea retta che passi per i punti medi di questi due spigoli e ruotare il cubo di 360°; i piani di riferimento di colore diverso ma di forma identica si ripeteranno due volte nella stessa posizione (le facce rosse e incolori, le facce verdi e blu, le facce incolori e gialle, tre serie di facce ripetute), questa linea retta immaginaria viene registrata come quarto asse secondario.
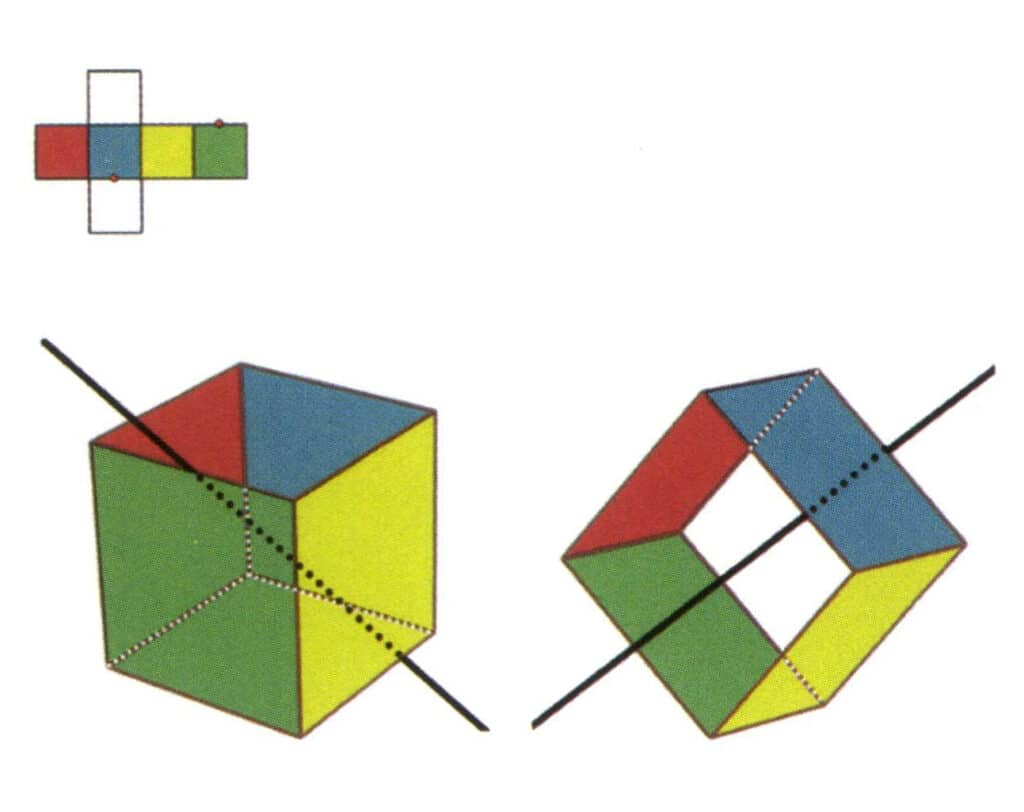
Figura 2-2-8 Il quinto asse secondario del cubo.
Selezionare i punti medi delle linee parallele come mostrato in figura, immaginare una linea retta che passi per i punti medi di questi due spigoli, ruotare il cubo di 360°, i piani di riferimento di colore diverso ma di forma identica si ripeteranno nella stessa posizione due volte (facce rosse e incolori, facce verdi e blu, facce incolori e gialle, tre serie di facce ripetute), questa linea retta immaginata viene registrata come quinto asse secondario.
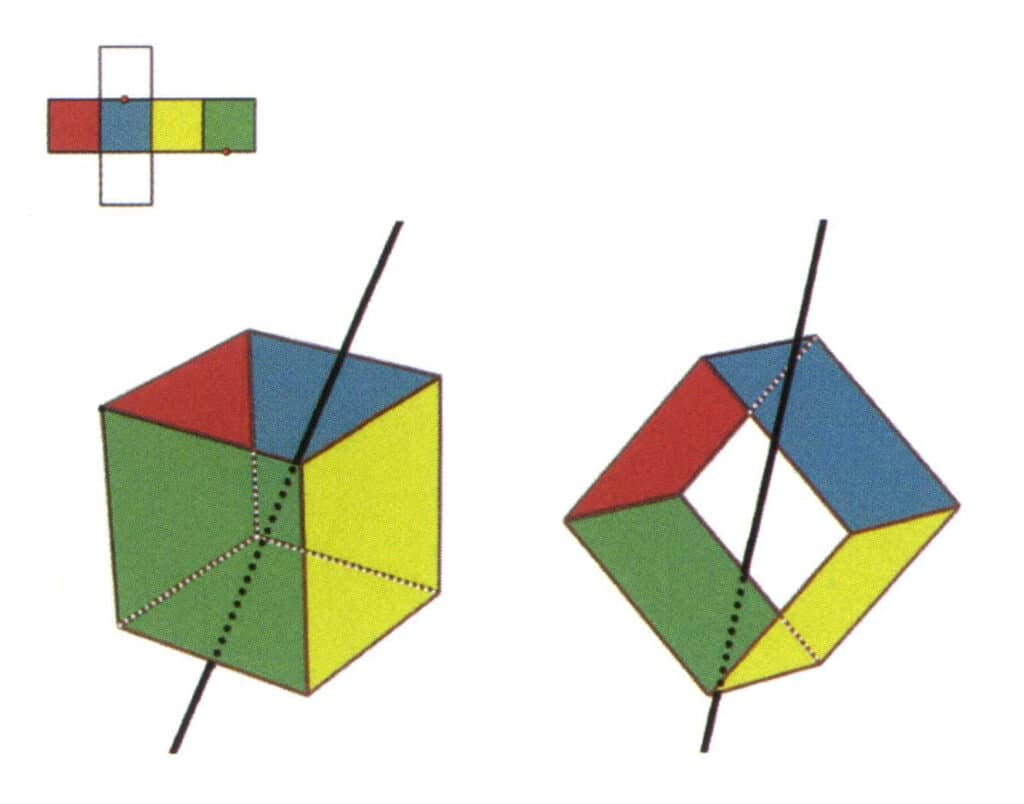
Figura 2-2-9 Il sesto asse secondario del cubo
Selezionare il punto medio delle linee parallele, come mostrato in figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base, di colore diverso ma di forma identica, si ripeteranno due volte nella stessa posizione (facce verdi e incolori, rosse e gialle, incolori e blu, tre serie di facce ripetute). Questa linea immaginaria viene registrata come sesto asse secondario.
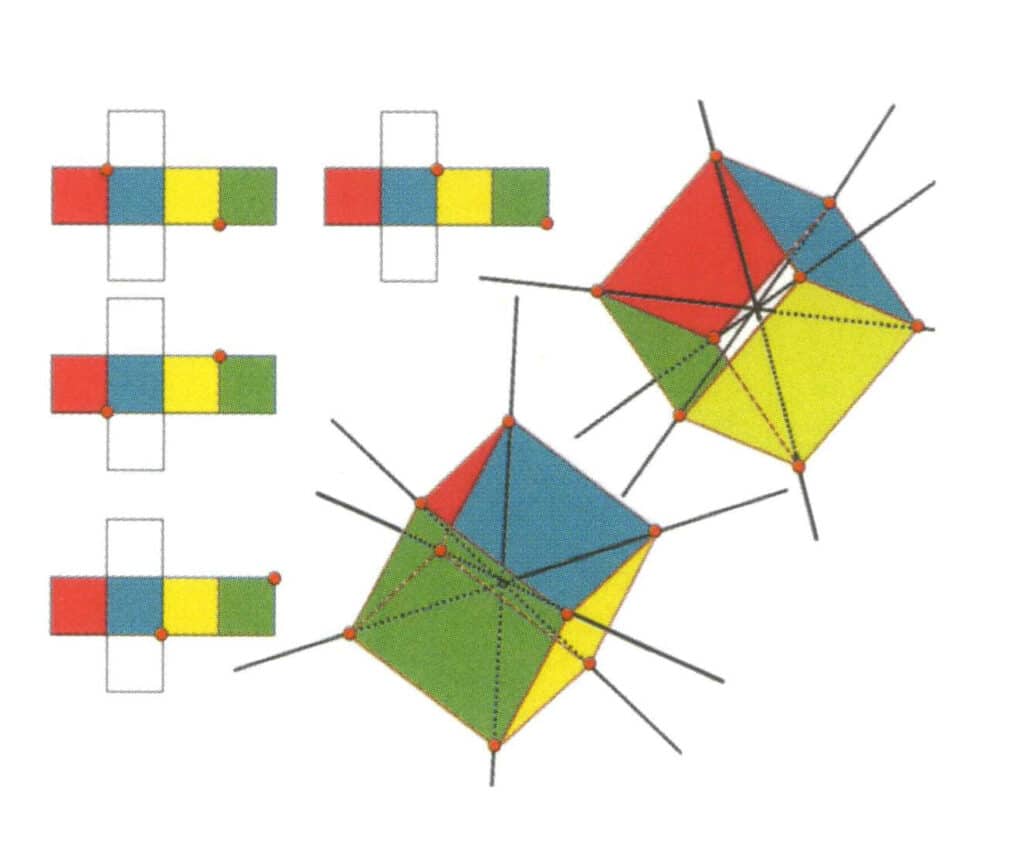
Figura 2-2-10 L'asse terziario del cubo
Il lato sinistro della figura mostra la vista dispiegata del cubo, con il punto rosso che indica il punto di intersezione tra la retta immaginaria e la linea degli spigoli. Il lato destro della figura mostra il cubo chiuso; i punti rossi indicano l'intersezione tra la retta immaginaria e gli spigoli. L'asse terziario può apparire nel punto medio delle facce di un triangolo equilatero parallelo, all'intersezione di tre o più facce parallele che assomigliano a un triangolo equilatero.
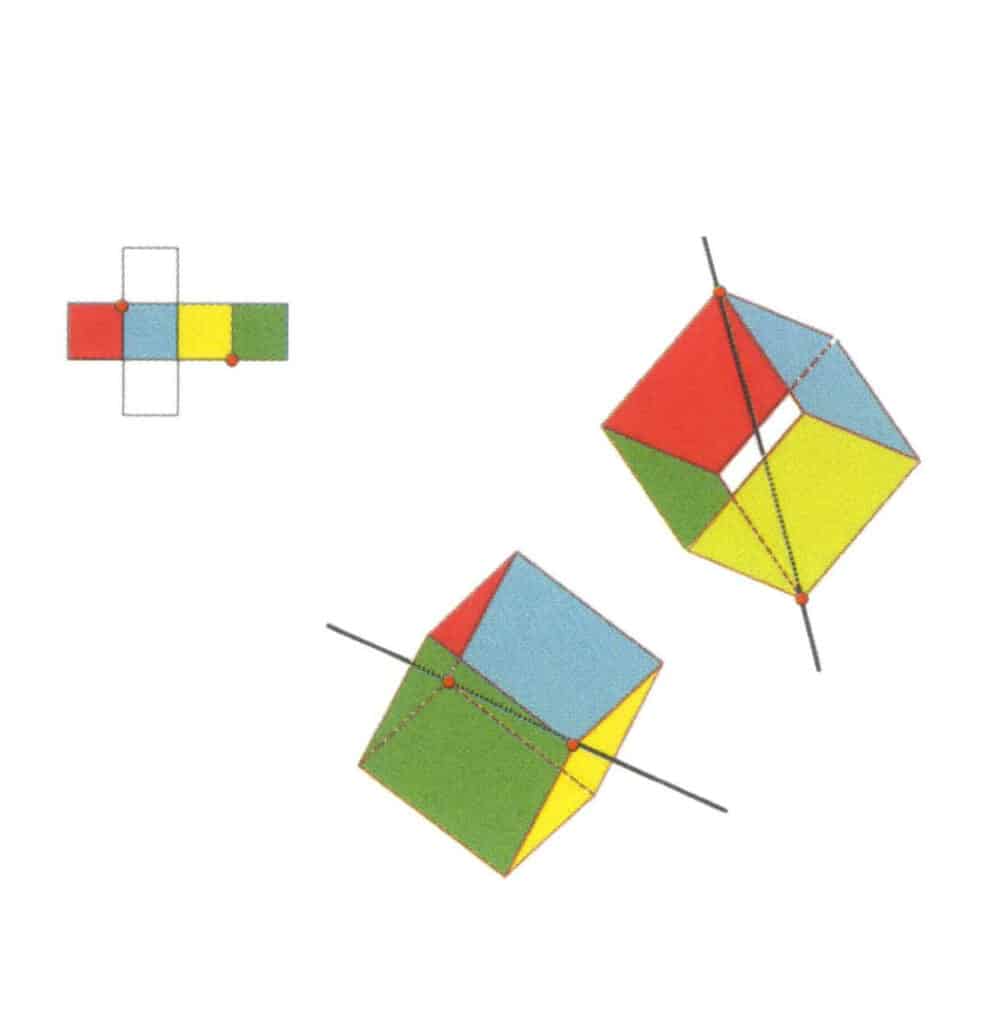
Figura 2-2-11 Il primo asse terziario del cubo.
Selezionare i punti di intersezione delle tre facce come mostrato in figura, immaginare una linea retta che passi per i punti medi di questi due spigoli, ruotare il cubo di 360°, i piani di riferimento di colore diverso ma di forma identica si ripeteranno nella stessa posizione per tre volte (facce rosse, incolori e blu, facce verdi, incolori e gialle, due serie di facce ripetute), questa linea retta immaginata è registrata come primo asse terziario
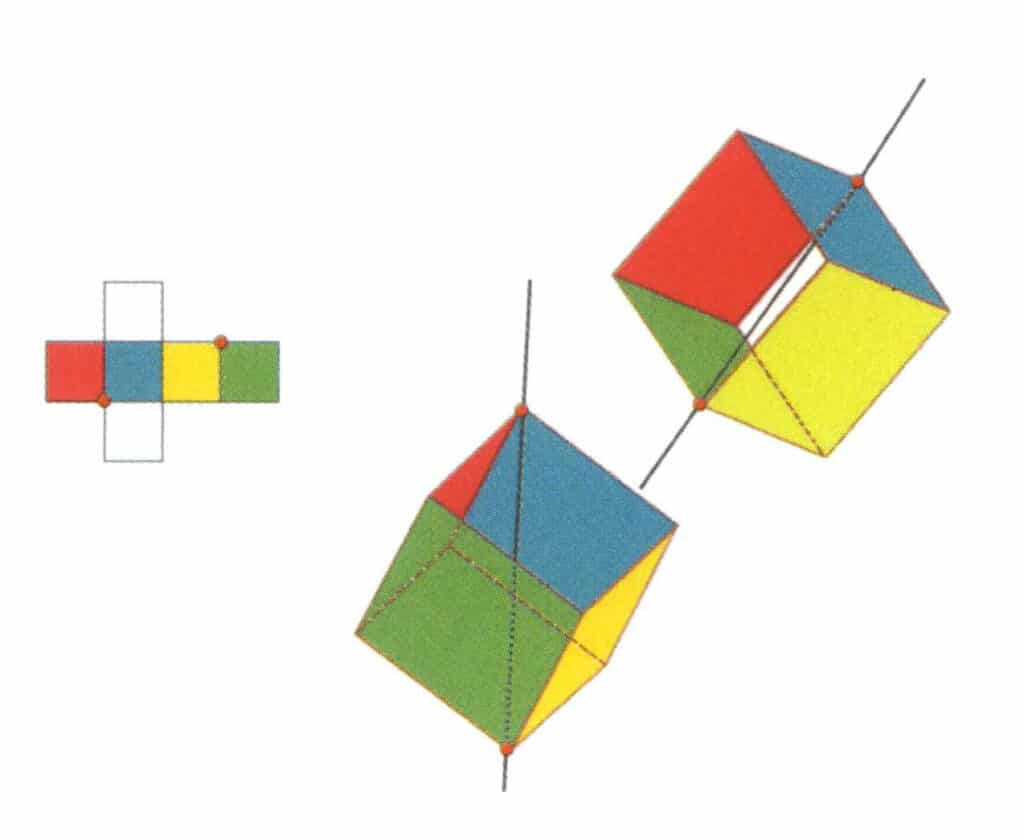
Figura 2-2-12 Il secondo asse terziario del cubo.
Selezionare i punti di intersezione delle tre facce, come mostrato in figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base di colore diverso ma di forma identica si ripeteranno nella stessa posizione per tre volte (facce rosse, incolori e blu; facce verdi, incolori e gialle, due serie di facce ripetute). Questa linea immaginaria viene registrata come secondo asse terziario.
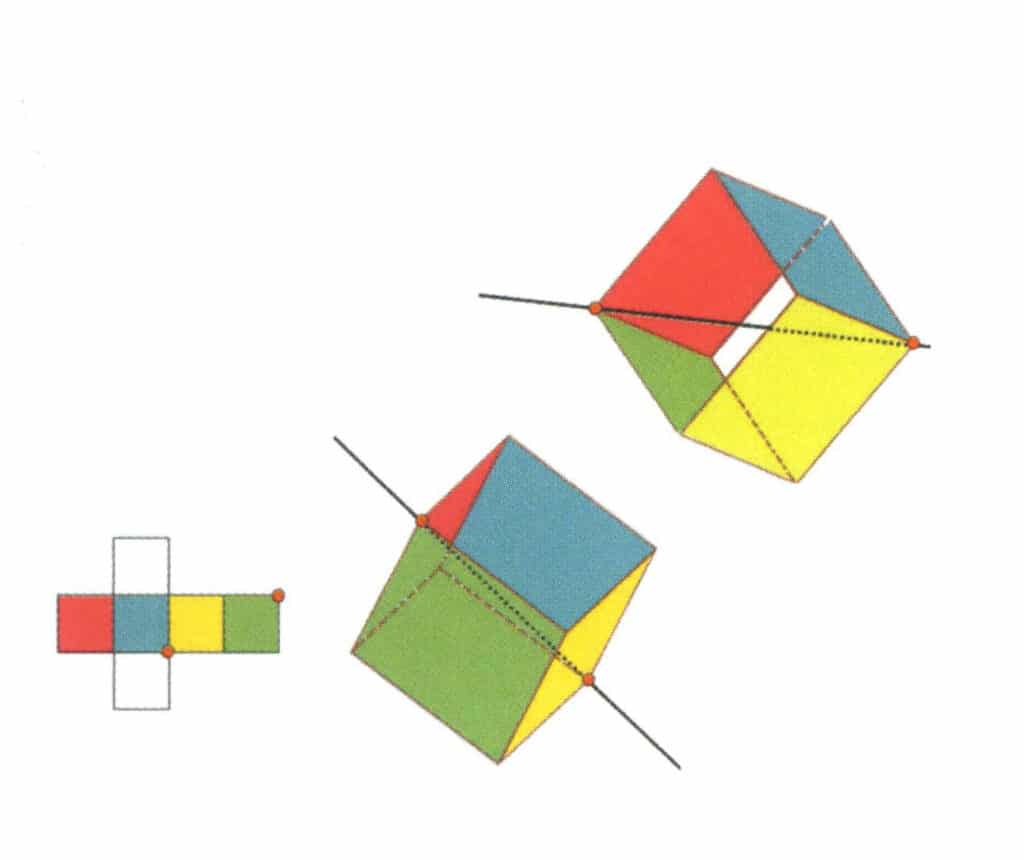
Figura 2-2-13 Il terzo asse terziario del cubo
Selezionare i punti di intersezione delle tre facce, come mostrato in figura. Immaginate una linea retta che passi per i punti medi di questi due spigoli, ruotando il cubo di 360°. I livelli di base di colore diverso ma di forma identica si ripeteranno nella stessa posizione per tre volte (facce rosse, incolori e verdi; facce blu, incolori e gialle, due serie di facce ripetute). Questa linea immaginaria viene registrata come terzo asse terziario.
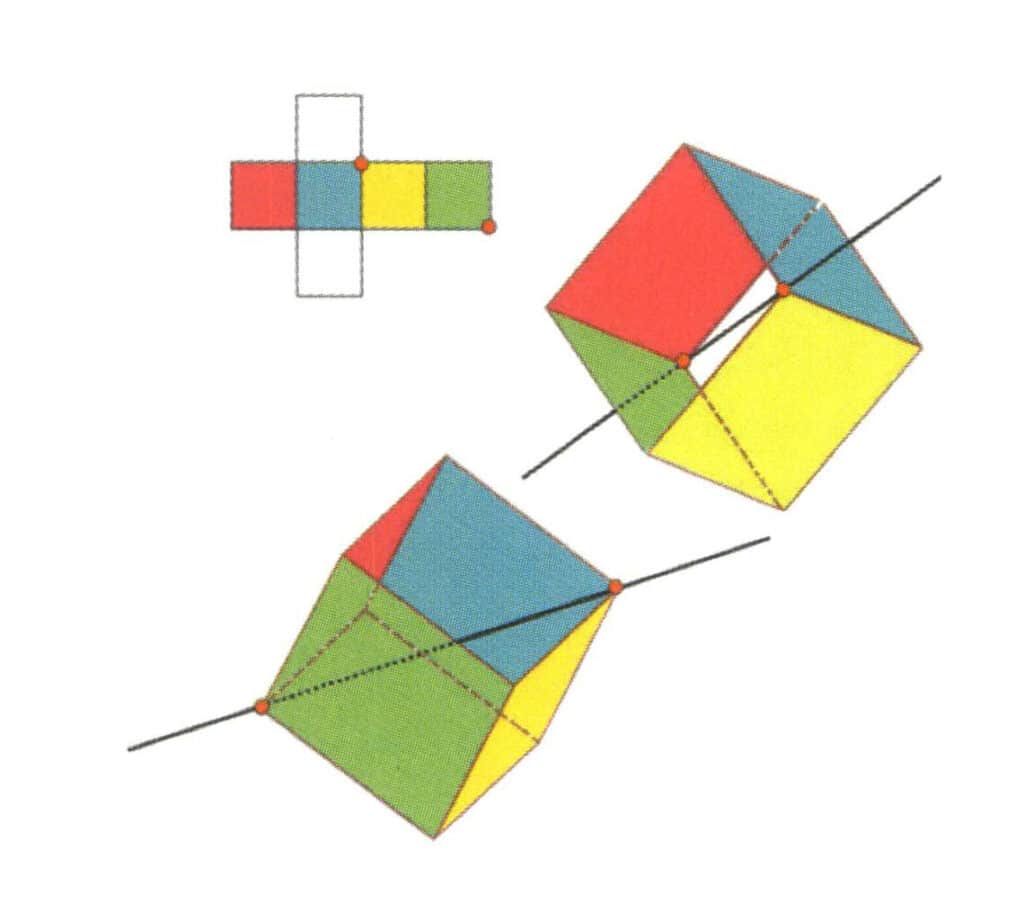
Figura 2-2-14 Quarto asse cubico del cubo.
Selezionare l'intersezione delle tre facce come mostrato in figura, supponendo che ci sia una linea retta attraverso il punto medio dei due spigoli ruota il cubo di 360°, con colori diversi ma con la stessa forma il livello di base sarà lo stesso. Ripetere la posizione tre volte (faccia rossa, incolore, verde, blu, incolore e gialla, due serie di facce ripetute). Questa linea immaginaria viene registrata come quarto asse cubico.
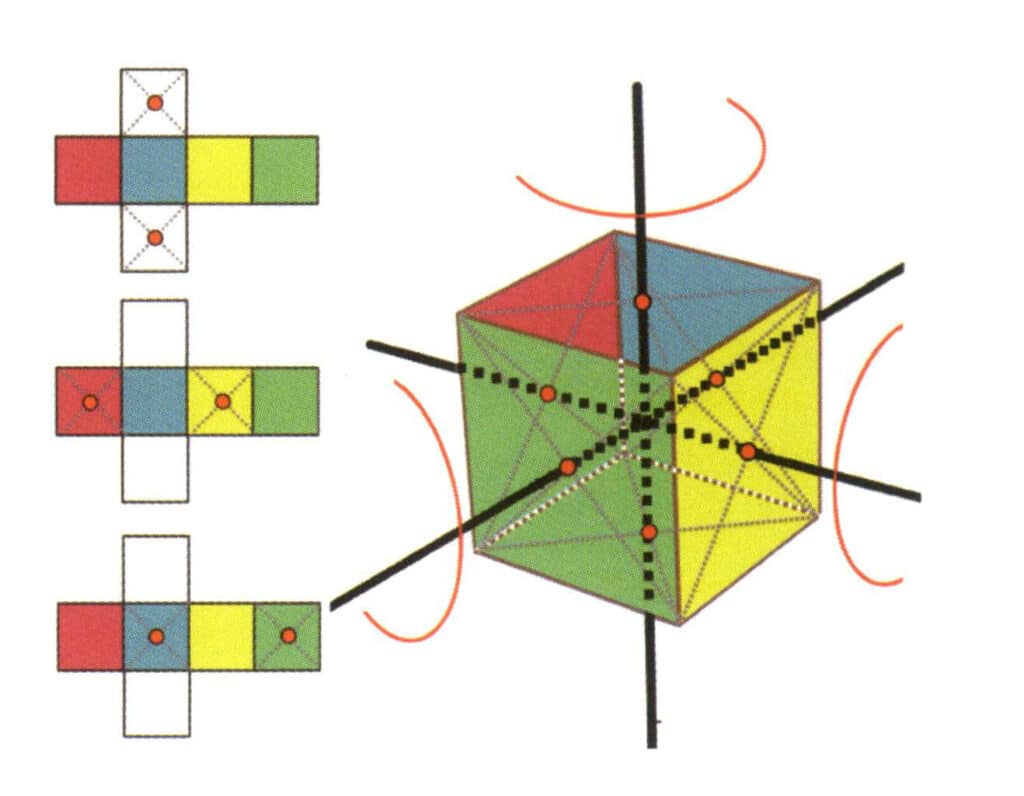
Figura 2-2-15 Quarto asse del cubo
Il lato sinistro della figura mostra la vista aperta del cubo, con i punti rossi che indicano i punti di intersezione della linea immaginaria con gli spigoli. Il lato destro della figura mostra un cubo chiuso, con i punti rossi che indicano i punti di intersezione della linea immaginaria e del piano. Il quarto asse può apparire nel punto medio di facce quadrate parallele, all'intersezione di tre o più facce parallele che assomigliano a un quadrato.
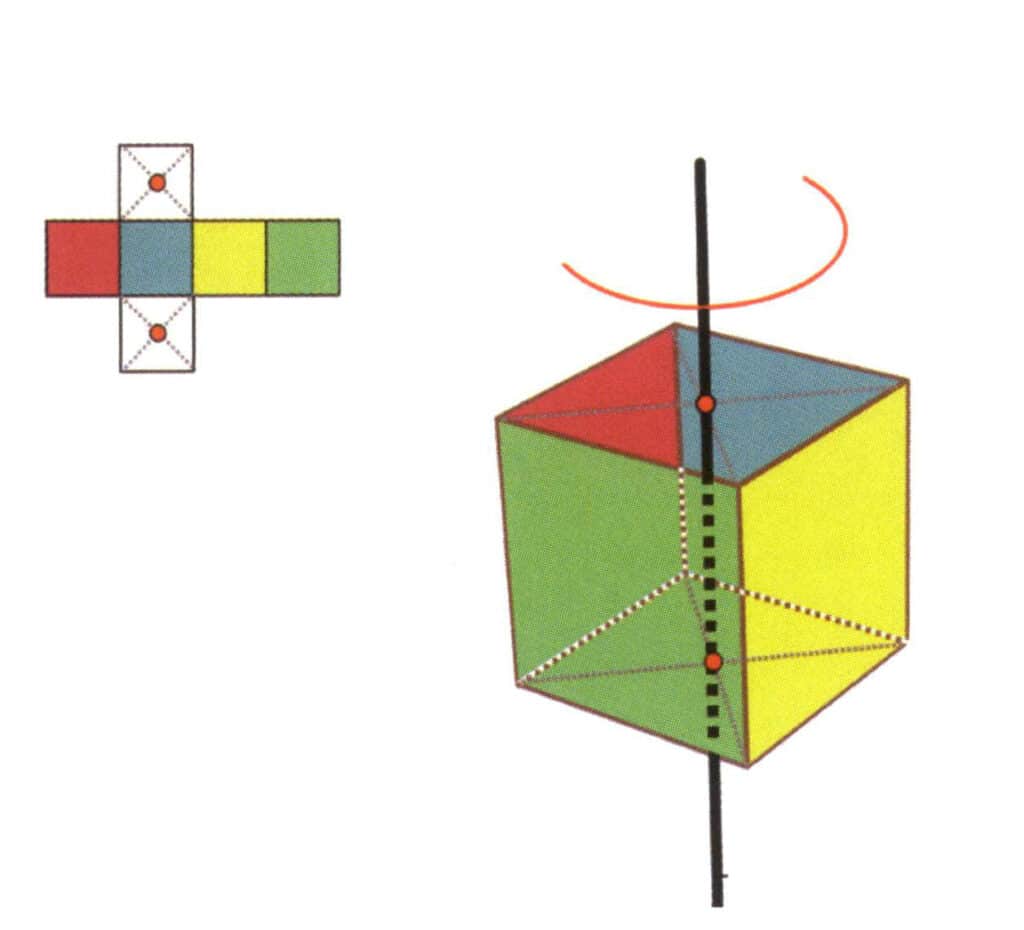
Figura 2-2-16 Il primo asse quartico del cubo
Scegliere i punti medi dei piani mostrati in figura, ipotizzare una linea retta passante per i punti medi dei due piani e ruotare il cubo di 360°. Le facce del piano di base, di colore diverso ma con la stessa forma, si ripeteranno quattro volte nella stessa posizione (facce rosse, blu, verdi e gialle) e questa ipotetica linea retta verrà registrata come una quadrupla assiale.
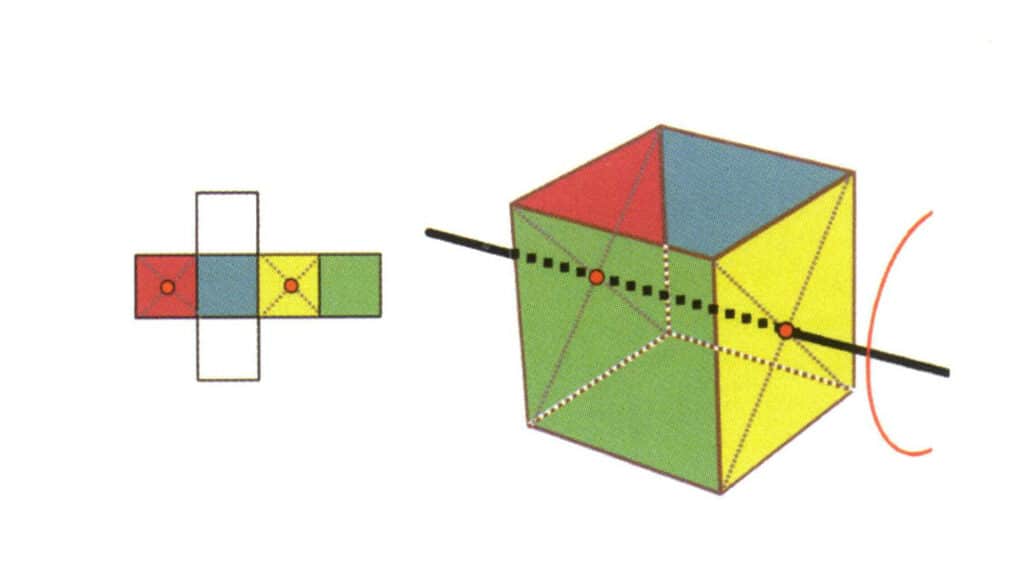
Figura 2-2-17 Il secondo asse quartico del cubo
Selezionare il punto medio del piano come mostrato in figura, immaginare una linea retta che attraversi il cubo e ruotare il cubo di 360°; la superficie del livello di base di colore diverso ma con la stessa forma sarà ripetuta quattro volte nella stessa posizione (incolore, faccia blu in alto, incolore, faccia verde in basso), e questa linea immaginaria sarà registrata come secondo asse quadrico.
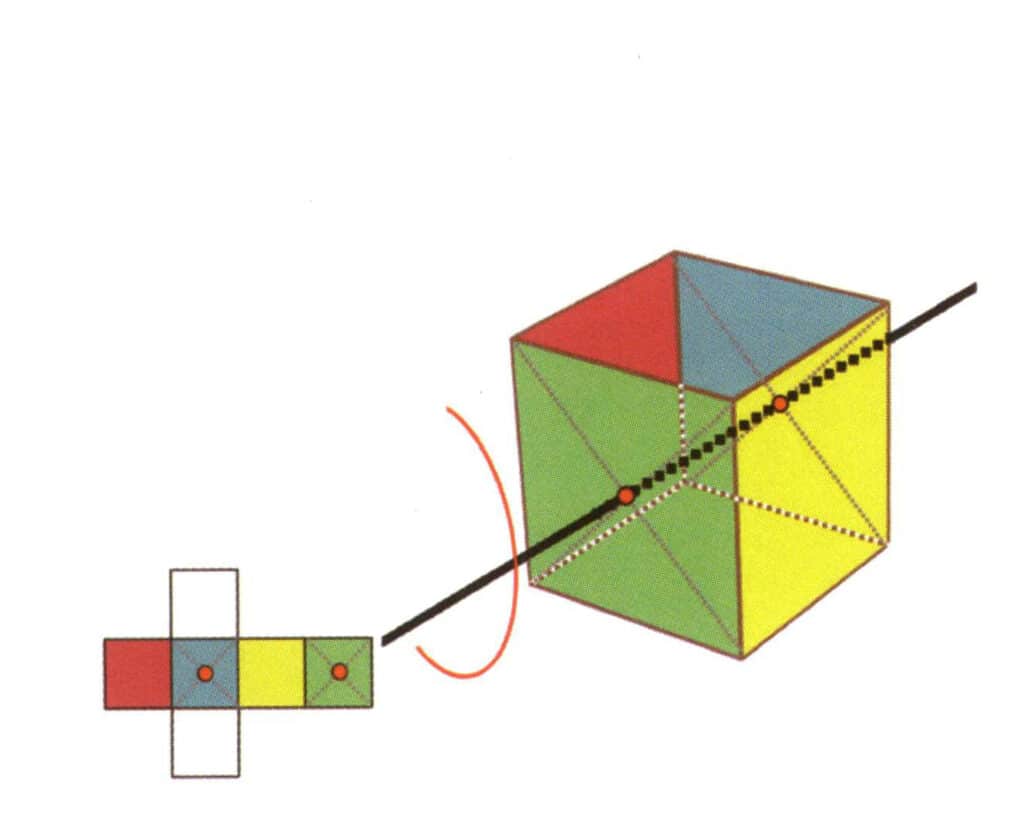
Figura 2-2-18 Terzo asse quartico del cubo
Selezionare il punto centrale del piano come mostrato in figura, immaginare una linea retta attraverso il cubo e ruotare il cubo di 360°. Il livello di base di colore diverso ma con la stessa forma sarà ripetuto quattro volte nella stessa posizione (incolore, faccia rossa in alto, incolore, faccia gialla in basso), e questa linea immaginaria sarà registrata come terzo, quarto asse
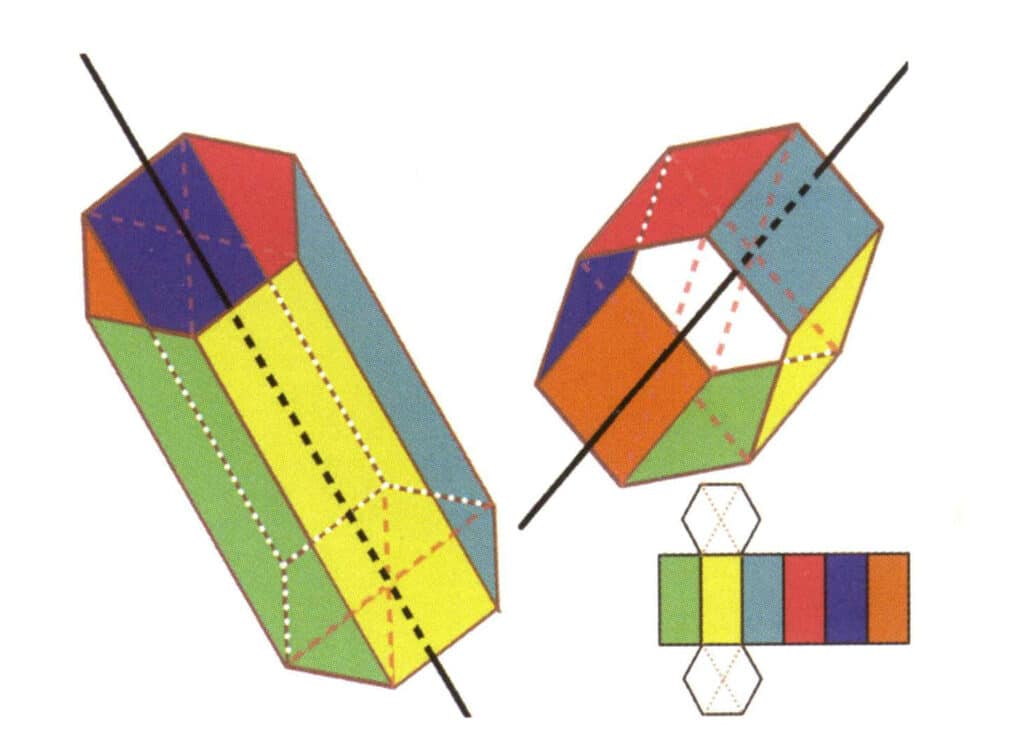
Figura 2-2-19 Sei assi di un prisma esagonale
Le linee nere a sinistra e in alto a destra rappresentano i sei assi del prisma esagonale. In basso a destra un'espansione del prisma esagonale. L'asse sestico può apparire nel punto medio delle facce di un esagono parallelo o nell'intersezione delle sei facce di un esagono.
(2) Considerazioni per trovare l'asse di simmetria.
Esistono cinque tipi di posizioni per l'asse di simmetria.
Il punto medio di due spigoli paralleli, come la posizione dell'asse secondario di un cubo.
Il punto medio di due piani paralleli, come la posizione dell'asse quartico di un cubo.
Tra due vertici (i punti di intersezione di più facce), come la posizione dell'asse terziario di un cubo.
Il punto medio tra un vertice e un piano parallelo, come la posizione dell'asse terziario di un tetraedro.
Il punto medio della linea del bordo e il punto medio del piano parallelo, come la posizione dell'asse secondario di un prisma triangolare.
② La selezione dell'asse di simmetria nella stessa direzione segue il principio del numero più basso. Ad esempio, secondo il principio del numero più basso, se una direzione trova sei assi di simmetria e tre assi di simmetria, alla fine verrà registrata come L³. Gli assi di simmetria nelle diverse direzioni devono essere registrati in base al numero trovato.
Si noti che, ad eccezione dell'asse di simmetria sestuplo e dell'asse di simmetria quadruplice, che non possono comparire contemporaneamente, e che può comparire solo un asse sestuplo, gli altri assi di simmetria possono coesistere in varie forme o istanze multiple.
③ Il livello di base deve essere selezionato come il piano unitario più piccolo; non è possibile selezionare come livello di base due o più piani intersecanti. In caso contrario, la precisione del giudizio sull'asse di simmetria ne risentirà.
Quando si registra il numero di assi di simmetria, è essenziale determinare il numero di volte in cui la stessa forma e dimensione del piano si ripete nella stessa posizione.
⑤ Se esiste un asse secondario di simmetria verticale Lⁿ(n = 3, 4 o 6), devono esistere n assi secondari verticali a Lⁿ.
2.2 Piano di simmetria
(1) Concetto e metodo di registrazione del piano di simmetria
Un piano di simmetria è un piano immaginario che, quando il cristallo viene tagliato lungo questo piano, permette a ciascuna metà del cristallo di essere l'immagine speculare dell'altra metà (Figura 2-2-20). Nella stessa struttura cristallina, tale piano può apparire al massimo 9 volte (Figura 2-2-21), il che significa che può essere tagliato in 9 modi diversi e le due metà possono coincidere completamente. Naturalmente, non tutte le strutture cristalline presentano piani di simmetria.
La lettera maiuscola P rappresenta il piano di simmetria. Alcuni cristalli presentano più piani di simmetria non coincidenti e il numero di questi piani di simmetria viene convenzionalmente scritto a sinistra della lettera P; ad esempio, quattro piani di simmetria sono rappresentati come 4P e un piano di simmetria è rappresentato come P.
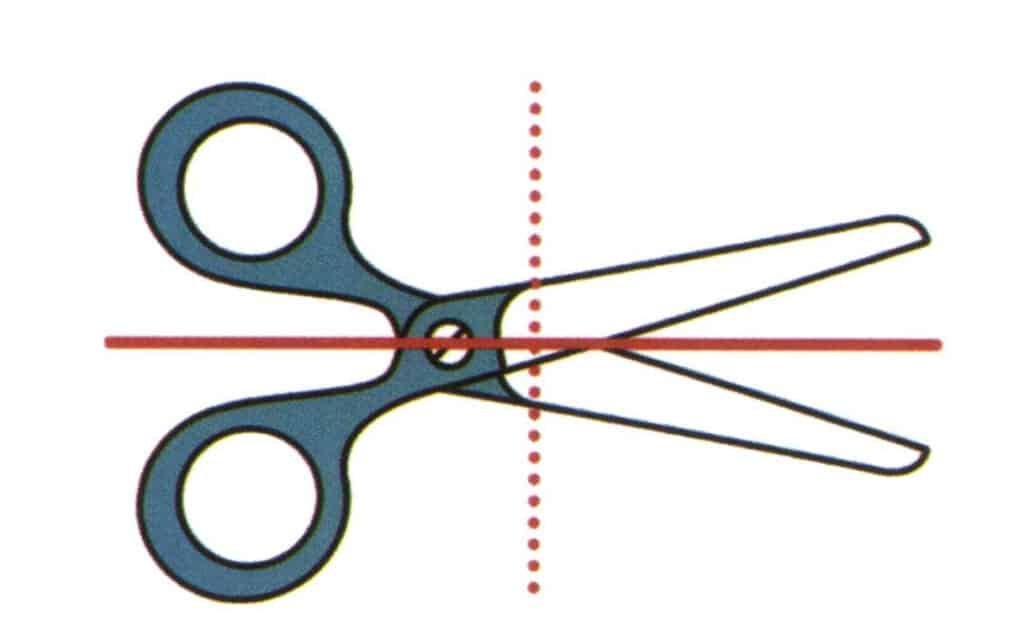
Figura 2-2-20 Immaginate un piano verticale di carta e un piano che si estende lungo la direzione della linea solida rossa, che divide le forbici in parti superiori e inferiori, le quali sono specularmente simmetriche. Questo piano immaginato è chiamato piano di simmetria. Immaginate un altro piano perpendicolare alla superficie della carta e che si estende lungo la direzione della linea rossa tratteggiata, che divide le forbici in due parti, una destra e una sinistra, ma le forme delle forbici sui lati sinistro e destro non sono simmetriche.
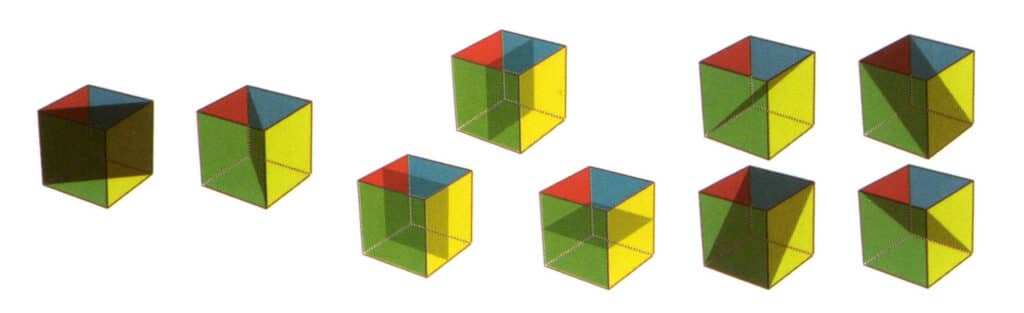
Figura 2-2-21 Nove piani di simmetria di un cubo
(2) Suggerimenti per trovare Piani di simmetria.
Il piano di simmetria è spesso parallelo e coincidente con l'asse di simmetria.
Il piano di simmetria è un piano immaginario che divide la geometria cristallina, diverso dal doppio piano parallelo della geometria.
③ Se un piano di simmetria contiene l'asse di simmetria Lⁿ, allora devono esistere n piani di simmetria contenenti Lⁿ.
(3) Punto Gruppo.
Il gruppo di punti è la somma di tutti gli elementi di simmetria di un cristallo. L'ordine di scrittura del gruppo di punti è asse di simmetria + piano di simmetria, ad esempio 3L²3P (Figura 2-2-22). Se un cristallo ha più assi di simmetria, è consuetudine registrarli da sinistra a destra, dall'asse di ordine superiore all'asse di ordine inferiore, e l'ordine dei piani di simmetria, ad esempio, L⁴4L²5P (Figura 2-2-23). Nei cristalli esistono 32 tipi di simmetria.
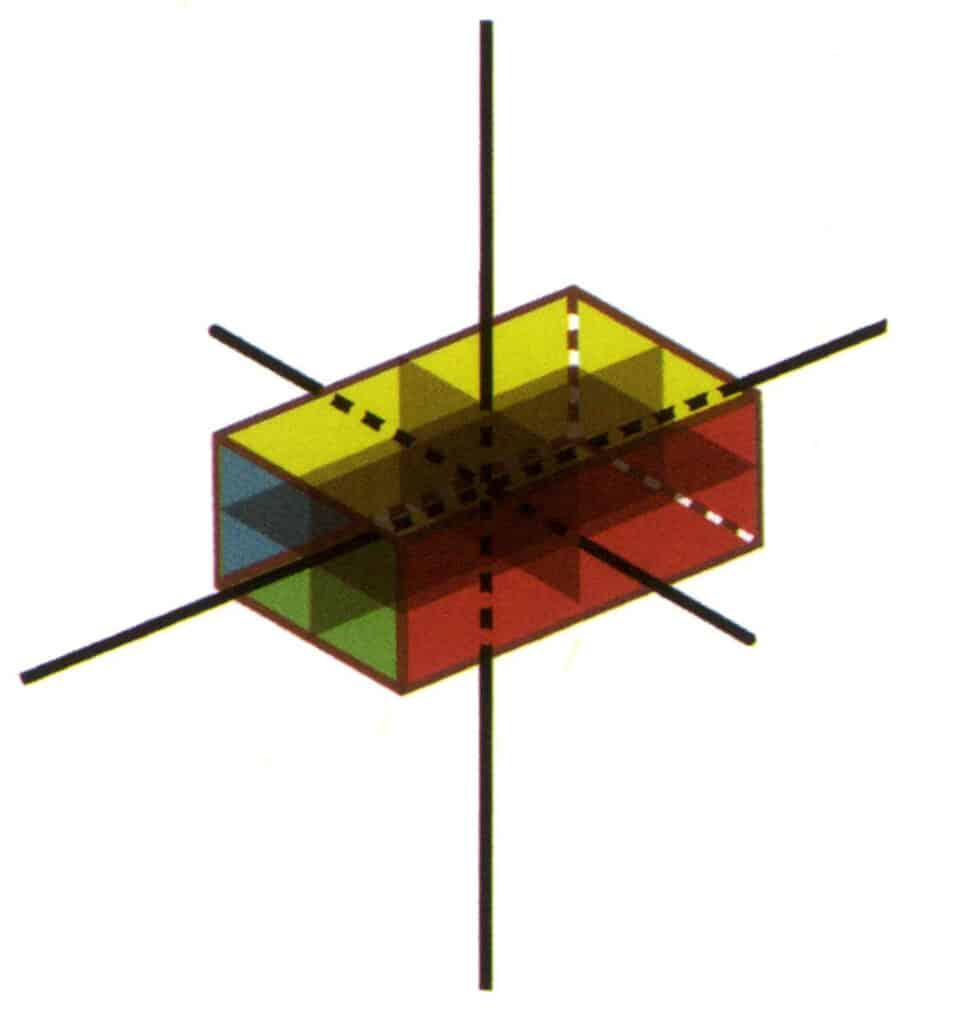
Figura 2-2-22 Gruppo di punti 3L²3P (cuboide rettangolare a sezione rettangolare)
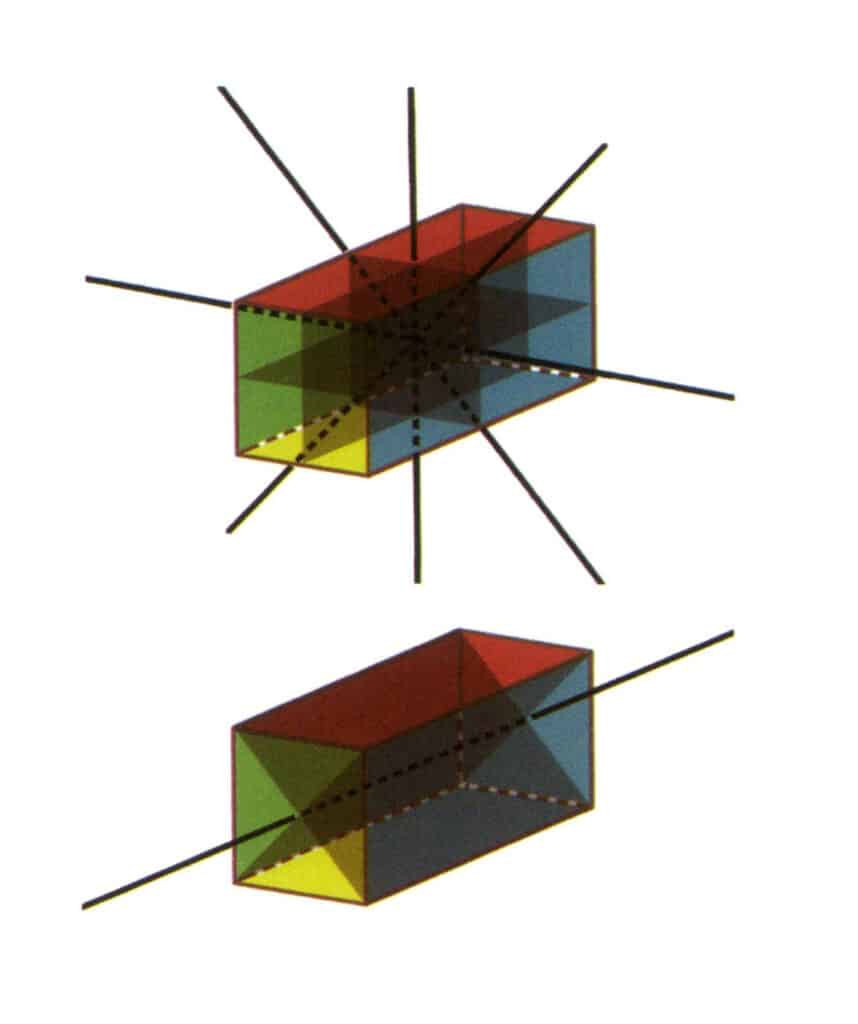
Figura 2-2-23 Gruppo di punti L⁴4L²5P (un prisma rettangolare a sezione quadrata), con quattro assi secondari e tre facce simmetriche in alto, e un quarto asse e due facce simmetriche in basso.
3. Classificazione dei cristalli
La simmetria fa parte della classificazione dei cristalli. Per descrivere la struttura cristallina delle gemme di cristallo naturali e artificiali in uno schema di classificazione dei cristalli, è necessario introdurre un altro concetto, quello di asse cristallino. L'asse cristallino è una linea immaginaria che attraversa la struttura cristallina, indicando la direzione in cui si ripetono i nodi del reticolo e la distanza relativa in cui i nodi si ripetono lungo tale direzione. L'asse del cristallo coincide con la normale dell'asse di simmetria o del piano di simmetria. Se non esiste un asse di simmetria o un piano di simmetria, l'asse del cristallo può essere selezionato in parallelo alla direzione del bordo del cristallo.
Sulla base degli elementi di simmetria e degli assi cristallini, il sistema accademico classifica i cristalli in tre famiglie cristalline e sette sistemi cristallini (Tabella 1).
Tabella 1: Punti chiave per la determinazione delle famiglie e dei sistemi di cristallo
| Famiglia di cristallo | Cristallo | Punti chiave per la determinazione | Varietà di gemme comuni |
|---|---|---|---|
| Sistema a cristalli di basso livello | Sistema triclino | Nessun secondo asse o piano di simmetria | Amazzonite, rodonite, turchese |
| Sistema cristallino monoclino | Nessun asse di ordine superiore, non più di un asse secondario e piano di simmetria | Giadeite, diopside, spodumene, epidoto | |
| Sistema cristallino ortorombico | Nessun asse di ordine superiore, più di un asse secondario o piano di simmetria | Olivina, topazio, saualpite (compresa la tanzanite), cordierite, crisoberillo, enstatite | |
| Famiglia di cristalli intermedi | Sistema cristallino tetragonale | 1 asse quadruplo (può essere rappresentato da L4) | Diamante |
| Sistema di cristalli trigonali | 1 assi trigonali (possono essere rappresentati da L3) | Corindone, rubino, zaffiro, tormalina, cristalli della famiglia del quarzo (come il cristallo, l'ametista, il citrino, ecc.), rodocrosite | |
| Sistema cristallino esagonale | 1 asse esagonale (può essere rappresentato da L6) | Acquamarina, smeraldo e altre gemme della famiglia della berillite, apatite | |
| Famiglia di cristalli avanzata | Sistema cristallino isometrico | 4 assi trigonali (possono essere rappresentati da 4L3) | Diamante, granato, spinello, fluorite |
4. Caratteristiche dei cristalli delle gemme comuni
Le gemme più comuni sono il diamante, lo spinello, la fluorite, il granato, la berillite, lo zircone, il corindone, la tormalina, il cristallo, il crisoberillo, il topazio, ecc. Ogni tipo di gemma ha le sue caratteristiche cristalline fisse.
Le gemme della famiglia dei cristalli di alto livello hanno per lo più un aspetto granulare e le varietà più comuni si presentano spesso in forme cristalline fisse (Tabella 2).
L'abito cristallino delle famiglie cristalline intermedie e basse è colonnare (Tabella 3).
Tabella 2: Caratteristiche comuni delle famiglie di cristalli di alto livello
| Nome del tono delle gemme | Classificazione dei cristalli | Caratteristiche importanti del cristallo | |||
|---|---|---|---|---|---|
| Nome del tono delle gemme | Classificazione dei cristalli | Abitudine al cristallo | Forme di cristallo comuni | Forme gemellari comuni | Modelli comuni di facce di cristallo |
| Diamante | Sistema cristallino isometrico | Forma cristallina granulare (Figura 2-2-24), comunemente osservata in granuli ottaedrici. | L'ottaedro è una forma cristallina comune, ma possono comparire anche forme cristalline più complesse, tra cui i dodecaedri rombici, spesso caratterizzati da facce cristalline arrotondate, che possono presentare una triplice simmetria. | Gemello triangolare piatto, a volte senza angoli concavi visibili (Figura 2-2-25) | La superficie mostra fosse di incisione triangolari invertite (Figure 2-2-26, 2-2-27) e altre facce del cristallo (Figure 2-2-28, 2-2-29). |
| Spinello | Abitudine cristallina granulare (Figura 2-2-30), comunemente vista in granuli ottaedrici | Spesso prodotti in forma ottaedrica, le facce dei cristalli possono essere molto piatte e apparire come lucidate (Figura 2-2-31). | I cristalli gemelli sono molto piatti, simili a una forma triangolare con gli angoli tagliati (Figura 2¬2-32). | Fosse di incisione visibili in superficie, alcune delle quali assomigliano a diamanti a forma di triangolo rovesciato (Figura 2-2-33) | |
| Fluorite | Forma cristallina granulare (Figura 2-2-34) | Forme cristalline ottaedriche e cubiche (Figura 2-2-35) | Gemellaggio interpenetrante | Segni di crescita a gradini quadrati, per lo più con lacune di scissione, bande di colore parallele alle direzioni delle sei facce del cubo | |
| Granato | Abitudine cristallina granulare, comunemente vista in grani dodecaedrici rombici (Figura 2-2-36) | Dodecaedro rombico o quadrato-trapezoedro | Raro | Sono visibili bande anulari concentriche con la stessa forma delle facce del cristallo (Figura 2-2-37). | |
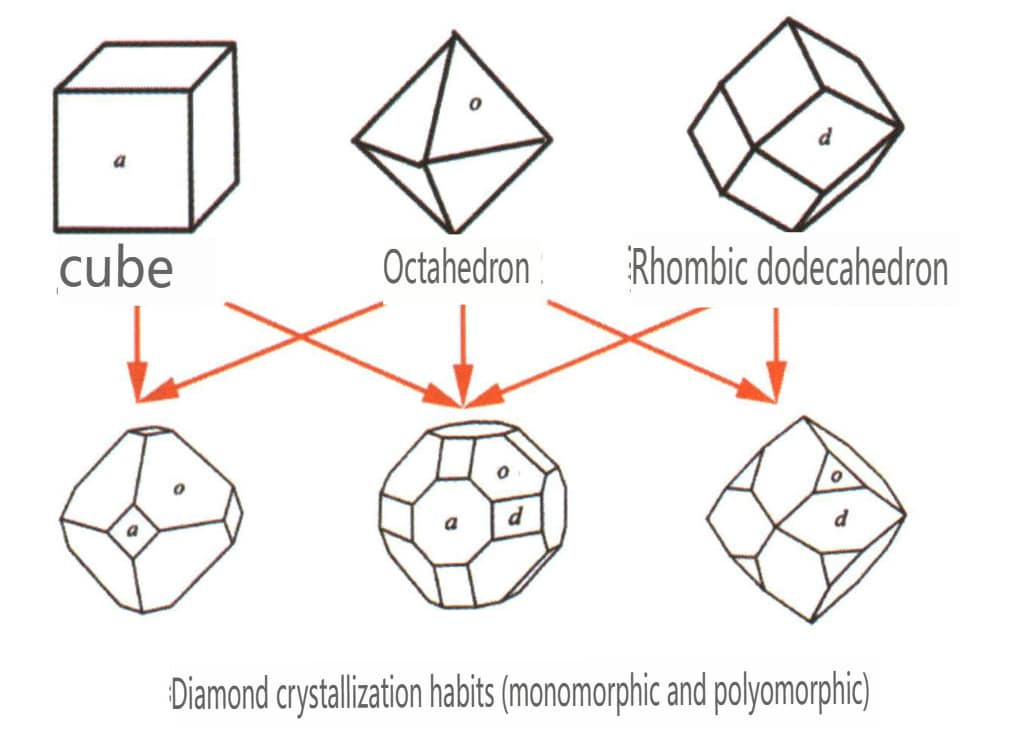
Figura 2-2-24 Abitudini del cristallo di diamante
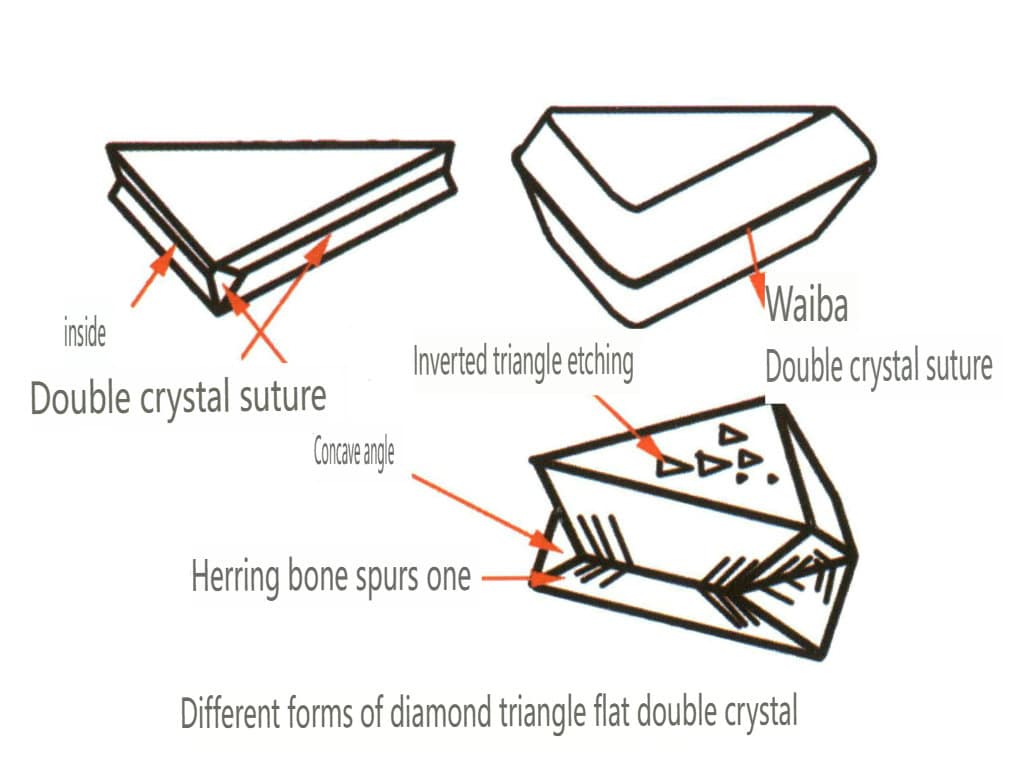
Figura 2-2-25 Abitudine del diamante gemello
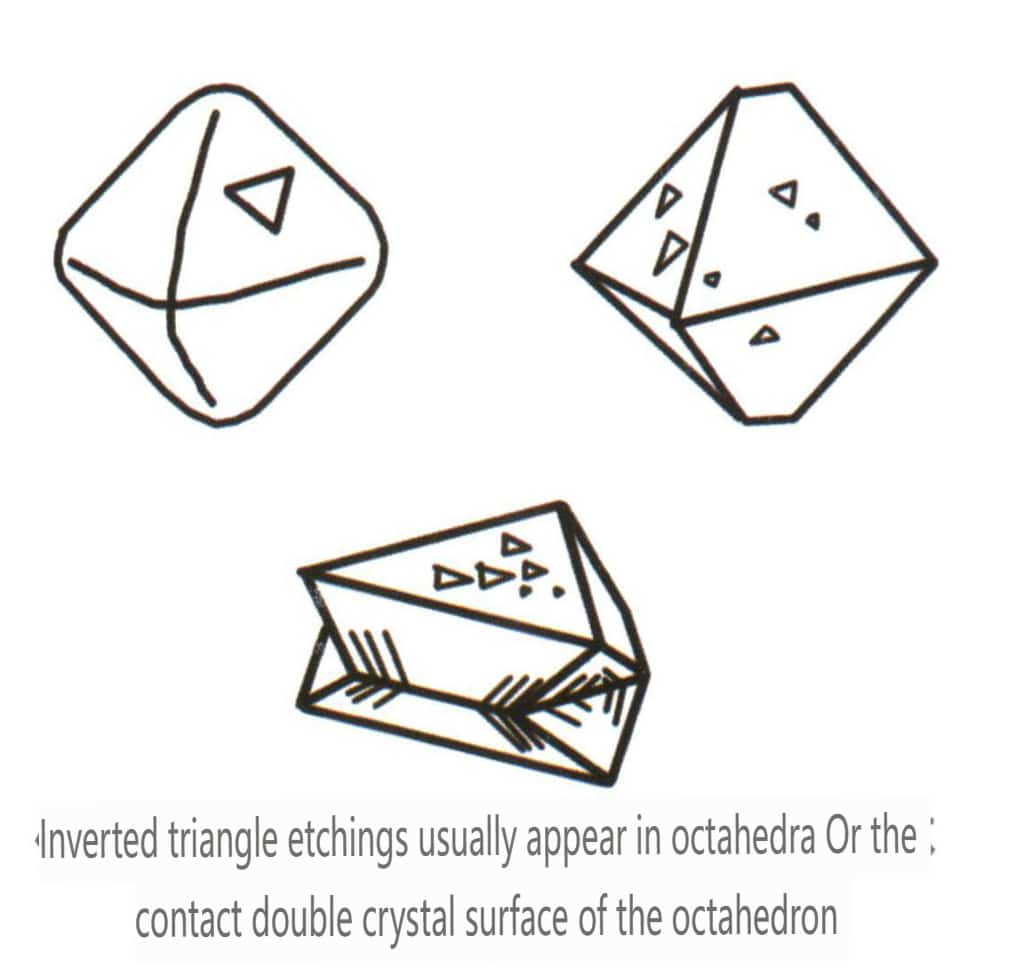
Figura 2-2-26 Figura di incisione a triangolo invertito delle facce del cristallo ottaedrico di diamante

Figura 2-2-27 Figura di incisione triangolare invertita sulla superficie di un cristallo ottaedrico di diamante
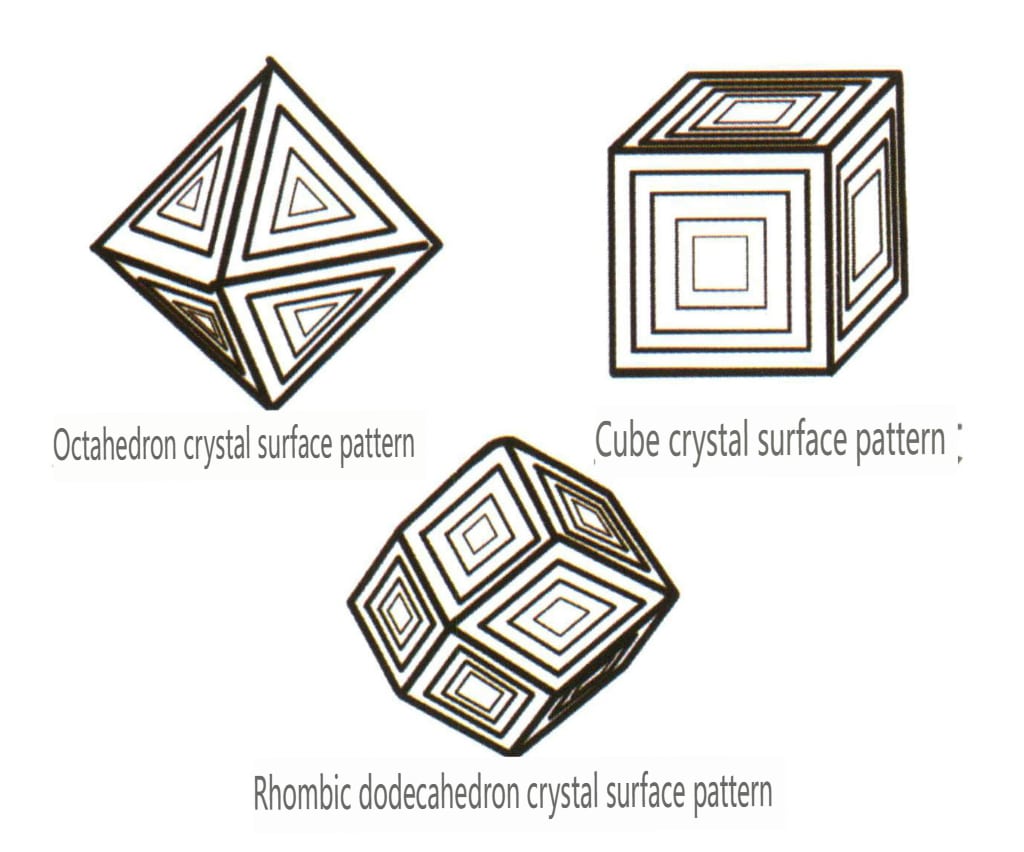
Figura 2-2-28 Figura di incisione a triangolo invertito delle facce del cristallo ottaedrico di diamante

Figura 2-2-29 Figura di incisione triangolare invertita sulla superficie di un cristallo ottaedrico di diamante
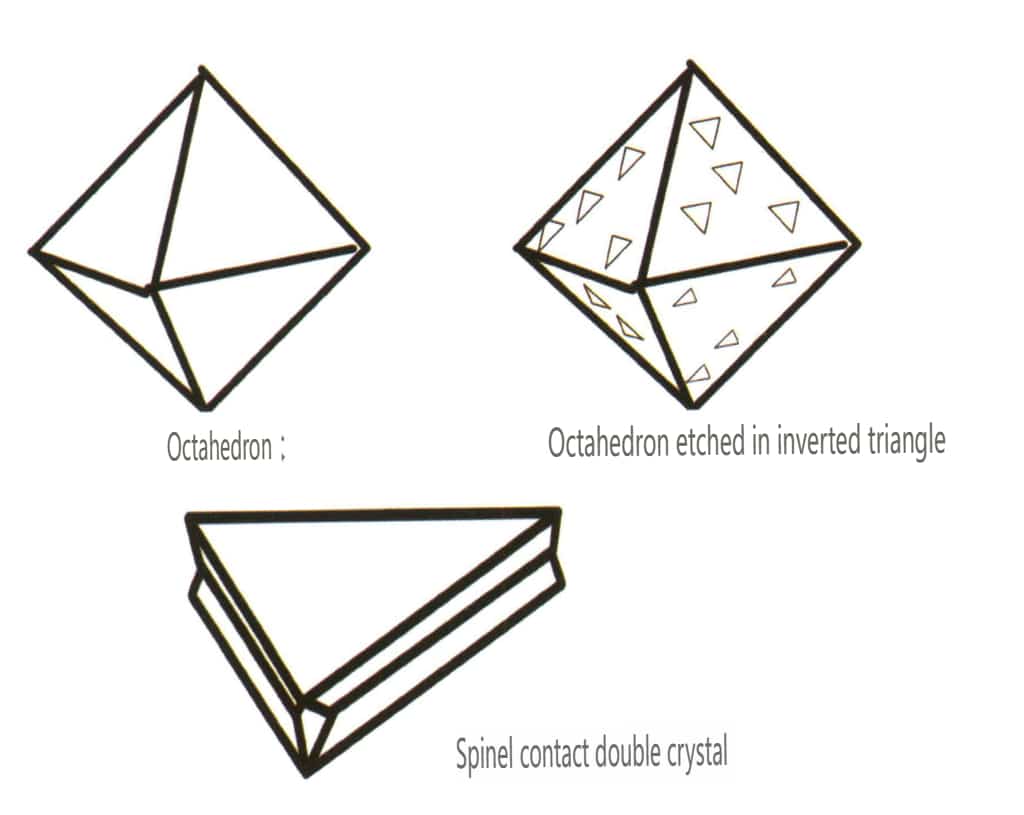
Figura 2-2-30 Abitudine cristallina dello spinello

Figura 2-2-31 Forme comuni di cristalli di spinello

Figura 2-2-32 Gemellaggio a contatto dello spinello
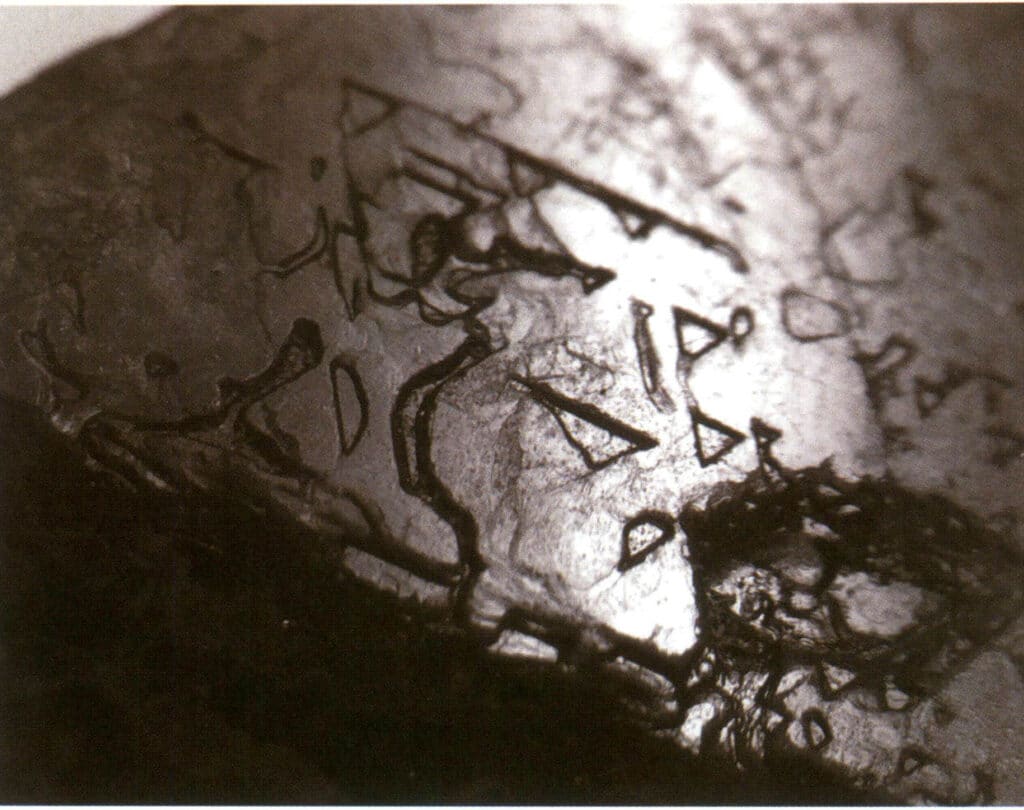
Figura 2-2-33 Schema di incisione triangolare invertita sulla superficie dello spinello
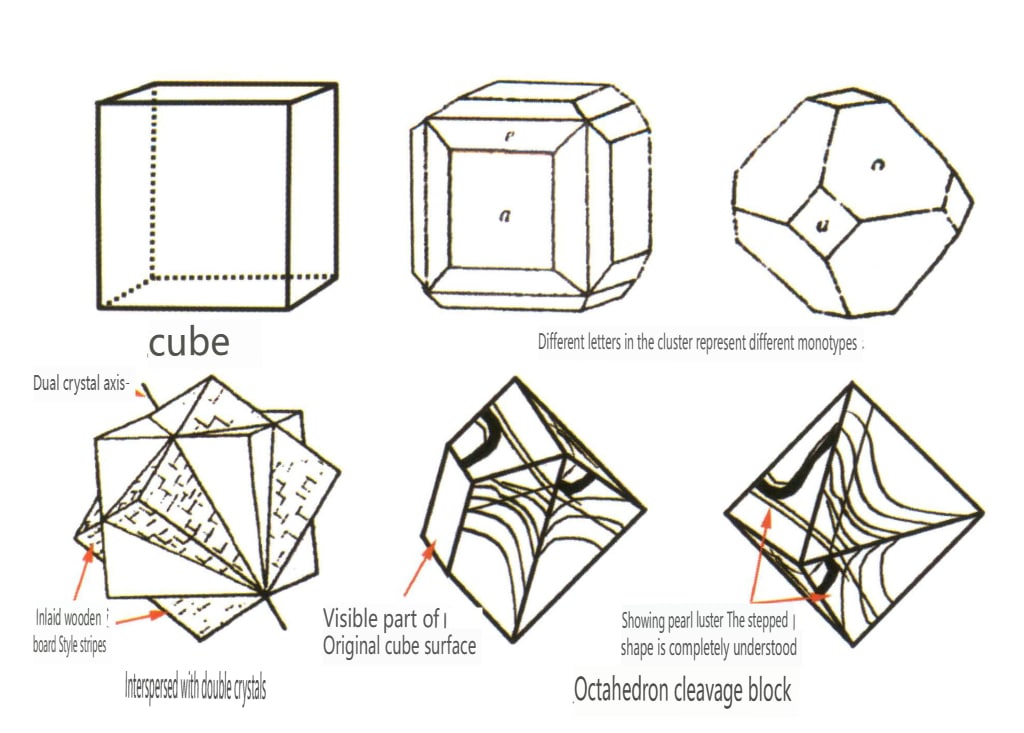
Figura 2-2-34 Abitudini cristalline della fluorite

Figura 2-2-35 Cristallo di fluorite
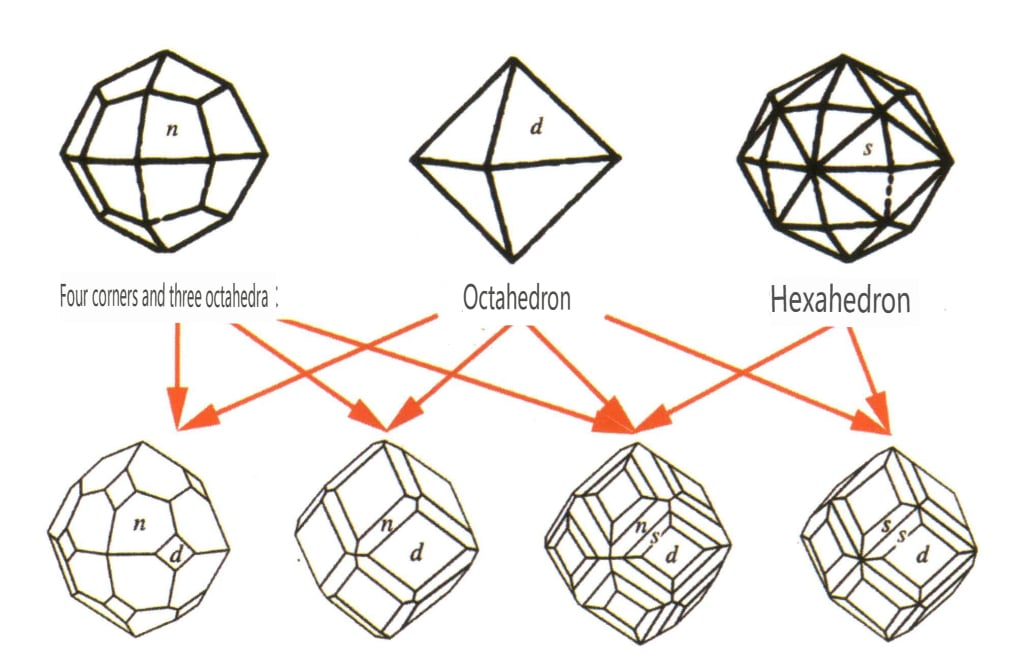
Figura 2-2-36 Abitudine del cristallo di granato

Figura 2-2-37 Bande anulari concentriche sulla superficie dei cristalli di granato che hanno la stessa forma delle facce del cristallo
Tabella 3: Caratteristiche comuni dei cristalli di gemma delle famiglie a cristallo intermedio e basso
| Nome del tono delle gemme | Classificazione dei cristalli | Caratteristiche importanti del cristallo | |||
|---|---|---|---|---|---|
| Nome del tono delle gemme | Classificazione dei cristalli | Abitudine al cristallo | Forme di cristallo comuni | Forme gemellari comuni | Modelli comuni di facce di cristallo |
| Beryl | Sistema cristallino esagonale | Forma cristallina colonnare (Figura 2-2-38) | Forma cristallina esagonale colonnare (Figure 2-2-39, 2-2-40) | Raro | Strisce longitudinali visibili |
| Pietra di piombo | Sistema cristallino tetragonale | Forma cristallina colonnare (Figura 2-2-41) | Una colonna quadrata con sezione trasversale quadrata, che appare insieme a un doppio cono quadrato (Figura 2-2-42) | Cristalli gemelli a forma di ginocchio visibili | Nessun modello speciale |
| Corindone | Sistema cristallino trigonale | Forma cristallina a placca, forma cristallina colonnare (Figura 2-2-43) | I rubini presentano spesso una forma di prisma esagonale (Figura 2-2-44), mentre gli zaffiri hanno spesso una forma di cristallo bipiramidale esagonale a botte (Figura 2-2-45). | I bi-cristalli più comuni. | Striature visibili. |
| Tormalina . | Forma cristallina colonnare (Figura 2-2-46) | Le facce del cristallo alle due estremità sono diverse e la sezione trasversale è un triangolo sferico (Figura 2-2-47). | Raro | Strisce longitudinali visibili (Figura 2-2-48) | |
| Quarzo (quarzo cristallino) | Forma cristallina colonnare (Figura 2-2-49) | La sezione trasversale è esagonale, le bipiramidi esagonali sono rare (Figure 2-2-50, 2-2-51), le monotiramidi esagonali sono comuni. | Contatto comune con i bicristalli (noti anche come bicristalli giapponesi) | Strisce orizzontali comuni sulle superfici dei cristalli | |
| Crisoberillo | Sistema cristallino trigonale | Caratteristiche della cristallizzazione colonnare (Figura 2-¬2-52) | Il monocristallino è raro | Il tri-cristallino è comune (Figura 2-2-53), gli angoli esagonali e concavi possono essere utilizzati come criteri di identificazione. | Le strisce di tri-cristallino possono essere utilizzate come criterio di identificazione. |
| Topazio | Forma cristallina colonnare (Figura 2-2-54) | La sezione trasversale è a forma di diamante e la parte superiore appare spesso come un involucro (Figura 2-2-55). | I bi-cristalli sono rari | Strisce longitudinali visibili | |
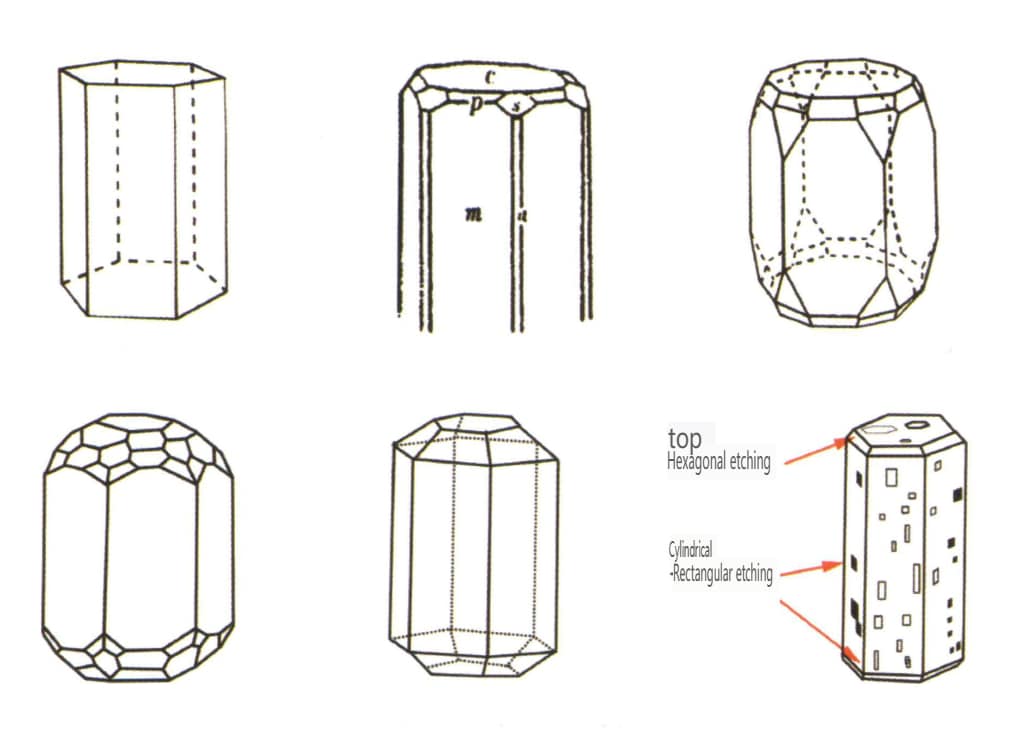
Figura 2-2-38 Abitudini cristalline del berillo

Figura 2-2-39 Forme comuni di cristalli di smeraldo

Figura 2-2-40 Forme comuni di cristalli di acquamarina
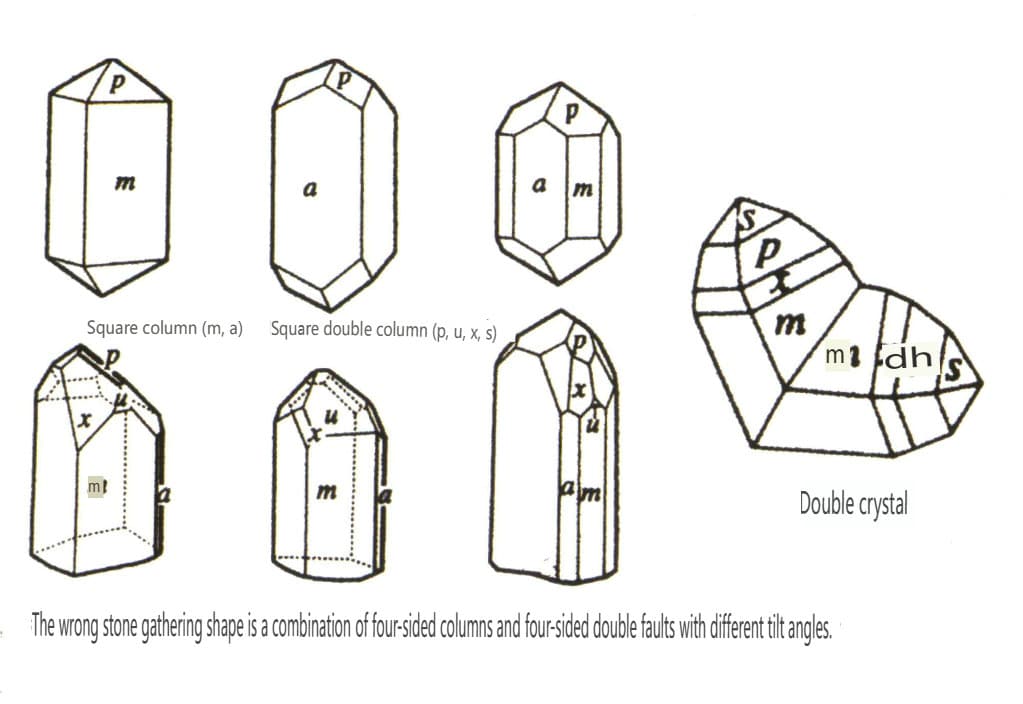
Figura 2-2-41 Abitudini dei cristalli di zircone

Figura 2-2-42 Cristallo di zircone
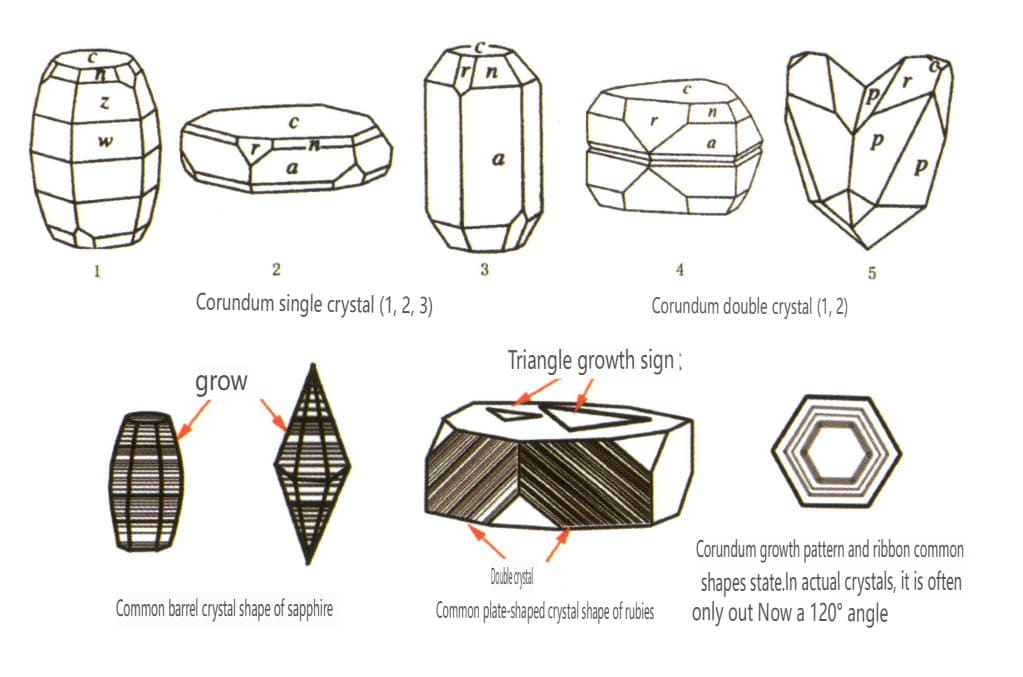
Figura 2-2-43 Abitudine al cristallo di corindone

Figura 2-2-44 Cristallo di rubino

Figura 2-2-45 Gemello meccanico del rubino
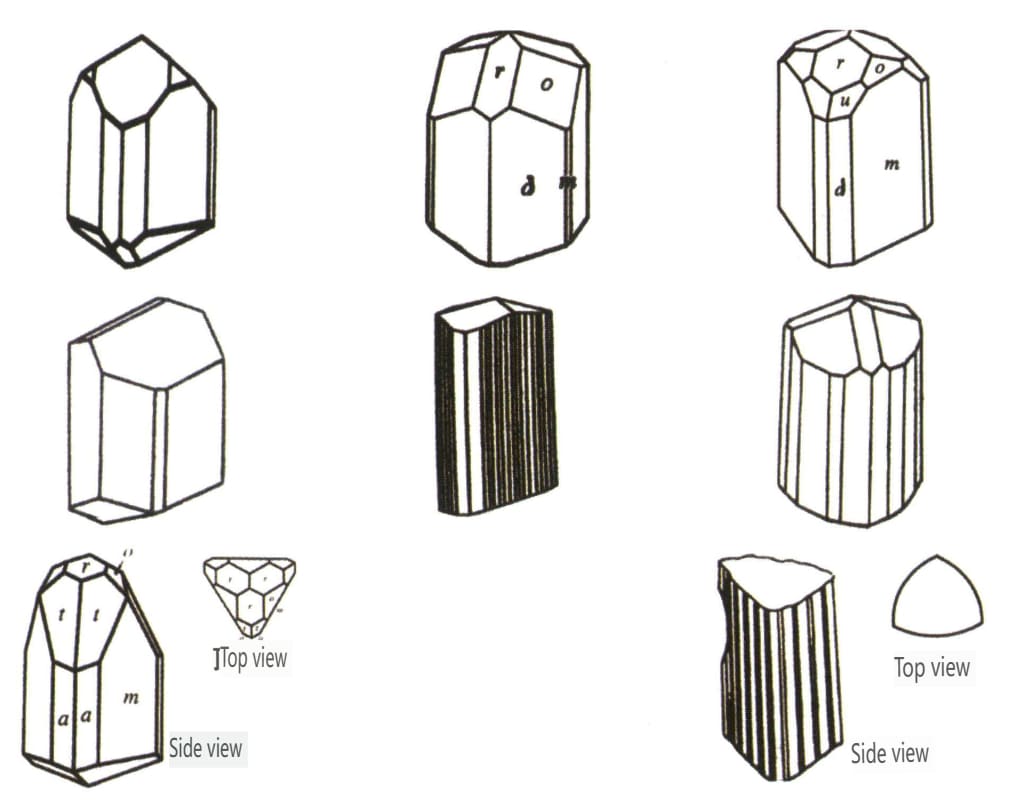
Figura 2-2-46 Abitudini dei cristalli di tormalina

Figura 2-2-47 Cristallo di tormalina

Figura 2-2-48 Strisce longitudinali superficiali del cristallo di tormalina
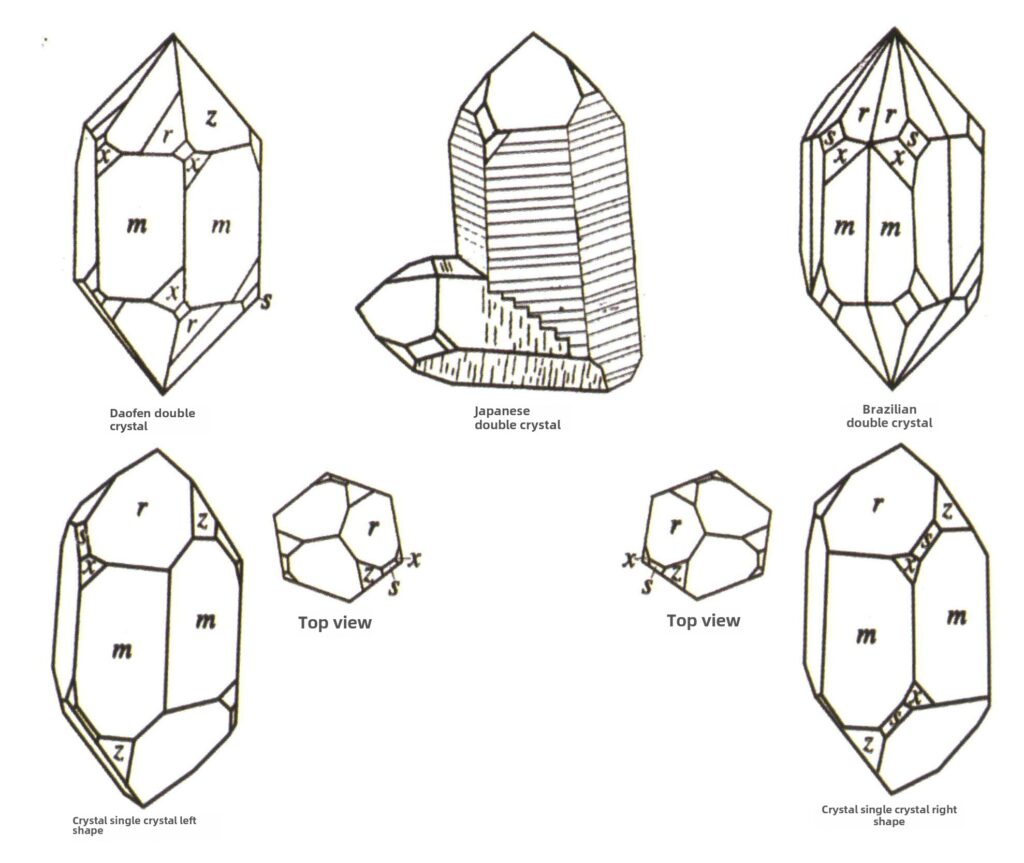
Figura 2-2-49 Abitudini di cristallizzazione del cristallo

Figura 2-2-50 corpo di cristallo

Figura 2-2-51 Corpo del cristallo
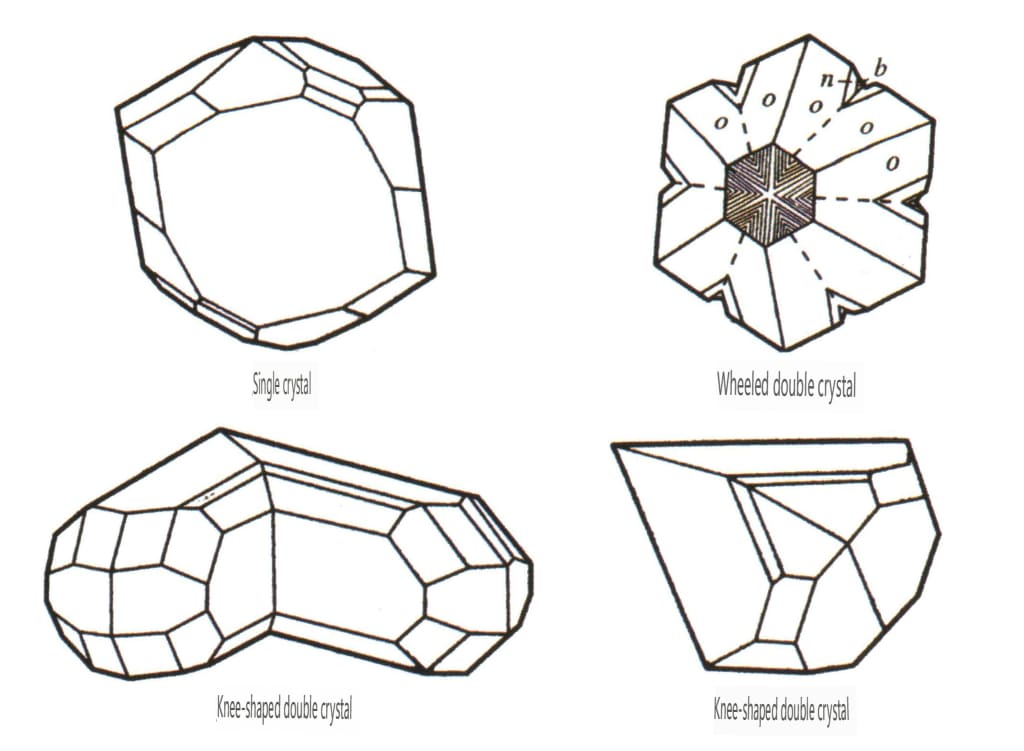
Figura 2-2-52 Abitudine cristallina del crisoberillo

Figura 2-2-53 Cristallo di crisoberillo
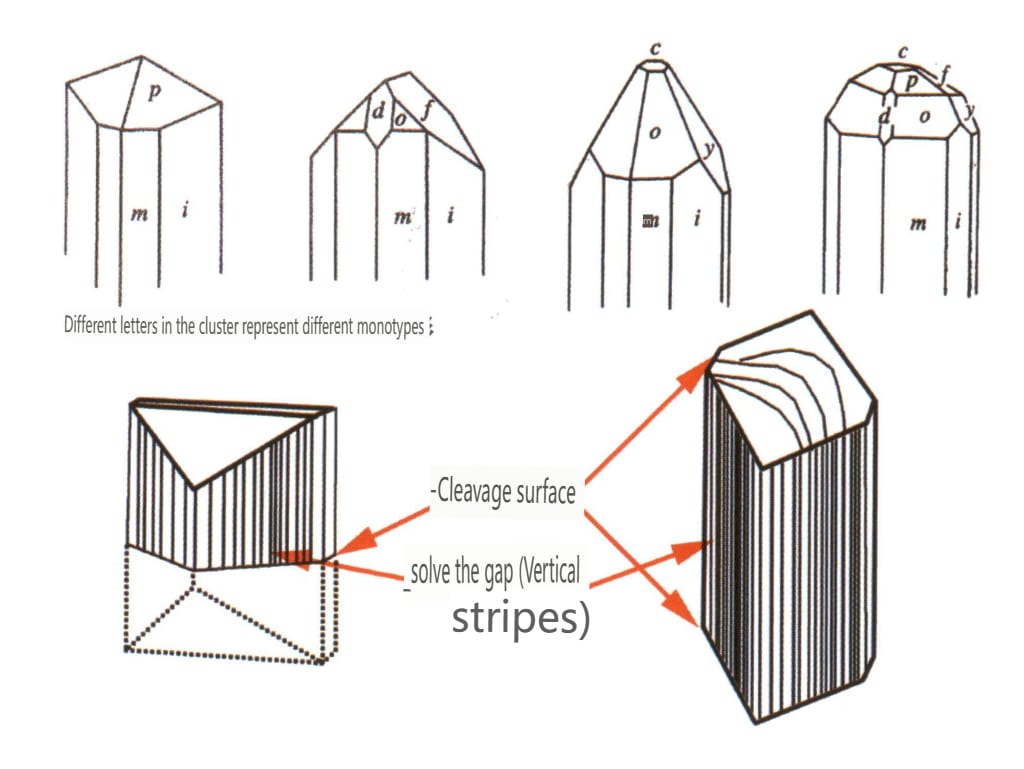
Figura 2-2-54 Abitudini cristalline del topazio

Figura 2-2-55 Cristallo di topazio
Sezione IV Perché i cristalli delle gemme crescono in modo diverso
Da un punto di vista microscopico, il cristallo di gemma è un solido composto da elementi di dimensioni diverse disposti secondo regole diverse. Da un punto di vista macroscopico, molte gemme hanno caratteristiche di forma cristallina a causa delle loro diverse composizioni. Tuttavia, esistono alcuni casi particolari, come l'eteromorfia. Per capire meglio perché i cristalli di gemma hanno un aspetto diverso, presenteremo qui cinque aspetti: eteromorfismo, isomorfismo, mescolanza meccanica molecolare, acqua nei minerali di gemma e composizione chimica delle gemme.
1. Eteromorfo
Sebbene alcuni minerali abbiano la stessa composizione chimica, hanno strutture cristalline (la disposizione degli elementi nello spazio tridimensionale) molto diverse e presentano differenze significative nelle proprietà fisiche e chimiche (Tabella 4). Questo fenomeno viene definito eteromorfismo, ad esempio il diamante e la grafite (Figura 2-2-56).
Il quarzo comune presenta il fenomeno dell'eteromorfismo. Sillimanite, andalusite e cianite sono un gruppo di varianti dell'eteromorfismo.
La trasformazione dell'eteromorfismo avviene in condizioni di stato solido. Durante il processo di trasformazione strutturale, la pressione può svilupparsi all'interno del cristallo, portando spesso alla formazione di gemellaggi all'interno del cristallo.

Tabella 4: Confronto delle proprietà di diamante e grafite
| Minerale | Diamante | Grafite |
|---|---|---|
| Componenti | Carbonio (C) | Carbonio (C) |
| Condizioni di formazione | Alta temperatura e alta pressione | Alta temperatura |
| Sistema cristallino, abitudine | Sistema cristallino isometrico, ottaedro, dodecaedro rombico | Sistema cristallino esagonale, stratificato |
| Colore | Incolore, giallo, blu, rosa, verde, ecc. | Nero |
| Lustro | Lucentezza adamantina | Lucentezza metallica |
| Trasparenza | Da trasparente a opaco | Opaco |
| Indice di rifrazione | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Proprietà meccaniche | Moderato clivaggio ottaedrico, durezza 10, densità 3,52 | Un insieme di scollature perfette, durezza 1, densità 2,10 |
| Altre proprietà | Eccellente conduttività termica; ad eccezione dei diamanti blu naturali che sono semiconduttori, i diamanti di altri colori sono isolanti. | Moderata conducibilità termica, buona conducibilità elettrica |
2. Isomorfismo
L'isomorfismo si riferisce al fenomeno per cui alcune particelle della struttura reticolare vengono sostituite da altre particelle con proprietà simili, con conseguenti lievi cambiamenti nei parametri reticolari e nelle proprietà fisiche e chimiche. Al contrario, la struttura cristallina rimane fondamentalmente invariata. Si può intendere che gli elementi del cristallo gemmato vengano sostituiti da altri elementi. Al contrario, lo schema di ripetizione degli elementi del cristallo di gemma rimane lo stesso, con leggere deviazioni nelle distanze tra gli atomi. Tuttavia, le proprietà fisico-chimiche del cristallo di gemma subiscono lievi cambiamenti (Figure 2-2-57 e 2-2-58).
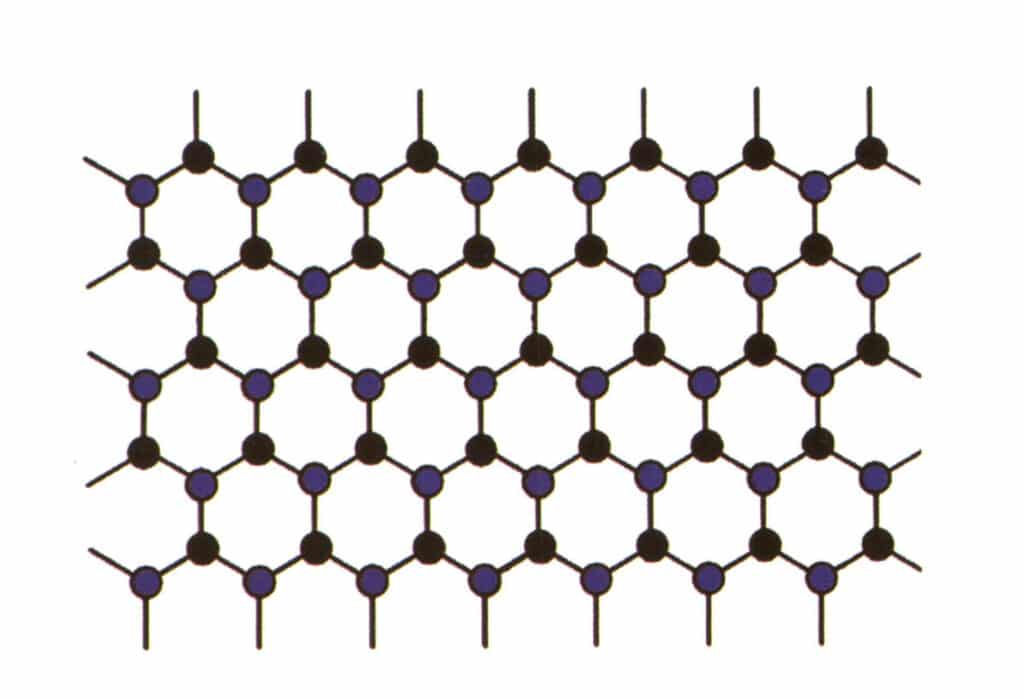
Figura 2-2-57 Diagramma di simulazione della struttura cristallina (il blu e il nero indicano le particelle degli elementi)
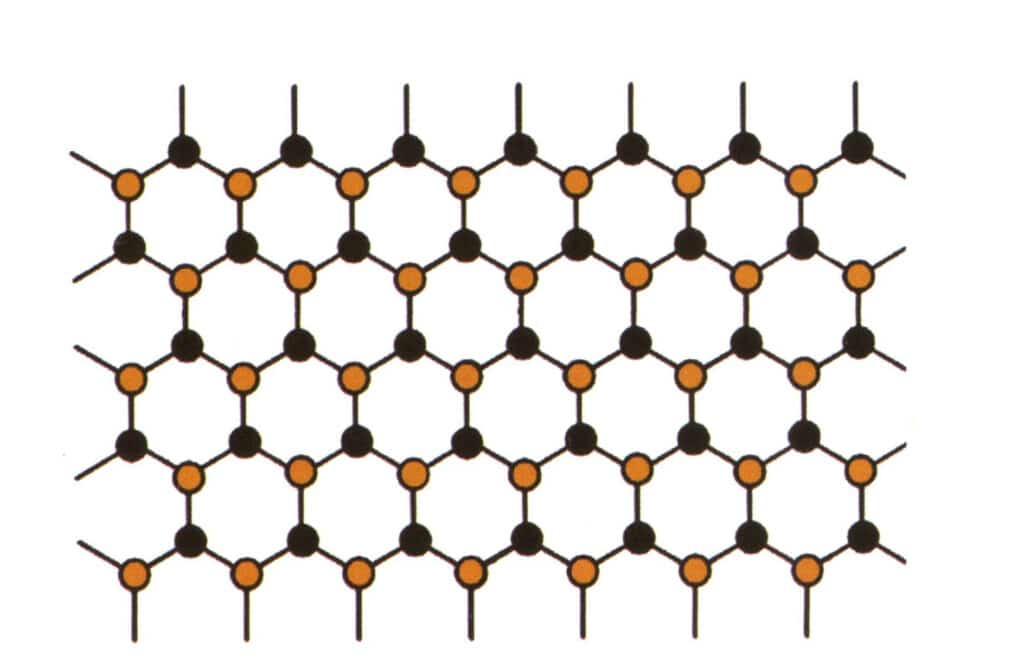
Figura 2-2-58 Diagramma di simulazione della struttura cristallina (il nero rappresenta le particelle elementari, il giallo rappresenta le nuove particelle elementari che sostituiscono parzialmente le particelle elementari blu, il giallo potrebbe non sostituire completamente tutte le particelle blu)
Il concetto di isomorfismo può spiegare perché le gemme della stessa famiglia possono avere così tanti colori e perché ci sono variazioni nell'indice di rifrazione e nella densità tra le gemme della stessa famiglia.
Una famiglia può essere intesa come un tipo di gemma in cui gli schemi di ripetizione degli elementi cristallini sono gli stessi, ma le forme fisiche e chimiche sono leggermente diverse. Ad esempio, la famiglia del corindone comprende due membri, il rubino e lo zaffiro, mentre la famiglia del berillo comprende le varietà smeraldo, acquamarina e morganite.
(1) Olivina
La composizione chimica dell'olivina è (Mg,Fe)₂SiO₄. Nella sua composizione si verifica la completa sostituzione isomorfa degli elementi Fe e Mg. Quando il contenuto di Fe nell'olivina aumenta, il colore dell'olivina diventa più scuro, l'indice di rifrazione aumenta e anche la densità aumenta.
(2) Corindone
Il corindone puro senza impurità (Al₂O₃) è incolore, mentre quando il Cr sostituisce l'Al, la gemma presenta una tonalità da rosa a rossa, nota come rubino. I colori rimanenti sono chiamati zaffiro, come lo zaffiro giallo-arancio o lo zaffiro incolore. Lo zaffiro comunemente chiamato zaffiro è in particolare lo zaffiro blu, dove Fe e Ti sostituiscono l'Al. Più alto è il contenuto di elementi coloranti nella gemma sostitutiva, più profondo è il colore della gemma; viceversa, più basso è il contenuto, più chiaro è il colore.
(3) Tormalina
La tormalina si riferisce allo stesso tipo di gemma della tormalina, dove tormalina è il suo nome mineralogico e tormalina è il suo nome gemmologico. La composizione chimica del berillo è (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), dove R è principalmente Mg , Fe , Cr , Li, Al , Mn, e gli elementi in R possono sostituirsi completamente o parzialmente l'uno all'altro, dando luogo a una varietà estremamente ampia di colori per la tormalina. Per esempio, quando R è principalmente Fe, il berillo presenta un colore blu intenso o addirittura nero; quando R è principalmente Mg, il berillo presenta un colore che va dal giallo al marrone; quando R è principalmente Li o Mn, il berillo presenta un colore rosa o azzurro; quando R è principalmente Cr, la tormalina presenta un verde intenso.
Da quanto detto sopra, si evince che la sostituzione di elementi con proprietà simili porta a colori più belli e brillanti nelle gemme.
3. Intermiscelazione meccanica molecolare
A volte, alcuni elementi entrano forzatamente tra gli elementi principali delle gemme disposte regolarmente. Tuttavia, la bassa percentuale di elementi che entrano non interrompe il modello ripetitivo degli elementi principali della gemma, ma ne provoca solo la deformazione (Figura 2-2-59). Questa situazione viene definita mescolanza meccanica molecolare, come ad esempio la mescolanza meccanica molecolare di azoto e boro nei diamanti, che produce diamanti blu, rosa e gialli, di grande valore.
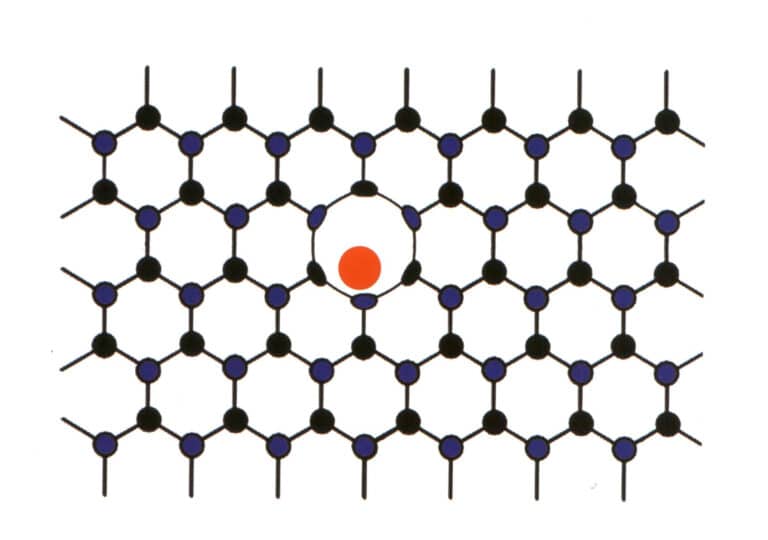
4. L'acqua nei minerali delle gemme
Alcune gemme contengono acqua, che è un componente importante dei minerali gemmari ed è strettamente correlata alle proprietà delle gemme. In base alla forma dell'acqua presente nei minerali gemmari e al suo ruolo nella struttura cristallina, l'acqua presente nelle gemme può essere suddivisa in due categorie: una è l'acqua di assorbimento, che non ha alcuna relazione con la struttura cristallina, e l'altra è l'acqua che partecipa alla struttura cristallina del minerale, tra cui l'acqua di cristallizzazione, l'acqua zeolitica, l'acqua interstrato e l'acqua di costituzione. L'acqua strettamente legata alle gemme comprende l'acqua di assorbimento, l'acqua di cristallizzazione e l'acqua di costituzione.
Uno è quello di assorbire l'acqua, come l'Opale (la composizione chimica è SiO₂ - nH₂O, n rappresenta il numero di H₂O, il contenuto è variabile) nella molecola d'acqua, che è una molecola d'acqua neutra meccanicamente adsorbita per particelle minerali o superfici di frattura. Quando la temperatura raggiunge i 100 ~ 110° gradi in condizioni di pressione normale, le molecole d'acqua possono tutte sfuggire e non danneggiano la struttura del reticolo cristallino, quindi per evitare che l'Opale nel contatore in un lungo periodo di esposizione alla luce forte crepa secca, dovrebbe mettere una tazza d'acqua nel contatore.
La seconda è l'acqua di cristallizzazione, come l'acqua di cristallizzazione del turchese [composizione chimica: CuAl₆(PO₄)₄(OH)₈-4H₂O, dove il contenuto di H₂O può raggiungere 19,47% ]. Questa molecola d'acqua neutra esiste in posizioni fisse all'interno del reticolo e funge da unità strutturale, facendo parte della composizione chimica del minerale. La temperatura alla quale l'acqua di cristallizzazione fuoriesce non supera generalmente i 600℃ e di solito fuoriesce a 100-200℃. Quando una gemma perde l'acqua di cristallizzazione, la sua struttura cristallina viene danneggiata, formando una nuova struttura.
La terza è l'acqua di costituzione, nota anche come acqua combinata, che partecipa al reticolo minerale sotto forma di plasma OH-, H⁺, H₃O⁺, con OH- che è il più comune. L'acqua di costituzione fa parte della composizione chimica del minerale, occupando posizioni fisse nella struttura reticolare con una proporzione definita nella sua composizione. L'acqua di costituzione richiede una temperatura più elevata per fuoriuscire e danneggiare la sua struttura, di solito intorno ai 600-1000℃. Quando una gemma perde l'acqua di costituzione, la sua struttura cristallina viene distrutta. Molte gemme contengono acqua di costituzione, come la tormalina [la composizione chimica è ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), dove R include principalmente Mg , Fe , Cr, Li, Al, Mn, ecc, e gli elementi in R possono sostituirsi completamente o parzialmente l'un l'altro], e il topazio [composizione chimica è Al₂SiO₄( F, OH) ₂ ].
5. La composizione chimica delle gemme
Le gemme, come altre sostanze, sono composte da elementi chimici. Ogni tipo di gemma ha una composizione chimica specifica e un certo intervallo di variazione, che determina le diverse caratteristiche e proprietà della gemma. Le gemme appartengono ai minerali e alle rocce e la classificazione della composizione chimica di una gemma può essere ricondotta alla composizione chimica dei minerali.
Attualmente, i principali metodi di classificazione dei minerali comprendono la classificazione in base alla composizione chimica (sistema Dana), la classificazione geochimica, la classificazione genetica, la classificazione applicativa e la classificazione cristallo-chimica. Il metodo ampiamente adottato è la classificazione chimica basata sulla composizione chimica e sulla struttura cristallina (sistema Hugo Strunz) (Tabella 5).
Tabella 5: Sistema di classificazione chimica dei cristalli minerali
| Sequenza di livelli | Base per la divisione | Esempio |
|---|---|---|
| Categoria principale | Tipo di composto | Sale contenente ossigeno Categoria principale |
| Classe | Tipi di anioni o anioni complessi | Classe dei silicati |
| (Sottocategoria) | Struttura del complesso anionico | Sottoclasse dei silicati quadro |
| Gruppo | Tipi di struttura cristallina e proprietà ioniche | Gruppo del corindone, gruppo del berillo, gruppo del granato |
| (Sottogruppo) | Tipi di cationi | Sottogruppo dei feldspati alcalini |
| Specie | Struttura cristallina e composizione chimica | Ortoclasio KAlSi3O8 |
| (Sottospecie) | Stessa struttura cristallina, diversa composizione o proprietà, morfologia | Adularia KAlSi3O8 |
















