Porque é que as pedras preciosas têm várias cores?
Introdução à teoria do campo cristalino, teoria das orbitais moleculares e teoria das bandas de energia
As cores das pedras preciosas são ricas e variadas, possuindo um encanto único que as pessoas sempre adoraram. A qualidade das pedras preciosas depende em grande parte da sua cor. A cor de uma pedra preciosa é um indicador importante na avaliação da pedra preciosa, e a maioria dos tratamentos de otimização para pedras preciosas envolve a alteração ou melhoria da sua cor. Por isso, compreender as causas da coloração das pedras preciosas é um pré-requisito crucial para o tratamento de otimização das pedras preciosas. Só dominando a forma como as pedras preciosas adquirem a sua cor é que se pode determinar se uma pedra preciosa pode ser optimizada, qual o esquema de otimização a adotar e qual o plano experimental a estabelecer. Existem cinco teorias comuns de coloração de pedras preciosas: teoria da mineralogia clássica, teoria do campo cristalino, teoria do orbital molecular, teoria da banda de energia e efeitos ópticos físicos. Estas teorias constituem as teorias de coloração das pedras preciosas naturais comuns, e o que se segue é uma breve introdução a estas cinco teorias de coloração.
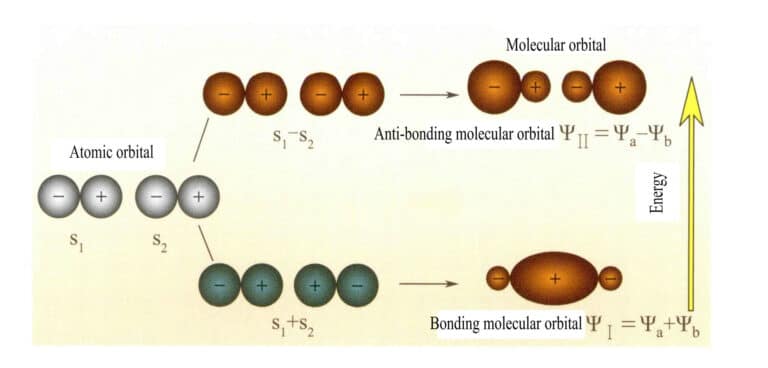
Orbitais moleculares formadas por duas orbitais atómicas s
Índice
Secção I Teoria do campo cristalino
Na década de 1930, os cientistas propuseram a teoria do campo cristalino para explicar as propriedades dos cristais. A teoria do campo cristalino é uma teoria que estuda as ligações químicas dos elementos de transição (complexos). Explica as propriedades físicas e químicas dos elementos de transição e dos elementos lantanídeos através da combinação de alguns pontos de vista da teoria eletrostática, da mecânica quântica e da teoria dos grupos (a teoria que estuda a simetria da matéria), centrando-se na influência dos ligandos nas orbitais d e f dos iões centrais. Na década de 1950, as pessoas aplicaram a teoria do campo cristalino aos complexos e propuseram a teoria do campo ligante. A teoria do campo ligante é um avanço da teoria do campo cristalino; considera tanto a influência do campo elétrico do ligante no ião central como o efeito de enchimento dos electrões do ligante no ião central, tornando-a mais completa do que a teoria do campo cristalino. No entanto, não existe uma diferença essencial entre as duas, e geralmente não são distinguidas no estudo de minerais inorgânicos.
1. Conceitos básicos da teoria dos campos cristalinos
Os iões dos metais de transição encontram-se no campo cristalino de aniões circundantes ou moléculas dipolares. A teoria do campo cristalino é um modelo eletrostático que vê o cristal como uma interação eletrostática entre iões positivos e negativos, em que o catião com carga positiva é designado por ião central e o anião com carga negativa é designado por ligando.
A aplicação da teoria do campo cristalino para explicar a cor dos minerais de pedras preciosas envolve principalmente os electrões d ou a energia do eletrão f dos iões dos elementos de transição. Por exemplo, as orbitais d têm cinco tipos: dxy, dxz, dyz, d , e d . Estas cinco orbitais d têm distribuições espaciais diferentes no estado iónico livre, mas têm a mesma energia. No entanto, sofrem alterações significativas sob a influência do campo do ligante. As cinco orbitais d degeneradas em energia do átomo central dividem-se sob a influência do campo elétrico negativo formado pelos ligandos circundantes. Algumas orbitais d aumentam a energia, enquanto outras diminuem a energia. Devido à divisão dos níveis de energia das orbitais d, os electrões nas orbitais d do átomo central reorganizam-se, ocupando preferencialmente as orbitais de menor energia, reduzindo assim a energia total do sistema e tornando o complexo mais estável.
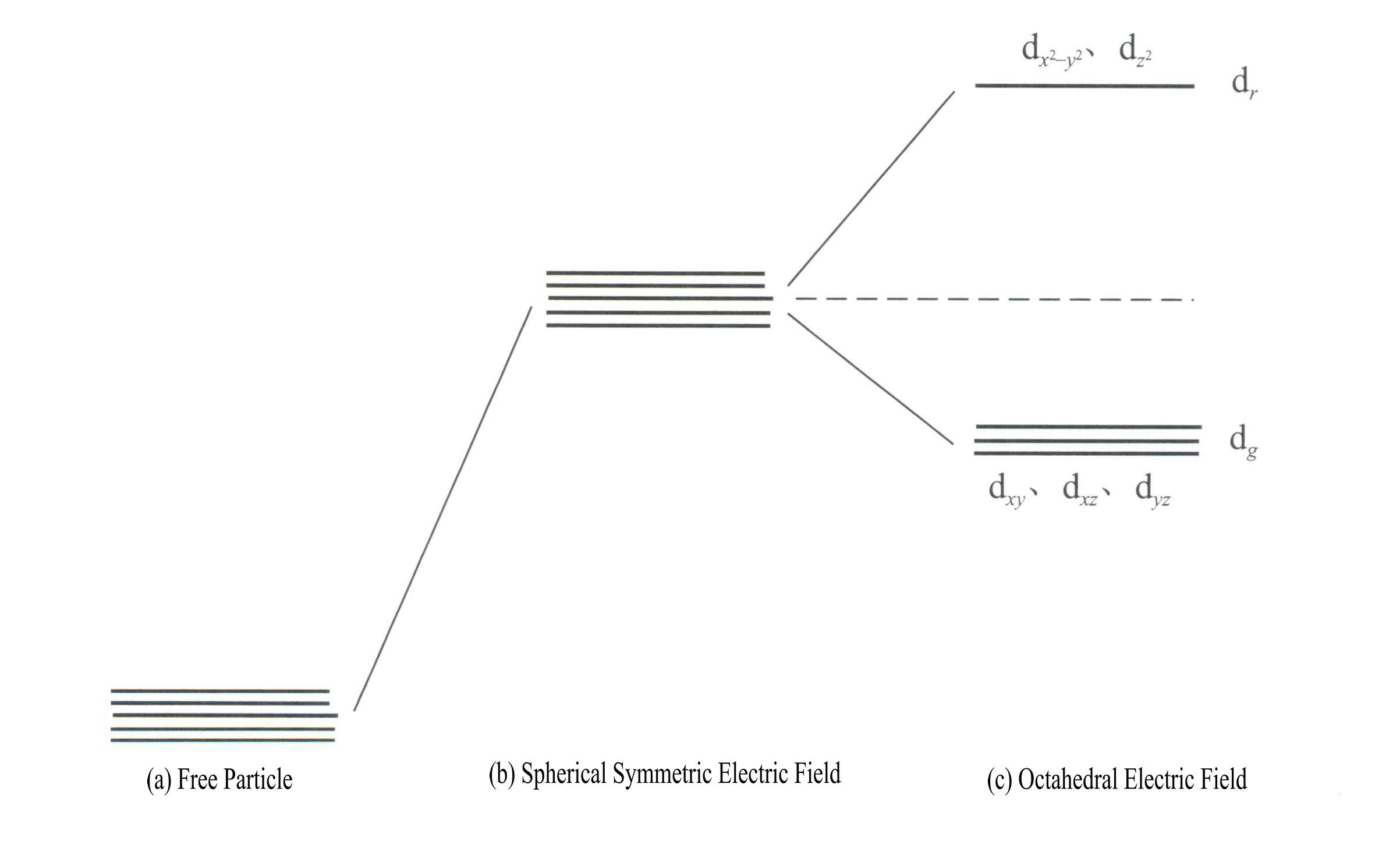
A energia das orbitais d é a mesma quando não há campo elétrico [Figura 3-19 (a)]; sob um campo eletrostático esfericamente simétrico, as orbitais d têm energia aumentada mas não se dividem [Figura 3-19 (b)]; quando o campo do ligando é octaédrico, divide-se em dr e dg. Destes, dr são compostas por orbitais d e d , com energia mais elevada; as orbitais dg são compostas por orbitais dxy, dxz, dyz.
Os iões dos metais de transição encontram-se no campo cristalino de aniões circundantes ou moléculas dipolares. A teoria do campo cristalino é um modelo eletrostático que vê o cristal como uma interação eletrostática entre iões positivos e negativos, em que o catião com carga positiva é designado por ião central e o anião com carga negativa é designado por ligando.
A aplicação da teoria do campo cristalino para explicar a cor dos minerais de pedras preciosas envolve principalmente os electrões d ou a energia do eletrão f dos iões dos elementos de transição. Por exemplo, as orbitais d têm cinco tipos: dxy, dxz, dyz, d , e d . Estas cinco orbitais d têm distribuições espaciais diferentes no estado iónico livre, mas têm a mesma energia. No entanto, sofrem alterações significativas sob a influência do campo do ligante. As cinco orbitais d degeneradas em energia do átomo central dividem-se sob a influência do campo elétrico negativo formado pelos ligandos circundantes. Algumas orbitais d aumentam a energia, enquanto outras diminuem a energia. Devido à divisão dos níveis de energia das orbitais d, os electrões nas orbitais d do átomo central reorganizam-se, ocupando preferencialmente as orbitais de menor energia, reduzindo assim a energia total do sistema e tornando o complexo mais estável.
A energia das orbitais d é a mesma quando não há campo elétrico [Figura 3-19 (a)]; sob um campo eletrostático esfericamente simétrico, as orbitais d têm energia aumentada mas não se dividem [Figura 3-19 (b)]; quando o campo do ligando é octaédrico, divide-se em dr e dg. Destes, dr são compostas por orbitais dx2– y2 e dz2
com maior energia; o dg são compostas por orbitais dxy, dxz, dyz. [Figura 3-19 (c)]
A diferença entre os níveis de energia mais alto e mais baixo após a divisão do orbital d é chamada de energia de separação △ . As energias de separação produzidas por diferentes configurações de campos ligantes não são as mesmas (Figura 3-20). A sua ordem de energia é:
Campo quadrado > Campo octaédrico > Campo tetraédrico

Mesmo para campos com a mesma configuração, podem também diferir devido às diferenças nos ligandos e iões centrais; quanto maior for, mais estável é o cristal. Os três factores seguintes determinam principalmente o tamanho da energia de separação do cristal:
(1) Cristais formados pelo mesmo elemento de transição; quando os ligandos são os mesmos, quanto maior a carga do ião central, maior a energia de separação △ . Quanto maior for a carga positiva do ião central, maior será a atração pelos ligandos, resultando numa menor distância entre o ião central e o núcleo do ligando, e quanto maior for a força repulsiva do campo cristalino gerada pelos ligandos sobre os electrões, maior será a energia de separação △ .
(2) Para cristais formados por iões diferentes com a mesma carga positiva e os mesmos ligandos, quanto maior for o raio do ião central, mais distantes estão as orbitais d do núcleo e maior é a energia de separação △ .
(3) Para cristais formados pelo mesmo ião central e diferentes ligandos, a energia de separação varia devido às diferentes intensidades do campo cristalino do ligando. Diferentes ligantes têm diferentes intensidades de campo, e a energia de separação △ varia com a intensidade do campo do ligante.
A energia de separação é utilizada para explicar qualitativamente a estabilidade dos cristais; não é necessário obter o valor absoluto △ , pois basta conhecer os valores relativos do cristal em diferentes condições.
Com base na energia relativa das orbitais d divididas, pode calcular-se a energia total dos iões do metal de transição nas orbitais d. Esta energia é menor do que antes da divisão, fornecendo assim energia adicional ao cristal, conhecida como energia de estabilização do campo cristalino, representada pelo símbolo CFSE. A Tabela 3-10 lista as energias de estabilização dos iões que contêm orbitais dn electrões em diferentes condições.
Tabela 3-10 Energias de estabilização do campo cristalino com diferentes ligandos (Wu Ruihua, 1994)
| dn | Campo fraco | Campo forte | ||||
|---|---|---|---|---|---|---|
| dn | Quadrado | Octaedro regular | Tetraedro regular | Quadrado | Octaedro regular | Tetraedro regular |
| d0 | 0 | 0 | 0 | 0 | 0 | 0 |
| d1 | 5.14 | 4 | 2.67 | 5.14 | 4 | 2.67 |
| d2 | 10.28 | 8 | 5.34 | 10.28 | 8 | 5.34 |
| d3 | 14.56 | 12 | 3.56 | 14.56 | 12 | 8.01 |
| d4 | 12.28 | 6 | 1.78 | 19.70 | 16 | 10.68 |
| d5 | 0 | 0 | 0 | 24.84 | 20 | 8.90 |
| d6 | 5.14 | 4 | 2.67 | 29.12 | 24 | 6.12 |
| d7 | 10.28 | 8 | 5.34 | 26.84 | 18 | 5.34 |
| d8 | 14.56 | 12 | 3.56 | 24.56 | 12 | 3.56 |
| d9 | 12.28 | 6 | 1.70 | 12.28 | 6 | 1.78 |
| d10 | 0 | 0 | 0 | 0 | 0 | 0 |
2. Caraterísticas de cor dos iões de metais de transição
Nas suas pedras preciosas coloridas, a cor da maioria das pedras preciosas é devida a iões metálicos de transição, e a cor das pedras preciosas está relacionada com o facto de os iões coloridos conterem electrões não emparelhados nas orbitais d ou f. As caraterísticas de coloração dos iões de metais de transição incluem principalmente os seguintes aspectos:
(1) A coloração dos iões de metais de transição está relacionada com os estados electrónicos da orbital d ou da orbital f. Quando os electrões da orbital d ou da orbital f estão cheios ou vazios, a pedra preciosa não apresenta cor. Por exemplo, o Cr6+, Ce4+e Cu+.
(2) Diferentes iões corantes exibem cores diferentes no mesmo material de pedra preciosa. Devido às diferentes energias de separação dos diferentes iões corantes, estes podem apresentar cores diferentes mesmo no mesmo material. Por exemplo, o Fe2+ produz uma cor azul-acinzentada ligeira no espinélio, enquanto o Cr3+ produz vermelho.
(3) Os iões corantes do mesmo elemento em diferentes estados de valência exibem frequentemente cores diferentes no mesmo material de pedra preciosa. Como a energia necessária para as transições do eletrão d do ião central é diferente, os comprimentos de onda da luz absorvida são diferentes, resultando em cores diferentes. Por exemplo, um castrum contendo Mn2+ apresenta uma tonalidade rosa suave, enquanto um berilo com Mn2+ apresenta um vermelho vivo, conhecido como berilo vermelho.
(4) Os iões corantes do mesmo elemento no mesmo estado de valência exibem frequentemente cores diferentes quando em diferentes configurações de ligandos. Por exemplo, o Co2+ na configuração tetraédrica do espinélio apresenta uma cor caraterística "azul diamante", enquanto que na configuração octaédrica da calcite aparece cor-de-rosa. O Fe2+ na olivina coordenada octaedricamente mostra um verde azeitona caraterístico, enquanto que na almandina coordenada cúbica distorcida, aparece vermelho profundo.
(5) O mesmo tipo de iões coloridos tem o mesmo estado de valência e a mesma geometria de coordenação, mas diferentes átomos de coordenação adjacentes exibem cores diferentes. Por exemplo, na coordenação tetraédrica do Co2+na esfalerite, Co2+ está ligado ao enxofre, mostrando-se verde, enquanto no espinélio, o Co2+ está ligado ao oxigénio, que se apresenta a azul.
(6) O mesmo tipo de iões coloridos com o mesmo estado de valência, geometria de coordenação e átomos adjacentes apresentam cores diferentes em pedras preciosas diferentes. A distorção da geometria de coordenação causada pelas diferentes composições químicas das pedras preciosas altera a natureza das ligações químicas entre o ião central e os ligandos de coordenação, alterando a energia de transição dos electrões d. Por exemplo, o Cr3+ aparece vermelho no rubi, verde na esmeralda e apresenta cores variáveis na alexandrite. A razão para tais mudanças no Cr3+ está relacionada com as suas caraterísticas e com os ligandos de coordenação adjacentes, com a análise de caraterísticas específicas que se segue.
① Cr3+ Caraterísticas:
Cr3+ tem uma estrutura eletrónica externa de 3s23p63d3com 11 electrões na camada exterior, pertencentes a uma estrutura irregular (8-18) de camadas electrónicas.
Esta estrutura tem um menor efeito de proteção no núcleo do que a estrutura de 8 electrões, resultando em Cr3+ com uma carga positiva efectiva mais elevada, enquanto o seu raio iónico é também mais pequeno, o que constitui as caraterísticas básicas do Cr3+: um forte campo elétrico positivo e orbitais d vazias. Cr3+ pode fornecer seis orbitais vazias para acomodar seis ligandos de coordenação, com uma configuração espacial octaédrica, pertencente a d2esp3 hibridação (Figura 3-21).
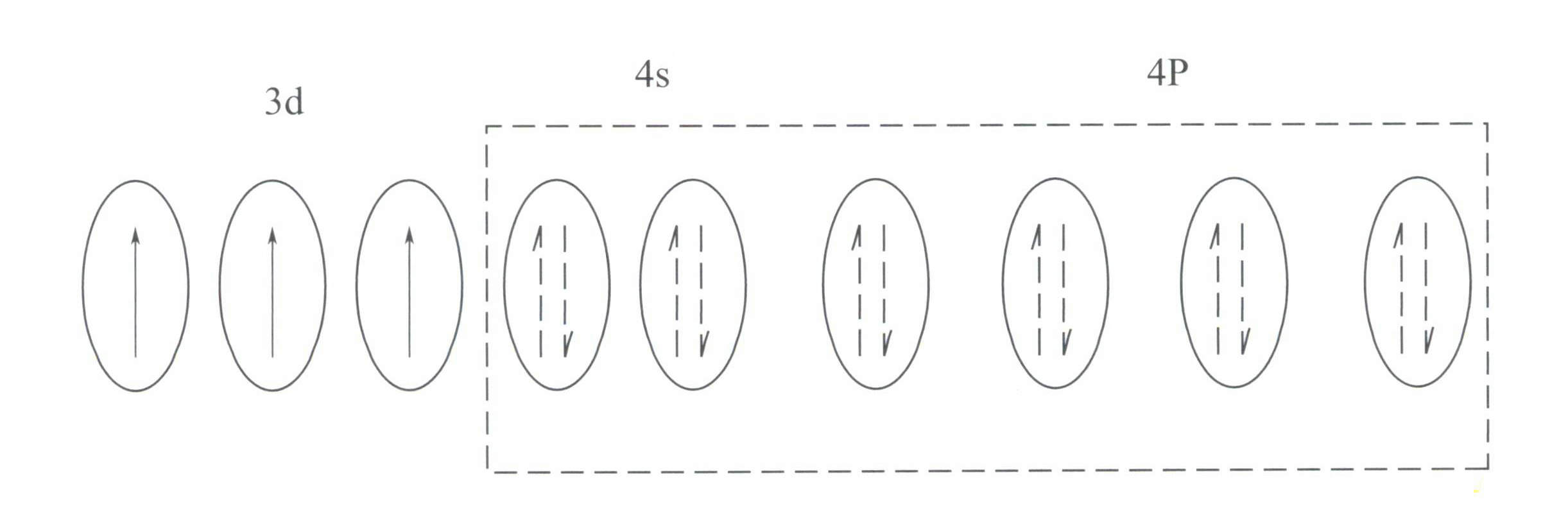
De acordo com a teoria do campo cristalino, num campo octaédrico, as orbitais d do Cr3+ pode dividir-se em energia inferior dƐ e a órbita de energia mais elevada dr órbita. Uma vez que os três electrões d do Cr3+ estão todos no dƐ e são todos electrões simples, as transições d-d podem ocorrer sob luz visível, fazendo com que as gemas contendo Cr3+ para exibir cor.
② O mecanismo de coloração do Cr3+:
No rubi O principal componente químico do rubi é o Al2O3. Quando uma pequena percentagem de Cr3+ substitui Al3+, produz uma cor vermelha brilhante. Na estrutura do rubi, devido ao maior raio do Cr3+ em comparação com o raio do Al3+, Cr3+ entra na rede do corindo, reduzindo a simetria em torno do óxido de alumínio.
As orbitais d do Cr3+ e quando os electrões do estado excitado regressam de D ou C para o estado fundamental A, têm de passar primeiro por B, libertando calor. Regressam de B para A, acompanhados de luminescência, emitindo fluorescência vermelha. Neste processo, os electrões absorvem energia luminosa, fazendo com que o rubi absorva o violeta D (400nm) e o amarelo-verde C (555nm) do espetro visível (Figura 3-22), formando uma banda de absorção.

Quando a luz branca passa através de um rubi, os fotões do espetro do roxo ao amarelo-verde são absorvidos, enquanto quase toda a luz vermelha e alguma luz azul passam, dando ao rubi uma cor vermelha profunda com um toque de roxo, conhecida como vermelho sangue de pombo.
Os rubis apresentam uma breve absorção de nível B, que se manifesta como fluorescência vermelha. Esta absorção de nível B que produz a fluorescência vermelha torna a cor do rubi mais viva; quanto mais elevado for o teor de iões de crómio, mais forte será a fluorescência.
Os iões de ferro na pedra preciosa podem suprimir a fluorescência da absorção de nível B, o que explica o fenómeno de os rubis parecerem mais escuros quando contêm impurezas de ferro.
③ Cr3+ O mecanismo de coloração das esmeraldas
O principal componente químico da esmeralda é o Be3Al2Si6O18, Cr3+que substitui o Al3+ na rede esmeralda, e o Cr3+ é também rodeado por um octaedro composto por seis iões de oxigénio, em que o Cr3+O comprimento da ligação -O é também bastante semelhante ao dos rubis. No entanto, em comparação com os rubis, as esmeraldas têm mais dois iões, Be2+ e Si4+. Na estrutura das esmeraldas, a natureza da ligação covalente entre os óxidos metálicos aumenta, enquanto as caraterísticas iónicas enfraquecem.
Pequenas alterações, como ligações químicas, levam a uma ligeira diminuição do Cr3+C e D, resultando numa ligeira deslocação da banda de absorção (Figura 3-23), bloqueando significativamente a transmissão da luz azul-púrpura (425nm) e amarelo-alaranjada (608nm) no espetro, enquanto aumenta a transmissão da luz azul-verde, formando assim o caraterístico verde-esmeralda.

A absorção de nível B da dioptase é quase inalterada. Quando o ferro impuro não tem efeito "inibidor" no componente esmeralda, a forte fluorescência vermelha faz com que o verde esmeralda caraterístico brilhe ainda mais.
④ Cr3+ O mecanismo da cor na alexandrite:
A cor da alexandrite também é causada pelo Cr3+ substituindo Al3+ em coordenação octaédrica distorcida. Devido ao facto de a composição química da alexandrite ser BeAL2O4A natureza das ligações químicas entre os seus iões metal-oxigénio situa-se entre a do rubi e a da esmeralda. Por conseguinte, as suas bandas de absorção também se situam entre as do rubi e da esmeralda, sendo as probabilidades de transmissão da luz azul-violeta e da luz amarelo-alaranjada aproximadamente iguais, tornando impossível determinar se a luz vermelha ou azul-verde é dominante (Figura 3-24).
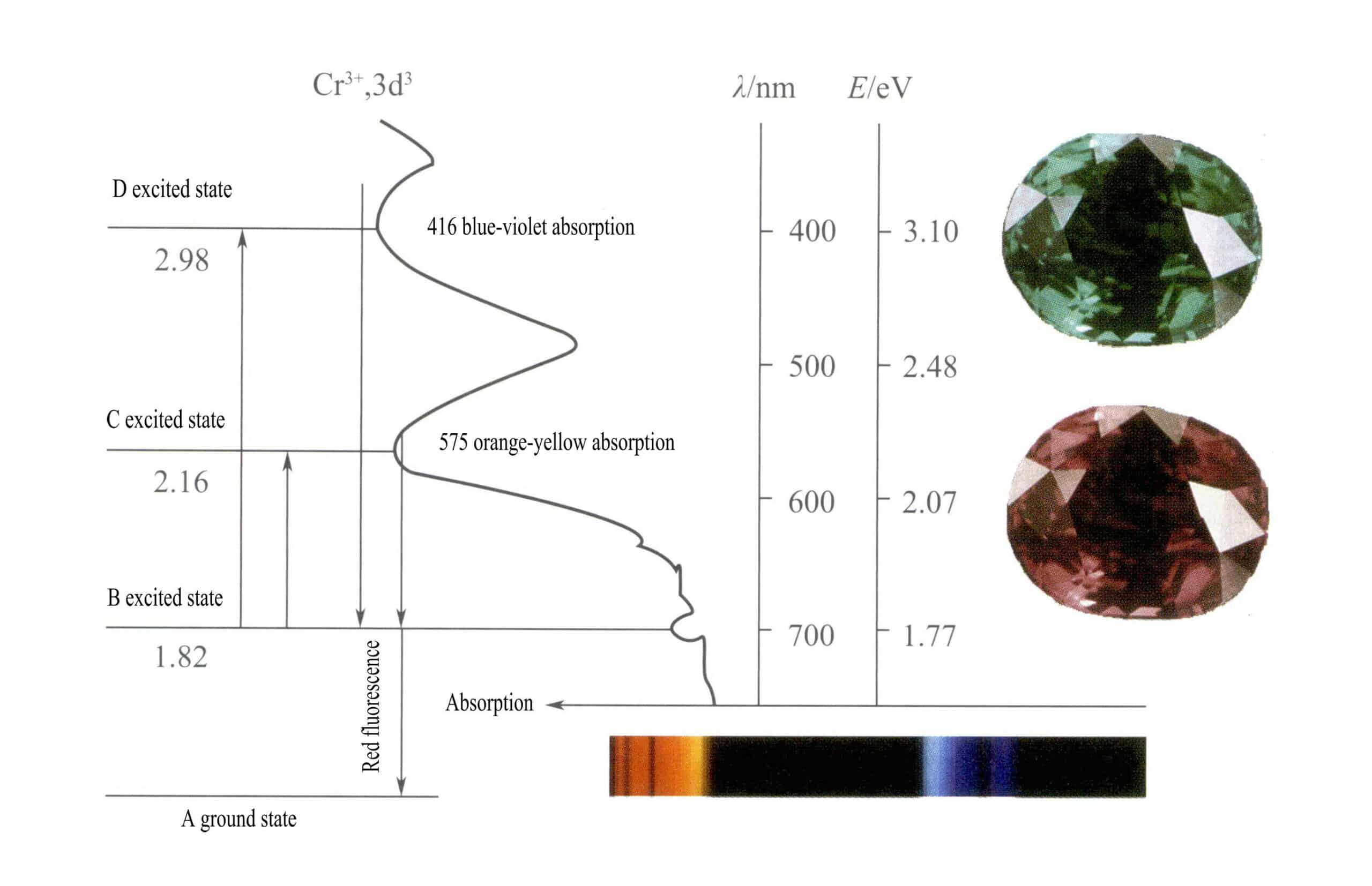
Por conseguinte, a cor da alexandrite só pode depender da distribuição de energia e da gama de cores da luz incidente, resultando assim no "efeito de mudança de cor" da alexandrite, ou seja, aparecendo verde à luz do dia com um alto componente de luz azul e vermelho em luz incandescente com um alto componente de luz vermelha. Por isso, a alexandrita é muitas vezes chamada "a esmeralda do dia e o rubi da noite".
O "efeito de mudança de cor" aparece em muitos tipos de pedras preciosas, como o corindo que muda de cor e a granada que muda de cor. Atualmente, o corindo que muda de cor sintetizado artificialmente é produzido utilizando o princípio da mudança de cor, empregando V3+ como ião corante para a síntese.
3. Cores dos minerais de pedras preciosas
As cores produzidas pelos componentes dos metais de transição podem ser inferidas a partir da composição química dos minerais das pedras preciosas. Por exemplo, a turquesa que contém Cu2+ deve ser azul, enquanto o Cu+ é incolor. A Tabela 3-11 lista as cores produzidas por componentes comuns de metais de transição em minerais de pedras preciosas naturais.
Tabela 3-11 Cores produzidas por componentes de metais de transição em minerais de pedras preciosas naturais
| Elemento | Cor | Minerais comuns |
|---|---|---|
| Cério (Ce) | Amarelo | Parisita |
| Crómio (Cr) | Vermelho, verde, laranja, etc. | Crocoisite, Crocoisite vermelha, Uvarovite |
| Cobalto (Co) | Azul | Espinélio sintético |
| Cobre (Cu) | Azul, Verde | Azurite, crisocola, turquesa malaquite, dioptase |
| Ferro (Fe) | Vermelho, verde, amarelo | Almandina, olivina, goetite |
| Manganês (Mn) | Rosa, laranja | Rodonite, espessartina |
| Níquel (Ni) | Verde | Bunsenite, Calcedónia |
A cor da maioria das pedras preciosas é causada pelas impurezas dos metais de transição que contêm. Por exemplo, os rubis parecem vermelhos devido a quantidades vestigiais de Cr3+. Vários factores influenciam a cor causada pelos iões de impureza na pedra preciosa. Por conseguinte, as impurezas podem produzir cores diferentes em pedras preciosas diferentes. Por exemplo, o Cr3+ aparece vermelho nos rubis e verde nas esmeraldas.
As mesmas impurezas podem não causar necessariamente a mesma cor de uma pedra preciosa. Por exemplo, a cor verde da maioria das esmeraldas é causada pelo Cr, enquanto a cor verde de algumas esmeraldas é parcial ou totalmente causada pelo vanádio (V).
A teoria do campo cristalino não só pode ser usada para explicar as cores das pedras preciosas produzidas por componentes ou impurezas de metais de transição, mas também as cores produzidas por defeitos estruturais (centros de cor); o processo específico de geração de cor pode ser referido no Capítulo 3.3 deste livro.
Existem também deficiências na explicação das cores dos minerais de pedras preciosas pela teoria do campo cristalino, que se reflectem principalmente nos seguintes aspectos:
(1) Os electrões do ião central d não estão completamente localizados nas suas orbitais originais. Podem também aparecer em torno dos átomos de coordenação, indicando uma interação covalente entre o átomo central e os ligandos.
(2) Considera apenas a interação eletrostática iónica entre o átomo central e os ligandos, ignorando completamente a interação de ligação covalente entre o átomo central e os ligandos. Na investigação física, os resultados dos cálculos quantitativos diferem muitas vezes significativamente das situações reais.
(3) As razões da cor dos minerais de pedras preciosas, para além da interação entre o ião central e os ligandos, podem também dever-se aos efeitos combinados dos defeitos estruturais e do campo cristalino.
Secção II Teoria das orbitais moleculares
Mulliken e Hund propuseram inicialmente a teoria das orbitais moleculares (teoria MO). Através da exploração contínua de muitos cientistas, desenvolveu-se uma teoria madura. As orbitais moleculares (MO) podem ser obtidas por combinações lineares de orbitais atómicas, um método comummente utilizado para construir orbitais moleculares. A partir de n orbitais atómicas, podem ser obtidas n orbitais moleculares e os coeficientes da combinação linear podem ser determinados utilizando o método variacional ou outros métodos. As orbitais moleculares formadas por duas orbitais atómicas, com níveis de energia inferiores aos das orbitais atómicas, são designadas por orbitais de ligação; as que têm níveis de energia superiores aos das orbitais atómicas são designadas por orbitais de anti-ligação; as que têm níveis de energia próximos das orbitais atómicas são geralmente orbitais de não-ligação.
A teoria do orbital molecular é uma teoria utilizada para explicar questões como a formação, estrutura e propriedades moleculares. Também pode explicar algumas das causas das cores das pedras preciosas, que foram desenvolvidas com base na teoria do campo cristalino e na teoria das orbitais moleculares dos metais de transição. As orbitais moleculares são uma extensão natural das orbitais atómicas. Numa molécula, os electrões já não pertencem a um átomo específico, mas movem-se ao longo de toda a gama molecular; por conseguinte, o movimento dos electrões numa molécula é descrito utilizando orbitais moleculares.
1. Conceitos básicos da teoria das orbitais moleculares
A teoria das orbitais moleculares postula que, depois de os átomos formarem uma molécula, os electrões deixam de pertencer às orbitais atómicas originais, tal como proposto pela teoria do campo cristalino, mas movem-se dentro de certas orbitais moleculares. As orbitais moleculares compõem uma molécula tal como as orbitais atómicas compõem um átomo. Os electrões de valência já não são considerados localizados em átomos individuais, mas movem-se por toda a molécula. A distribuição de electrões na molécula pode ser tratada de acordo com os princípios de distribuição de electrões nos átomos (o princípio da energia mínima e a regra de Hund).
A combinação linear de orbitais atómicas numa molécula forma orbitais moleculares. O número de orbitais moleculares é igual ao número de orbitais atómicas antes da combinação. A combinação de orbitais atómicas em orbitais moleculares efectivas deve obedecer aos três princípios seguintes:
(1) Princípio da correspondência de simetria: Apenas as orbitais atómicas com a mesma simetria podem formar orbitais moleculares.
(2) Princípio da Proximidade Energética: Apenas as orbitais atómicas com energias semelhantes se podem combinar para formar orbitais moleculares efectivas.
(3) Princípio da Sobreposição Máxima: Em condições de simetria, quanto maior for a sobreposição das orbitais atómicas, mais a energia das orbitais moleculares resultantes diminui e mais estável é a ligação química resultante.
A orbital molecular ψ é a função de onda de um único eletrão. Pode ser representada como uma combinação linear de orbitais atómicas, correspondendo cada orbital a uma energia específica, que é a soma das energias cinética e potencial do eletrão que se move no campo elétrico molecular. Duas orbitais atómicas, a e b, através de combinações lineares sobrepostas, produzem duas orbitais moleculares ψI e ψII :
ψI=ψa + ψb (3-5)
ψII = ψa - ψb (3-6)
Quando as orbitais moleculares com electrões são preenchidas primeiro, as orbitais de ligação ψI são preenchidas em primeiro lugar. Quando os electrões preenchem orbitais moleculares de igual energia, de acordo com a regra de Hund, devem também ocupar, tanto quanto possível, orbitais moleculares diferentes com a mesma direção de spin.
As orbitais moleculares ψI obtidas pela adição de duas funções orbitais atómicas (Equação 3-5) são chamadas orbitais moleculares de ligação. As orbitais moleculares ψII obtidas por subtração de duas funções orbitais atómicas (Equação 3-6) são designadas por orbitais moleculares anti-ligação. A energia das orbitais moleculares de ligação é inferior à das orbitais moleculares de anti-ligação e inferior às energias das duas orbitais atómicas originais. Assim, tal como no caso do preenchimento de orbitais atómicas, ao preencher orbitais moleculares, os electrões são primeiro colocados em orbitais de ligação, e uma orbital molecular pode acomodar dois electrões com spins opostos. Quando os electrões preenchem orbitais moleculares de igual energia, de acordo com a regra de Hund, devem também ocupar, tanto quanto possível, orbitais moleculares diferentes com a mesma direção de spin. As orbitais moleculares formadas por duas orbitais atómicas s são mostradas na Figura 3-25.

As orbitais p e as orbitais d podem também formar orbitais moleculares de diferentes níveis de energia; por exemplo, a combinação de orbitais moleculares diatómicas no O2 moléculas é relativamente complexo.
Em experiências, mediram-se as propriedades magnéticas destes dois electrões individuais, o que deu um forte apoio à teoria das orbitais moleculares. Ao contrário das moléculas compostas pelos mesmos átomos, as compostas por dois ou mais átomos diferentes têm níveis de energia de orbitais moleculares mais complexos, mas o princípio é o mesmo.
2. Caraterísticas da coloração por transferência de carga
Esta teoria das orbitais moleculares, em que toda a molécula partilha electrões, é também considerada como a transição de electrões de uma orbital atómica para outra, conhecida como transferência de carga. A transferência de carga pode ocorrer em interações metal-metal (M-M), não-metal-não-metal (L-L) e não-metal-metal (L-M). Entre elas, L-L, M-L, estes dois tipos de ligação são frequentemente ligações covalentes. O2 pertence à transferência de carga L-L, que é uma ligação covalente.
(1) Transferência de carga metal-metal (transferência de carga M - M)
Este tipo de transferência de carga ocorre geralmente entre iões de metais de transição comuns. A maioria das causas de coloração das pedras preciosas coloridas é produzida por transferência de carga metal-metal. A transferência de carga M-M inclui principalmente os seguintes tipos: Fe2+ - Fe3+/Fe3+ - Fe2+; Ti3+ - Ti4+ / Ti4+- T3+ ;Fe2+ - T4+/Fe3+ - T3+; Mn2+ - Mn4+/Mn3+ - Mn3+ . A transferência de carga entre metais divide-se em dois tipos: transferência de carga entre átomos homonucleares e transferência de carga entre átomos heteronucleares.
① Transferência de carga entre átomos isoelectrónicos
A transferência de carga entre átomos isoelectrónicos ocorre entre dois átomos do mesmo elemento metálico de transição em diferentes estados de oxidação. Por exemplo, o Fe2+ e Fe3+ sofrem transferência de carga em diferentes condições redox, absorvendo energia e produzindo cor. A cor azul-púrpura da iolite é produzida pela transferência de carga de iões de ferro em diferentes estados de oxidação. Fe3+ e Fe2+ estão em posições tetraédricas e octaédricas, respetivamente, com dois ligandos ligados por arestas. Quando a luz visível incide sobre a iolite, um eletrão d do Fe2+ absorve luz de uma determinada energia e transita para Fe3+absorvendo luz amarela a 588nm e produzindo uma cor azul-púrpura. A água-marinha, a turmalina verde e outras também podem exibir cor devido à transferência de carga entre iões de ferro.
② Transferência de carga entre heteroátomos
As safiras azuis exemplificam mais tipicamente a cor produzida pela transferência de carga entre dois tipos de iões de metais de transição. Os poliedros de coordenação dos iões de metais de transição estão ligados por arestas ou faces, facilitando a transferência de carga entre metais.
Por exemplo, nas safiras, quando os iões de ferro e os iões de titânio entram nos octaedros ligados, tanto o Fe como o Ti existem em dois estados de oxidação:
Fe2+ + Ti4+ baixa energia (3-7)
Fe3+ + Ti3+ alta energia (3-8)
A transição da equação (3-7) para a equação (3-8) requer a absorção de uma certa quantidade de energia luminosa, resultando numa banda de absorção alargada que vai do amarelo ao vermelho. Em contraste, a maior parte da luz azul passa através da pedra preciosa, dando-lhe uma aparência azul.
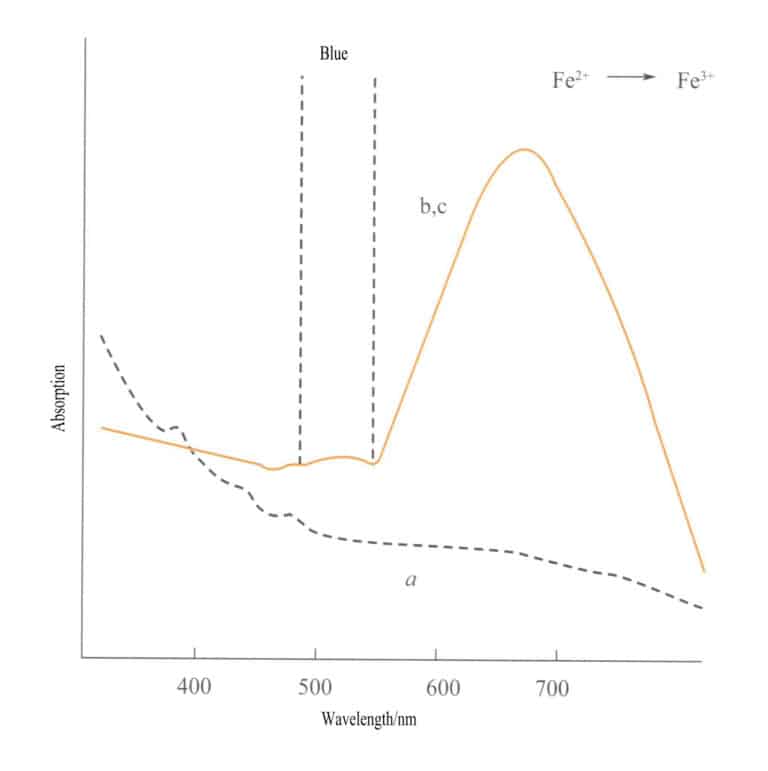
A transferência de carga entre diferentes estados de valência tem uma forte direccionalidade, e as pedras preciosas que exibem cor devido a este mecanismo apresentam frequentemente pleocroísmo. Por exemplo, a água-marinha colorida por Fe2+→ Fe3+ A transferência de carga mostra a cor estritamente ao longo da direção do eixo ótico. A Figura 3-26 mostra que a água-marinha aparece amarela nos planos b e c. Ao mesmo tempo, não existe essa transferência ao longo da direção do eixo a, o que resulta na ausência de absorção de luz e, por conseguinte, na ausência de cor ao longo da direção do eixo a.
(2) Transferência de carga de não-metal para metal (L-M)
Este tipo de transferência de carga L-M ocorre frequentemente entre iões de oxigénio e iões metálicos, e algumas pedras preciosas que contêm oxigénio são coloridas por transferência de carga de não-metal para metal, como o O2–→ Fe3+, O2- →Cr6+, O2-→Mn6+, O →V5+.
No espetro de absorção dos óxidos de ferro simples (Figura 3-27), aparecem duas bandas de absorção fracas na região do infravermelho da ilmenite, hematite e lepidocrocite (transições electrónicas d - d). Uma banda de absorção forte aparece na gama de ondas curtas, produzida pelo O2-→Fe3+ transferência de carga, e esta banda de absorção determina as cores caraterísticas destes compostos: castanho-avermelhado, castanho e castanho-amarelado.
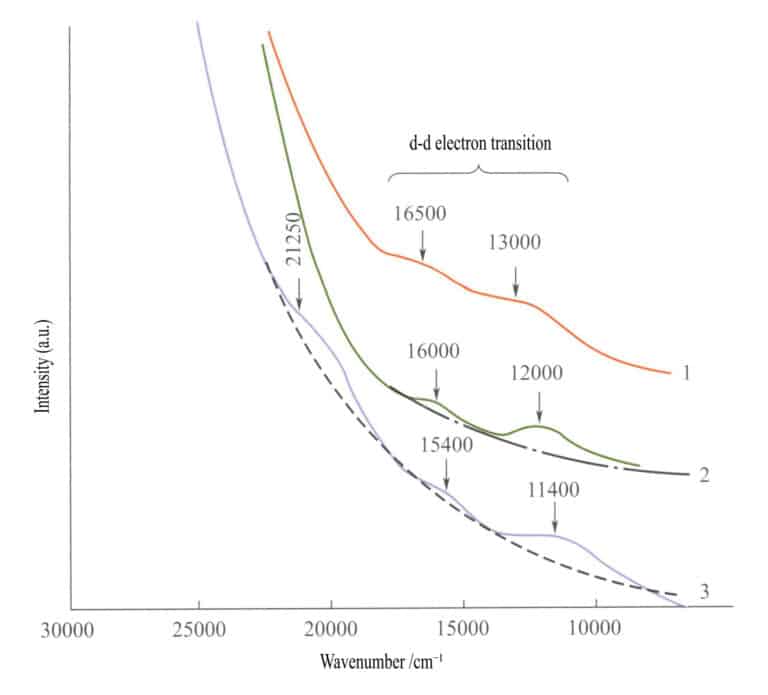
1 -Iilmenite; 2 - Hematite; 3 - Lepidocrocite
O berilo amarelo obtém a sua cor do O2–→ Fe3+ transferência de carga. Na estrutura do berilo amarelo, o O2–→ Fe3+ A forte absorção de transferência de carga pode estender-se desde o extremo ultravioleta até ao extremo azul do espetro visível, absorvendo o roxo e o azul, resultando numa cor amarela.
A safira, que tem um ambiente de coordenação completamente diferente do berilo, também pode produzir as mesmas bandas de absorção espetral que o berilo, resultando em amarelo, que também é um resultado de O2–→ Fe3+ transferência de carga.
De acordo com a teoria do campo cristalino, alguns minerais de pedras preciosas não contêm electrões não emparelhados e não podem produzir cor. Por exemplo, as camadas electrónicas da crocoite (PbCrO4), Pb2+, Cr6+e O2– estão cheios. Ainda assim, no CrO42- são "orbitais moleculares", que correspondem aos estados excitados durante a formação do O2-→Cr6+ formando bandas de absorção e apresentando cor de laranja.
L→M A transferência de carga também inclui a transferência de enxofre para o metal, como na pirite comum; este fenómeno ótico causado pela transferência é mais fácil de compreender quando discutido utilizando a teoria das bandas.
(3) Transferência de carga de não-metal para não-metal (L-L)
A teoria das orbitais moleculares sugere que a cor azul profunda do lápis-lazúli se deve aos níveis de energia de excitação dos átomos S3- grupo atómico.
Na grafite, os anéis de seis átomos de carbono estão dispostos em camadas. Ao longo desta camada, os electrões podem mover-se livremente, o que resulta numa forte absorção de luz, anisotropia e condutividade.
Algumas pedras preciosas orgânicas, como o âmbar e as pérolas, têm electrões que se movem e se excitam através dos grupos atómicos de pigmentos orgânicos em orbitais moleculares partilhados, causando a absorção de luz visível e produzindo cor. Por exemplo, o "amarelo mel" do âmbar, as cores do coral e algumas conchas e pérolas coloridas.
Os mecanismos de cor das pedras preciosas comuns são apresentados na Tabela 3-12.
Tabela 3-12 Classificação dos mecanismos de cor das pedras preciosas comuns
| Transferência de carga metal - metal | Fe2+ - Fe3+ /Fe3+ - Fe2+ : iolite (azul), berthierite (azul), Magnetite (preto), etc. |
| Fe2+ -Ti4+/Fe3+ - Ti3+ : Cianite (azul), Safira (azul) | |
| Mn2+-Mn4+/Mn3+-Mn3+: Manganite (preto), Bixbyite (preto) | |
| Transferência de carga de não-metal para metal | O2- -Fe3+: Berilo amarelo dourado, safira amarela dourada, ilmenite, hematite, lepidocrocite, etc. |
| O2- - Cr6+: Crocoite (laranja) | |
| O2- -V5+:Vanadinite (laranja) | |
| Enxofre a metal: pirite, marcassite, etc. (ver semicondutor com lacuna) | |
| Transferência de carga não-metal - não-metal | S3-: Lápis-lazúli (azul) |
| Π eletrónico: grafite (preto) | |
| As cores de algumas pedras preciosas orgânicas, como o âmbar e o coral. |
Copywrite @ Sobling.Jewelry - Fabricante de jóias personalizadas, fábrica de jóias OEM e ODM
Secção III Teoria das bandas de energia
A teoria das bandas de energia é um modelo mecânico quântico para estudar materiais de pedras preciosas, que é uma extensão e expansão da teoria orbital molecular. O estudo da teoria das bandas de energia pode explicar melhor o mecanismo de cor de algumas pedras preciosas naturalmente coloridas.
1. Conceitos básicos da teoria das bandas de energia
A teoria das bandas de energia é uma teoria aproximada utilizada para estudar as leis do movimento dos electrões nos sólidos. Os sólidos são compostos por átomos, que incluem os núcleos atómicos e os electrões mais externos, todos eles em constante movimento. A teoria das bandas postula que os electrões nos sólidos não estão ligados a um átomo específico, mas são partilhados por todo o cristal e movem-se dentro do campo potencial periódico do espaço tridimensional do cristal. A amplitude do movimento dos electrões está dentro do campo potencial periódico da rede, permitindo que a distribuição espacial das órbitas dos electrões exceda a das moléculas, atingindo um máximo. Os níveis de energia dos electrões individuais são alargados em bandas de energia.
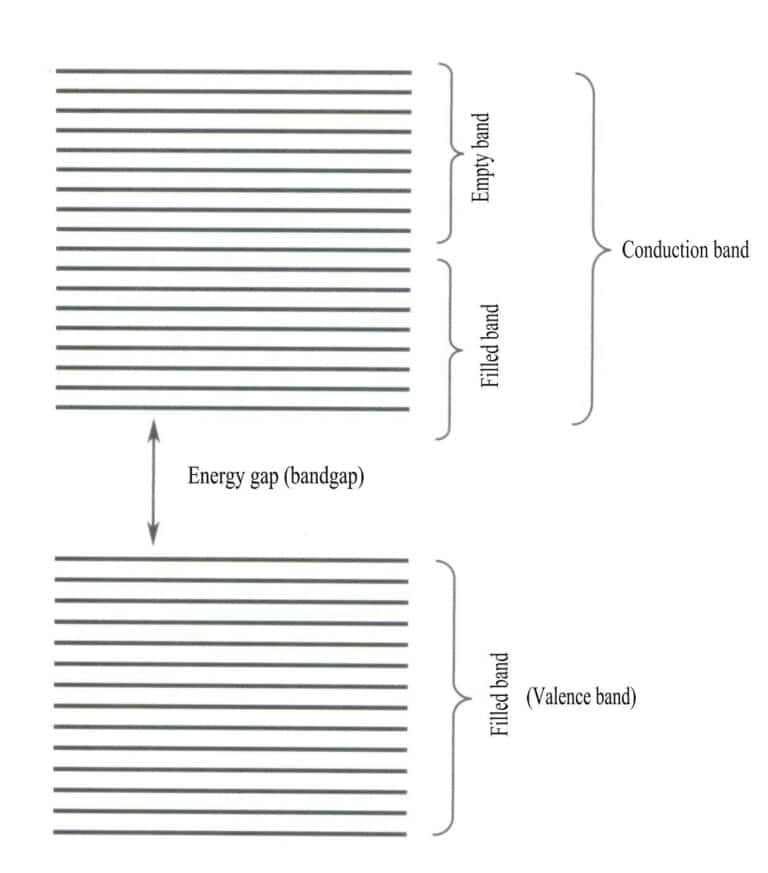
A teoria das bandas aborda principalmente as transições de electrões entre estados não-locais, em que todos os electrões de valência devem pertencer a toda a rede sólida. De acordo com a teoria das bandas, os materiais sólidos podem ser divididos em diferentes bandas de energia com base no facto de as orbitais atómicas estarem ou não preenchidas: uma banda preenchida é formada pelos níveis de energia das orbitais atómicas que estão totalmente ocupadas por electrões, representando uma banda de baixa energia; uma banda vazia é formada por níveis de energia que não estão totalmente ocupados por electrões, representando uma banda de alta energia. A diferença de energia entre estes dois tipos de bandas é designada por "intervalo de banda" (Figura 3-28).
Quando todas as bandas de energia de um material estão preenchidas, este é um não-condutor; quando parcialmente preenchido com electrões, é um condutor. Os defeitos da rede introduzem níveis de energia adicionais no cristal, permitindo que os electrões entrem nesses níveis de energia, resultando numa condutividade condicional.
2. Caraterísticas das transições de intervalo de banda
Alguns minerais de pedras preciosas contêm elementos do Grupo IV A da tabela periódica, como o diamante e a moissanite, que se ligam principalmente de forma covalente. Existem também outros minerais, como o sulfureto de cádmio (CdS), cujas cores podem ser explicadas pela teoria das bandas.
Os electrões absorvem a energia da luz e movem-se entre as bandas de valência e de condução, formando "transições de banda interna". A probabilidade de ocorrerem transições está intimamente relacionada com a diferença de energia entre as bandas de valência e de condução, conhecida como energia de hiato (Eg) (Figura 3-29).

A Figura 3-29 (a) é um diagrama de bandas típico de um semicondutor. Com base no tamanho da energia do intervalo de banda do cristal, este pode ser dividido em três tipos: intervalo de banda larga, intervalo de banda estreita e intervalo de banda média. Um intervalo de banda larga tem uma energia de intervalo de banda superior à energia da luz visível; quando a energia do intervalo de banda excede a energia da luz visível, a luz visível não é absorvida e passa completamente, tornando o mineral incolor. Por exemplo, a energia de hiato do diamante Eg é de cerca de 5,5eV, tornando-o incolor.
A energia de bandgap dos materiais de bandgap estreito é inferior à da luz visível, fazendo com que toda a luz visível seja absorvida, resultando em cores cinzento-esverdeadas ou pretas escuras. Por exemplo, a energia de bandgap da galena é Eg inferior a 0,4eV, que parece ser cinzento-chumbo. Quando este "semicondutor de banda estreita" tem uma forma geométrica adequada, apresenta propriedades de retificação e amplificação.
A energia dos materiais com intervalo de banda médio está exatamente dentro da gama de luz visível e os minerais de gema apresentam várias cores. A sua sequência de cores é mostrada na Figura 3-29 (c), variando de vermelho-amarelo a verde-azul e roxo. Por exemplo, a energia de bandgap (Eg) do sulfureto de cádmio (CdS) é de aproximadamente 2,5eV, que absorve a luz azul e violeta, aparecendo amarelo. A energia de bandgap do cinábrio é de cerca de 2eV, permitindo apenas a passagem da luz vermelha, aparecendo assim vermelho. A energia de bandgap do orpiment é de cerca de 2,5eV, aparecendo amarelo.
Outra categoria de minerais de gema naturais explicada pela teoria das bandas é a cor dos materiais de grande intervalo de energia que contêm impurezas. Por exemplo, no caso de um diamante com impurezas, a energia de banda larga do diamante é de aproximadamente 5,5eV, e a luz visível não é absorvida ao passar pelo diamante; o diamante puro é incolor, mas a situação muda quando contém impurezas.
(1) O mecanismo de cor dos diamantes amarelos
Os átomos de azoto substituem as posições dos átomos de carbono. Uma vez que os átomos de azoto têm mais um eletrão do que os átomos de carbono, este eletrão extra forma um nível de energia de impureza no intervalo de energia, conhecido como nível de energia do dador, com os átomos de azoto a actuarem como "dadores".
A existência deste nível de impureza reduz a energia do intervalo de banda para 4eV[ [Figura 3-30 (a)]. Pode ser ainda mais baixa, permitindo-lhe absorver a luz ultravioleta e um pouco de luz violeta de 3eV, fazendo com que o diamante pareça amarelo.
Este efeito é forte; ter um átomo de azoto por cada cem mil átomos de carbono pode tornar o diamante amarelo profundo. No entanto, a redução do intervalo de banda é ainda insuficiente para tornar o diamante condutor à temperatura ambiente.
(2) Mecanismo da cor nos diamantes azuis
Como o boro tem menos um eletrão do que o carbono, forma um "nível aceitador" no intervalo de banda do diamante. Não tem electrões extra, mas pode aceitar electrões da banda de valência de um diamante, criando buracos na banda de valência [Figura 3-30 (b)] e formando uma banda de energia de impureza cerca de 0,4eV acima da banda de valência conhecida como nível aceitador.

O nível de energia do aceitador não é simples; é uma estrutura complexa de bandas de energia de impurezas que podem produzir o azul. O nível de energia do aceitador cria "buracos" na banda de valência, o que permite que este diamante azul "buraco" tipo II b conduza eletricidade.
Um átomo de boro entre cada milhão de átomos de carbono pode formar o azul. Devido ao maior teor de alumínio neste diamante azul e porque o alumínio tem menos um eletrão na camada exterior do que o carbono, pensava-se anteriormente que o alumínio desempenhava o papel de aceitador. No entanto, as experiências actuais provaram que é o boro e não o alumínio.
Os diamantes azuis condutores tipo II b são naturalmente azuis, e a sua condutividade é uma das diferenças em relação aos diamantes azuis irradiados (centros de cor). Esta propriedade é frequentemente utilizada para distinguir entre os dois tipos de diamantes. No entanto, os diamantes amarelos doadores de azoto não conduzem eletricidade, pelo que este método não pode ser utilizado para os diferenciar dos diamantes amarelos irradiados.
3. Minerais de pedra preciosa coloridos por transições de banda
A teoria das bandas de energia pode explicar parte da formação da cor das pedras preciosas naturais. Uma vez que a energia do intervalo de bandas é uma propriedade inerente ao cristal e não se altera devido a condições externas, a cor das pedras preciosas tem uma boa estabilidade. A condutividade do cristal pode ser determinada com base no facto de as bandas de energia do cristal estarem cheias de electrões. A Tabela 3-13 lista os tipos de cores das pedras preciosas que podem ser explicados pela teoria das bandas e as suas propriedades de condutividade.
Tabela 3-13 Tipos de cores de gemas explicadas pela teoria das bandas e sua condutividade
| Condutores (cores metálicas e brilho metálico) | Elemento | Cobre, ouro, ferro, prata, mercúrio, etc. |
| Liga metálica | Amálgama, ferro níquel meteorito | |
| Semicondutores | Intervalo de banda estreito | Cinzento opaco a preto: altaite, galena |
| Cor metálica opaca: cobaltina, marcassite, pirite, smaltite | ||
| Diferencial de banda moderado | Vermelho: cinábrio, proustita, pirargirite | |
| Laranja: Realgar | ||
| Amarelo: Sulfureto de cádmio, realgar, enxofre | ||
| Grande intervalo de banda | Incolor: diamante, esfalerite | |
| Semicondutores de banda larga contendo impurezas | Impureza doadora: Diamante dopado com azoto (amarelo) | |
| Impurezas no hospedeiro: diamante com boro (azul) |
A cor das pedras preciosas causada por transições de banda está relacionada com a estrutura e o tipo de ligação no momento da formação da pedra preciosa. Tem pouca relação com impurezas e defeitos cristalinos posteriores. O tamanho da energia do intervalo de banda das pedras preciosas é fixo. Não se altera com as propriedades do material da pedra preciosa, pelo que os métodos de otimização convencionais geralmente não podem melhorar a cor das pedras preciosas.
Secção IV Efeitos ópticos físicos
A maioria das pedras preciosas naturais pode causar a absorção selectiva da luz, e diferentes pedras preciosas absorvem a luz visível em diferentes comprimentos de onda, resultando em cores diferentes. Para além da absorção selectiva da luz, a estrutura interna dos cristais de pedras preciosas também pode causar efeitos ópticos físicos, levando a diferentes cores nas pedras preciosas.
1. Minerais de pedras preciosas relacionados com efeitos ópticos físicos
As cores produzidas por efeitos ópticos físicos são formadas devido à dispersão, interferência, difração e outras razões da luz causadas pela estrutura ou composição do cristal e pelas inclusões. Trata-se apenas de um efeito ótico que pode ser explicado pela teoria ótica física. Diferentes pedras preciosas podem produzir cores diferentes sob os mesmos efeitos ópticos. Para além dos oligoelementos comuns que causam a cor, as razões para as cores produzidas por efeitos ópticos físicos estão principalmente relacionadas com a estrutura interna e as propriedades físicas das pedras preciosas. Os tipos de minerais de pedras preciosas que causam cores devido a efeitos ópticos físicos estão listados na Tabela 3-14.
Tabela 3-14 Tipos de minerais de gema causados por efeitos ópticos físicos
| Função | Propriedades ópticas e cor | Minerais de gema |
|---|---|---|
| Dispersão Dispersão | Cintilante | "Fogo" em pedras preciosas de dispersão, como diamantes, zircão, rutilo e titanato de estrôncio |
| Azul | Pedra da lua, quartzo azul, opala | |
| Púrpura | Fluorite (dispersão de microcristais de cálcio) | |
| Vermelho | Vidro rubi, dispersão de microcristais de cobre ou ouro | |
| Branco | Quartzo leitoso | |
| Efeito olho de gato | água-marinha olho-de-gato, piroxénio olho-de-gato, etc. | |
| Efeito de luz das estrelas | Vários efeitos estelares do corindo e da granada | |
| Brilho | Brilho das pérolas, da apofilite, etc. | |
| Cintilação | Brilho de aventurina, obsidiana, etc. | |
| Difração por interferência | As cores espectrais puras da película fina | O arco-íris da calcopirite, a película descolorida numa fissura de quartzo irisado |
| Efeitos de interferência | Mudança de cor da opala, o efeito da labradorite | |
| Inclusão | Azul | Dumortierite em quartzo |
| Verde | Calcedónia verde e veios de níquel em calcedónia verde, fucsite em quartzo-estrela | |
| Laranja | Óxido de ferro hidratado na opala de fogo e na calcedónia cor de carne | |
| Vermelho | Flocos de hematite em ortoclase |
2. Efeitos de interferência e difração
(1) Efeitos de interferência
Os fenómenos de interferência ocorrem quando dois feixes de luz se propagam ao longo do mesmo caminho ótico ou em direcções paralelas. Um fenómeno de interferência comum nas pedras preciosas é a iridescência. Por exemplo, no quartzo iridescente, as cores de interferência dependem da espessura da película, do índice de refração da película e da natureza da luz incidente.
As cores de interferência das pérolas são formadas pela sobreposição alternada de camadas concêntricas de duas substâncias com índices de refração diferentes (aragonite e nacrum), em que a luz incidente é reflectida a partir das superfícies entre as camadas alternadas, e a luz reflectida interfere com a luz incidente para produzir belas cores de interferência.
(2) Efeitos de difração
A difração refere-se ao fenómeno físico em que as ondas de luz se desviam da sua propagação original em linha reta ao encontrarem obstáculos. Em física, as ondas de luz sofrem diferentes graus de curvatura e dispersão quando passam por obstáculos como fendas, pequenos orifícios ou discos. Se for colocado um obstáculo entre a fonte de luz e o ecrã de observação, aparecerão regiões claras e escuras no ecrã de observação e os limites destas regiões não são nítidos, formando um padrão complexo de claro e escuro. Este fenómeno é designado por difração. Estes fenómenos podem ocorrer sempre que as ondas de luz encontram obstáculos ao longo do seu percurso de propagação. O fator mais importante na produção de difração é a presença de grelhas de difração periodicamente espaçadas nos minerais de pedras preciosas.
① Mudança de cor da opala
Na opala, as esferas de sílica que contêm água têm diâmetros iguais e estão dispostas numa estrutura regular de camadas alternadas, formando grelhas de difração periodicamente espaçadas. Quando a luz entra na opala, ocorre difração, mudando de cor (Figuras 3-31, 3-32). Os tipos de cores e o grau de mudança de cor dependem principalmente do espaçamento interplanar das esferas de sílica empilhadas.
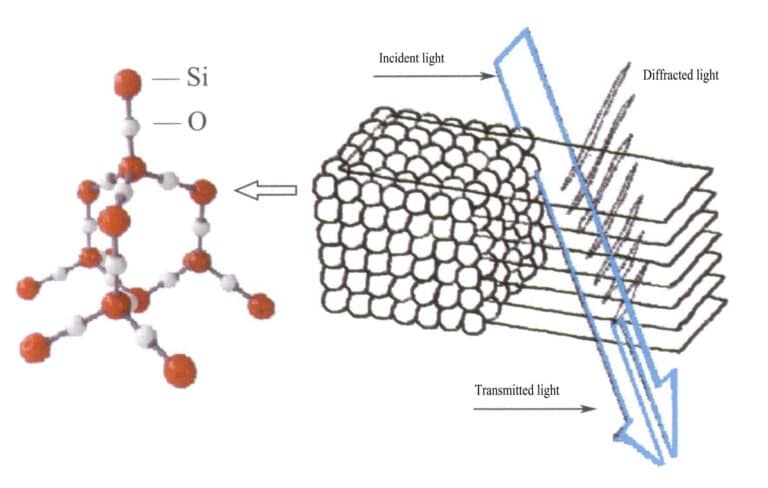

Por exemplo, a opala com uma estrutura de placa plana cúbica de face centrada e um espaçamento de rede de 3×10-10m apresenta cores que vão do verde ao vermelho; este tipo de opala com um espaçamento de rede de 2,5×10-10m apresenta cores que vão do azul ao amarelo.
② Efeito Labradorite
A labradorita também exibe efeitos semelhantes aos da opala (Figura 3-33). A labradorita também é conhecida como espectrólito porque pode brilhar com a luz colorida do sol. Vários tipos de labradorite da Finlândia podem exibir uma gama de cores espectrais, um fenómeno conhecido como "efeito labradorite". O efeito de mudança de cor na labradorite é devido a pequenas camadas de plagioclase fundidas com diferentes composições. As ligeiras diferenças no índice de refração entre os diferentes feldspatos causam interferência e difração da luz, resultando em luminescência e mudança de cor. As cores produzidas por esta estrutura estão relacionadas com a espessura relativa das camadas e os seus índices de refração. Ocasionalmente, a andradite do México também apresenta fenómenos de difração.

3. Dispersão e Inclusões
(1) Dispersão
A dispersão ocorre geralmente quando a estrutura interna dos materiais de gema é irregular ou quando o tamanho dos componentes excede os limites das condições de difração. Os efeitos de cor produzidos pela dispersão estão relacionados com o tamanho e a forma das partículas do material da gema. Quando a luz incidente interage com partículas irregularmente dispostas, mais pequenas do que o comprimento de onda da luz visível, as ondas de luz de alta energia transmitidas são mais fortes do que as ondas de luz de baixa energia, o que significa que, na maioria dos casos, apenas se vêem o roxo e o azul. Por exemplo, o SiO2 As pequenas esferas na opala têm diâmetros mais pequenos do que o comprimento de onda da luz visível e, quando o tamanho das partículas dispersoras é próximo do comprimento de onda da luz visível, também podem ocorrer cores dispersas.
Por exemplo, a fluorite púrpura é causada por irradiação radioactiva que expulsa átomos de flúor, resultando em átomos de cálcio que se ligam a átomos de flúor condensando-se em placas hexagonais de tamanho comparável ao comprimento de onda da luz visível. A interação entre as placas de cálcio e as ondas de luz produz dispersão. Absorve algumas ondas de luz, criando um forte pico de absorção na região da luz verde a vermelha, permitindo a passagem da luz púrpura e produzindo a cor púrpura.
Uma vez que partículas do mesmo tamanho de elementos metálicos podem produzir efeitos de cor semelhantes, e partículas metálicas diferentes podem produzir cores diferentes, algumas imitações de pedras preciosas são fabricadas utilizando esta propriedade.
Por exemplo, o vidro "rubi" é produzido pela adição de partículas de cobre ou ouro ao vidro, resultando numa cor vermelha semelhante à dos rubis. Quando o material da gema contém inclusões, microfissuras ou bolhas maiores do que o comprimento de onda da luz visível, as ondas de luz interagem com estas partículas dispersoras, fazendo com que as ondas de luz dispersas se recombinem, produzindo uma luz leitosa translúcida. Por exemplo, certas imitações de pedra da lua.
O efeito de luar da pedra da lua também é produzido pela dispersão da luz (Figura 3-34). A pedra da lua é um feldspato alcalino, um composto formado por camadas paralelas alternadas de feldspato rico em potássio e rico em sódio. A espessura da camada intermédia varia tipicamente entre 50 e 1000 nm, com camadas mais finas capazes de produzir dispersão. A mesma cor de dispersão pode também ocorrer na plagioclase, conhecida como "efeito labradorite".
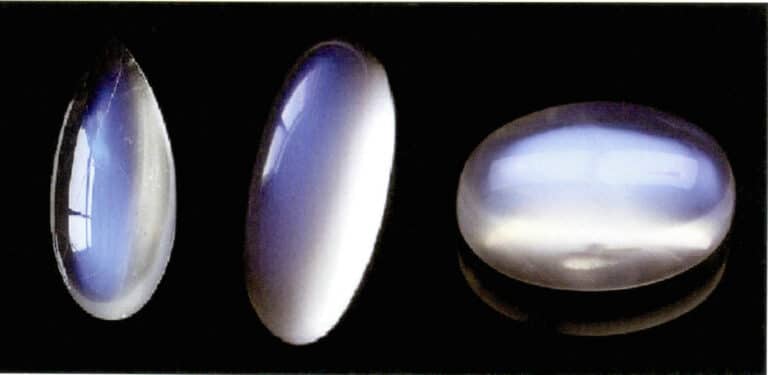
Uma disposição especialmente orientada das partículas dispersoras pode produzir efeitos ópticos caraterísticos. Por exemplo, quando as partículas de dispersão estão em forma fibrosa paralela, produzem um efeito de olho de gato ou de estrela, como as safiras estrela e os olhos de gato de quartzo. Quando as partículas de dispersão são suficientemente grandes para serem distinguidas a olho nu, podem produzir um "efeito goldstone", como a pedra-sol (Figura 3-35) e o vidro goldstone.

(2) Inclusões
A cor e os fenómenos ópticos produzidos pelas inclusões são um tipo especial de dispersão. As inclusões com cor incorporadas em cristais principais quase incolores apresentarão a cor das inclusões, tais como a calcedónia com bandas de níquel e o óxido de ferro (II) contendo água (FeO - H2O) calcedónia cor de carne; a cor da ortoclase de Madagáscar e de alguma cordierite é formada por inclusões ligeiramente maiores, mas ainda assim microscópicas, de hematite que criam tonalidades vermelhas; inclusões submicroscópicas de hidróxido férrico colorem frequentemente a opala de fogo.
Os diamantes apresentam frequentemente cores diferentes devido à presença de numerosas inclusões. Os diamantes coloridos por inclusões podem ser pretos, vermelho-alaranjados e vermelho-marrons. Quando um diamante contém inúmeras inclusões minerais escuras e opacas, ele aparece preto; quando examinado com luz forte transmitida, muitas inclusões escuras podem ser observadas, e o diamante aparece cinza escuro; outro tipo são as inclusões secundárias que ocorrem nas fissuras do diamante. Quando as fendas se desenvolvem e são preenchidas com estas inclusões coloridas, o diamante aparece castanho-avermelhado ou laranja-avermelhado, o que também é conhecido como um diamante "oxidado".
4. Dispersão
O fenómeno de decomposição da luz branca em várias cores espectrais através de um objeto chama-se dispersão. A dispersão das pedras preciosas refere-se à propriedade da luz se dispersar em diferentes comprimentos de onda de cores espectrais ao passar pelos planos inclinados das pedras preciosas transparentes. Devido aos diferentes comprimentos de onda da luz monocromática que constituem a luz branca e que se propagam a diferentes velocidades e índices de refração em diferentes materiais, a luz branca pode ser decomposta em várias cores espectrais em determinadas condições. O tamanho do valor de dispersão de uma pedra preciosa é determinado pelas suas propriedades físicas; cada pedra preciosa tem o seu valor de dispersão inerente, que não se altera com as propriedades da pedra preciosa. O encanto único dos diamantes está intimamente relacionado com o seu elevado valor de dispersão (0,044).
A maioria dos simuladores de diamante tem um valor de dispersão mais alto, como o valor de dispersão do zircão de 0,039 e o valor de dispersão da moissanita sintética de 0,104. A comparação dos valores de dispersão dos diamantes e suas pedras preciosas simuladoras comuns é mostrada na Tabela 3-15.
Quadro 3-15 Comparação dos valores de dispersão dos diamantes e das suas pedras preciosas simuladoras comuns
| Nome da pedra preciosa | Valor de dispersão |
|---|---|
| Diamante | 0.044 |
| Zircão | 0.039 |
| Corindo | 0.018 |
| Espinélio | 0.020 |
| Topázio | 0.014 |
| Berilo | 0.014 |
| Cristal | 0.014 |
| Rútilo sintético | 0.280 |
| Titanato de estrôncio sintético | 0.190 |
| Moissanite sintética | 0.104 |
A dispersão é normalmente referida como o "fogo" das pedras preciosas. Por exemplo, os diamantes têm um elevado valor de dispersão e o seu fogo é muito pronunciado, reforçando o já real estatuto dos diamantes e mostrando o seu encanto único.
Existem muitos tipos de cores produzidas por efeitos ópticos físicos, todos eles explicáveis pela teoria ótica física. Exceptuando a dispersão, que é uma propriedade inerente à própria pedra preciosa, outros fenómenos são causados por alterações estruturais após a formação da pedra preciosa e as diferenças nas inclusões mecânicas. A compreensão das várias causas das cores das pedras preciosas fornece uma base teórica para otimizar o tratamento das pedras preciosas naturais e sintéticas.