宝石結晶学のすべてを知るための1回
結晶学の形態、種類、分類、違いについての総合ガイドブック
地球は無数の分子と原子で構成されている。現代の科学的研究により、自然界に存在する固体物質はさまざまな化学元素から構成されていることが判明した。X線分析の結果、ある種の固体物質の元素に含まれる原子は、整然と規則正しく並んでいることがわかった。このような物質は結晶または結晶と呼ばれ、原子格子が整然と並んでいる状態を結晶構造と呼ぶ(図2-1-1)。
自然界や研究所で成長する宝石材料のほとんどは結晶である。この章では、結晶の概念、分類、結晶と宝石学の基本用語の関係について説明します。

目次
第1節 結晶の概念と説明
宝石というと、その輝きや半透明の特徴を思い浮かべることが多い(図2-1-2)。地質学者や宝石学者から見ると、最も愛されている宝石は、幾何学的な固体である結晶に属する。結晶の美しさの本質は、実は幾何学的な美しさにある。

1.結晶の概念
結晶は、最も容易に連想でき、自然界で最も一般的に見出される。結晶は地球上の7大陸すべてに存在し、自然界に存在する場合、幾何学的な多面体の形をとることが多い(図2-1-3)。一般に結晶と呼ばれる。その後、この用語は、ダイヤモンドやアクアマリンの結晶のように、幾何学的な多面体形状を持つ自然界に存在する固体物質を指すようになった(図2-1-4)。結晶はまた、表面が不規則、不揃い、磨耗、破損、人工的な加工が施されているが、原子配列が規則的なパターンを保っている固体物質を指すこともある。結晶学者たちは、すべての結晶は6つの基本的な性質、すなわち、自己限定性、均一性、異方性、対称性、安定性、固定融点を備えていると考えている。
自己限定性とは、化学元素が幾何学的な多面体形状を自発的に形成する性質を指す。この性質は、元素によって結晶の幾何学的形状が異なる理由を説明することができる。
結晶の物理的・化学的性質がすべて同じであること。この性質は、異なる鉱物の結晶を見分け、識別するのに役立ちます。
異方性とは、元素の配列が異なる方向に変化する性質のことで、方向によって物性にわずかな違いが生じる。ダイヤモンドの硬度が最も高く、切断や研磨が可能なのは、この性質のためである。
対称性とは、結晶中の同じ部分や性質が規則正しく繰り返される性質を指す。この性質は結晶にとって極めて重要かつ特殊であり、本章の第2節で詳しく説明する。
安定性とは、結晶の内部エネルギーが最小であることによる結晶の安定性のこと。結晶の内部エネルギーが高くて不均一だと、それだけで割れやすくなる。フラムフュージョン法で合成されたルビー結晶が、常に完全ではなく半分に見えるのは、この性質によるものである。
固定融点とは、結晶の融点が一定であるという性質を指す。

図2-1-3 ガーネット(左側が結晶、右側が研磨されたガーネット)

図2-1-4 アクアマリン・クリスタル
2.結晶の理想形
結晶学で取り上げられる結晶は、主に理想単結晶である。理想単結晶とは、内部構造が空間格子の規則に厳密に従うもので、その形状が規則的な幾何学的組合せ形であるものと定義される。理想単結晶の形は単純形と組合せ形に分けられる。
(1) シンプルなフォーム
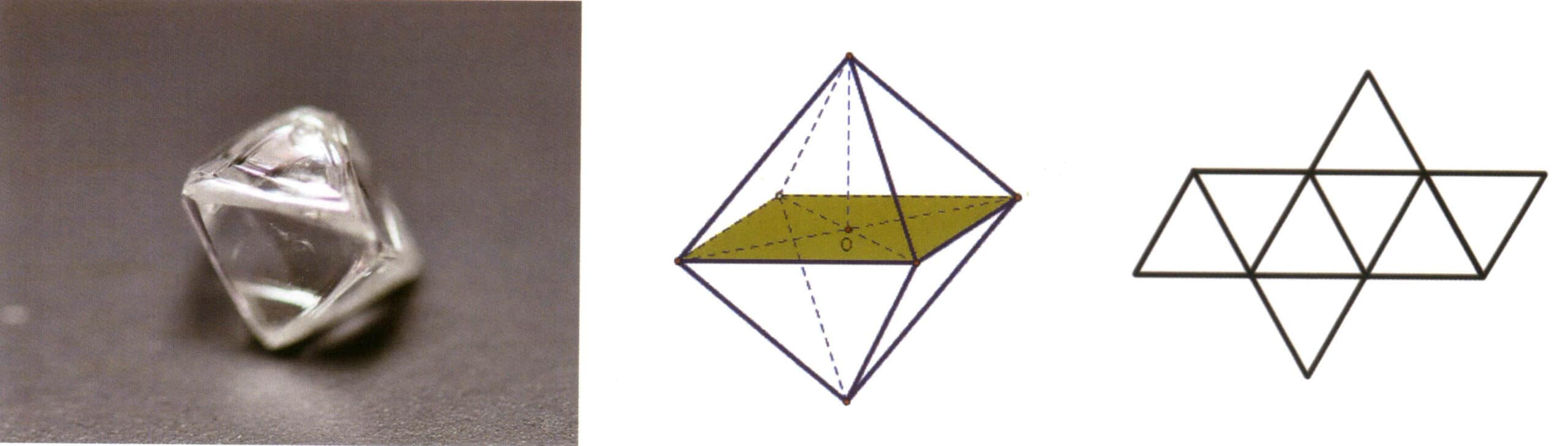
単純形とは、対称要素で結ばれた結晶面群の組み合わせのことで、理想的な状態では同じ形と大きさの結晶面からなる幾何学体と理解できる(図2-1-5)。結晶には47種類の単純形がある。
シンプル・フォームを識別するための重要なポイントは、結晶中のすべての結晶面が同じ形と大きさであること、そして結晶面の向きが異なることがあることです。
(2) コンビネーション フォーム
単純形の集合体は組合せ形と呼ばれ、2つ以上の異なる単純形からなる。すべての単純形が自由に組合せ形にできるわけではなく、同じ点群を持つ単純形だけが集合できる(図2-1-6~2-1-8)。
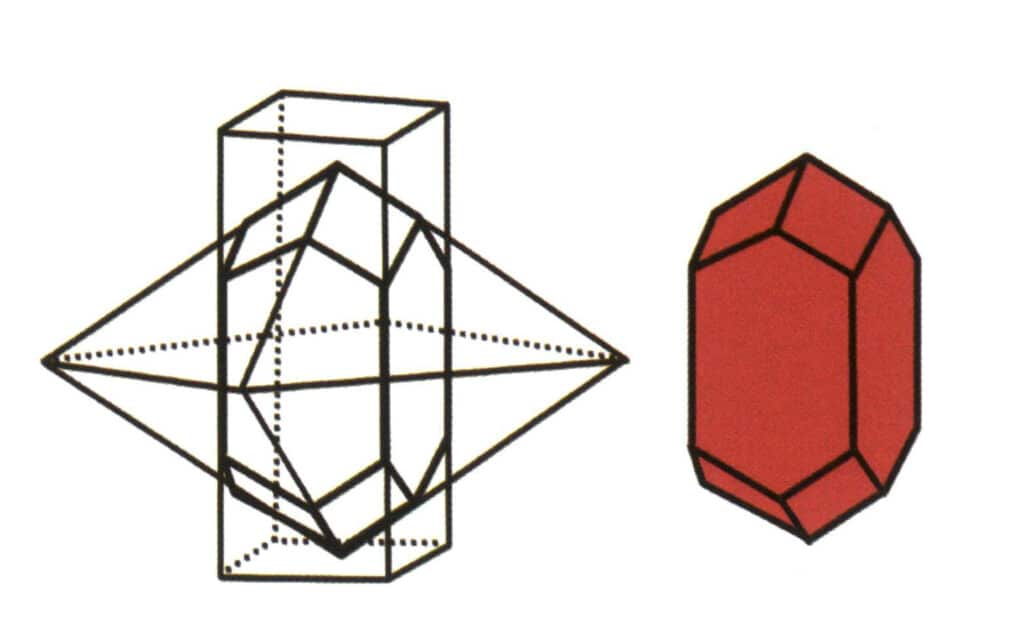
図2-1-6 正四角柱と正四角錐の組み合わせ
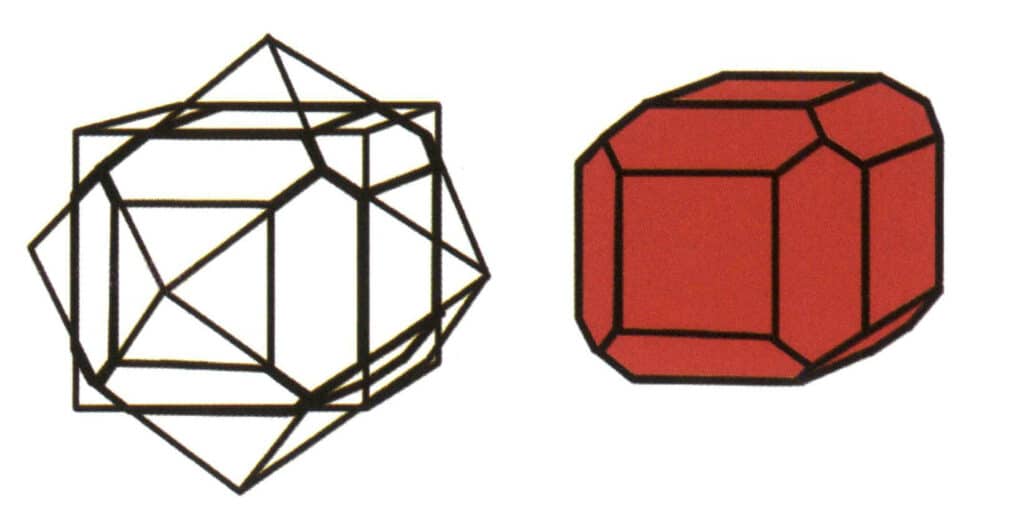
図2-1-7 立方体と菱形12面体の組み合わせ
コンビネート形状の識別の重要なポイントは、結晶中に2つ以上の異なる形状の結晶面が存在することである。
自然界で単結晶が発見される場合、単結晶の理想的な形態(図2-1-9)とは必ず大きな違いがあり、例えば、単結晶の面が必ずしも同じ形や大きさでなかったり、結晶面が消失していたりすることを歪んだ結晶と表現する。

歪んだ結晶は、成長環境の影響を受けて自然界で生成される本物の結晶とも言える。理想的な結晶において、一定の角度で繰り返される複数の結晶面は、必ずしも同じ形や大きさであるとは限らない。それでも、同じ種類の結晶であれば、同じ単相の結晶面は同じパターンと物理的性質を持たなければならない。対応する結晶面間の角度は変化せず、結晶自体の固有の対称性を反映している。現実に見られる結晶は、程度の差こそあれ歪んでいる。
双晶は、成長環境の影響を受けて自然界で実際に生成される結晶とも言える。理想的な結晶において一定の角度で繰り返される複数の結晶面は、必ずしも同じ形や大きさであるとは限らない。それでも、同じ種類の結晶であれば、同じ形の面は同じパターンと物理的性質を持たなければならない。対応する結晶面間の角度は変化せず、結晶自体の固有の対称性を反映している。現実に見られる結晶は、程度の差こそあれ、すべて双晶である。
3.結晶の結晶化習性
自然界で形成される結晶は、決して完璧な形にはならない。岩に囲まれた岩層の隙間で成長すれば、結晶の自然な形は歪んでしまう。実験室で培養された結晶でさえ、重力の影響で変形する。科学者たちが求める完璧な形の結晶を育成できるのは、国際宇宙ステーションの無重力環境下だけなのだ。
結晶の形は不完全だが、鉱物の結晶の種類はそれぞれ、異なる成長や集まり方、癖をする傾向がある。
各鉱物は特定の条件下で形成される傾向があり、その習性は形成条件を反映している。石英のように、形成条件が複雑で変化しやすい鉱物もある。そのため、石英にも複数の癖がある。
一般に、結晶癖とは、ある結晶が特定の外部条件下で特定の形状を形成する傾向を持つ特性を指す。時には、その結晶の単純な形の一般的なタイプを指すこともある。
三次元空間における結晶の発達の度合いに基づいて、結晶癖は3つの基本タイプに分けられる。
(1)ユニ-方向性エクステンション
結晶は一方向に延び、柱状、針状、繊維状などに現れる。ベリル、トルマリン、角閃石、マラカイトなどの鉱物はこのような習性を示すことが多い(図2-1-10~図2-1-11)。

図2-1-10 柱状アクアマリン(上)とその結晶癖図(下)

図2-1-11 繊維状マラカイト(上)とその結晶癖図(下)
(2) Bi-方向性エクステンション
結晶は平面に延び、板状、シート状、鱗片状などに現れるが、これは鉄マンガン、雲母、プランバゴ、タンザナイトなどの鉱物がよく示す習性である(図2-1-12)。
(3) トライ-方向アイソメトリック
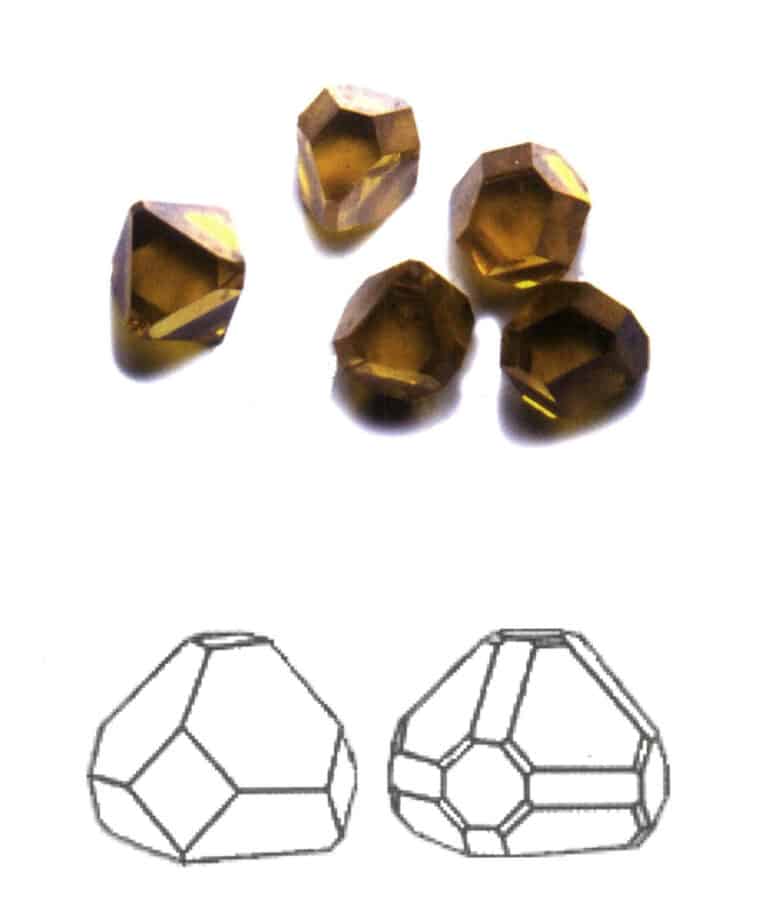
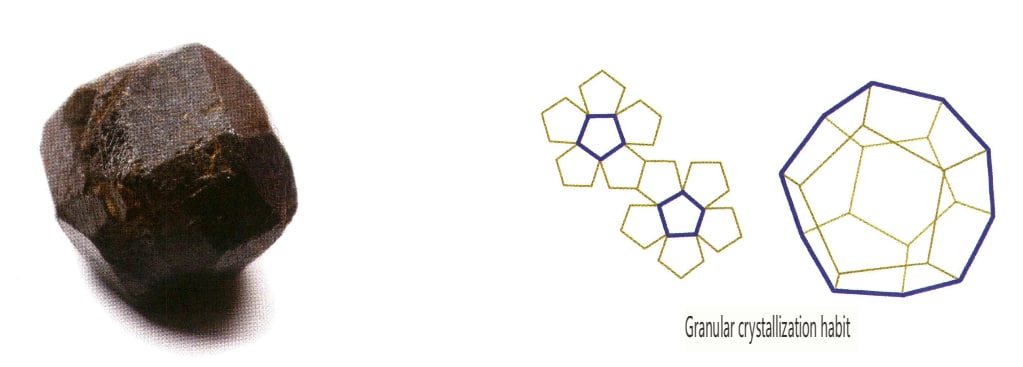
スピネル、ガーネット、ダイヤモンド、黄鉄鉱、蛍石など、結晶は3方向に均一に発達し、等尺性の粒状を呈するが、しばしばこのような習性を示す(図2-1-13、2-1-14)。

図2-1-12 タンザナイトの板状晶癖(上)と晶癖図(下)

図2-1-13 宝石スピネルの八面体晶癖(上)とその晶癖図(下)
さらに、短柱状、板状柱状、帯状、厚板状などの過渡的なタイプもある。
結晶の化学組成と構造は主に結晶癖を決定する。また、ダイヤモンドと人工ダイヤモンド結晶の結晶形状の違いなど、結晶形成時の外部条件(温度、圧力、濃度、粘度、不純物など)とも密接な関係があります。
4.結晶の規則的な凝集
自然界には、単結晶(図2-1-15)や、2つ以上の単結晶が一緒に成長して全体を形成しているものがあります。このように複数の結晶が集まって成長する現象を結晶凝集といいます。結晶の集合体には、不規則型と規則型があります。不規則型結晶集合体は集合体として理解できますが、これについては第3章で詳しく説明します。規則的な結晶凝集では、平行凝集、双結晶、過成長、相互成長の4種類が一般的です(図2-1-16~図2-1-18)。本節では、主に二結晶と呼ばれるタイプの規則的凝集について述べる。

図2-1-15 単結晶(トルマリン)
図2-1-16 平行凝集(同じ種類の結晶が空間的に平行に複数成長することを平行凝集という。この時、成長した結晶の対応する結晶面と結晶端は全て平行になります)。

図2-1-17 双晶(スピネル)

図2-1-18 過成長(ある種の結晶が他の結晶の表面で特定の結晶学的方向に成長すること、エピタキシャル成長とも呼ばれる)
双結晶とは、2つ以上の同じ結晶が一定の対称規則に従って規則正しく集合したもの。(双軸、双面)隣接する2つの個体の対応する面、辺、角は完全に平行ではない。それでも、回転や回転反転などの対称操作によって互いを反映させることができ、2つの個体を一致させたり整列させたりすることができる。
4.1 双結晶を識別するためのポイント
双晶に見られる凹角(図2-1-19)。
スタイロライト:スタイロライトの両面の結晶面のミクロ形態などが不連続である(図2-1-20)。
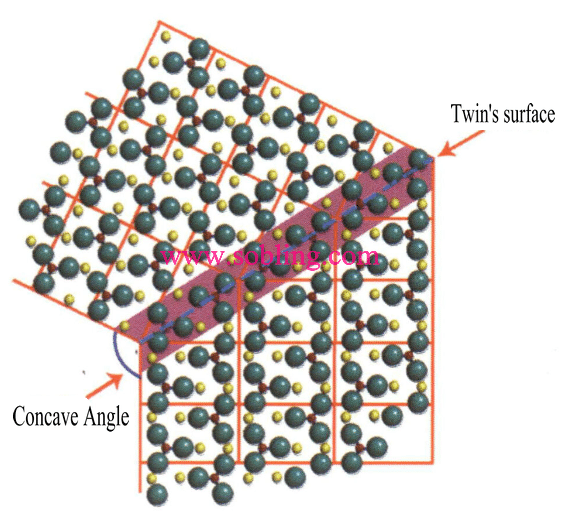
図2 - 1-19 ツインの凹角
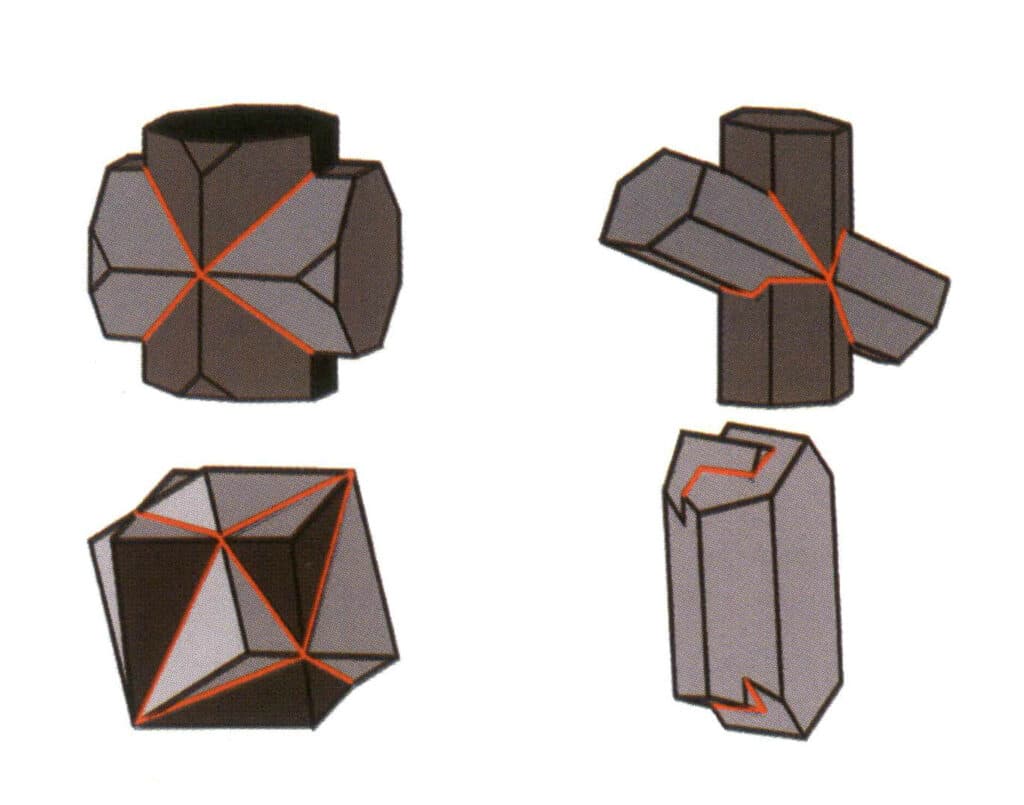
図2-1-20 スタイロライト(図中の異なる色は異なる結晶を表し、赤い線は双晶のスタイロライトを示す)
双晶条線:結晶面や劈開面に微細な双晶筋が見られる(図2-1-21)
エッチ図形:エッチ図形: エッチ図形の出現は双晶の存在を示す(図 2-1-22)

図2-1-21 多合成双生児の模式図

図2-1-22 逆三角形のピットを持つスピネルの表面。
擬似対称性の出現:結晶単結晶が本来持っている点群とは矛盾する対称関係が出現すること(図 2-1-23~ 図 2-1-24) ⑤擬似対称性の出現:結晶単結晶が本来持っている点群とは矛盾する対称関係が出現すること。

図2-1-23 クリソベリルの単結晶

図2-1-24 クリソベリルの膝状双晶
双晶は、その積層特性から、接触双晶(図2-1-25~図2-1-26)、多合成双晶(図2-1-27)、相互貫入双晶(図2-1-28)、三重項結晶(図2-1-29)、複合双晶の5種類に分けられ、このうち最初の4種類が一般的である。


図2-1-26 スピネルの接触双晶(上)とその模式図(下)

図2-1-27 ラブラドライトの多合成双晶(上)とその模式図(下)
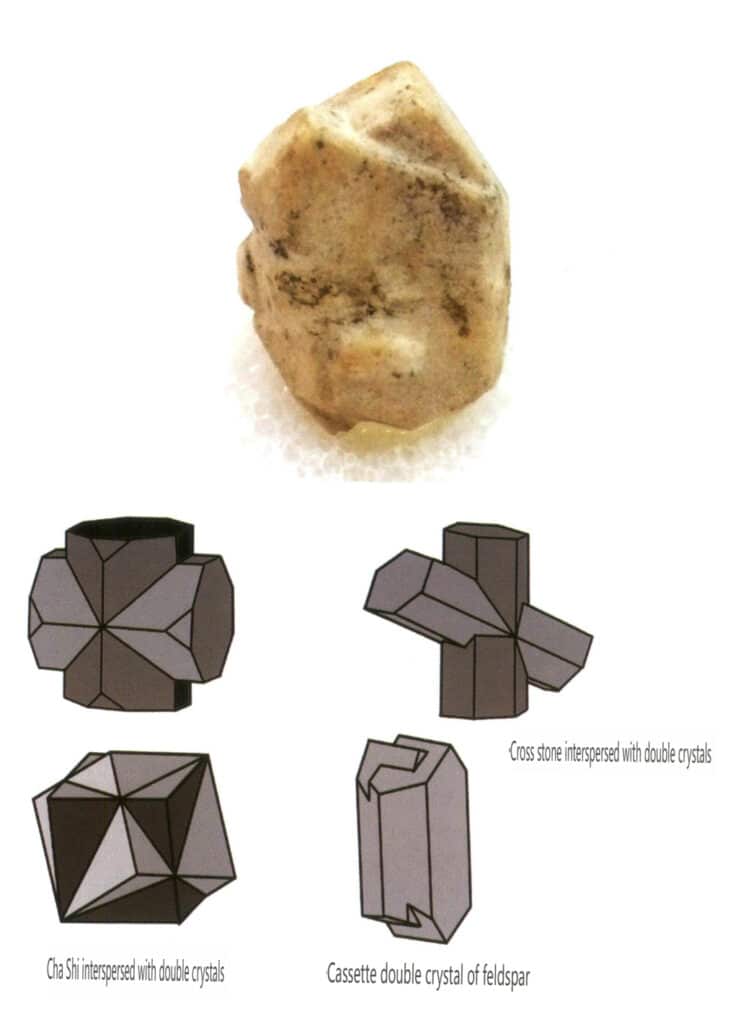
図2-1-28 長石双晶(上)と他種双晶の相互貫入模式図(下)

図2-1-29 クリソベリルの三元双晶(上)とその模式図(下)
4.2 双結晶の形成
結晶成長中に形成されるもので、双晶の原石から発達する場合と、双晶の位置に依存して成長する小さな結晶から発達する場合がある。
α石英がβ石英に変化して双晶を形成するなど、異形変態の過程で形成される。
機械的作用によって形成されるもので、結晶の一部が一定方向の平面に沿って滑り、方解石の双晶のような変形双晶を形成する。
5.クリスタル・フェイス・パターン
自然界で発見される結晶は、不完全な形(図2-1-30)や特殊な表面模様を持つことが多い。時には、結晶が集まって成長し(図2-1-31)、立方体や六角柱のような、私たちがよく知っている標準的な幾何学的多面体とは大きな違いを示すことが多い。このような現象を結晶の実形と呼ぶ。結晶の実形には、歪結晶、凸結晶、曲結晶、浮遊結晶、結晶面縞、エッチ図形、双晶縞など、結晶学上詳細な分類がある。

図 2-1-30 ルビー・クリスタル

図2-1-31 黄鉄鉱の結晶(左は複数の黄鉄鉱の結晶が一緒に成長したもの、右は単一の黄鉄鉱の結晶)
このセクションでは、主に実際の結晶における結晶面パターンについて説明します。
理論的には、結晶面は滑らかで平らである。しかし、実際に結晶が成長したり溶解したりする際には、表面には一般に結晶面パターンと呼ばれる、わずかに凹凸のある規則的な模様が残ることが多い。結晶面パターンには、成長条線、成長層、スパイラルパターン、成長ヒロック、エッチング図形などがある。本書で取り上げる結晶面パターンは、主に肉眼や低倍率の条件下で観察できる結晶面の縞模様やエッチ図形を指す。
結晶面縞とは、異なる単結晶が収束と成長を交互に繰り返すことにより、結晶表面に平行な直線が連続することを指す。コンビネート縞」とも呼ばれ、結晶表面にのみ見られるもので、成長縞とも呼ばれる。例えば、水晶の六角柱の結晶面には、六角柱と菱形十二面体の微細な結晶面が交互に発達して集合横縞となることが多い(図2-1-32)。

エッチ図形とは、結晶が形成された後、腐食によって結晶面に残る特異な形状のピット(エッチピット)を指す。エッチ図形は、結晶面内の元素粒子の配置によって制御される。従って、エッチ形状の形状や方向は、異なる鉱物や同じ結晶の単一形態によって異なる。例えば、ダイヤモンド単結晶の場合、八面体結晶では三角形のピット(図2-1-33)、立方体結晶面では四角形のピット、四角形のピットが重なった格子状のパターン、菱形十二面体では線状のパターンや微小な円盤状のパターンが見られます(図2-1-34)。

図2-1-33 ダイヤモンド八面体結晶上の可視逆三角形ピット

図2-1-34 菱形12面体結晶に見られる線状の模様
同じ結晶形の同じ結晶面のエッチ図形だけが同じになることがあるので、エッチ図形は鉱物の同定や結晶面が同じ単一形に属するかどうかの判断によく使われる(図2-1-35~図2-1-42)。

図2-1-35 蛍石水晶象嵌フローリング風ストライプ

図2-1-36 ルビーのナチュラル・トライアングル・エッチ図形(ルビーによく見られる横縞、菱面体方向に平行な成長線、三角形や六角形のナチュラル・エッチ図形)

図2-1-37 トルマリンの表面縦縞

図2-1-38 結晶表面の横縞

図 2-1-39 結晶表面のエッチング図形

図2-1-40 トパーズの表面縦縞

図2-1-41 トパーズ結晶のトポグラフ画像

図 2-1-42 スピネルのエッチング図
第II部 47 クリスタルフォームの種類
結晶学には146の異なる単一形があり、それらは独立して存在するときの幾何学的形状に基づいて47の幾何学的形に分類することができる。これらの幾何学的形態には次のような名前が付けられている:
三角柱、正方晶、六角柱、菱面体二角錐など、断面形状の特徴によって名付けられる。
円柱、二重円錐、立方体など、単体の形状によって命名。
単面体、八面体など、幾何学的な面の数によって命名される。
菱形面体、五面体など、幾何学的な面の形によって命名される。
結晶学において単一形は、一般形と特殊形、閉鎖形と開放形、規則形と不規則形、左利き形と右利き形の4つのカテゴリーに分けられる。この章では、閉形と開形について簡単に説明する。
閉形とは、結晶面が閉じた空間を取り囲むことができるものをいい、多面体型、斜多面体型、両錐体型の3つに大別され、全部で30種類ある。各分類はさらに細かく分類され、例えば多面体型は四面体型、八面体型、立方体型などに細分される(図2-1-43~2-1-48)。

図 2-1-43 四面体クラス
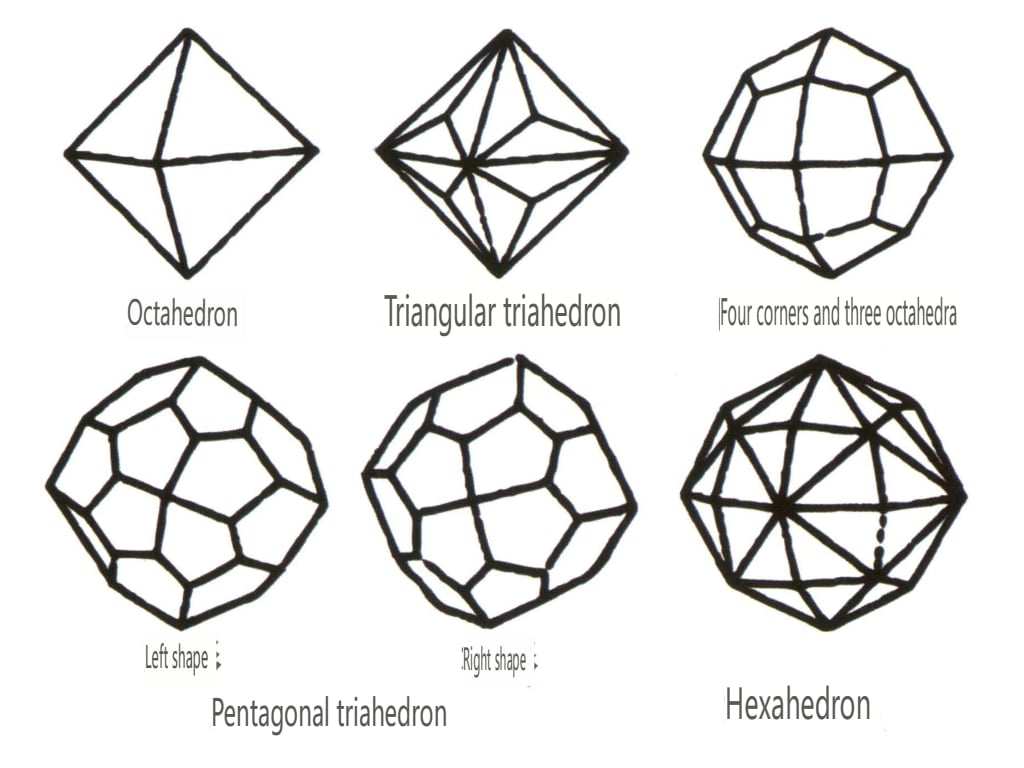
図2-1-44 正八面体クラス
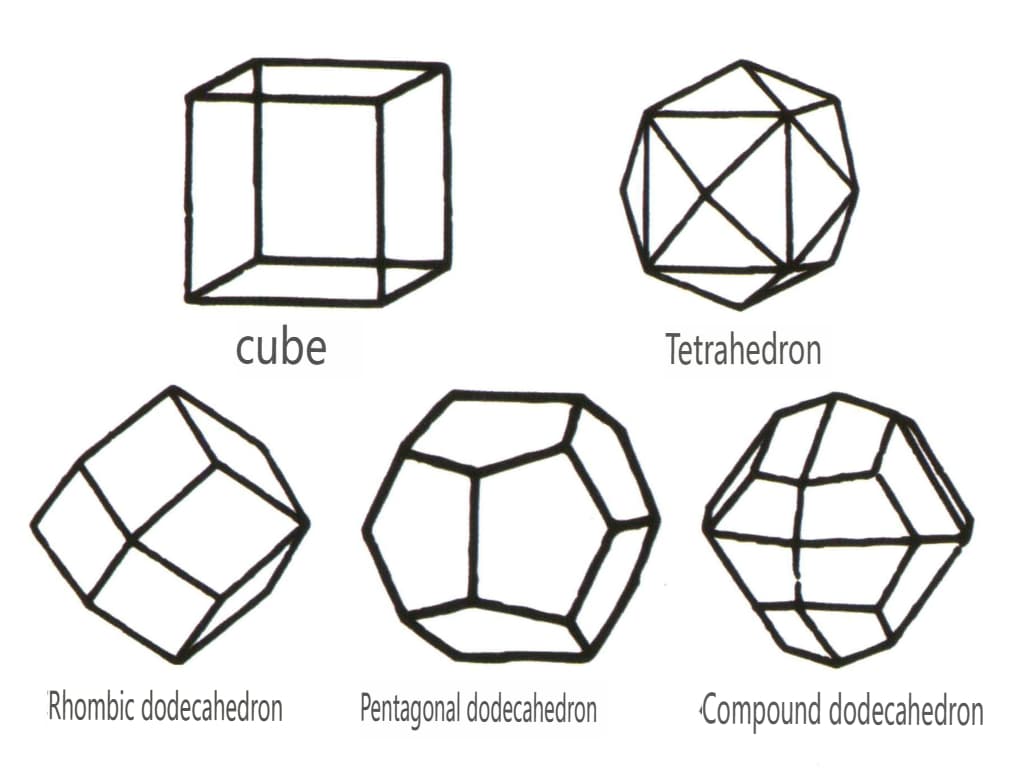
図 2-1-45 立方体クラスと正十二面体クラス
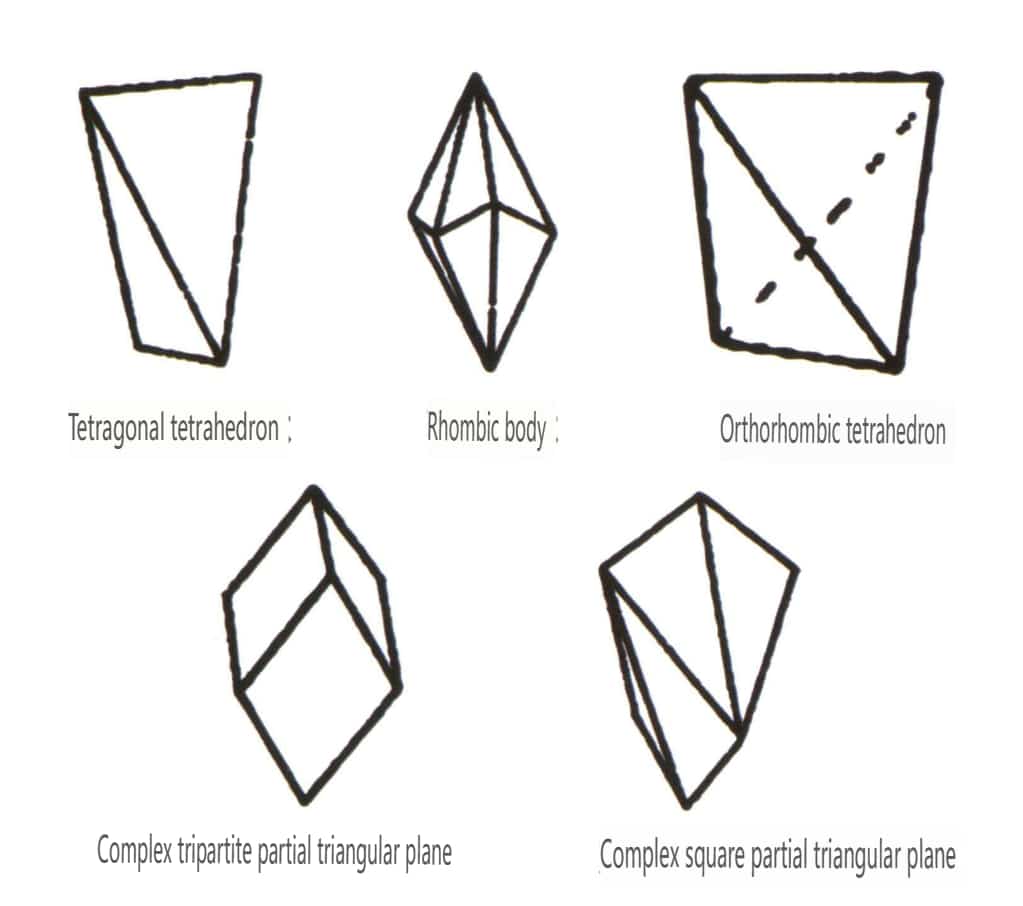
図 2-1-46 その他の多面体タイプ
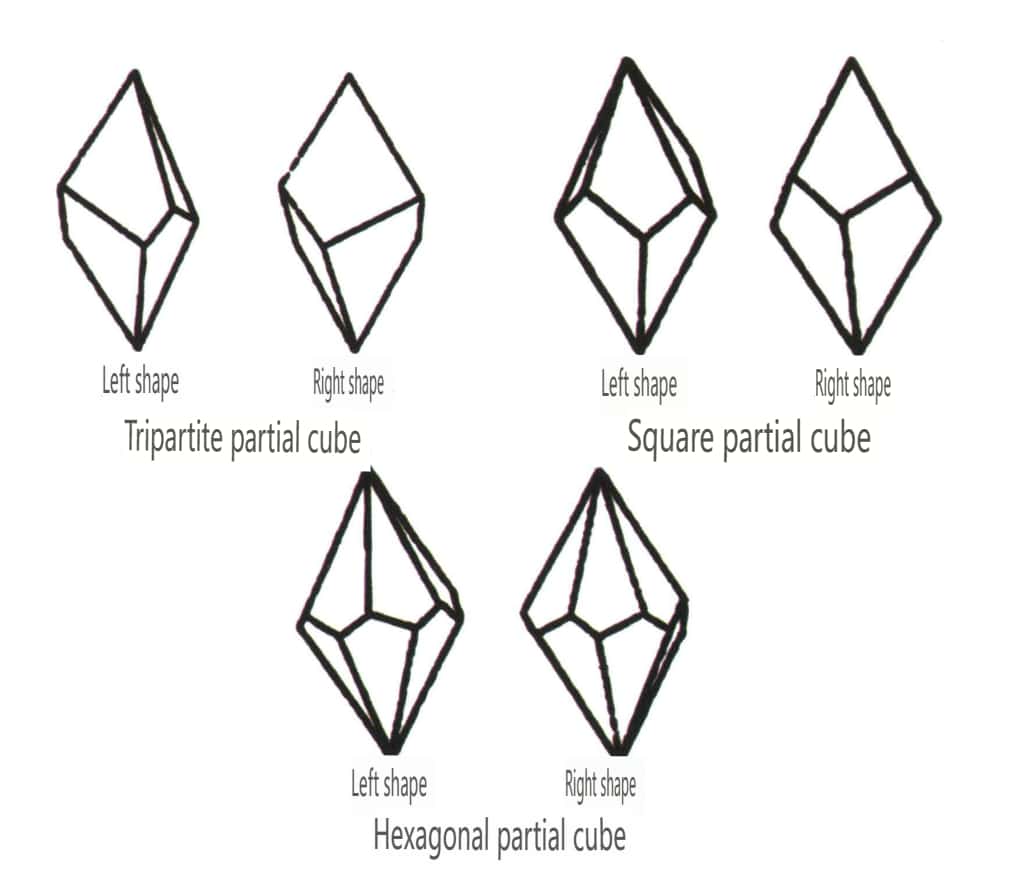
図 2-1-47 斜めの組合せ形 クラス
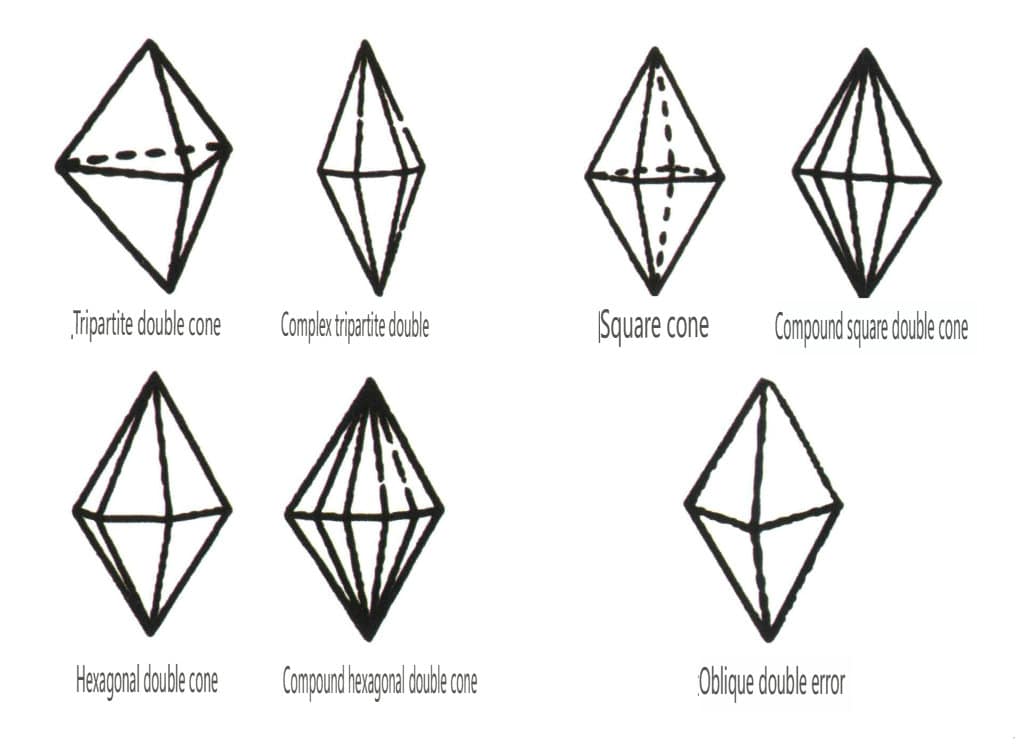
図 2-1-48 二重ピラミッド型クラス
オープン・フォームとは、結晶面が閉じた空間を囲むことができないものを指し、シングル・フェイス、ダブル・フェイス、柱状クラス、シングル・ピラミッド・クラスの4つに大別され、合計17種類に分類される(図2-1-49、図2-1-51)。
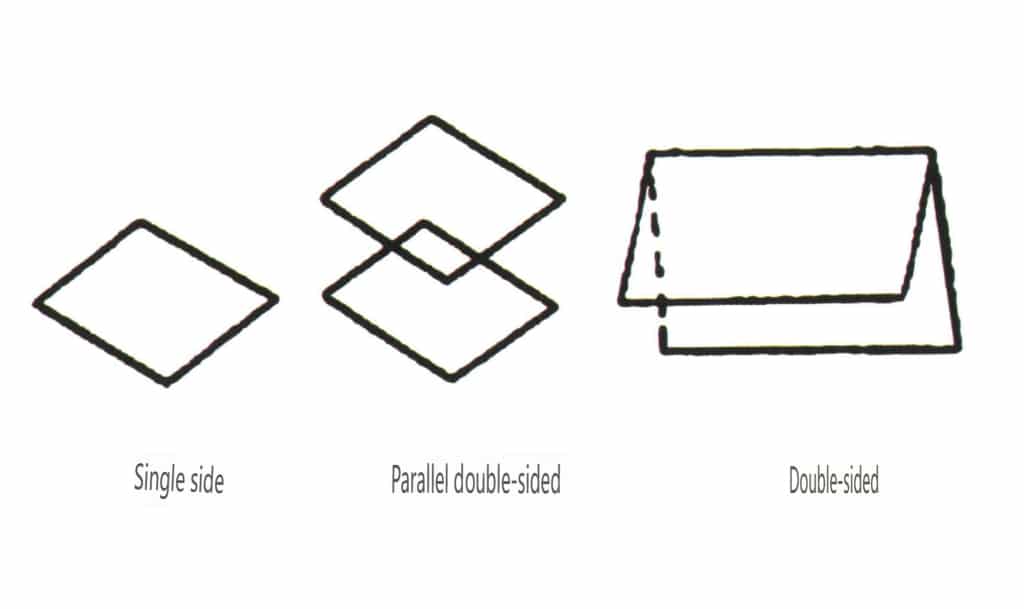
図 2-1-49 片面と両面
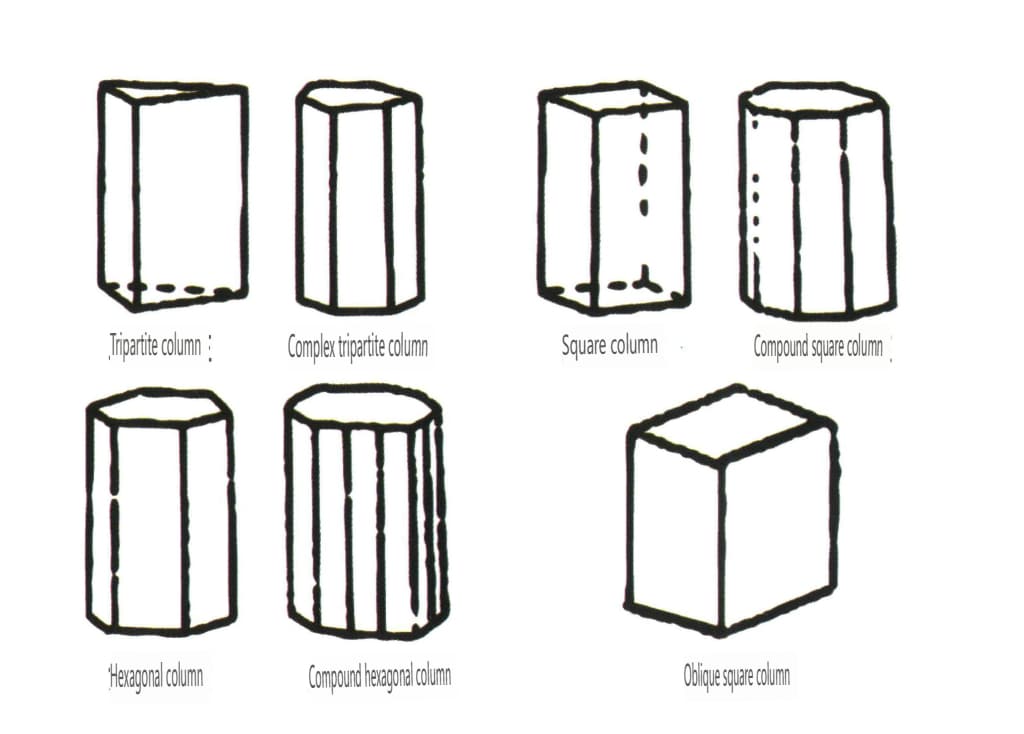
図 2-1-50 コラム

セクション III 結晶の分類
1.結晶の対称性
対称性とは、本物の結晶や未加工の宝石素材を研究する際に関わる抽象的な概念である。これは、結晶構造がそれを通過する方向または平面によって参照されるときに示される繰り返しを記述します。これは結晶の分類の基礎となる。
結晶の対称性は、微視的な観点からは結晶構造の反復性を表す方法として理解され、巨視的な観点からは、ある規則に従って、形や大きさは同じだが方向が異なる可能性のある2つ以上の幾何学的な面の反復として理解される。この繰り返しのパターンは、対称軸や対称面を用いて記述することができ、各対称軸や対称面は対称要素と呼ばれる。物体の対称性を観察したり推測したりする場合、この行為は対称性の操作を行うことと表現される。
2.結晶の対称要素
結晶学では、対称軸、対称面、回転対称軸、対称中心の4つの対称要素がある。これは対称軸と対称面の2つの対称要素に関わる。
2.1 対称軸
(1) 対称軸の概念とその表記法。
対称軸は想像上の直線であり、格子構造をこの想像上の直線を中心に360°回転させたとき、ベースレベル(図2-2-1~図2-2-2)が同じ位置に現れる回数を示す。この回数は、2 回、3 回、4 回、6 回の 4 通りしかない。また、幾何学的本体の中心を通る仮想線で、この線に沿って幾何学的本体を360°回転させると理解することもできる。ある角度を回転させた後の幾何学体の形状が、最初の0度での幾何学体の形状と一致しているとする。その場合、この仮想線を対称軸と呼ぶ。
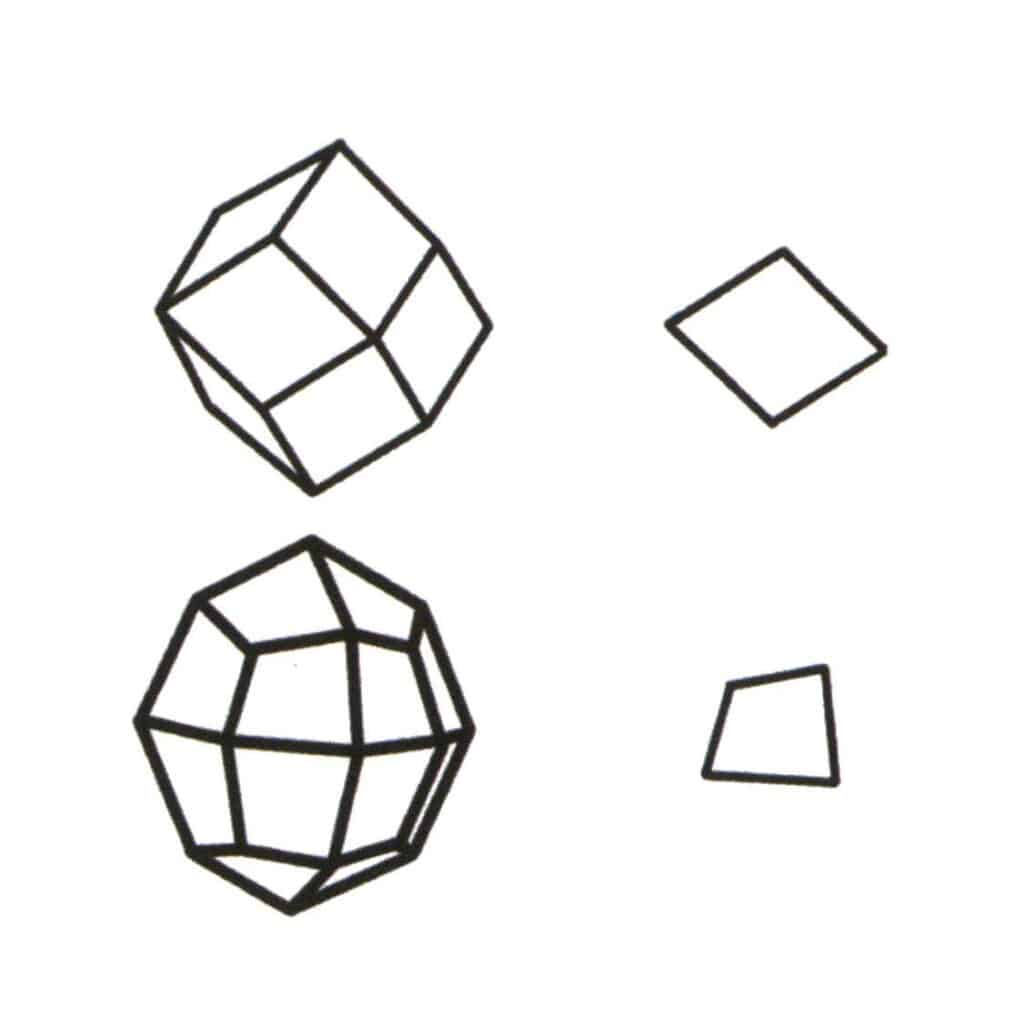
図 2-2-1 シングルフォームのベースレベルの選択
単一形状の基底面は、シンプレックスを構成する最小の繰り返し平面である。図の左上はひし形の12面体で、1種類の面で構成される閉じた図形である。最小の繰り返し平面は右上のひし形なので、ひし形12面体の基底面はひし形である。 図の左下は四辺形正八面体で、1種類の面で構成される閉じた図形です。最小の繰り返し平面は右下の四辺形なので、四辺形八面体の基底準位は四辺形である。
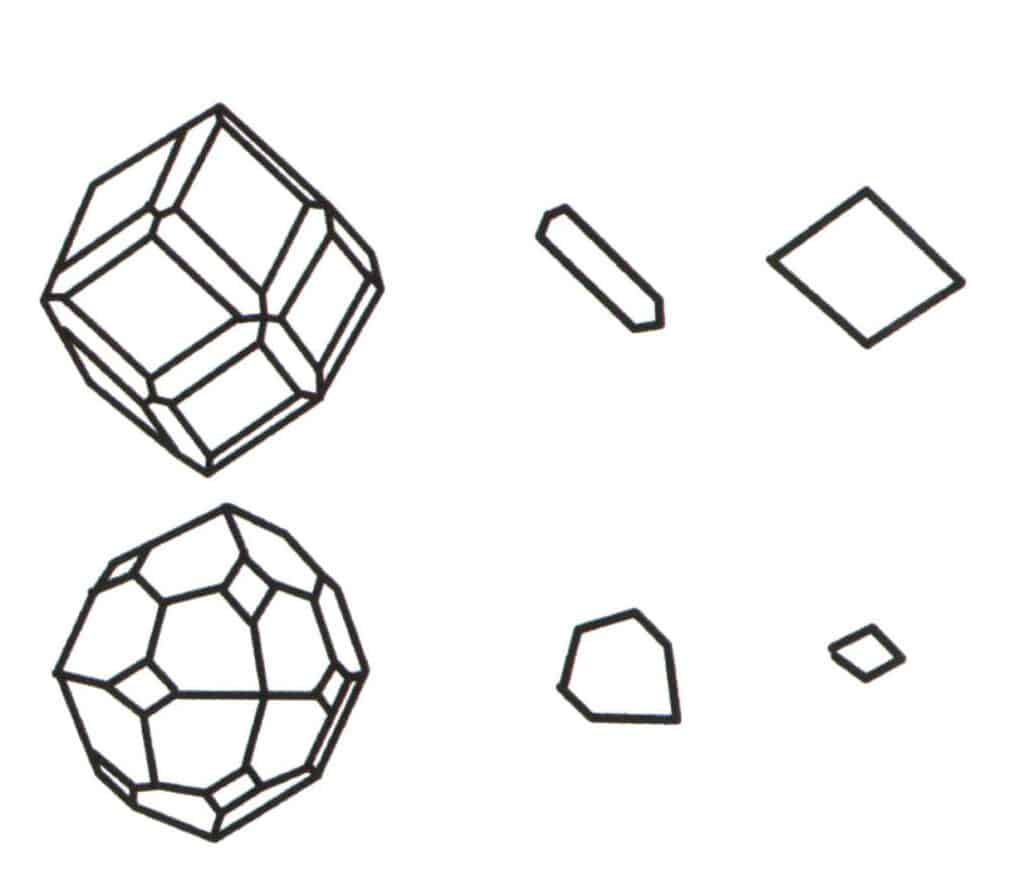
図 2-2-2 ポリトープの基底レベルの選択
複数の単純形の集合体が組合せ形を形成し、組合せ形の基底レベルの選択は、組合せ形を形成するために組み合わされる単一形の判断である。 図の左から1番目の列は組合せ形(正12面体と正14面体の単形の集合によって形成される)を表し、この幾何学体は2種類の面からなる閉じた図形である。六角形は2列目の最小反復面を表し、3列目の右側のひし形を表す。したがって、1列目の組合せ形の基本水準は六角形かひし形のどちらかである。対称軸を計算するとき、対称性を記録するための基本水準として選択できる形状は1つだけである。
対称軸は大文字のLで表され、その順番は次の通りである。 n Lの右上にL_207Fと書く。例えば、2倍軸はL²、3倍軸はL³、4倍軸はL⁴、6倍軸はL⁶と表します。L⁶, L⁴, L³は習慣的に高次の軸と呼ばれています。
結晶は異なる方向に対称軸を持つことがあり、これらの対称軸が一致しない数は、慣例的にLの左側に書かれる。例えば、6つの二次軸は6L²(図2-2-3から図2-2-9)、3つの三次軸は3L³(図2-2-10から図2-2-14)、4つの三次軸は4L³(図2-2-15から図2-2-18)、1つの六角軸はL⁶(図2-2-19)と表されます。
結晶が複数の対称軸を持つ場合、記録された方法は左から右へ降順に並べ、対応する軸の左側に対称軸の数を書きます。例えば、L⁶6L²、3L⁴4L³6L²。
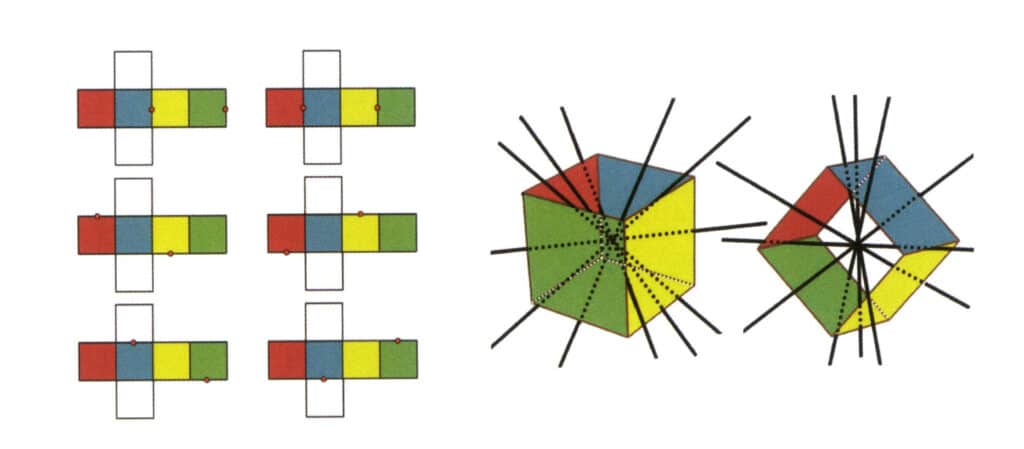
図 2-2-3 キューブの第二軸
図の左側は立方体の展開図を示し、赤い点は仮想線と辺の交点を示す。 図の右側は閉じた立方体を示しており、二次軸は平行な辺の中点、平行な長方形の面の中点、または長方形に似た3つ以上の平行な面の交点に現れることがある。 の交点に現れることがある。
コピーライト @ Sobling.Jewelry - ジュエリー カスタムジュエリーメーカー、OEMおよびODMジュエリー工場
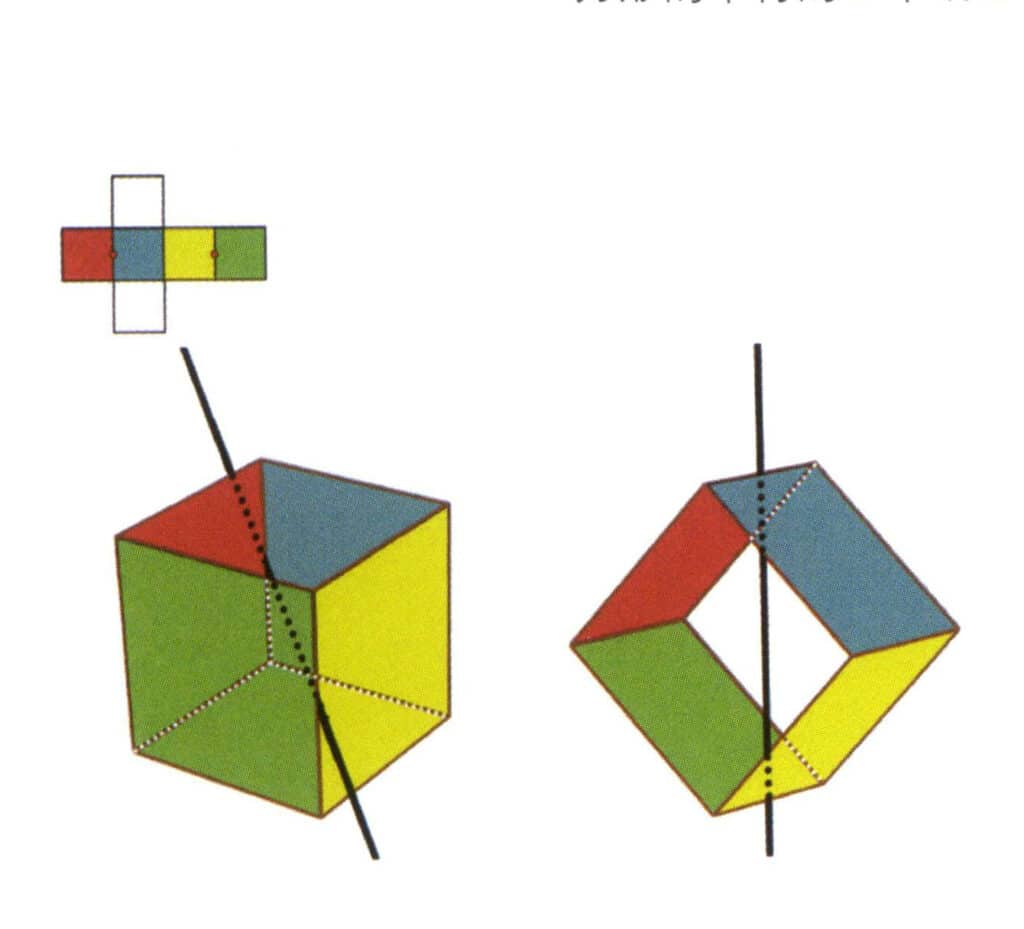
図 2-2-4 立方体の第 1 副軸
図のように、平行線の中点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形の基本レベルは、同じ位置で2回繰り返される(赤と青の面、黄と緑の面、2つの無色の面、そして3組の繰り返しの面)。イマジナリーラインは位置も角度も変わっていないので、3組の繰り返しの面が現れるが、二次軸は1回しか記録されない)。このイマジナリーラインが二次軸として記録される。
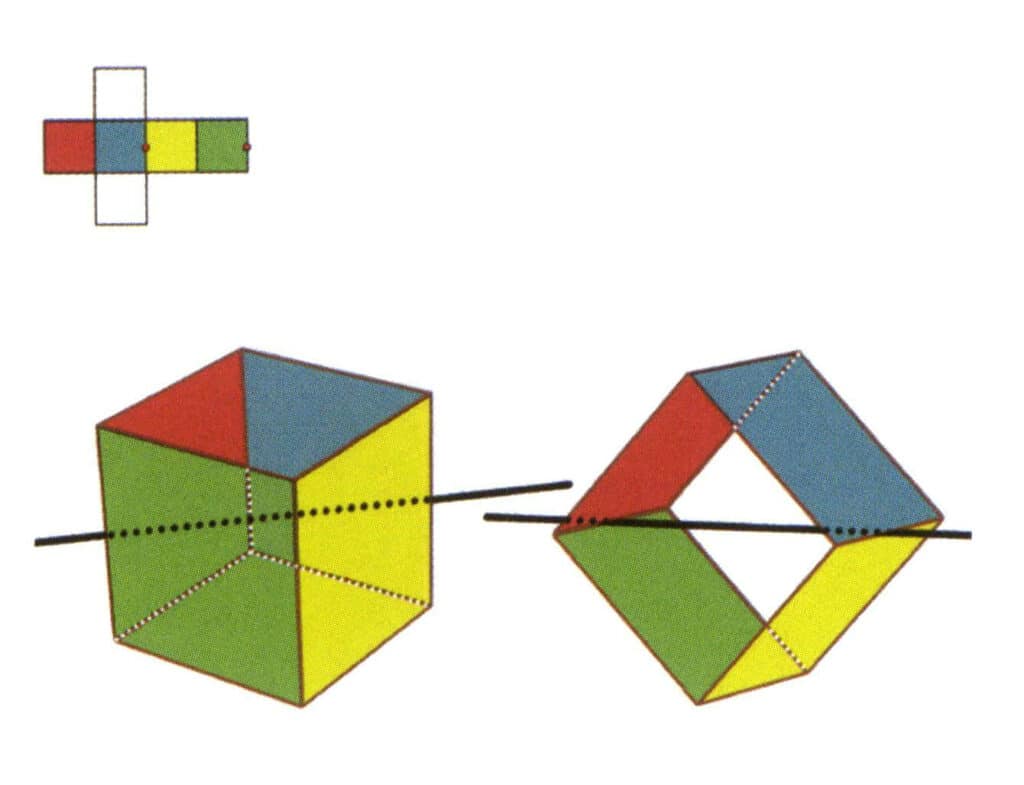
図 2-2-5 立方体の第二の二次軸
図のように、平行線の中点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形状の基本レベルは、同じ位置で2回繰り返される(赤と緑の面、黄と青の面、2つの無色の面、3組の繰り返しの面)。この想像上の線が第二の副軸として記録される。
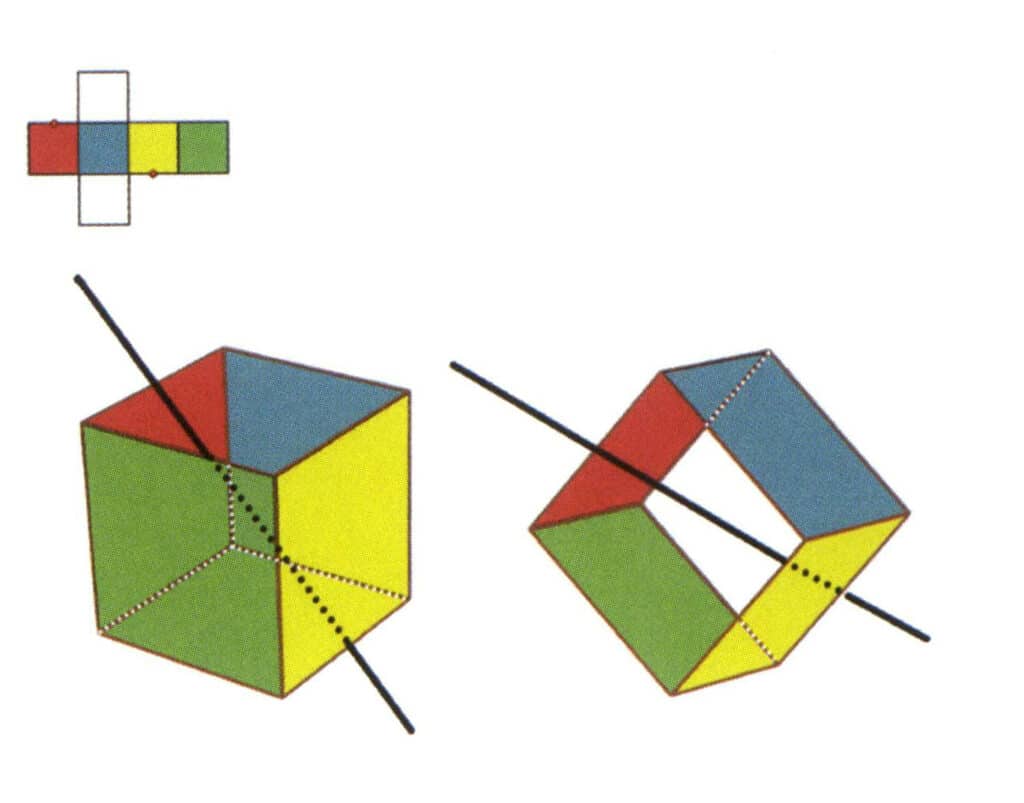
図 2-2-6 キューブの第 3 の副軸。
図のように、平行線の中点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形状の底辺が同じ位置で2回繰り返される(赤と無色の面、緑と青の面、無色と黄色の面、3組の繰り返しの面)。この想像上の線は、第3の副軸として記録される。
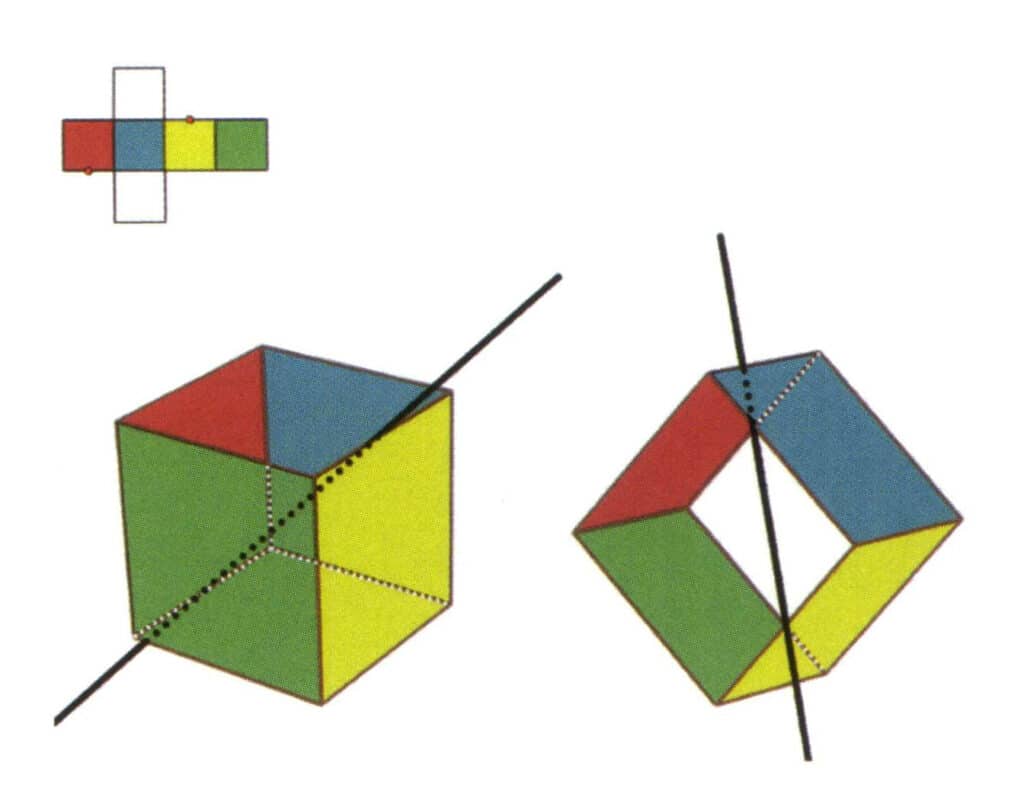
図 2-2-7 立方体の第 4 の副軸
図のように平行線の中点を選択し、この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形の基準面は、同じ位置で2回繰り返される(赤と無色の面、緑と青の面、無色と黄色の面、3組の繰り返される面)。
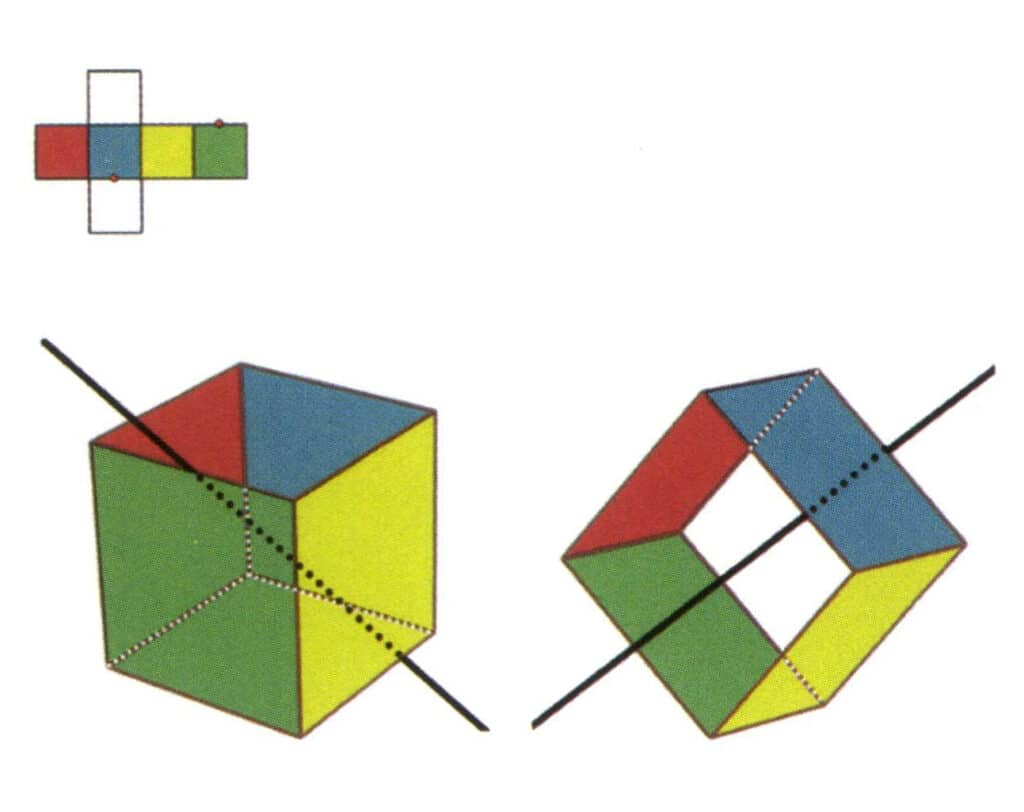
図 2-2-8 キューブの第 5 の副軸。
図のように平行線の中点を選択し、この2つの辺の中点を通る直線を想像し、立方体を360°回転させると、色は異なるが同じ形の基準面が同じ位置で2回繰り返される(赤と無色の面、緑と青の面、無色と黄色の面、3組の繰り返される面)。
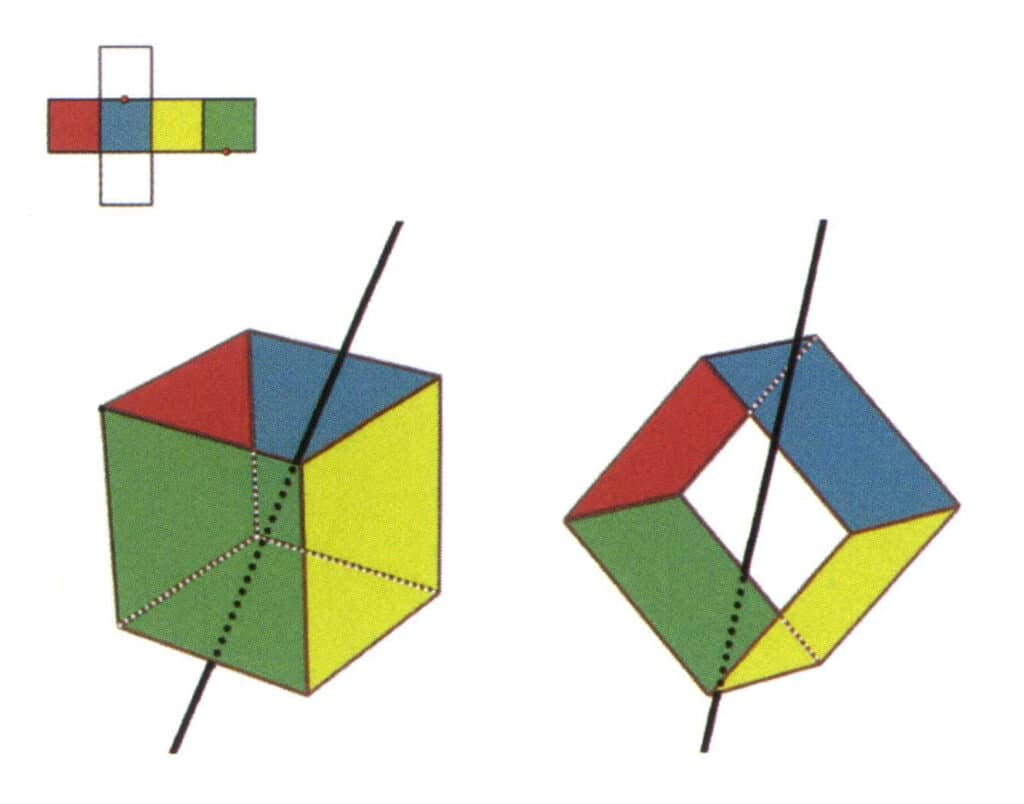
図 2-2-9 立方体の第 6 の副軸
図のように、平行線の中点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形の底辺が、同じ位置で2回繰り返される(緑と無色の面、赤と黄色の面、無色と青の面、3組の繰り返される面)。この想像上の線が6番目の副軸として記録される。
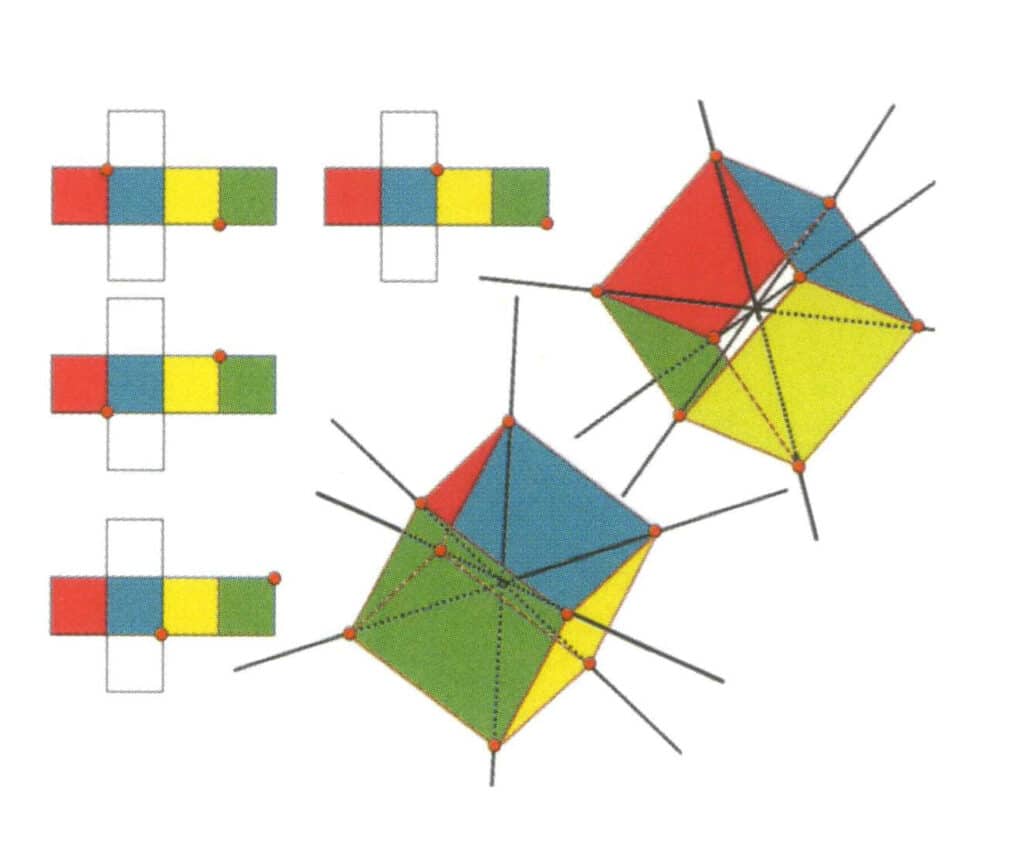
図 2-2-10 立方体の三次軸
図の左側は立方体の展開図であり、赤い点は仮想直線と辺の線の交点を示す。 図の右側は閉じた立方体で、赤い点は想像上の直線と辺の交点を示す。 三次軸は、平行な正三角形の面の中点、正三角形に似た3つ以上の平行な面の交点に現れることがある。
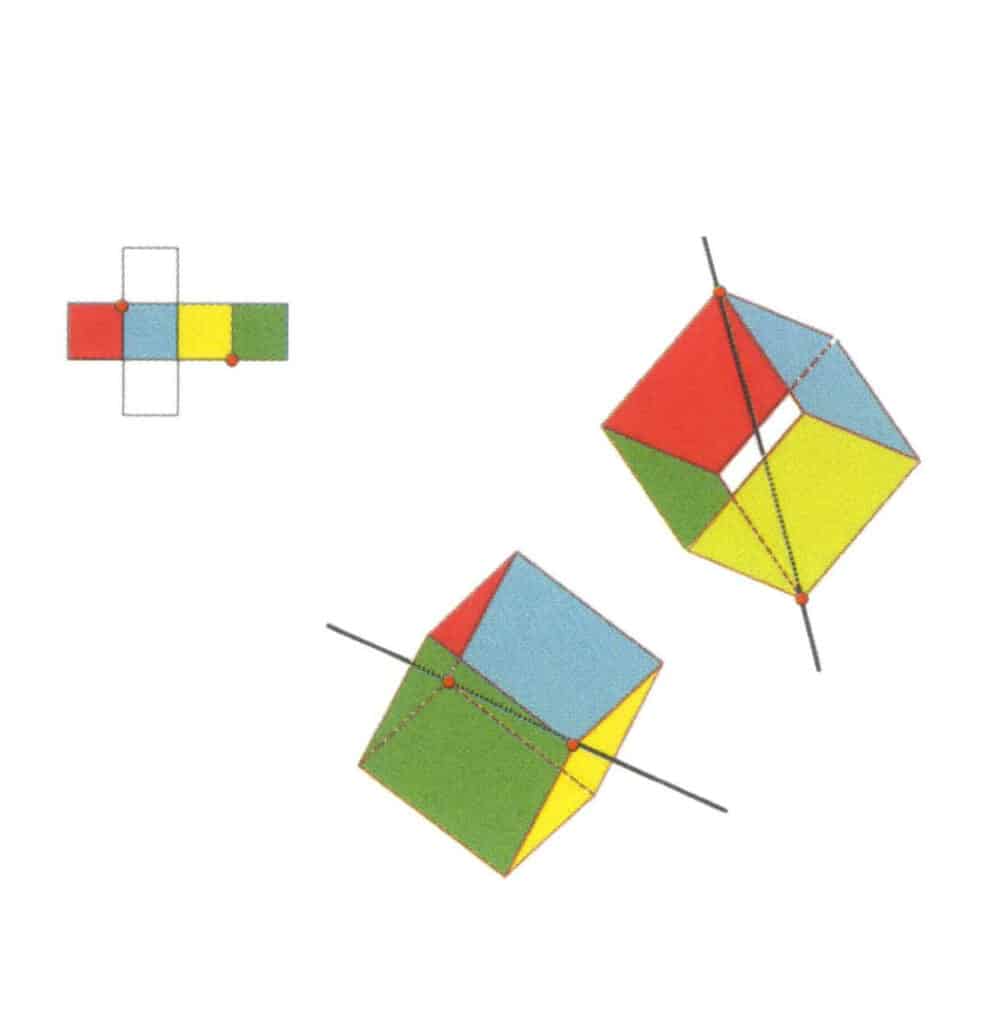
図 2-2-11 立方体の第 3 軸。
図に示すように3つの面の交点を選択し、これらの2つの辺の中点を通る直線を想像し、立方体を360°回転させると、色は異なるが同じ形の基準面が同じ位置で3回繰り返される(赤、無色、青の面、緑、無色、黄色の面、2組の繰り返される面)。
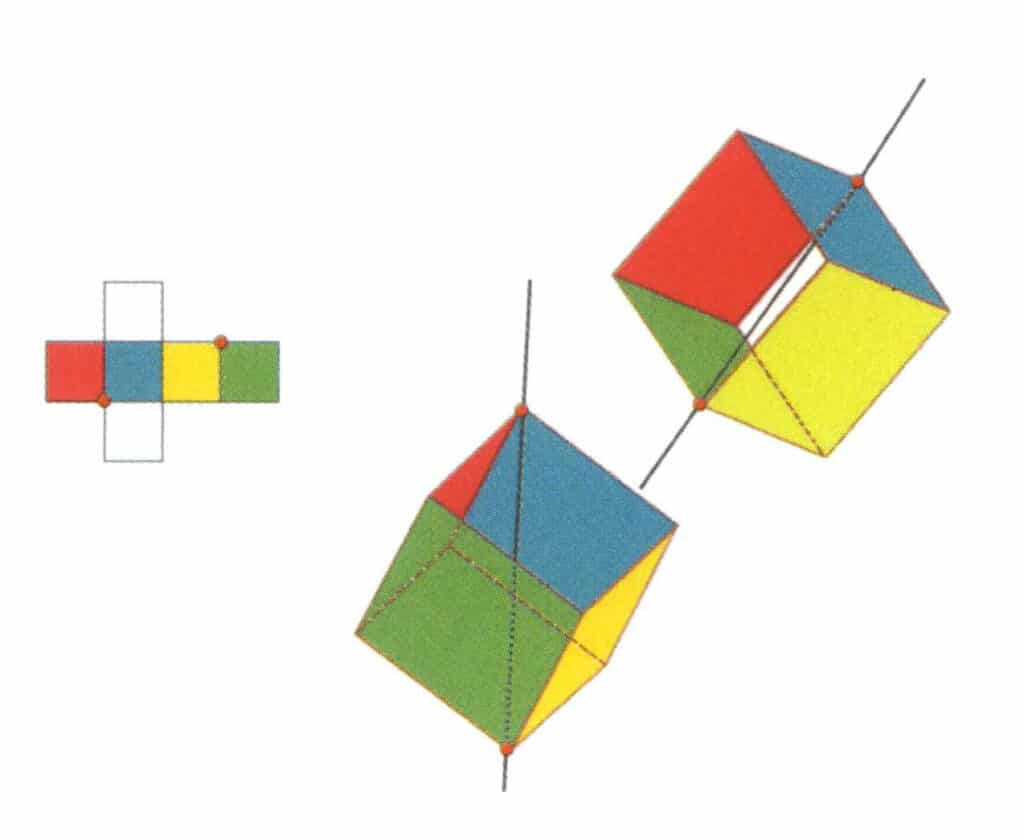
図 2-2-12 立方体の第 2 の 3 次軸。
図に示すように、3つの面の交点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形の底辺が、同じ位置で3回繰り返される(赤、無色、青の面、緑、無色、黄の面、2組の繰り返しの面)。この想像上の線が第二の三次軸として記録される。
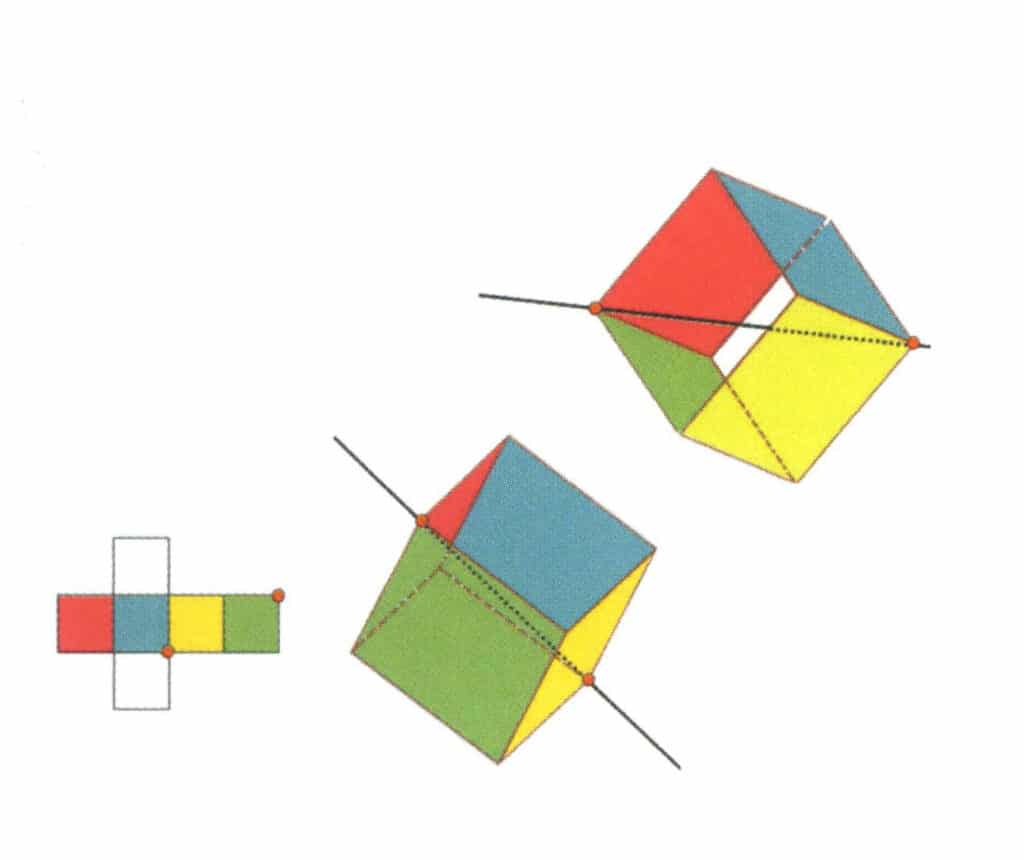
図 2-2-13 立方体の第 3 次軸
図に示すように、3つの面の交点を選択する。この2つの辺の中点を通る直線を想像し、立方体を360°回転させる。色は違うが同じ形の底辺が同じ位置で3回繰り返される(赤、無色、緑の面、青、無色、黄色の面、2組の繰り返しの面)。この想像上の線が第3の3次軸として記録される。
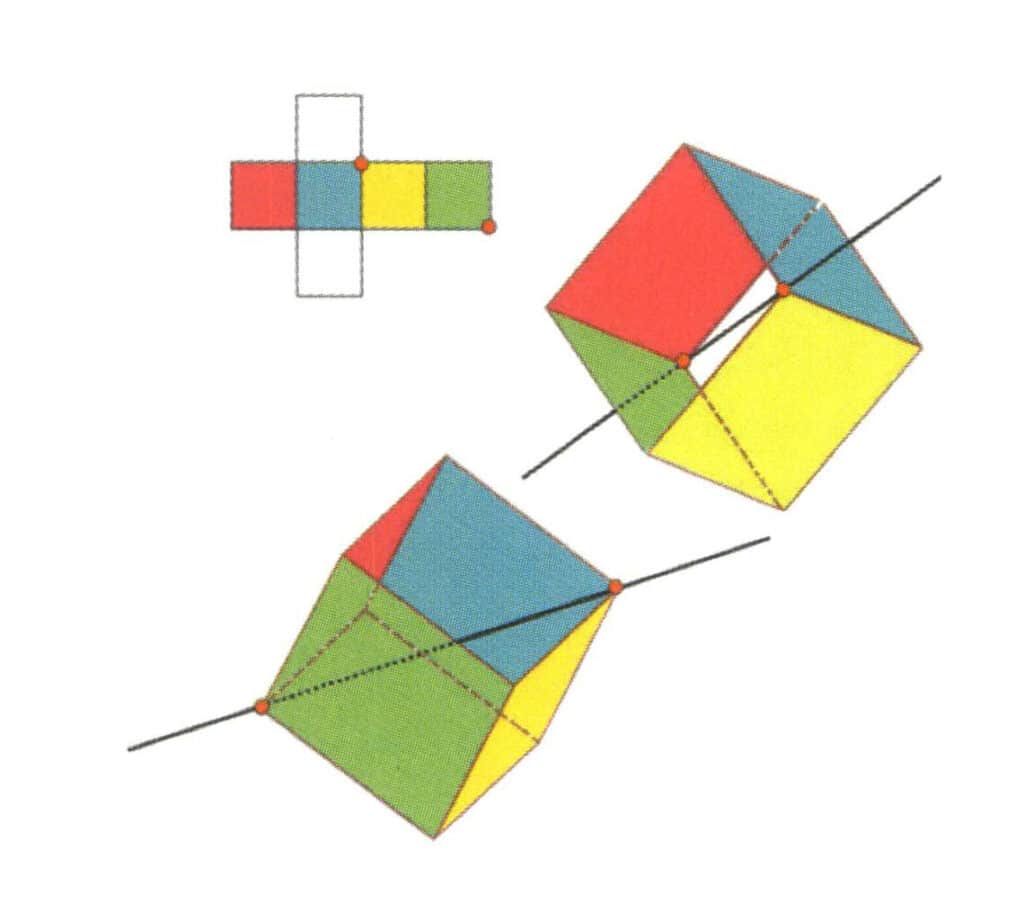
図 2-2-14 立方体の第 4 立方軸。
図のように3つの面の交点を選ぶ。2つの辺の中点を通る1本の直線があると仮定すると、立方体は360°回転し、色は異なるがベースレベルは同じ形になる。この位置を3回繰り返す(赤、無色、緑の面、青、無色、黄色の面を2セット繰り返す)。この想像上の線を第4の立方体の軸として記録する。
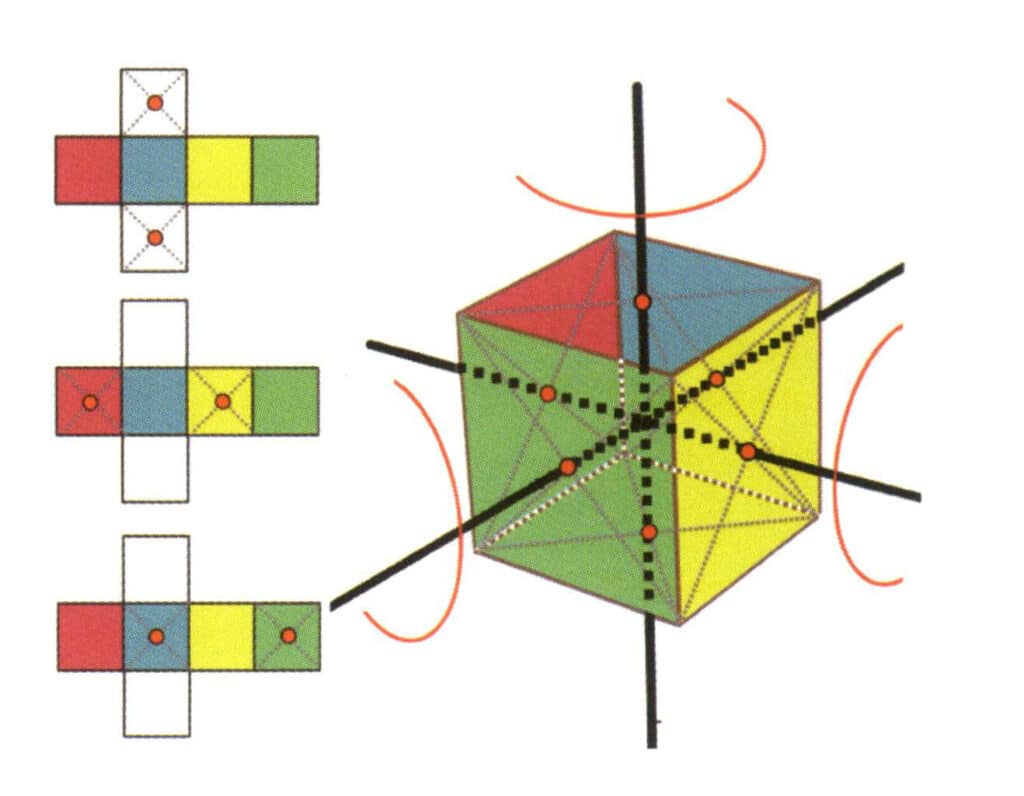
図 2-2-15 キューブの第 4 軸
図の左側は立方体の展開図で、赤い点は仮想線と辺の交点を示す。 図の右側は閉じた立方体を示し、赤い点は想像線と平面の交点を示す。 第4の軸は、平行な正方形の面の中点、正方形に似た3つ以上の平行な面の交点に現れることがある。
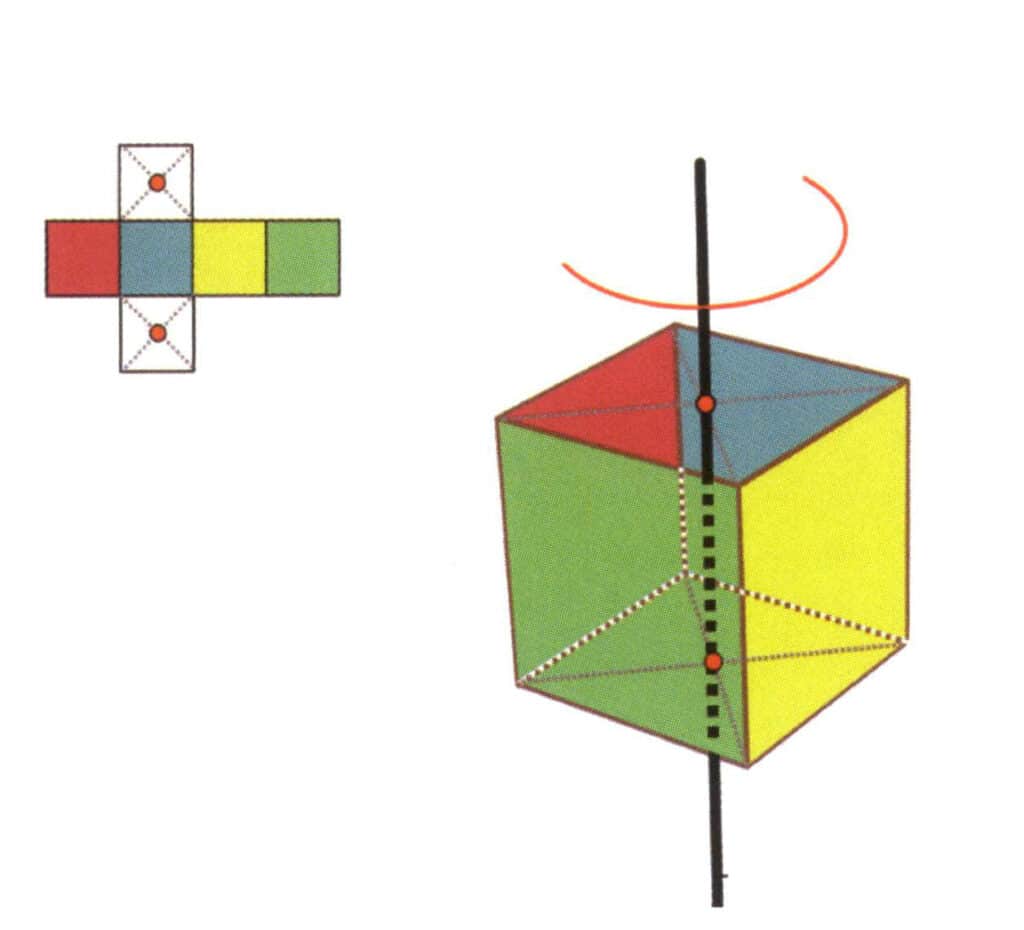
図2-2-16 立方体の第一四分軸
図に示す平面の中点を選び、2つの平面の中点を通る直線があると仮定し、立方体を360°回転させる。色は異なるが同じ形の底辺の面は、同じ位置で4回繰り返されることになり(赤、青、緑、黄色の面)、この仮想の直線は4重軸として記録される。
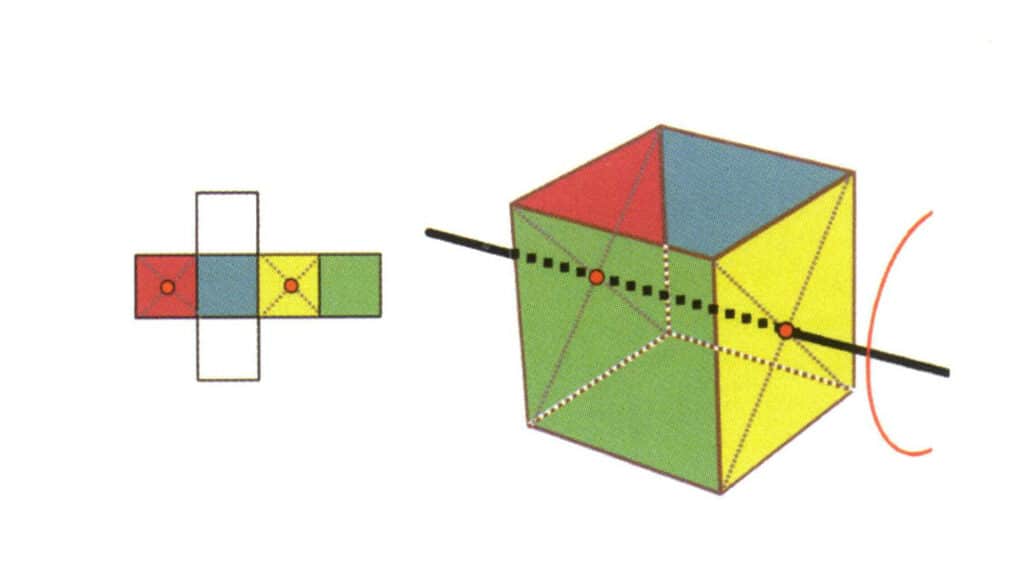
図2-2-17 立方体の第二四分軸
図のように平面の中点を選択し、立方体を通る直線を想像し、立方体を360°回転させる。色は異なるが同じ形状の底面が同じ位置で4回繰り返され(上は無色で青い面、下は無色で緑の面)、この想像上の線が2つ目の4角軸として記録される。
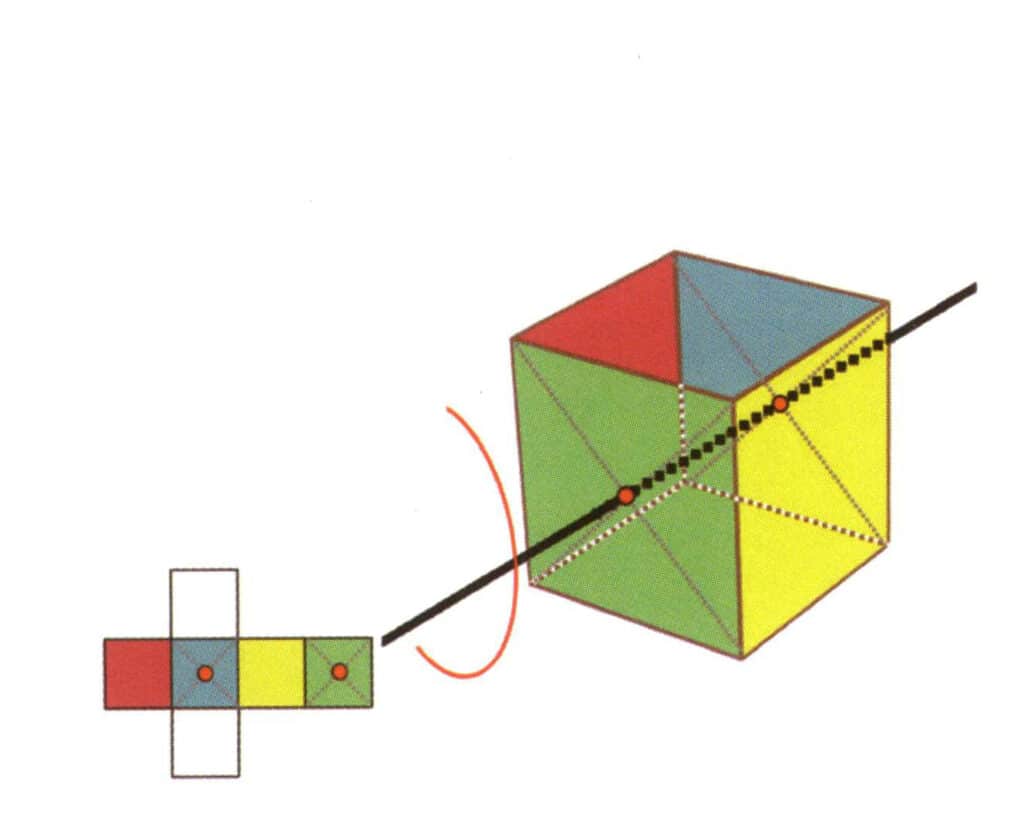
図 2-2-18 立方体の第 3 の 4 次軸
図のように平面の中点を選び、立方体を通る直線を想像し、立方体を360°回転させる。色は違うが形は同じベースレベルが同じ位置で4回繰り返され(上は無色で赤い面、下は無色で黄色い面)、この想像上の線が3本目、4本目の軸として記録される。
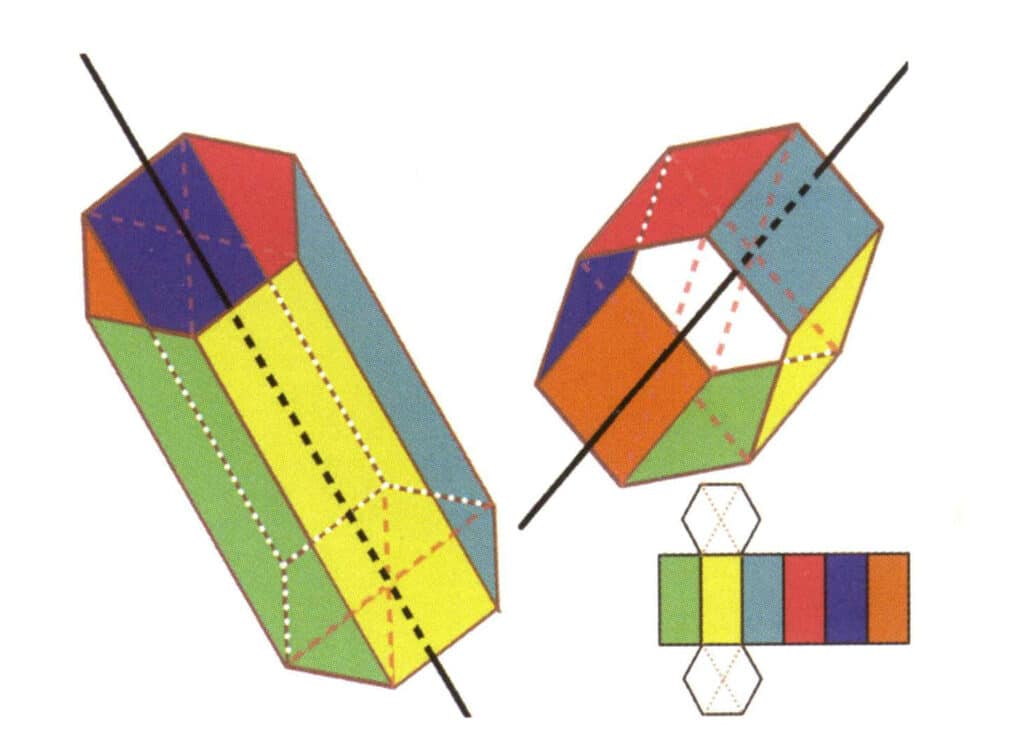
図2-2-19 六角柱の6つの軸
左と右上の黒い線は六角柱の6つの軸を表している。 右下は六角柱の拡大図。 六角柱の軸は、平行な六角形の面の中点や、六角形の6つの面の交点に現れることがある。
(2) 対称軸を見つけるための考察。
対称軸の位置は5種類ある。
立方体の二次軸の位置など、2つの平行な辺の中点。
立方体の4分軸の位置など、2つの平行な平面の中点。
立方体の3次軸の位置など、2つの頂点(複数の面の交点)の間。
頂点と平行面との中点。例えば、正四面体の三次軸の位置。
三角柱の二次軸位置のように、エッジラインの中点と平行面の中点を指す。
同じ方向の対称軸の選択は、最小数の原則に従う。例えば、最小数の原則に従えば、ある方向に6本の対称軸が見つかり、3本の対称軸が見つかれば、それは最終的にL³として記録される。異なる方向の対称軸は、見つかった数に従って記録されるべきである。
注意しなければならないのは、6重の対称軸と4重の対称軸は同時に現れることはなく、6重の対称軸は1つしか現れないが、それ以外の対称軸はさまざまな形で、あるいは複数の例で共存しうるということだ。
ベースレベルは最小単位平面として選択する。そうでない場合、対称軸判定の精度に影響する。
対称軸の数を記録する場合、平面の同じ形や大きさが同じ位置で繰り返される回数を決定することが不可欠である。
垂直対称の二次軸L_207(n = 3, 4 or 6)がある場合、L_207Fに垂直な二次軸がn本なければならない。
2.2 平面 対称性の
(1) 平面の概念と記録方法 対称性の
対称面とは架空の平面のことで、この平面に沿って結晶を切断すると、結晶の半分がもう半分の鏡像になる(図2-2-20)。同じ結晶構造において、このような平面は最大で9回現れることがあります(図2-2-21)。つまり、9通りの切り方が可能で、2つの半分が完全に一致することもあります。もちろん、すべての結晶構造に対称面があるわけではない。
大文字のPは対称面を表す。結晶の中には、複数の非対称面を持つものがあり、これらの対称面の数は慣例的にPの左側に書かれる。例えば、4つの対称面は4Pと表され、1つの対称面はPと表される。
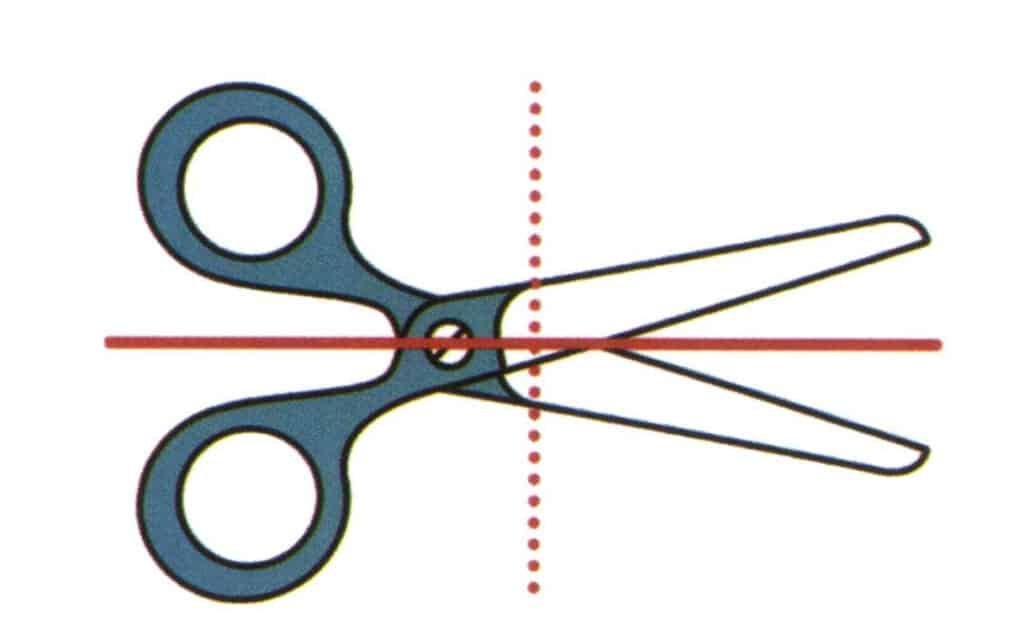
図2-2-20 紙の垂直な平面と、ハサミを上下に分割する赤い実線の方向に伸びる平面を想像し、上下の部分が鏡面対称であるとする。この想像上の平面を対称平面と呼ぶ。 紙面に垂直で、ハサミを左右に分ける赤い破線の方向に伸びる別の平面を想像するが、左右のハサミの形は対称ではない。
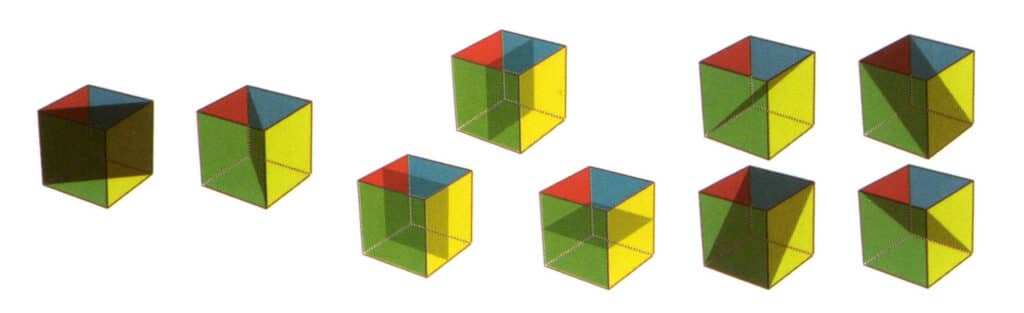
図2-2-21 立方体の9つの対称面
(2) 見つけるためのヒント 対称性の平面。
対称面は多くの場合、対称軸と平行で一致する。
対称面とは、結晶形状を分割する仮想の平面のことで、幾何学の平行二平面とは異なる。
対称平面が対称軸L_207Fを含むなら、L_207Fを含む対称平面はn個なければならない。
(3) ポイント グループだ。
点群は結晶中のすべての対称要素の総和である。点群の書き方は対称軸+対称面の順で、例えば3L²3Pのように書きます(図2-2-22)。結晶に複数の対称軸がある場合は、左から右へ、高次の軸から低次の軸へ、対称面の順序は、例えば、L⁴4L²5Pのように記録するのが通例です(図2-2-23)。結晶には32種類の対称性がある。
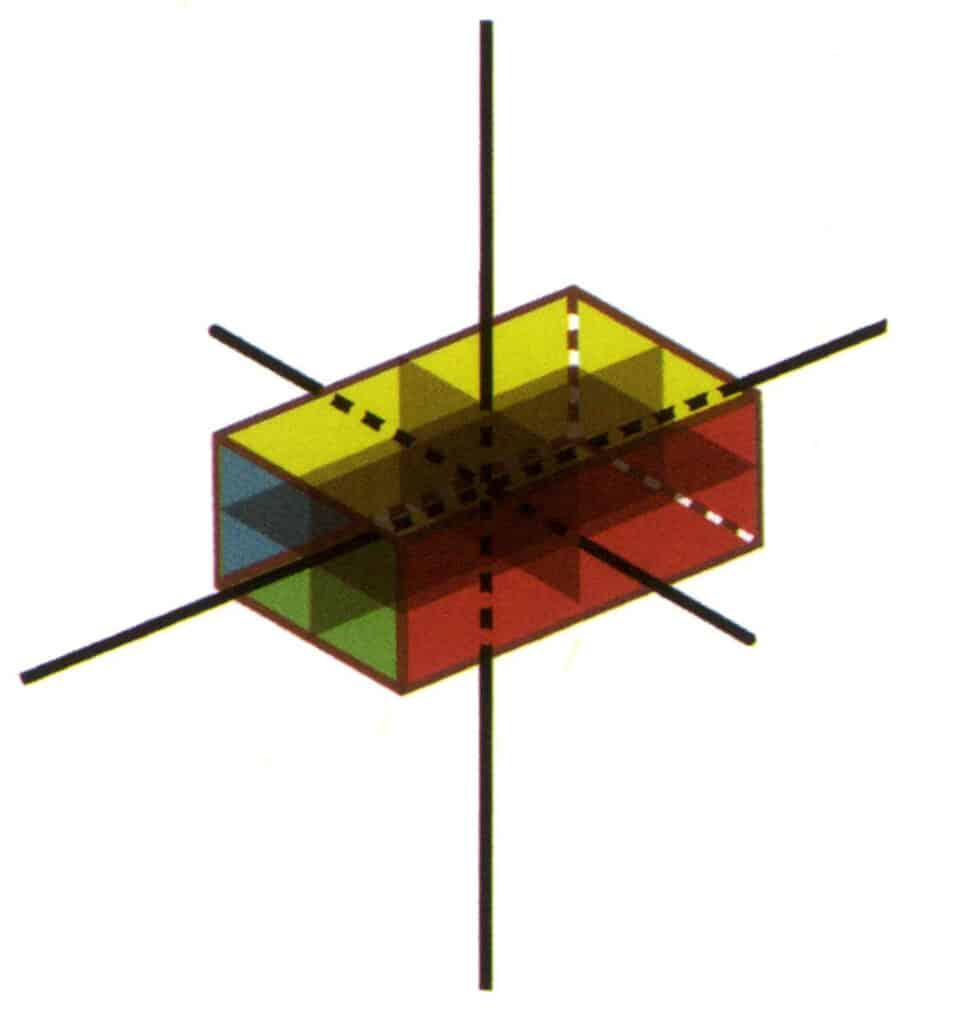
図2-2-22 3L²3P点群(断面が長方形の立方体)
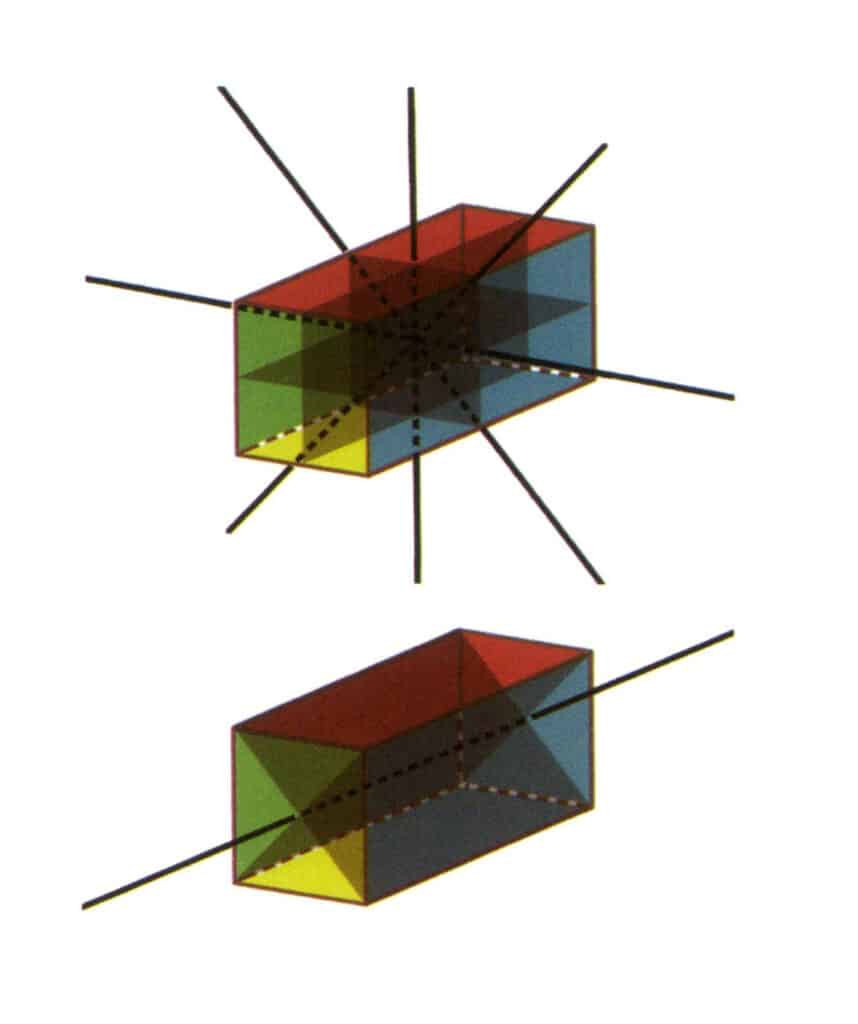
図2-2-23 L⁴4L²5P点群(断面が正方形の直方体)で、上部に4つの第2軸と3つの対称面、下部に1つの第4軸と2つの対称面を持つ。
3.結晶の分類
対称性は結晶分類の一部である。結晶分類法において、天然水晶と人工水晶の宝石の結晶構造を説明するためには、もう一つの概念-結晶軸-を導入する必要がある。結晶軸とは、結晶構造を通る仮想の線であり、格子の節点が繰り返される方向と、その方向に沿って節点が繰り返される相対的な距離を示す。結晶軸は対称軸または対称面の法線と一致する。対称軸や対称面がない場合、結晶軸は結晶端の方向と平行に選択することができる。
対称元素と結晶軸に基づいて、学問体系は結晶を3つの結晶族と7つの結晶系に分類している(表1)。
表1:クリスタル・ファミリーとシステムを決定するためのポイント
| クリスタル・ファミリー | クリスタル | 決定のポイント | 一般的な宝石の品種 |
|---|---|---|---|
| 低レベル水晶振動子システム | 三斜晶系 | 第2軸または対称面なし | アマゾナイト、ロードナイト、ターコイズ |
| 単斜晶系 | 高次軸なし、2次軸と対称面は1つまで | ヒスイ輝石、ダイオプサイド、スポジュメン、エピドート | |
| 斜方晶系 | 高次軸、2つ以上の副軸、対称面はない | カンラン石、トパーズ、サアルパイト(タンザナイトを含む)、コーディエライト、クリソベリル、エンスタタイト | |
| 中級クリスタル・ファミリー | 正方晶系 | 1四重軸(Lで表すことができる4) | ダイヤモンド |
| 三斜晶系 | 1 三角軸(Lで表すことができる3) | コランダム、ルビー、サファイア、トルマリン、水晶系の結晶(水晶、アメジスト、シトリンなど)、ロードクロサイト | |
| 六方晶系 | 1六角軸(Lで表すことができる6) | アクアマリン、エメラルド、その他のベリライト系宝石、アパタイト | |
| アドバンスド・クリスタル・ファミリー | アイソメトリック結晶系 | 4つの三角軸(4Lで表すことができる3) | ダイヤモンド、ガーネット、スピネル、蛍石 |
4.一般的な宝石の結晶の特徴
一般的な宝石には、ダイヤモンド、スピネル、蛍石、ガーネット、ベリライト、ジルコン、コランダム、トルマリン、水晶、クリソベリル、トパーズなどがある。宝石の各タイプは、独自の固定結晶特性を持っています。
ハイレベル・クリスタル・ファミリーの宝石は、そのほとんどが結晶癖のある粒状で、一般的な品種は固定した結晶形で現れることが多い(表2)。
中級および低級結晶ファミリーの結晶癖は柱状である(表3)。
表2:ハイレベル水晶ファミリーの共通水晶特性
| ジェムトーン名 | 水晶の分類 | クリスタルの重要な特性 | |||
|---|---|---|---|---|---|
| ジェムトーン名 | 水晶の分類 | クリスタルの習慣 | 一般的な結晶形 | 一般的な双子の形 | 一般的なクリスタル・フェイス・パターン |
| ダイヤモンド | アイソメトリック結晶系 | 粒状結晶の習性(図2-2-24)、一般に八面体の顆粒で見られる | 八面体は一般的な結晶形であるが、菱形十二面体など、より複雑な結晶形も現れることがあり、しばしば丸みを帯びた結晶面を特徴とし、3回対称性を示すことがある。 | 三角形の平たい双子で、凹角が見えないこともある(図2-2-25)。 | 表面には逆三角形のエッチングピット(図2-2-26、2-2-27)、その他の結晶面模様(図2-2-28、2-2-29)が見られる。 |
| スピネル | 粒状結晶の習性(図2-2-30)、一般に八面体の顆粒で見られる | 八面体の形で生成することが多く、結晶面は非常に平坦で、研磨したように見えることがある(図2-2-31)。 | 双晶は非常に平らで、角を落とした三角形のような形をしている(図2¬2-32)。 | 表面から見えるエッチング・ピット(逆三角形のダイヤモンドのようなものもある)(図2-2-33 | |
| 蛍石 | 粒状結晶(図2-2-34) | 八面体と立方体の結晶形(図2-2-35) | 相互貫通ツインニング | 正方形の段差のある成長痕、多くは劈開の隙間、立方体の6つの面の方向に平行な色帯。 | |
| ガーネット | 粒状結晶で、一般に菱形12面体の結晶が見られる(図2-2-36) | 菱形正十二面体または正方形台形正十二面体 | 希少 | 結晶面と同じ形状の同心円状の輪帯が見える(図2-2-37) | |
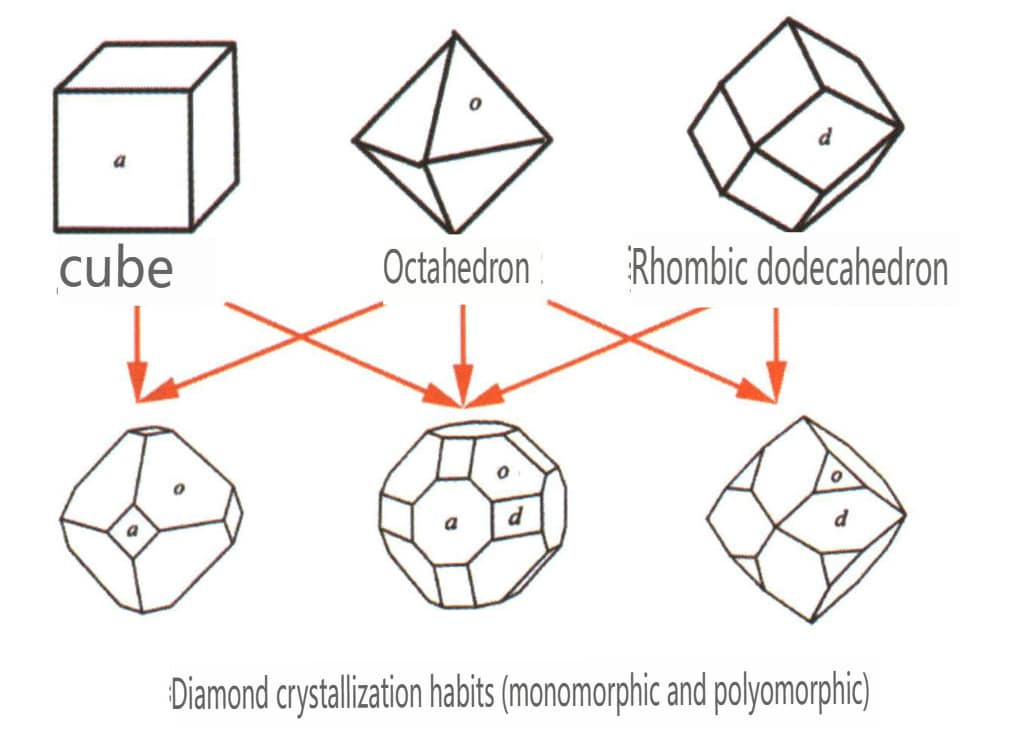
図2-2-24 ダイヤモンドの結晶癖
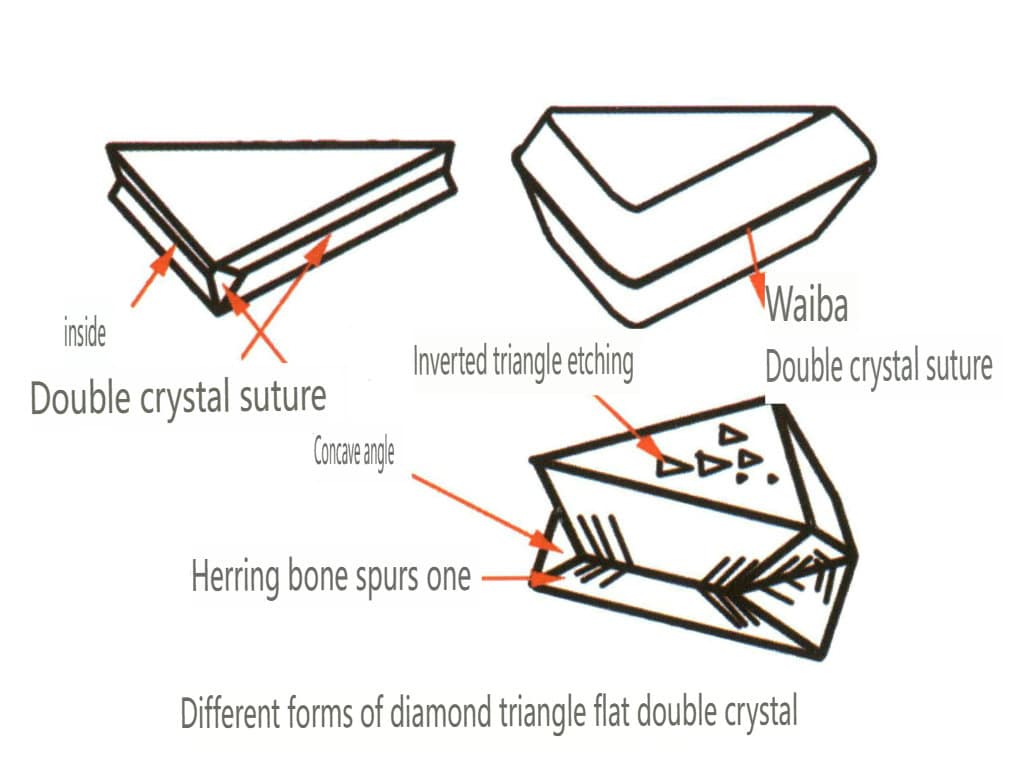
図2-2-25 ダイヤモンド・ツイン・ハビット
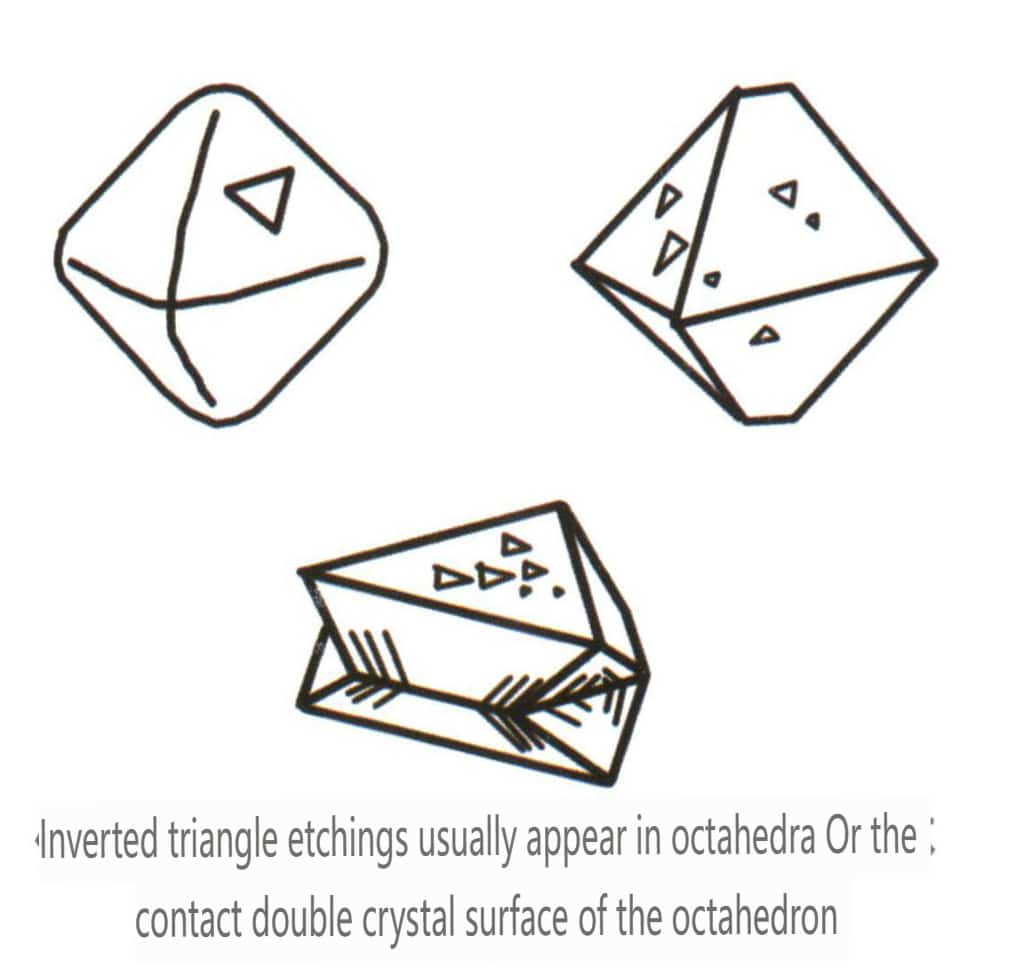
図2-2-26 ダイヤモンド八面体結晶面の逆三角形エッチング図

図2-2-27 ダイヤモンド八面体結晶表面の逆三角形エッチ図形
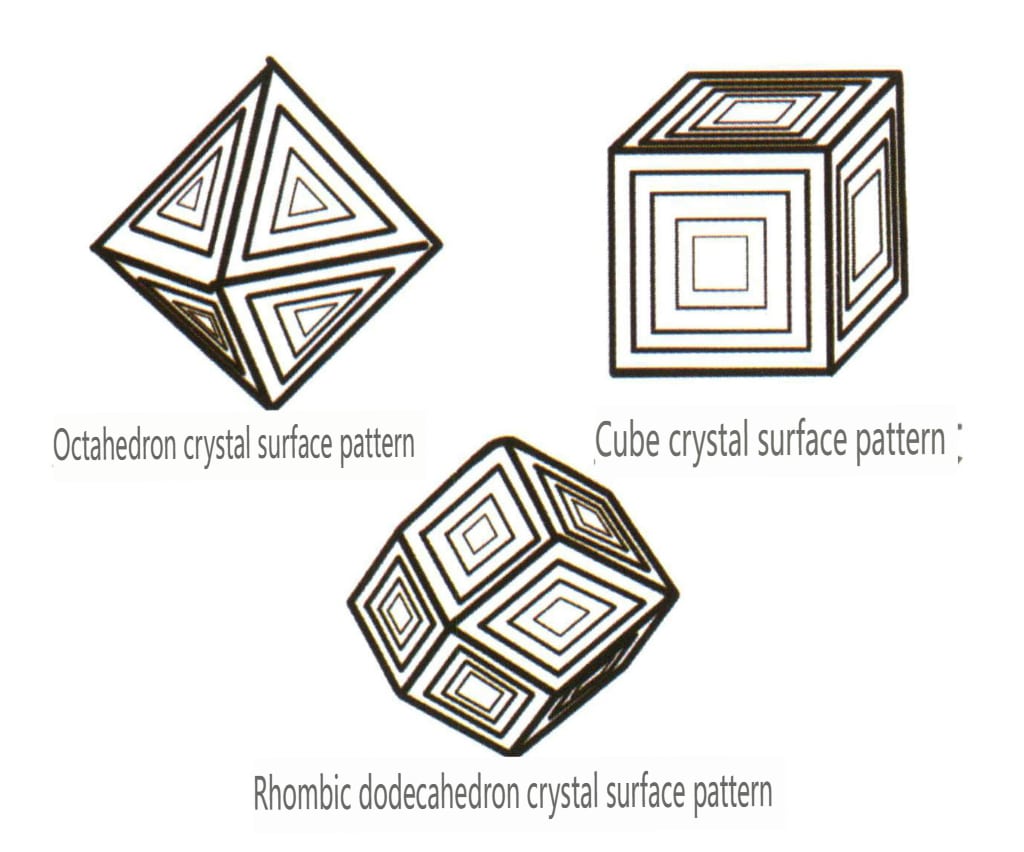
図2-2-28 ダイヤモンド八面体結晶面の逆三角形エッチング図

図2-2-29 ダイヤモンド八面体結晶表面の逆三角形エッチ図形
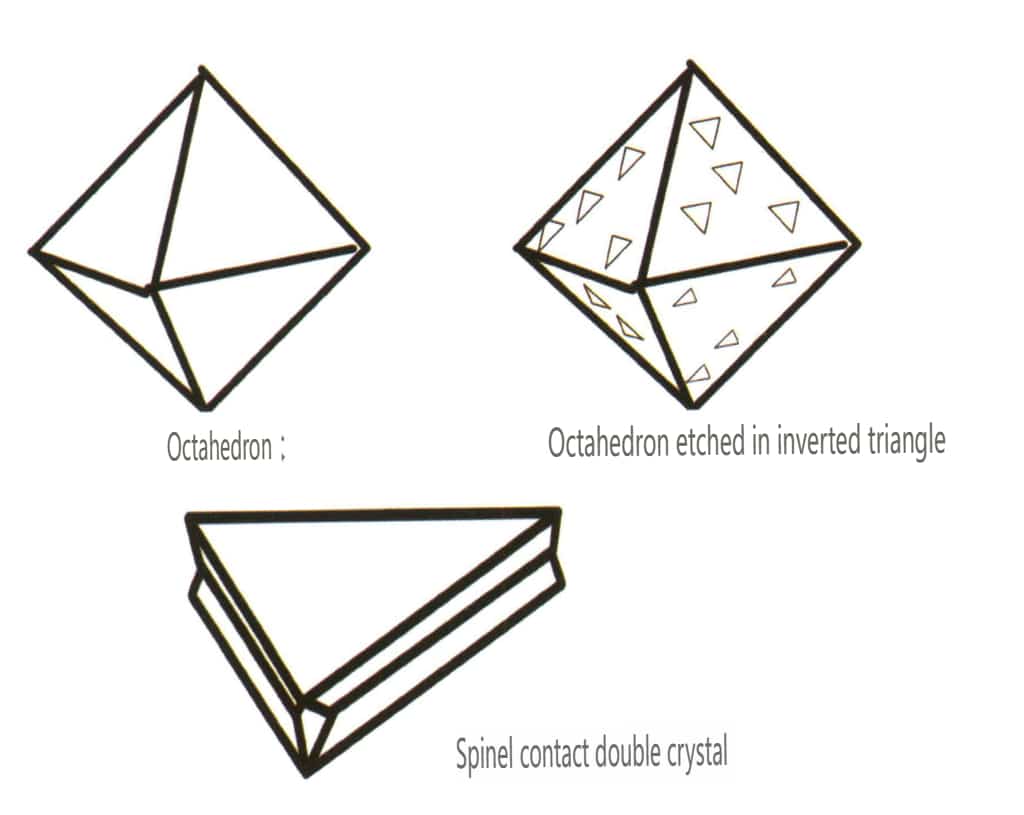
図2-2-30 スピネル晶癖

図2-2-31 スピネル結晶の一般的な形態

図2-2-32 スピネルの接触双晶化
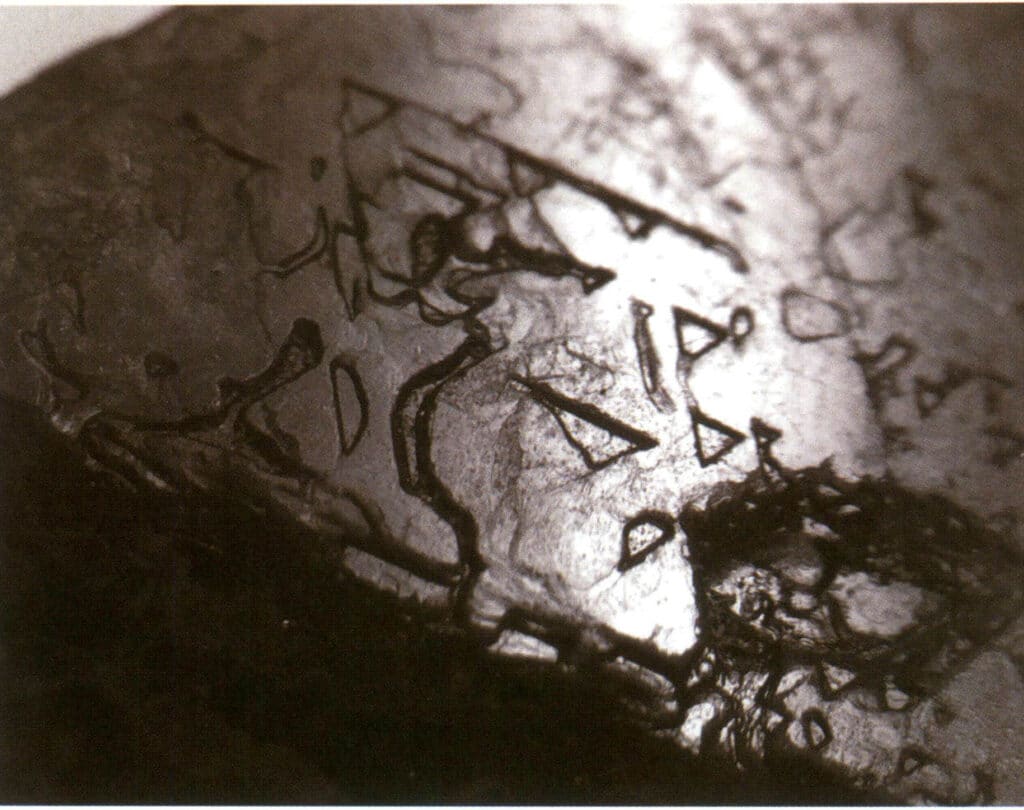
図 2-2-33 スピネル表面の逆三角形エッチング図形パターン
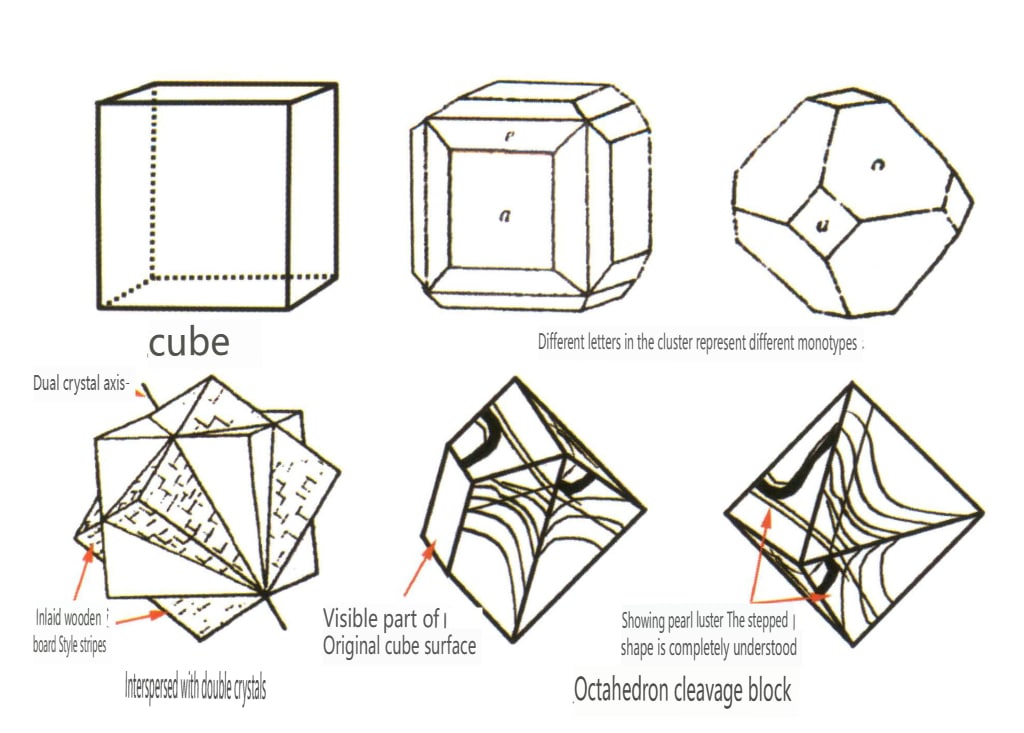
図2-2-34 蛍石の結晶癖

図2-2-35 蛍石結晶
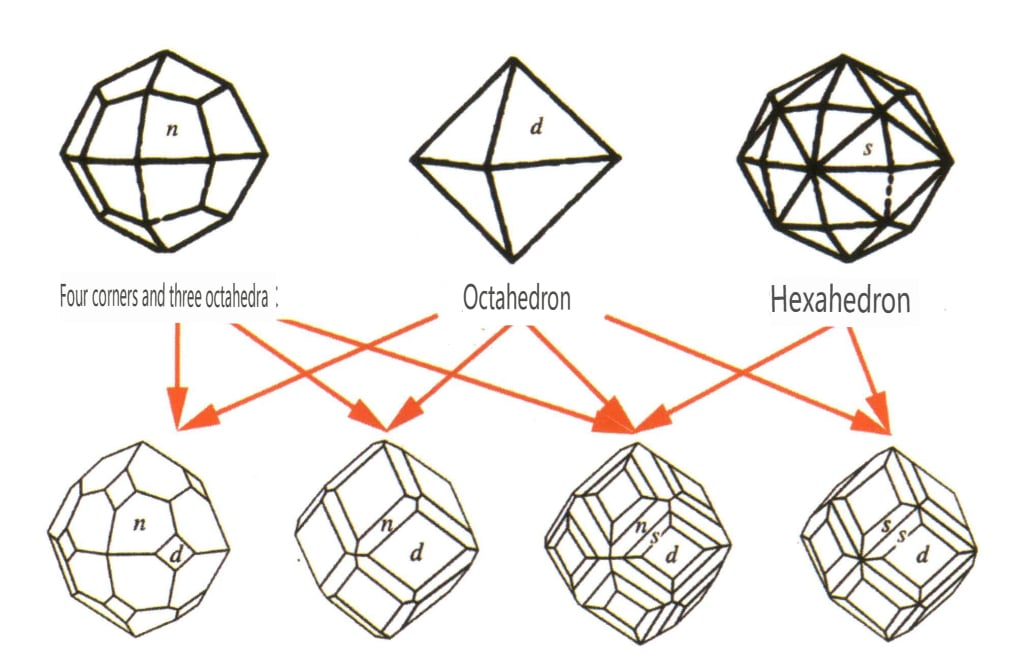
図2-2-36 ガーネットの結晶癖

図2-2-37 ガーネット結晶表面に見られる結晶面と同じ形状の同心円状の輪帯
表3: 中間結晶系と低結晶系に共通する宝石の結晶特性
| ジェムトーン名 | 水晶の分類 | クリスタルの重要な特性 | |||
|---|---|---|---|---|---|
| ジェムトーン名 | 水晶の分類 | クリスタルの習慣 | 一般的な結晶形 | 一般的な双子の形 | 一般的なクリスタル・フェイス・パターン |
| ベリル | 六方晶系 | 柱状晶癖(図2-2-38) | 六方柱状結晶(図2-2-39、2-2-40) | 希少 | 目に見える縦縞 |
| 鉛石 | 正方晶系 | 柱状晶癖(図2-2-41) | 断面が正方形の柱が、正方形のダブルコーンとともに現れる(図2-2-42)。 | 目に見える膝状の双晶 | 特別なパターンなし |
| コランダム | 三方晶系 | 板状晶癖、柱状晶癖(図2-2-43) | ルビーは六角柱の形状を示すことが多く(図2-2-44)、サファイアは六角両錐の樽型の結晶形を示すことが多い(図2-2-45)。 | よく見られる双結晶。 | 目に見える筋。 |
| トルマリン . | 柱状晶癖(図2-2-46) | 両端の結晶面が異なり、断面は球面三角形である(図2-2-47)。 | 希少 | 目に見える縦縞(図2-2-48) | |
| 水晶 | 柱状晶癖(図2-2-49) | 断面は六角形で、六角形の二角錐はまれで(図2-2-50、2-2-51)、六角形の一角錐が一般的である。 | 双結晶(日本の双結晶とも呼ばれる)との一般的な接触 | 結晶表面によく見られる横縞 | |
| クリソベリル | 三方晶系 | 柱状結晶化特性(図2-¬2-52) | 単結晶は希少 | 三結晶が一般的で(図2-2-53)、六角形と凹角が識別基準として使用できる。 | 三結晶の縞模様は、識別基準として使用できる。 |
| トパーズ | 柱状晶癖(図2-2-54) | 断面は菱形で、上部は封筒状に見えることが多い(図2-2-55)。 | 双結晶は珍しい | 目に見える縦縞 | |
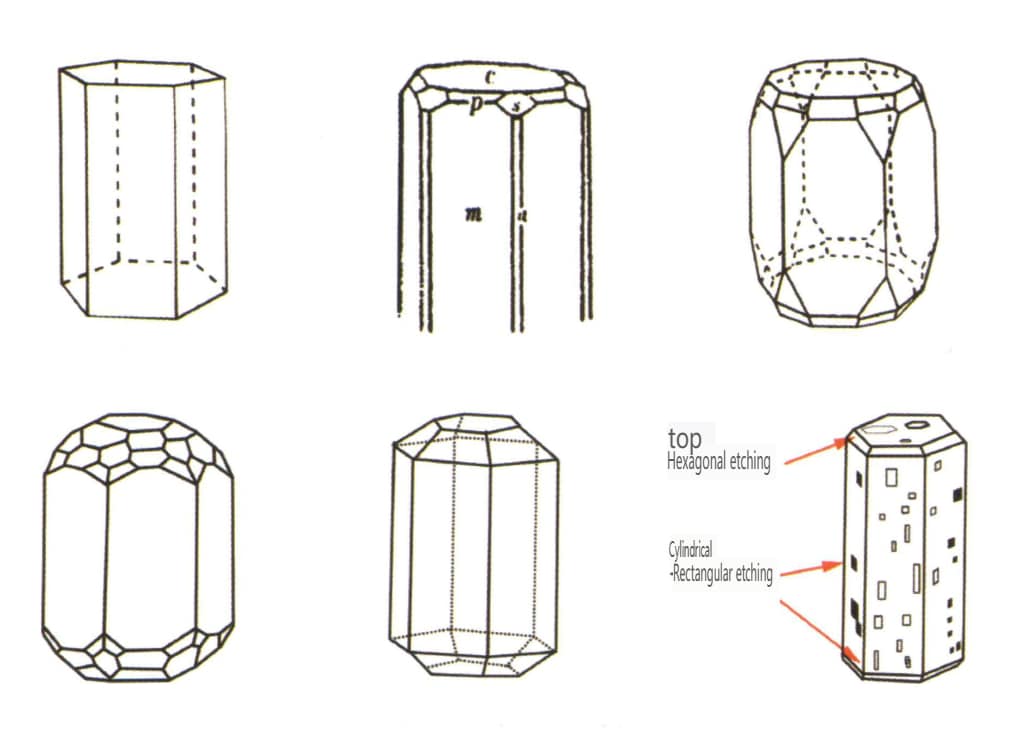
図2-2-38 ベリルの結晶癖

図2-2-39 エメラルドの一般的な結晶の形

図2-2-40 アクアマリンの一般的な結晶形
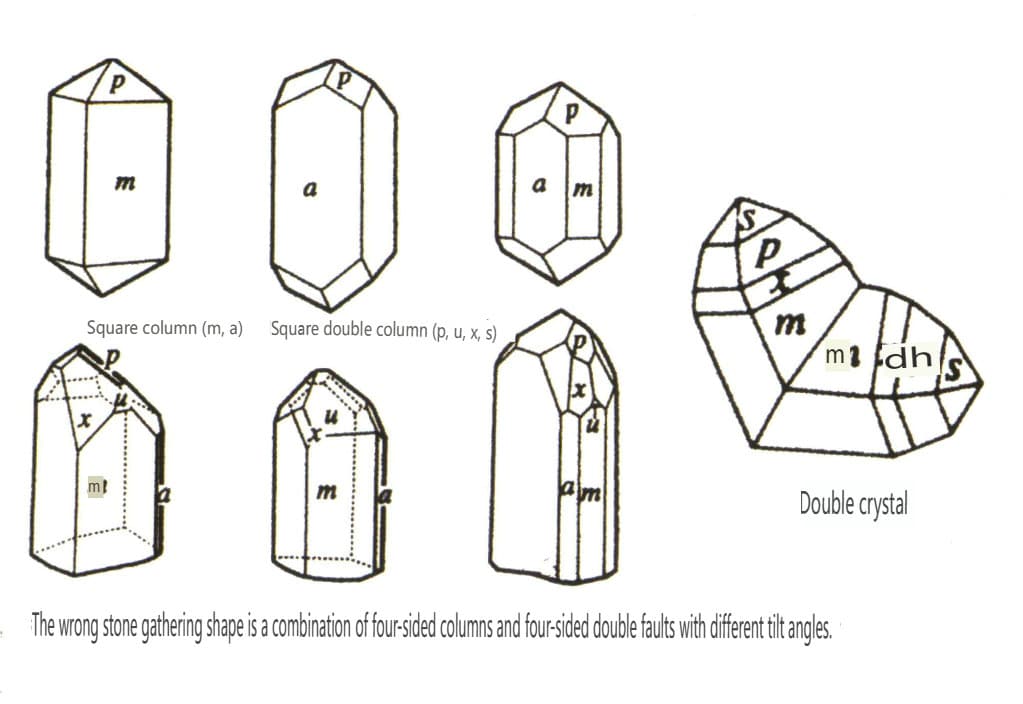
図 2-2-41 ジルコンの結晶癖

図2-2-42 ジルコン結晶
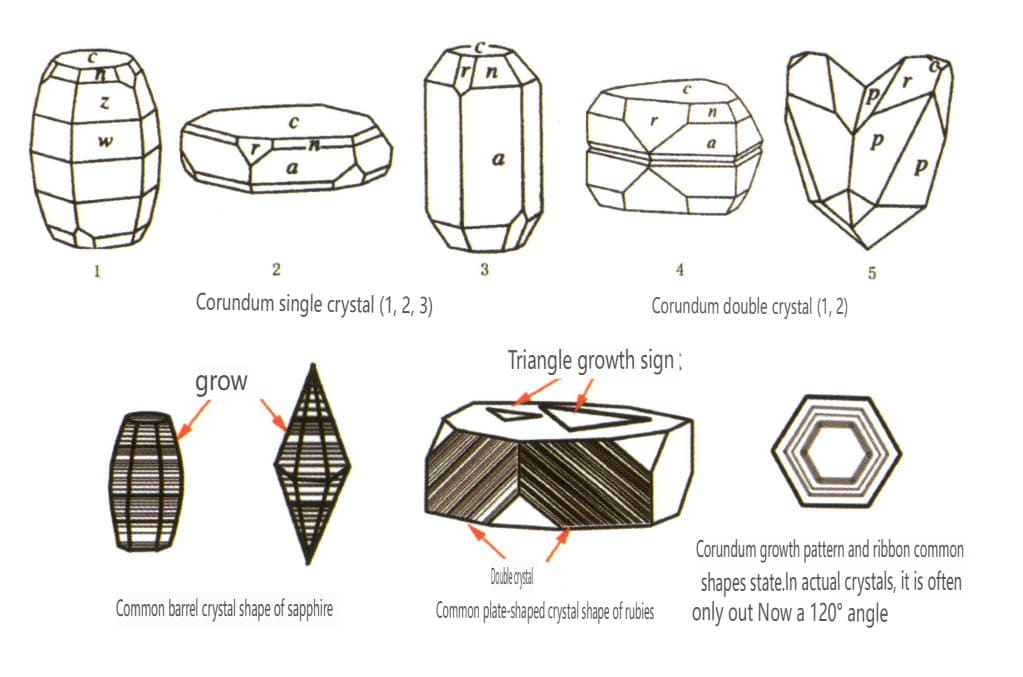
図2-2-43 コランダムの結晶癖

図 2-2-44 ルビー・クリスタル

図 2-2-45 ルビーのメカニカル・ツイン
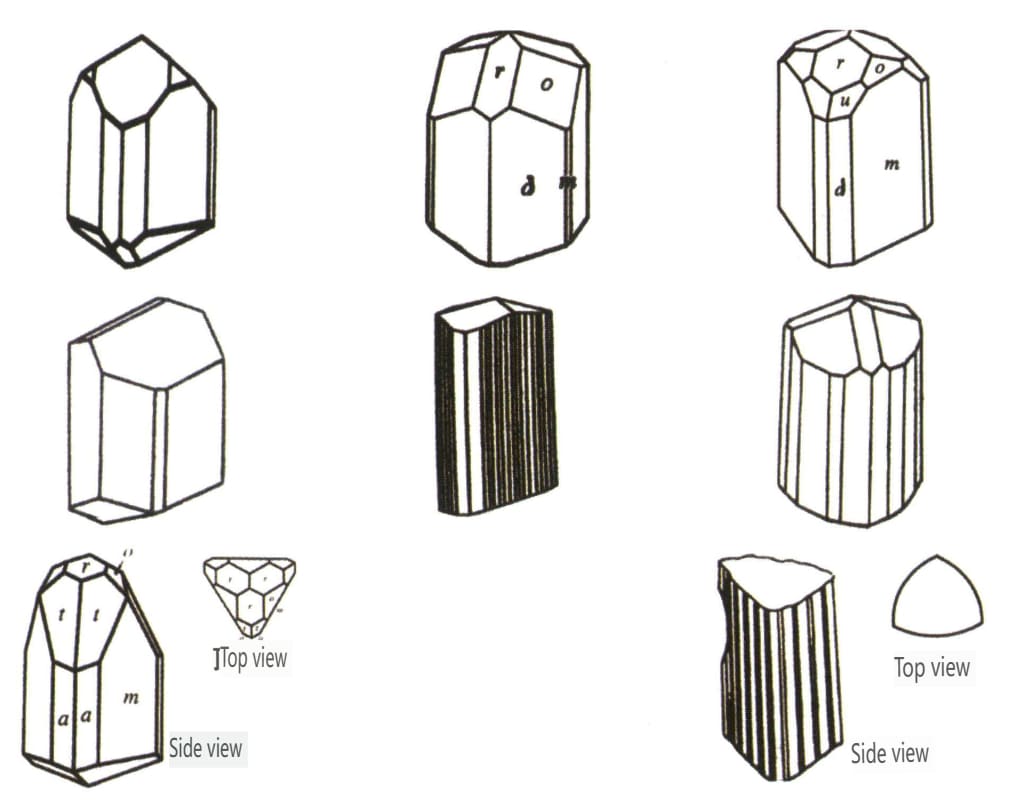
図 2-2-46 トルマリンの結晶癖

図2-2-47 トルマリン結晶

図2-2-48 トルマリン結晶の表面縦縞
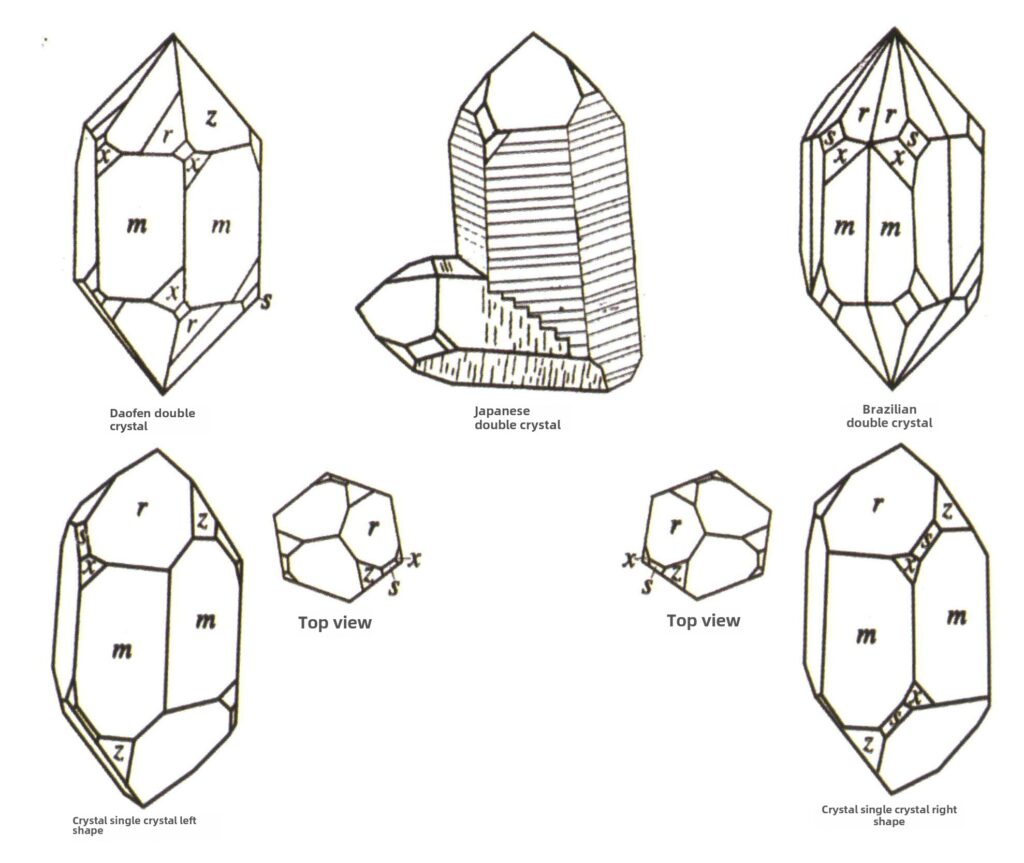
図 2-2-49 結晶の晶癖

図 2-2-50 クリスタル・ボディ

図 2-2-51 クリスタル・ボディ
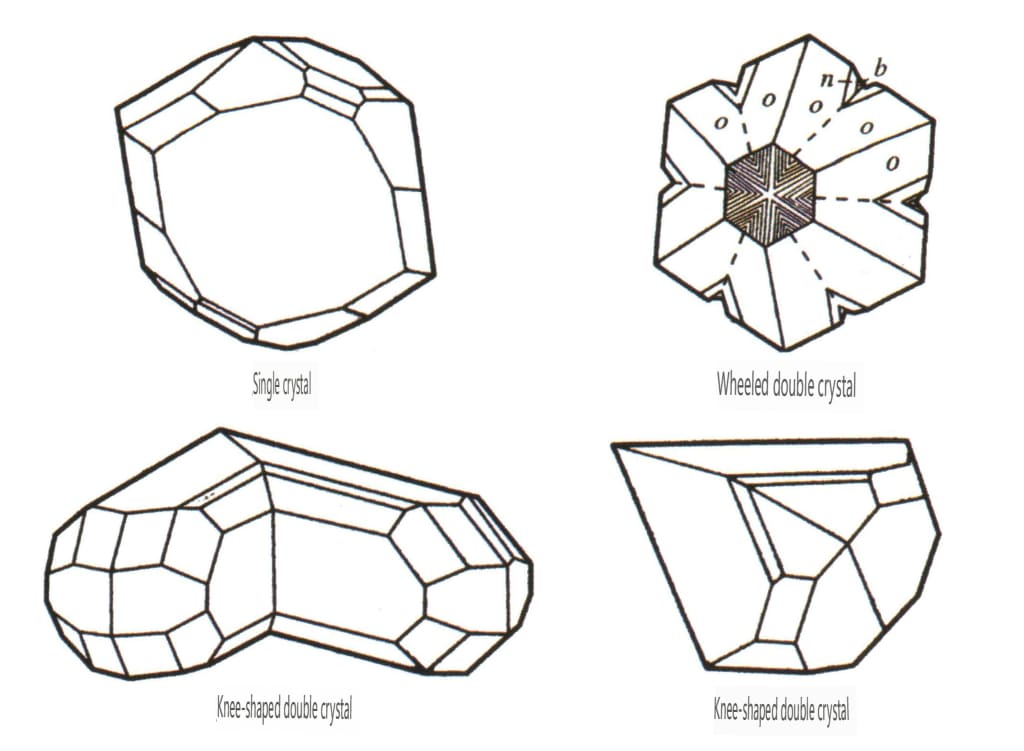
図2-2-52 クリソベリルの結晶癖

図2-2-53 クリソベリルの結晶
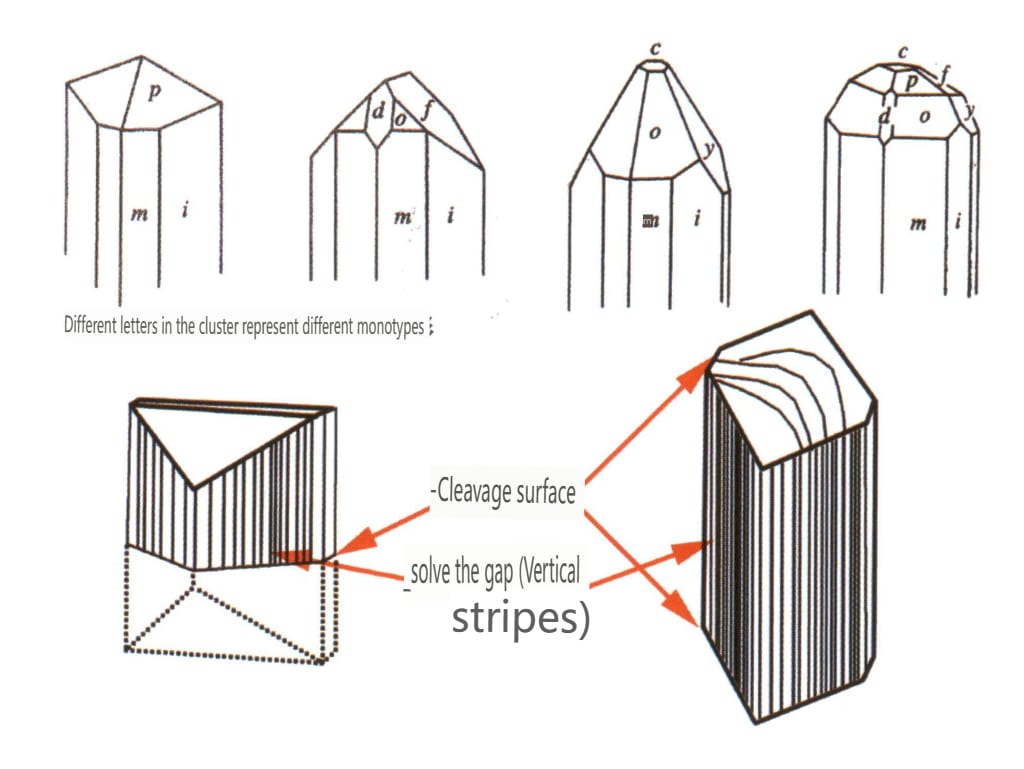
図2-2-54 トパーズの結晶癖

図 2-2-55 トパーズ・クリスタル
第四節 宝石の結晶はなぜ成長するのか?
微視的に見れば、宝石の結晶は異なる大きさの元素が異なる規則で配列された固体である。巨視的に見れば、多くの宝石はその組成の違いから結晶形状の特徴を持っている。しかし、異形などの特殊なケースも存在する。ここでは、宝石の結晶の形が異なる理由をよりよく理解するために、「異形」「同形」「分子力学的相互混合」「宝石鉱物に含まれる水」「宝石の化学組成」の5つの側面から紹介する。
1.異形
鉱物の中には、化学組成は同じでも、結晶構造(三次元空間における元素の配置)が大きく異なり、物理的・化学的性質が大きく異なるものがあります(表4)。この現象を異形性と呼び、例えばダイヤモンドとグラファイトがそうである(図2-2-56)。
一般的な石英には異形という現象がある。シリマナイト、アンダリュサイト、カイヤナイトは異形変種のグループである。
異形構造の変換は固体状態で起こる。構造変換の過程で、結晶内に圧力が発生し、結晶内部に双晶が形成されることがよくある。

表4:ダイヤモンドとグラファイトの特性の比較
| ミネラル | ダイヤモンド | グラファイト |
|---|---|---|
| コンポーネント | カーボン(C) | カーボン(C) |
| 結成条件 | 高温・高圧 | 高温 |
| 水晶系、癖 | 等角結晶系、八面体、菱形十二面体 | 六方晶系、層状 |
| カラー | 無色、黄色、青色、ピンク色、緑色など。 | ブラック |
| 光沢 | アダマンティンの輝き | メタリックな光沢 |
| 透明性 | 透明から不透明 | 不透明 |
| 屈折率 | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| 機械的特性 | 中程度の八面体劈開、硬度10、密度3.52 | 完全な劈開、硬度1、密度2.10 |
| その他の物件 | 優れた熱伝導性。半導体である天然ブルーダイヤモンドを除き、他の色のダイヤモンドは絶縁体である。 | 中程度の熱伝導性、良好な電気伝導性 |
2.同型
同型性とは、格子構造中の一部の粒子が、類似した性質を持つ他の粒子と置き換わることで、格子定数や物理的・化学的性質がわずかに変化する現象を指す。対照的に、結晶構造は基本的に変化しない。これは、宝石の結晶に含まれる元素が他の元素に置き換えられていると理解できる。対照的に、宝石結晶の元素の繰り返しパターンは、原子間の距離にわずかなずれがあるだけで変わりません。それでも、宝石の結晶の物理化学的性質はわずかに変化する(図 2-2-57~図 2-2-58)。
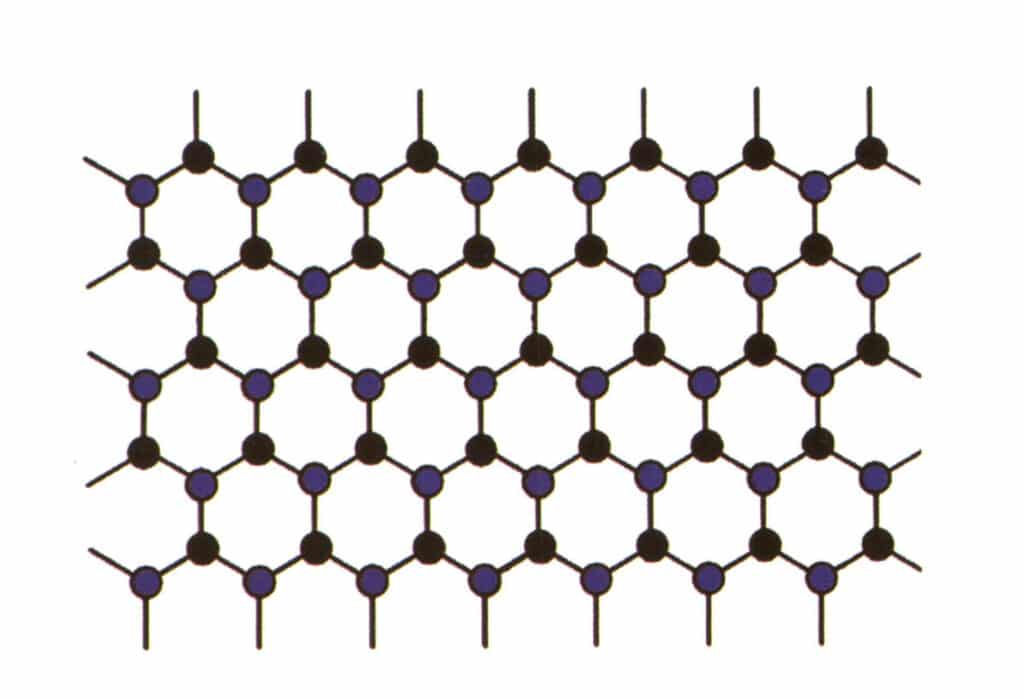
図 2-2-57 結晶構造シミュレーション図(青と黒は要素粒子)
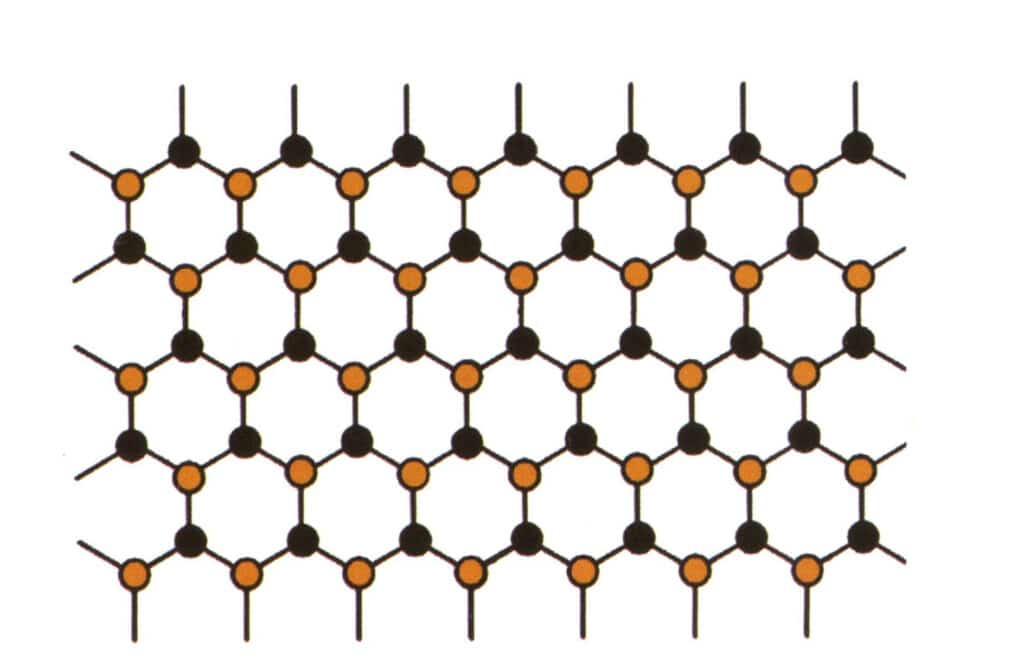
図 2-2-58 結晶構造シミュレーション図(黒色は元素粒子、黄色は青色元素粒子の一部を置換する新元素粒子、黄色はすべての青色粒子を完全に置換しない場合がある。)
同型性という概念は、なぜ同じ系列の宝石に多くの色があるのか、なぜ同じ系列の宝石に屈折率や密度の違いがあるのかを説明することができる。
ファミリーは、結晶元素の繰り返しパターンは同じであるが、物理的および化学的形態がわずかに異なる宝石の種類として理解することができる。例えば、コランダム・ファミリーにはルビーとサファイアがあり、ベリル・ファミリーにはエメラルド、アクアマリン、モルガナイトがある。
(1) オリビン
カンラン石の化学組成は(Mg,Fe)₂SiO₄。その組成において、FeとMg元素の完全な同型置換が起こる。カンラン石中のFe含有量が増加すると、カンラン石の色が濃くなり、屈折率が増加し、密度も増加する。
(2)コランダム
不純物を含まない純粋なコランダム(Al₂O₃)は無色で、CrがAlに置き換わると、ルビーと呼ばれるバラ色から赤色の色合いを呈する。残りの色はサファイアと呼ばれ、オレンジイエローのサファイアや無色のサファイアなどがある。一般にサファイアと呼ばれるものは、特にブルーサファイアで、Alの代わりにFeとTiが含まれている。代替宝石中の着色元素の含有量が多いほど、宝石の色は濃くなり、逆に含有量が少ないほど色は薄くなる。
(3) トルマリン
トルマリンはトルマリンと同種の宝石を指し、トルマリンは鉱物学名、トルマリンは宝石学名である。ベリルの化学組成は、(Na, Ca)R₃Al₃Si₆₁O₈(O, OH, F)であり、Rは主にMg , Fe , Cr , Li, Al , Mnであり、Rに含まれる元素は完全に、または部分的に互いに置換することができるため、トルマリンの色は極めて多様である。例えば、Rが主にFeの場合、ベリルは深い青色、あるいは黒色を呈し、Rが主にMgの場合、ベリルは黄色から褐色を呈し、Rが主にMgの場合、ベリルは黄色から褐色を呈する。 R が主にLiまたはMnの場合、ベリルはローズまたはライトブルーを呈し、Rが主にCrの場合、トルマリンはディープグリーンを呈する。
以上のことから、似た性質を持つ元素を代用することで、宝石の色がより美しく鮮やかになることがわかる。
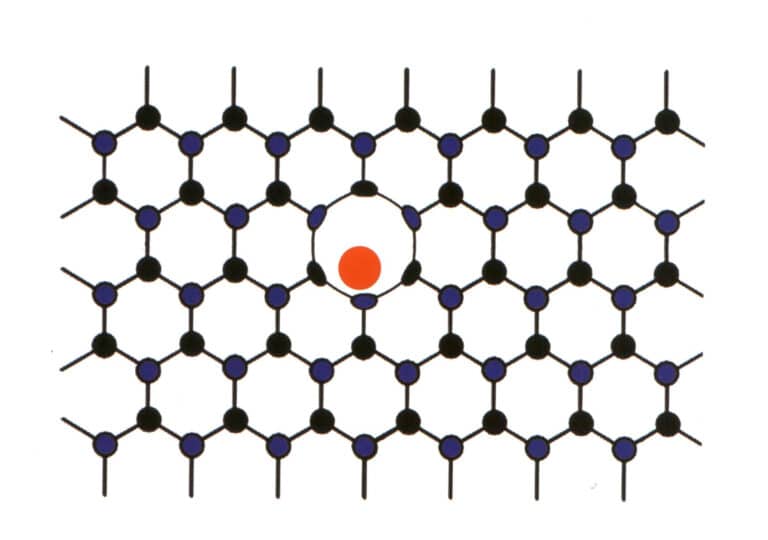
3.分子メカニカル混合
規則正しく並んだ宝石の主成分の間に、ある元素が無理やり入り込むことがある。しかし、入り込んだ元素の割合が低いため、宝石の主成分の繰り返しパターンが崩れることはなく、変形を起こすだけである(図2-2-59)。このような状態を分子力学的混在といい、例えばダイヤモンドでは窒素とホウ素が分子力学的混在を起こし、ブルー、ピンク、イエローのダイヤモンドが生成され、高い価値を持つ。
4.宝石鉱物に含まれる水
宝石の中には、宝石鉱物の重要な成分であり、宝石の性質と密接に関係する水を含むものがある。宝石に含まれる水は、その形態と結晶構造における役割から、結晶構造とは無関係な吸収水と、結晶化水、ゼオライト水、層間水、構成水など鉱物の結晶構造に関与する水に分けられる。宝石と密接に関係する水には、吸収水、結晶化水、体質水などがある。
一つはオパール(化学組成はSiO₂ - nH₂O、nはH₂Oの数を表し、含有量は可変である)のような水分子を吸収することであり、中性水分子は機械的に鉱物の粒子や亀裂の表面に吸着する。常圧で温度が100 ~ 110°に達すると、水分子はすべて脱出することができ、結晶格子構造を損傷しないので、強い光の暴露乾燥亀裂の長い時間のカウンターのオパールを避けるために、カウンターの中に水のカップを置く必要があります。
第二は、ターコイズの結晶水[化学組成はCuAl₆(PO₄)₈(OH)₄-4H₂O で、H₂Oの含有量は19.47%に達する]のような結晶化水である。この中性の水分子は格子内の固定位置に存在し、鉱物の化学組成の一部である構造単位としての役割を果たす。結晶化した水が抜け出る温度は一般的に600℃を超えず、通常は100~200℃で抜け出る。宝石が結晶水を失うと、結晶構造が損傷し、新しい構造が形成される。
第三は、構成水であり、結合水とも呼ばれ、OH-、H⁺、H₃O⁺プラズマの形で鉱物の格子に参加し、OH-が最も一般的である。構造水は鉱物の化学組成の一部であり、その組成の中で定義された割合で格子構造の固定された位置を占める。構造水は、その構造から抜け出し、損傷を与えるために高い温度を必要とし、通常は約600~1000℃である。宝石が構造水を失うと、その結晶構造は破壊される。多くの宝石は、トルマリン[化学組成は(Na、Ca)R₃Al₃Si₆₁O₁₈(O、OH、F)であり、Rは主にMg、Fe、Cr、Li、Al、Mnなどを含む、を含み、Rの元素は互いに完全または部分的に置換できる]、トパーズ[化学組成はAl₂SiO₄( F, OH)₂ ]。
5.宝石の化学組成
宝石は、他の物質と同様、化学元素から構成されている。宝石の各タイプは、その特定の化学組成と一定の変動範囲を持っており、それが宝石の様々な特性や性質を決定する。宝石は鉱物と岩石に属し、宝石の化学組成の分類は鉱物の化学組成にまで遡ることができる。
現在、鉱物の主な分類法には、化学組成による分類(ダナ系)、地球化学的分類、遺伝学的分類、応用分類、結晶化学的分類などがある。広く採用されているのは、化学組成と結晶構造に基づく化学的分類(ヒューゴ・シュトルツ方式)である(表5)。
表5:鉱物結晶化学分類システム
| レベルシーケンス | 分割の根拠 | 例 |
|---|---|---|
| 主要カテゴリー | 複合タイプ | 含酸素塩 大分類 |
| クラス | 陰イオンまたは複合陰イオンの種類 | ケイ酸塩クラス |
| (サブカテゴリー) | アニオン性錯体構造 | フレームワーク珪酸塩サブクラス |
| グループ | 結晶構造の種類とイオン特性 | コランダムグループ、ベリルグループ、ガーネットグループ |
| (サブグループ) | 陽イオンの種類 | アルカリ長石サブグループ |
| 種目 | 特定の結晶構造と化学組成 | オルソクレーズ KAlSi3O8 |
| 亜種 | 結晶構造は同じだが、組成や特性、形態が異なる。 | アデュラリア KAlSi3O8 |