Why Gemstones have multiple Colors?
Introduction of Crystal Field Theory & Molecular Orbital Theory & Energy Band Theory
The colors of gemstones are rich and varied, possessing a unique charm that people have always loved. The quality of gemstones largely depends on their color. The color of a gemstone is an important indicator in gemstone evaluation, and most optimization treatments for gemstones involve changing or improving their color. Therefore, understanding the causes of gemstone coloration is a crucial prerequisite for gemstone optimization treatment. Only by mastering how gemstones acquire their color can one determine whether a gemstone can be optimized, which optimization scheme to adopt, and which experimental plan to establish. There are five common theories of gemstone coloration: classical mineralogy theory, crystal field theory, molecular orbital theory, energy band theory, and physical optical effects. These theories constitute the coloration theories of common natural gemstones, and the following is a brief introduction to these five coloration theories.
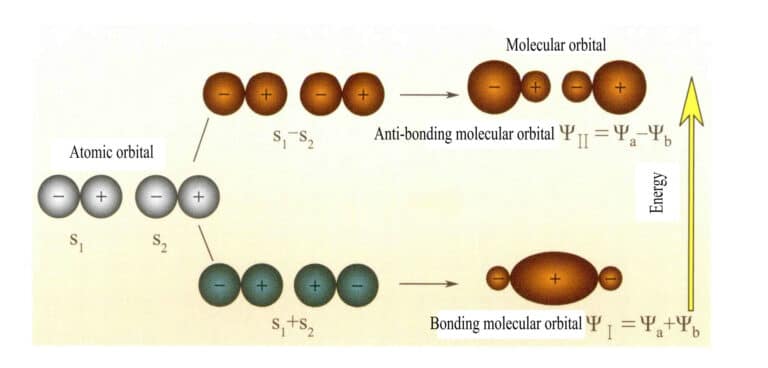
Molecular orbitals formed by two s atomic orbitals
Tartalomjegyzék
Section I Crystal Field Theory
Scientists in the 1930s proposed Crystal field theory to explain the properties of crystals. Crystal field theory is a theory that studies the chemical bonds of transition elements (complexes). It explains the physical and chemical properties of transition elements and lanthanide elements by combining some viewpoints of electrostatic theory, quantum mechanics, and group theory (the theory that studies the symmetry of matter), focusing on the influence of ligands on the d and f orbitals of the central ions. By the 1950s, people applied crystal field theory to complexes and proposed ligand field theory. Ligand field theory is an advancement of crystal field theory; it considers both the influence of the ligand’s electric field on the central ion and the filling effect of the ligand’s electrons on the central ion, making it more complete than crystal field theory. However, there is no essential difference between the two, and they are generally not distinguished in the study of inorganic minerals.
1. Basic Concepts of Crystal Field Theory
The ions of transition metals are in the crystal field of surrounding anions or dipole molecules. Crystal field theory is an electrostatic model that views the crystal as an electrostatic interaction between positive and negative ions, where the positively charged cation is called the central ion, and the negatively charged anion is called the ligand.
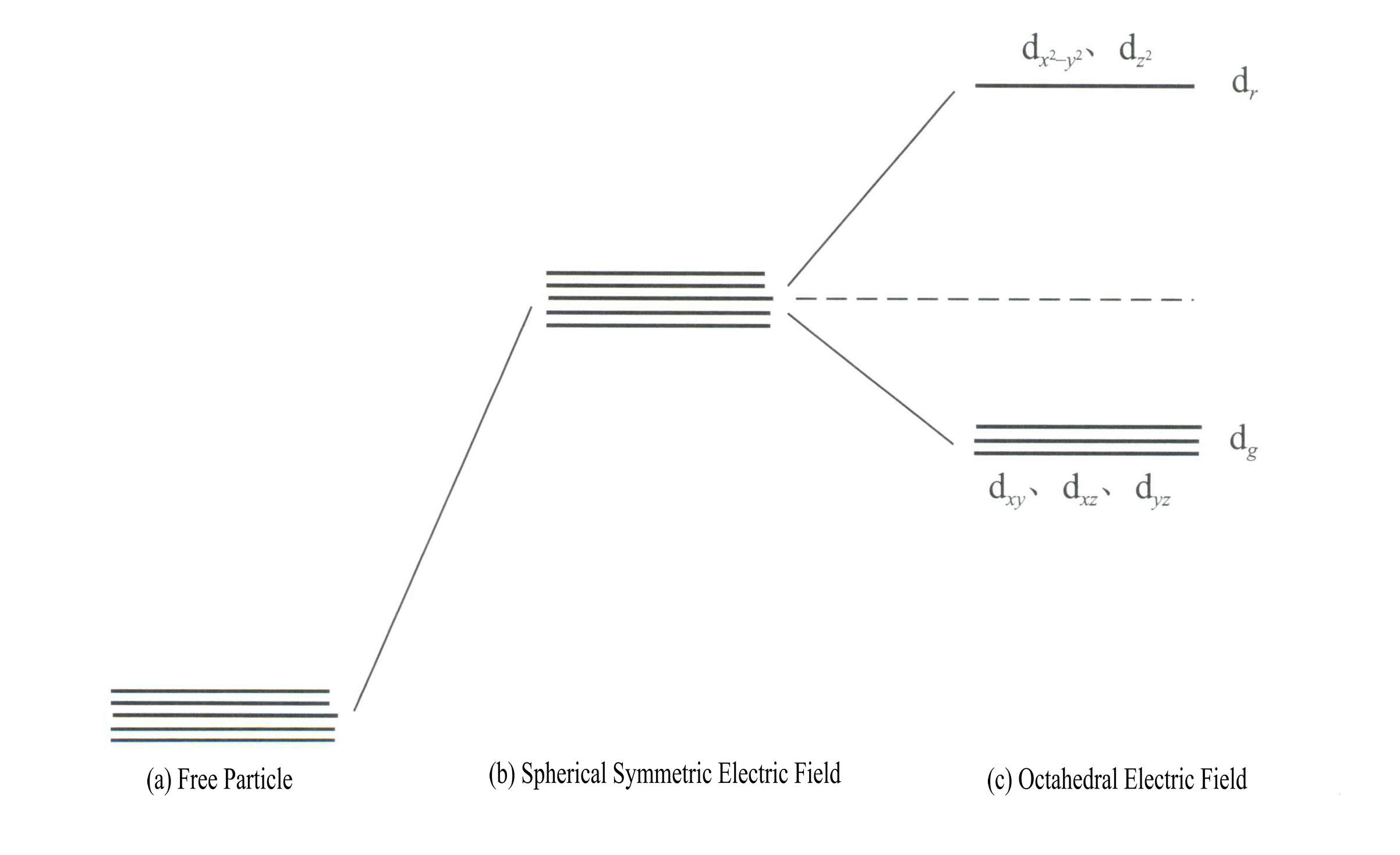
Applying crystal field theory to explain the color of gemstone minerals mainly involves the d electrons or f electron energy of transition element ions. For example, the d orbitals have five types: dxy, dxz, dyz, d , and d . These five d orbitals have different spatial distributions in the free ion state but have the same energy. However, they undergo significant changes under the influence of the ligand field. The five energy-degenerate d orbitals of the central atom split under the influence of the negative electric field formed by surrounding ligands. Some d orbitals have increased energy, while others have decreased energy. Due to the splitting of the d orbital energy levels, the electrons in the central atom’s d orbitals will rearrange, preferentially occupying the lower energy orbitals, thereby reducing the system’s total energy and making the complex more stable.
The energy of the d orbitals is the same when there is no electric field [Figure 3-19 (a)]; under a spherically symmetric electrostatic field, the d orbitals have increased energy but will not split [Figure 3-19 (b)]; when the ligand field is octahedral, it splits into dr and dg. Of these, dr orbitals are composed of d and d , with higher energy; the lower-energy dg orbitals are composed of dxy, dxz, dyz.
The ions of transition metals are in the crystal field of surrounding anions or dipole molecules. Crystal field theory is an electrostatic model that views the crystal as an electrostatic interaction between positive and negative ions, where the positively charged cation is called the central ion, and the negatively charged anion is called the ligand.
Applying crystal field theory to explain the color of gemstone minerals mainly involves the d electrons or f electron energy of transition element ions. For example, the d orbitals have five types: dxy, dxz, dyz, d , and d . These five d orbitals have different spatial distributions in the free ion state but have the same energy. However, they undergo significant changes under the influence of the ligand field. The five energy-degenerate d orbitals of the central atom split under the influence of the negative electric field formed by surrounding ligands. Some d orbitals have increased energy, while others have decreased energy. Due to the splitting of the d orbital energy levels, the electrons in the central atom’s d orbitals will rearrange, preferentially occupying the lower energy orbitals, thereby reducing the system’s total energy and making the complex more stable.
The energy of the d orbitals is the same when there is no electric field [Figure 3-19 (a)]; under a spherically symmetric electrostatic field, the d orbitals have increased energy but will not split [Figure 3-19 (b)]; when the ligand field is octahedral, it splits into dr and dg. Of these, dr orbitals are composed of dx2– y2 and dz2
, with higher energy; the lower-energy dg orbitals are composed of dxy, dxz, dyz. [Figure 3-19 (c)]
The difference between the highest and lowest energy levels after d orbital splitting is called the separation energy △ . The separation energies produced by different configurations of ligand fields are not the same (Figure 3-20). Their energy order is:
Square field > Octahedral field > Tetrahedral field

Even for fields of the same configuration, they may also differ due to the differences in ligands and central ions; the larger it is, the more stable the crystal. The following three factors mainly determine the size of the crystal separation energy:
(1) Crystals formed by the same transition element; when the ligands are the same, the higher the charge of the central ion, the greater the separation energy △ . The higher the positive charge of the central ion, the greater the attraction to the ligands, resulting in a smaller distance between the central ion and the ligand nucleus, and the greater the repulsive force of the crystal field generated by the ligands on the electrons, the greater the separation energy △ .
(2) For crystals formed by different ions with the same positive charge and the same ligands, the larger the radius of the central ion, the further the d orbitals are from the nucleus, and the greater the separation energy △ .
(3) For crystals formed by the same central ion and different ligands, the separation energy varies due to the differing strengths of the ligand’s crystal field. Different ligands have different field strengths, and the separation energy △ varies with the ligand’s field strength.
The separation energy is used to qualitatively explain the stability of crystals; it is not necessary to obtain the absolute value △ , as knowing the relative values of the crystal under different conditions is sufficient.
Based on the relative energy of the split d orbitals, the total energy of transition metal ions in the d orbitals can be calculated. This energy is lower than before the splitting, thus providing additional energy to the crystal, known as the crystal field stabilization energy, represented by the symbol CFSE. Table 3-10 lists the stabilization energies of ions containing dn electrons under different conditions.
Table 3-10 Crystal Field Stabilization Energies under Different Ligands (Wu Ruihua, 1994)
| dn | Weak Field | Strong Field | ||||
|---|---|---|---|---|---|---|
| dn | Négyzet | Regular Octahedron | Regular Tetrahedron | Négyzet | Regular Octahedron | Regular Tetrahedron |
| d0 | 0 | 0 | 0 | 0 | 0 | 0 |
| d1 | 5.14 | 4 | 2.67 | 5.14 | 4 | 2.67 |
| d2 | 10.28 | 8 | 5.34 | 10.28 | 8 | 5.34 |
| d3 | 14.56 | 12 | 3.56 | 14.56 | 12 | 8.01 |
| d4 | 12.28 | 6 | 1.78 | 19.70 | 16 | 10.68 |
| d5 | 0 | 0 | 0 | 24.84 | 20 | 8.90 |
| d6 | 5.14 | 4 | 2.67 | 29.12 | 24 | 6.12 |
| d7 | 10.28 | 8 | 5.34 | 26.84 | 18 | 5.34 |
| d8 | 14.56 | 12 | 3.56 | 24.56 | 12 | 3.56 |
| d9 | 12.28 | 6 | 1.70 | 12.28 | 6 | 1.78 |
| d10 | 0 | 0 | 0 | 0 | 0 | 0 |
2. Color Characteristics of Transition Metal Ions
In his colored gemstones, the color of most gemstones is due to transition metal ions, and the color of the gemstones is related to whether the coloring ions contain unpaired electrons in the d or f orbitals. The coloring characteristics of transition metal ions mainly include the following aspects:
(1) The coloration of transition metal ions is related to the electronic states of the d orbital or f orbital. When the d orbital or f orbital electrons are filled or empty, the gemstone will not exhibit color. For example, Cr6+, Ce4+, és Cu+.
(2) Different coloring ions exhibit different colors in the same gemstone material. Due to the different separation energies of different coloring ions, they can present different colors even in the same material. For instance, Fe2+ produces a slightly grayish-blue color in spinel, while Cr3+ produces red.
(3) Coloring ions of the same element in different valence states often exhibit different colors in the same gemstone material. Because the energy required for the d-electron transitions of the central ion is different, the absorbed wavelengths of light are different, resulting in different colors. For example, a castrum containing Mn2+ presents a soft pink hue, while a beryl containing Mn2+ presents bright red, known as red beryl.
(4) Coloring ions of the same element in the same valence state often exhibit different colors when in different configurations of ligands. For example, Co2+ in the tetrahedral configuration of spinel shows a characteristic “diamond blue” color, while in the octahedral configuration of calcite, it appears pink. Fe2+ in the octahedrally coordinated olivine shows a characteristic olive green, while in the distorted cubic coordinated almandine, it appears deep red.
(5) The same type of colored ions have the same valence state and coordination geometry, but different adjacent coordinating atoms exhibit different colors. For example, in the tetrahedral coordination of Co2+, in sphalerite, Co2+ is connected to sulfur, showing green, while in spinel, Co2+ is connected to oxygen, showing blue.
(6) The same type of colored ions with the same valence state, coordination geometry, and adjacent atoms exhibit different colors in different gemstones. The distortion of the coordination geometry caused by the different chemical compositions of the gemstones changes the nature of the chemical bonds between the central ion and the coordinating ligands, altering the transition energy of the d electrons. For example, Cr3+ appears red in ruby, green in emerald, and shows variable colors in alexandrite. The reason for such changes in Cr3+ is related to its characteristics and the adjacent coordinating ligands, with specific feature analysis as follows.
① Cr3+ Characteristics:
Cr3+ has an outer electron shell structure of 3s23p63d3, with 11 electrons in the outer shell, belonging to an irregular (8-18) electron shell structure.
This structure has a smaller shielding effect on the nucleus than the 8-electron shell structure, resulting in Cr3+ having a higher effective positive charge, while its ionic radius is also smaller, which forms the basic characteristics of Cr3+: a strong positive electric field and empty d orbitals. Cr3+ can provide six empty orbitals to accommodate six coordinating ligands, with a spatial configuration of octahedral, belonging to d2sp3 hybridization (Figure 3-21).
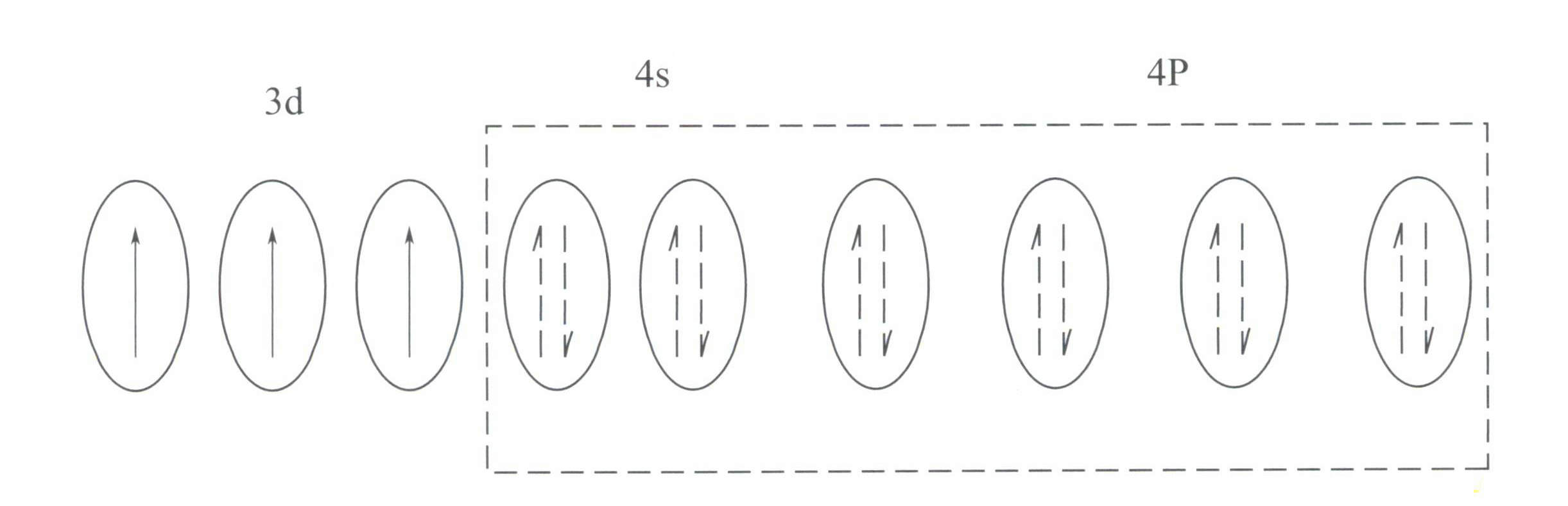
According to crystal field theory, in an octahedral field, the d orbitals of Cr3+ can split into lower energy dƐ orbit and higher energy dr orbit. Since the three d electrons of Cr3+ are all in the dƐ orbital and are all single electrons, d-d transitions can occur under visible light, causing gems containing Cr3+ to exhibit color.
② The coloring mechanism of Cr3+:
In ruby The main chemical component of ruby is Al2O3. When a few percent of Cr3+ replaces Al3+, it produces a bright red color. In the structure of ruby, due to the larger radius of Cr3+ compared to the radius of Al3+, Cr3+ enters the corundum lattice, reducing the symmetry around aluminum oxide.
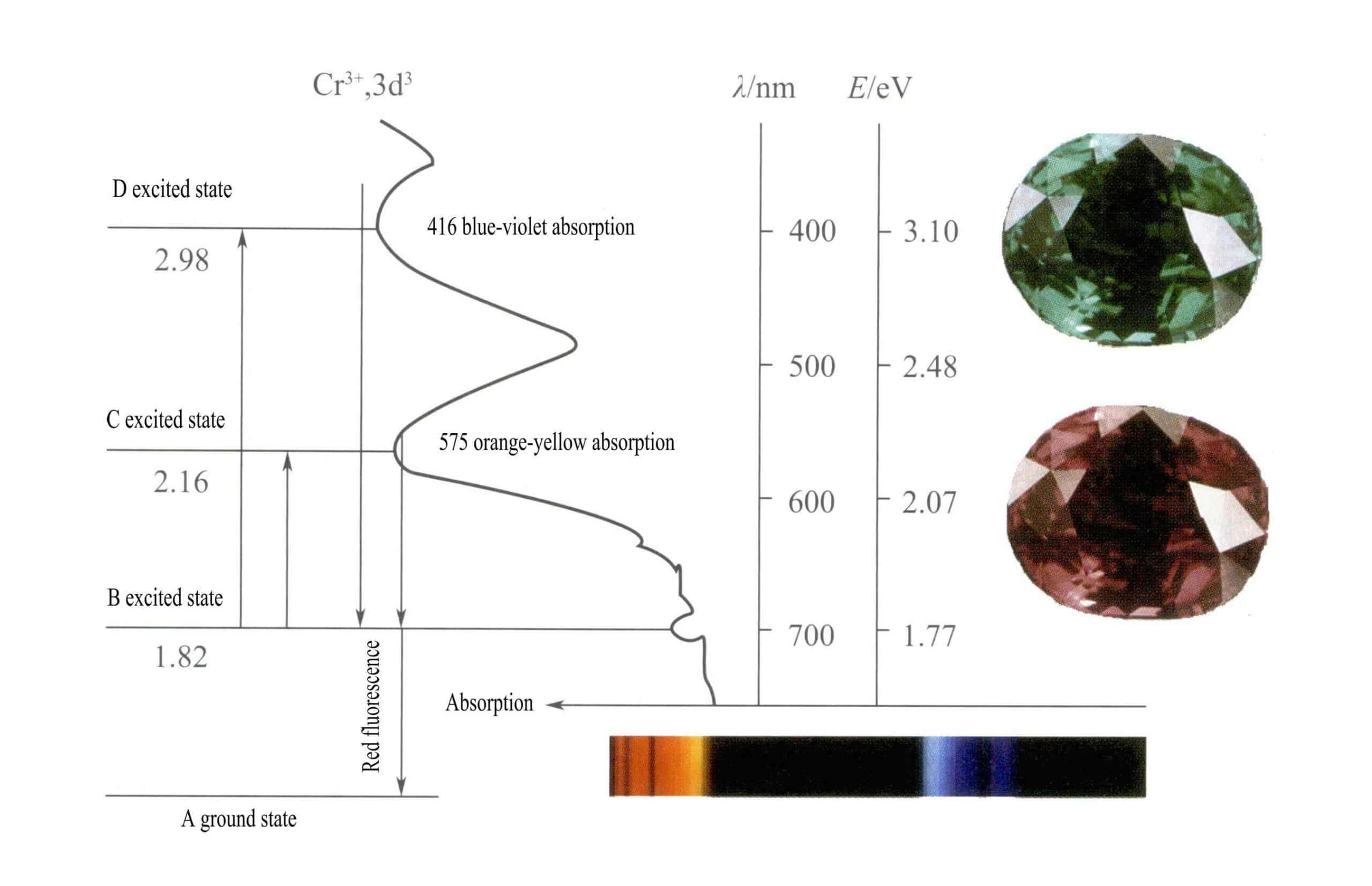
The d orbitals of Cr3+ split, and when excited state electrons return from D or C to the ground state A, they must first pass through B, releasing heat. They return from B to A, accompanied by luminescence, emitting red fluorescence. In this process, electrons absorb light energy, causing ruby to absorb D violet (400nm) and C yellow-green (555nm) visible spectrum (Figure 3-22), forming an absorption band.

When white light passes through a ruby, photons in the spectrum from purple to yellow-green are absorbed, while almost all red light and some blue light pass through, giving the ruby a deep red color with a hint of purple, known as pigeon blood red.
Rubies exhibit a brief B-level absorption, manifested as red fluorescence. This B-level absorption that produces red fluorescence makes the color of the ruby more vivid; the higher the chromium ion content, the stronger the fluorescence.
Iron ions in the gemstone can suppress the fluorescence of B-level absorption, explaining the phenomenon of rubies appearing darker when containing iron impurities.
③ Cr3+ The coloring mechanism in emeralds
The main chemical component of emerald is Be3Al2Si6O18, Cr3+, which replaces Al3+ in the emerald lattice, and Cr3+ is also surrounded by an octahedron composed of six oxygen ions, where the Cr3+-O bond length is also quite similar to that in rubies. However, compared to rubies, emeralds have two more ions, Be2+ and Si4+. In the structure of emeralds, the covalent bond nature between metal oxides increases, while the ionic characteristics weaken.
Minor changes like chemical bonds lead to a slight decrease in Cr3+C level and D level energy, resulting in a slight shift of the absorption band (Figure 3-23), significantly blocking the transmission of blue-purple (425nm) and orange-yellow (608nm) light in the spectrum, while increasing the transmission of blue-green light, thus forming the characteristic emerald green.

The B-level absorption of dioptase is almost unchanged. When impurity iron has no “inhibitory” effect in the emerald component, the strong red fluorescence makes the characteristic emerald green shine even brighter.
④ Cr3+ The color mechanism in alexandrite:
The color of alexandrite is also caused by Cr3+ Al helyettesítésére3+ in distorted octahedral coordination. Due to the chemical composition of alexandrite being BeAL2O4, the nature of the chemical bonds between its metal-oxygen ions lies between that of ruby and emerald. Therefore, its absorption bands also lie between those of ruby and emerald, with the transmission probabilities of blue-violet and orange-yellow light being roughly equal, making it impossible to determine whether red or blue-green light is dominant (Figure 3-24).
Therefore, the color of alexandrite can only depend on the energy distribution and color range of the incident light, thus resulting in the “color-changing effect” of alexandrite, i.e., appearing green in daylight with a high blue light component and red in incandescent light with a high red light component. Therefore, alexandrite is often called “the emerald of the day and the ruby of the night.”
The “color change effect” appears in many types of gemstones, such as color-changing corundum and color-changing garnet. Currently, artificially synthesized color-changing corundum is produced using the principle of color change, employing V3+ as the coloring ion for synthesis.
3. Colors of Gemstone Minerals
The colors produced by transition metal components can be inferred from the chemical composition of gemstone minerals. For example, turquoise containing Cu2+ must be blue, while Cu+ is colorless. Table 3-11 lists the colors produced by common transition metal components in natural gemstone minerals.
Table 3-11 Colors Produced by Transition Metal Components in Natural Gemstone Minerals
| Elem | Színes | Common Minerals |
|---|---|---|
| Cerium (Ce) | Sárga | Parisite |
| Króm (Cr) | Red, Green, Orange, etc. | Crocoisite, Red Crocoisite, Uvarovite |
| Cobalt (Co) | Kék | Szintetikus spinell |
| Copper (Cu) | Blue, Green | Azurite, chrysocolla , Turquoise malachite, Dioptase |
| Iron (Fe) | Red, green, yellow | Almandine, olivine, goethite |
| Manganese (Mn) | Rózsaszín, narancssárga | Rhodonite, spessartine |
| Nikkel (Ni) | Zöld | Bunsenite, Chalcedony |
The color of most gemstones is caused by the transition metal impurities they contain. For example, rubies appear red due to trace amounts of Cr3+. Various factors influence the color caused by impurity ions in the gemstone. Therefore, impurities may produce different colors in different gemstones. For instance, Cr3+ appears red in rubies and green in emeralds.
The same impurities may not necessarily cause the same color of a gemstone. For example, the green color of most emeralds is caused by Cr, while some emeralds’ green color is partially or entirely caused by vanadium (V).
The crystal field theory can not only be used to explain the gemstone colors produced by transition metal components or impurities but also the colors produced by structural defects (color centers); the specific process of color generation can be referred to in Chapter 3.3 of this book.
There are also shortcomings in the explanation of gemstone mineral colors by crystal field theory, mainly reflected in the following aspects:
(1) The electrons of the central ion d are not completely localized in their original orbitals. They can also appear around the coordinating atoms, indicating a covalent interaction between the central atom and the ligands.
(2) It only considers the electrostatic ionic interaction between the central atom and the ligands, completely ignoring the covalent bonding interaction between the central atom and the ligands. In physical research, the results of quantitative calculations often differ significantly from actual situations.
(3) The reasons for the color of gemstone minerals, in addition to the interaction between the central ion and the ligands, may also be due to the combined effects of structural defects and the crystal field.
Section II Molecular Orbital Theory
Mulliken and Hund initially proposed molecular orbital theory (MO theory). Through the continuous exploration of many scientists, it has developed into a mature theory. Molecular orbitals (MOs) can be obtained by linear combinations of atomic orbitals, a commonly used method for constructing molecular orbitals. From n atomic orbitals, n molecular orbitals can be obtained, and the linear combination coefficients can be determined using the variational method or other methods. Molecular orbitals formed by two atomic orbitals, with energy levels lower than those of the atomic orbitals, are called bonding orbitals; those with energy levels higher than the atomic orbitals are called antibonding orbitals; those with energy levels close to the atomic orbitals are generally non-bonding orbitals.
Molecular orbital theory is a theory used to explain issues such as molecular formation, structure, and properties. It can also explain some of the causes of gemstone colors, which have been developed based on crystal field theory and transition metal molecular orbital theory. Molecular orbitals are a natural extension of atomic orbitals. In a molecule, electrons no longer belong to a specific atom but move across the entire molecular range; therefore, the movement of electrons in a molecule is described using molecular orbitals.
1. Basic Concepts of Molecular Orbital Theory
The molecular orbital theory posits that after atoms form a molecule, electrons no longer belong to the original atomic orbitals as proposed by crystal field theory but move within certain molecular orbitals. Molecular orbitals compose a molecule just as atomic orbitals compose an atom. Valence electrons are no longer considered localized within individual atoms but move throughout the entire molecule. The electron distribution in the molecule can be treated according to the principles of electron distribution in atoms (the principle of minimum energy and Hund’s rule).
The linear combination of atomic orbitals in a molecule forms molecular orbitals. The number of molecular orbitals equals the number of atomic orbitals before the combination. The combination of atomic orbitals into effective molecular orbitals must adhere to the following three principles:
(1) Symmetry Matching Principle: Only atomic orbitals with the same symmetry can form molecular orbitals.
(2) Energy Proximity Principle: Only atomic orbitals with similar energies can combine to form effective molecular orbitals.
(3) Maximum Overlap Principle: Under symmetry matching, the greater the overlap of atomic orbitals, the more the energy of the resulting molecular orbitals decreases and the more stable the resulting chemical bond.
Molecular orbital ψ is the wave function of a single electron. It can be represented as a linear combination of atomic orbitals, with each orbital corresponding to a specific energy, which is the sum of the kinetic and potential energy of the electron moving in the molecular electric field. Two atomic orbitals, a and b, through overlapping linear combinations, produce two molecular orbitals ψI and ψII :
ψI=ψa + ψb (3-5)
ψII = ψa – ψb (3-6)
When molecular orbitals with electrons are filled first, the bonding orbitals ψI are filled first. When electrons fill molecular orbitals of equal energy, according to Hund’s rule, they should also occupy different molecular orbitals with the same spin direction as much as possible.
The molecular orbitals ψI obtained by adding two atomic orbital functions (Equation 3-5) are called bonding molecular orbitals. The molecular orbitals ψII obtained by subtracting two atomic orbital functions (Equation 3-6) are called antibonding molecular orbitals. The energy of bonding molecular orbitals is lower than that of antibonding molecular orbitals and lower than the energies of the original two atomic orbitals. Thus, just like in the case of filling atomic orbitals, when filling molecular orbitals, electrons are first placed in bonding orbitals, and a molecular orbital can accommodate two electrons with opposite spins. When electrons fill molecular orbitals of equal energy, according to Hund’s rule, they should also occupy different molecular orbitals with the same spin direction as much as possible. The molecular orbitals formed by two s atomic orbitals are shown in Figure 3-25.

p Orbitals and d orbitals can also form molecular orbitals of different energy levels; for example, the combination of diatomic molecular orbitals in O2 molecules is relatively complex.
In experiments, the magnetic properties of these two single electrons were measured, providing strong support for molecular orbital theory. Unlike molecules composed of the same atoms, those composed of two or more different atoms have more complex molecular orbital energy levels, but the principle is the same.
2. Charge Transfer Coloration Characteristics
This theory of molecular orbitals, where the entire molecule shares electrons, is also regarded as the transition of electrons from one atomic orbital to another, known as charge transfer. Charge transfer can occur in metal-metal (M-M), non-metal-non-metal (L-L), and non-metal-metal (L-M) interactions. Among them, L-L, M-L these two types of bonding are often primarily covalent bonds. O2 belongs to L-L charge transfer, which is a covalent bond.
(1) Metal-Metal Charge Transfer ( M – M Charge Transfer)
This type of charge transfer generally occurs between common transition metal ions. Most of the coloration causes of colored gemstones are produced by metal-metal charge transfer. M-M Charge transfer mainly includes the following types: Fe2+ – Fe3+/Fe3+ – Fe2+; Ti3+ – Ti4+ / Ti4+– T3+ ;Fe2+ – T4+/Fe3+ – T3+; Mn2+ – Mn4+/Mn3+ – Mn3+ . Charge transfer between metals is divided into two types: charge transfer between homonuclear atoms and charge transfer between heteronuclear atoms.
① Charge transfer between isoelectronic atoms
Charge transfer between isoelectronic atoms occurs between two atoms of the same transition metal element in different oxidation states. For example, Fe2+ és Fe3+ undergo charge transfer under different redox conditions, absorbing energy and producing color. The blue-purple color of iolite is produced by the charge transfer of iron ions in different oxidation states. Fe3+ és Fe2+ are in tetrahedral and octahedral positions, respectively, with two ligands connected by edges. When visible light shines on iolite, one d electron of Fe2+ absorbs light of a certain energy and transitions to Fe3+, absorbing yellow light at 588nm and producing a blue-purple color. Aquamarine, green tourmaline, and others can also exhibit color due to charge transfer between iron ions.
② Charge transfer between heteroatoms
Blue sapphires most typically exemplify the color produced by charge transfer between two types of transition metal ions. The coordination polyhedra of transition metal ions are connected by edges or faces, facilitating charge transfer between metals.
For example, In sapphires, when iron ions and titanium ions enter the connected octahedra, both Fe and Ti exist in two oxidation states:
Fe2+ + Ti4+ low energy (3-7)
Fe3+ + Ti3+ high energy (3-8)
Transitioning from equation (3-7) to equation (3-8) requires absorbing a certain amount of light energy, resulting in a broad absorption band that ranges from yellow to red. In contrast, most blue light passes through the gemstone, giving it a blue appearance.
Charge transfer between different valence states has a strong directionality, and gemstones that exhibit color due to this mechanism often display pleochroism. For example, aquamarine colored by Fe2+→ Fe3+ charge transfer shows color strictly along the optical axis direction. Figure 3-26 shows that aquamarine appears yellow in the b and c planes. At the same time, there is no such transfer along the a-axis direction, resulting in no light absorption and, therefore, no color along the a-axis direction.
(2) Non-metal to metal (L-M) charge transfer
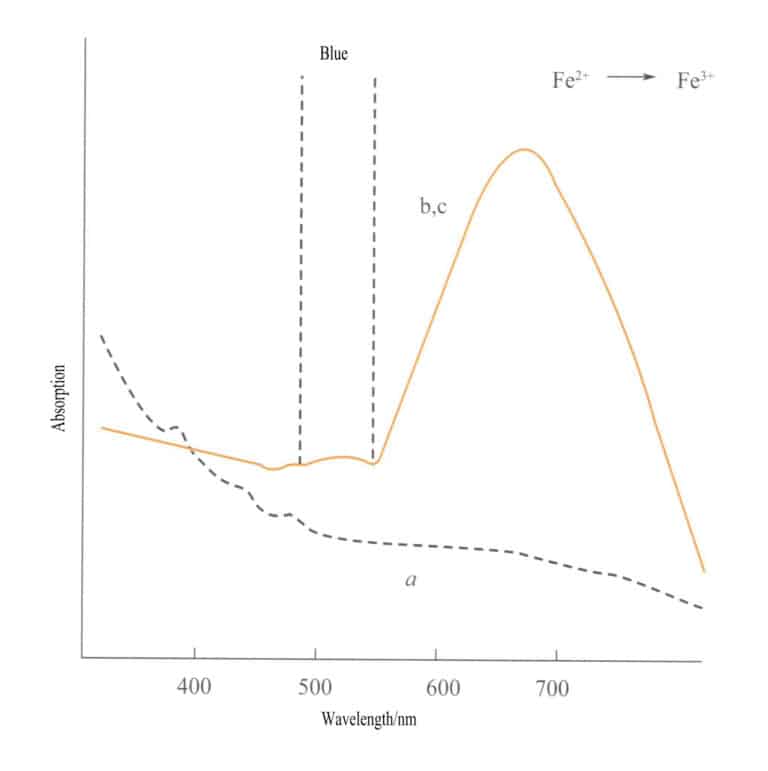
This type of L-M charge transfer often occurs between oxygen and metal ions, and some oxygen-containing gemstones are colored by non-metal to metal charge transfer, such as O2–→ Fe3+, O2- →Cr6+, O2-→Mn6+, O →V5+.
In the absorption spectrum of simple iron oxides (Figure 3-27), two weak absorption bands appear in the infrared region of ilmenite, hematite, and lepidocrocite ( d — d electronic transitions). A strong absorption band appears in the shortwave range, produced by O2-→Fe3+ charge transfer, and this absorption band determines the characteristic colors of these compounds: reddish-brown, brown, and yellow-brown.
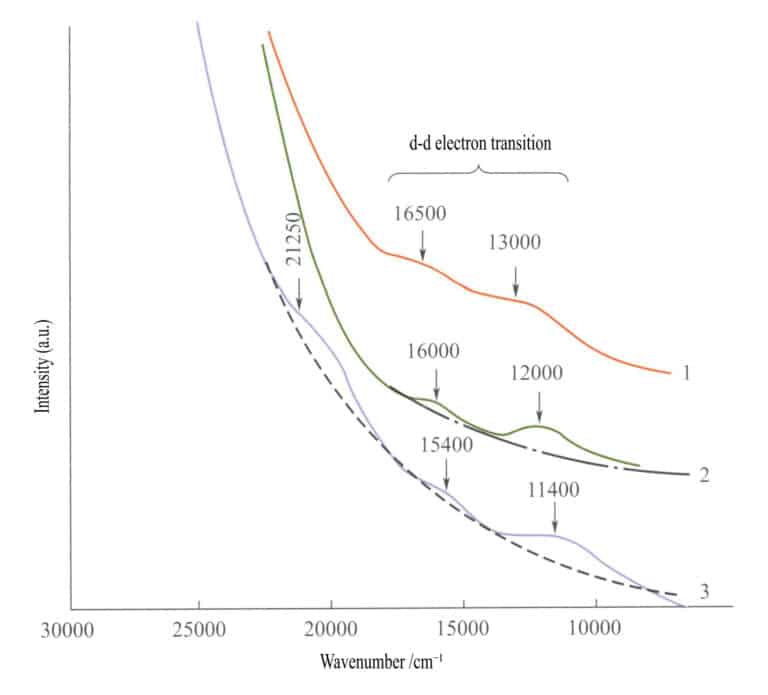
1 -Iilmenite; 2 – Hematite; 3 – Lepidocrocite
Yellow beryl gets its color from O2–→ Fe3+ charge transfer. In the structure of yellow beryl, O2–→ Fe3+ strong charge transfer absorption can extend from the ultraviolet end into the blue end of the visible spectrum, absorbing purple and blue, resulting in a yellow color.
Sapphire, which has a completely different coordination environment from beryl, can also produce the same spectral absorption bands as beryl, resulting in yellow, which is also a result of O2–→ Fe3+ charge transfer.
According to crystal field theory, some gemstone minerals do not contain unpaired electrons and cannot produce color. For example, the electronic layers of crocoite (PbCrO4), Pb2+, Cr6+, and O2– are full. Still, in the CrO42- atomic cluster are “molecular orbitals,” which correspond to the excited states during O2-→Cr6+ transfer, forming absorption bands and presenting orange.
L→M Charge transfer also includes the transfer of sulfur to metal, like in common pyrite; this optical phenomenon caused by the transfer is easier to understand when discussed using band theory.
(3) Non-metal to non-metal (L-L) charge transfer
Molecular orbital theory suggests that the deep blue color of lapis lazuli is due to the excitation energy levels of the S3- atomic group.
In graphite, the rings of six carbon atoms are arranged in layers. Along this layer, electrons can move to some extent freely, resulting in strong light absorption, anisotropy, and conductivity.
Some organic gemstones, such as amber and pearls, have electrons that move and excite through the atomic groups of organic pigments in shared molecular orbitals, causing the absorption of visible light and producing color. For example, the “honey yellow” of amber, the colors of coral, and some shells and colored pearls.
The color mechanisms of common gemstones are shown in Table 3-12.
Table 3-12 Classification of Color Mechanisms of Common Gemstones
| Metal - Metal Charge Transfer | Fe2+ - Fe3+ /Fe3+ - Fe2+ : iolite (blue), berthierite (blue), Magnetite (black), etc. |
| Fe2+ -Ti4+/Fe3+ - Ti3+ : Kyanite (blue), Sapphire (blue) | |
| Mn2+-Mn4+/Mn3+-Mn3+: Manganite (black), Bixbyite (black) | |
| Non-metal to metal charge transfer | O2- -Fe3+: Golden yellow beryl, golden yellow sapphire, ilmenite, hematite, lepidocrocite , etc. |
| O2- - Cr6+: Crocoite (orange) | |
| O2- -V5+:Vanadinite (orange) | |
| Sulfur to metal: pyrite, marcasite, etc. (see semiconductor with gap) | |
| Non-metal - non-metal charge transfer | S3-: Lapis lazuli (blue) |
| Π electronic: graphite (black) | |
| The colors of some organic gemstones such as amber and coral. |
Copywrite @ Sobling.Jewelry - Egyedi ékszergyártó, OEM és ODM ékszergyár
Section III Energy Band Theory
Energy band theory is a quantum mechanical model for studying gemstone materials, which is a further extension and expansion of molecular orbital theory. The study of energy band theory can better explain the color mechanism of some naturally colored gemstones.
1. Basic concepts of energy band theory
Energy band theory is an approximate theory used to study the laws of electron motion in solids. Solids are composed of atoms, which include atomic nuclei and outermost electrons, all of which are in a constant state of motion. Band theory posits that electrons in solids are not bound to a specific atom but are shared by the entire crystal and move within the periodic potential field of the three-dimensional space of the crystal. The range of electron motion is within the periodic potential field of the lattice, allowing the spatial distribution of electron orbits to exceed that of molecules, reaching a maximum. The energy levels of individual electrons are broadened into energy bands.
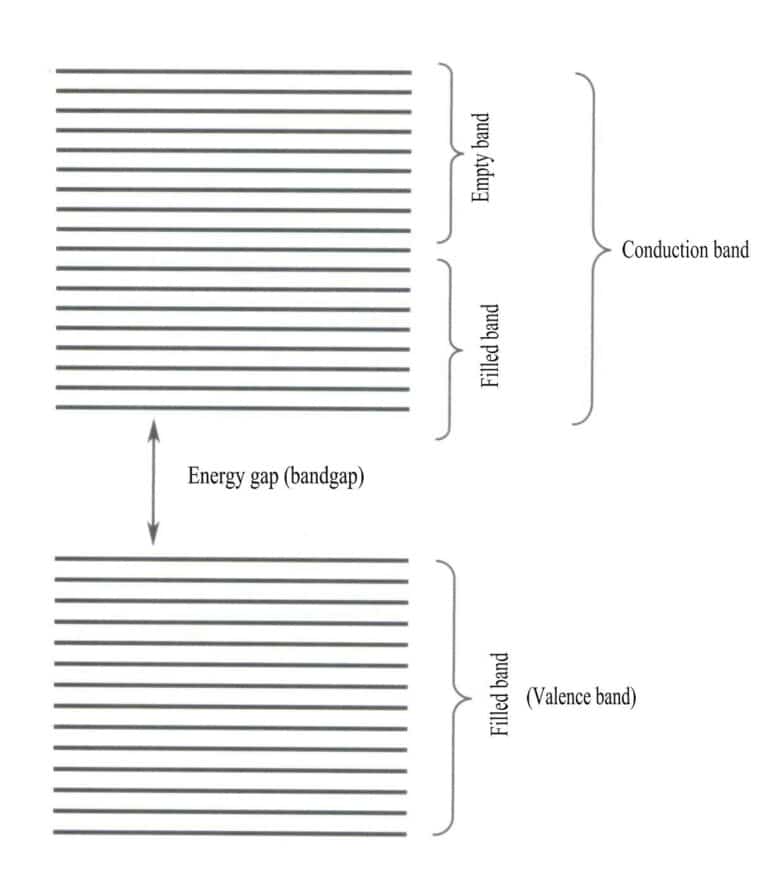
Band theory mainly discusses electron transitions between non-local states, where all valence electrons should belong to the entire solid lattice. According to band theory, solid materials can be divided into different energy bands based on whether the atomic orbitals are filled: a filled band is formed by the energy levels of atomic orbitals that are fully occupied by electrons, representing a low-energy band; an empty band is formed by energy levels that are not fully occupied by electrons, representing a high-energy band. The energy difference between these two types of bands is called the “band gap” (Figure 3-28).
When all energy bands of a material are filled, it is a non-conductor; when partially filled with electrons, it is a conductor. Lattice defects introduce additional energy levels in the crystal, allowing electrons to enter these energy levels, resulting in conditional conductivity.
2. Characteristics of Band Gap Transitions
Some gemstone minerals contain elements from Group IV A of the periodic table, such as diamond and moissanite, which primarily bond covalently. There are also other minerals, such as Cadmium sulfide (CdS), whose colors can be explained by band theory.
Electrons absorb light energy and move between the valence and conduction bands, forming “internal band transitions.” The likelihood of transitions is closely related to the energy difference between the valence and conduction bands, known as the band gap energy (Eg) (Figure 3-29).

Figure 3-29 (a) is a typical semiconductor band diagram. Based on the size of the crystal’s band gap energy, it can be divided into three types: wide band gap, narrow band gap, and medium band gap. A wide band gap has a band gap energy greater than the energy of visible light; when the band gap energy exceeds the energy of visible light, visible light is not absorbed and passes through completely, making the mineral colorless. For example, the band gap energy of diamond Eg is about 5.5eV, making it colorless.
The bandgap energy of narrow bandgap materials is less than that of visible light, causing all visible light to be absorbed, resulting in dark gray-green or black colors. For example, the bandgap energy of galena is Eg less than 0.4eV, which appears to be lead gray. When this “narrow bandgap semiconductor” is in an appropriate geometric shape, it exhibits rectifying and amplifying properties.
Medium bandgap materials’ energy is exactly within the visible light range, and gem minerals display various colors. Their color sequence is shown in Figure 3-29 (c), ranging from red-yellow to green-blue to purple. For example, the bandgap energy (Eg) of Cadmium sulfide (CdS) is approximately 2.5eV, which absorbs blue and violet light, appearing yellow. The bandgap energy of cinnabar is about 2eV, allowing only red light to pass through, thus appearing red. The bandgap energy of orpiment is about 2.5eV, appearing yellow.
Another category of natural gem minerals explained by band theory is the color of wide bandgap materials containing impurities. For example, in the case of a diamond with impurities, the bandgap energy of the diamond is Eg approximately 5.5eV, and visible light is not absorbed when passing through the diamond; pure diamond is colorless, but the situation changes when it contains impurities.
(1) The color mechanism of yellow diamonds
Nitrogen atoms replace the positions of carbon atoms. Since nitrogen atoms have one more electron than carbon atoms, this extra electron forms an impurity energy level in the bandgap, known as the donor energy level, with nitrogen atoms acting as “donors.”
The existence of this impurity level reduces the energy of the band gap to 4eV[ [Figure 3-30 (a)]. It can be even lower, allowing it to absorb ultraviolet light and a bit of 3eV violet light, causing the diamond to appear yellow.
This effect is strong; having one nitrogen atom for every hundred thousand carbon atoms can make the diamond deep yellow. However, the band gap reduction is still insufficient to make the diamond conductive at room temperature.
(2) Mechanism of color in blue diamonds
Since boron has one less electron than carbon, it forms an “acceptor level” in the band gap of diamond. It does not have extra electrons, but it can accept electrons from the valence band of a diamond, creating holes in the valence band [Figure 3-30 (b)] and forming an impurity energy band about 0.4eV above the valence band known as the acceptor level.

The acceptor energy level is not simple; it is a complex structure of impurity energy bands that can produce blue. The acceptor energy level creates “holes” in the valence band, which allows this “hole” type II b blue diamond to conduct electricity.
One boron atom among every million carbon atoms can form blue. Due to the higher aluminum content in this blue diamond and because aluminum has one less outer layer electron than carbon, aluminum was previously thought to play the acceptor role. Still, current experiments have proven that it is boron, not aluminum.
Type II b conductive blue diamonds are naturally blue, and their conductivity is one of the differences from irradiated blue diamonds (color centers). This property is often used to distinguish between the two types of diamonds. However, yellow nitrogen donor diamonds do not conduct electricity, so this method cannot be used to differentiate them from irradiated yellow diamonds.
3. Gemstone minerals colored by band transitions
Energy band theory can explain part of the color formation of natural gemstones. Since the band gap energy is an inherent property of the crystal and does not change due to external conditions, the color of gemstones has good stability. The crystal’s conductivity can be determined based on whether the energy bands in the crystal are filled with electrons. Table 3-13 lists the types of gemstone colors that can be explained by band theory and their conductivity properties.
Table 3-13 Types of Gem Colors Explained by Band Theory and Their Conductivity
| Conductors (Metal Colors and Metallic Luster) | Elem | Copper, Gold, Iron, Silver, Mercury, etc. |
| Ötvözet | Amalgam, Meteorite nickel iron | |
| Félvezető | Narrow Band Gap | Opaque gray to black: altaite, galena |
| Opaque metallic color: cobaltine, marcasite, pyrite, smaltite | ||
| Moderate band gap | Red: cinnabar, proustite, pyrargyrite | |
| Orange: Realgar | ||
| Yellow: Cadmium sulfide, realgar, sulfur | ||
| Wide bandgap | Colorless: diamond, sphalerite | |
| Impurity-containing wide bandgap semiconductors | Donor impurity: Nitrogen-doped diamond (yellow) | |
| Impurities in the host: Boron-containing diamond (blue) |
The color of gemstones caused by band transitions is related to the structure and bonding type at the time of gemstone formation. It has little relation to later impurities and crystal defects. The size of the band gap energy of gemstones is fixed. It does not change with the properties of the gemstone material, so conventional optimization methods generally cannot improve the color of gemstones.
Section IV Physical Optical Effects
Most natural gemstones can cause selective absorption of light, and different gemstones absorb visible light at different wavelengths, resulting in different colors. In addition to selective light absorption, the internal structure of gemstone crystals can also cause physical optical effects, leading to different colors in gemstones.
1. Gemstone minerals related to physical optical effects
The colors produced by physical optical effects are formed due to the dispersion, interference, diffraction, and other reasons of light caused by the crystal structure or composition and inclusions. This is merely an optical effect that can be explained by physical optical theory. Different gemstones can produce different colors under the same optical effects. In addition to the common trace elements that cause color, the reasons for colors produced by physical optical effects are mainly related to the gemstones’ internal structure and physical properties. The types of gemstone minerals that cause colors due to physical optical effects are listed in Table 3-14.
Table 3-14 Types of Gem Minerals Caused by Physical Optical Effects
| Function | Optical Properties and Color | Gem Minerals |
|---|---|---|
| Dispersion Scattering | Shimmering | "Fire" in dispersion gemstones, such as diamonds, zircon, rutile, and strontium titanate |
| Kék | Moonstone, blue quartz, opal | |
| Purple | Fluorite (scattering of microcrystals of calcium) | |
| Red | Ruby glass, scattering of microcrystals of copper or gold | |
| Fehér | Milky quartz | |
| Cat's eye effect | cat's eye aquamarine, cat's eye pyroxene, etc. | |
| Starlight effect | Various star effects of corundum and garnet | |
| Luster | Luster of pearls, apophyllite, etc. | |
| Sparkle | Sparkle of aventurine, obsidian, etc. | |
| Interference Diffraction | The pure spectral colors of thin film | The rainbow of chalcopyrite, the discolored film in a iris quartz fissure |
| Interference effects | Color-changing of opal, the effect of labradorite | |
| Befogadás | Kék | Dumortierite in quartz |
| Zöld | Green chalcedony and nickel veins in green chalcedony, fuchsite in star-quartz | |
| Narancs | Hydrated iron oxide in fire opal and flesh-colored chalcedony | |
| Red | Hematite flakes in orthoclase |
2. Interference and Diffraction Effects
(1) Interference Effects
Interference phenomena occur when two beams of light propagate along the same optical path or in parallel directions. A common interference phenomenon in gemstones is iridescence. For example, in iridescent quartz, the interference colors depend on the thickness of the film, the refractive index of the film, and the nature of the incident light.
The interference colors of pearls are formed by the concentric layered alternating superposition of two substances with different refractive indices (aragonite and nacrum), where the incident light is reflected from the surfaces between the alternating layers, and the reflected light interferes with the incident light to produce beautiful interference colors.
(2) Diffraction Effects
Diffraction refers to the physical phenomenon where light waves deviate from their original straight-line propagation when encountering obstacles. In physics, light waves undergo varying degrees of bending and scattering when passing through obstacles such as slits, small holes, or disks. If an obstacle is placed between the light source and the observation screen, bright and dark regions will appear on the observation screen, and the boundaries of these regions are not sharp, forming a complex pattern of light and dark. This phenomenon is called diffraction. Such phenomena can occur whenever light waves encounter obstacles along their propagation path. The most important factor in producing diffraction is the presence of periodically spaced diffraction gratings in gemstone minerals.
① Opal Color Change
In opal, the water-containing silica spheres have equal diameters and are arranged in a regular alternating layered structure, forming periodically spaced diffraction gratings. When light enters the opal, diffraction occurs, changing color (Figures 3-31, 3-32). The types of colors and the degree of color change mainly depend on the interplanar spacing of the stacked silica spheres.
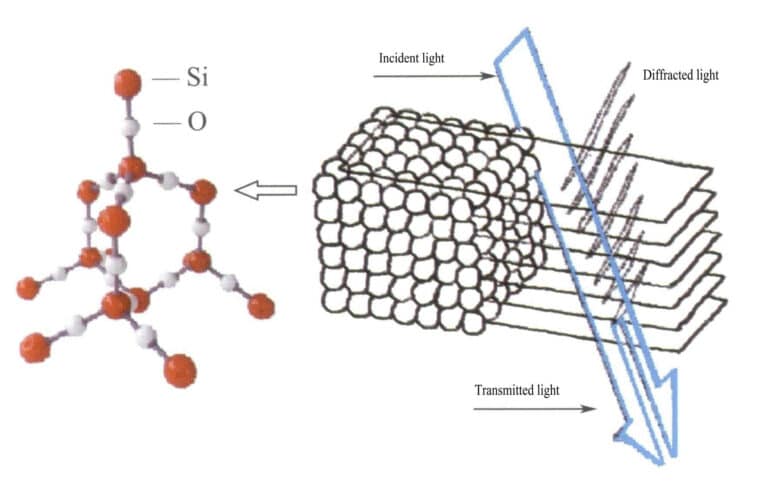

For example, opal with a face-centered cubic flat plate structure and a lattice spacing of 3×10-10m shows colors ranging from green to red; this type of opal with a lattice spacing of 2.5×10-10m shows colors ranging from blue to yellow.
② Labradorite Effect
Labradorite also exhibits effects similar to opal (Figure 3-33). Labradorite is also known as spectrolite because it can flash with the colorful light of the sun. Various types of labradorite from Finland can display a range of spectral colors, a phenomenon known as the “labradorite effect.” The color change effect in labradorite is due to small interlayer melts of plagioclase with different compositions. The slight differences in refractive index among the different feldspars cause interference and diffraction of light, resulting in luminescence and color change. The colors produced by this structure are related to the relative thickness of the layers and their refractive indices. Occasionally, andradite from Mexico also exhibits diffraction phenomena.

3. Scattering and Inclusions
(1) Szóródás
Scattering generally occurs when the internal structure of gem materials is irregular or when the size of the components exceeds the limits of diffraction conditions. The color effects produced by scattering are related to the particle size and shape of the gem material. When incident light interacts with irregularly arranged particles smaller than the wavelength of visible light, the transmitted high-energy light waves are stronger than the low-energy light waves, meaning that in most cases, only purple and blue can be seen. For example, the SiO2 small spheres in opal have diameters smaller than the wavelength of visible light, and when the size of the scattering particles is close to the wavelength of visible light, scattering colors can also occur.
For example, purple fluorite is caused by radioactive irradiation expelling fluorine atoms, resulting in calcium atoms that bond with fluorine atoms condensing into hexagonal plates of a size comparable to the wavelength of visible light. The interaction between the calcium plates and light waves produces scattering. It absorbs some light waves, creating a strong absorption peak in the green-to-red light region, allowing purple light to pass through and produce the purple color.
Since particles of the same size of metal elements can produce similar color effects, and different metal particles can produce different colors, some imitation gems are manufactured using this property.
For example, “ruby” glass is produced by adding copper or gold particles to glass, resulting in a red color similar to that of rubies. When the gem material contains inclusions, micro-cracks, or bubbles larger than the wavelength of visible light, the light waves interact with these scattering particles, causing the scattered light waves to recombine, producing a translucent milky light. For example, certain moonstone imitations.
The moonlight effect of moonstone is also produced by the scattering of light (Figure 3-34). Moonstone is an alkaline feldspar, a composite formed by alternating parallel layers of potassium-rich and sodium-rich feldspar. The interlayer thickness typically ranges from 50~1000nm, with thinner layers capable of producing scattering. The same scattering color can also occur in plagioclase, known as the “labradorite effect.”
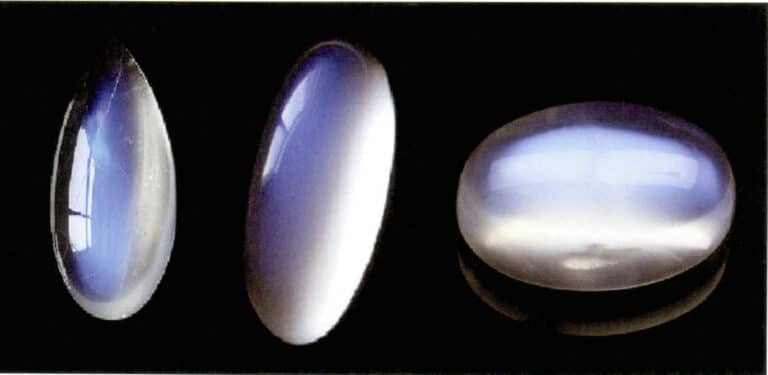
A specially oriented arrangement of scattering particles can produce characteristic optical effects. For example, when the scattering particles are in parallel fibrous form, they produce a cat’s eye or star effects, such as star sapphires and quartz cat’s eyes. When the scattering particles are large enough to be distinguished by the naked eye, they can produce a “goldstone effect,” such as sunstone (Figure 3-35) and goldstone glass.

(2) Tartalmak
The color and optical phenomena produced by inclusions are a special type of scattering. Inclusions with color embedded in nearly colorless main crystals will present the color of the inclusions, such as nickel-bearing banded chalcedony and water-containing iron(II) oxide (FeO • H2O) flesh-colored chalcedony; the color of orthoclase from Madagascar and some cordierite is formed by slightly larger, yet still microscopic inclusions of hematite that create red hues; sub-microscopic inclusions of ferric hydroxide often color fire opal.
Diamonds often exhibit different colors due to the presence of numerous inclusions. The diamonds colored by inclusions can be black, orange-red, and brown-red. When a diamond contains countless dark opaque mineral inclusions, it appears black; when examined with strong transmitted light, many dark inclusions can be observed, and the diamond appears dark gray; another type is secondary inclusions that occur in the cracks of the diamond. When the cracks develop and are filled with these colored inclusions, the diamond appears brown-red or orange-red, which is also known as an “oxidized” diamond.
4. Dispersion
The phenomenon of decomposing white light into various spectral colors through an object is called dispersion. The dispersion of gemstones refers to the property of light dispersing into different wavelengths of spectral colors when passing through the inclined planes of transparent gemstones. Due to the different wavelengths of the monochromatic light that make up white light propagating at different speeds and refractive indices in different materials, white light can be decomposed into various spectral colors under certain conditions. The size of a gemstone’s dispersion value is determined by its physical properties; each gemstone has its inherent dispersion value, which does not change with the properties of the gemstone. The unique charm of diamonds is closely related to their high dispersion value (0.044).
Most diamond simulants have a higher dispersion value, such as zircon’s dispersion value of 0.039 and synthetic moissanite’s dispersion value of 0.104. The comparison of the dispersion values of diamonds and their common simulant gemstones is shown in Table 3-15.
Table 3-15 Comparison of the dispersion values of diamonds and their common simulant gemstones
| Drágakő neve | Diszperziós érték |
|---|---|
| Diamond | 0.044 |
| Cirkon | 0.039 |
| Korund | 0.018 |
| Spinell | 0.020 |
| Topáz | 0.014 |
| Beryl | 0.014 |
| Crystal | 0.014 |
| Szintetikus rutil | 0.280 |
| Synthetic strontium titanate | 0.190 |
| Synthetic moissanite | 0.104 |
Dispersion is commonly referred to as the “fire” of gemstones. For example, diamonds have a high dispersion value, and their fire is very pronounced, enhancing the already royal status of diamonds and showcasing their unique charm.
There are many types of colors produced by physical optical effects, all of which can be explained by physical optical theory. Except for dispersion, which is an inherent property of the gemstone itself, other phenomena are caused by structural changes after the formation of the gemstone and the differences in mechanical inclusions. Understanding the various causes of gemstone colors provides a theoretical basis for optimizing the treatment of natural and synthetic gemstones.