Une fois pour tout savoir sur la cristallographie des pierres précieuses
Un guide complet sur les formes, les types, les classifications et les différences de la cristallographie.
La Terre est composée d'innombrables molécules et atomes. La recherche scientifique moderne a découvert que les matériaux solides dans la nature sont constitués de différents éléments chimiques. Les résultats des analyses aux rayons X montrent que les atomes des éléments de certains matériaux solides sont disposés de manière ordonnée et régulière. Ces matériaux sont classés comme cristallins ou appelés cristaux, et leur réseau atomique ordonné est appelé structure cristalline (figure 2-1-1).
La plupart des matériaux gemmes qui poussent dans la nature et dans les laboratoires sont cristallins. Ce chapitre aborde le concept des cristaux, leur classification et la relation entre les cristaux et la terminologie de base de la gemmologie.

Table des matières
Section ⅠLe concept et la description des cristaux
Lorsque nous évoquons les pierres précieuses, nous pensons souvent à leurs caractéristiques étincelantes et translucides (figure 2-1-2). Du point de vue des géologues et des gemmologues, la plupart des pierres précieuses bien-aimées appartiennent à une forme géométrique de solide, les cristaux. L'essence de la beauté des cristaux est, en fait, la beauté de la géométrie.

1. Le concept de cristal
Les cristaux sont les éléments les plus faciles à associer et les plus courants dans la nature. On trouve des cristaux sur les sept continents de la Terre et, dans la nature, ils prennent souvent la forme de polyèdres géométriques (figure 2-1-3). Ils sont communément appelés cristaux. Plus tard, ce terme a été étendu pour désigner les substances solides naturelles ayant des formes géométriques polyédriques, telles que les cristaux de diamant et d'aigue-marine (figure 2-1-4). Les cristaux peuvent également décrire des matériaux solides dont la surface est irrégulière, inégale, usée, cassée ou traitée artificiellement, mais dont l'arrangement atomique suit toujours un modèle régulier. Les cristallographes estiment que tous les cristaux possèdent six caractéristiques fondamentales : autolimitation, uniformité, anisotropie, symétrie, stabilité et point de fusion fixe.
① L'autolimitation fait référence à la propriété des éléments chimiques de former spontanément des formes géométriques polyédriques. Cette propriété peut expliquer pourquoi des éléments différents ont des formes géométriques cristallines différentes.
② L'uniformité est la propriété qu'ont toutes les parties d'un cristal d'avoir les mêmes propriétés physiques et chimiques. Cette propriété peut nous aider à distinguer et à identifier différents cristaux minéraux.
③ L'anisotropie désigne la propriété selon laquelle la disposition des éléments varie dans différentes directions, ce qui entraîne de légères différences dans les propriétés physiques en fonction de la direction. Cette propriété peut expliquer pourquoi les diamants les plus durs peuvent être taillés et polis.
④ La symétrie fait référence à la propriété selon laquelle les parties ou propriétés identiques d'un cristal sont répétées de façon régulière. Cette propriété est extrêmement importante et particulière pour les cristaux et sera développée dans la deuxième section de ce chapitre.
⑤ La stabilité désigne la stabilité d'un cristal résultant de son énergie interne minimale. Si l'énergie interne d'un cristal est élevée et inégale, il est susceptible de se fissurer de lui-même. Cette propriété peut expliquer pourquoi les cristaux de rubis synthétisés par la technique de fusion à la flamme semblent toujours être à moitié plutôt que complets.
⑥ Le point de fusion fixe fait référence à la propriété d'un cristal d'avoir un point de fusion fixe.

Figure 2-1-3 Grenat (la partie gauche est le cristal, la partie droite est le grenat poli)

Figure 2-1-4 Cristal aigue-marine
2. La forme idéale des cristaux
Les cristaux étudiés en cristallographie sont principalement des monocristaux idéaux. Un monocristal idéal est défini comme un cristal dont la structure interne suit strictement les règles des réseaux spatiaux et dont la forme est une forme géométrique combinée régulière. Les formes de monocristaux idéaux sont divisées en deux types : les formes simples et les formes combinées.
(1) Formulaire simple
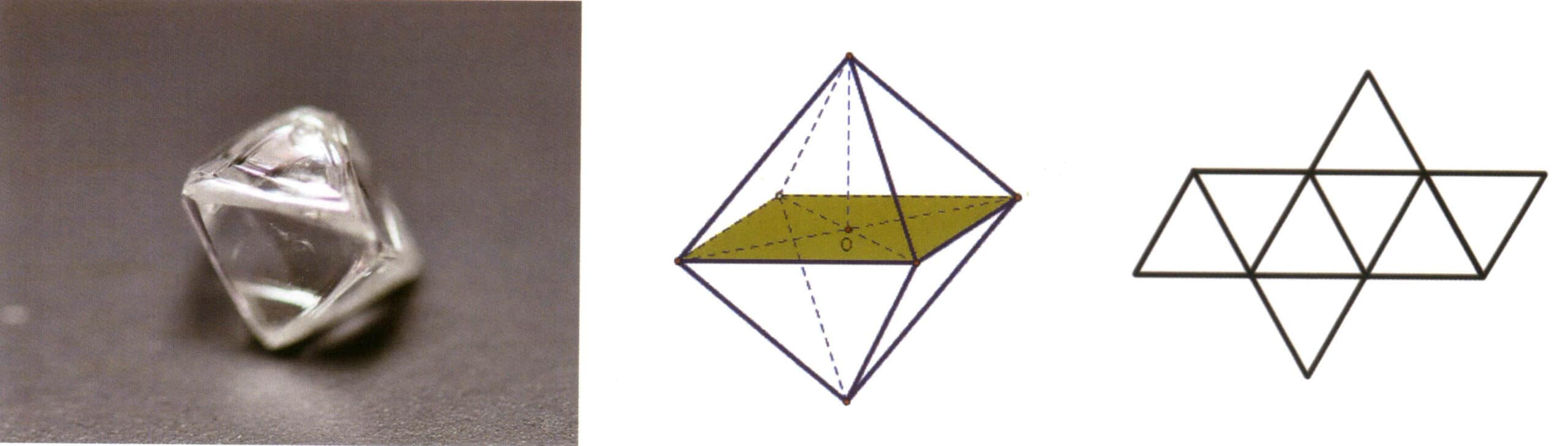
Une forme simple désigne une combinaison d'un groupe de faces cristallines reliées par des éléments de symétrie, qui peut être considérée comme un corps géométrique composé de faces cristallines de même forme et de même taille dans un état idéal (figure 2-1-5). Il existe 47 types de formes simples dans les cristaux.
Les points clés pour identifier les formes simples sont les suivants : toutes les faces cristallines du cristal ont la même forme et la même taille, et les faces cristallines peuvent être orientées différemment.
(2) Combiner Formulaire
L'agrégation de formes simples est appelée forme combinée, composée de deux ou plusieurs formes simples différentes. Toutes les formes simples ne peuvent pas être combinées librement en forme combinée ; seules les formes simples ayant le même groupe de points peuvent s'agréger (figures 2-1-6 à 2-1-8).
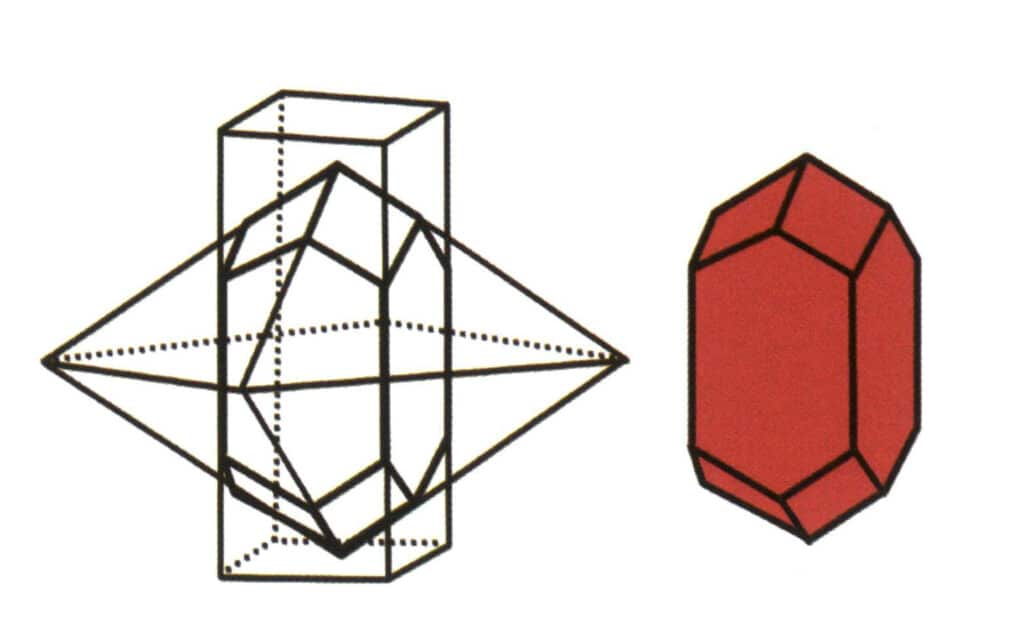
Figure 2-1-6 Combinaison de prismes tétragonaux et de dipyramides tétragonaux
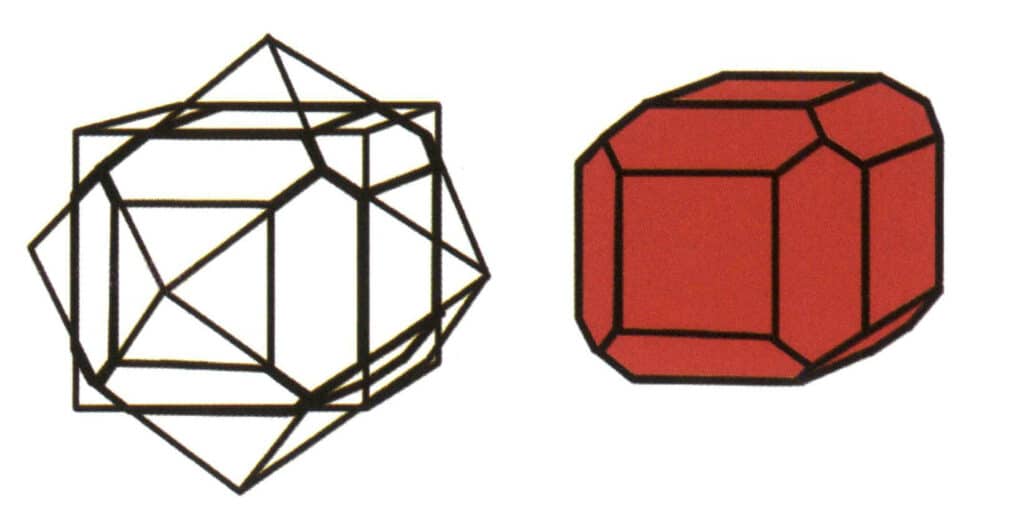
Figure 2-1-7 Combinaison de cubes et de dodécaèdres rhombiques
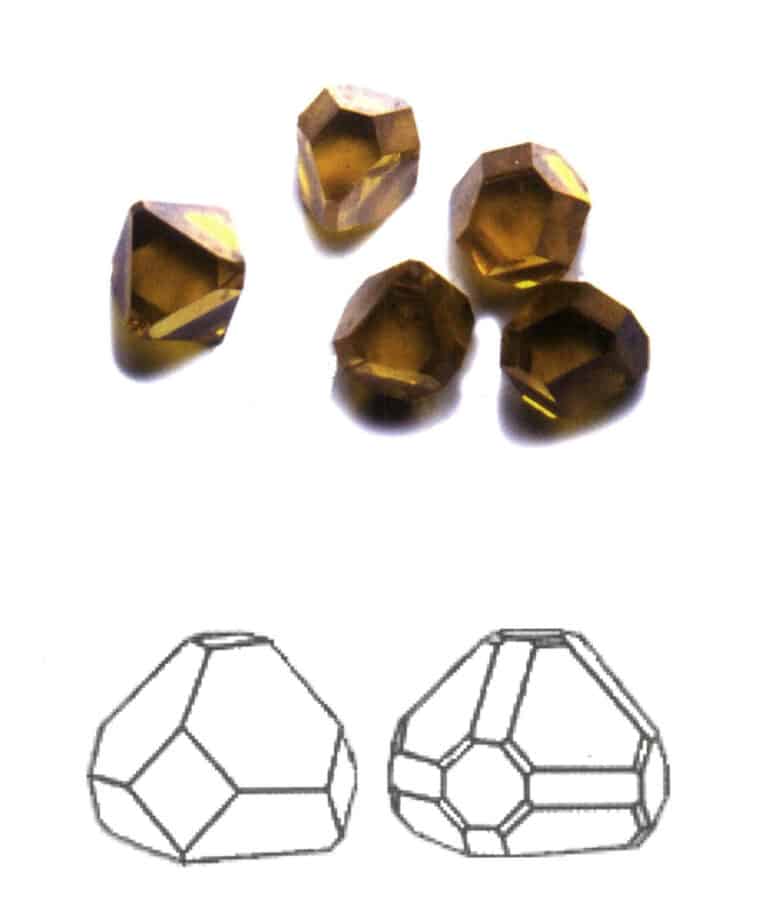
Le point clé de l'identification de la forme combinée est la présence de deux ou plusieurs faces cristallines de formes différentes dans le cristal.
Lorsque l'on trouve des cristaux uniques dans la nature, ils présentent toujours une différence significative par rapport à la morphologie idéale des cristaux uniques (figure 2-1-9), par exemple une face unique n'ayant pas nécessairement la même forme et la même taille et la disparition de faces cristallines, ce qui est décrit comme des cristaux déformés.

Les cristaux déformés peuvent également être décrits comme de véritables cristaux produits dans la nature, influencés par l'environnement de croissance. Les multiples faces cristallines qui se répètent à des angles fixes dans les cristaux idéaux n'ont pas nécessairement la même forme et la même taille. Néanmoins, pour un même type de cristal, les faces cristallines d'un même monomorphe doivent avoir le même motif et les mêmes propriétés physiques. Les angles entre les faces cristallines correspondantes restent inchangés, reflétant la symétrie inhérente au cristal lui-même. Les cristaux que l'on trouve dans la réalité sont déformés à des degrés divers.
Les cristaux jumelés peuvent également être décrits comme des cristaux réels produits dans la nature, influencés par l'environnement de croissance. Les multiples faces cristallines qui se répètent à des angles fixes dans les cristaux idéaux n'ont pas nécessairement la même forme ni la même taille. Néanmoins, pour un même type de cristal, les faces de même forme doivent avoir les mêmes motifs et les mêmes propriétés physiques. Les angles entre les faces correspondantes du cristal restent inchangés, reflétant la symétrie inhérente au cristal lui-même. Les cristaux que l'on trouve dans la réalité sont tous, à des degrés divers, jumeaux.
3. Les habitudes de cristallisation des cristaux
Les cristaux formés dans la nature ne peuvent jamais atteindre une forme parfaite. S'ils poussent dans les interstices des couches rocheuses, entourés de roches, la forme naturelle du cristal sera déformée. Même les cristaux cultivés en laboratoire se déforment sous l'effet de la gravité. Ce n'est que dans les conditions de gravité zéro de la Station spatiale internationale que les scientifiques peuvent cultiver les cristaux de forme parfaite qu'ils recherchent.
Bien que les formes des cristaux soient imparfaites, chaque type de cristal minéral a tendance à croître ou à se regrouper de différentes manières ou habitudes.
Chaque minéral tend à se former dans des conditions spécifiques, et ses habitudes reflètent les conditions de sa formation. Certains minéraux, comme le quartz, ont des conditions de formation complexes et variables. Le quartz possède donc lui aussi de multiples habitudes.
En général, les habitudes cristallines font référence aux caractéristiques d'un certain cristal tendant à prendre une forme spécifique dans certaines conditions extérieures. Parfois, il s'agit des types courants de la forme simple de ce cristal.
En fonction du degré de développement des cristaux dans l'espace tridimensionnel, les habitudes cristallines sont divisées en trois types fondamentaux.
(1) Uni-Extension directionnelle
Les cristaux s'étendent dans une seule direction et se présentent sous forme de colonnes, d'acicules, de fibres, etc. Les minéraux tels que le béryl, la tourmaline, la hornblende et la malachite présentent souvent cette forme (figures 2-1-10 à 2-1-11).

Figure 2-1-10 Aigue-marine colonnaire (en haut) et son diagramme d'habitudes cristallines (en bas)

Figure 2-1-11 Malachite fibreuse (en haut) et son diagramme de comportement cristallin (en bas)
(2) Bi-Extension directionnelle
Les cristaux s'étendent dans un plan, apparaissant sous forme de plaques, de feuilles, d'écailles, etc. Des minéraux comme la wolframite, le mica, le plumbago et la tanzanite présentent souvent cette caractéristique (figure 2-1-12).
(3) Tri-isométrique directionnelle
Les cristaux se développent uniformément dans trois directions, présentant des formes isométriques et granuleuses, comme le spinelle, le grenat, le diamant, la pyrite et la fluorine, qui présentent souvent ce type de structure (figures 2-1-13, 2-1-14).

Figure 2-1-12 Le comportement cristallin en forme de plaque de la tanzanite (en haut) et son diagramme de comportement cristallin (en bas)

Figure 2-1-13 Le comportement cristallin octaédrique de la pierre précieuse spinelle (en haut) et son diagramme de comportement cristallin (en bas)
En outre, il existe des types transitoires tels que les formes colonnaires courtes, les formes colonnaires en plaques, les formes en bandes et les formes en plaques épaisses.
La composition chimique et la structure du cristal déterminent principalement la forme du cristal. Elle est également étroitement liée aux conditions extérieures lors de la formation du cristal (température, pression, concentration, viscosité et impuretés), ce qui explique les différences de forme entre les diamants et les cristaux de diamants synthétiques.
4. Agrégation régulière de cristaux
Dans la nature, on peut trouver des cristaux individuels (figure 2-1-15) et deux ou plusieurs cristaux individuels qui se développent ensemble pour former un tout. Ce phénomène de croissance de plusieurs cristaux est appelé agrégation cristalline. L'agrégation de cristaux peut être classée en deux catégories : les agrégations irrégulières et les agrégations régulières. L'agrégation cristalline irrégulière peut être considérée comme un collectif, ce que nous verrons plus en détail au chapitre 3. Dans l'agrégation cristalline régulière, il existe quatre types courants : l'agrégation parallèle, les bicristaux, la surcroissance et l'intercroissance (figures 2-1-16 à 2-1-18). Cette section traite principalement du type d'agrégation régulière connu sous le nom de bicristaux.

Figure 2-1-15 Monocristal (Tourmaline)
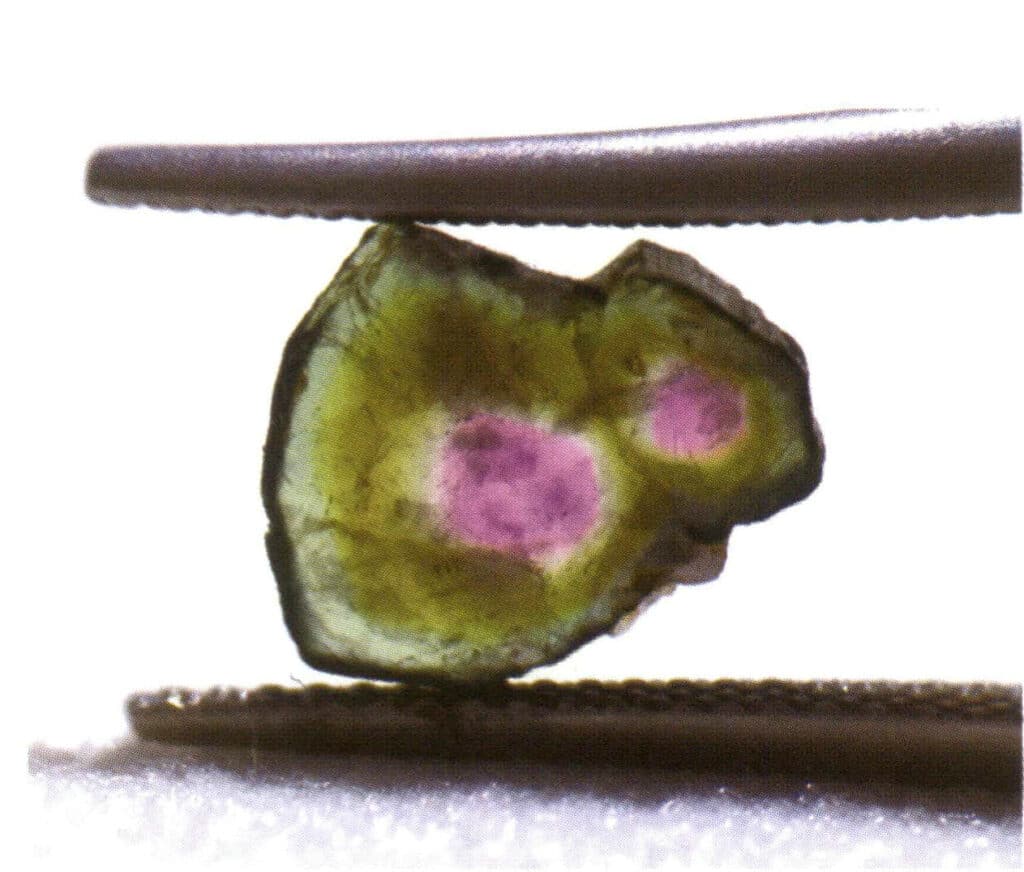
Figure 2-1-16 Agrégation parallèle (Lorsque plusieurs cristaux du même type croissent parallèlement dans l'espace, on parle d'agrégation parallèle. À ce moment-là, les faces cristallines et les arêtes correspondantes des cristaux cultivés sont toutes parallèles les unes aux autres).

Figure 2-1-17 Cristal double (spinelle)

Figure 2-1-18 Surcroissance (un type de cristal se développe à la surface d'un autre cristal dans une direction cristallographique spécifique, également connue sous le nom de croissance épitaxiale)
Les bicristaux sont l'agrégation régulière de deux ou plusieurs cristaux identiques selon certaines règles de symétrie. (Axe jumeau, plan jumeau) Les faces, arêtes et angles correspondants des deux individus adjacents ne sont pas complètement parallèles. Néanmoins, ils peuvent se refléter l'un l'autre grâce à des opérations symétriques telles que la rotation et l'inversion de rotation, ce qui permet aux deux individus de coïncider ou de s'aligner.
4.1 Points clés pour l'identification des bicristaux
① Angles concaves visibles dans les cristaux jumelés (Figure 2-1-19).
② Stylolite : La micro-morphologie et les autres caractéristiques des surfaces cristallines des deux côtés de la stylolite sont discontinues (figure 2-1-20).
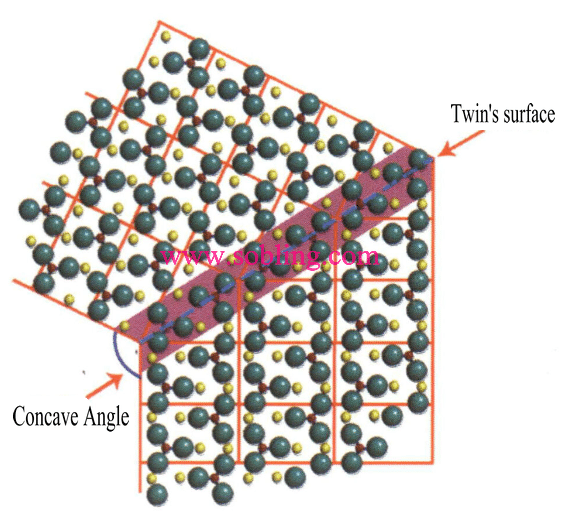
Figure 2 - 1-19 Angle concave du jumeau
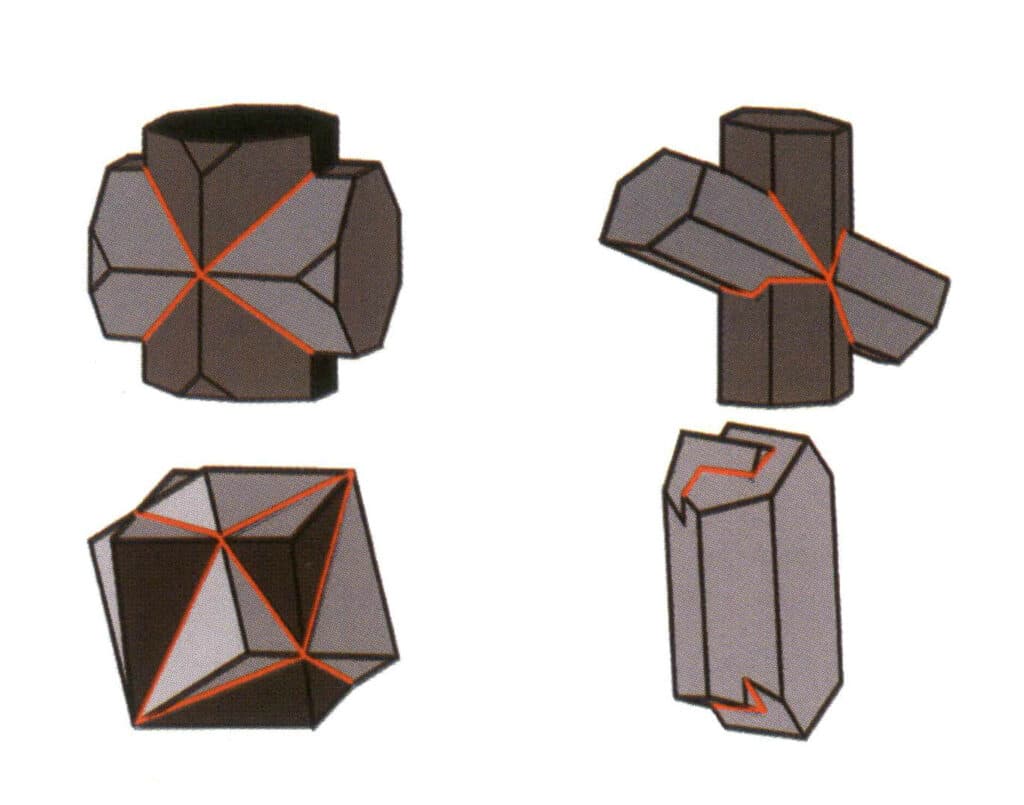
Figure 2-1-20 Stylolite (les différentes couleurs de la figure représentent différents cristaux ; les lignes rouges indiquent la stylolite jumelle)
③ Stries de maclage : Les faces cristallines ou les plans de clivage présentent de fines stries de maclage (figure 2-1-21).
④ Figure de gravure : L'apparition de la figure de gravure indique la présence d'un jumelage (figure 2-1-22).

Figure 2-1-21 Schéma des jumeaux polysynthétiques

Figure 2-1-22 Surface d'un spinelle avec des piqûres triangulaires inversées.
⑤ L'apparition d'une pseudo-symétrie : l'émergence de relations de symétrie incompatibles avec le groupe ponctuel inhérent au monocristal (figure 2-1-23 à figure 2-1-24).

Figure 2-1-23 Cristal unique de chrysobéryl

Figure 2-1-24 Jumeau de chrysobéryl en forme de genou
Les jumeaux sont divisés en cinq types en fonction de leurs caractéristiques d'empilement : jumeaux de contact (figure 2-1-25 à figure 2-1-26), jumeaux polysynthétiques (figure 2-1-27), jumeaux interpénétrés (figure 2-1-28), cristal triplet (figure 2-1-29) et jumeaux complexes, parmi lesquels les quatre premiers types sont les plus courants.


Figure 2-1-26 Torsion de contact du spinelle (en haut) et son schéma (en bas)

Figure 2-1-27 Jumelle polysynthétique de la labradorite (en haut) et son schéma (en bas)
Figure 2-1-28 Cristaux jumeaux de feldspath (en haut) et schéma de cristaux jumeaux interpénétrés d'autres types (en bas)

Figure 2-1-29 Jumelage trigonal du chrysobéryl (en haut) et son schéma (en bas)
4.2 La formation de bicristaux
① Formé lors de la croissance du cristal, il peut se développer à partir de germes cristallins jumeaux ou de petits cristaux qui croissent de manière dépendante en fonction de la position du jumeau.
② Formé au cours du processus de transformation de l'hétéromorphisme, par exemple lorsque le quartz α se transforme en quartz β, formant ainsi des jumeaux.
③ Formé par action mécanique, où une partie du cristal glisse le long d'un certain plan directionnel pour former des jumeaux de déformation, tels que les jumeaux de calcite.
5. Modèles de face en cristal
Lorsque des cristaux sont découverts dans la nature, ils présentent souvent des formes incomplètes (figure 2-1-30) et des motifs de surface particuliers. Parfois, ils se développent en grappes (figure 2-1-31), qui présentent souvent des différences significatives par rapport aux polyèdres géométriques standard que nous connaissons, tels que les cubes et les prismes hexagonaux. Ce phénomène est appelé la forme réelle des cristaux. La forme réelle des cristaux fait l'objet d'une classification détaillée en cristallographie : cristaux déformés, cristaux convexes, cristaux courbes, cristaux flottants, bandes sur la face des cristaux, figures de gravure, stries de jumelage, etc.

Figure 2-1-30 Cristal de Rubis

Figure 2-1-31 Cristaux de pyrite (à gauche, plusieurs cristaux de pyrite se développent ensemble et à droite, un seul cristal de pyrite)
Cette section traite principalement des motifs de face de cristal dans la forme réelle des cristaux.
En théorie, les plans cristallins sont lisses et plats. Cependant, au cours de la croissance ou de la dissolution des cristaux, la surface laisse souvent des motifs réguliers légèrement inégaux, communément appelés motifs de face de cristal. Les motifs de la face du cristal comprennent les stries de croissance, les couches de croissance, les motifs en spirale, les buttes de croissance et les figures de gravure. Les motifs de face cristalline abordés dans cet ouvrage se réfèrent principalement aux stries de face cristalline et aux figures de gravure qui peuvent être observées à l'œil nu ou dans des conditions de faible grossissement.
Les bandes de face de cristal désignent une série de lignes droites parallèles sur la surface du cristal, dues à la convergence répétée et à la croissance alternée de différentes formes simples. Également connues sous le nom de "bandes combinées", ces bandes ne sont visibles que sur les surfaces cristallines, également appelées bandes de croissance. Par exemple, la face cristalline prismatique hexagonale du quartz présente souvent des faces cristallines fines prismatiques hexagonales et dodécaédriques rhombiques alternativement développées en bandes transversales agrégées (figure 2-1-32).

Les figures de gravure désignent les piqûres de forme spécifique (c'est-à-dire les piqûres de gravure) laissées sur la face du cristal en raison de la corrosion après la formation du cristal. Les figures d'attaque sont contrôlées par la disposition des particules élémentaires dans la face du cristal. Ainsi, les formes et les orientations des figures d'attaque varient selon les minéraux et les formes individuelles d'un même cristal. Par exemple, les figures d'attaque sur différentes formes uniques de cristaux de diamant varient ; des piqûres triangulaires peuvent être observées sur les cristaux octaédriques (figure 2-1-33), des piqûres quadrilatérales sur les faces cubiques, des piqûres quadrilatérales se chevauchant forment un motif en forme de grille, et des motifs linéaires ou des motifs microscopiques en forme de disque peuvent être observés sur les dodécaèdres rhombiques (figure 2-1-34).

Figure 2-1-33 Puits triangulaires inversés visibles sur le cristal octaédrique de diamant

Figure 2-1-34 Texture linéaire visible sur les cristaux dodécaédriques en forme de diamant
Seules les figures de gravure sur la même face cristalline de la même forme peuvent être identiques, c'est pourquoi les figures de gravure sont souvent utilisées pour identifier les minéraux et déterminer si les faces cristallines appartiennent à la même forme unique (Figure 2-1-35 à Figure 2-1-42).

Figure 2-1-35 Plancher en bois incrusté de cristaux de fluorine, avec bandes de style

Figure 2-1-36 Figure de gravure naturelle triangulaire dans un rubis (bandes horizontales communes dans les rubis, lignes de croissance parallèles à la direction rhomboédrique, gravures naturelles de formes triangulaires ou hexagonales)

Figure 2-1-37 Rayures longitudinales superficielles de la tourmaline

Figure 2-1-38 bandes horizontales à la surface du cristal

Figure 2-1-39 Figures de gravure sur la surface du cristal

Figure 2-1-40 Stries longitudinales de surface de la topaze

Figure 2-1-41 Image topographique d'un cristal de topaze

Figure 2-1-42 Figures de gravure du spinelle
Section II 47 Types de formes de cristaux
La cristallographie compte 146 formes individuelles différentes, qui peuvent être classées en 47 formes géométriques sur la base de leurs formes géométriques lorsqu'elles existent indépendamment les unes des autres. Ces formes géométriques sont nommées de la manière suivante :
① Nommé en fonction des caractéristiques de la forme de la section transversale, comme le prisme trigonal, le prisme tétragonal, le prisme hexagonal, la bipyramide rhomboédrique, etc.
② Nommée selon la forme de la forme unique, telle que cylindre, double cône, cube, etc.
③ Nommés en fonction du nombre de faces géométriques, tels que face unique, octaèdre, etc.
④ Nommés en fonction de la forme des faces géométriques, tels que rhomboèdre, pentacontaèdre, etc.
En cristallographie, les formes simples sont divisées en quatre catégories : formes générales et formes spéciales, formes fermées et formes ouvertes, formes régulières et formes irrégulières, formes gauches et formes droites. Ce chapitre aborde brièvement les formes fermées et les formes ouvertes.
Les formes fermées désignent celles dont les faces cristallines peuvent enfermer un espace fermé, divisé en trois catégories principales : les classes polyédriques, les classes polyédriques asymétriques et les classes bipyramidales, soit un total de 30 types. Chaque catégorie a des classifications plus détaillées ; par exemple, la classe polyédrique est subdivisée en classe tétraédrique, classe octaédrique, classe cubique, etc. (figures 2-1-43 à 2-1-48).

Figure 2-1-43 Classe de tétraèdre
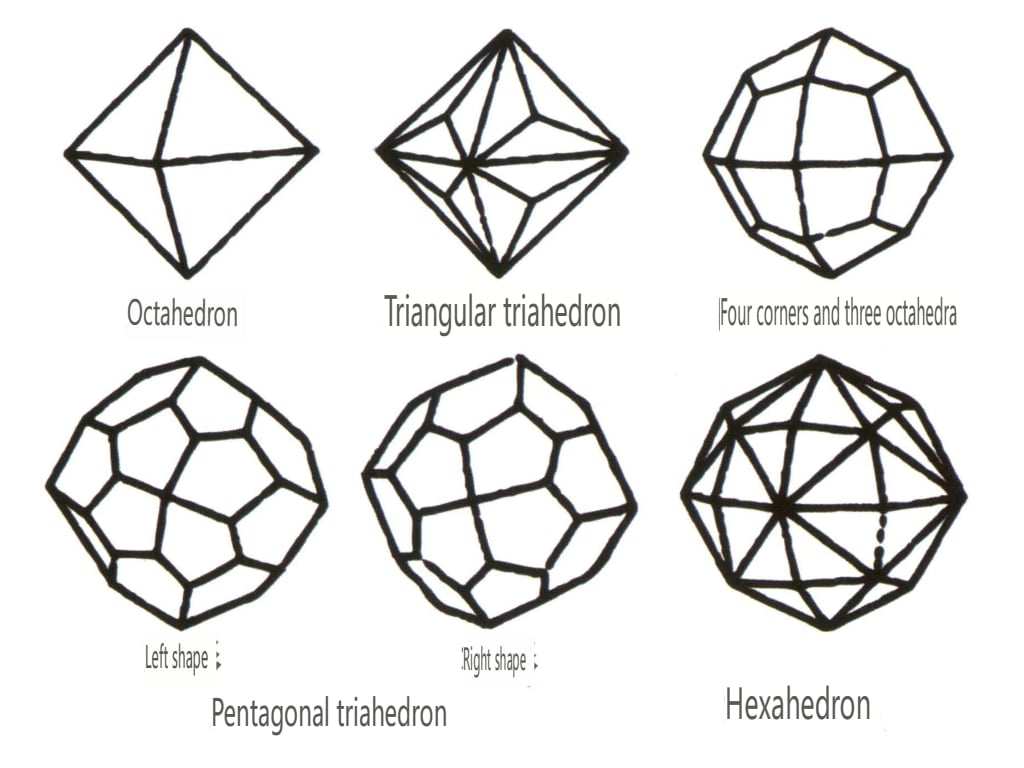
Figure 2-1-44 Classe 0ctaédrique
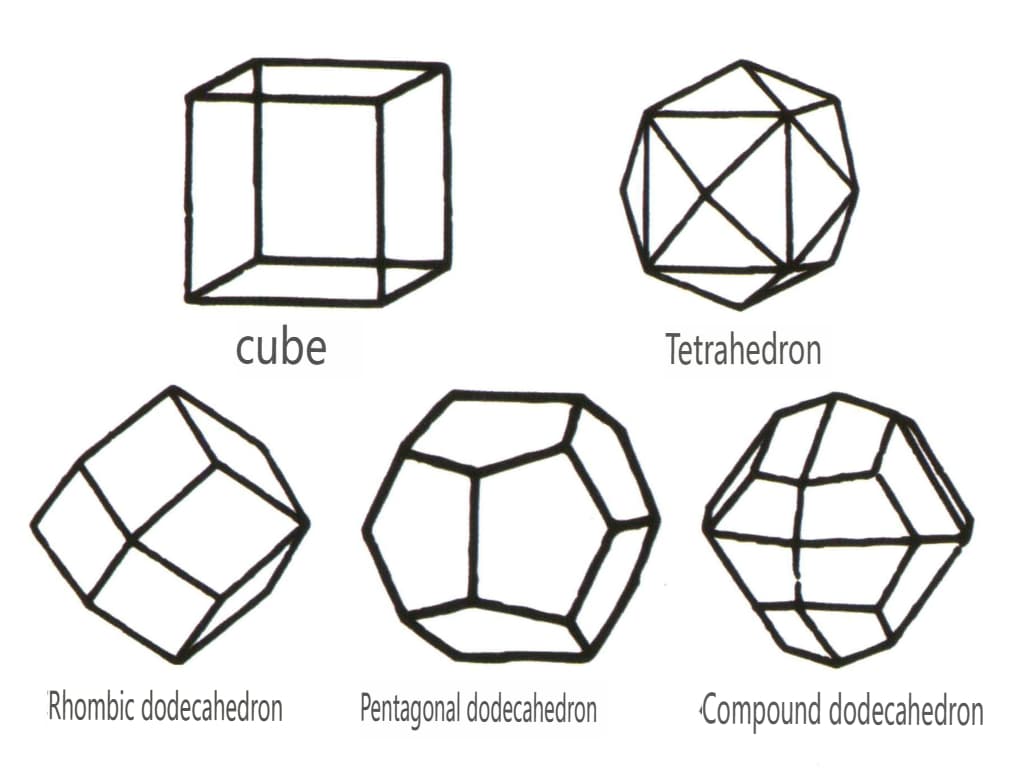
Figure 2-1-45 Classes cubiques et dodécaédriques
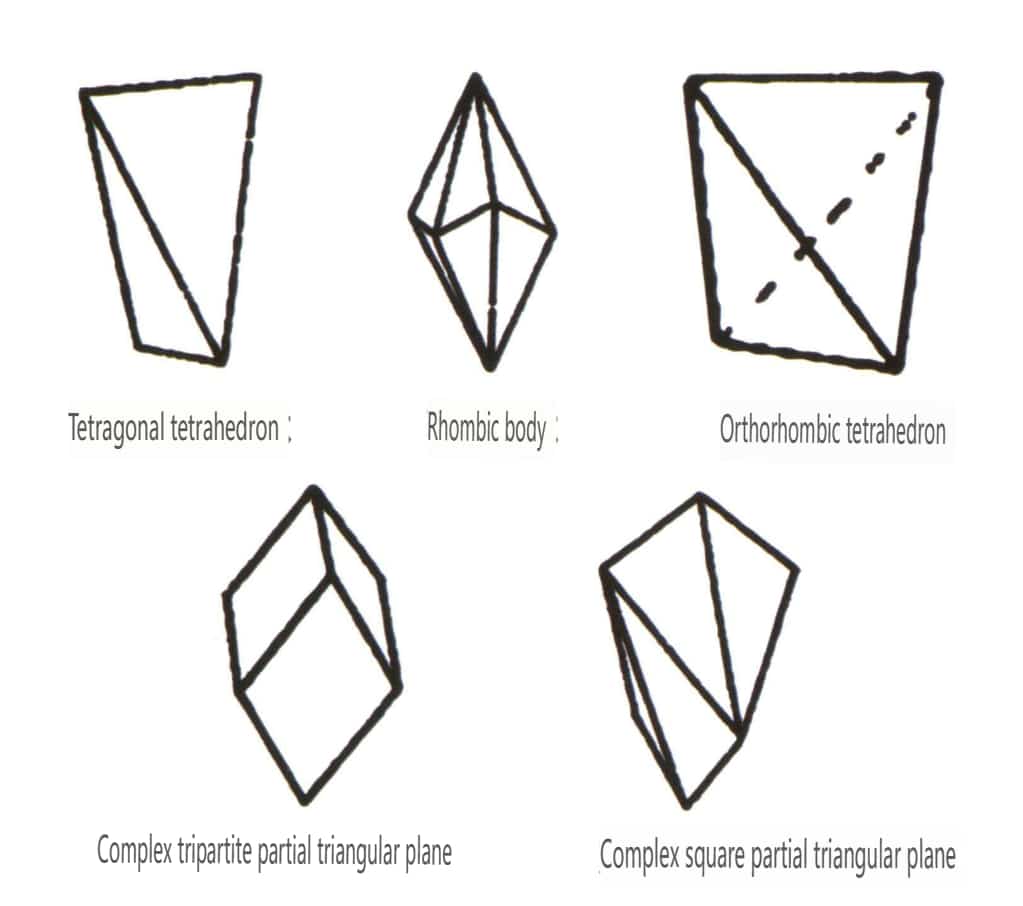
Figure 2-1-46 Autres types de polyèdres
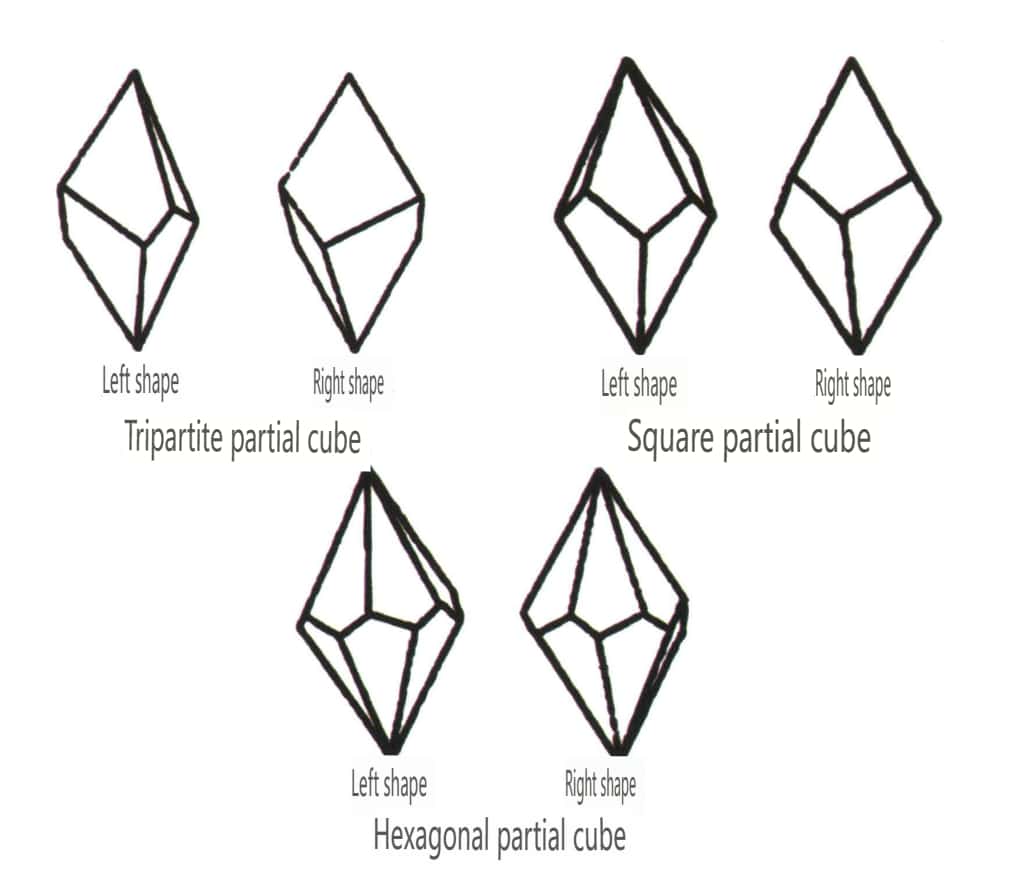
Figure 2-1-47 Forme combinée oblique Classe
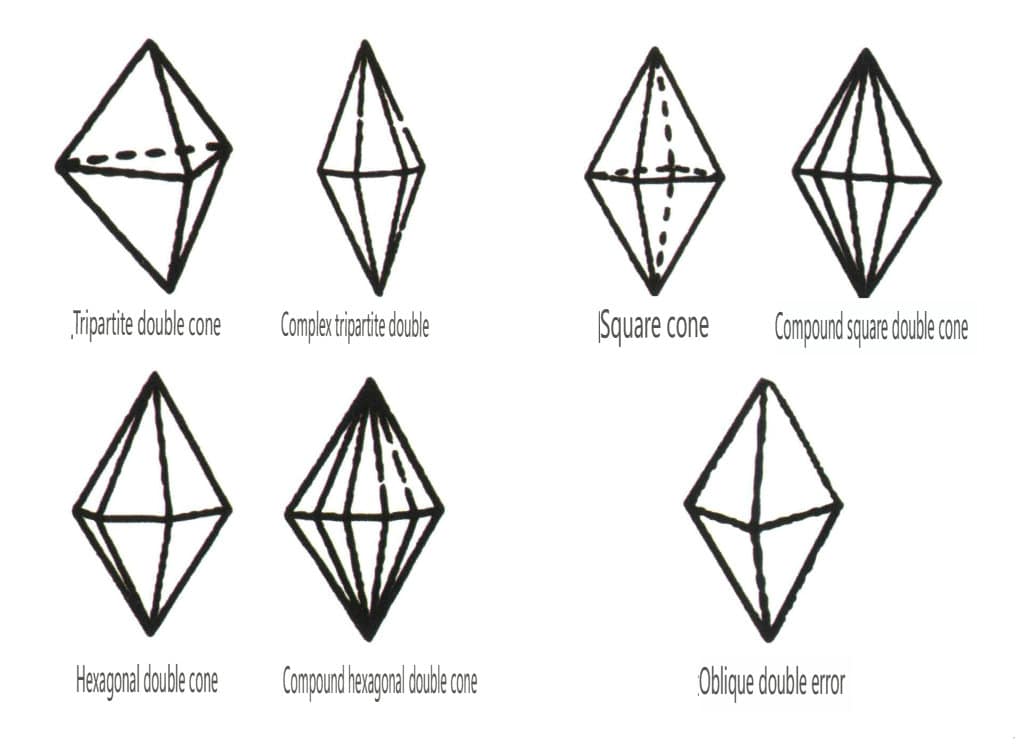
Figure 2-1-48 Classe pyramidale double
Les formes ouvertes sont celles dont les faces cristallines ne peuvent pas enfermer un espace fermé. Elles sont divisées en quatre catégories principales : simple face, double face, classes colonnaires et classes pyramidales simples, soit un total de 17 types (figures 2-1-49 et 2-1-51).
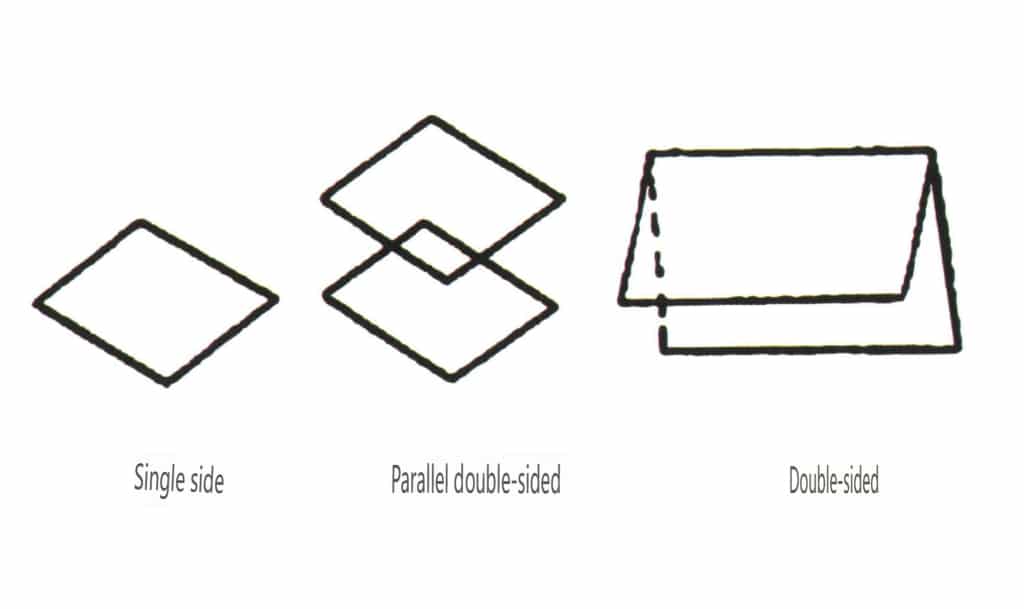
Figure 2-1-49 Simple face et double face
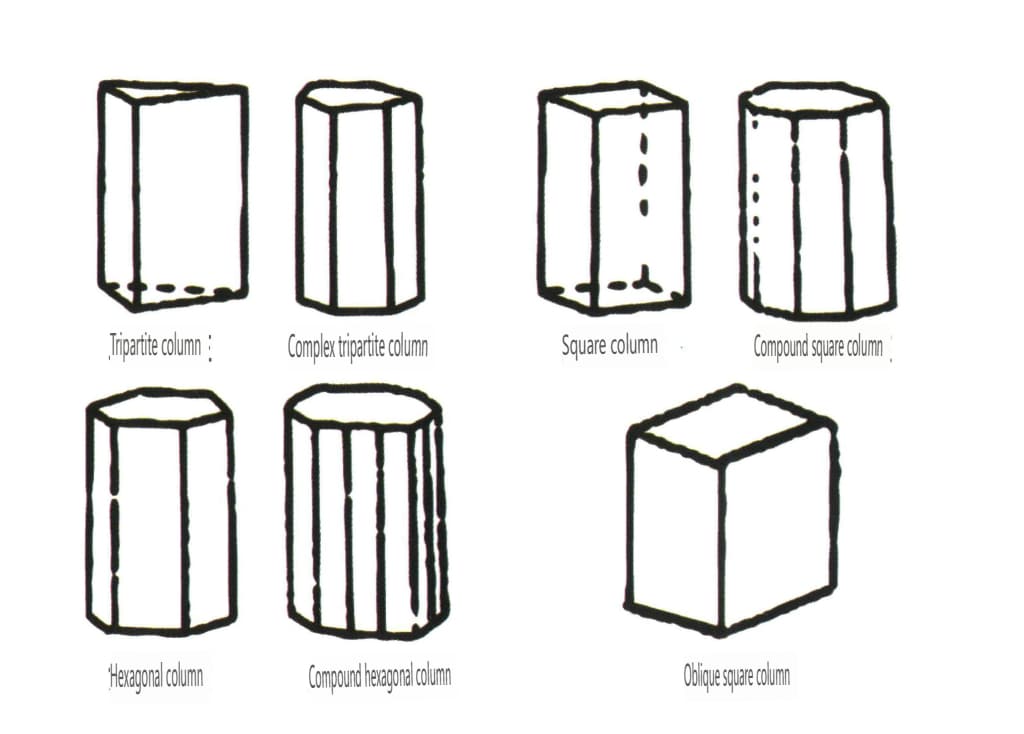
Figure 2-1-50 Colonnes

Section III Classification des cristaux
1. Symétrie des cristaux
La symétrie est un concept abstrait utilisé dans l'étude des cristaux réels et des pierres précieuses non traitées. Elle décrit la répétition observée lorsque la structure cristalline est référencée par une direction ou un plan qui la traverse. C'est la base de la classification des cristaux.
La symétrie d'un cristal peut être considérée, d'un point de vue microscopique, comme une méthode permettant de décrire le caractère répétitif de la structure cristalline et, d'un point de vue macroscopique, comme la répétition de deux ou plusieurs faces géométriques qui ont la même forme et la même taille, mais qui peuvent différer dans leur direction, selon certaines règles. Ce modèle de répétition peut être décrit à l'aide d'axes et de plans de symétrie, chaque axe ou plan de symétrie étant appelé élément de symétrie. Lorsqu'on observe ou déduit la symétrie d'un objet, cette action est décrite comme une opération sur la symétrie.
2. Éléments de symétrie des cristaux
En cristallographie, il existe quatre éléments de symétrie : l'axe de symétrie, le plan de symétrie, les axes de symétrie de rotation et le centre de symétrie. Cette étude portera sur les deux éléments de symétrie que sont l'axe de symétrie et le plan de symétrie.
2.1 Axe de symétrie
(1) Le concept d'axe de symétrie et leur notation.
L'axe de symétrie est une ligne droite imaginaire qui indique le nombre de fois où le niveau de base (figures 2-2-1 à figure 2-2-2) apparaît dans la même position lorsque la structure en treillis est tournée de 360° autour de cette ligne imaginaire. Ce nombre ne peut être que de 2, 3, 4 ou 6 fois dans 4 cas. Il peut également être considéré comme une ligne imaginaire passant par le centre du corps géométrique, faisant tourner le corps géométrique de 360° autour de cette ligne. Supposons que la forme du corps géométrique après une rotation d'un certain angle soit cohérente avec la forme du corps géométrique à zéro degré initial. Dans ce cas, cette ligne imaginaire est appelée axe de symétrie.
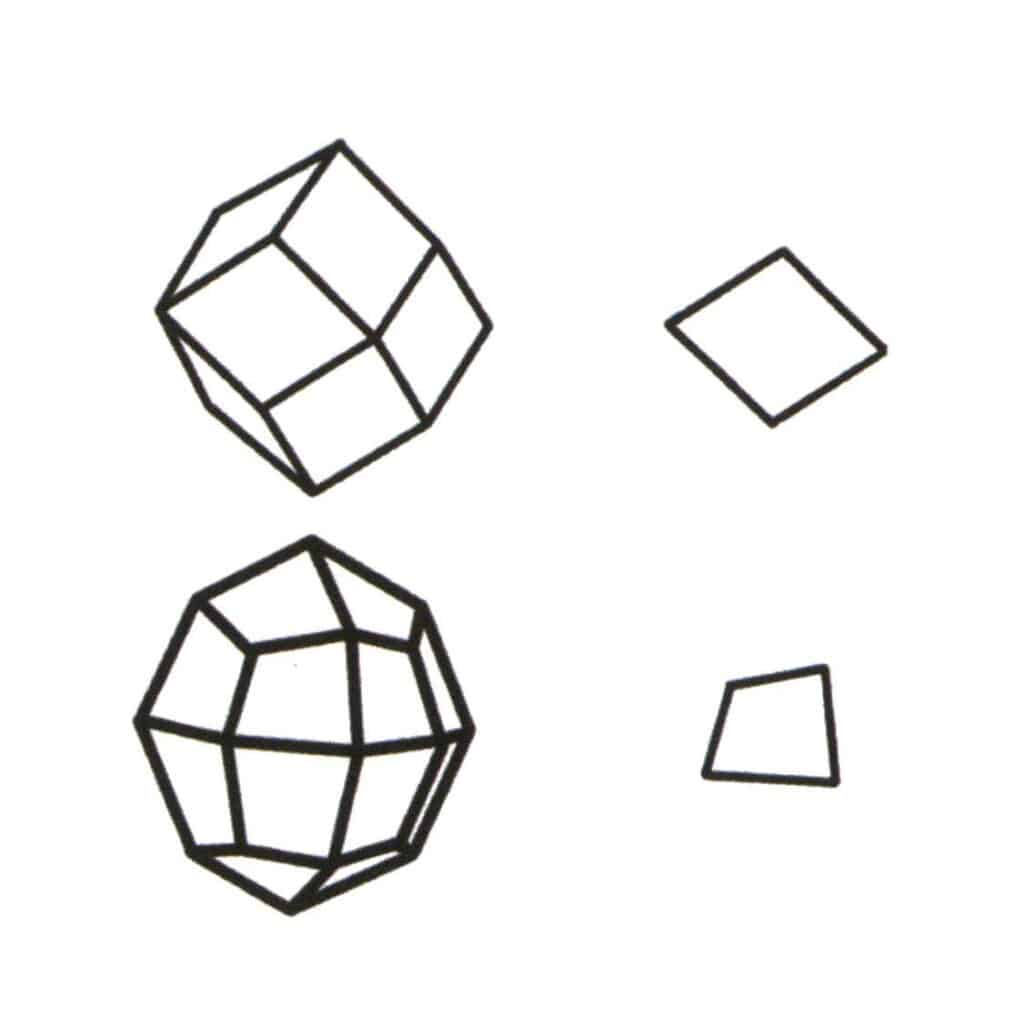
Figure 2-2-1 Sélection du niveau de base pour le formulaire unique.
Le niveau de base d'une forme simple est le plus petit plan répétitif qui compose le simplexe. La partie supérieure gauche de la figure montre un dodécaèdre rhombique, qui est une forme fermée composée d'un seul type de face. Le plus petit plan répétitif est le losange représenté en haut à droite, de sorte que le niveau de base du dodécaèdre rhombique est le losange. La partie inférieure gauche de la figure montre un octaèdre quadrilatéral, qui est une forme fermée composée d'un seul type de face. Le plus petit plan répétitif est le quadrilatère représenté en bas à droite, de sorte que le niveau de base de l'octaèdre quadrilatéral est le quadrilatère.
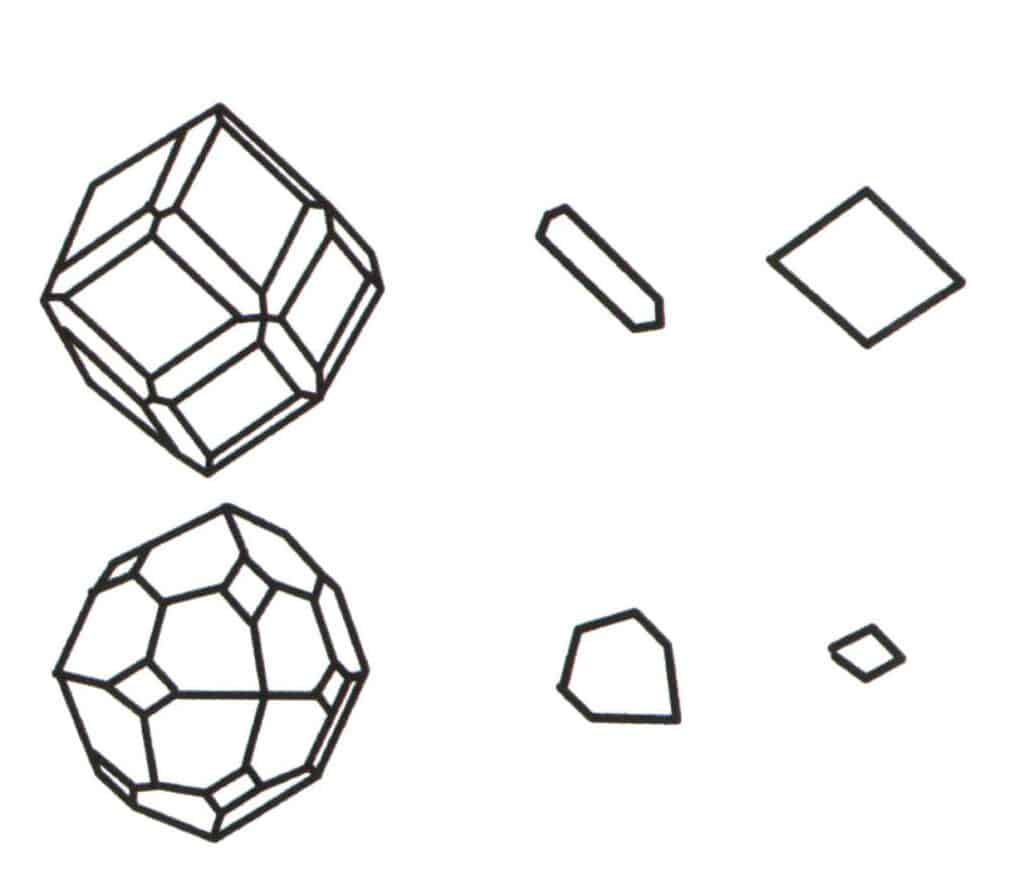
Figure 2-2-2 Sélection du niveau de base du polytope.
L'agrégation de plusieurs formes simples forme une forme combinée, et le choix du niveau de base de la forme combinée est le jugement des formes simples qui se combinent pour former la forme combinée. La première colonne en partant de la gauche dans la figure représente une forme combinée (formée par l'agrégation des formes simples d'un dodécaèdre et d'un tétraèdre), et ce corps géométrique est une figure fermée composée de deux types de faces. L'hexagone représente le plan répétitif minimal dans la deuxième colonne et le rhombe à droite dans la troisième colonne. Par conséquent, le niveau de base de la forme combinée de la première colonne est soit l'hexagone, soit le losange. Lors du calcul de l'axe de symétrie, une seule forme peut être sélectionnée comme niveau de base pour l'enregistrement de la symétrie.
L'axe de symétrie est représenté par la lettre majuscule L, avec l'ordre de l'axe n écrit dans le coin supérieur droit de L, représenté par Lⁿ. Par exemple, un axe double est représenté par L², un axe triple par L³, un axe quadruple par L⁴ et un axe sextuple par L⁶. L⁶, L⁴, L³ est habituellement désigné comme un axe d'ordre supérieur.
Les cristaux peuvent avoir des axes de symétrie dans différentes directions, et le nombre de ces axes de symétrie non coïncidents est conventionnellement écrit à gauche de L. Par exemple, six axes secondaires sont représentés par 6L² (figure 2-2-3 à figure 2-2-9), trois axes tertiaires sont représentés par 3L³ (figure 2-2-10 à figure 2-2-14), quatre axes tertiaires sont représentés par 4L³ (figure 2-2-15 à figure 2-2-18) et un axe hexagonal est représenté par L⁶ (figure 2-2-19).
Lorsqu'un cristal possède plusieurs axes de symétrie, la méthode enregistrée les classe de gauche à droite dans l'ordre décroissant, le nombre d'axes de symétrie étant inscrit sur le côté gauche de l'axe correspondant, par exemple, L⁶6L², 3L⁴4L³6L².
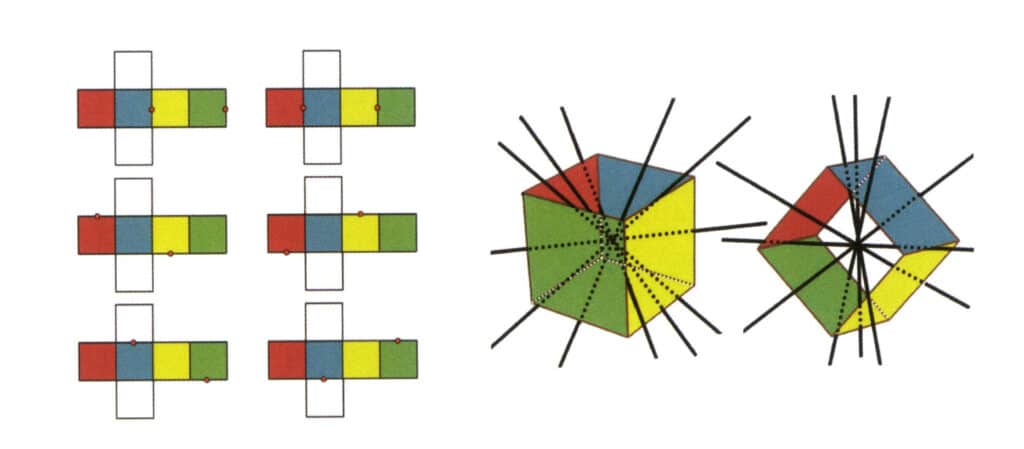
Figure 2-2-3 Axe secondaire du cube
La partie gauche de la figure montre la vue dépliée d'un cube, les points rouges indiquant les points d'intersection de la ligne imaginaire et des arêtes. La partie droite de la figure montre un cube fermé, où l'axe secondaire peut apparaître au milieu de lignes d'arêtes parallèles, au milieu de faces rectangulaires parallèles ou aux points d'intersection de trois faces parallèles ou plus ressemblant à un rectangle. ou plus de faces parallèles ressemblant à un rectangle.
Copywrite @ Sobling.Jewelry - Fabricant de bijoux sur mesure, usine de bijoux OEM et ODM
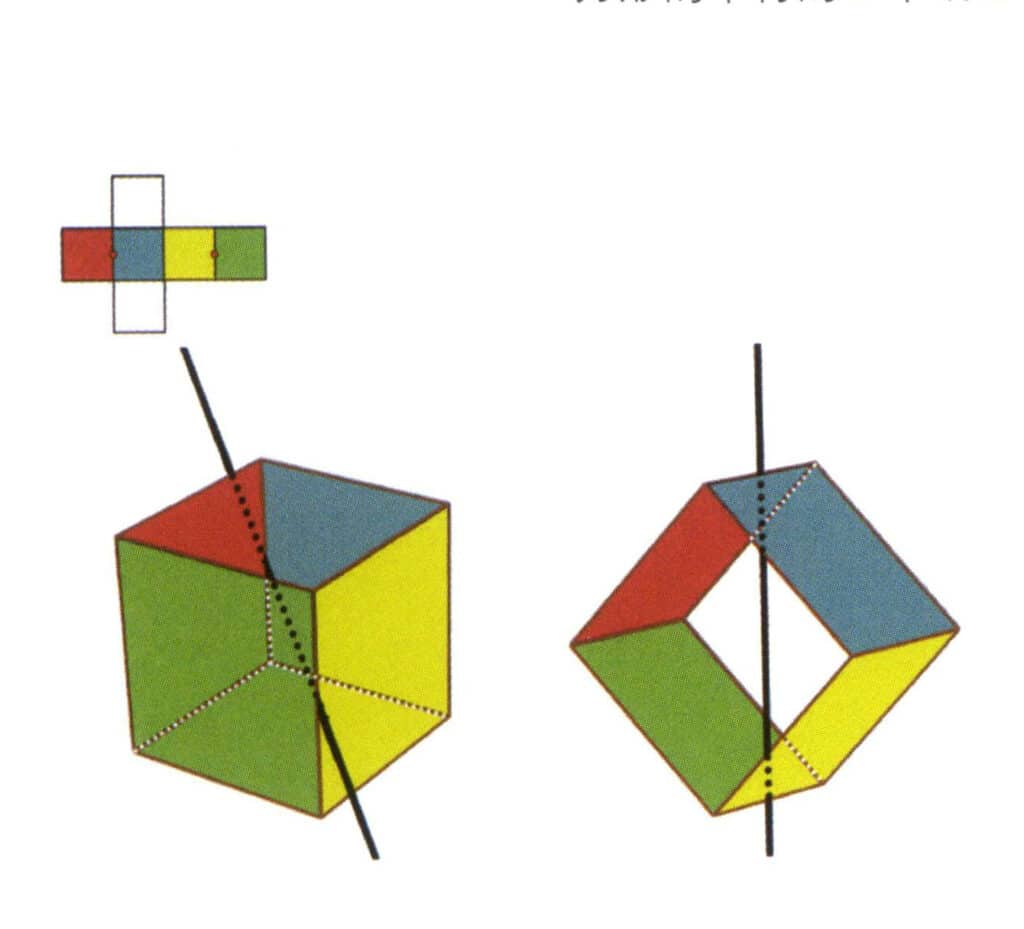
Figure 2-2-4 Le premier axe secondaire du cube
Sélectionnez le point médian des lignes parallèles, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant tourner le cube de 360°. Les niveaux de base de couleurs différentes mais de même forme se répéteront deux fois au même endroit (les faces rouge et bleue, les faces jaune et verte, les deux faces incolores et trois ensembles de faces répétées. Bien que trois séries de faces répétées apparaissent puisque la ligne imaginaire n'a pas changé de position et d'angle, l'axe secondaire n'est enregistré qu'une seule fois). Cette ligne imaginaire est enregistrée comme axe secondaire.
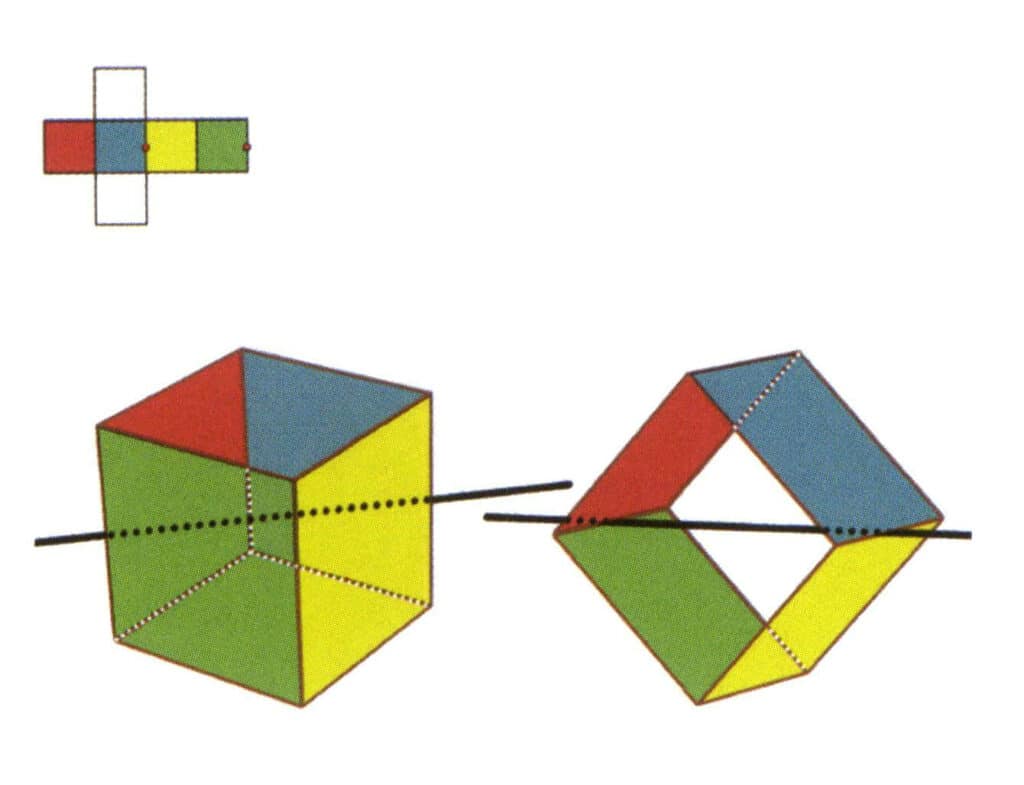
Figure 2-2-5 Le deuxième axe secondaire du cube
Sélectionnez le point médian des lignes parallèles, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant tourner le cube de 360°. Les niveaux de base de couleurs différentes mais de même forme se répètent deux fois au même endroit (les faces rouge et verte, les faces jaune et bleue, les deux faces incolores et trois ensembles de faces répétées). Cette ligne imaginaire est enregistrée comme deuxième axe secondaire.
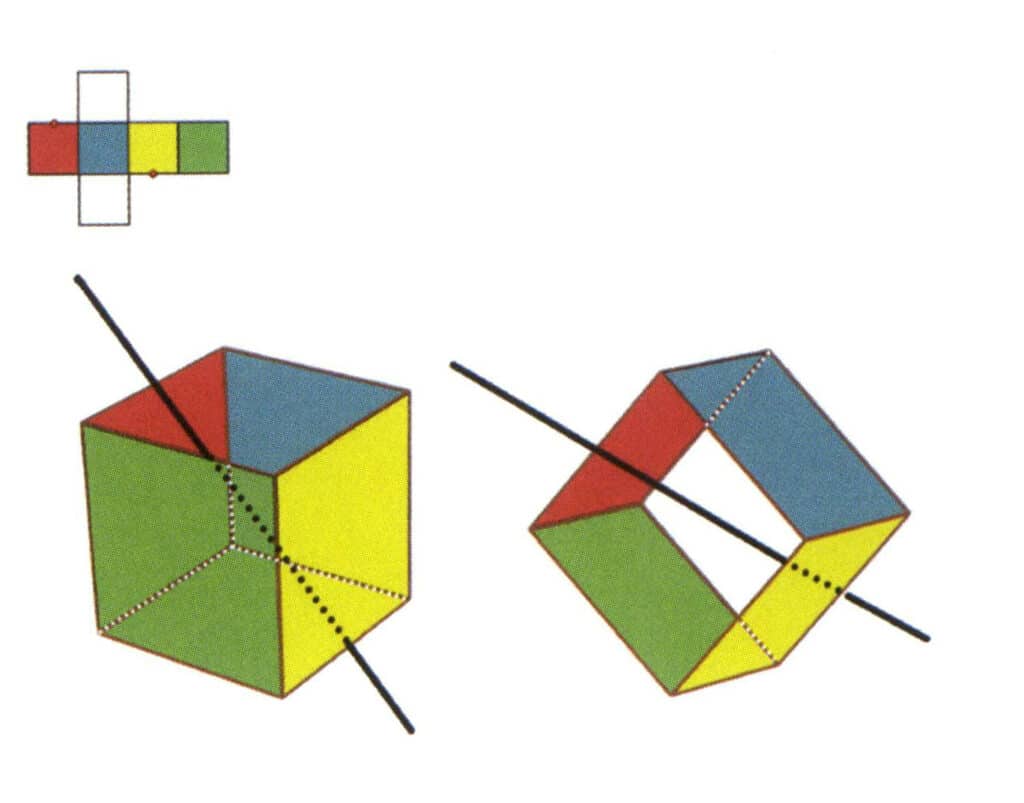
Figure 2-2-6 Le troisième axe secondaire du cube.
Sélectionnez le point médian des lignes parallèles, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant pivoter le cube de 360°. Les niveaux de base ont des couleurs différentes, mais la même forme se répète deux fois dans la même position (les faces rouge et incolore, les faces verte et bleue, les faces incolore et jaune, trois ensembles de faces répétées). Cette ligne imaginaire est enregistrée comme troisième axe secondaire.
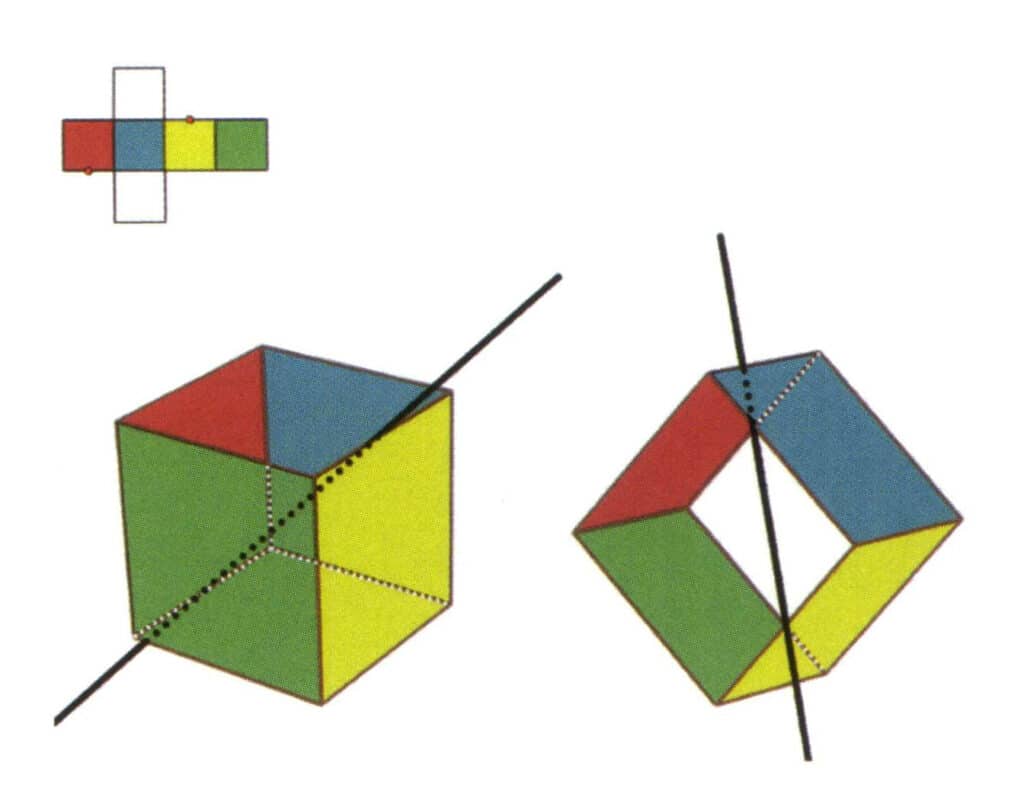
Figure 2-2-7 Le quatrième axe secondaire du cube
Sélectionnez le point médian des lignes parallèles comme indiqué sur la figure, imaginez une ligne droite passant par les points médians de ces deux arêtes et faites pivoter le cube de 360° ; les plans de référence de couleur différente mais de forme identique se répètent deux fois dans la même position (les faces rouge et incolore, les faces verte et bleue, les faces incolore et jaune, trois ensembles de faces répétées), cette ligne droite imaginaire est enregistrée comme le quatrième axe secondaire.
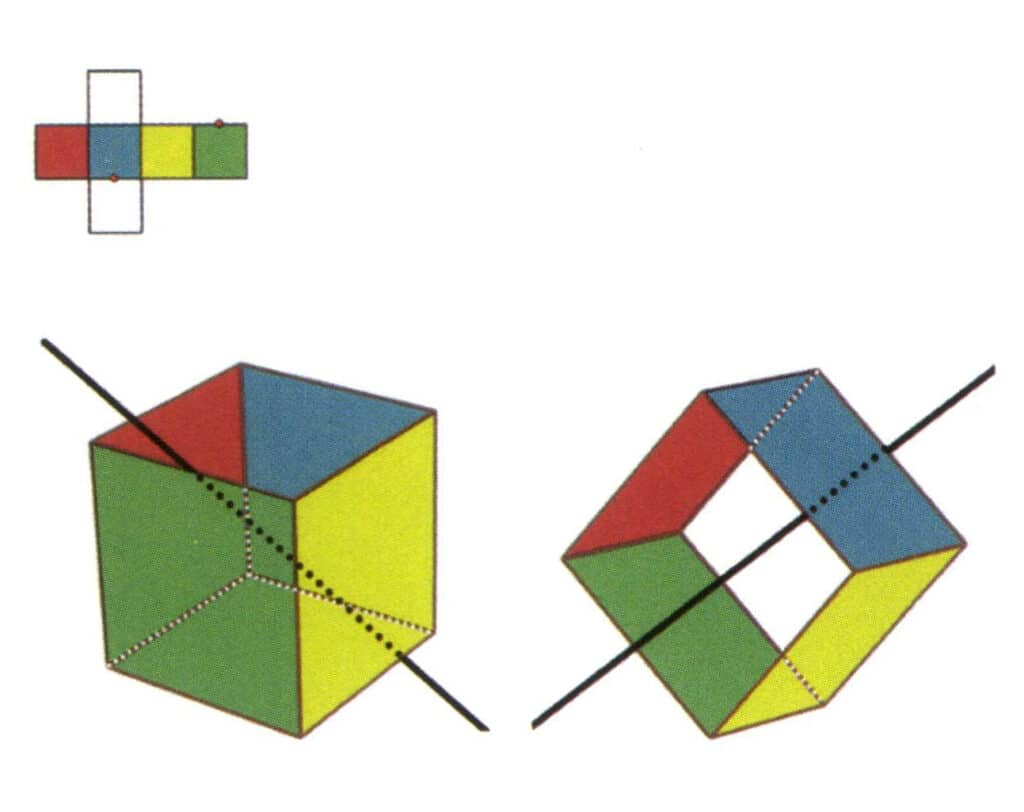
Figure 2-2-8 Le cinquième axe secondaire du cube.
Sélectionnez les points médians des lignes parallèles comme indiqué sur la figure, imaginez une ligne droite passant par les points médians de ces deux arêtes, faites pivoter le cube de 360°, les plans de référence de couleur différente mais de forme identique se répéteront deux fois dans la même position (faces rouges et incolores, faces vertes et bleues, faces incolores et jaunes, trois ensembles de faces répétées), cette ligne droite imaginée est enregistrée comme le cinquième axe secondaire.
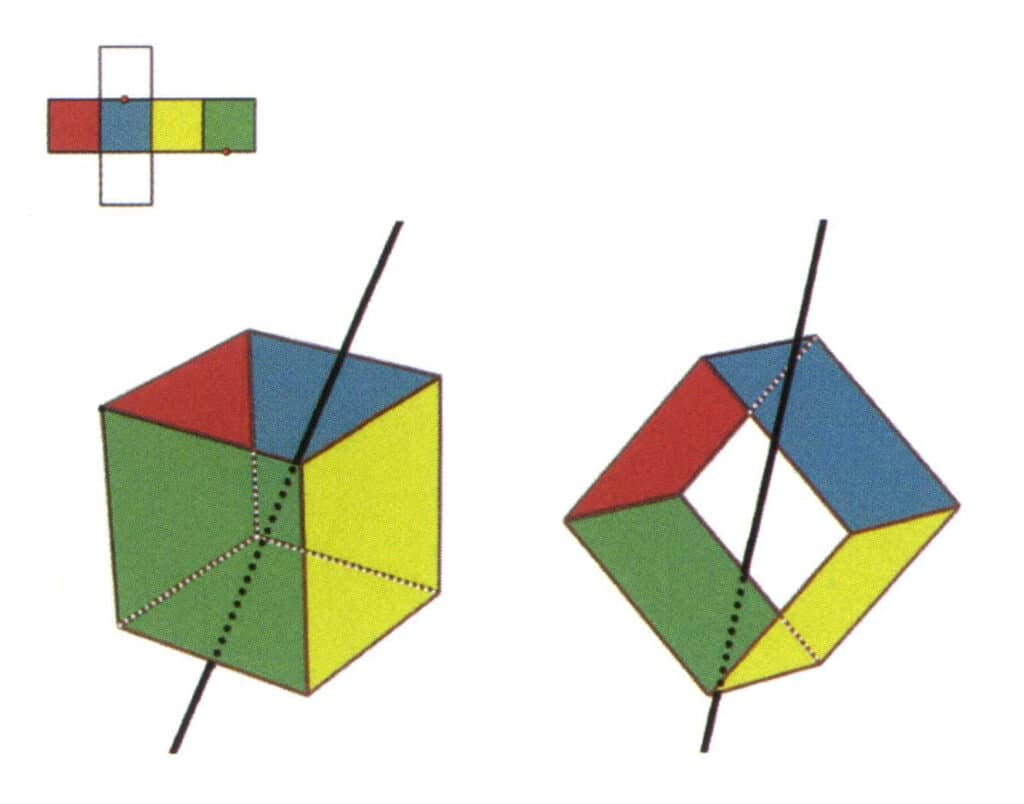
Figure 2-2-9 Le sixième axe secondaire du cube
Sélectionnez le point médian des lignes parallèles, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant pivoter le cube de 360°. Les niveaux de base de couleur différente mais de forme identique se répètent deux fois au même endroit (faces vertes et incolores, faces rouges et jaunes, faces incolores et bleues, trois séries de faces répétées). Cette ligne imaginaire est enregistrée comme le sixième axe secondaire.
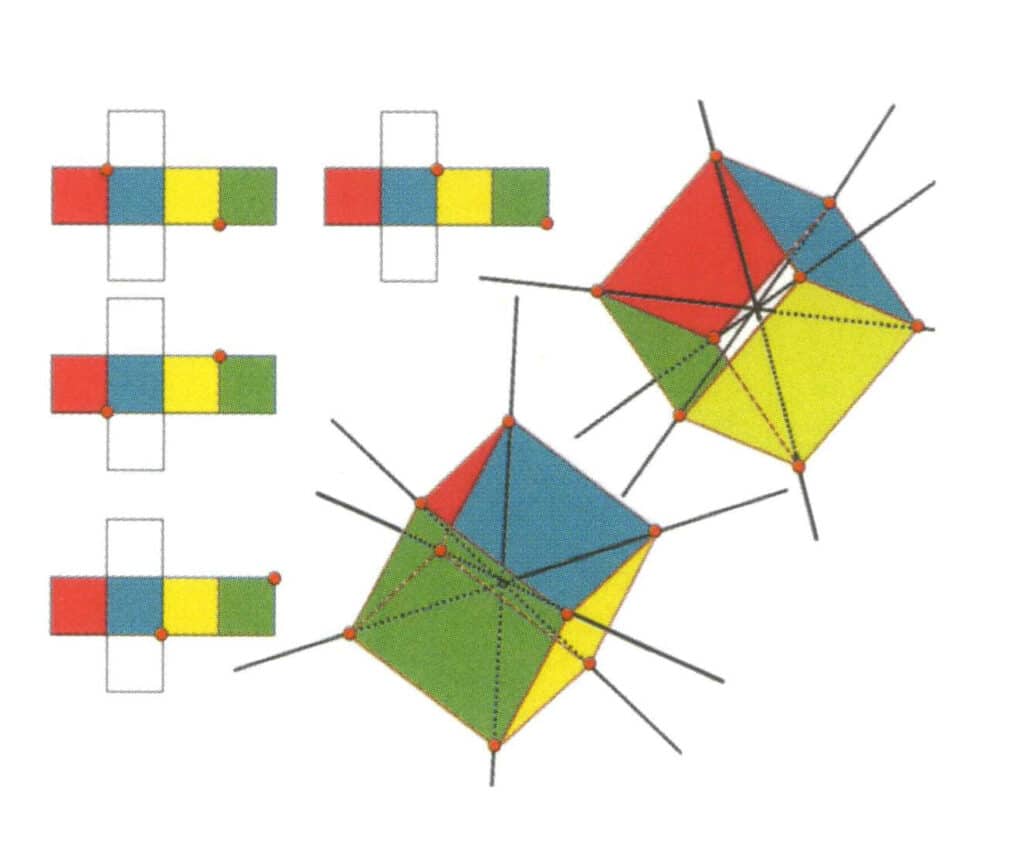
Figure 2-2-10 L'axe tertiaire du cube
La partie gauche de la figure montre la vue dépliée du cube, le point rouge indiquant le point d'intersection de la ligne imaginaire et de la ligne d'arête. La partie droite de la figure montre le cube fermé ; les points rouges indiquent l'intersection de la ligne droite imaginaire et des arêtes. L'axe tertiaire peut apparaître au milieu des faces d'un triangle équilatéral parallèle, à l'intersection de trois ou plusieurs faces parallèles ressemblant à un triangle équilatéral.
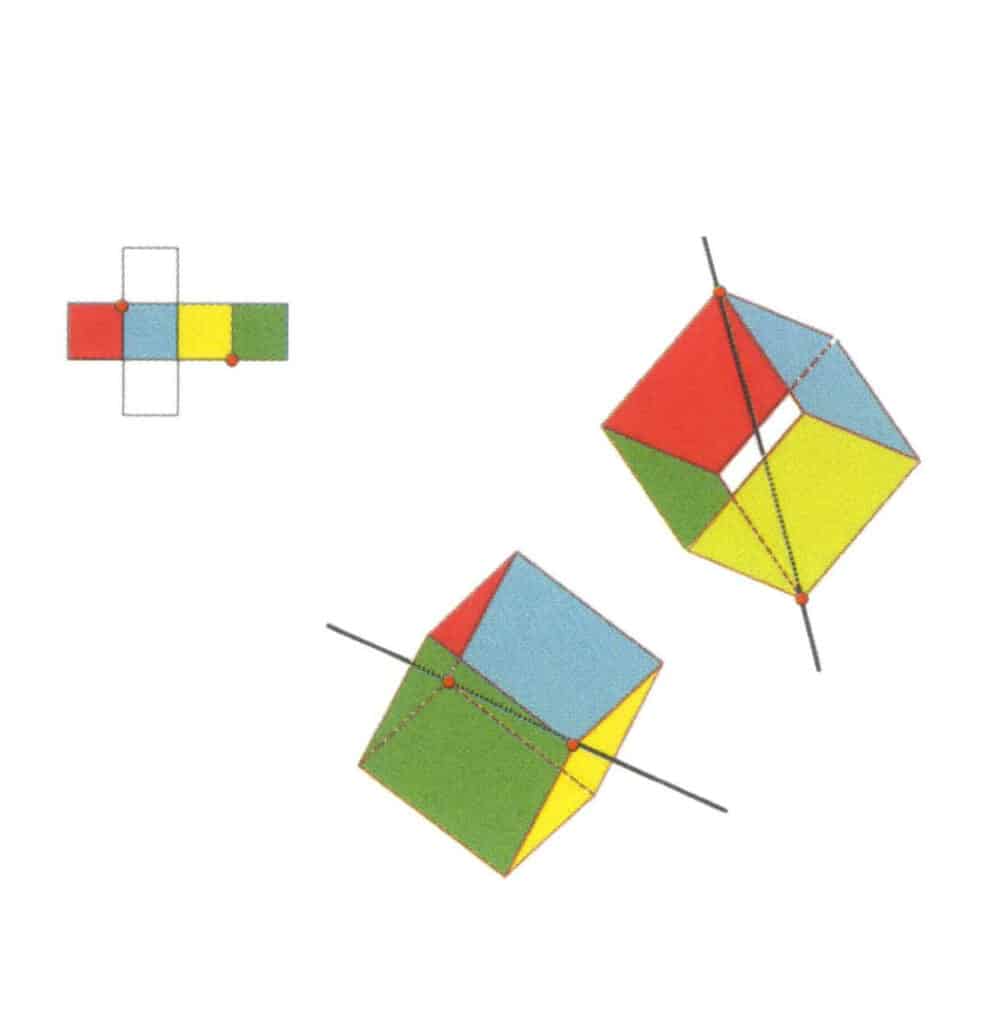
Figure 2-2-11 Le premier axe tertiaire du cube.
Sélectionnez les points d'intersection des trois faces comme indiqué sur la figure, imaginez une ligne droite passant par les points médians de ces deux arêtes, faites pivoter le cube de 360°, les plans de référence de couleur différente mais de forme identique se répètent dans la même position trois fois (faces rouges, incolores et bleues, faces vertes, incolores et jaunes, deux ensembles de faces répétées), cette ligne droite imaginée est enregistrée comme le premier axe tertiaire.
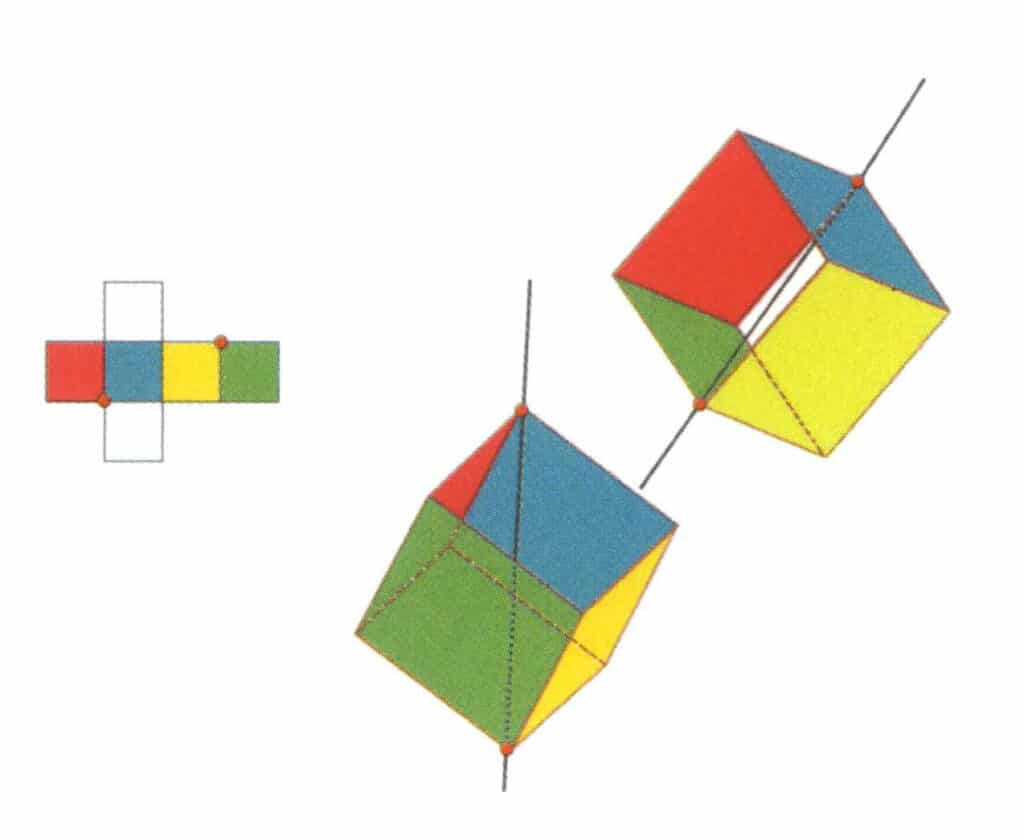
Figure 2-2-12 Le deuxième axe tertiaire du cube.
Sélectionnez les points d'intersection des trois faces, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant pivoter le cube de 360°. Les niveaux de base de couleur différente mais de forme identique se répètent trois fois au même endroit (faces rouges, incolores et bleues ; faces vertes, incolores et jaunes, deux ensembles de faces répétées). Cette ligne imaginaire est enregistrée comme le deuxième axe tertiaire.
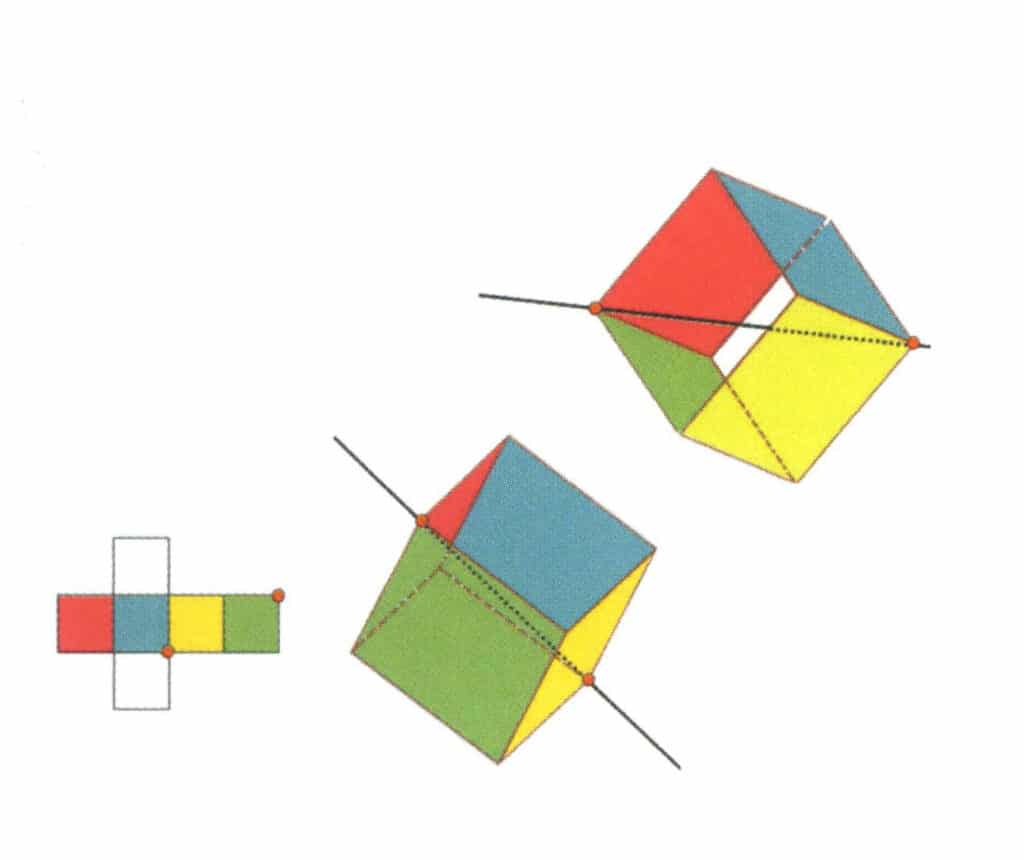
Figure 2-2-13 Le troisième axe tertiaire du cube
Sélectionnez les points d'intersection des trois faces, comme indiqué sur la figure. Imaginez une ligne droite passant par les points médians de ces deux arêtes, faisant pivoter le cube de 360°. Les niveaux de base de couleur différente mais de forme identique se répètent trois fois au même endroit (faces rouge, incolore et verte ; faces bleue, incolore et jaune, deux ensembles de faces répétées). Cette ligne imaginaire est enregistrée comme le troisième axe tertiaire.
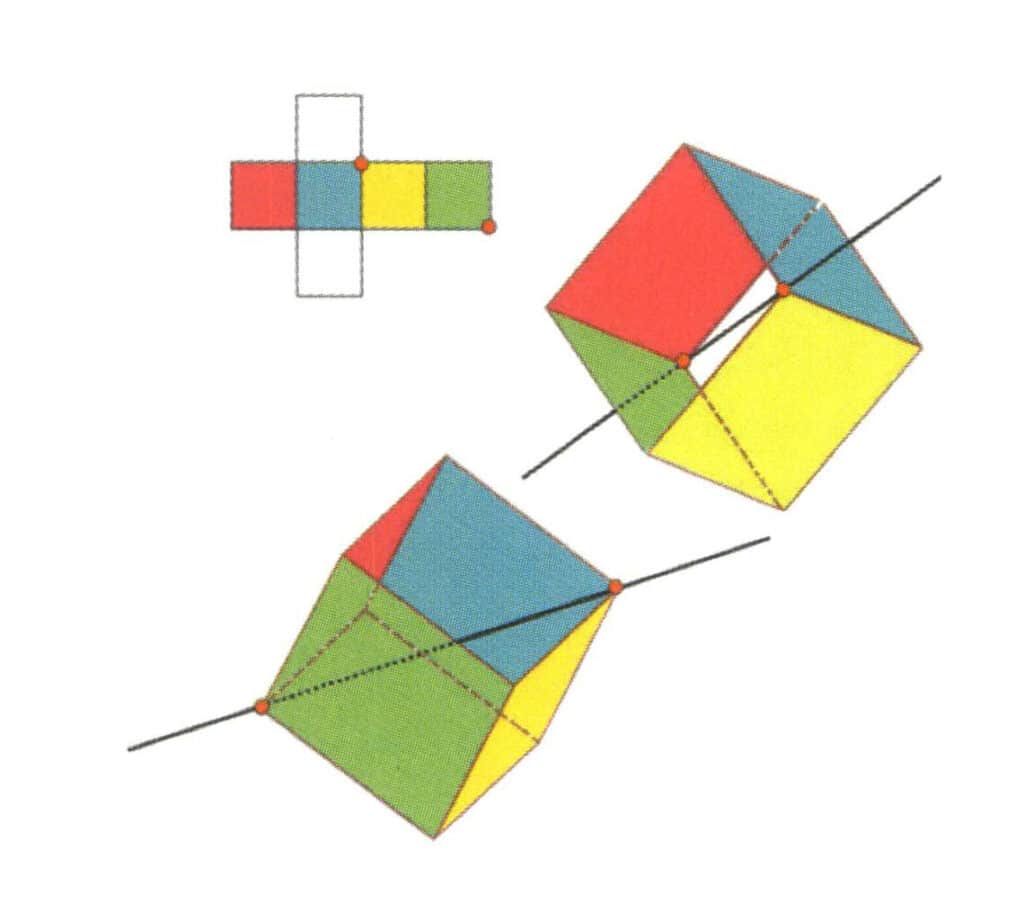
Figure 2-2-14 Quatrième axe cubique du cube.
Sélectionnez l'intersection des trois faces comme indiqué sur la figure, en supposant qu'il existe une ligne droite passant par le point médian des deux arêtes, faites pivoter le cube de 360°, des couleurs différentes mais la même forme, le niveau de base sera le même. Répétez la position trois fois (faces rouge, incolore, verte, bleue, incolore et jaune, deux séries de faces répétées). Cette ligne imaginaire est enregistrée comme le quatrième axe du cube.
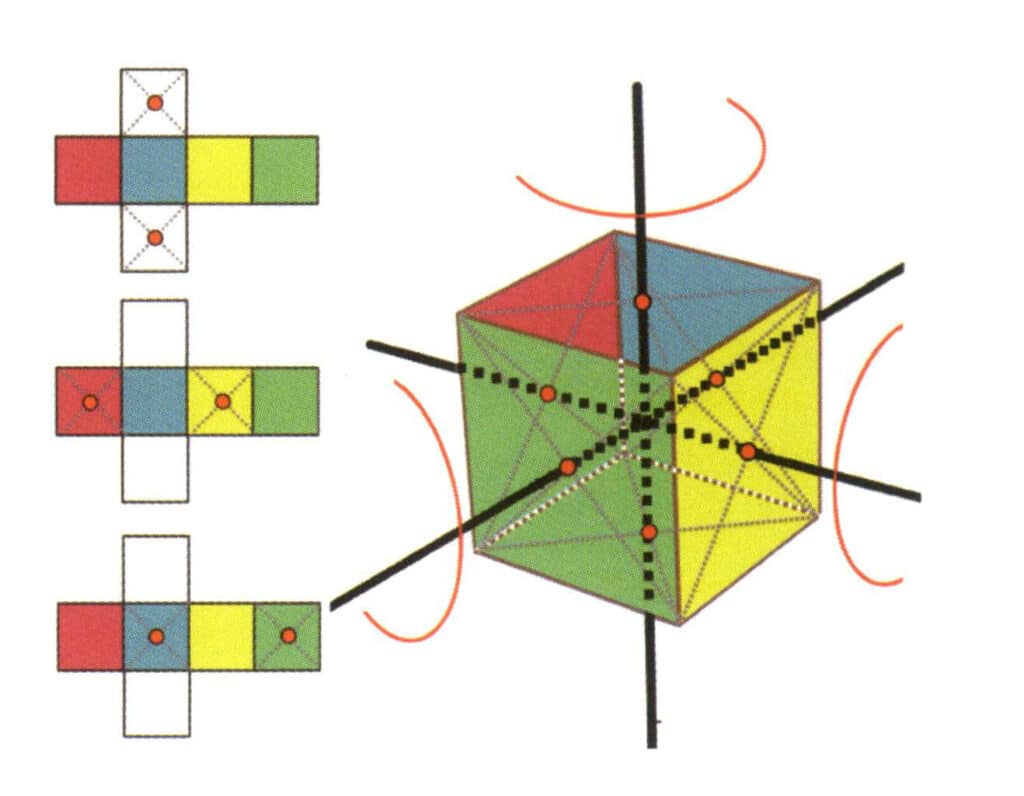
Figure 2-2-15 Quatrième axe du cube
La partie gauche de la figure montre la vue dépliée du cube, les points rouges indiquant les points d'intersection de la ligne imaginaire et des arêtes. La partie droite de la figure montre un cube fermé, les points rouges indiquant les points d'intersection de la ligne imaginaire et du plan. Le quatrième axe peut apparaître au point médian de faces carrées parallèles, à l'intersection de trois faces parallèles ou plus qui ressemblent à un carré.
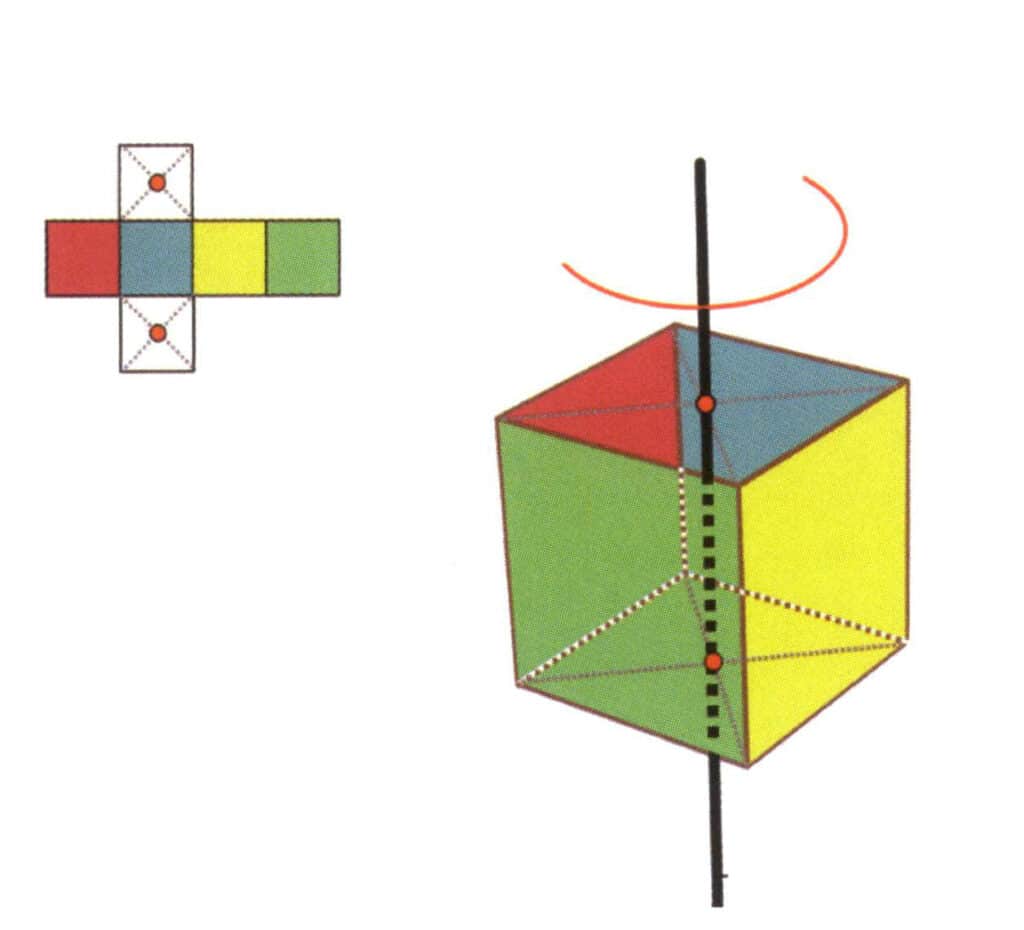
Figure 2-2-16 Le premier axe quartique du cube
Choisissez les points médians des plans représentés sur la figure, supposez qu'il existe une ligne droite passant par les points médians des deux plans et faites pivoter le cube de 360°. Les faces de couleur différente mais de même forme du niveau de base seront répétées quatre fois dans la même position (faces rouge, bleue, verte et jaune), et cette ligne droite hypothétique est enregistrée comme une quadruple axiale.
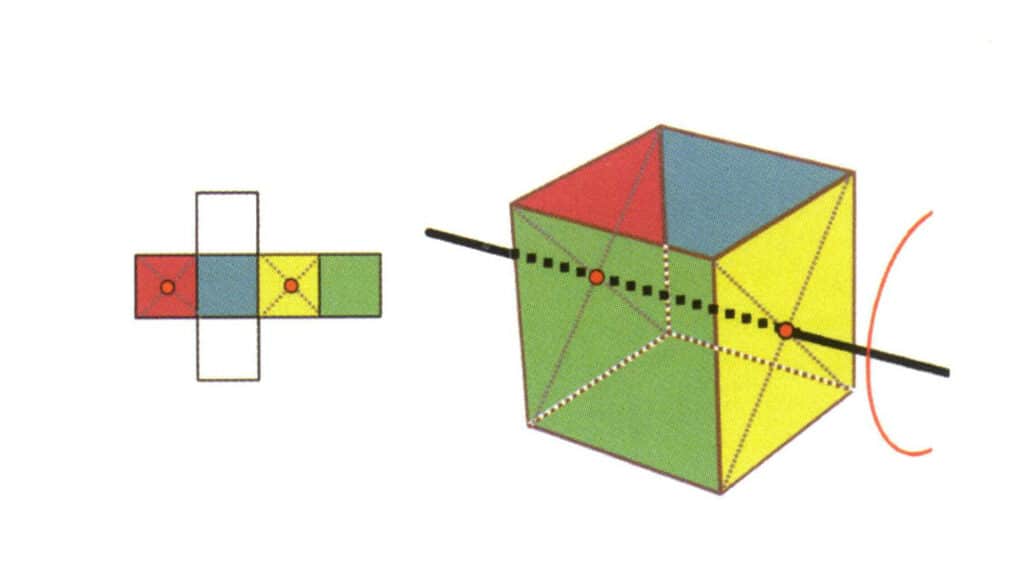
Figure 2-2-17 Le deuxième axe quartique du cube
Sélectionnez le point médian du plan comme indiqué sur la figure, imaginez une ligne droite traversant le cube et faites pivoter le cube de 360° ; la surface de base de couleurs différentes mais de même forme sera répétée quatre fois dans la même position (incolore, face bleue en haut, incolore, face verte en bas), et cette ligne imaginaire sera enregistrée comme le deuxième axe quadrique.
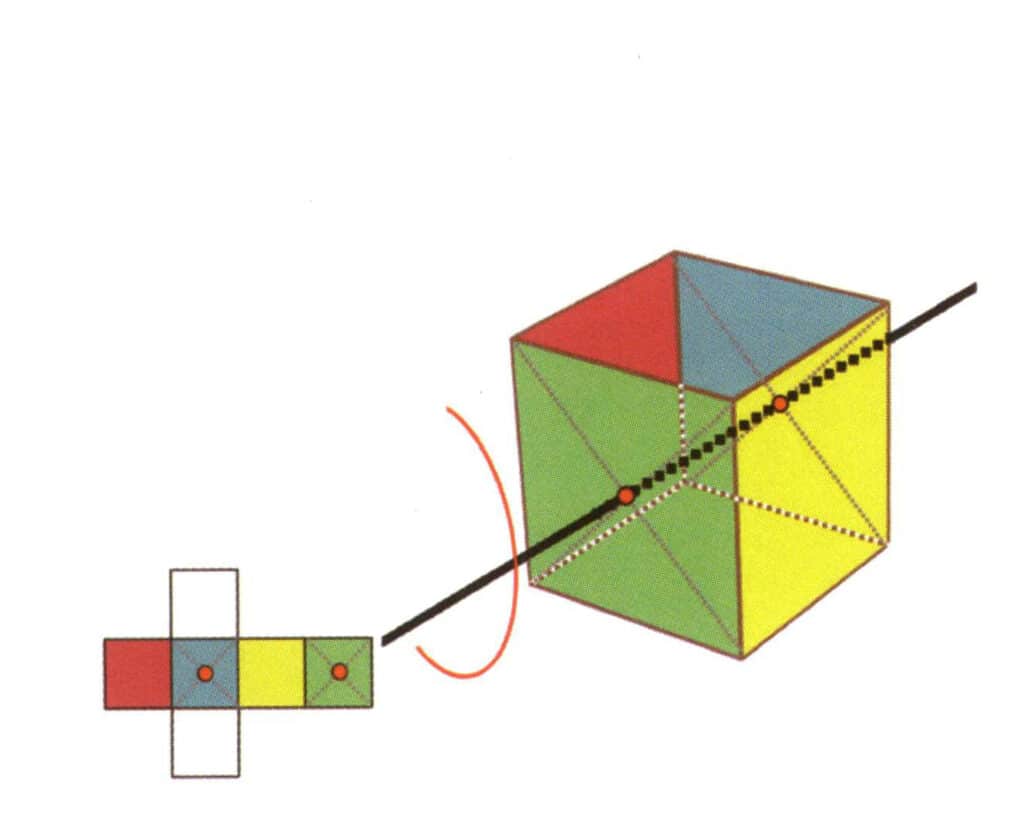
Figure 2-2-18 Troisième axe quartique du cube
Sélectionnez le point médian du plan comme indiqué sur la figure, imaginez une ligne droite à travers le cube et faites tourner le cube de 360°. Le niveau de base de couleurs différentes mais de même forme sera répété quatre fois dans la même position (incolore, face rouge en haut, incolore, face jaune en bas), et cette ligne imaginaire sera enregistrée comme troisième, quatrième axe.
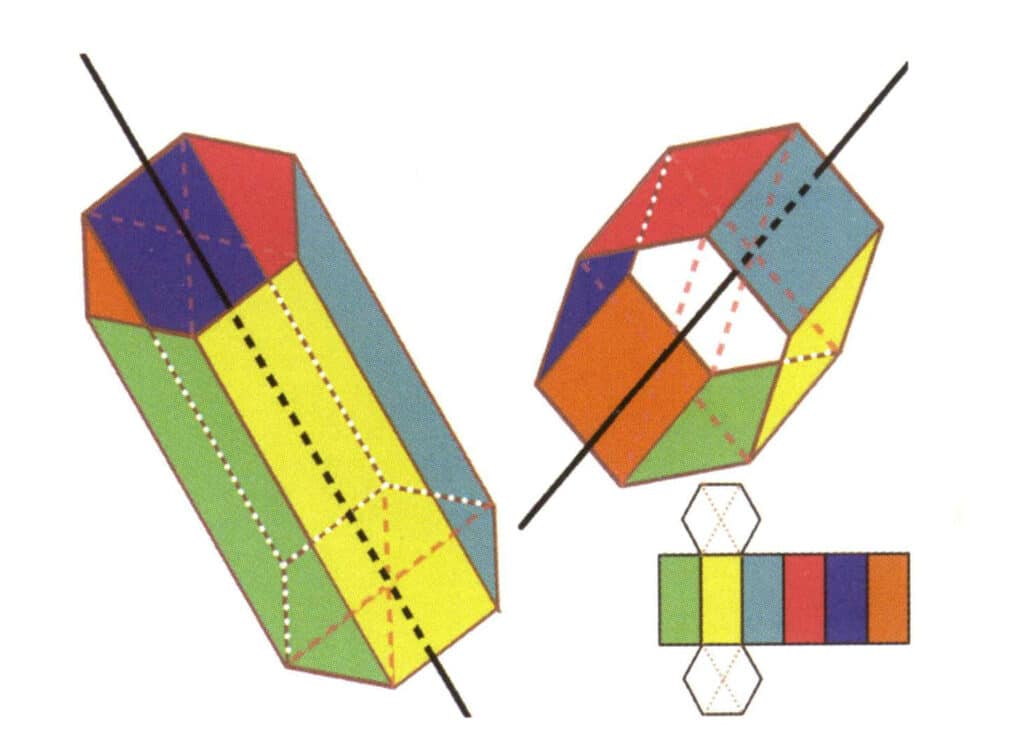
Figure 2-2-19 Six axes d'un prisme hexagonal
Les lignes noires à gauche et en haut à droite représentent les six axes du prisme hexagonal. La partie inférieure droite est une expansion du prisme hexagonal L'axe sextique peut apparaître au point médian des faces d'un hexagone parallèle ou à l'intersection des six faces d'un hexagone.
(2) Considérations pour trouver l'axe de symétrie.
① Il existe cinq types de positions pour l'axe de symétrie.
Le point médian de deux arêtes parallèles, comme la position de l'axe secondaire d'un cube.
Le point médian de deux plans parallèles, comme la position de l'axe quartique d'un cube.
Entre deux sommets (points d'intersection de plusieurs faces), comme la position de l'axe tertiaire d'un cube.
Le point médian entre un sommet et un plan parallèle, comme la position de l'axe tertiaire d'un tétraèdre.
Le point médian de la ligne de bord et le point médian du plan parallèle, comme la position de l'axe secondaire d'un prisme triangulaire.
② La sélection de l'axe de symétrie dans la même direction suit le principe du plus petit nombre. Par exemple, selon le principe du plus petit nombre, si une direction trouve six axes de symétrie et trois axes de symétrie, elle sera finalement enregistrée comme L³. Les axes de symétrie dans différentes directions doivent être enregistrés en fonction du nombre trouvé.
Il convient de noter qu'à l'exception de l'axe de symétrie sextuple et de l'axe de symétrie quadruple, qui ne peuvent apparaître simultanément, et qu'un seul axe sextuple peut apparaître, d'autres axes de symétrie peuvent coexister sous diverses formes ou dans des cas multiples.
③ Le niveau de base doit être choisi comme le plus petit plan de l'unité ; deux ou plusieurs plans se croisant ne peuvent pas être choisis comme niveau de base. Dans le cas contraire, la précision de l'évaluation de l'axe de symétrie s'en trouvera affectée.
④ Lors de l'enregistrement du nombre d'axes de symétrie, il est essentiel de déterminer le nombre de fois où la même forme et la même taille du plan sont répétées dans la même position.
⑤ S'il existe un axe secondaire de symétrie verticale Lⁿ(n = 3, 4 ou 6), il doit y avoir n axes secondaires verticaux par rapport à Lⁿ.
2.2 Plan de la symétrie
(1) Concept et méthode d'enregistrement du plan de la symétrie
Un plan de symétrie est un plan imaginaire qui, lorsque le cristal est coupé le long de ce plan, permet à chaque moitié du cristal d'être une image miroir de l'autre moitié (figure 2-2-20). Dans une même structure cristalline, un tel plan peut apparaître au maximum 9 fois (figure 2-2-21), ce qui signifie qu'il peut être coupé en deux de 9 façons différentes et que les deux moitiés peuvent coïncider complètement. Bien entendu, toutes les structures cristallines ne présentent pas de plans de symétrie.
La lettre majuscule P représente le plan de symétrie. Certains cristaux possèdent plusieurs plans de symétrie non coïncidents, et le nombre de ces plans de symétrie est conventionnellement écrit à gauche de P ; par exemple, quatre plans de symétrie sont représentés par 4P, et un plan de symétrie est représenté par P.
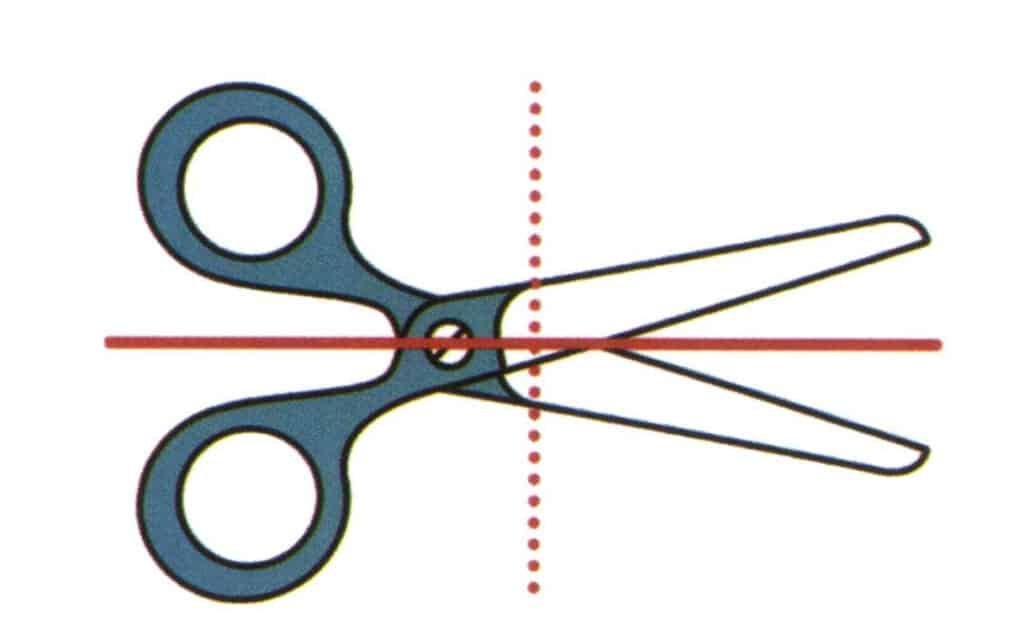
Figure 2-2-20 Imaginez un plan vertical de papier et un plan s'étendant le long de la direction de la ligne continue rouge, qui divise les ciseaux en parties supérieure et inférieure, et les parties supérieure et inférieure sont symétriques. Ce plan imaginé est appelé plan de symétrie. Imaginez un autre plan perpendiculaire à la surface du papier et s'étendant le long de la direction de la ligne pointillée rouge, qui divise les ciseaux en parties gauche et droite, mais les formes des ciseaux sur les côtés gauche et droit ne sont pas symétriques.
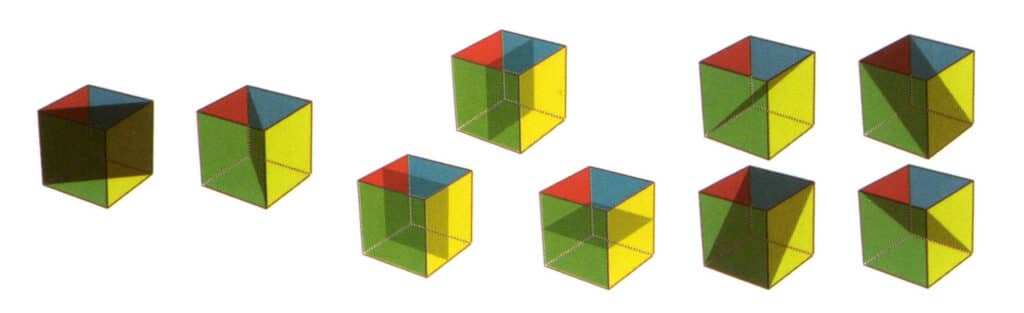
Figure 2-2-21 Neuf plans de symétrie d'un cube
(2) Conseils pour trouver Les plans de symétrie.
① Le plan de symétrie est souvent parallèle et coïncide avec l'axe de symétrie.
② Le plan de symétrie est un plan imaginaire qui divise la géométrie cristalline, ce qui est différent du double plan parallèle en géométrie.
③ Si un plan de symétrie contient l'axe de symétrie Lⁿ, alors il doit y avoir n plans de symétrie contenant Lⁿ.
(3) Point Le groupe.
Le groupe de points est la somme de tous les éléments de symétrie d'un cristal. L'ordre d'écriture du groupe de points est axe de symétrie + plan de symétrie, par exemple 3L²3P (figure 2-2-22). Si un cristal possède plusieurs axes de symétrie, il est d'usage de les noter de gauche à droite, de l'axe d'ordre supérieur à l'axe d'ordre inférieur, et l'ordre des plans de symétrie, par exemple, L⁴4L²5P (figure 2-2-23). Il existe 32 types de symétrie dans les cristaux.
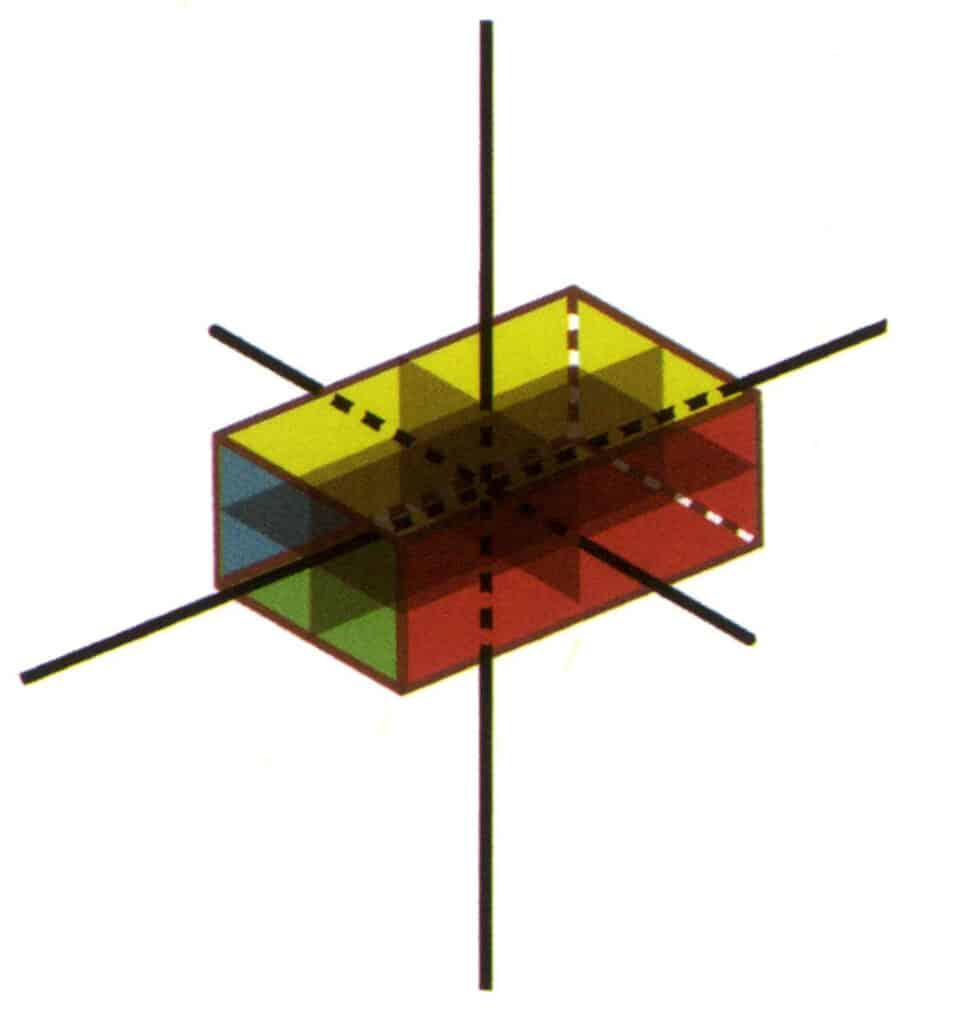
Figure 2-2-22 Groupe de points 3L²3P (cuboïde rectangulaire avec une section transversale rectangulaire)
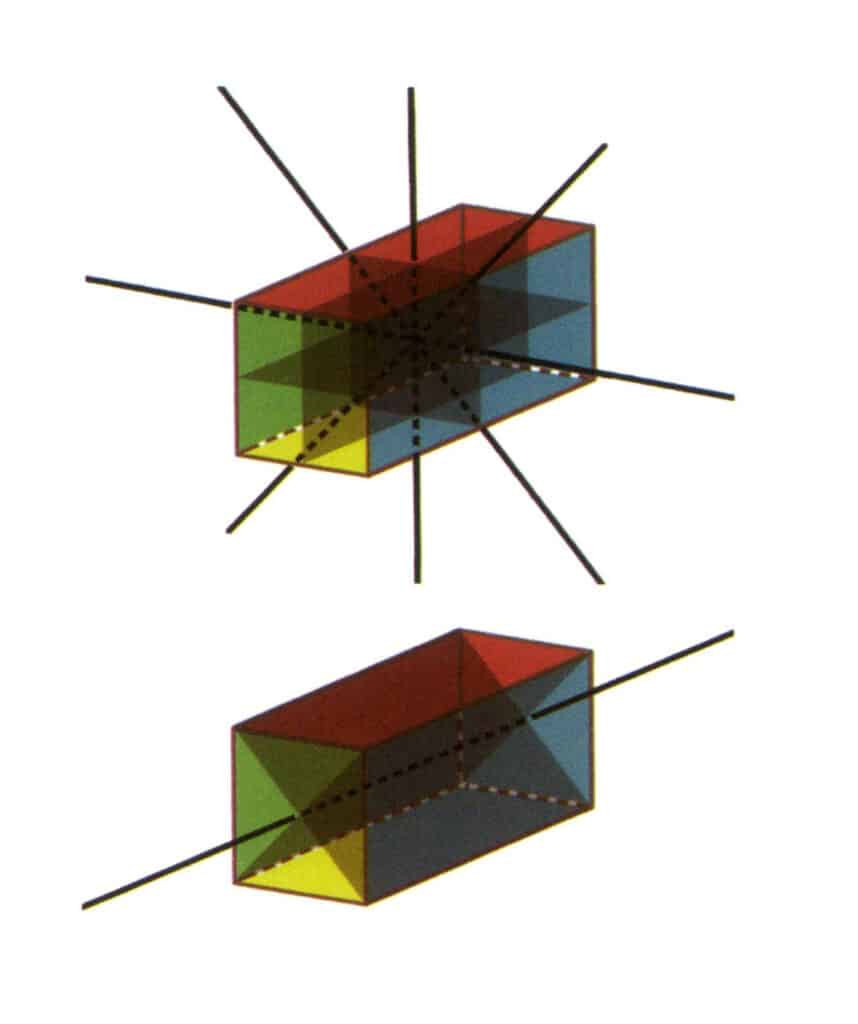
Figure 2-2-23 Groupe de points L⁴4L²5P (prisme rectangulaire à section carrée), avec quatre deuxièmes axes et trois faces symétriques en haut, et un quatrième axe et deux faces symétriques en bas.
3. Classification des cristaux
La symétrie fait partie de la classification des cristaux. Un autre concept - l'axe cristallin - doit être introduit pour décrire la structure cristalline des pierres précieuses naturelles et artificielles dans un système de classification des cristaux. L'axe cristallin est une ligne imaginaire traversant la structure cristalline et indiquant la direction dans laquelle les nœuds du réseau se répètent et la distance relative à laquelle les nœuds se répètent le long de cette direction. L'axe cristallin coïncide avec la normale de l'axe de symétrie ou du plan de symétrie. En l'absence d'axe de symétrie ou de plan de symétrie, l'axe du cristal peut être choisi parallèlement à la direction du bord du cristal.
Sur la base des éléments de symétrie et des axes cristallins, le système académique classe les cristaux en trois familles de cristaux et sept systèmes cristallins (tableau 1).
Tableau 1 : Points clés pour déterminer les familles et les systèmes de cristaux
| Famille de cristal | Cristal | Points clés pour la détermination | Variétés de pierres précieuses communes |
|---|---|---|---|
| Système de cristaux de bas niveau | Système triclinique | Pas de deuxième axe ou de plan de symétrie | Amazonite, rhodonite, Turquoise |
| Système cristallin monoclinique | Pas d'axes supérieurs, pas plus d'un axe secondaire et d'un plan de symétrie | Jadéite, diopside, spodumène, épidote | |
| Système cristallin orthorhombique | Pas d'axes supérieurs, plus d'un axe secondaire ou d'un plan de symétrie | Olivine, topaze, saualpite (y compris tanzanite), cordiérite, chrysobéryl, enstatite | |
| Famille de cristaux intermédiaires | Système cristallin tétragonal | 1 axe quadruple (peut être représenté par L4) | Diamant |
| Système cristallin trigonal | 1 (peut être représenté par L3) | Corindon, rubis, saphir, tourmaline, cristaux de la famille des quartz (tels que cristal, améthyste, citrine, etc.), rhodochrosite. | |
| Système cristallin hexagonal | 1 axe hexagonal (peut être représenté par L6) | Aigue-marine, émeraude et autres pierres précieuses de la famille des bérylites, apatite | |
| Famille de cristaux avancés | Système cristallin isométrique | 4 axes trigonaux (pouvant être représentés par 4L3) | Diamant, grenat, spinelle, spath fluor |
4. Caractéristiques communes des cristaux de pierres précieuses
Les pierres précieuses les plus courantes sont le diamant, le spinelle, le spath fluor, le grenat, la bérylite, le zircon, le corindon, la tourmaline, le cristal, le chrysobéryl, la topaze, etc. Chaque type de pierre précieuse possède ses propres caractéristiques cristallines.
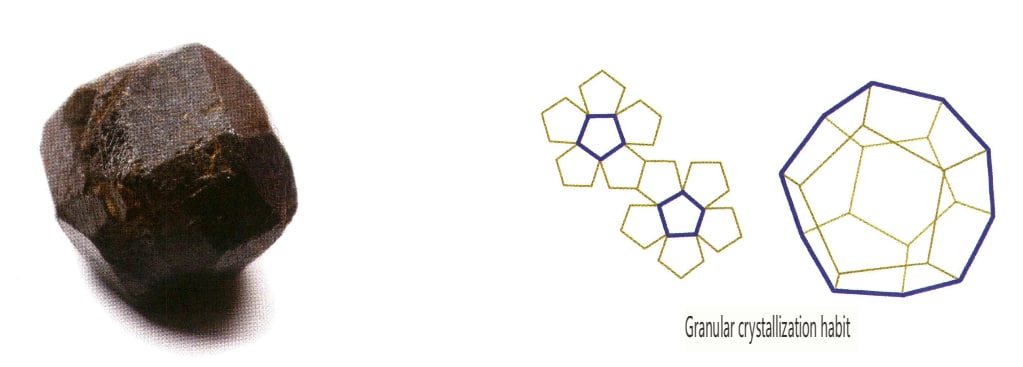
Les pierres précieuses de la famille des cristaux de haut niveau ont le plus souvent un comportement cristallin granuleux, et les variétés communes apparaissent souvent sous des formes cristallines fixes (tableau 2).
Le comportement cristallin des familles de cristaux de niveau intermédiaire et inférieur est colonnaire (tableau 3).
Tableau 2 : Caractéristiques communes des familles de cristaux de haut niveau
| Nom de la tonalité des pierres précieuses | Classification des cristaux | Caractéristiques importantes du cristal | |||
|---|---|---|---|---|---|
| Nom de la tonalité des pierres précieuses | Classification des cristaux | L'habitude du cristal | Formes cristallines courantes | Formes jumelles courantes | Modèles courants de faces de cristal |
| Diamant | Système cristallin isométrique | Structure cristalline granulaire (figure 2-2-24), couramment observée sous forme de granules octaédriques. | L'octaèdre est une forme cristalline courante, mais des formes cristallines plus complexes, notamment des dodécaèdres rhombiques, peuvent également apparaître, présentant souvent des faces cristallines arrondies, qui peuvent présenter une symétrie triple | Jumeau plat triangulaire, parfois sans angles concaves visibles (figure 2-2-25) | La surface présente des piqûres de gravure triangulaires inversées (figures 2-2-26, 2-2-27) et d'autres motifs de faces cristallines (figures 2-2-28, 2-2-29). |
| Spinelle | Forme cristalline granuleuse (figure 2-2-30), généralement observée sous forme de granules octaédriques. | Souvent produites sous forme octaédrique, les faces cristallines peuvent être très plates, comme si elles étaient polies (figure 2-2-31) | Les cristaux jumeaux sont très plats, ressemblant à une forme triangulaire dont les coins ont été coupés (Figure 2¬2-32). | Puits de gravure visibles en surface, certains ressemblant à des diamants en forme de triangle inversé (figure 2-2-33) | |
| Fluorite | Cristaux granuleux (Figure 2-2-34) | Formes cristallines octaédriques et cubiques (figure 2-2-35) | Jumelage interpénétré | Marques de croissance en gradins carrés, la plupart avec des lacunes de clivage, bandes de couleur parallèles aux directions des six faces du cube | |
| Grenat | Habitude cristalline granulaire, communément observée dans les grains dodécaédriques rhombiques (Figure 2-2-36). | Dodécaèdre rhombique ou trapèze carré | Rare | Bandes annulaires concentriques visibles ayant la même forme que les faces du cristal (figure 2-2-37) | |
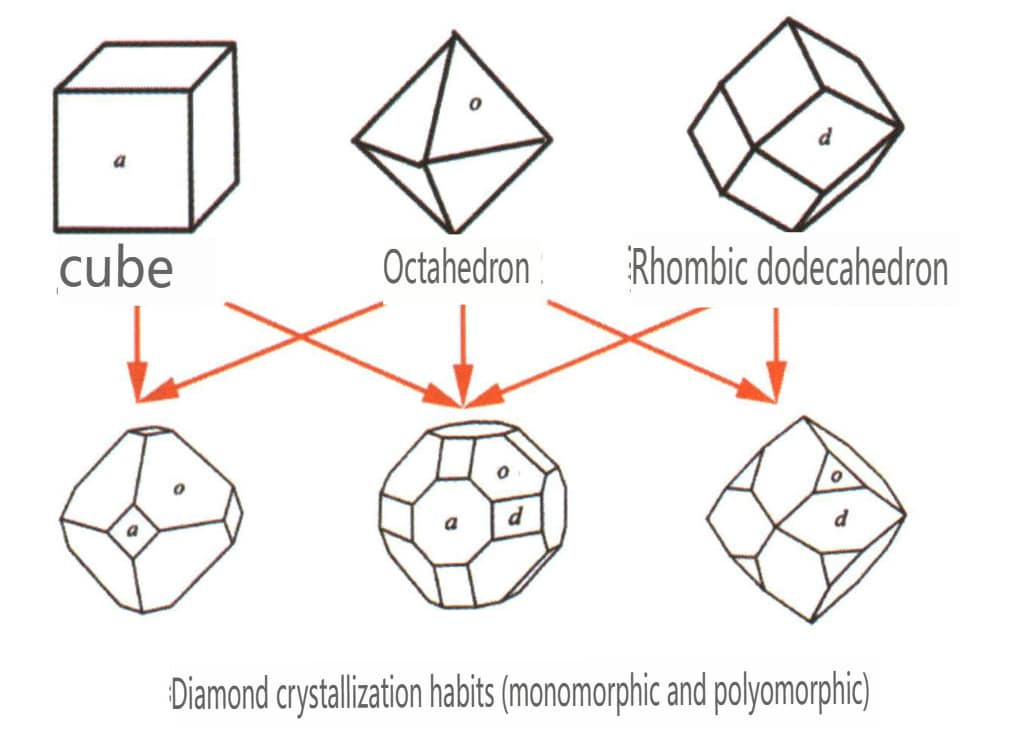
Figure 2-2-24 Habitudes du cristal de diamant
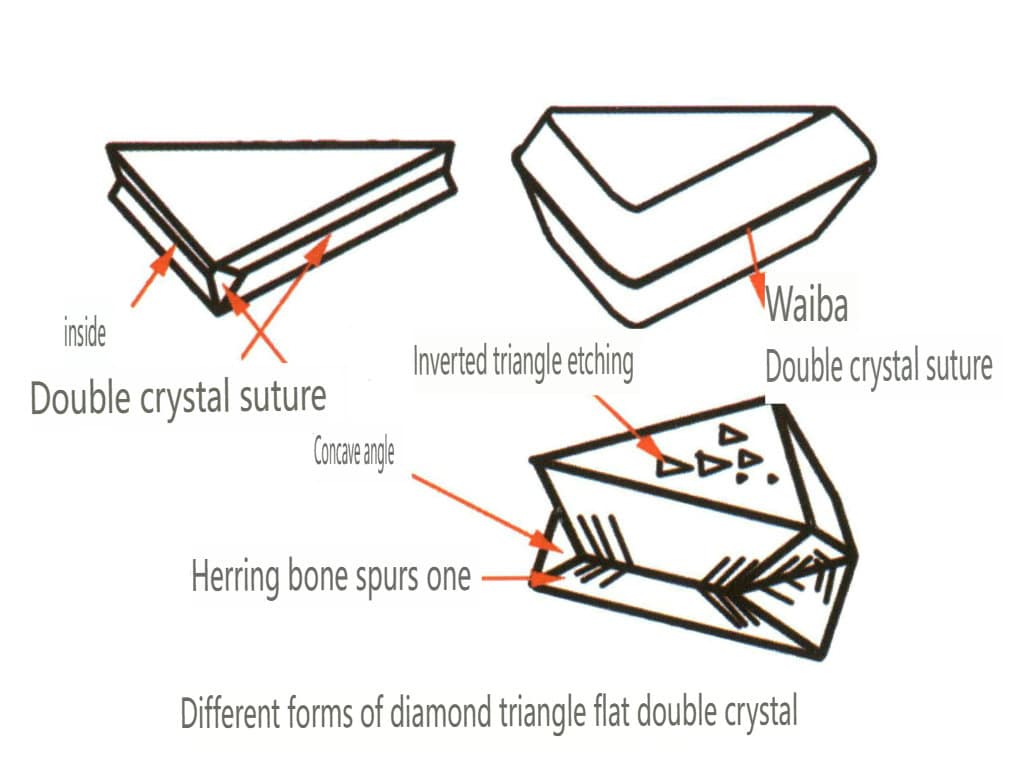
Figure 2-2-25 Habitation jumelée en forme de diamant
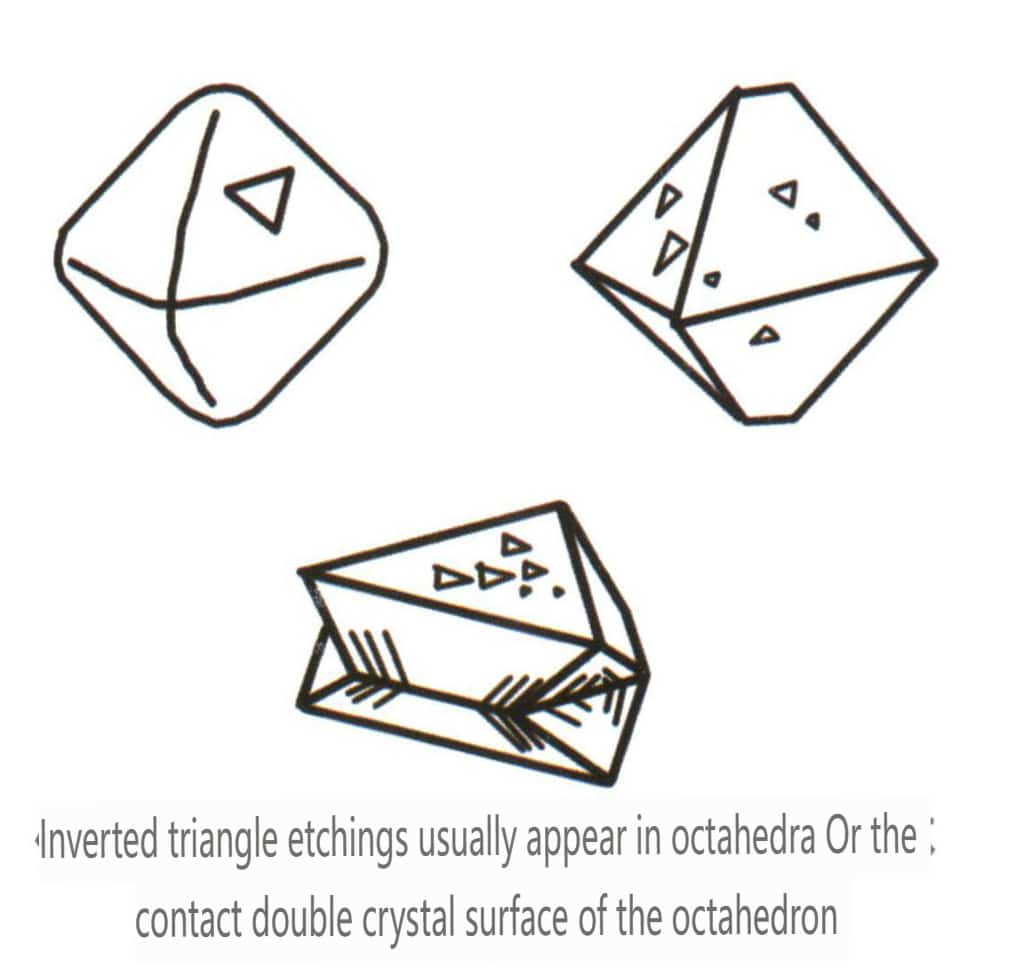
Figure 2-2-26 Figure de gravure en triangle inversé des faces cristallines octaédriques du diamant

Figure 2-2-27 Figure de gravure triangulaire inversée sur la surface d'un cristal octaédrique de diamant
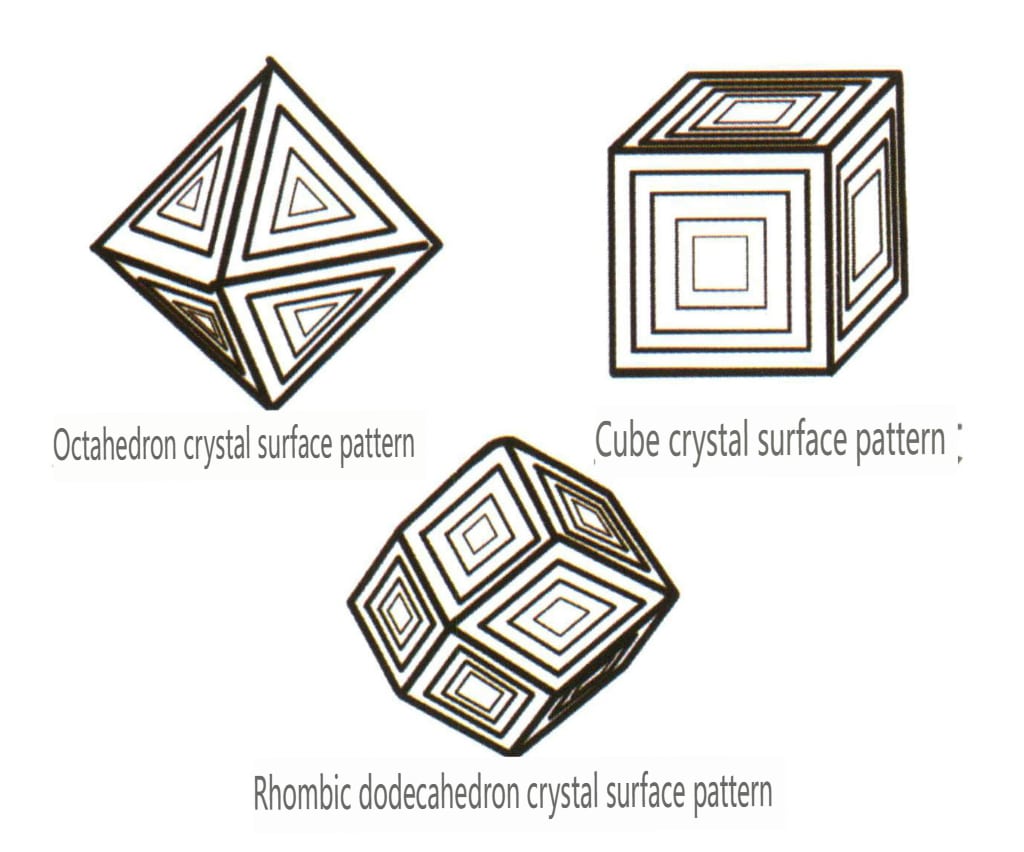
Figure 2-2-28 Figure de gravure en triangle inversé des faces cristallines octaédriques du diamant

Figure 2-2-29 Figure de gravure triangulaire inversée sur la surface d'un cristal octaédrique de diamant
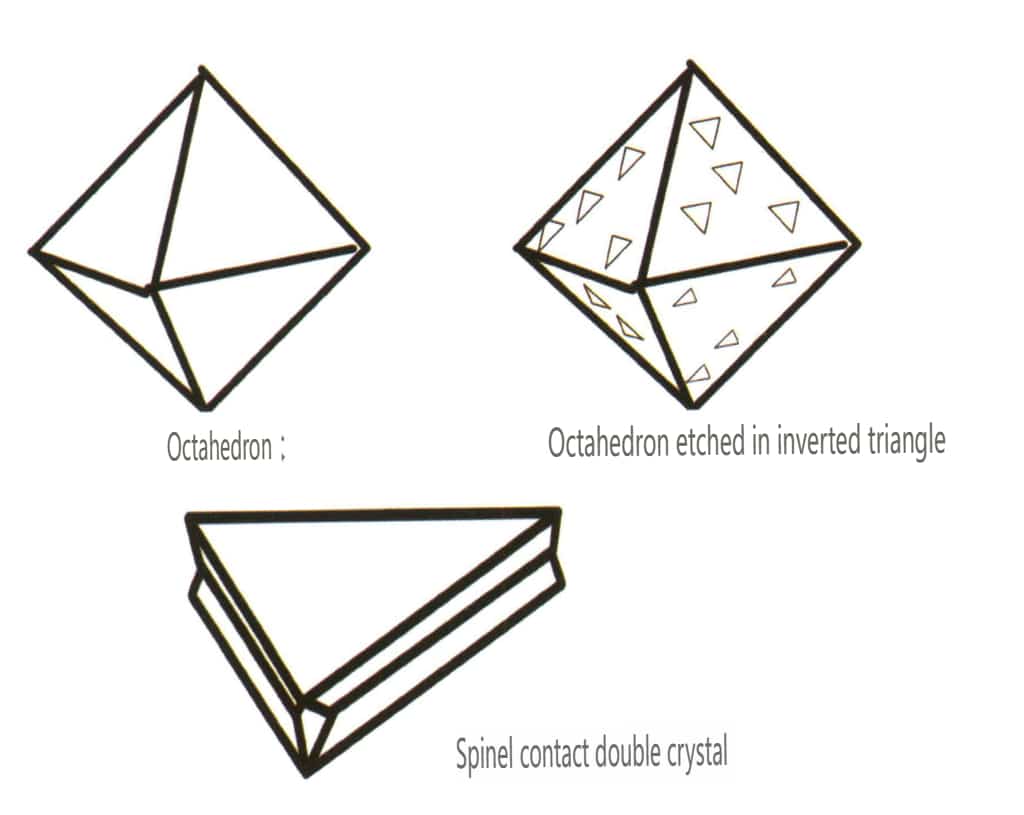
Figure 2-2-30 Habitudes cristallines du spinelle

Figure 2-2-31 Formes courantes de cristaux de spinelle

Figure 2-2-32 Torsion de contact du spinelle
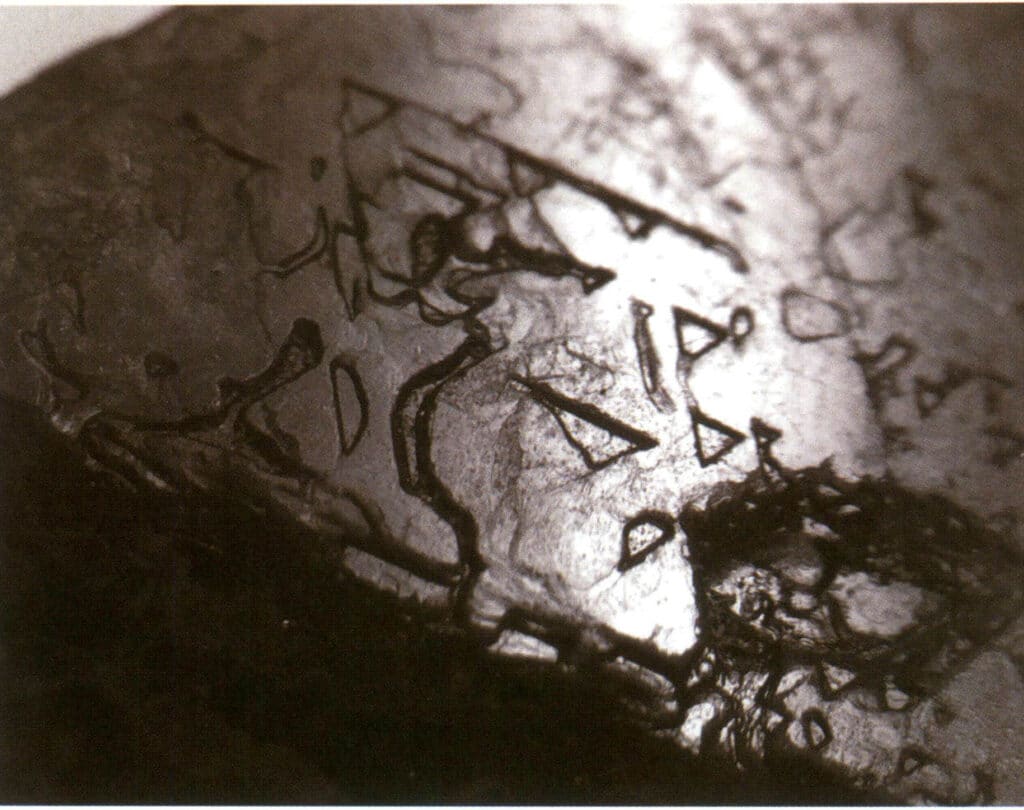
Figure 2-2-33 Figure de gravure triangulaire inversée à la surface du spinelle
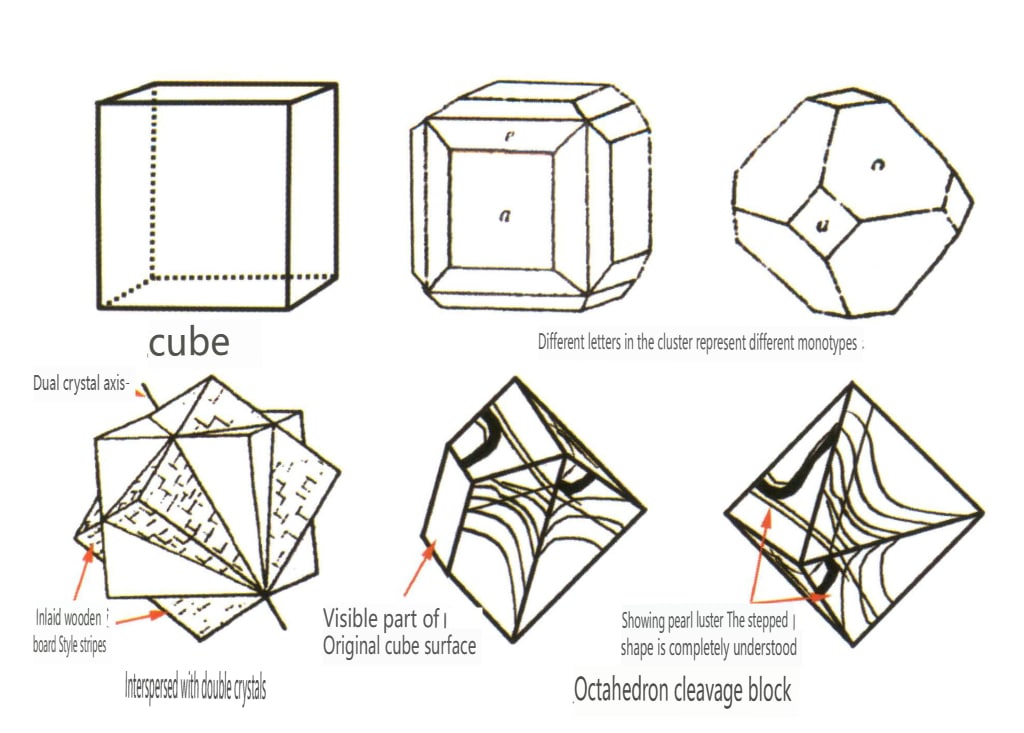
Figure 2-2-34 Habitudes cristallines de la fluorine

Figure 2-2-35 Cristal de fluorine
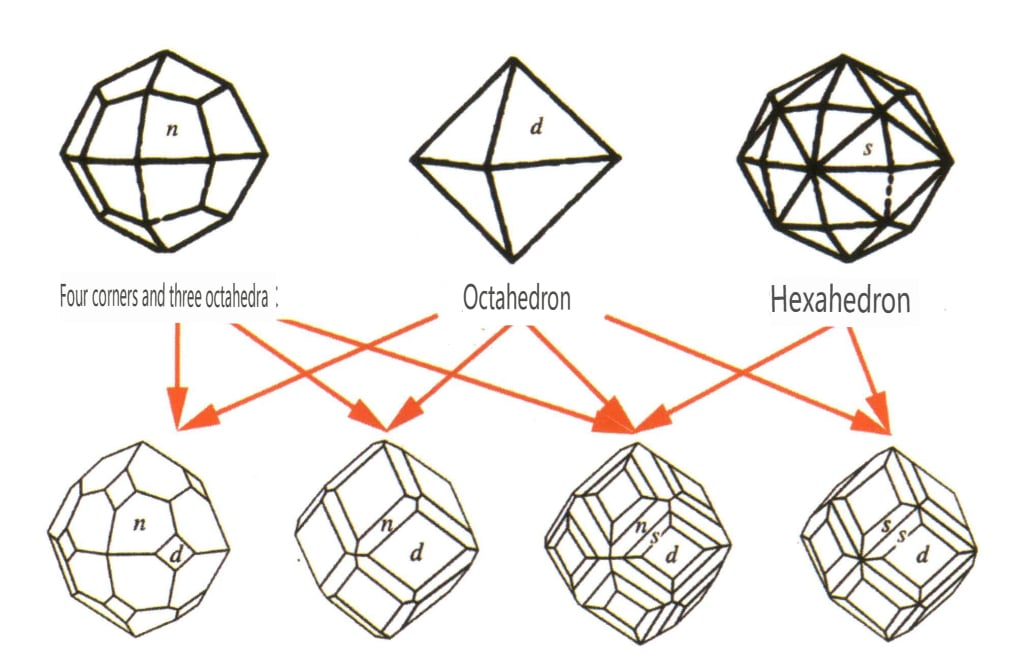
Figure 2-2-36 Habitudes cristallines du grenat

Figure 2-2-37 Bandes annulaires concentriques à la surface des cristaux de grenat qui ont la même forme que les faces du cristal
Tableau 3 : Caractéristiques communes des familles de cristaux intermédiaires et faibles
| Nom de la tonalité des pierres précieuses | Classification des cristaux | Caractéristiques importantes du cristal | |||
|---|---|---|---|---|---|
| Nom de la tonalité des pierres précieuses | Classification des cristaux | L'habitude du cristal | Formes cristallines courantes | Formes jumelles courantes | Modèles courants de faces de cristal |
| Béryl | Système cristallin hexagonal | Cristaux colonnaires (figure 2-2-38) | Forme cristalline hexagonale (figures 2-2-39, 2-2-40) | Rare | Bandes longitudinales visibles |
| Pierre de plomb | Système cristallin tétragonal | Structure cristalline colonnaire (figure 2-2-41) | Une colonne carrée à section carrée, apparaissant avec un double cône carré (figure 2-2-42). | Cristaux jumeaux visibles en forme de genou | Pas de motifs particuliers |
| Corindon | Système cristallin trigonal | Cristaux en forme de plaques, cristaux en forme de colonnes (Figure 2-2-43) | Les rubis présentent souvent une forme de prisme hexagonal (figure 2-2-44), tandis que les saphirs présentent souvent une forme cristalline hexagonale bipyramidale en tonneau (figure 2-2-45). | Bi-cristaux couramment observés. | Stries visibles. |
| Tourmaline . | Cristaux colonnaires (figure 2-2-46) | Les faces cristallines aux deux extrémités sont différentes et la section transversale est un triangle sphérique (figure 2-2-47) | Rare | Bandes longitudinales visibles (figure 2-2-48) | |
| Quartz (quartz cristallin) | Cristaux colonnaires (figure 2-2-49) | La section transversale est hexagonale, les bipyramides hexagonaux sont rares (figures 2-2-50, 2-2-51), les monopyramides hexagonaux sont fréquents. | Contact commun avec les bicristaux (également connus sous le nom de bicristaux japonais) | Rayures horizontales courantes sur les surfaces cristallines | |
| Chrysobéryl | Système cristallin trigonal | Caractéristiques de la cristallisation en colonne (Figure 2-¬2-52) | Le monocristallin est rare | La forme tricristalline est courante (figure 2-2-53), les angles hexagonaux et concaves peuvent être utilisés comme critères d'identification. | Les bandes tri-cristallines peuvent être utilisées comme critères d'identification. |
| Topaze | Cristaux colonnaires (figure 2-2-54) | La section transversale est en forme de losange et le sommet a souvent l'apparence d'une enveloppe (figure 2-2-55) | Les bi-cristaux sont rares | Bandes longitudinales visibles | |
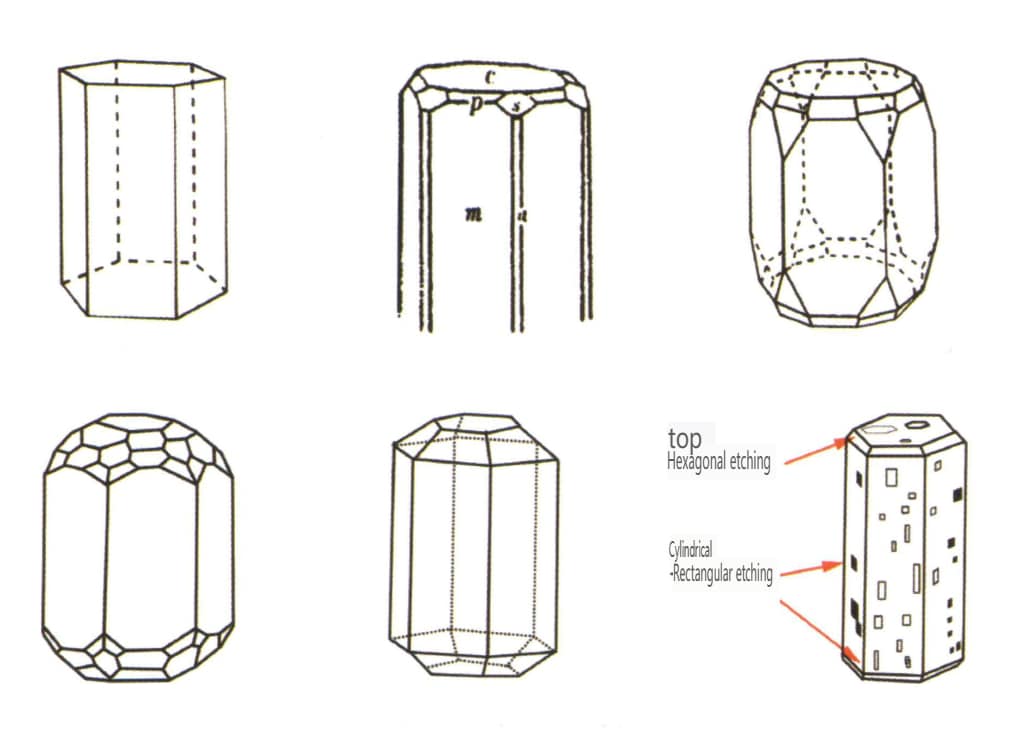
Figure 2-2-38 Habitudes cristallines du béryl

Figure 2-2-39 Formes courantes de cristaux d'émeraude

Figure 2-2-40 Formes courantes de cristaux d'aigue-marine
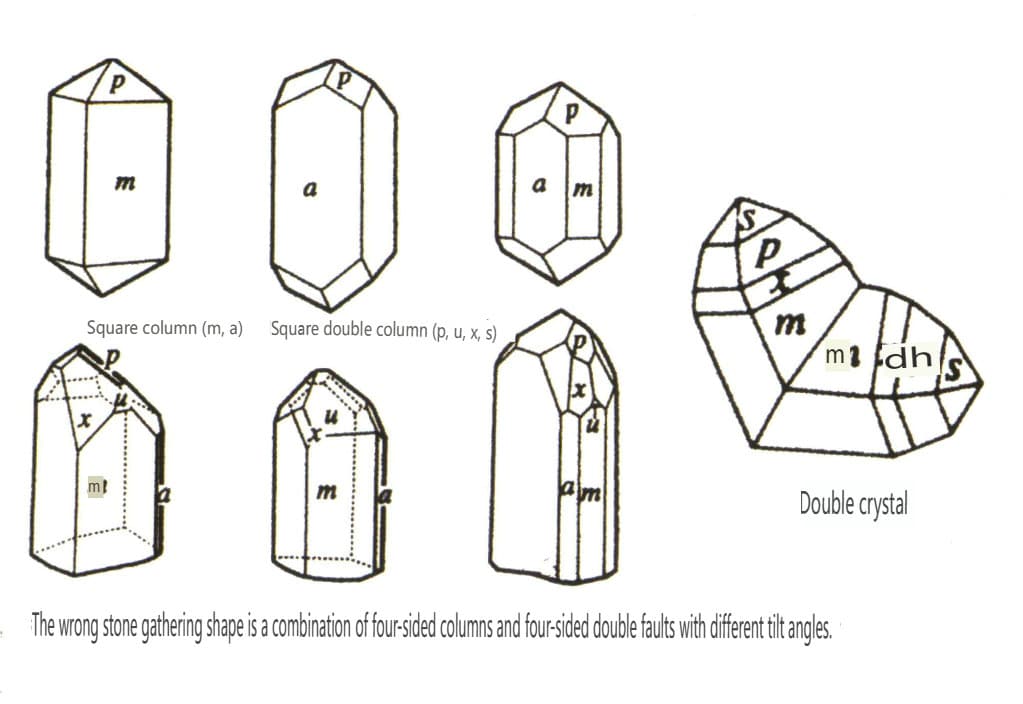
Figure 2-2-41 Habitudes cristallines du zircon

Figure 2-2-42 Cristal de zircon
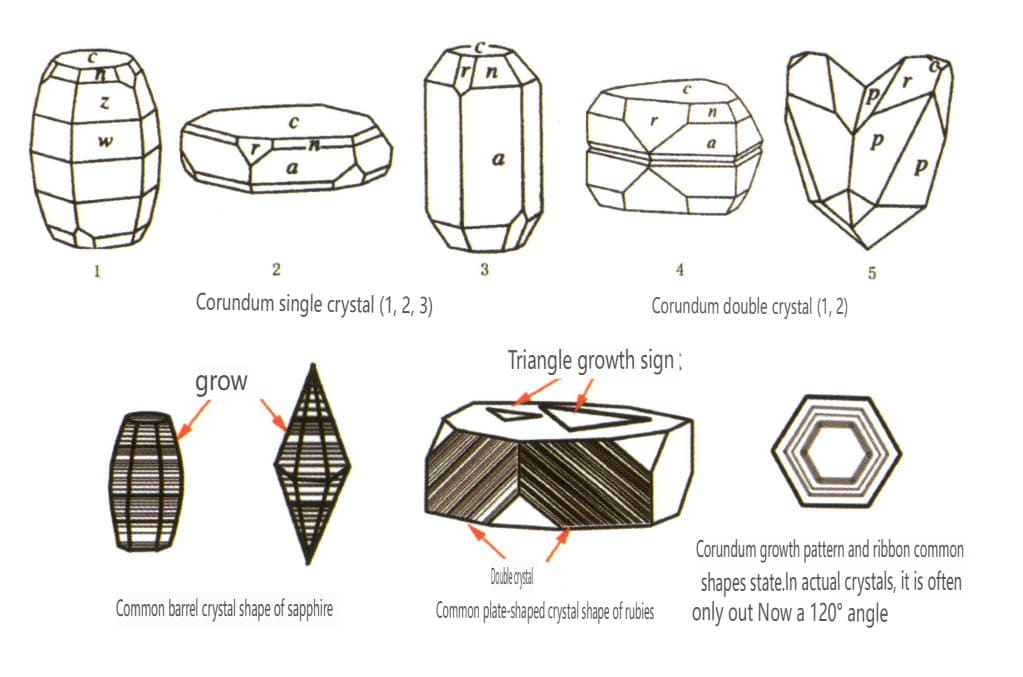
Figure 2-2-43 Habitude du cristal de corindon

Figure 2-2-44 Cristal de Rubis

Figure 2-2-45 Jumelle mécanique du rubis
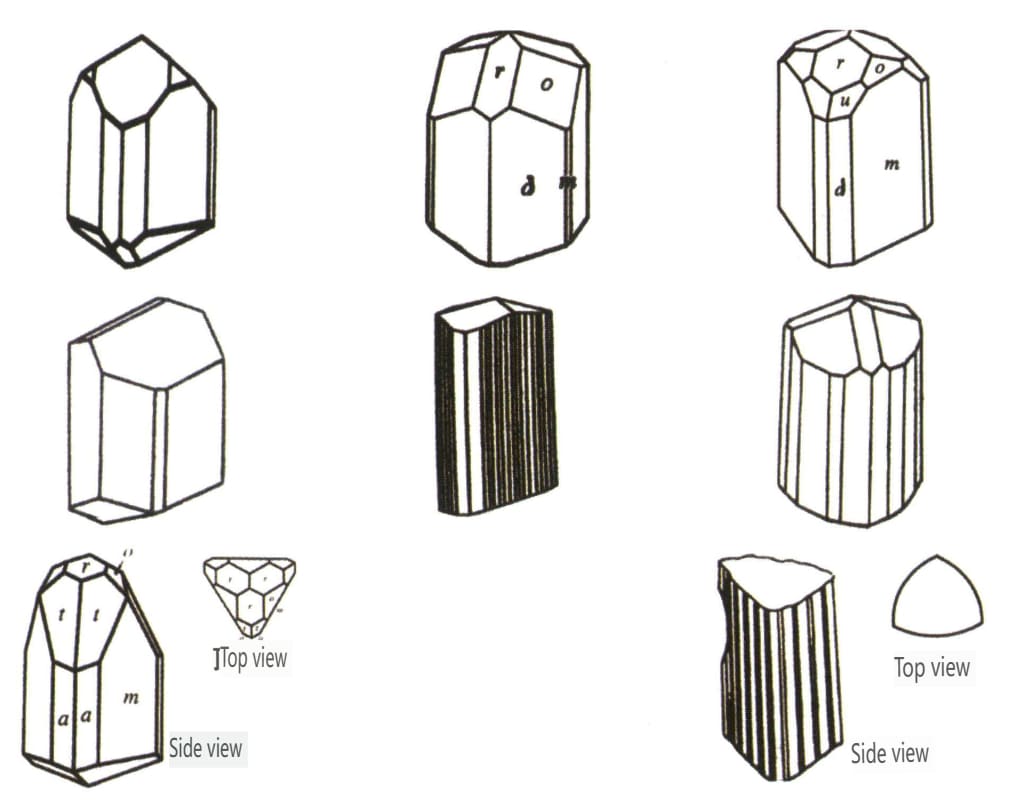
Figure 2-2-46 Habitudes cristallines de la tourmaline

Figure 2-2-47 Cristal de tourmaline

Figure 2-2-48 Bandes longitudinales de surface du cristal de tourmaline
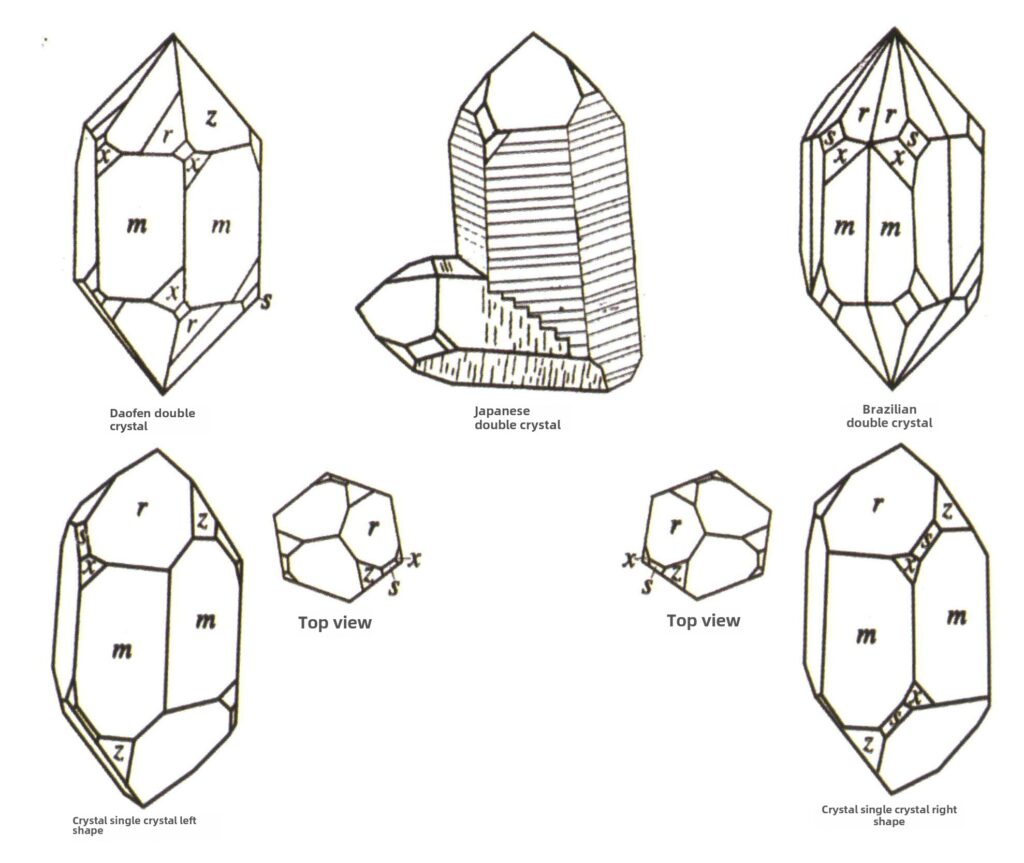
Figure 2-2-49 Habitudes de cristallisation des cristaux

Figure 2-2-50 corps de cristal

Figure 2-2-51 Corps du cristal
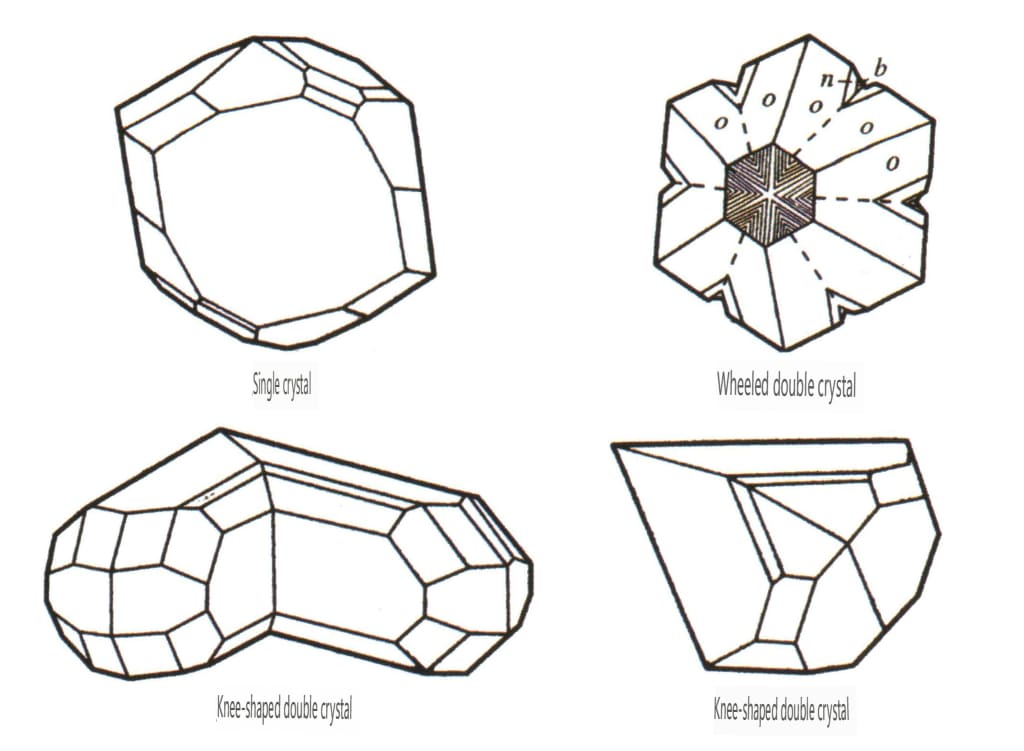
Figure 2-2-52 Morphologie du chrysobéryl

Figure 2-2-53 Cristal de chrysobéryl
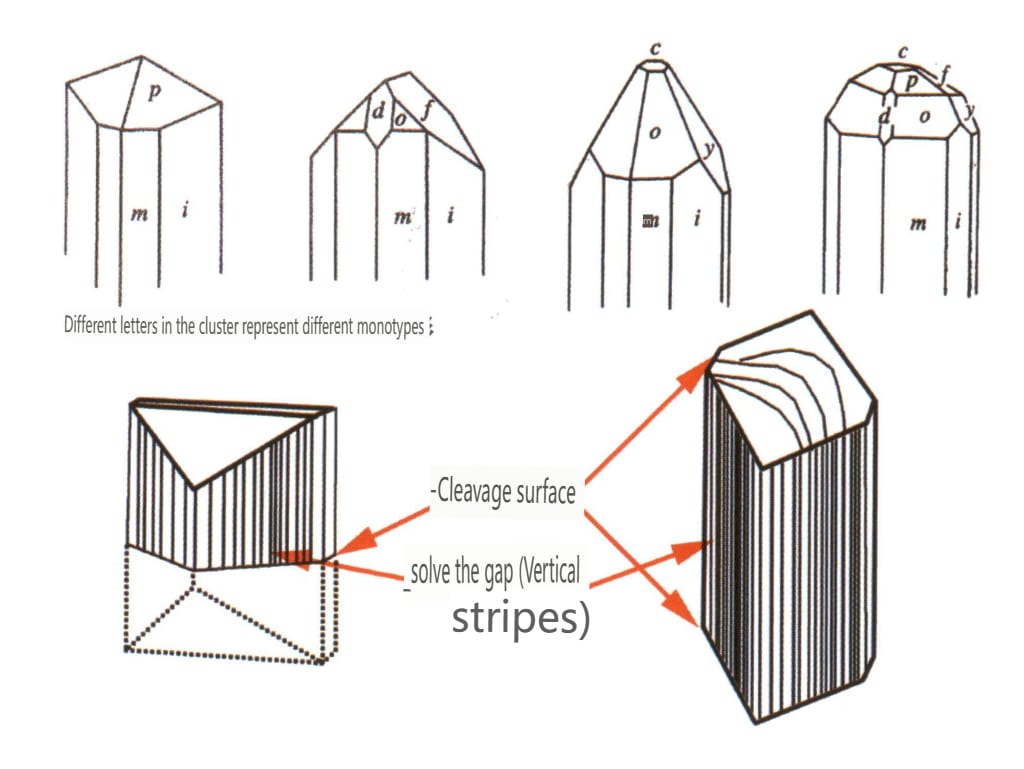
Figure 2-2-54 Habitudes cristallines de la topaze

Figure 2-2-55 Cristal de topaze
Section IV Pourquoi les cristaux de pierres précieuses poussent-ils différemment ?
D'un point de vue microscopique, le cristal de gemme est un solide composé d'éléments de tailles différentes disposés selon des règles différentes. D'un point de vue macroscopique, de nombreuses gemmes présentent des caractéristiques de forme cristalline en raison de leurs différentes compositions. Toutefois, il existe des cas particuliers, tels que l'hétéromorphisme. Pour mieux comprendre pourquoi les cristaux de gemmes ont un aspect différent, nous présenterons ici cinq aspects : l'hétéromorphisme, l'isomorphisme, le mélange mécanique moléculaire, l'eau dans les minéraux de gemmes et la composition chimique des pierres précieuses.
1. Hétéromorphes
Bien que certains minéraux aient la même composition chimique, ils ont des structures cristallines (l'arrangement des éléments dans l'espace tridimensionnel) très différentes et présentent des différences significatives en termes de propriétés physiques et chimiques (tableau 4). Ce phénomène est appelé hétéromorphisme, par exemple le diamant et le graphite (figure 2-2-56).
Le quartz commun présente le phénomène d'hétéromorphisme. La sillimanite, l'andalousite et le disthène constituent un groupe de variantes d'hétéromorphisme.
La transformation de l'hétéromorphisme se produit à l'état solide. Au cours du processus de transformation structurelle, une pression peut se développer à l'intérieur du cristal, conduisant souvent à la formation de jumeaux à l'intérieur du cristal.

Tableau 4 : Comparaison des propriétés du diamant et du graphite
| Minéraux | Diamant | Graphite |
|---|---|---|
| Composants | Carbone (C) | Carbone (C) |
| Conditions de formation | Haute température et haute pression | Haute température |
| Système cristallin, habitude | Système cristallin isométrique, octaèdre, dodécaèdre rhombique | Système cristallin hexagonal, en couches |
| Couleur | Incolore, jaune, bleu, rose, vert, etc. | Noir |
| Éclat | Éclat adamantin | Éclat métallique |
| Transparence | Transparent à opaque | Opaque |
| Indice de réfraction | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Propriétés mécaniques | Clivage octaédrique modéré, dureté 10, densité 3.52 | Un ensemble de clivages parfaits, dureté 1, densité 2.10 |
| Autres biens | Excellente conductivité thermique ; à l'exception des diamants bleus naturels qui sont semi-conducteurs, les diamants d'autres couleurs sont isolants. | Conductivité thermique modérée, bonne conductivité électrique |
2. Isomorphisme
L'isomorphisme désigne le phénomène par lequel certaines particules de la structure du réseau sont remplacées par d'autres particules ayant des propriétés similaires, ce qui entraîne de légères modifications des paramètres du réseau et des propriétés physiques et chimiques. En revanche, la structure cristalline reste fondamentalement inchangée. On peut considérer que les éléments du cristal de la pierre précieuse sont remplacés par d'autres éléments. En revanche, le schéma répétitif des éléments du cristal de pierre précieuse reste le même, avec de légères déviations dans les distances entre les atomes. Cependant, les propriétés physico-chimiques du cristal de pierre précieuse subissent de légères modifications (figure 2-2-57 à figure 2-2-58).
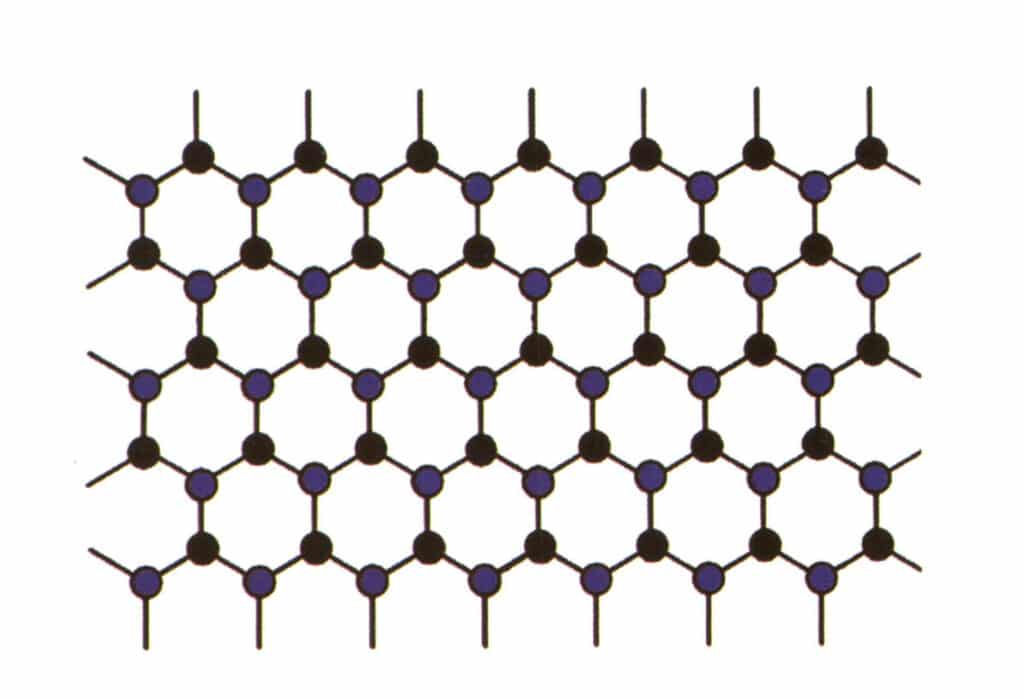
Figure 2-2-57 Diagramme de simulation de la structure cristalline (le bleu et le noir indiquent les particules des éléments)
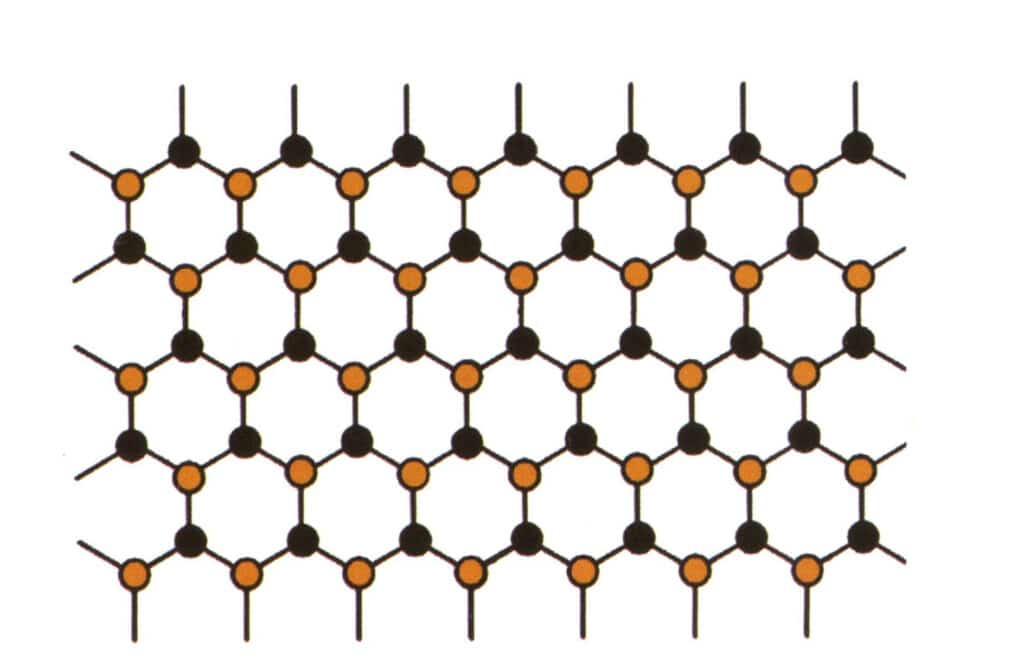
Figure 2-2-58 Diagramme de simulation de la structure cristalline (le noir représente les particules élémentaires, le jaune représente les nouvelles particules élémentaires qui remplacent partiellement les particules élémentaires bleues, le jaune peut ne pas remplacer complètement toutes les particules bleues).
Le concept d'isomorphisme peut expliquer pourquoi les pierres précieuses d'une même famille peuvent avoir autant de couleurs et pourquoi il existe des variations d'indice de réfraction et de densité entre les pierres précieuses d'une même famille.
Une famille peut être considérée comme un type de pierre précieuse dont les motifs répétitifs des éléments cristallins sont les mêmes, mais dont les formes physiques et chimiques sont légèrement différentes. Par exemple, la famille des corindons comprend deux membres, le rubis et le saphir, tandis que la famille des béryls comprend les variétés d'émeraude, d'aigue-marine et de morganite.
(1) Olivine
La composition chimique de l'olivine est (Mg,Fe)₂SiO₄. La substitution isomorphe complète des éléments Fe et Mg se produit dans sa composition. Lorsque la teneur en Fe de l'olivine augmente, la couleur de l'olivine devient plus foncée, l'indice de réfraction augmente et la densité augmente également.
(2) Corindon
Le corindon pur sans impureté (Al₂O₃) est incolore, et lorsque le Cr remplace l'Al, la gemme présente une teinte rose-rouge à rouge, connue sous le nom de rubis. Les autres couleurs sont appelées saphir, comme le saphir jaune orangé ou le saphir incolore. Le saphir communément appelé est spécifiquement le saphir bleu, où le Fe et le Ti remplacent l'Al. Plus la teneur en éléments colorants de la gemme de substitution est élevée, plus la couleur de la gemme est profonde ; inversement, plus la teneur est faible, plus la couleur est claire.
(3) Tourmaline
La tourmaline désigne le même type de gemme que la tourmaline, la tourmaline étant son nom minéralogique et la tourmaline son nom gemmologique. La composition chimique du béryl est (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), où R est principalement Mg , Fe , Cr , Li, Al , Mn, et les éléments de R peuvent se substituer totalement ou partiellement les uns aux autres, ce qui donne à la tourmaline une très grande variété de couleurs. Par exemple, lorsque R est principalement composé de Fe, le béryl présente une couleur bleu foncé ou même noire ; lorsque R est principalement composé de Mg, le béryl présente une couleur jaune à brune ; lorsque R est principalement composé de Mg, le béryl présente une couleur jaune à brune. R est principalement Li ou Mn, le béryl présente une couleur rose ou bleu clair ; lorsque R est principalement Cr, la tourmaline présente un vert profond.
Il ressort de ce qui précède que la substitution d'éléments aux propriétés similaires permet d'obtenir des couleurs plus belles et plus brillantes dans les gemmes.
3. Mélange mécanique moléculaire
Parfois, certains éléments pénètrent de force entre les éléments principaux des pierres précieuses disposées régulièrement. Cependant, la faible proportion d'éléments entrant ne perturbe pas le motif répétitif des éléments principaux de la pierre précieuse, mais provoque seulement une déformation (figure 2-2-59). Cette situation est appelée mélange mécanique moléculaire, comme le mélange mécanique moléculaire de l'azote et du bore dans les diamants, qui produit des diamants bleus, roses et jaunes, d'une grande valeur.
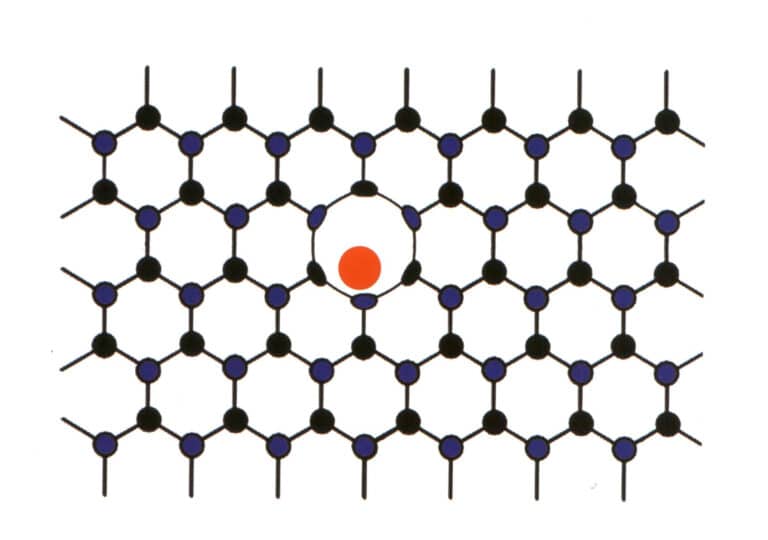
4. L'eau dans les minéraux
Certaines pierres précieuses contiennent de l'eau, qui est un composant important des minéraux gemmes et qui est étroitement liée aux propriétés des pierres précieuses. En fonction de la forme de l'eau présente dans les minéraux et de son rôle dans la structure cristalline, l'eau des pierres précieuses peut être divisée en deux catégories : l'eau d'absorption, qui n'est pas liée à la structure cristalline, et l'eau qui participe à la structure cristalline du minéral, y compris l'eau de cristallisation, l'eau zéolitique, l'eau intercalaire et l'eau de constitution. L'eau étroitement liée aux pierres précieuses comprend l'eau d'absorption, l'eau de cristallisation et l'eau de constitution.
La première consiste à absorber l'eau, comme l'opale (composition chimique : SiO₂ - nH₂O, n représentant le nombre de H₂O, la teneur est variable) dans la molécule d'eau, qui est une molécule d'eau neutre adsorbée mécaniquement sur les particules minérales ou les surfaces de rupture. Lorsque la température atteint 100 ~ 110° degrés sous une pression normale, les molécules d'eau peuvent toutes s'échapper et ne pas endommager la structure du réseau cristallin, de sorte que pour éviter que l'opale dans le comptoir dans une longue période d'exposition à la lumière forte fissure sèche, devrait mettre une tasse d'eau dans le comptoir.
La deuxième est l'eau de cristallisation, comme l'eau de cristallisation de la turquoise [composition chimique : CuAl₆(PO₄)₄(OH)₈-4H₂O, où la teneur en H₂O peut atteindre 19,47% ]. Cette molécule d'eau neutre existe dans des positions fixes au sein du réseau et sert d'unité structurelle, faisant partie de la composition chimique du minéral. La température à laquelle l'eau de cristallisation s'échappe ne dépasse généralement pas 600℃ et s'échappe habituellement entre 100 et 200℃. Lorsqu'une pierre précieuse perd son eau de cristallisation, sa structure cristalline est endommagée, formant une nouvelle structure.
La troisième est l'eau de constitution, également appelée eau combinée, qui participe au réseau minéral sous forme de plasma OH-, H⁺, H₃O⁺, OH- étant le plus courant. L'eau de constitution fait partie de la composition chimique du minéral, occupant des positions fixes dans la structure du réseau avec une proportion définie dans sa composition. L'eau structurelle nécessite une température plus élevée pour s'échapper et endommager sa structure, généralement autour de 600 -1000℃. Lorsqu'une pierre précieuse perd de l'eau de constitution, sa structure cristalline est détruite. De nombreuses pierres précieuses contiennent de l'eau de constitution, comme la tourmaline [la composition chimique est ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), où R comprend principalement Mg , Fe , Cr, Li, Al, Mn, etc, et les éléments de R peuvent se substituer totalement ou partiellement les uns aux autres], et la topaze [composition chimique : Al₂SiO₄( F, OH) ₂ ].
5. La composition chimique des pierres précieuses
Les pierres précieuses, comme les autres substances, sont composées d'éléments chimiques. Chaque type de gemme a une composition chimique spécifique et une certaine plage de variation, qui détermine les diverses caractéristiques et propriétés de la gemme. Les pierres précieuses font partie des minéraux et des roches, et la classification de la composition chimique d'une pierre précieuse remonte à la composition chimique des minéraux.
Actuellement, les principales méthodes de classification des minéraux comprennent la classification par composition chimique (système Dana), la classification géochimique, la classification génétique, la classification par application et la classification cristallochimique. La méthode la plus largement adoptée est la classification chimique basée sur la composition chimique et la structure cristalline (système Hugo Strunz) (tableau 5).
Tableau 5 : Système de classification chimique des cristaux minéraux
| Séquence de niveaux | Base de la division | Exemple |
|---|---|---|
| Catégorie principale | Type de composé | Sel contenant de l'oxygène Catégorie principale |
| Classe | Types d'anions ou d'anions complexes | Classe de silicate |
| (Sous-catégorie) | Structure du complexe anionique | Sous-classe des silicates-cadres |
| Groupe | Types de structures cristallines et propriétés ioniques | Groupe des corindons, groupe des béryls, groupe des grenats |
| (Sous-groupe) | Types de cations | Sous-groupe des feldspaths alcalins |
| Espèce | Structure cristalline et composition chimique déterminées | Orthoclase KAlSi3O8 |
| (sous-espèce) | Même structure cristalline, composition ou propriétés différentes, morphologie | Adularia KAlSi3O8 |