Una vez para saberlo todo sobre Cristalografía de piedras preciosas
Una guía completa sobre formas, tipos, clasificaciones y diferencias de la cristalografía
La Tierra está compuesta de innumerables moléculas y átomos. La investigación científica moderna ha descubierto que los materiales sólidos de la naturaleza están formados por diferentes elementos químicos. Los resultados de los análisis con rayos X muestran que los átomos de los elementos de ciertos materiales sólidos están dispuestos de forma ordenada y regular. Estos materiales se clasifican como cristalinos o se denominan cristales, y su red atómica ordenada se denomina estructura cristalina (Figura 2-1-1).
La mayoría de los materiales gema que crecen en la naturaleza y en los laboratorios son cristalinos. En este capítulo se tratará el concepto de cristal, su clasificación y la relación entre los cristales y la terminología básica en gemología.

Índice
Sección ⅠEl concepto y la descripción de los cristales
Cuando mencionamos las gemas, a menudo pensamos en sus características brillantes y translúcidas (Figura 2-1-2). Desde la perspectiva de los geólogos y gemólogos, las gemas más queridas pertenecen a una forma geométrica de sólido: los cristales. La esencia de la belleza de los cristales es, de hecho, la belleza de la geometría.

1. El concepto de cristal
Los cristales son los más fáciles de asociar y los que más comúnmente se encuentran en la naturaleza. Los cristales se encuentran en los siete continentes de la Tierra y, cuando se hallan en la naturaleza, suelen adoptar la forma de poliedros geométricos (Figura 2-1-3). Se les suele denominar cristales. Más tarde, este término se amplió para referirse a sustancias sólidas naturales con formas poliédricas geométricas, como los cristales de diamante y aguamarina (Figura 2-1-4). Los cristales también pueden describir materiales sólidos con superficies irregulares, desiguales, desgastadas, rotas o procesadas artificialmente, pero con una disposición atómica que sigue un patrón regular. Los cristalógrafos creen que todos los cristales poseen seis características básicas: autolimitación, uniformidad, anisotropía, simetría, estabilidad y punto de fusión fijo.
① La autolimitación se refiere a la propiedad de los elementos químicos de formar espontáneamente formas geométricas poliédricas. Esta propiedad puede explicar por qué distintos elementos tienen formas geométricas cristalinas diferentes.
② La uniformidad se refiere a la propiedad de que todas las propiedades físicas y químicas de las partes del cristal son iguales. Esta propiedad puede ayudarnos a distinguir e identificar diferentes cristales minerales.
③ La anisotropía se refiere a la propiedad por la que la disposición de los elementos varía en distintas direcciones, dando lugar a ligeras diferencias en las propiedades físicas según la dirección. Esta propiedad puede explicar por qué los diamantes de mayor dureza pueden cortarse y pulirse.
④ La simetría se refiere a la propiedad por la que partes o propiedades idénticas de un cristal se repiten siguiendo un patrón regular. Esta propiedad es extremadamente importante y especial para los cristales, y se explicará con más detalle en la segunda sección de este capítulo.
⑤ La estabilidad se refiere a la estabilidad de un cristal resultante de su mínima energía interna. Si la energía interna de un cristal es alta y desigual, es propenso a agrietarse por sí solo. Esta propiedad puede explicar por qué los cristales de rubí sintetizados mediante la técnica de flamefusión siempre parecen estar a la mitad en lugar de completos.
⑥ Punto de fusión fijo se refiere a la propiedad de que un cristal tiene un punto de fusión fijo.

Figura 2-1-3 Granate (a la izquierda el cristal, a la derecha el granate pulido)

Figura 2-1-4 Cristal de aguamarina
2. La forma ideal de los cristales
Los cristales que se analizan en cristalografía son principalmente monocristales ideales. Un monocristal ideal se define como aquel cuya estructura interna sigue estrictamente las reglas de los entramados espaciales y cuya forma es una forma combinada geométrica regular. Las formas de los monocristales ideales se dividen en dos tipos: formas simples y formas combinadas.
(1) Formulario simple
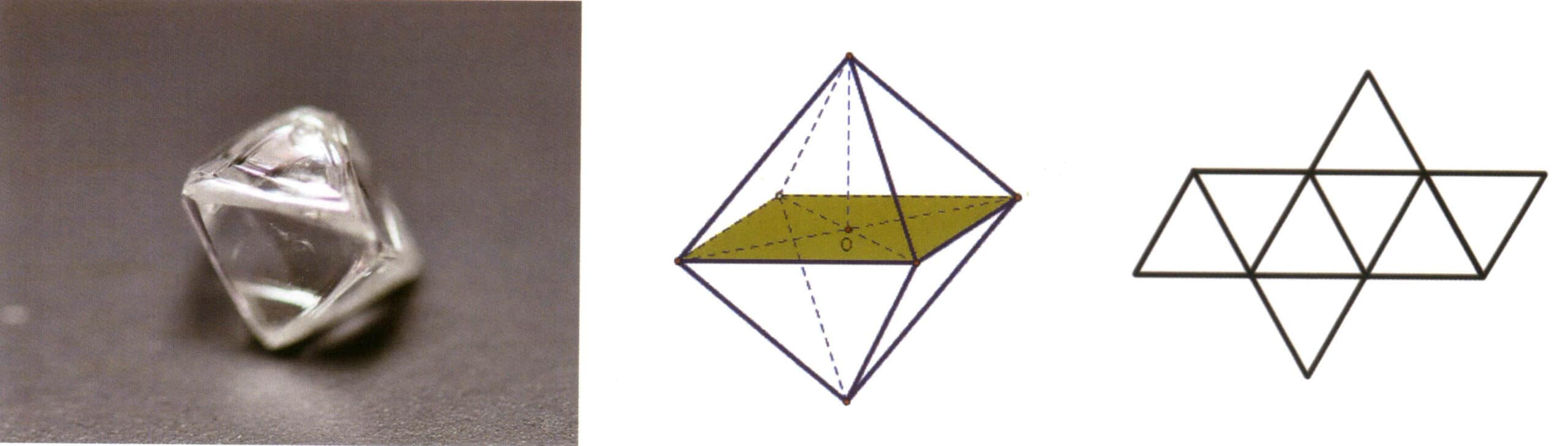
Una forma simple se refiere a una combinación de un grupo de caras cristalinas conectadas por elementos de simetría, que puede entenderse como un cuerpo geométrico compuesto por caras cristalinas de la misma forma y tamaño en un estado ideal (Figura 2-1-5). Existen 47 tipos de formas simples en los cristales.
Los puntos clave para identificar las formas simples son: todas las caras del cristal tienen la misma forma y tamaño, y las caras del cristal pueden estar orientadas de forma diferente.
(2) Combinar Formulario
La agregación de formas simples se denomina forma combinada, compuesta por dos o más formas simples diferentes. No todas las formas simples pueden combinarse libremente en una forma combinada; sólo las formas simples con el mismo grupo de puntos pueden agregarse (figuras 2-1-6 a 2-1-8).
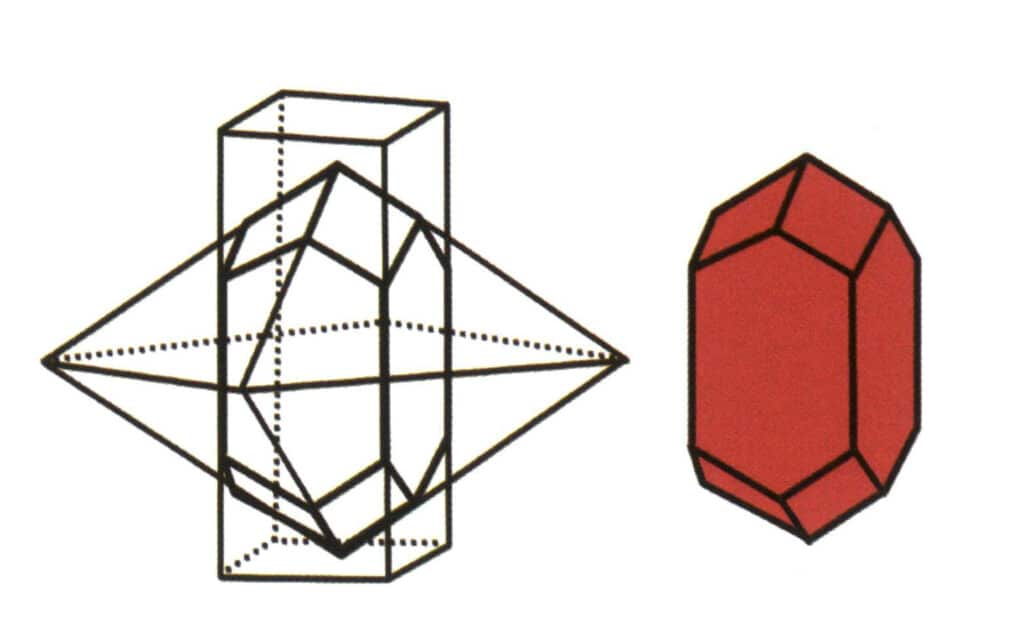
Figura 2-1-6 Combinación de prismas tetragonales y dipiramidales tetragonales
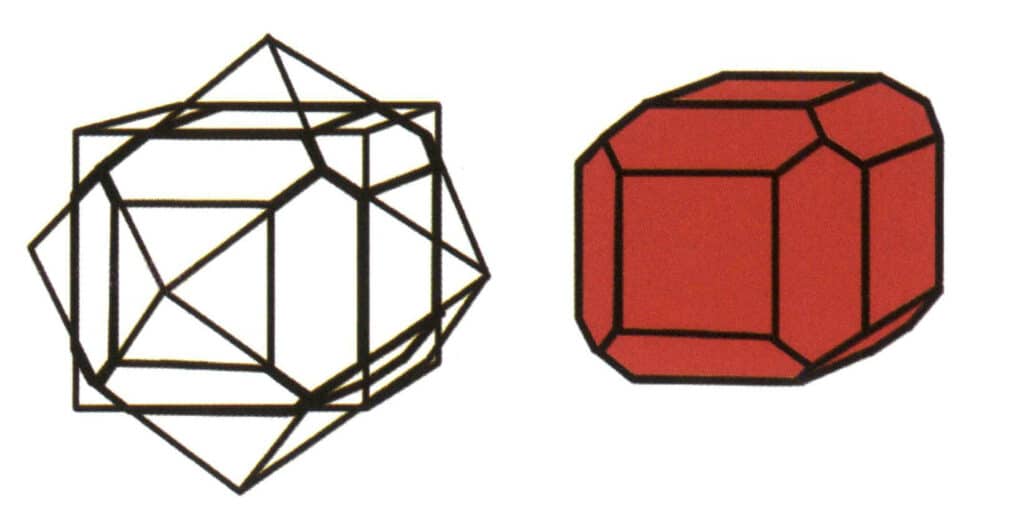
Figura 2-1-7 Combinación de cubos y dodecaedros rómbicos
El punto clave de la identificación de formas combinadas es la presencia de dos o más caras cristalinas de formas diferentes en el cristal.
Cuando se encuentran monocristales en la naturaleza, siempre presentan una diferencia significativa respecto a la morfología ideal de los monocristales (Figura 2-1-9), como por ejemplo que una sola cara no tenga necesariamente la misma forma y tamaño y la desaparición de caras cristalinas, lo que se describe como cristales distorsionados.

Los cristales distorsionados también pueden describirse como cristales reales producidos en la naturaleza, influidos por el entorno de crecimiento. Las múltiples caras cristalinas que se repiten en ángulos fijos en los cristales ideales pueden no tener necesariamente la misma forma y tamaño. Aun así, para un mismo tipo de cristal, las caras cristalinas del mismo monomorfo deben tener el mismo patrón y las mismas propiedades físicas. Los ángulos entre las caras cristalinas correspondientes permanecen invariables, lo que refleja la simetría inherente al propio cristal. Los cristales que se encuentran en la realidad están distorsionados en diversos grados.
Los cristales maclados también pueden describirse como cristales reales producidos en la naturaleza, influidos por el entorno de crecimiento. Las múltiples caras del cristal que se repiten en ángulos fijos en los cristales ideales pueden no tener necesariamente la misma forma y tamaño. Aun así, para un mismo tipo de cristal, las caras de la misma forma deben tener los mismos patrones y propiedades físicas. Los ángulos entre las caras correspondientes del cristal permanecen invariables, lo que refleja la simetría inherente al propio cristal. Los cristales que se encuentran en la realidad son todos, en diversos grados, maclados.
3. Los hábitos de cristalización de los cristales
Los cristales formados en la naturaleza nunca pueden alcanzar una forma perfecta. Si crecen en los huecos de las capas rocosas, rodeados de roca, la forma natural del cristal se distorsionará. Incluso los cristales cultivados en un laboratorio se deformarán debido a la influencia de la gravedad. Sólo en las condiciones de gravedad cero de la Estación Espacial Internacional pueden los científicos cultivar los cristales de forma perfecta que buscan.
Aunque las formas de los cristales son imperfectas, cada tipo de cristal mineral tiende a crecer o agruparse de formas o hábitos diferentes.
Cada mineral tiende a formarse en condiciones específicas, y sus hábitos reflejan las condiciones de su formación. Algunos minerales, como el cuarzo, presentan condiciones de formación complejas y variables. Por ello, el cuarzo también posee múltiples hábitos.
En general, los hábitos cristalinos se refieren a las características de un determinado cristal que tiende a formar una forma específica en determinadas condiciones externas. A veces, se refiere a los tipos comunes de la forma simple de ese cristal.
En función del grado de desarrollo de los cristales en el espacio tridimensional, los hábitos cristalinos se dividen en tres tipos básicos.
(1) Uni-extensión direccional
Los cristales se extienden en una dirección, apareciendo en formas columnares, aciculares, fibrosas, etc. Minerales como el berilo, la turmalina, la hornblenda y la malaquita presentan a menudo este hábito (figuras 2-1-10 a 2-1-11).

Figura 2-1-10 Aguamarina columnar (arriba) y su diagrama de hábito cristalino (abajo)

Figura 2-1-11 Malaquita fibrosa (arriba) y su diagrama de hábito cristalino (abajo)
(2) Bi-extensión direccional
Los cristales se extienden en un plano, apareciendo en forma de placas, láminas, escamas, etc., ya que minerales como la wolframita, la mica, el plumbago y la tanzanita suelen presentar este hábito (figura 2-1-12).
(3) Tri-isométrico direccional
Los cristales se desarrollan uniformemente en tres direcciones, presentando formas isométricas y granulares, como la espinela, el granate, el diamante, la pirita y la fluorita, que a menudo exhiben este hábito (Figuras 2-1-13, 2-1-14).

Figura 2-1-12 El hábito cristalino en forma de placa de la tanzanita (arriba) y su diagrama de hábito cristalino (abajo)

Figura 2-1-13 El hábito cristalino octaédrico de la piedra preciosa espinela (arriba) y su diagrama de hábito cristalino (abajo).
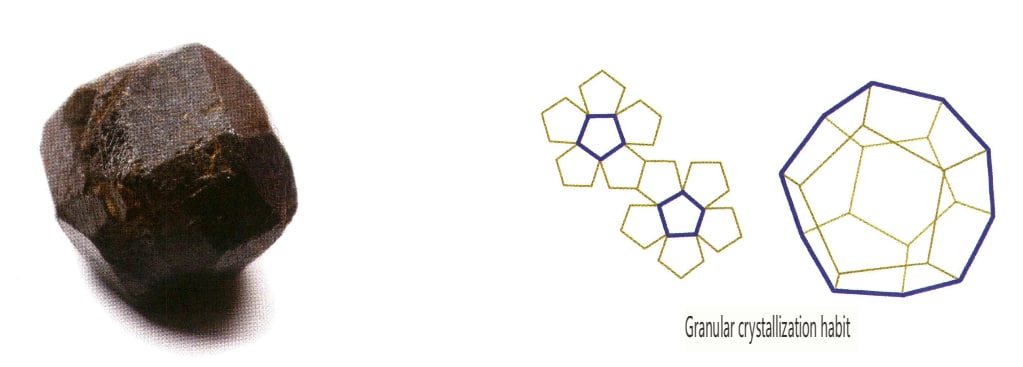
Además, existen tipos transicionales como las formas columnares cortas, columnares en placa, en tira y en placa gruesa.
La composición química y la estructura del cristal determinan principalmente el hábito cristalino. También está estrechamente relacionado con las condiciones externas durante la formación del cristal (como la temperatura, la presión, la concentración, la viscosidad y las impurezas), como las diferencias en las formas cristalinas entre los diamantes y los cristales de diamante sintético.
4. Agregación regular de cristales
En la naturaleza, podemos encontrar cristales individuales (Figura 2-1-15) y dos o más cristales individuales que crecen juntos para formar un todo. Este fenómeno de crecimiento conjunto de múltiples cristales se denomina agregación cristalina. La agregación de cristales puede clasificarse en irregular y regular. La agregación cristalina irregular puede entenderse como un colectivo, sobre el que se profundizará en el Capítulo Tres. En la agregación cristalina regular, existen cuatro tipos comunes: agregación paralela, bicristales, sobrecrecimiento e intercrecimiento (Figuras 2-1-16 a 2-1-18). En esta sección se analiza principalmente el tipo de agregación regular conocido como bicristales.

Figura 2-1-15 Monocristal (Turmalina)
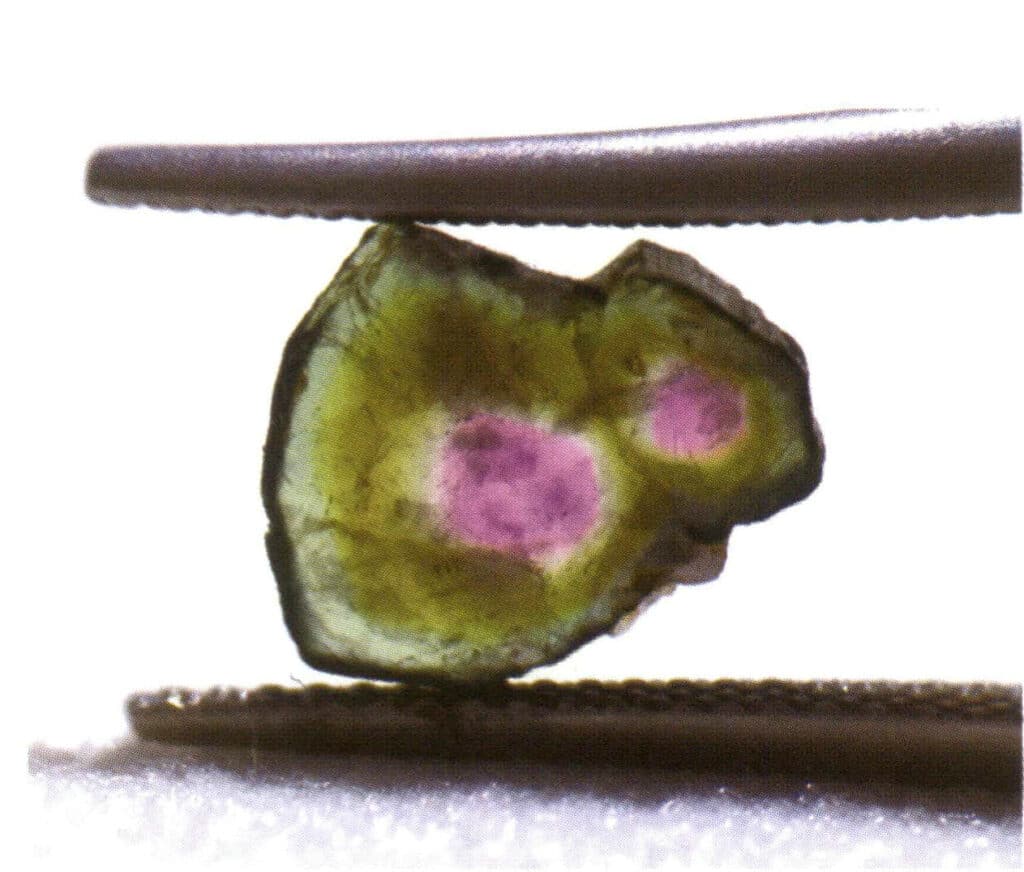
Figura 2-1-16 Agregación paralela (Cuando varios cristales del mismo tipo crecen paralelos en el espacio, se denomina agregación paralela. En este momento, las caras y aristas correspondientes de los cristales crecidos son todas paralelas entre sí).

Figura 2-1-17 Cristal gemelo (Espinela)

Figura 2-1-18 Sobrecrecimiento (un tipo de cristal crece sobre la superficie de otro cristal en una dirección cristalográfica específica, también conocido como crecimiento epitaxial).
Los bicristales son la agregación regular de dos o más cristales idénticos según ciertas reglas de simetría. (Eje gemelo, plano gemelo) Las caras, aristas y ángulos correspondientes de los dos individuos adyacentes no son completamente paralelos. Aún así, pueden reflejarse mutuamente mediante operaciones simétricas como la rotación y la inversión de la rotación, lo que permite que los dos individuos coincidan o se alineen.
4.1 Puntos clave para identificar los bicristales
① Ángulos cóncavos visibles en cristales maclados (Figura 2-1-19).
② Estilolita: La micromorfología y otras características de las superficies cristalinas de ambas caras del estilolito son discontinuas (Figura 2-1-20).
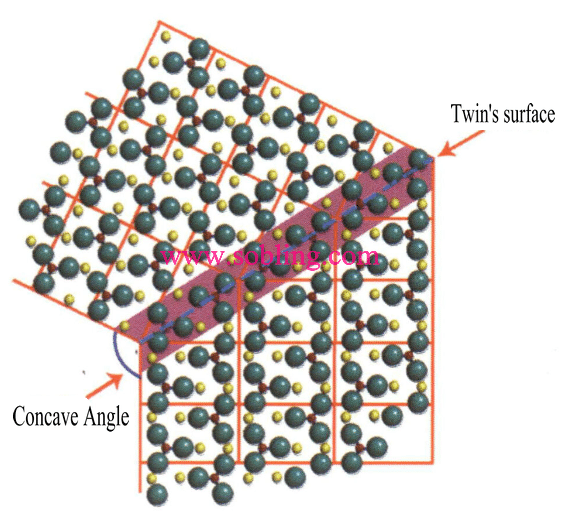
Figura 2 - 1-19 Ángulo cóncavo del gemelo
Figura 2-1-20 Estilolita (los distintos colores de la figura representan cristales diferentes; las líneas rojas indican la estilolita maclada).
③ Estrías de macla: Las caras de los cristales o los planos de clivaje muestran finas estrías de maclado (Figura 2-1-21)
④ Figura de mordentado: La aparición de la figura de grabado indica la presencia de maclado (Figura 2-1-22)

Figura 2-1-21 Diagrama esquemático de gemelos polisintéticos

Figura 2-1-22 Superficie de espinela con picaduras triangulares invertidas.
⑤ Aparición de pseudosimetría: aparición de relaciones de simetría incoherentes con el grupo puntual inherente al cristal monocristalino (Figura 2-1-23 a Figura 2-1-24).

Figura 2-1-23 Cristal único de crisoberilo

Figura 2-1-24 Gemelo en forma de rodilla de crisoberilo
Las maclas se dividen en cinco tipos en función de sus características de apilamiento: maclas de contacto (Figura 2-1-25 a Figura 2-1-26), maclas polisintéticas (Figura 2-1-27), maclas interpenetrantes (Figura 2-1-28), cristal triple (Figura 2-1-29) y maclas complejas, entre las que son comunes los cuatro primeros tipos.


Figura 2-1-26 Hermanamiento por contacto de la espinela (arriba) y su esquema (abajo)

Figura 2-1-27 Gemelo polisintético de labradorita (arriba) y su esquema (abajo)
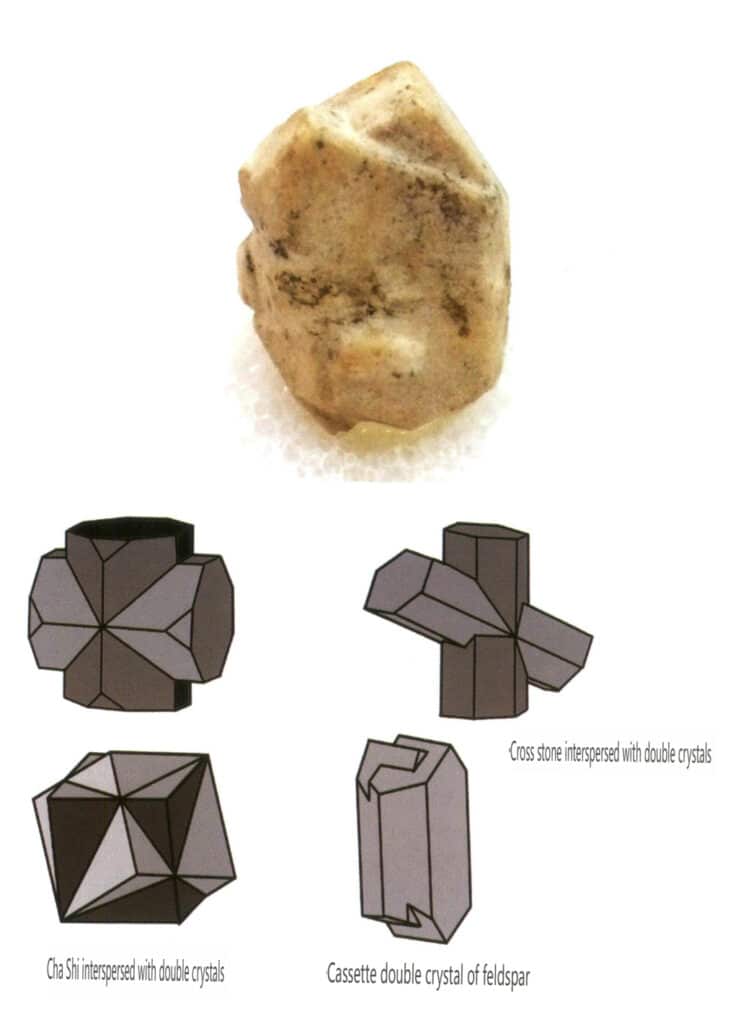
Figura 2-1-28 Cristales Gemelos de Feldespato (arriba) y Esquema de Cristales Gemelos Interpenetrantes de Otros Tipos (abajo)

Figura 2-1-29 Macla trigonal del crisoberilo (arriba) y su esquema (abajo)
4.2 La formación de bicristales
① Formado durante el crecimiento del cristal, puede desarrollarse a partir de gérmenes cristalinos gemelos o de pequeños cristales que crecen de forma dependiente según la posición del gemelo.
② Se forma durante el proceso de transformación del heteromorfismo, como cuando el cuarzo α se transforma en cuarzo β, formando maclas.
③ Formado por acción mecánica, donde una parte del cristal se desliza a lo largo de un determinado plano direccional para formar maclas de deformación, como las maclas de la calcita.
5.Patrones de cara de cristal
Cuando se descubren cristales en la naturaleza, suelen tener formas incompletas (Figura 2-1-30) y patrones superficiales especiales. A veces, crecen juntos en grupos (Figura 2-1-31), que a menudo muestran diferencias significativas respecto a los poliedros geométricos estándar con los que estamos familiarizados, como los cubos y los prismas hexagonales. Este fenómeno se denomina forma real de los cristales. La forma real de los cristales tiene una clasificación detallada en cristalografía, como cristales distorsionados, cristales convexos, cristales curvos, cristales flotantes, rayas en las caras de los cristales, figuras grabadas, estrías de macla, etc.

Figura 2-1-30 Cristal de rubí

Figura 2-1-31 Cristales de pirita (la izquierda muestra múltiples cristales de pirita creciendo juntos, y la derecha muestra un único cristal de pirita).
En esta sección se analizan principalmente los patrones de las caras de los cristales en su forma real.
En teoría, los planos de los cristales son lisos y planos. Sin embargo, durante el crecimiento o la disolución real de los cristales, la superficie suele dejar tras de sí patrones regulares ligeramente irregulares, comúnmente denominados patrones de caras de cristal. Los patrones de las caras de los cristales incluyen estrías de crecimiento, capas de crecimiento, patrones en espiral, lomas de crecimiento y figuras grabadas. Los patrones de las caras de los cristales que se tratan en este libro se refieren principalmente a las estrías de las caras de los cristales y a las figuras grabadas que pueden observarse a simple vista o en condiciones de bajo aumento.
Las rayas de la cara del cristal hacen referencia a una serie de líneas rectas paralelas en la superficie del cristal debidas a la convergencia repetida y al crecimiento alterno de diferentes formas simples. También conocidas como "rayas combinadas", sólo se observan en las superficies cristalinas, también llamadas rayas de crecimiento. Por ejemplo, la cara cristalina prismática hexagonal del cuarzo tiene a menudo caras cristalinas finas prismáticas hexagonales y dodecaédricas rómbicas desarrolladas alternativamente en bandas transversales agregadas (Figura 2-1-32).

Las figuras grabadas se refieren a las picaduras de forma específica (es decir, picaduras grabadas) que quedan en la cara del cristal debido a la corrosión después de que se haya formado el cristal. La disposición de las partículas elementales dentro de la cara del cristal controla las figuras de corrosión. Por lo tanto, las formas y orientaciones de las figuras de grabado varían entre los distintos minerales y formas individuales del mismo cristal. Por ejemplo, las figuras grabadas en diferentes formas individuales de cristales de diamante varían; se pueden ver picaduras triangulares en cristales octaédricos (Figura 2-1-33), picaduras cuadriláteras en caras cúbicas, picaduras cuadriláteras superpuestas que forman un patrón en forma de cuadrícula, y patrones de líneas o patrones microscópicos en forma de disco se pueden ver en dodecaedros rómbicos (Figura 2-1-34).

Figura 2-1-33 Punteaduras triangulares invertidas visibles en el cristal octaédrico de diamante

Figura 2-1-34 Textura lineal visible en cristales dodecaédricos romboédricos
Sólo las figuras grabadas en la misma cara cristalina de la misma forma pueden ser iguales, por lo que las figuras grabadas se utilizan a menudo para identificar minerales y determinar si las caras cristalinas pertenecen a la misma forma única (Figura 2-1-35 a Figura 2-1-42).

Figura 2-1-35 Rayas estilo suelo de madera con incrustaciones de cristal de fluorita

Figura 2-1-36 Figura de grabado triangular natural en rubí (rayas horizontales comunes en rubíes, líneas de crecimiento paralelas a la dirección romboédrica, grabados naturales de forma triangular o hexagonal).

Figura 2-1-37 Rayas longitudinales superficiales de la turmalina

Figura 2-1-38 rayas horizontales en la superficie del cristal

Figura 2-1-39 Figuras grabadas en la superficie del cristal

Figura 2-1-40 Estrías longitudinales superficiales del topacio

Figura 2-1-41 Imagen topográfica de un cristal de topacio

Figura 2-1-42 Figuras de grabado de la espinela
Sección II 47 Tipos de formas de cristal
Existen 146 formas simples diferentes en cristalografía, que pueden clasificarse en 47 formas geométricas basadas en sus formas geométricas cuando existen de forma independiente. Estas formas geométricas se denominan de las siguientes maneras:
① Denominado según las características de la forma de la sección transversal, como prisma trigonal, prisma tetragonal, prisma hexagonal, bipirámide romboédrica, etc.
② Se denomina según la forma de la forma simple, como cilindro, doble cono, cubo, etc.
③ Se denominan según el número de caras geométricas, como cara única, octaedro, etc.
④ Se denominan según la forma de las caras geométricas, como romboedro, pentacontaedro, etc.
En cristalografía, las formas simples se dividen en cuatro categorías: formas generales y formas especiales, formas cerradas y formas abiertas, formas regulares y formas irregulares, formas zurdas y formas diestras. En este capítulo se tratarán brevemente las formas cerradas y las formas abiertas.
Las formas cerradas se refieren a aquellas cuyas caras cristalinas pueden encerrar un espacio cerrado, divididas en tres categorías principales: clases poliédricas, clases poliédricas oblicuas y clases bipiramidales, con un total de 30 tipos. Cada categoría tiene clasificaciones más detalladas; por ejemplo, la clase poliédrica se subdivide en clase tetraédrica, clase octaédrica, clase cúbica, etc. (Figuras 2-1-43 a 2-1-48).

Figura 2-1-43 Clase tetraedro
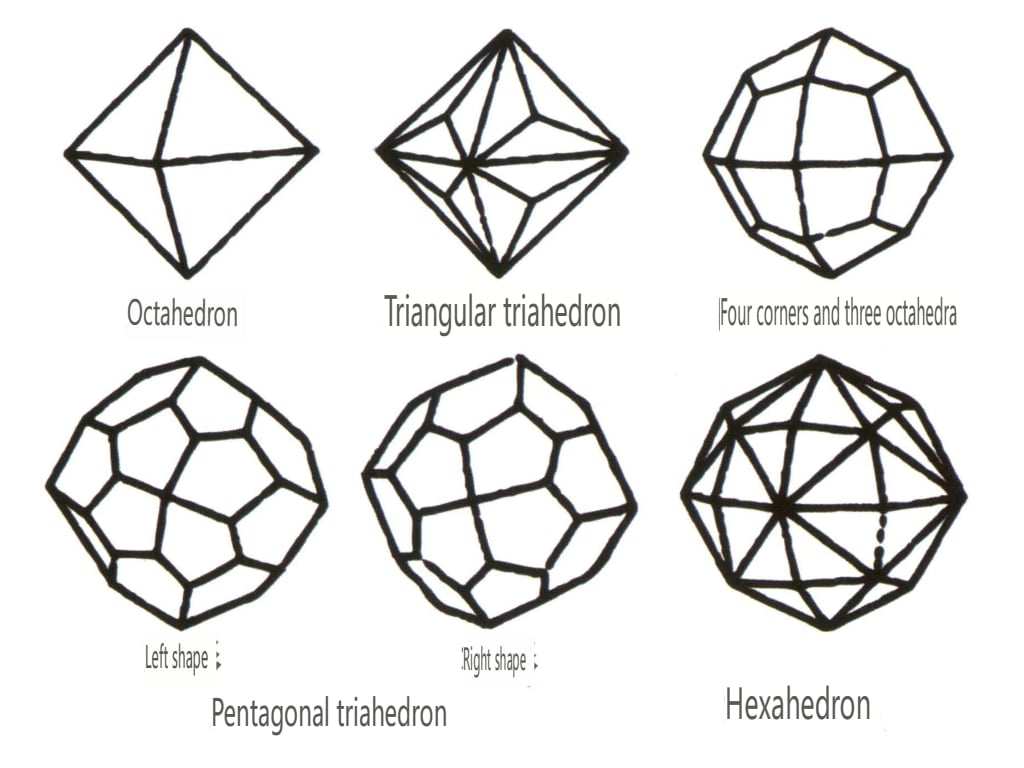
Figura 2-1-44 Clase 0ctaédrica
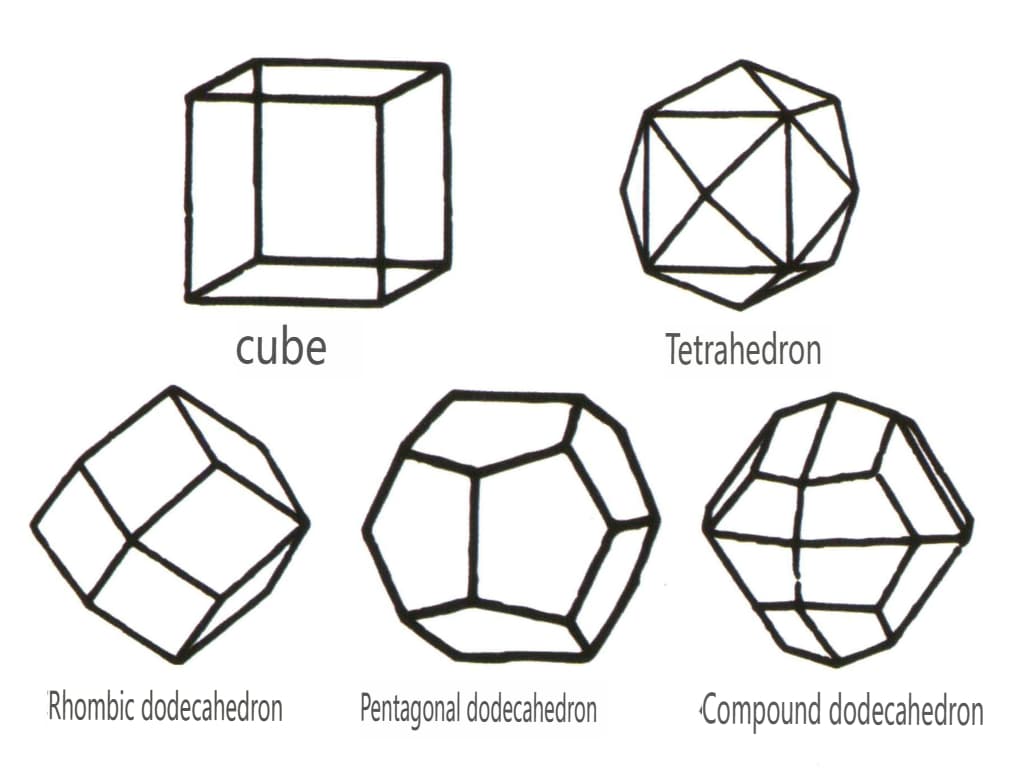
Figura 2-1-45 Clases cúbicas y dodecaédricas
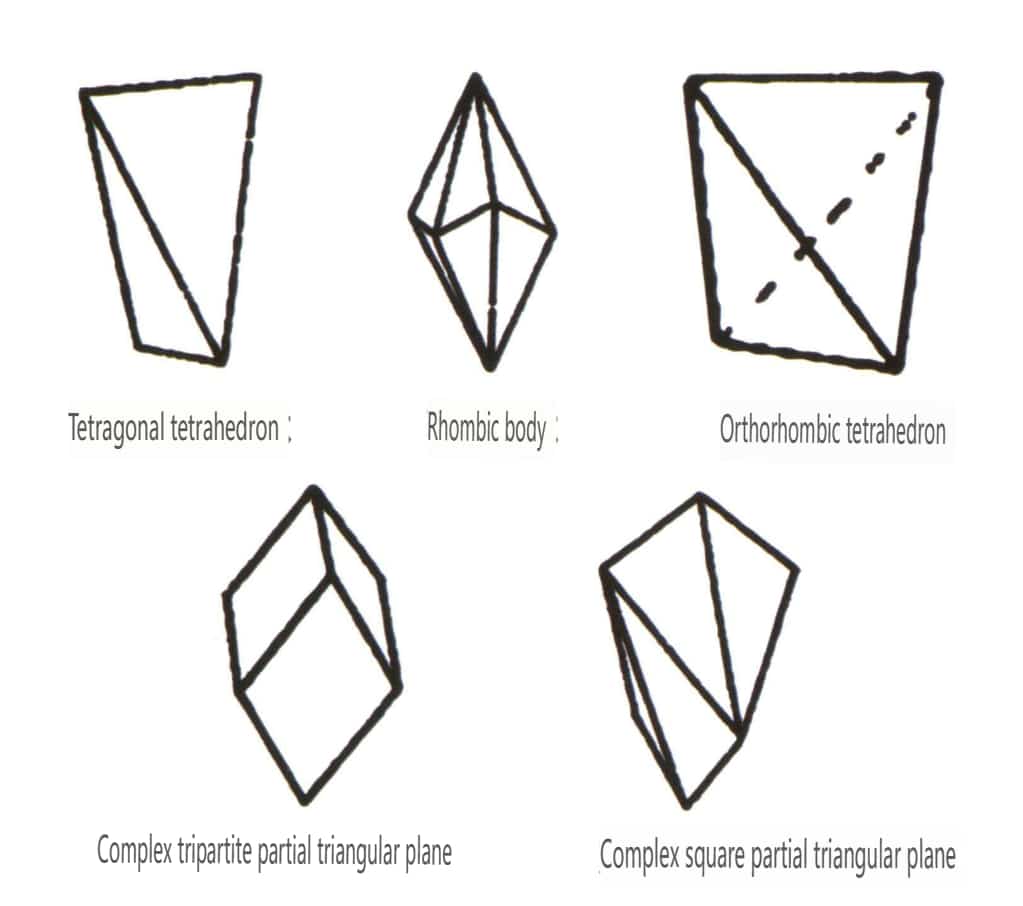
Figura 2-1-46 Otros tipos poliédricos
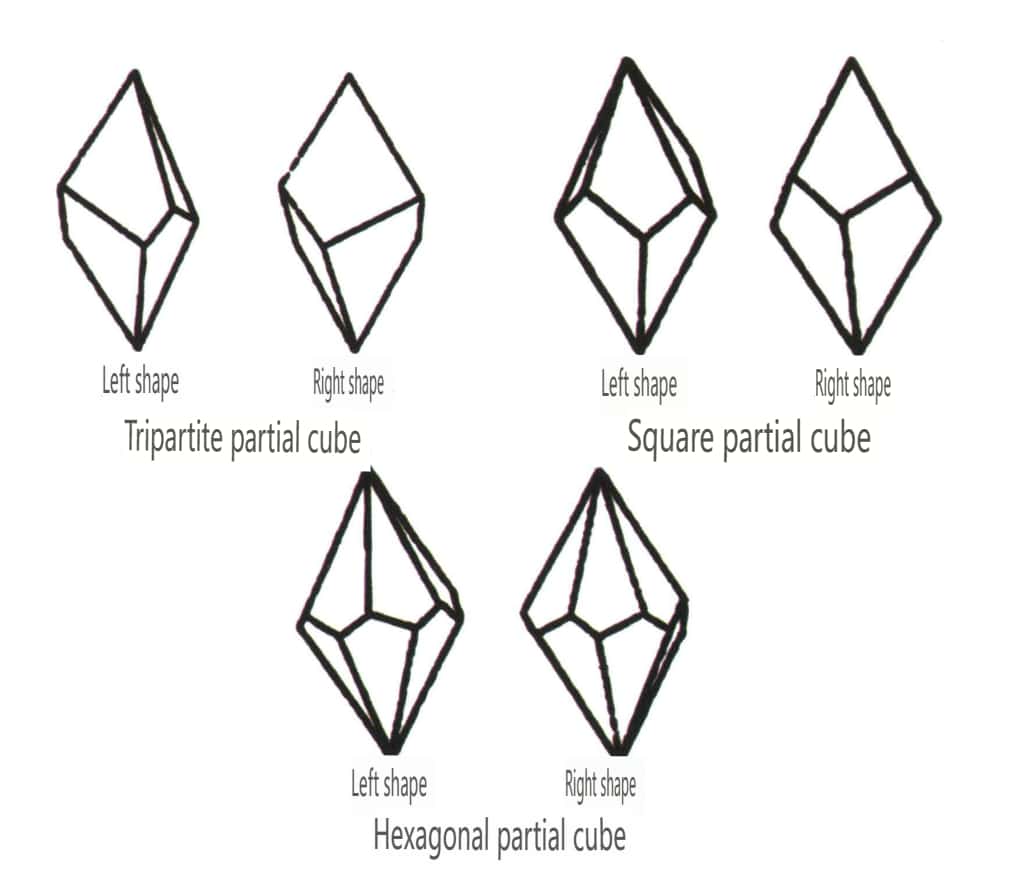
Figura 2-1-47 Forma combinada oblicua Clase
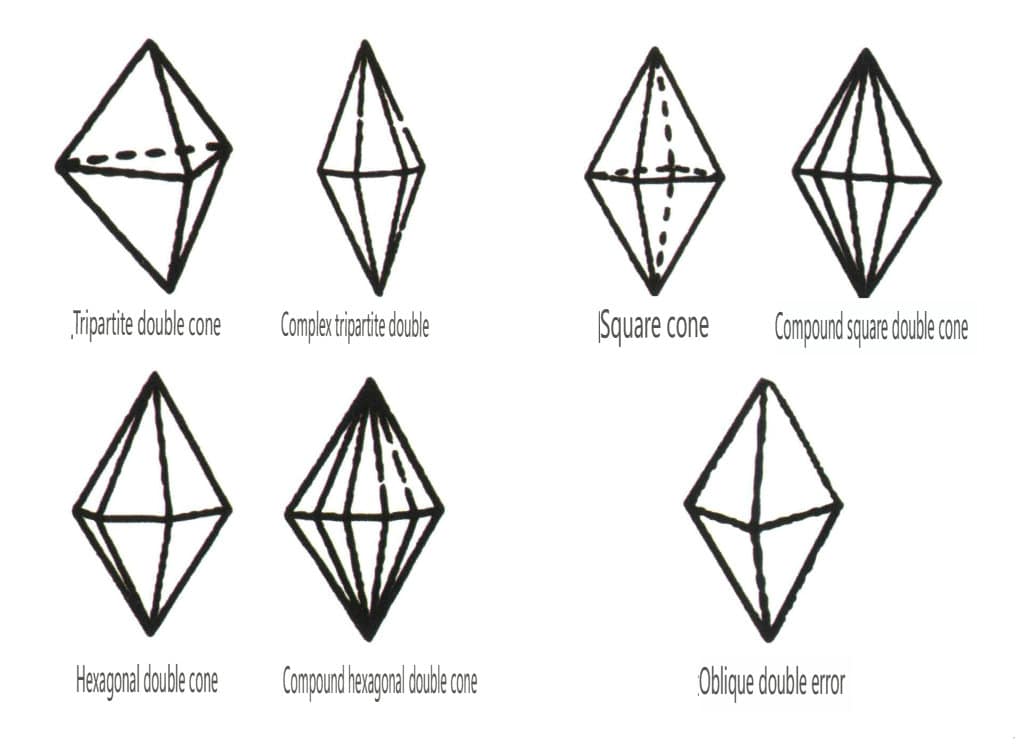
Figura 2-1-48 Clase piramidal doble
Las formas abiertas se refieren a aquellas cuyas caras cristalinas no pueden encerrar un espacio cerrado, divididas en cuatro categorías principales: cara simple, cara doble, clases columnares y clases piramidales simples, totalizando 17 tipos (Figuras 2-1-49 y 2-1-51).
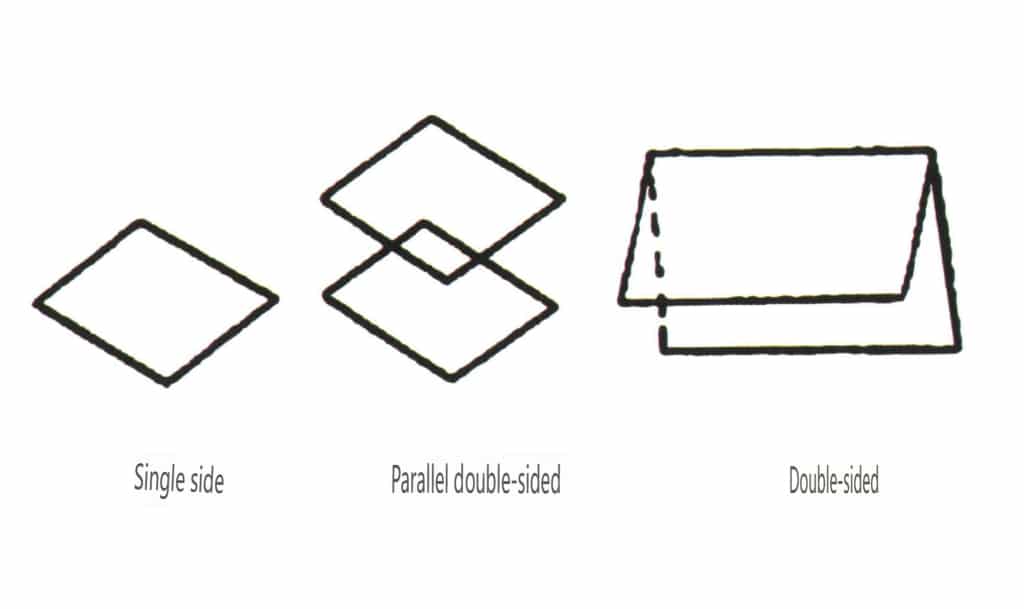
Figura 2-1-49 Una cara y dos caras
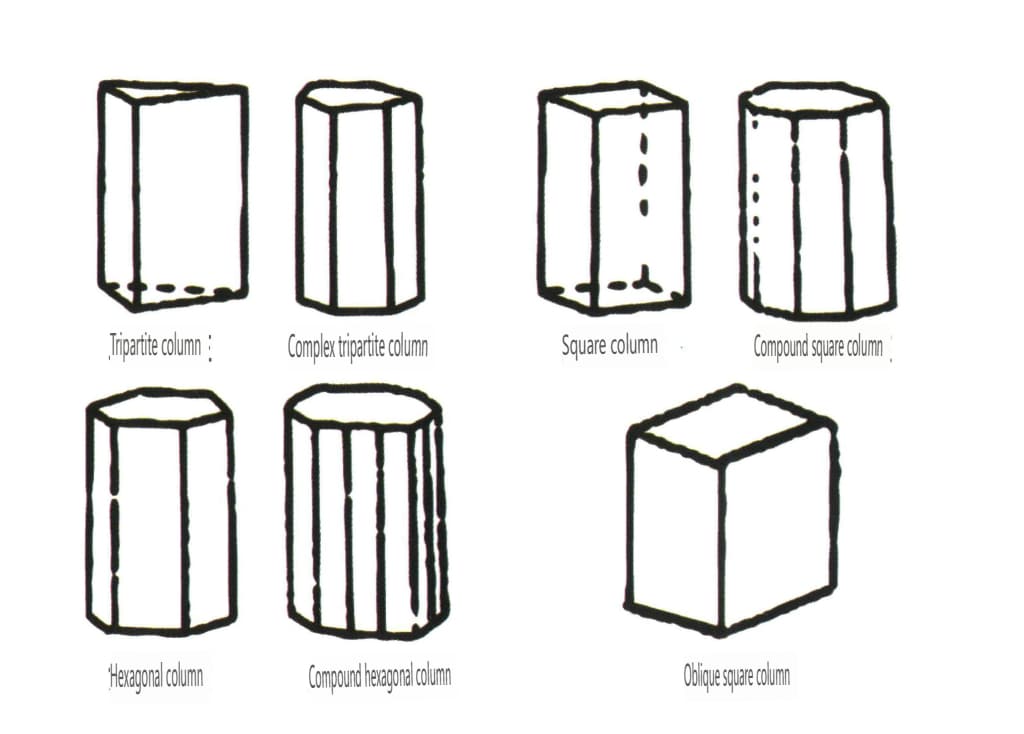
Figura 2-1-50 Columnas

Sección III Clasificación de los cristales
1. Simetría de los cristales
La simetría es un concepto abstracto que interviene en el estudio de los cristales reales y los materiales de las piedras preciosas sin procesar. Describe la repetición exhibida cuando la estructura cristalina está referenciada por una dirección o plano que la atraviesa. Es la base de la clasificación de los cristales.
La simetría de un cristal puede entenderse desde una perspectiva microscópica como un método para describir la repetitividad de la estructura cristalina y desde una perspectiva macroscópica como la repetición de dos o más caras geométricas que son iguales en forma y tamaño pero pueden diferir en dirección, de acuerdo con ciertas reglas. Este patrón de repetición puede describirse mediante ejes de simetría y planos de simetría, denominándose a cada eje de simetría o plano de simetría elemento de simetría. Al observar o inferir la simetría de un objeto, esta acción se describe como realizar operaciones sobre la simetría.
2. Elementos de simetría de los cristales
En cristalografía, existen cuatro elementos de simetría: eje de simetría, plano de simetría, ejes de simetría de rotoinversión y centro de simetría. Aquí se tratarán los dos elementos de simetría: eje de simetría y plano de simetría.
2.1 Eje de simetría
(1) El concepto de eje de simetría y su notación.
El eje de simetría es una línea recta imaginaria que indica el número de veces que el nivel de base (Figuras 2-2-1 a Figura 2-2-2) aparece en la misma posición cuando la estructura de celosía gira 360° alrededor de esta línea imaginaria. Este número sólo puede ser 2, 3, 4 ó 6 veces en 4 casos. También puede entenderse como una línea imaginaria que pasa por el centro del cuerpo geométrico, girando el cuerpo geométrico a lo largo de esta línea 360°. Supongamos que la forma del cuerpo geométrico después de rotar un cierto ángulo es consistente con la forma del cuerpo geométrico en los cero grados iniciales. En ese caso, esta línea imaginaria se denomina eje de simetría.
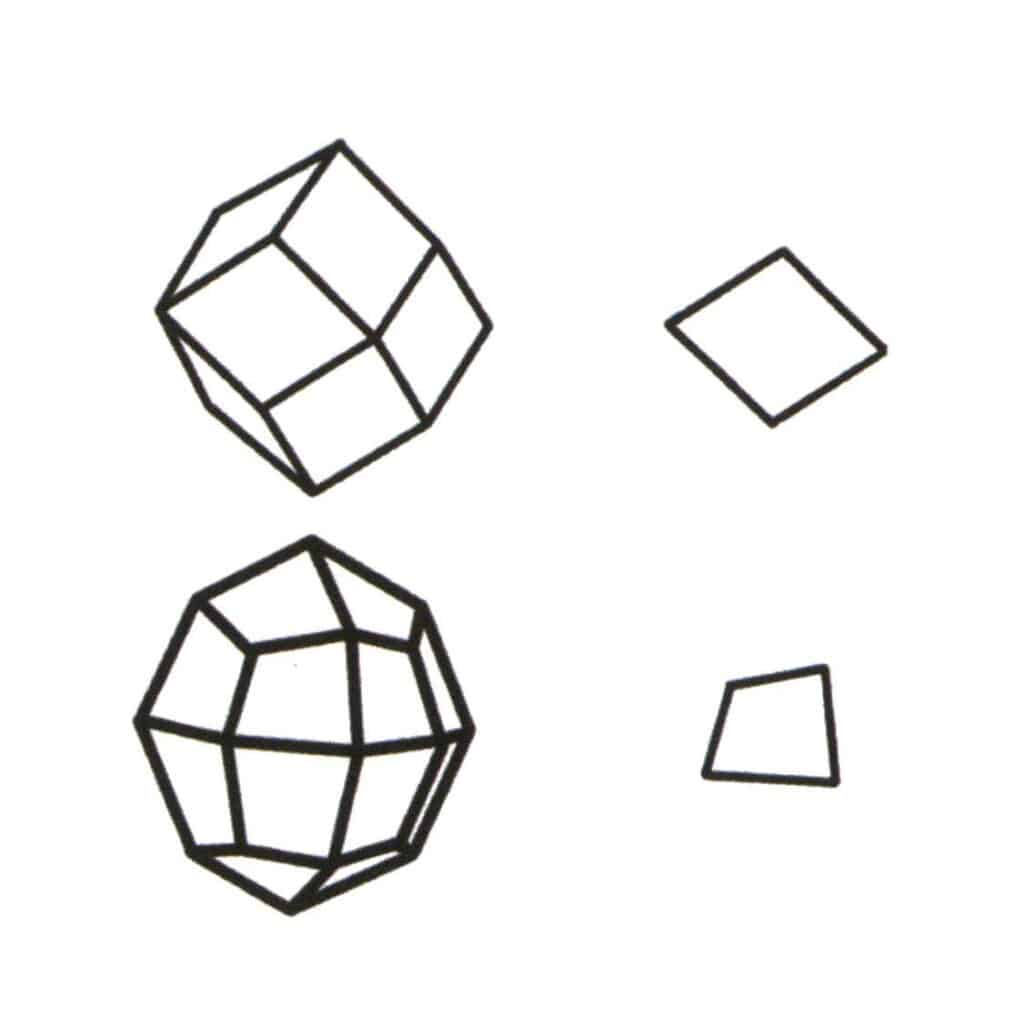
Figura 2-2-1 Selección del nivel de base para el formulario único.
El nivel base de la forma simple es el plano repetido más pequeño que compone el simplex. La parte superior izquierda de la figura muestra un dodecaedro rómbico, que es una forma cerrada compuesta por un tipo de caras. El plano que se repite más pequeño es el rombo que se muestra en la parte superior derecha, por lo que el nivel base del dodecaedro rómbico es el rombo. La parte inferior izquierda de la figura muestra un octaedro cuadrilátero, que es una forma cerrada compuesta por un tipo de caras. El plano de repetición más pequeño es el cuadrilátero mostrado en la parte inferior derecha, por lo que el nivel base del octaedro cuadrilátero es el cuadrilátero.
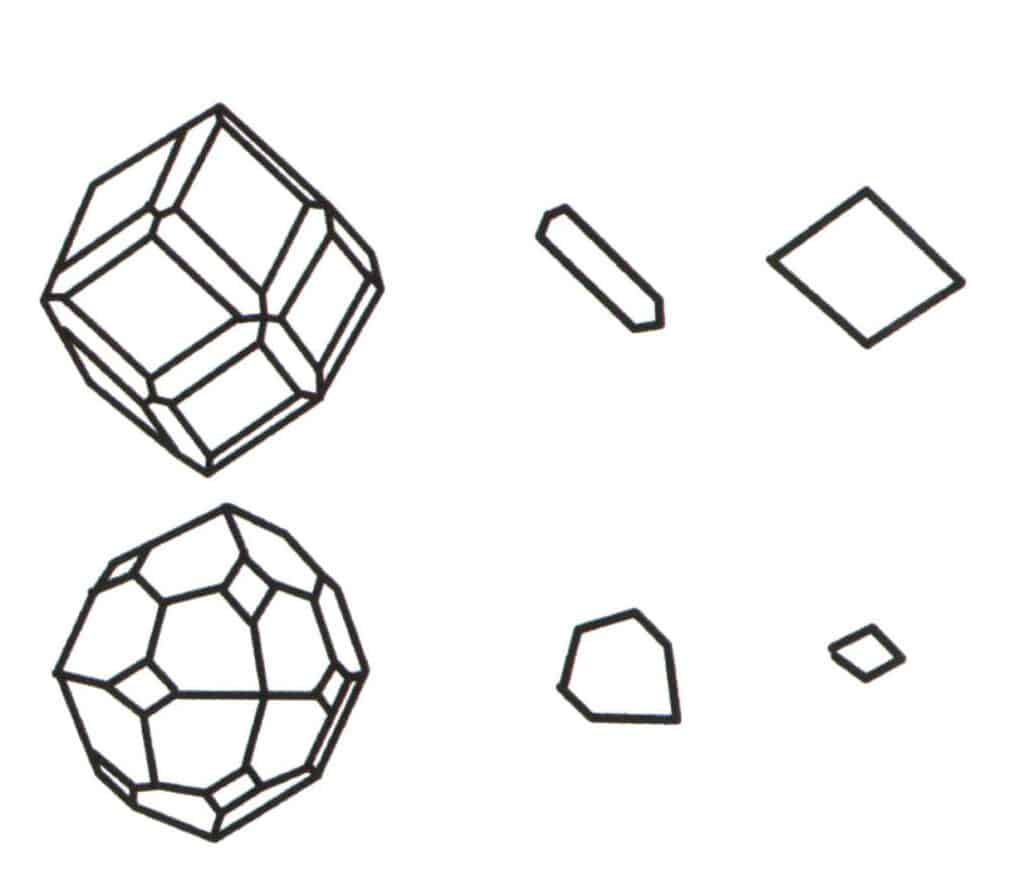
Figura 2-2-2 Selección del nivel base del politopo.
La agregación de múltiples formas simples forma una forma combinada, y la elección del nivel base para la forma combinada es el juicio de la forma simple que se combina para formar la forma combinada. La primera columna de la izquierda en la figura representa una forma combinada (formada por la agregación de formas simples de un dodecaedro y un tetraedro), y este cuerpo geométrico es una figura cerrada compuesta por dos tipos de caras. El hexágono representa el plano mínimo de repetición en la segunda columna y el rombo a la derecha en la tercera columna. Por lo tanto, el plano base de la forma combinada de la primera columna es el hexágono o el rombo. Al calcular el eje de simetría, sólo puede seleccionarse una forma como nivel base para el registro de simetría.
El eje de simetría se representa con la letra L mayúscula, con el orden del eje n escrito en la esquina superior derecha de L, escrito como Lⁿ. Por ejemplo, un eje doble se representa como L², un eje triple como L³, un eje cuádruple como L⁴ y un eje séxtuple como L⁶. L⁶, L⁴, L³ se denomina habitualmente eje de orden superior.
Los cristales pueden tener ejes de simetría en distintas direcciones, y el número de estos ejes de simetría no coincidentes se escribe convencionalmente a la izquierda de L. Por ejemplo, seis ejes secundarios se representan como 6L² (Figura 2-2-3 a Figura 2-2-9), tres ejes terciarios se representan como 3L³ (Figura 2-2-10 a Figura 2-2-14), cuatro ejes terciarios se representan como 4L³ (Figura 2-2-15 a Figura 2-2-18), y un eje hexagonal se representa como L⁶ (Figura 2-2-19).
Cuando un cristal tiene múltiples ejes de simetría, el método registrado los ordena de izquierda a derecha en orden descendente, con el número de ejes de simetría escrito a la izquierda del eje correspondiente, por ejemplo, L⁶6L², 3L⁴4L³6L².
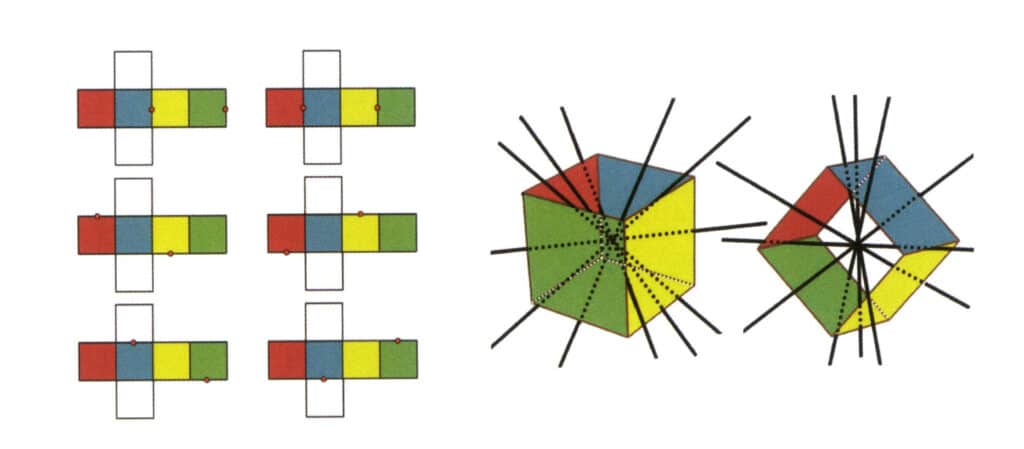
Figura 2-2-3 Eje secundario del cubo
La parte izquierda de la figura muestra la vista desplegada de un cubo, con puntos rojos que indican los puntos de intersección de la línea imaginaria y las aristas. La parte derecha de la figura muestra un cubo cerrado, en el que el eje secundario puede aparecer en el punto medio de líneas de aristas paralelas, en el punto medio de caras rectangulares paralelas o en los puntos de intersección de tres o más caras paralelas que se asemejan a un rectángulo.
Copywrite @ Sobling.Jewelry - Fabricante de joyería personalizada, fábrica de joyería OEM y ODM
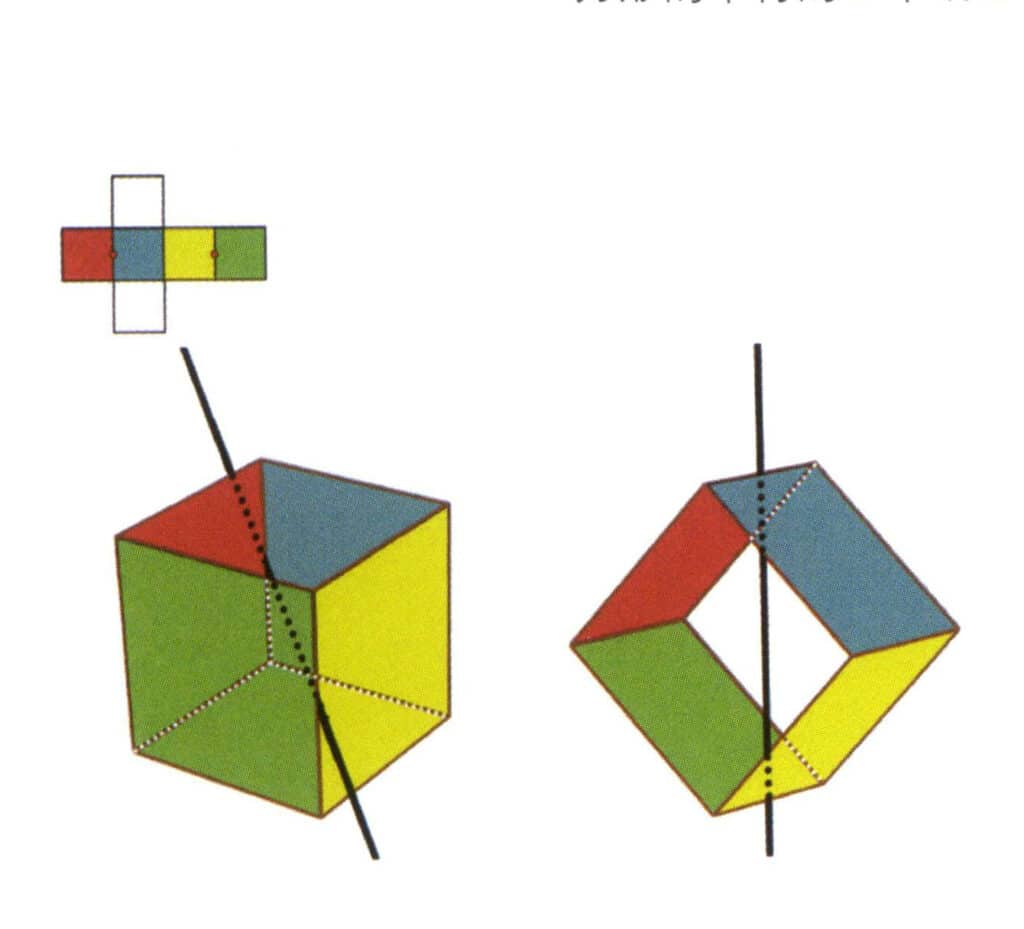
Figura 2-2-4 El primer eje secundario del cubo
Selecciona el punto medio de las líneas paralelas, como se muestra en la figura. Imagina una línea recta que pase por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles base con diferentes colores pero la misma forma se repetirán dos veces en la misma posición (las caras roja y azul, las caras amarilla y verde, las dos caras incoloras, y tres conjuntos de caras repetidas. Aunque aparecerán tres conjuntos de caras repetidas, ya que la línea imaginaria no ha cambiado de posición ni de ángulo, el eje secundario se registra una sola vez). Esta línea imaginaria se registra como eje secundario.
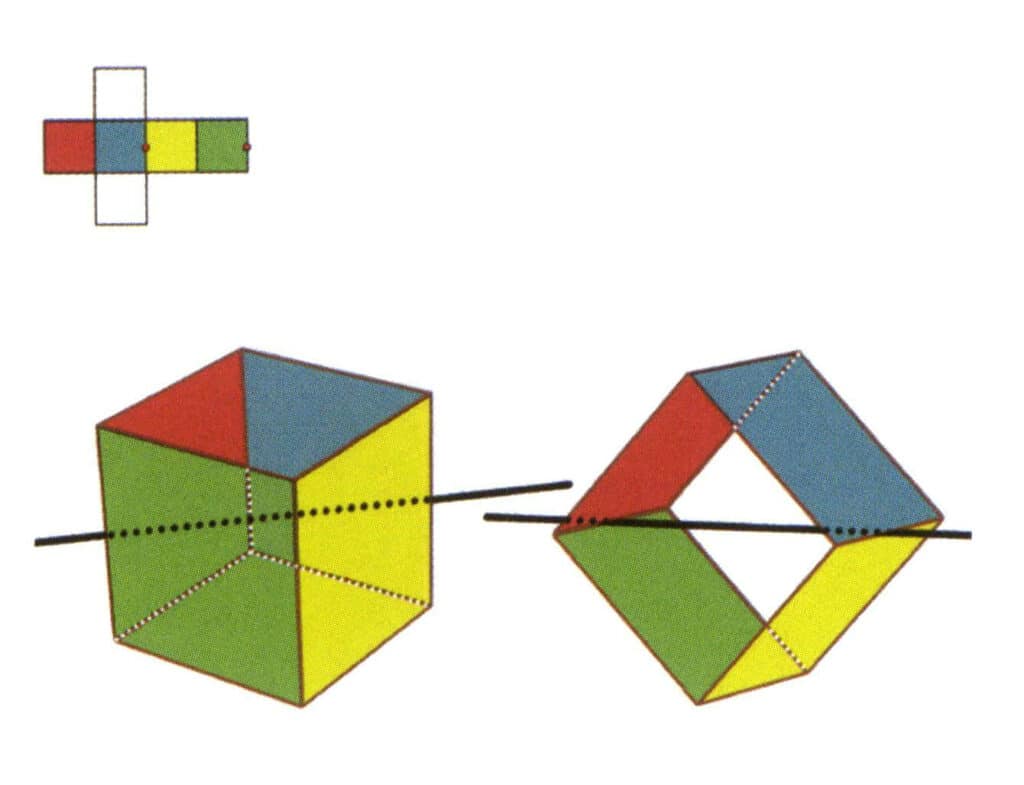
Figura 2-2-5 El segundo eje secundario del cubo
Selecciona el punto medio de las líneas paralelas, como se muestra en la figura. Imagina una línea recta que pase por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles base con diferentes colores pero la misma forma se repetirán dos veces en la misma posición (las caras roja y verde, las caras amarilla y azul, las dos caras incoloras y tres conjuntos de caras repetidas). Esta línea imaginaria se registra como segundo eje secundario.
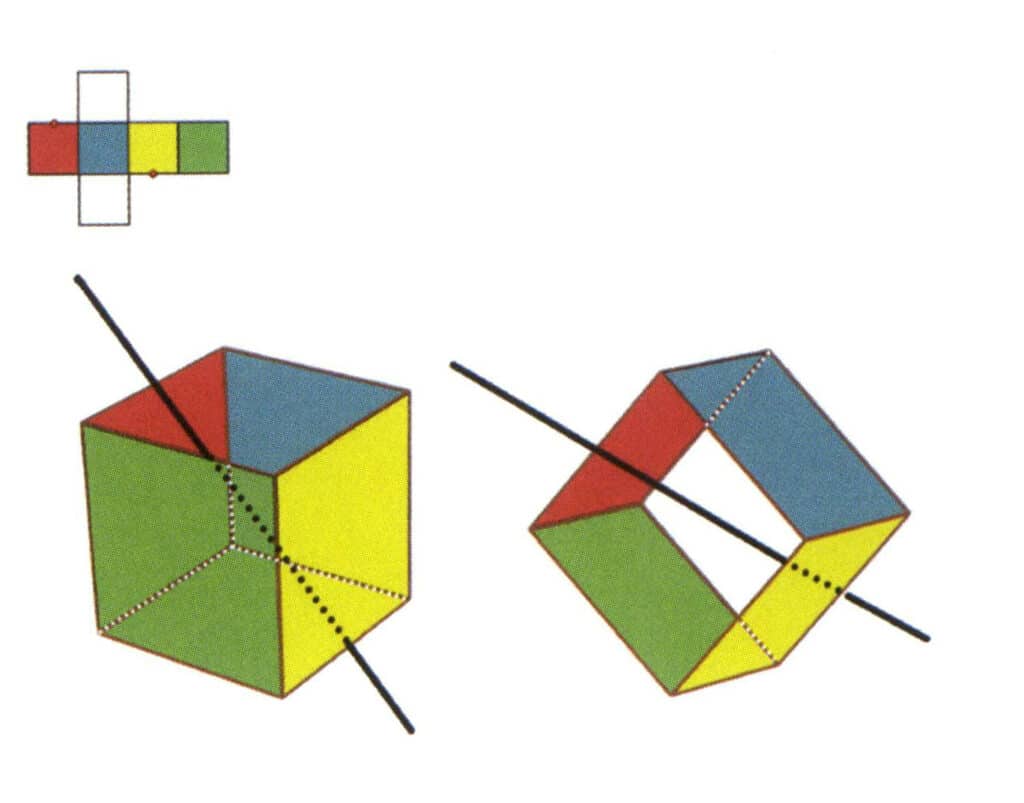
Figura 2-2-6 El tercer eje secundario del cubo.
Selecciona el punto medio de las líneas paralelas, como se muestra en la figura. Imagina una línea recta que pasa por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles de base con diferentes colores, pero la misma forma se repetirá dos veces en la misma posición (las caras roja e incolora, las caras verde y azul, las caras incolora y amarilla, tres conjuntos de caras repetidas). Esta línea imaginaria se registra como el tercer eje secundario
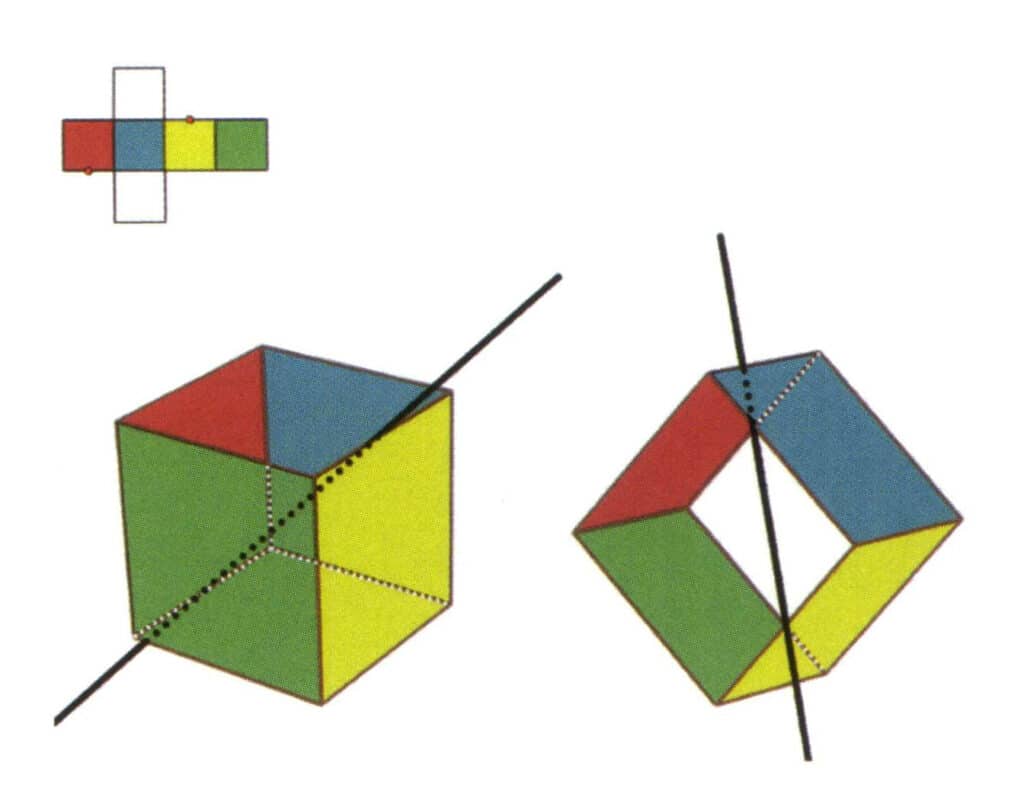
Figura 2-2-7 El cuarto eje secundario del cubo
Selecciona el punto medio de las líneas paralelas como se muestra en la figura, imagina una línea recta que pase por los puntos medios de estas dos aristas, y gira el cubo 360°; los planos de referencia de colores diferentes pero de forma idéntica se repetirán en la misma posición dos veces (las caras roja e incolora, las caras verde y azul, las caras incolora y amarilla, tres conjuntos de caras repetidas), esta línea recta imaginaria se registra como el cuarto eje secundario.
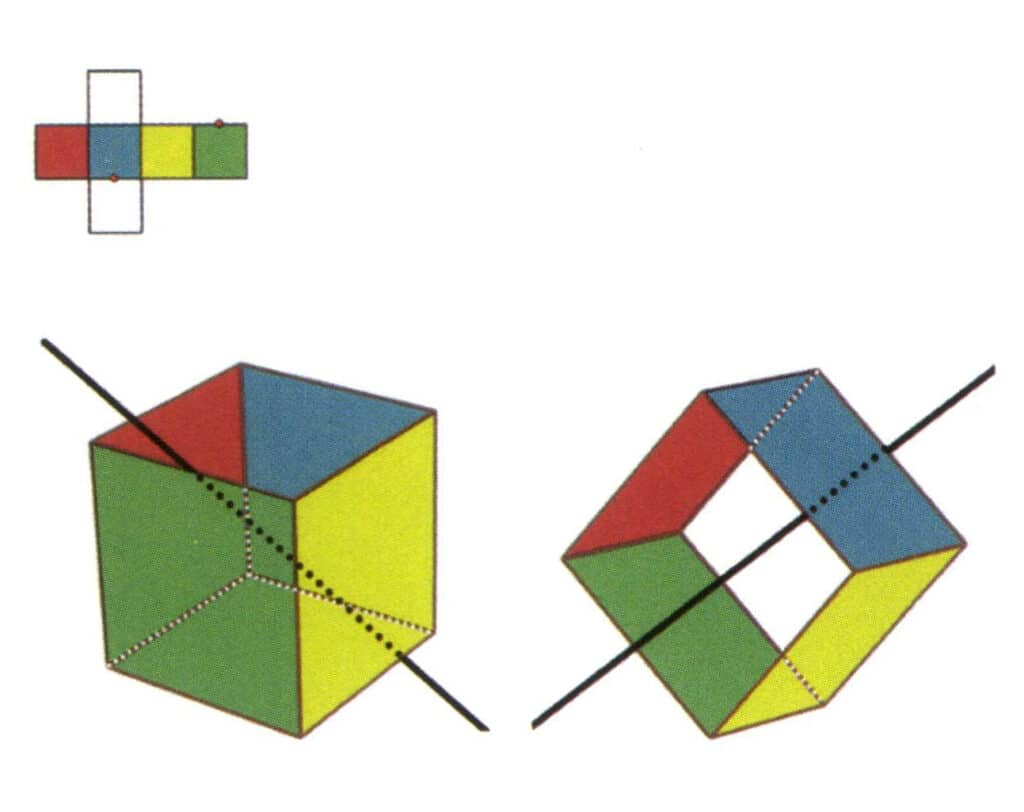
Figura 2-2-8 El quinto eje secundario del cubo.
Seleccione los puntos medios de las líneas paralelas como se muestra en la figura, imagine una línea recta que pase por los puntos medios de estas dos aristas, gire el cubo 360°, los planos de referencia de colores diferentes pero de forma idéntica se repetirán en la misma posición dos veces (caras rojas e incoloras, caras verdes y azules, caras incoloras y amarillas, tres conjuntos de caras repetidas), esta línea recta imaginada se registra como el quinto eje secundario.
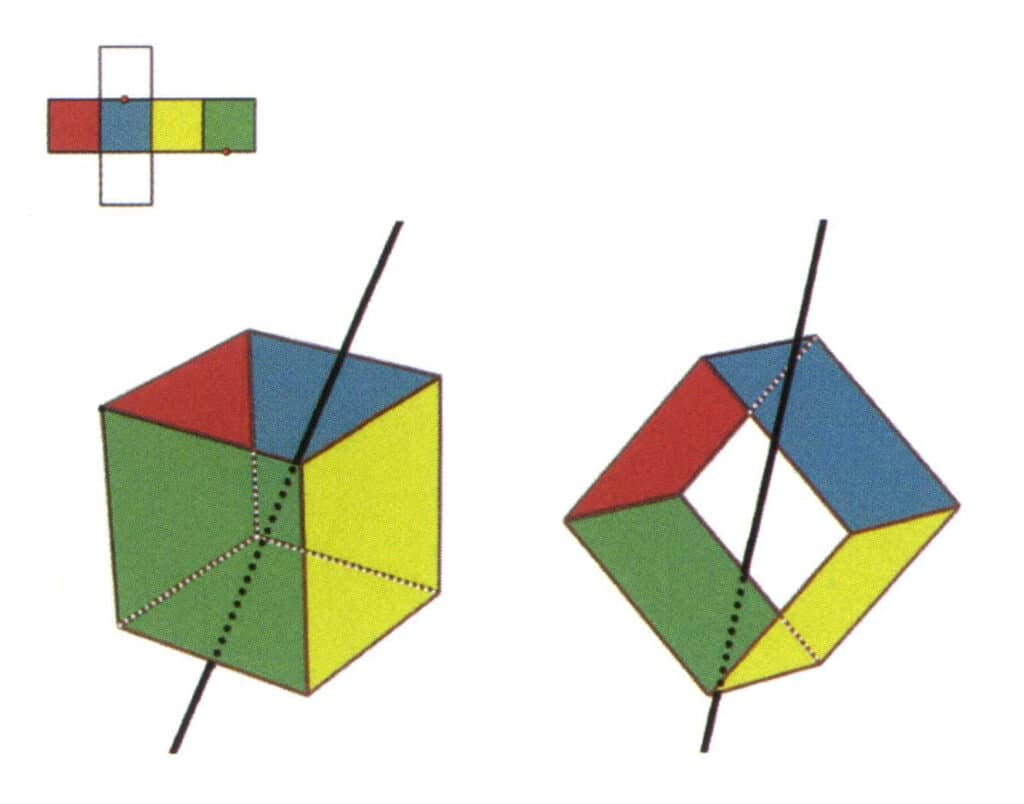
Figura 2-2-9 El sexto eje secundario del cubo
Selecciona el punto medio de las líneas paralelas, como se muestra en la figura. Imagina una línea recta que pasa por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles de base, de colores diferentes pero de forma idéntica, se repetirán en la misma posición dos veces (caras verde e incolora, caras roja y amarilla, caras incolora y azul, tres conjuntos de caras repetidas). Esta línea imaginaria se registra como sexto eje secundario.
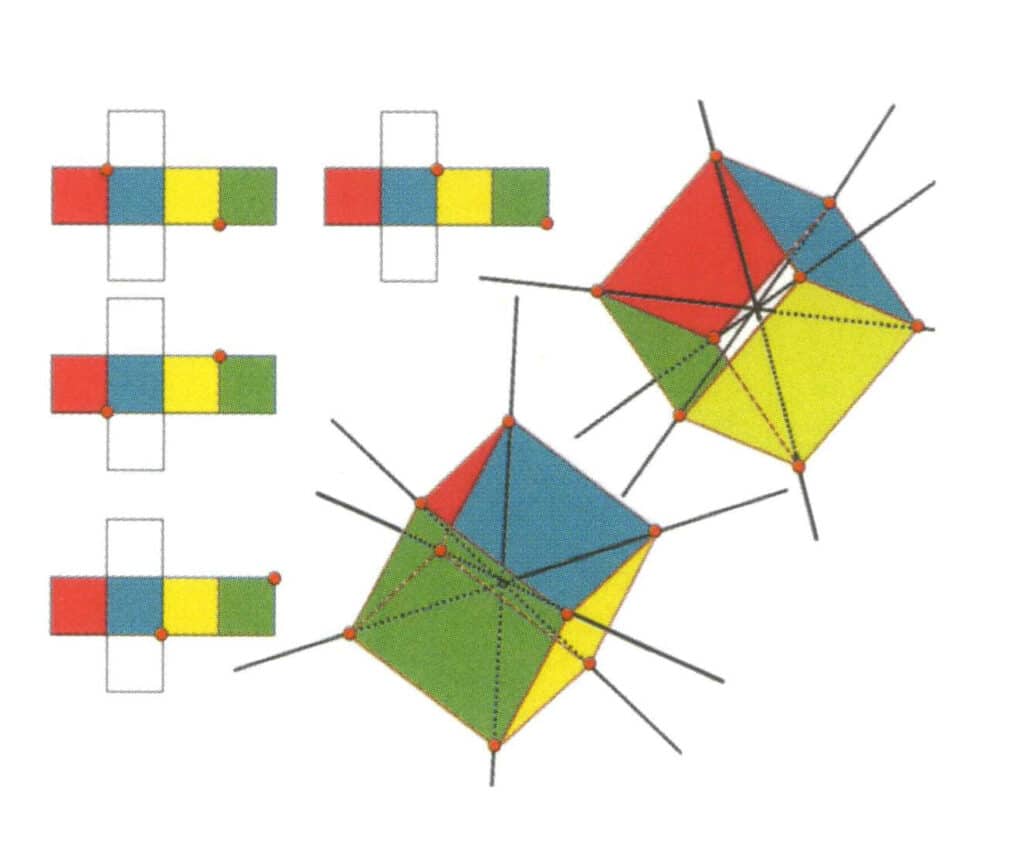
Figura 2-2-10 El eje terciario del cubo
La parte izquierda de la figura muestra la vista desplegada del cubo; el punto rojo indica el punto de intersección de la recta imaginaria y la arista. La parte derecha de la figura muestra el cubo cerrado; los puntos rojos indican la intersección de la recta imaginaria y las aristas. El eje terciario puede aparecer en el punto medio de las caras de un triángulo equilátero paralelo, en la intersección de tres o más caras paralelas que se asemejan a un triángulo equilátero.
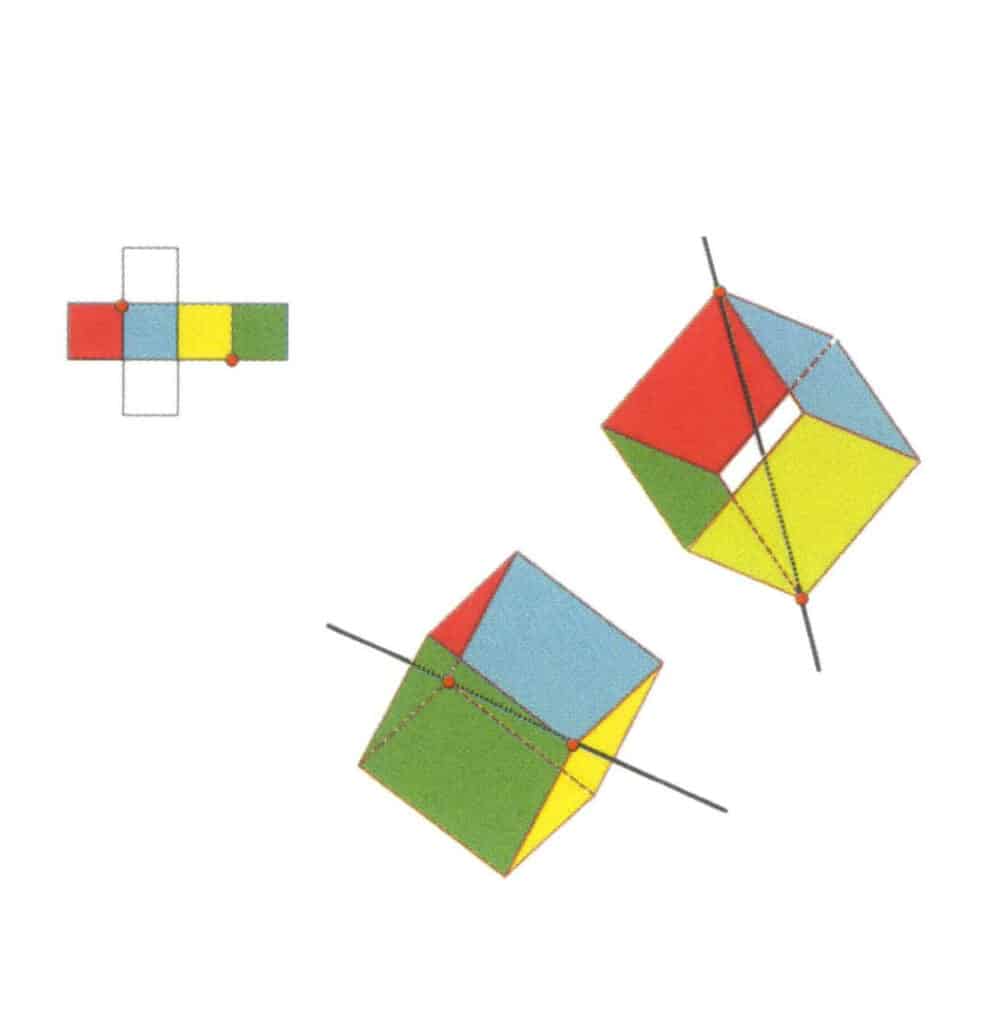
Figura 2-2-11 El primer eje terciario del cubo.
Selecciona los puntos de intersección de las tres caras como se muestra en la figura, imagina una línea recta que pase por los puntos medios de estas dos aristas, gira el cubo 360°, los planos de referencia de diferente color pero idéntica forma se repetirán en la misma posición tres veces (caras roja, incolora y azul, caras verde, incolora y amarilla, dos conjuntos de caras repetidas), esta línea recta imaginada se registra como el primer eje terciario
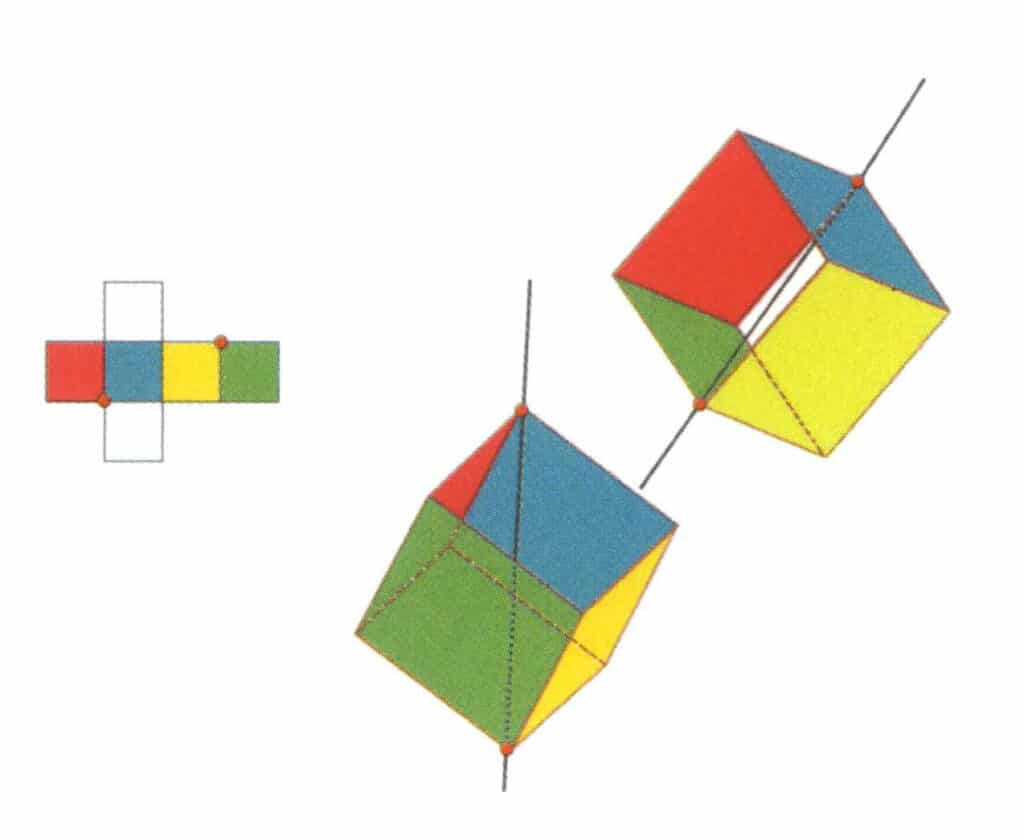
Figura 2-2-12 El segundo eje terciario del cubo.
Selecciona los puntos de intersección de las tres caras, como se muestra en la figura. Imagina una línea recta que pase por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles de base, de colores diferentes pero de forma idéntica, se repetirán en la misma posición tres veces (caras roja, incolora y azul; caras verde, incolora y amarilla, dos conjuntos de caras repetidas). Esta línea imaginaria se registra como segundo eje terciario.
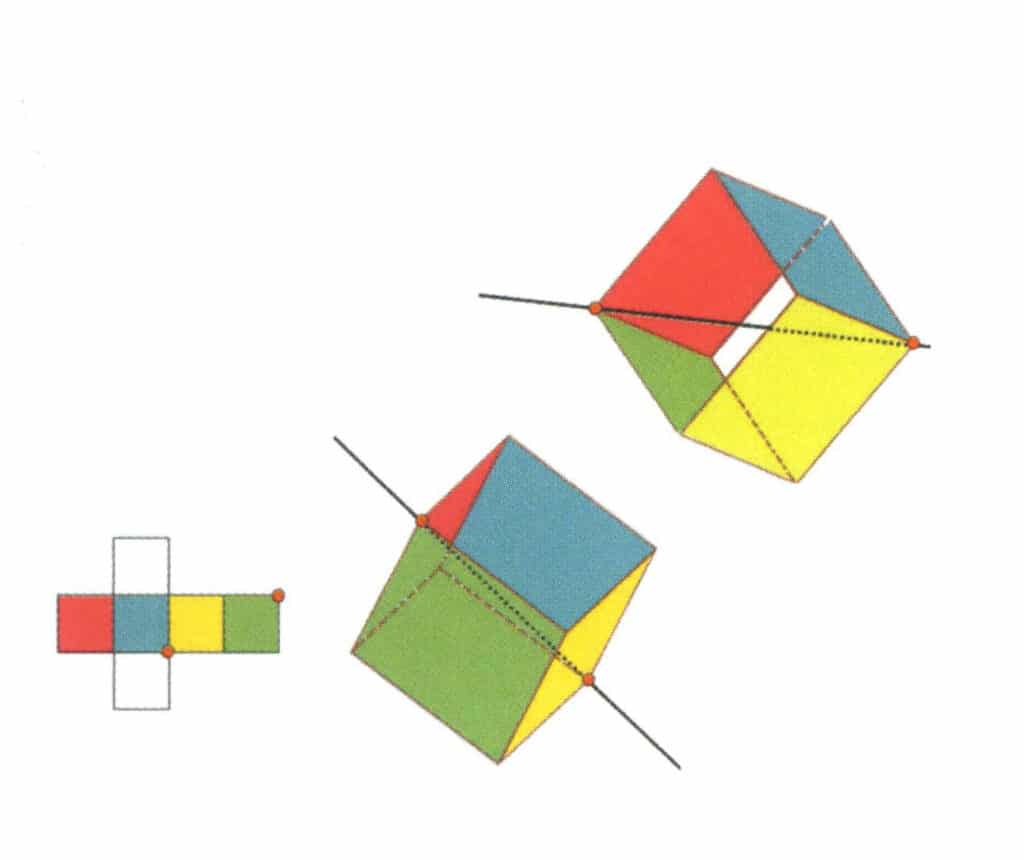
Figura 2-2-13 El tercer eje terciario del cubo
Selecciona los puntos de intersección de las tres caras, como se muestra en la figura. Imagina una línea recta que pase por los puntos medios de estas dos aristas, girando el cubo 360°. Los niveles de base, de colores diferentes pero de forma idéntica, se repetirán en la misma posición tres veces (caras roja, incolora y verde; caras azul, incolora y amarilla, dos conjuntos de caras repetidas). Esta línea imaginaria se registra como tercer eje terciario.
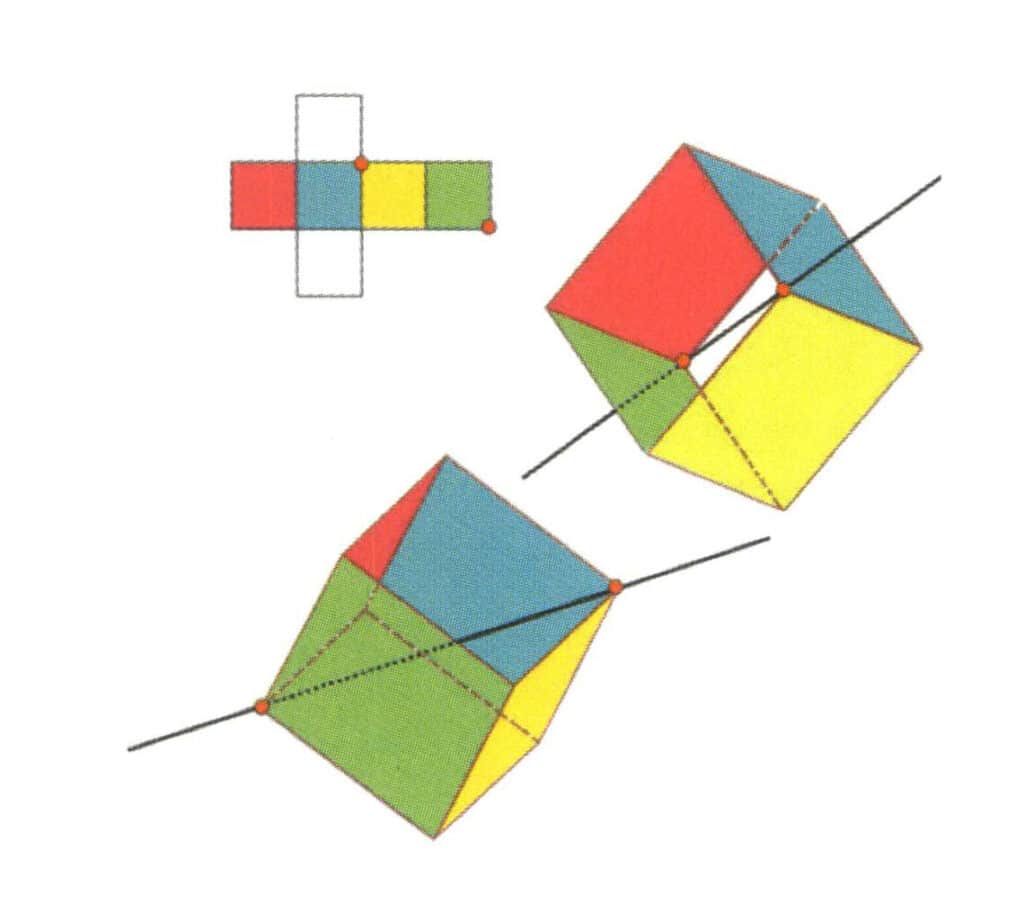
Figura 2-2-14 Cuarto eje cúbico del cubo.
Seleccione la intersección de las tres caras como se muestra en la figura, suponiendo que hay una línea recta a través del punto medio de los dos bordes gira el cubo 360 °, diferentes colores, pero el mismo nivel de base de forma será la misma. Repite la posición tres veces (cara roja, incolora, verde, cara azul, incolora y amarilla, dos conjuntos de caras repetidas). Esta línea imaginaria se registra como el cuarto eje cúbico.
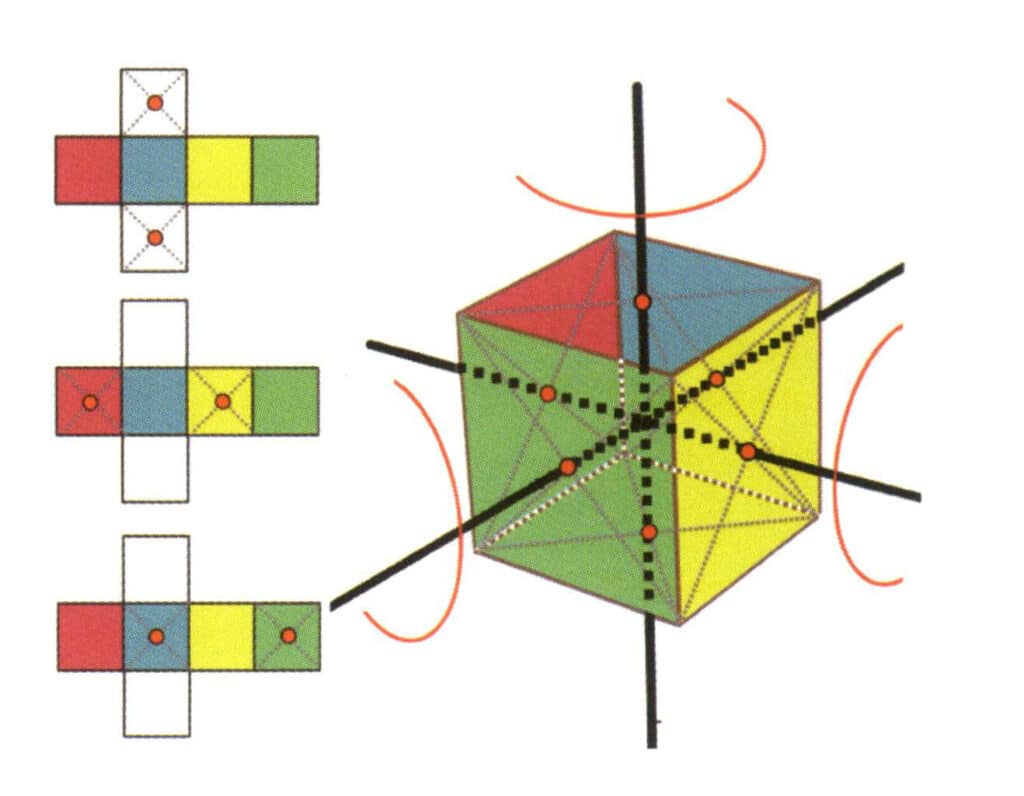
Figura 2-2-15 Cuarto eje del cubo
La parte izquierda de la figura muestra la vista desplegada del cubo, con los puntos rojos indicando los puntos de intersección de la línea imaginaria y las aristas. La parte derecha de la figura muestra un cubo cerrado, con los puntos rojos indicando los puntos de intersección de la línea imaginaria y el plano. El cuarto eje puede aparecer en el punto medio de las caras cuadradas paralelas, en la intersección de tres o más caras paralelas que se asemejan a un cuadrado.
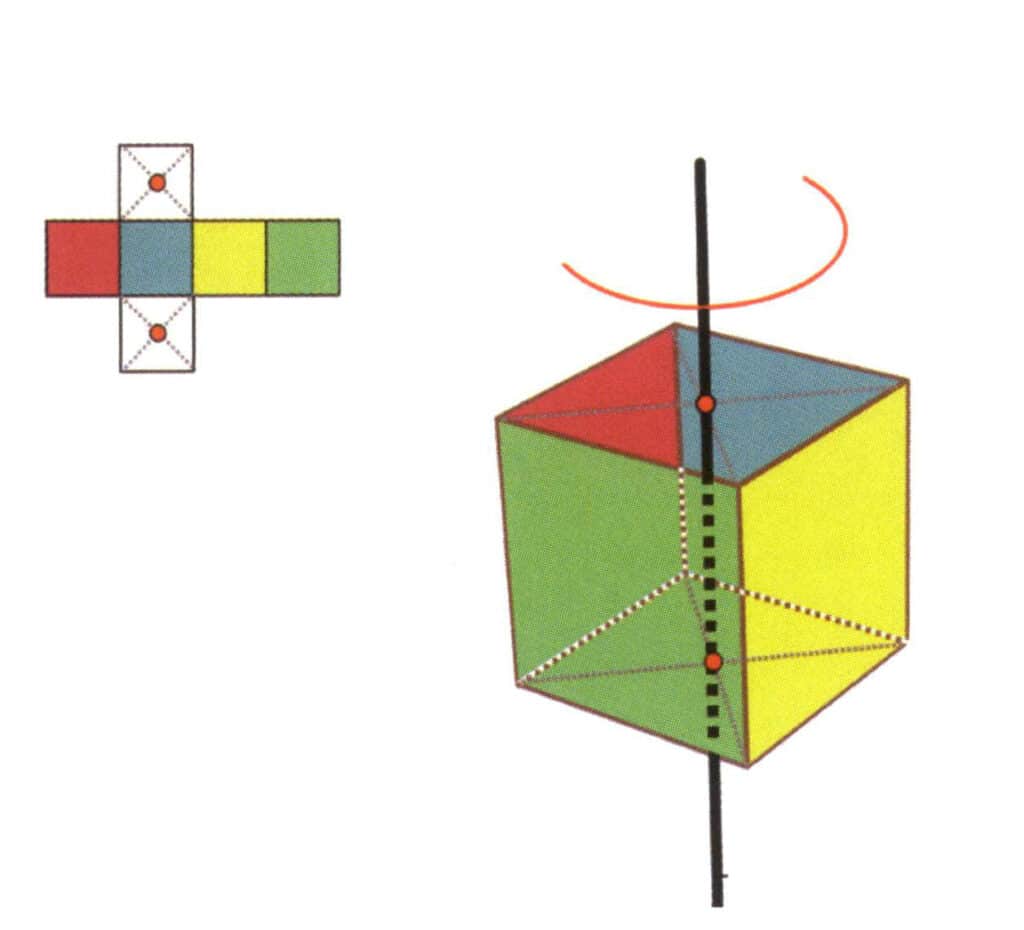
Figura 2-2-16 El primer eje cuártico del cubo
Elige los puntos medios de los planos mostrados en la figura, supone que existe una línea recta que pasa por los puntos medios de los dos planos y gira el cubo 360°. Las caras del plano base, de distinto color pero con la misma forma, se repetirán en la misma posición cuatro veces (caras roja, azul, verde y amarilla), y esta hipotética línea recta se registra como un cuádruple axial.
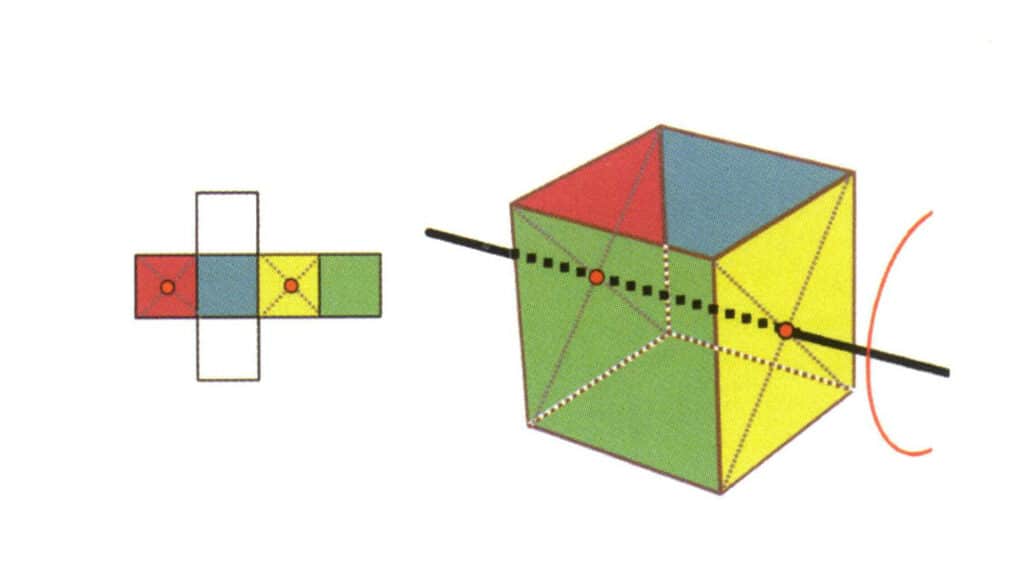
Figura 2-2-17 El segundo eje cuártico del cubo
Seleccione el punto medio del plano como se muestra en la figura, imagine una línea recta que atraviese el cubo y gire el cubo 360°; la superficie del nivel de base de diferentes colores pero la misma forma se repetirá cuatro veces en la misma posición (incolora, cara azul en la parte superior, incolora, cara verde en la parte inferior), y esta línea imaginaria se registrará como el segundo eje cuádrico.
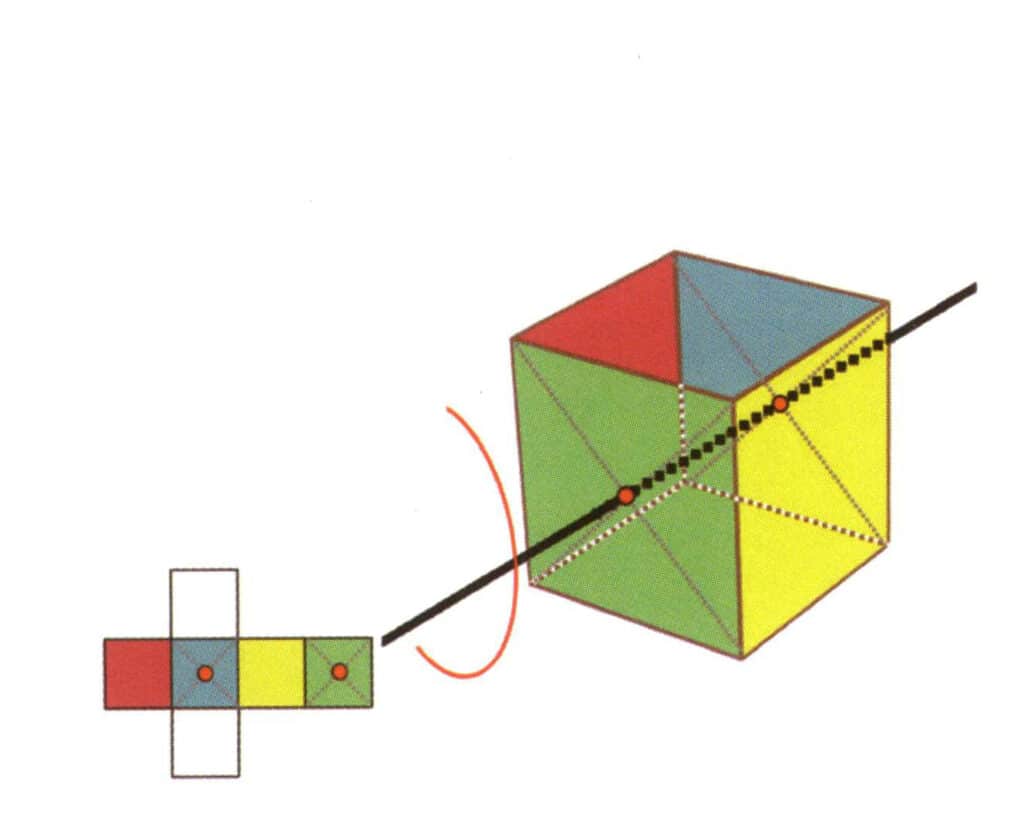
Figura 2-2-18 Tercer eje cuártico del cubo
Selecciona el punto medio del plano como se muestra en la figura, imagina una línea recta que atraviese el cubo y gíralo 360°. El plano base de diferentes colores pero la misma forma se repetirá cuatro veces en la misma posición (incoloro, cara roja en la parte superior, incoloro, cara amarilla en la parte inferior), y esta línea imaginaria se registrará como el tercer, cuarto eje
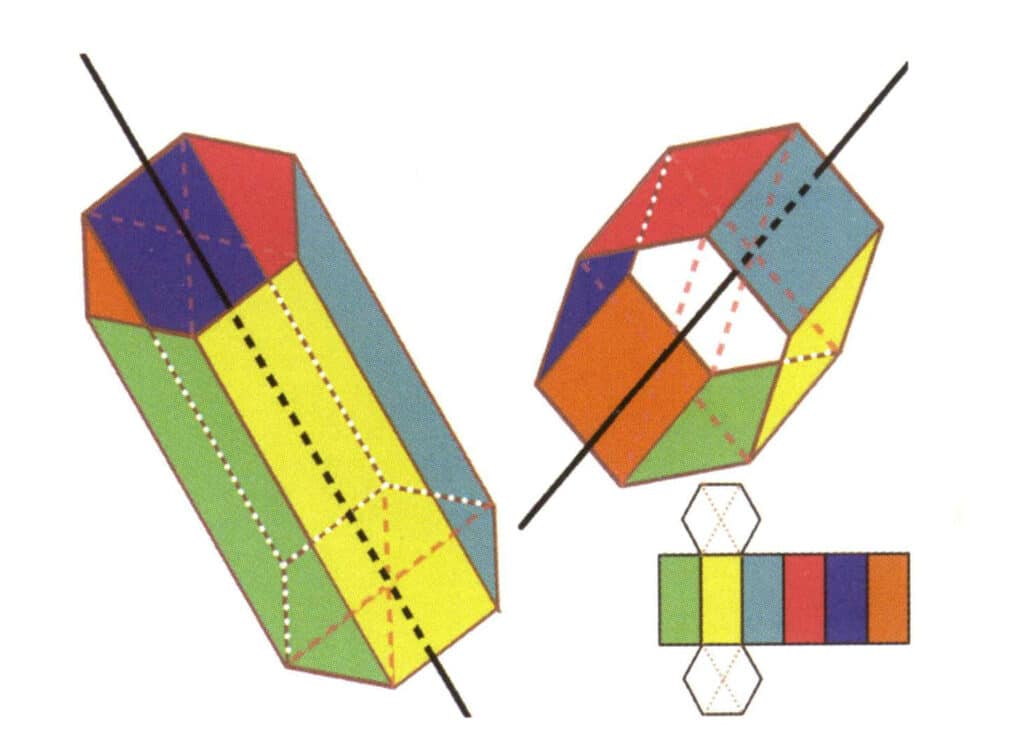
Figura 2-2-19 Seis ejes de un prisma hexagonal
Las líneas negras de la izquierda y la parte superior derecha representan los seis ejes del prisma hexagonal. La parte inferior derecha es una ampliación del prisma hexagonal El eje sexta puede aparecer en el punto medio de las caras de un hexágono paralelo o en la intersección de las seis caras de un hexágono.
(2) Consideraciones para encontrar el eje de simetría.
① Existen cinco tipos de posiciones para el eje de simetría.
Punto medio de dos aristas paralelas, como la posición del eje secundario de un cubo.
Punto medio de dos planos paralelos, como la posición del eje cuártico de un cubo.
Entre dos vértices (los puntos de intersección de varias caras), como la posición del eje terciario de un cubo.
Punto medio entre un vértice y un plano paralelo, como la posición del eje terciario de un tetraedro.
El punto medio de la línea de arista y el punto medio del plano paralelo, como la posición del eje secundario de un prisma triangular.
② La selección del eje de simetría en la misma dirección sigue el principio del número más bajo. Por ejemplo, según el principio del menor número, si en una dirección se encuentran seis ejes de simetría y en otra tres ejes de simetría, se registrará finalmente como L³. Los ejes de simetría en diferentes direcciones deben registrarse según el número encontrado.
Cabe señalar que, salvo el eje de simetría séxtuple y el eje de simetría cuádruple, que no pueden aparecer simultáneamente, y sólo puede aparecer un eje séxtuple, los demás ejes de simetría pueden coexistir en diversas formas o instancias múltiples.
③ El nivel base debe seleccionarse como el plano unitario más pequeño; no pueden seleccionarse como nivel base dos o más planos que se crucen. De lo contrario, afectará a la precisión de la evaluación del eje de simetría.
④ Al registrar el número de ejes de simetría, es esencial determinar el número de veces que se repite la misma forma y tamaño del plano en la misma posición.
⑤ Si hay un eje secundario de simetría vertical Lⁿ(n = 3, 4 ó 6), debe haber n ejes secundarios verticales a Lⁿ.
2.2 Plano de Simetría
(1) Concepto y método de registro del plano de Simetría
Un plano de simetría es un plano imaginario que, cuando se corta el cristal a lo largo de este plano, permite que cada mitad del cristal sea una imagen especular de la otra mitad (Figura 2-2-20). En la misma estructura cristalina, un plano de este tipo puede aparecer un máximo de 9 veces (Figura 2-2-21), lo que significa que se puede bisecar de 9 maneras diferentes, y las dos mitades pueden coincidir completamente. Por supuesto, no todas las estructuras cristalinas tienen planos de simetría.
La letra P mayúscula representa el plano de simetría. Algunos cristales tienen múltiples planos de simetría no coincidentes, y el número de estos planos de simetría se escribe convencionalmente a la izquierda de P; por ejemplo, cuatro planos de simetría se representan como 4P, y un plano de simetría se representa como P.
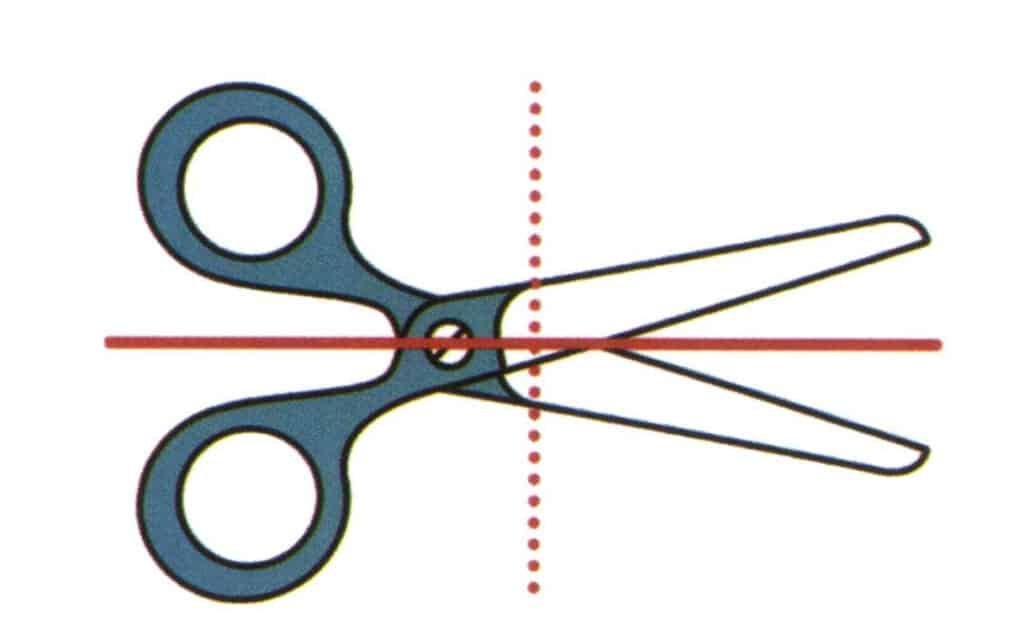
Figura 2-2-20 Imagine un plano vertical de papel y un plano que se extiende a lo largo de la dirección de la línea sólida roja, que divide las tijeras en partes superior e inferior, y las partes superior e inferior son simétricas en espejo. Este plano imaginado se llama plano de simetría. Imagina otro plano perpendicular a la superficie del papel y que se extiende a lo largo de la dirección de la línea discontinua roja, que divide las tijeras en partes izquierda y derecha, pero las formas de las tijeras en los lados izquierdo y derecho no son simétricas.
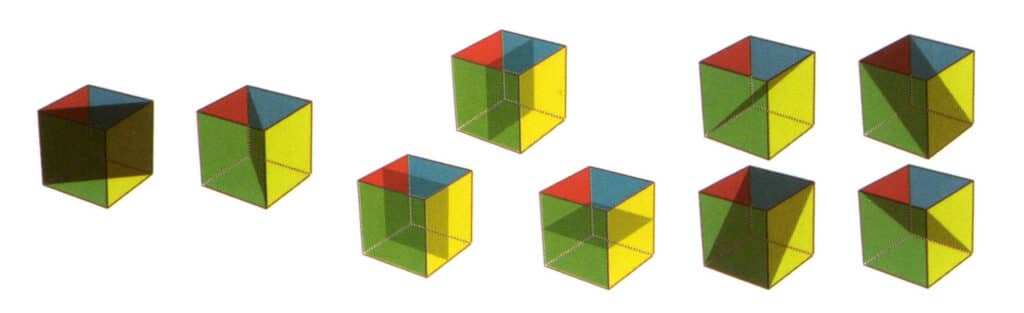
Figura 2-2-21 Nueve planos de simetría de un cubo
(2) Consejos para encontrar Planos de simetría.
① El plano de simetría suele ser paralelo y coincidente con el eje de simetría.
② El plano de simetría es un plano imaginario que divide la geometría cristalina, que es diferente del plano doble paralelo en geometría.
③ Si un plano de simetría contiene al eje de simetría Lⁿ, entonces debe haber n planos de simetría que contengan a Lⁿ.
(3) Punto Grupo.
El grupo de puntos es la suma de todos los elementos de simetría de un cristal. El orden de escritura del grupo de puntos es eje de simetría + plano de simetría, por ejemplo, 3L²3P (Figura 2-2-22). Si un cristal tiene varios ejes de simetría, se acostumbra a registrarlos de izquierda a derecha, del eje de orden superior al eje de orden inferior, y el orden de los planos de simetría, por ejemplo, L⁴4L²5P (Figura 2-2-23). Existen 32 tipos de simetría en los cristales.
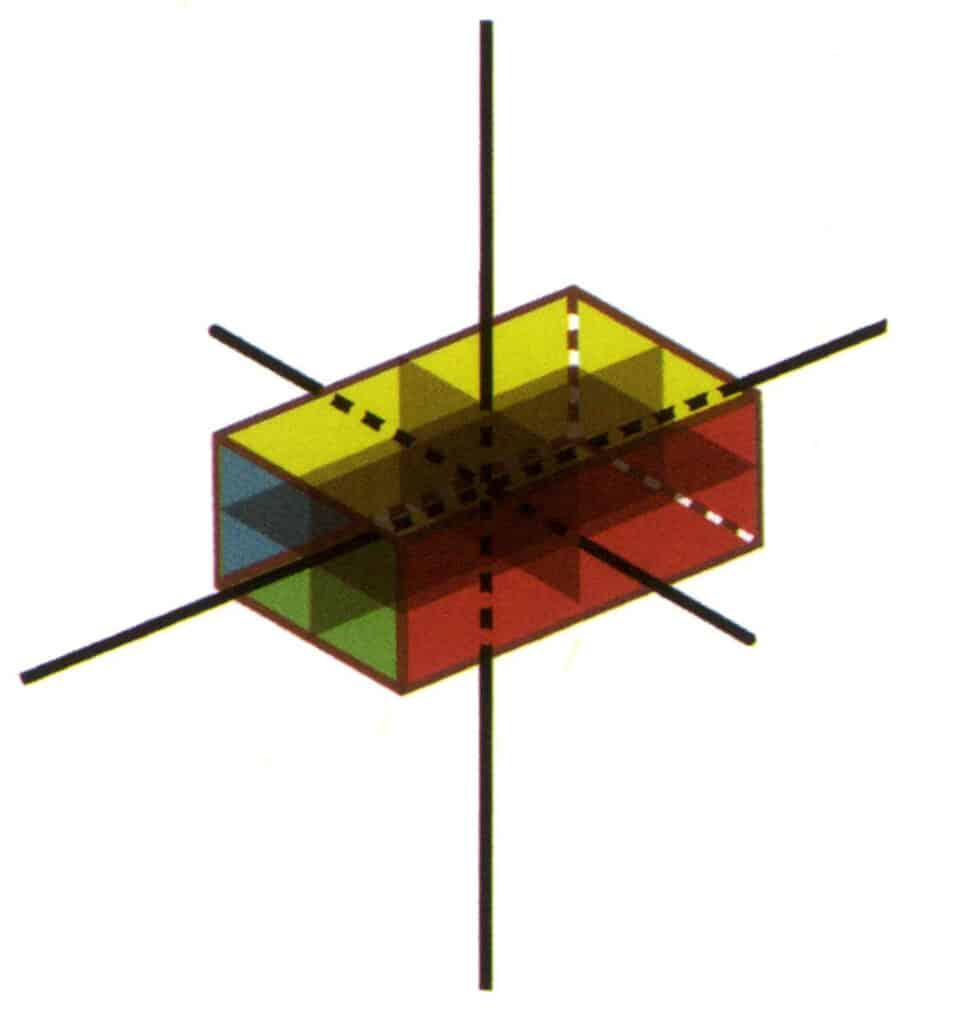
Figura 2-2-22 Grupo de puntos 3L²3P(cuboide rectangular con sección transversal rectangular)
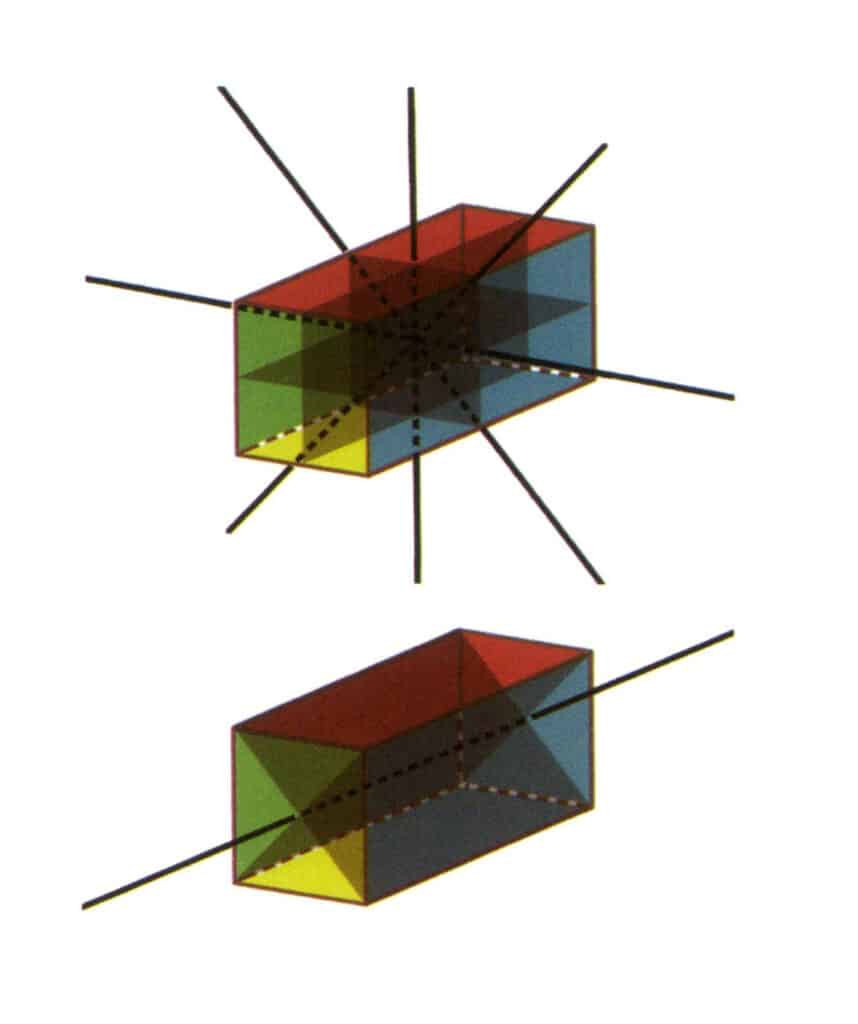
Figura 2-2-23 Grupo de puntos L⁴4L²5P(prisma rectangular de sección cuadrada), con cuatro segundos ejes y tres caras simétricas en la parte superior, y un cuarto eje y dos caras simétricas en la parte inferior.
3. Clasificación de los cristales
La simetría forma parte de la clasificación de los cristales. Es necesario introducir otro concepto, el eje cristalino, para describir la estructura cristalina de las gemas naturales y artificiales en un esquema de clasificación de cristales. El eje del cristal es una línea imaginaria que atraviesa la estructura cristalina e indica la dirección en la que se repiten los nodos de la red y la distancia relativa a la que se repiten los nodos a lo largo de esa dirección. El eje del cristal coincide con la normal del eje de simetría o el plano de simetría. Si no hay eje de simetría o plano de simetría, el eje cristalino puede seleccionarse en paralelo a la dirección del borde del cristal.
Basándose en los elementos de simetría y los ejes cristalinos, el sistema académico clasifica los cristales en tres familias cristalinas y siete sistemas cristalinos (Tabla 1).
Cuadro 1: Puntos clave para determinar las familias de cristales y los sistemas
| Familia de cristal | Cristal | Puntos clave para la determinación | Variedades comunes de piedras preciosas |
|---|---|---|---|
| Sistema de cristales de bajo nivel | Sistema triclínico | Sin segundo eje ni plano de simetría | Amazonita, rodonita, Turquesa |
| Sistema cristalino monoclínico | Sin ejes de orden superior, sin más de un eje secundario y plano de simetría | Jadeíta, diópsido, espodumeno, epidota | |
| Sistema cristalino ortorrómbico | No hay ejes de orden superior, más de un eje secundario o plano de simetría | Olivino, topacio, saualpita (incluida la tanzanita), cordierita, crisoberilo, enstatita | |
| Familia de cristales intermedios | Sistema cristalino tetragonal | 1 cuádruple Eje (puede representarse por L4) | Diamante |
| Sistema de cristales trigonales | 1 ejes trigonales (pueden representarse por L3) | Corindón, rubí, zafiro, turmalina , cristales de la familia del cuarzo (como el cristal, la amatista, el citrino, etc.), rodocrosita | |
| Sistema cristalino hexagonal | 1 eje hexagonal (puede representarse por L6) | Aguamarina, esmeralda y otras gemas de la familia de las berilitas, apatito | |
| Familia de cristales avanzados | Sistema isométrico de cristales | 4 ejes trigonales (pueden representarse por 4L3) | Diamante, granate, espinela, fluorita |
4. Características comunes de los cristales de las piedras preciosas
Las piedras preciosas más comunes son el diamante, la espinela, la fluorita, el granate, la berilita, el circón, el corindón, la turmalina, el cristal, el crisoberilo, el topacio, etc. Cada tipo de piedra preciosa tiene sus propias características cristalinas fijas.
Las gemas de la familia de los cristales de alto nivel son en su mayoría de hábito cristalino granular, y las variedades comunes suelen aparecer en formas cristalinas fijas (Tabla 2).
El hábito cristalino de las familias de cristales intermedios y bajos es columnar (Tabla 3).
Tabla 2: Características comunes de las familias de cristales de alto nivel
| Gemas tono Nombre | Clasificación de los cristales | Características importantes del cristal | |||
|---|---|---|---|---|---|
| Gemas tono Nombre | Clasificación de los cristales | Hábito de cristal | Formas cristalinas comunes | Formas comunes de gemelos | Patrones comunes de caras de cristal |
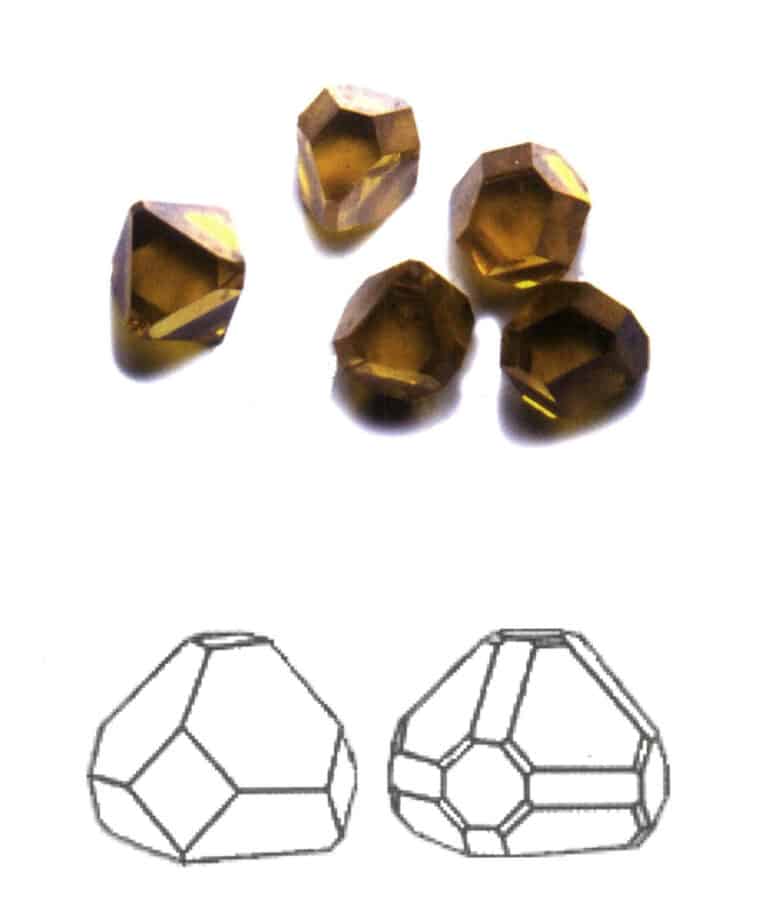
| Diamante | Sistema isométrico de cristales | Hábito cristalino granular (Figura 2-2-24), comúnmente visto en gránulos octaédricos. | El octaedro es una forma cristalina común, pero también pueden aparecer formas cristalinas más complejas, como los dodecaedros rómbicos, a menudo con caras cristalinas redondeadas, que pueden presentar una simetría triple. | Gemelo plano triangular, a veces sin ángulos cóncavos visibles (Figura 2-2-25) | La superficie muestra picaduras de grabado triangulares invertidas (Figuras 2-2-26, 2-2-27) y otros patrones de caras cristalinas (Figuras 2-2-28, 2-2-29). |
| Espinela | Hábito cristalino granular (Figura 2-2-30), comúnmente visto en gránulos octaédricos. | A menudo se producen en forma octaédrica, las caras del cristal pueden ser muy planas, pareciendo como si estuvieran pulidas (Figura 2-2-31) | Los cristales maclados son muy planos y se asemejan a una forma triangular con las esquinas cortadas (Figura 2¬2-32) | Punteaduras de grabado visibles en superficie, algunas de las cuales se asemejan a diamantes en forma de triángulo invertido (Figura 2-2-33). | |
| Fluorita | Hábito cristalino granular (Figura 2-2-34) | Formas cristalinas octaédricas y cúbicas (Figura 2-2-35) | Hermanamiento interpenetrante | Marcas de crecimiento de escalones cuadrados, en su mayoría con huecos de clivaje, bandas de color paralelas a las direcciones de las seis caras del cubo. | |
| Granate | Hábito cristalino granular, comúnmente visto en granos dodecaédricos rómbicos (Figura 2-2-36). | Dodecaedro rómbico o trapezoedro cuadrado | Raro | Bandas anulares concéntricas visibles con la misma forma que las caras del cristal (Figura2-2-37). | |
Figura 2-2-24 Hábitos del cristal de diamante
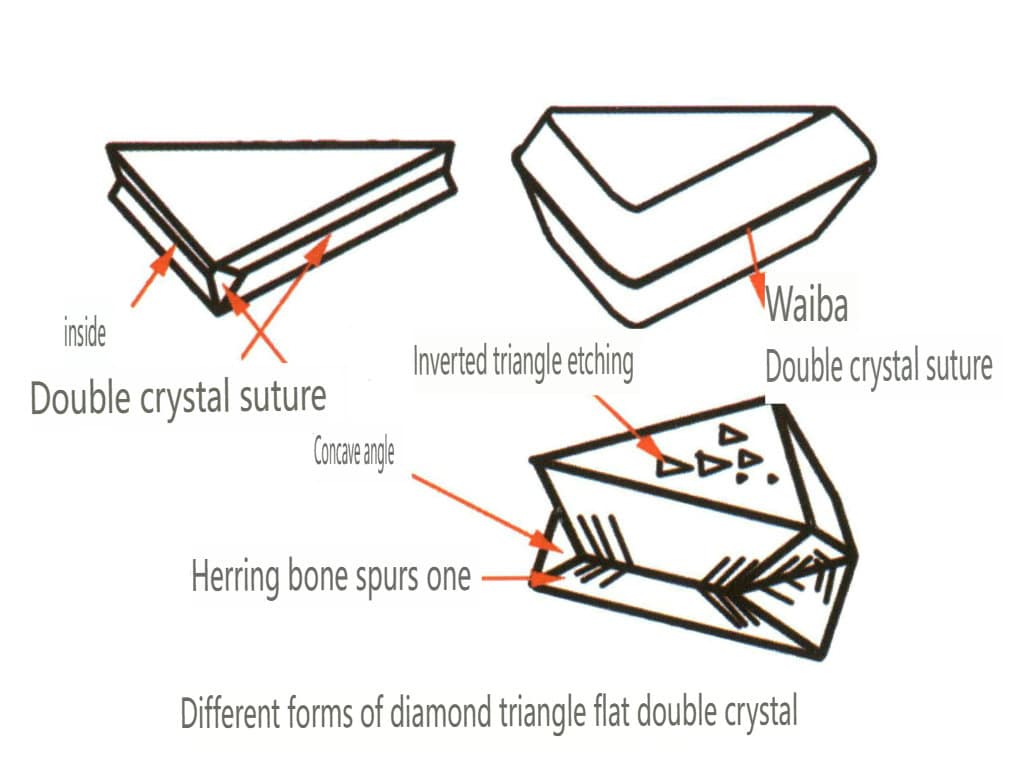
Figura 2-2-25 Hábito Gemelo Diamante
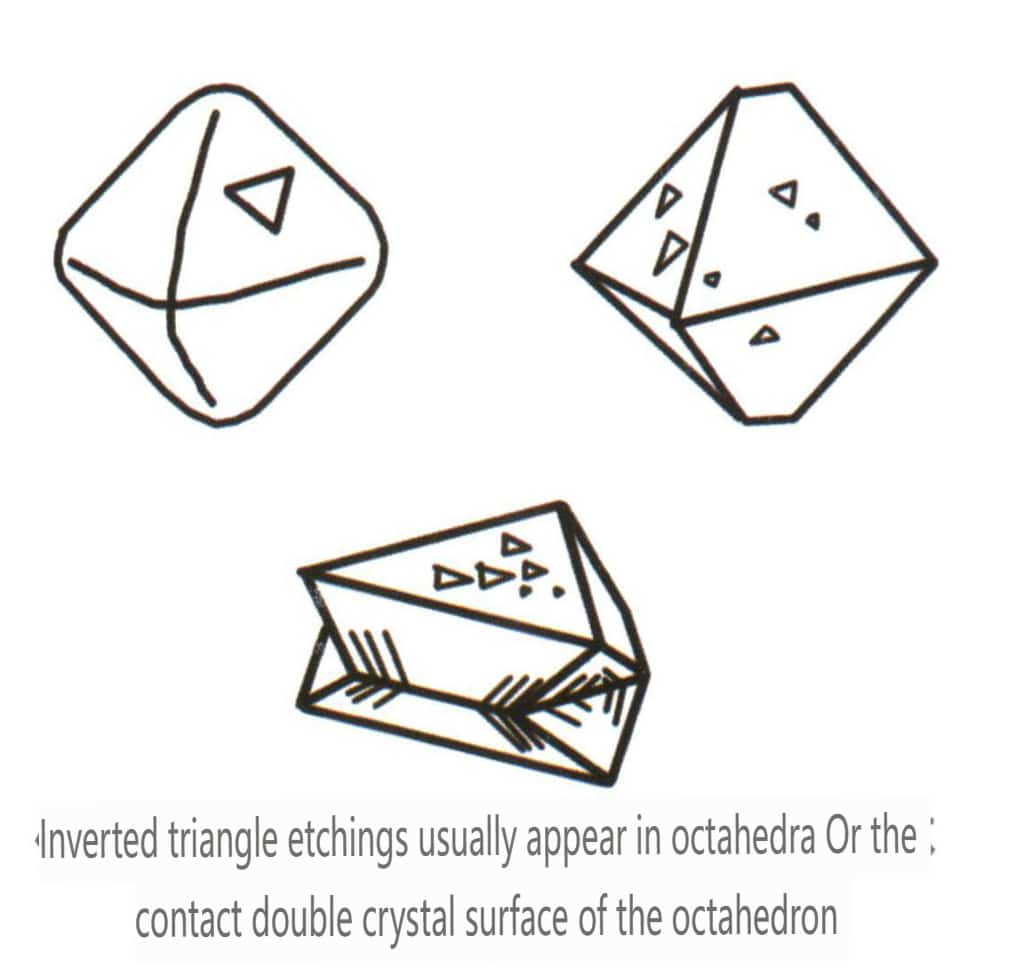
Figura 2-2-26 Figura de grabado de triángulo invertido de caras de cristal octaédrico de diamante

Figura 2-2-27 Figura de grabado triangular invertida en la superficie de un cristal octaédrico de diamante.
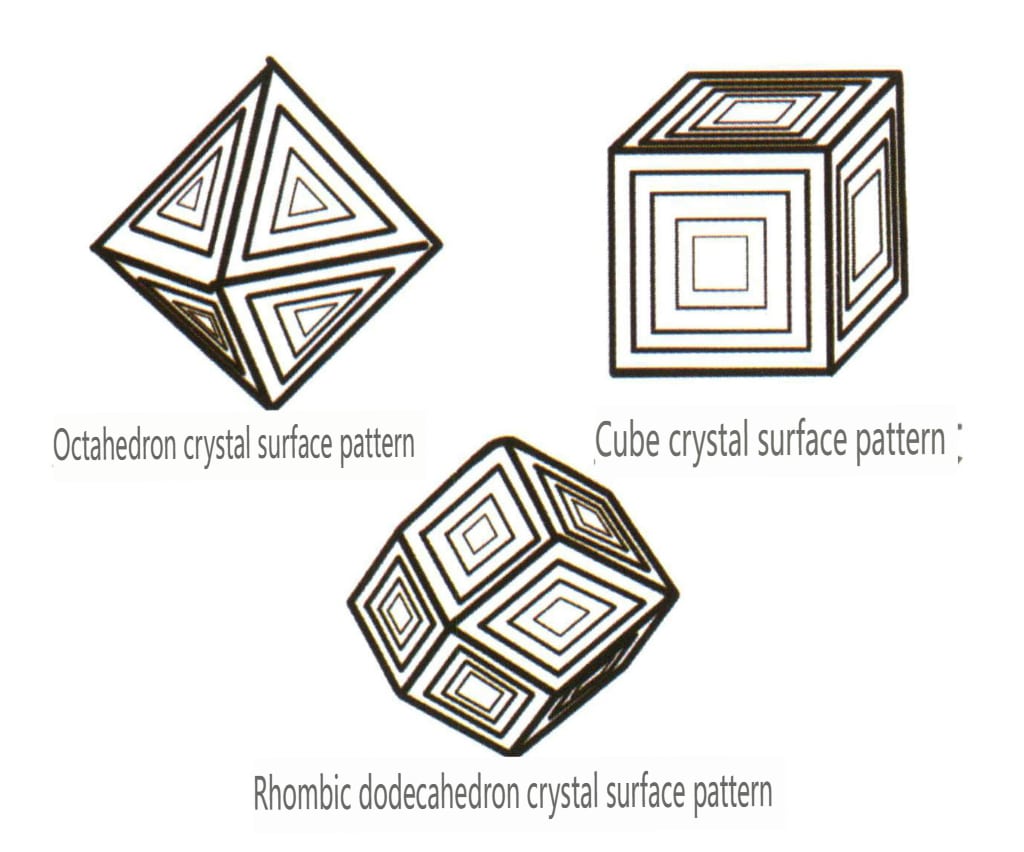
Figura 2-2-28 Figura de grabado de triángulo invertido de caras de cristal octaédrico de diamante

Figura 2-2-29 Figura de grabado triangular invertida en la superficie de un cristal octaédrico de diamante.
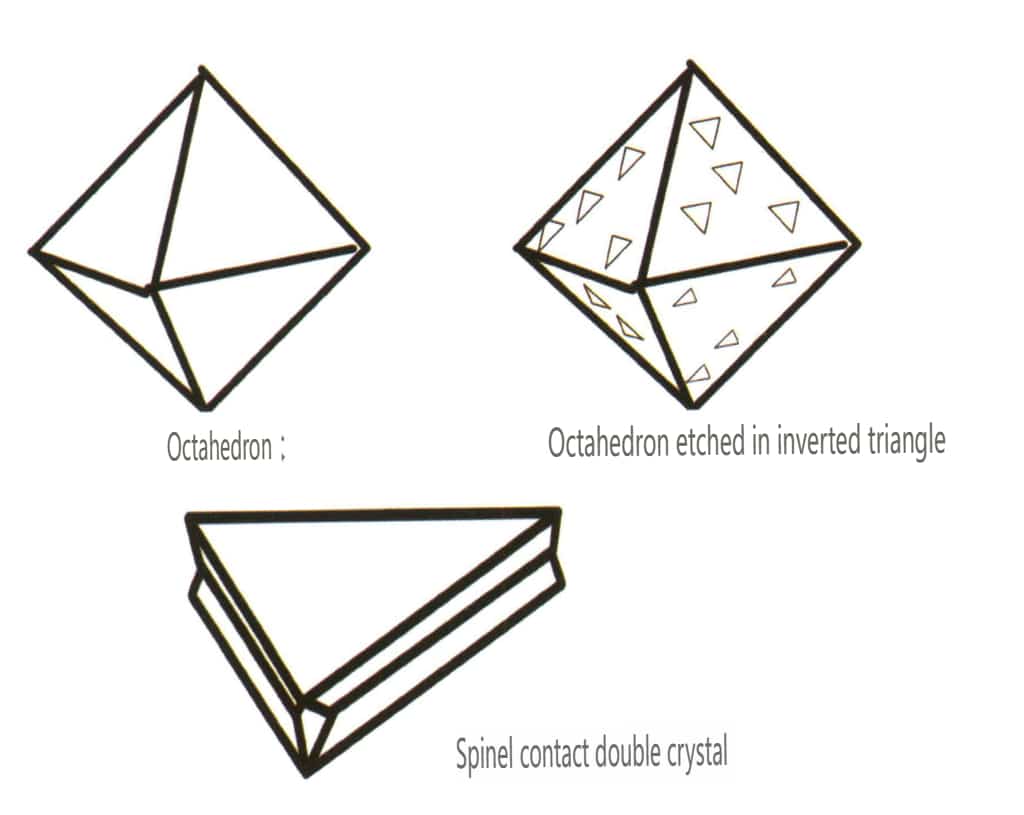
Figura 2-2-30 Hábito cristalino de la espinela

Figura 2-2-31 Formas comunes de los cristales de espinela

Figura 2-2-32 Hermanamiento por contacto de la espinela
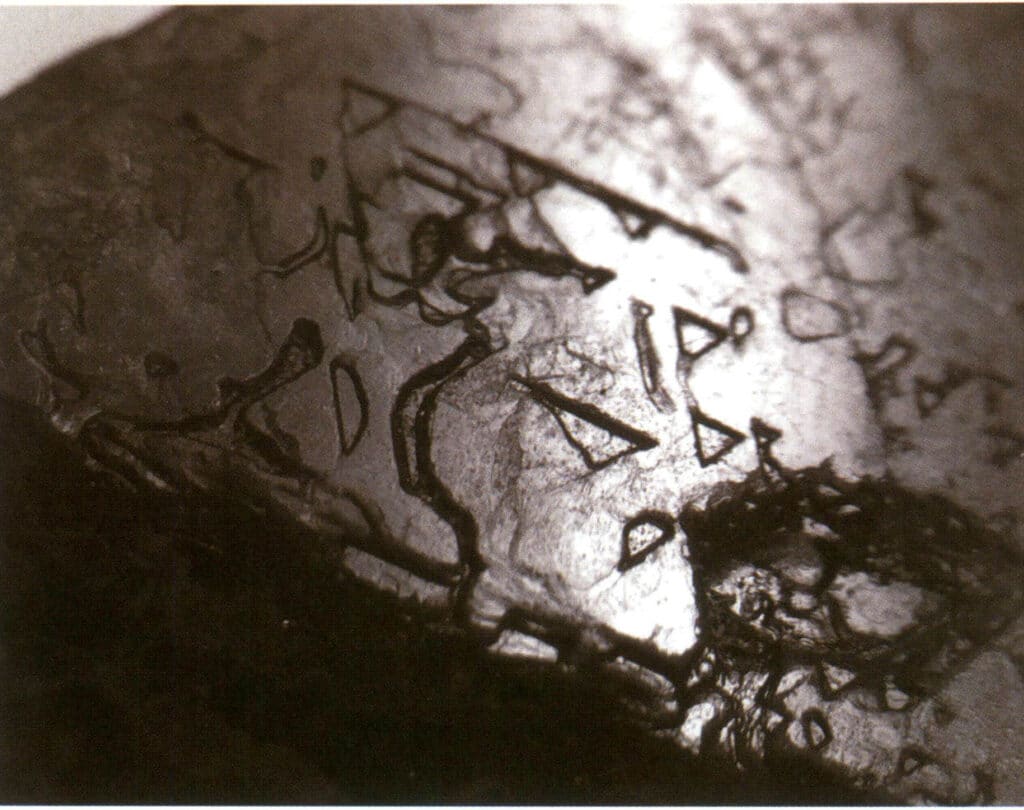
Figura 2-2-33 Patrón de grabado triangular invertido en la superficie de la espinela
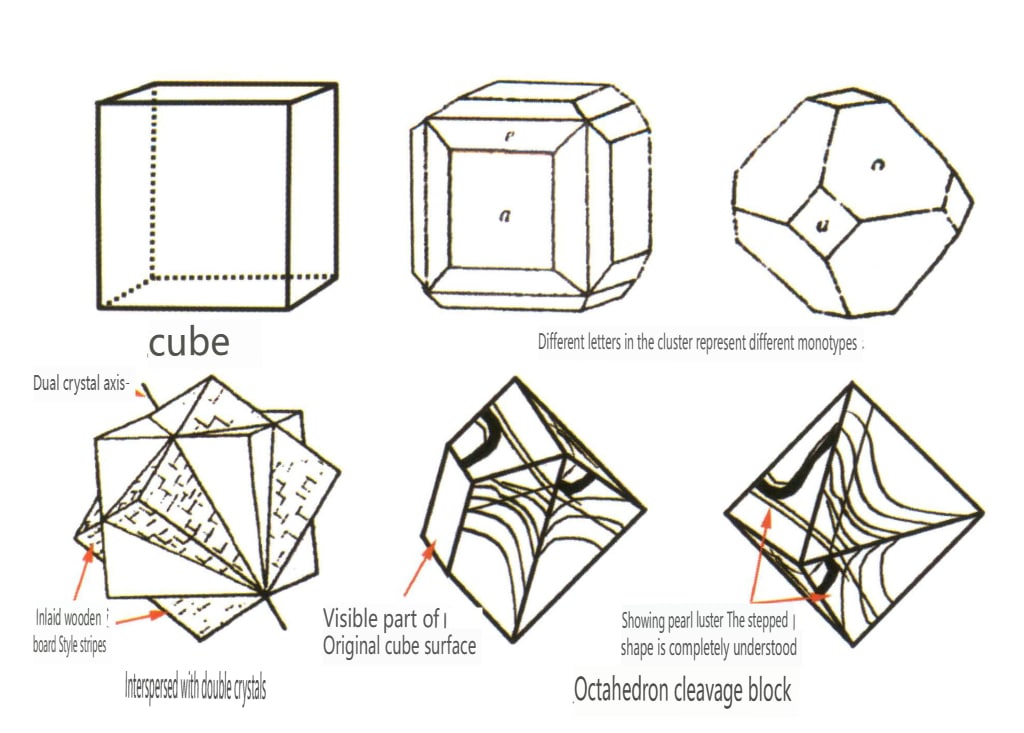
Figura 2-2-34 Hábitos cristalinos de la fluorita

Figura 2-2-35 Cristal de Fluorita
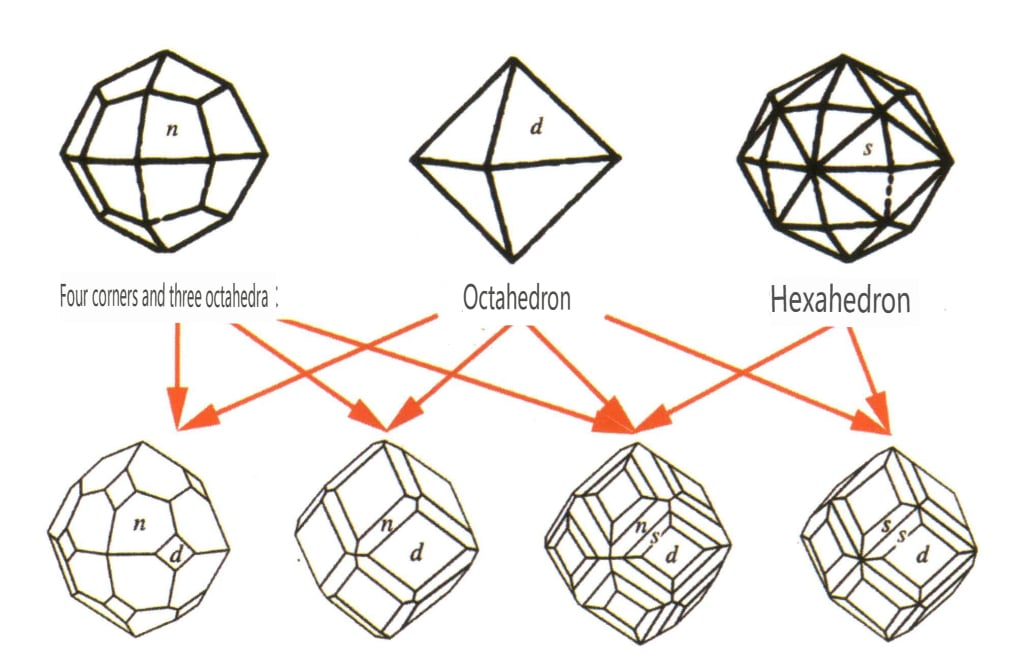
Figura 2-2-36 Hábito del cristal de granate

Figura 2-2-37 Bandas anulares concéntricas en la superficie de cristales de granate que tienen la misma forma que las caras del cristal.
Tabla 3: Características comunes de los cristales gema de las familias de cristales intermedios y bajos
| Gemas tono Nombre | Clasificación de los cristales | Características importantes del cristal | |||
|---|---|---|---|---|---|
| Gemas tono Nombre | Clasificación de los cristales | Hábito de cristal | Formas cristalinas comunes | Formas comunes de gemelos | Patrones comunes de caras de cristal |
| Beryl | Sistema cristalino hexagonal | Hábito cristalino columnar (Figura 2-2-38) | Forma cristalina columnar hexagonal (Figuras 2-2-39, 2-2-40) | Raro | Rayas longitudinales visibles |
| Piedra de plomo | Sistema cristalino tetragonal | Hábito cristalino columnar (Figura 2-2-41) | Columna cuadrada de sección cuadrada que aparece junto a un doble cono cuadrado (figura 2-2-42). | Cristales gemelos visibles en forma de rodilla | Sin patrones especiales |
| Corindón | Sistema cristalino trigonal | Hábito cristalino en forma de placa, hábito cristalino columnar (Figura 2-2-43) | Los rubíes suelen presentar una forma de prisma hexagonal (figura 2-2-44), mientras que los zafiros suelen exhibir una forma de cristal hexagonal bipiramidal en barril (figura 2-2-45) | Bicristales comúnmente vistos. | Estrías visibles. |
| Turmalina . | Hábito cristalino columnar (Figura 2-2-46) | Las caras del cristal en ambos extremos son diferentes, y la sección transversal es un triángulo esférico (Figura 2-2-47) | Raro | Rayas longitudinales visibles (Figura 2-2-48) | |
| Cuarzo (cuarzo cristalino) | Hábito cristalino columnar (Figura 2-2-49) | La sección transversal es hexagonal, las bipirámides hexagonales son raras (Figuras 2-2-50, 2-2-51), las monopirámides hexagonales son comunes | Contacto habitual con bicristales (también conocidos como bicristales japoneses) | Rayas horizontales comunes en superficies de cristal | |
| Crisoberilo | Sistema cristalino trigonal | Características de la cristalización columnar (Figura 2-¬2-52) | El monocristalino es raro | El tricristalino es común (Figura 2-2-53), los ángulos hexagonales y cóncavos pueden utilizarse como criterios de identificación | Las rayas del tricristalino pueden utilizarse como criterio de identificación |
| Topacio | Hábito cristalino columnar (Figura 2-2-54) | La sección transversal tiene forma de diamante y la parte superior suele tener aspecto envolvente (Figura 2-2-55). | Los bicristales son raros | Rayas longitudinales visibles | |
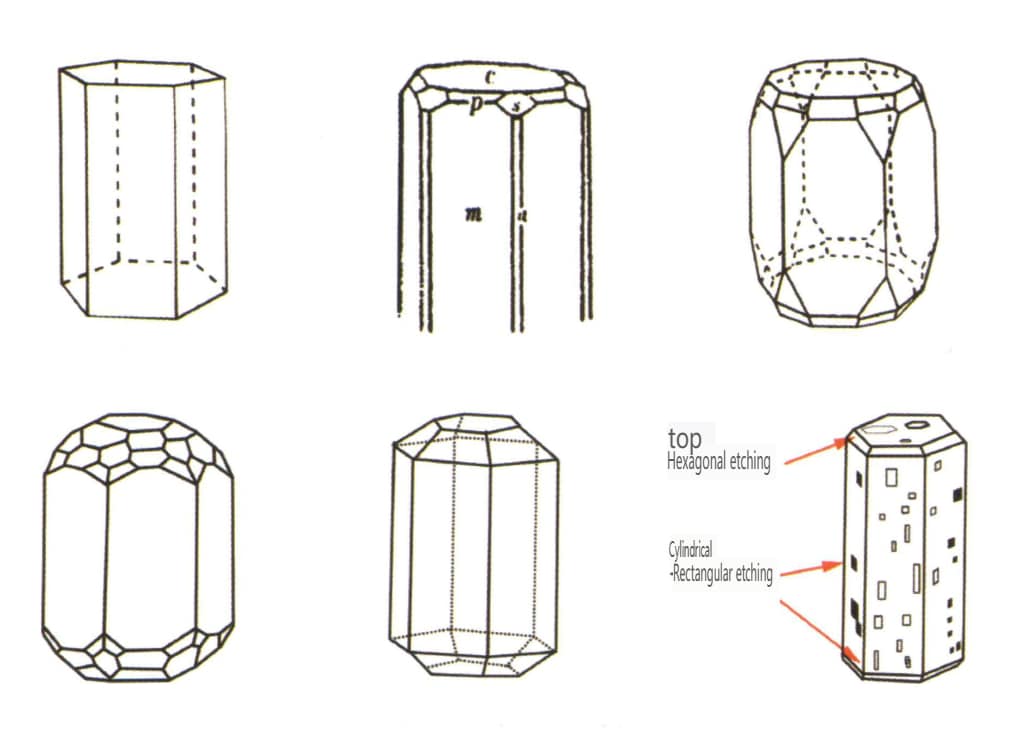
Figura 2-2-38 Hábito cristalino del berilo

Figura 2-2-39 Formas comunes de cristales de esmeralda

Figura 2-2-40 Formas comunes de los cristales de aguamarina
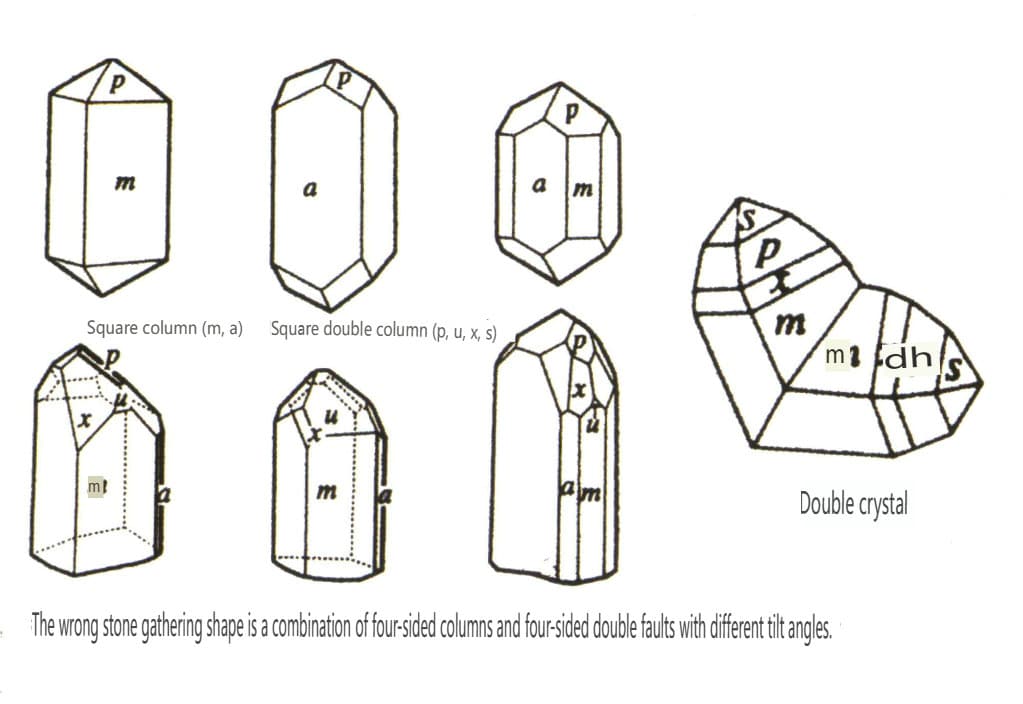
Figura 2-2-41 Hábitos cristalinos del circón

Figura 2-2-42 Cristal de circón
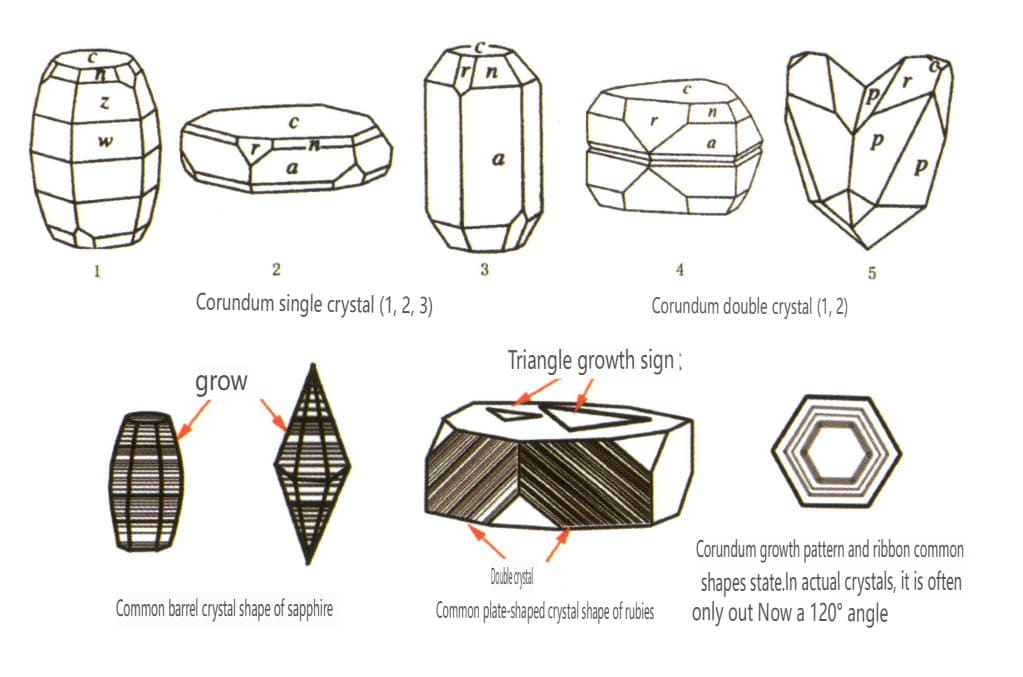
Figura 2-2-43 Hábito cristalino del corindón

Figura 2-2-44 Cristal de rubí

Figura 2-2-45 Gemelo mecánico del rubí
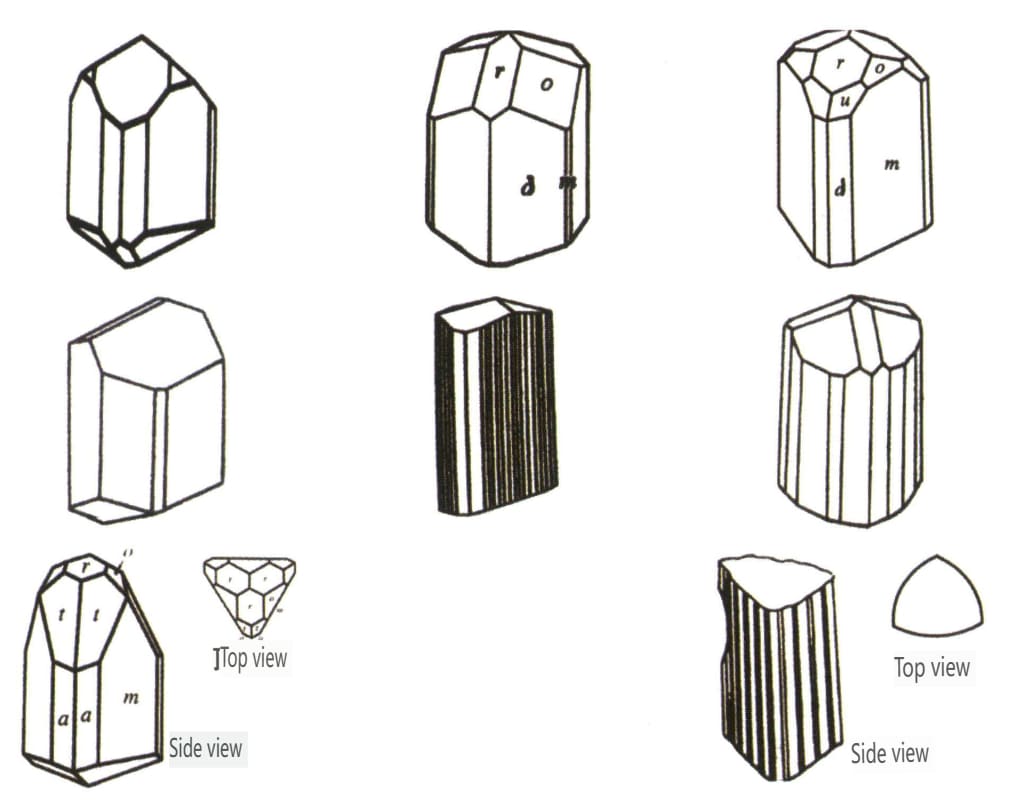
Figura 2-2-46 Hábitos del cristal de turmalina

Figura 2-2-47 Cristal de turmalina

Figura 2-2-48 Rayas longitudinales superficiales del cristal de turmalina
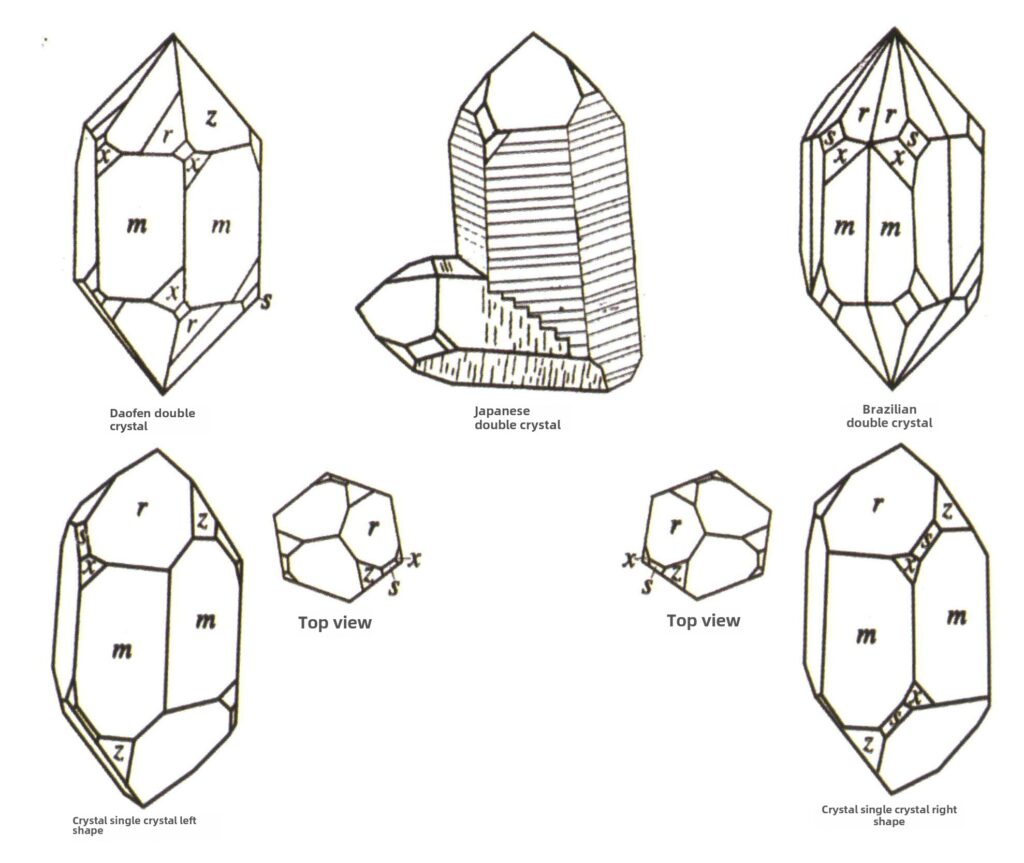
Figura 2-2-49 Hábitos de cristalización de los cristales

Figura 2-2-50 Cuerpo de cristal

Figura 2-2-51 Cuerpo del cristal
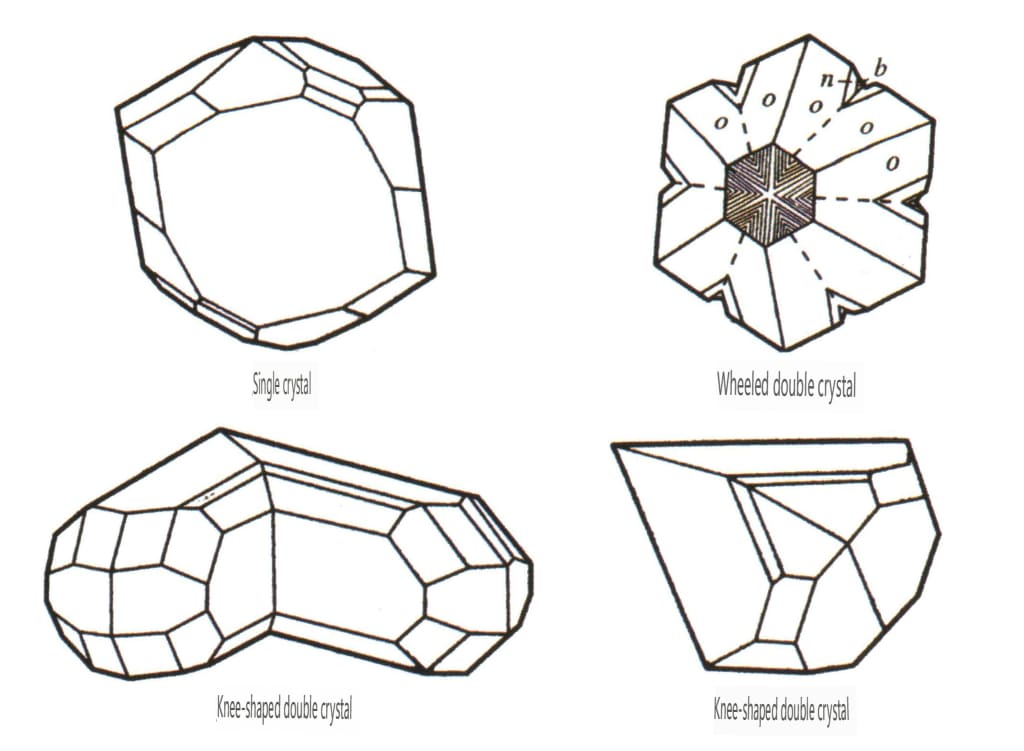
Figura 2-2-52 Hábito cristalino del crisoberilo

Figura 2-2-53 Cristal de crisoberilo
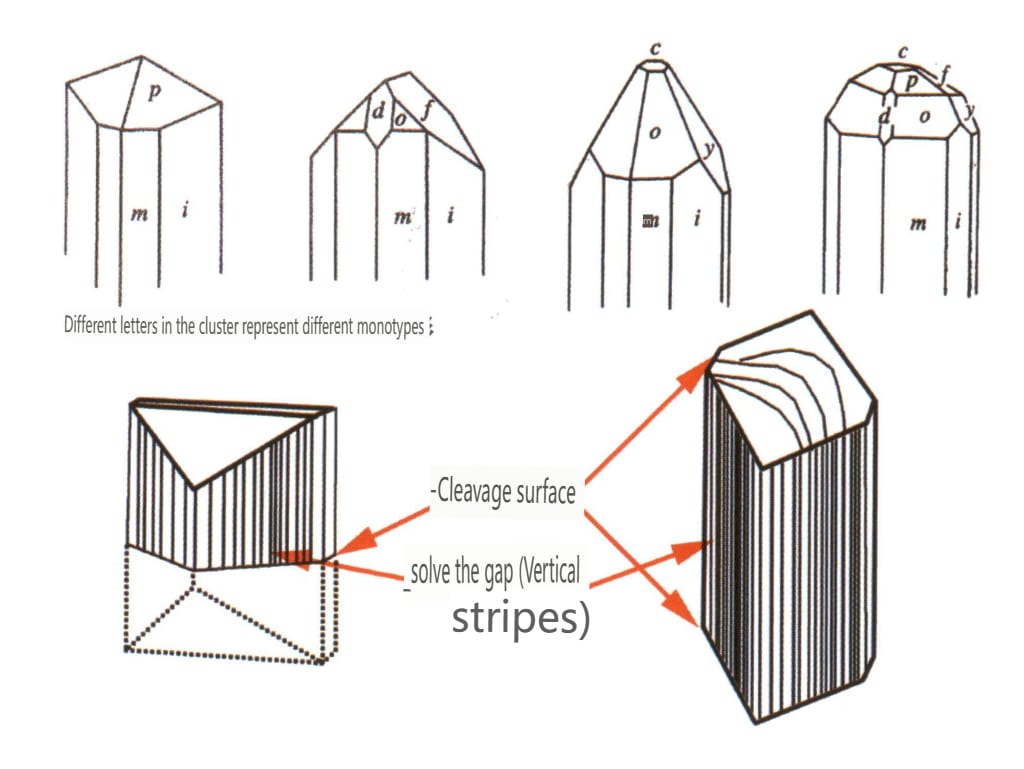
Figura 2-2-54 Hábitos cristalinos del topacio

Figura 2-2-55 Cristal topacio
Sección IV ¿Por qué los cristales de las piedras preciosas crecen de forma diferente?
Desde un punto de vista microscópico, el cristal de gema es un sólido compuesto por elementos de distintos tamaños dispuestos según distintas reglas. Desde un punto de vista macroscópico, muchas gemas presentan características de forma cristalina debido a sus diferentes composiciones. Sin embargo, existen algunos casos especiales, como los heteromórficos. Para entender mejor por qué los cristales de las gemas tienen un aspecto diferente, aquí presentaremos cinco aspectos: heteromorfía, isomorfismo, entremezcla mecánica molecular, agua en los minerales gema y composición química de las gemas.
1. Heteromórfico
Aunque algunos minerales tienen la misma composición química, presentan estructuras cristalinas (la disposición de los elementos en el espacio tridimensional) muy diferentes y muestran diferencias significativas en sus propiedades físicas y químicas (Tabla 4). Nos referimos a este fenómeno como heteromorfismo, por ejemplo, el diamante y el grafito (Figura 2-2-56).
El cuarzo común presenta el fenómeno del heteromorfismo. La silimanita, la andalucita y la cianita son un grupo de variantes del heteromorfismo.
La transformación del heteromorfismo se produce en condiciones de estado sólido. Durante el proceso de transformación estructural, puede desarrollarse presión dentro del cristal, lo que a menudo conduce a la formación de maclas dentro del cristal.

Tabla 4: Comparación de las propiedades del diamante y el grafito
| Mineral | Diamante | Grafito |
|---|---|---|
| Componentes | Carbono (C) | Carbono (C) |
| Condiciones de formación | Alta temperatura y alta presión | Alta temperatura |
| Sistema cristalino, hábito | Sistema cristalino isométrico, octaedro, dodecaedro rómbico | Sistema cristalino hexagonal, estratificado |
| Color | Incoloro, amarillo, azul, rosa, verde, etc. | Negro |
| Lustre | Brillo adamantino | Brillo metálico |
| Transparencia | De transparente a opaco | Opaco |
| Índice de refracción | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Propiedades mecánicas | Hendidura octaédrica moderada, dureza 10, densidad 3.52 | Un conjunto de hendidura perfecta, dureza 1, densidad 2.10 |
| Otras propiedades | Excelente conductividad térmica; salvo los diamantes azules naturales que son semiconductores, los diamantes de otros colores son aislantes. | Conductividad térmica moderada, buena conductividad eléctrica |
2. Isomorfismo
El isomorfismo se refiere al fenómeno por el que algunas partículas de la estructura reticular se sustituyen por otras partículas con propiedades similares, lo que provoca ligeros cambios en el parámetro reticular y en las propiedades físicas y químicas. En cambio, la estructura cristalina permanece fundamentalmente inalterada. Puede entenderse como la sustitución de los elementos del cristal de la gema por otros elementos. En cambio, el patrón de repetición de los elementos del cristal de la piedra preciosa sigue siendo el mismo, con ligeras desviaciones en las distancias entre los átomos. Aun así, las propiedades físico-químicas del cristal de gema sufren ligeros cambios (Figura 2-2-57 a Figura 2-2-58).
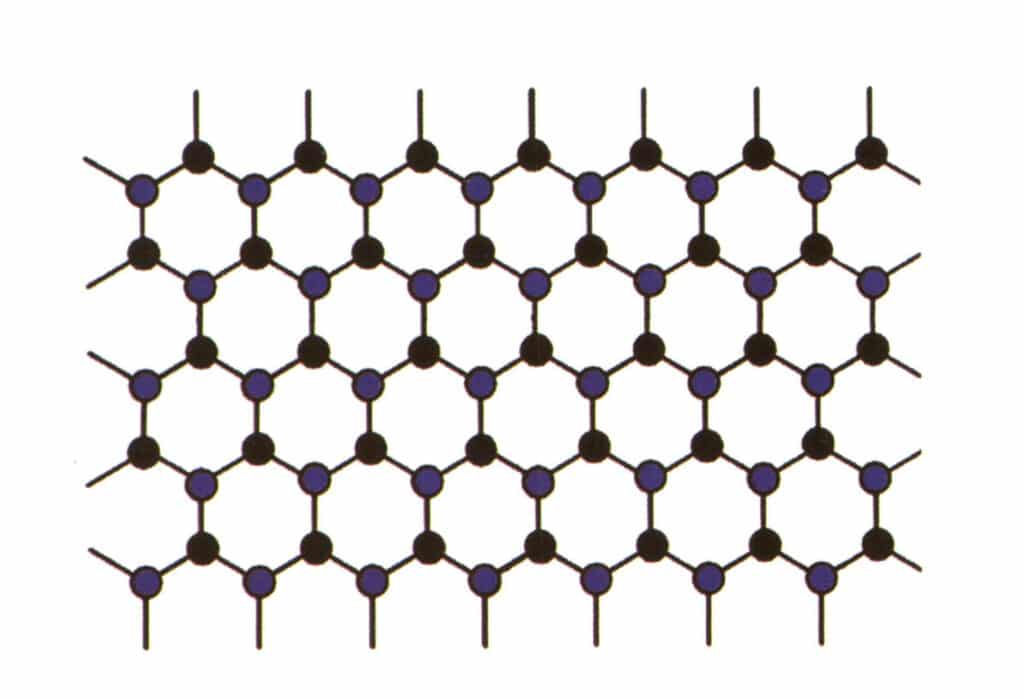
Figura 2-2-57 Diagrama de simulación de la estructura cristalina (el azul y el negro indican las partículas del elemento)
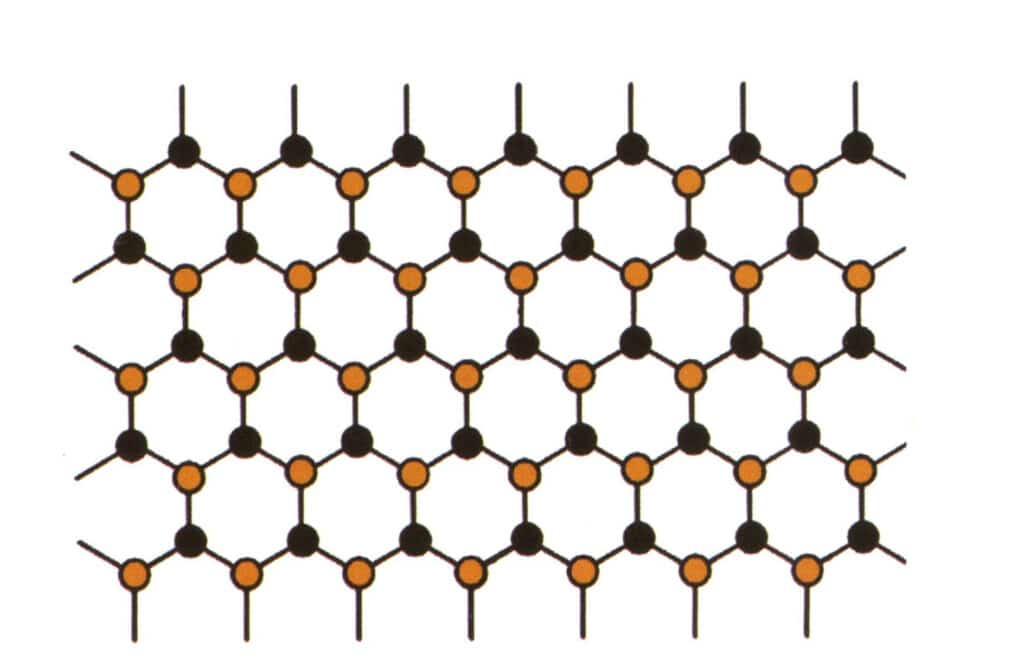
Figura 2-2-58 Diagrama de simulación de la estructura cristalina (el negro representa las partículas elementales, el amarillo representa las nuevas partículas elementales que sustituyen parcialmente a las partículas elementales azules, el amarillo puede no sustituir completamente a todas las partículas azules).
El concepto de isomorfismo puede explicar por qué las piedras preciosas de la misma familia pueden tener tantos colores y por qué hay variaciones en el índice de refracción y la densidad entre las piedras preciosas de la misma familia.
Una familia puede entenderse como un tipo de piedra preciosa en la que los patrones de repetición de los elementos cristalinos son los mismos, pero las formas físicas y químicas son ligeramente diferentes. Por ejemplo, la familia del corindón incluye dos miembros, el rubí y el zafiro, mientras que la familia del berilo incluye las variedades de esmeralda, aguamarina y morganita.
(1) Olivino
La composición química del olivino es (Mg,Fe)₂SiO₄. En su composición se produce la sustitución isomórfica completa de los elementos Fe y Mg. A medida que aumenta el contenido de Fe en el olivino, el color del olivino se vuelve más oscuro, aumenta el índice de refracción y también aumenta la densidad.
(2) Corindón
El corindón puro sin impurezas (Al₂O₃) es incoloro, y cuando el Cr sustituye al Al, la gema presenta un tono entre rojo rosado y rojo, conocido como rubí. El resto de colores se denominan zafiro, como el zafiro amarillo anaranjado o el zafiro incoloro. El comúnmente denominado zafiro es concretamente el zafiro azul, en el que el Fe y el Ti sustituyen al Al. Cuanto mayor sea el contenido de los elementos colorantes en la gema sustituta, más intenso será el color de la gema; por el contrario, cuanto menor sea el contenido, más claro será el color.
(3) Turmalina
Se refiere al mismo tipo de gema que la turmalina, siendo turmalina su nombre mineralógico y turmalina su nombre gemológico. La composición química del berilo es (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), donde R es principalmente Mg , Fe , Cr , Li, Al , Mn, y los elementos de R pueden sustituirse total o parcialmente entre sí, lo que da lugar a una amplísima variedad de colores para la turmalina. Por ejemplo, cuando R es principalmente Fe, el berilo presenta un color azul intenso o incluso negro; cuando R es principalmente Mg, el berilo presenta un color entre amarillo y marrón; cuando R es principalmente Li o Mn, el berilo presenta un color rosa o azul claro; cuando R es principalmente Cr, la turmalina presenta un verde intenso.
De lo anterior se desprende que la sustitución de elementos con propiedades similares da lugar a colores más bellos y brillantes en las gemas.
3. Entremezclado mecánico molecular
A veces, ciertos elementos entran a la fuerza entre los elementos principales de piedras preciosas dispuestas regularmente. Sin embargo, la baja proporción de los elementos que entran no altera el patrón repetitivo de los elementos principales de la piedra preciosa, sólo causa deformación (figura 2-2-59). Esta situación se denomina entremezcla mecánica molecular, como la entremezcla mecánica molecular del nitrógeno y el boro en los diamantes, que produce diamantes azules, rosas y amarillos, de gran valor.
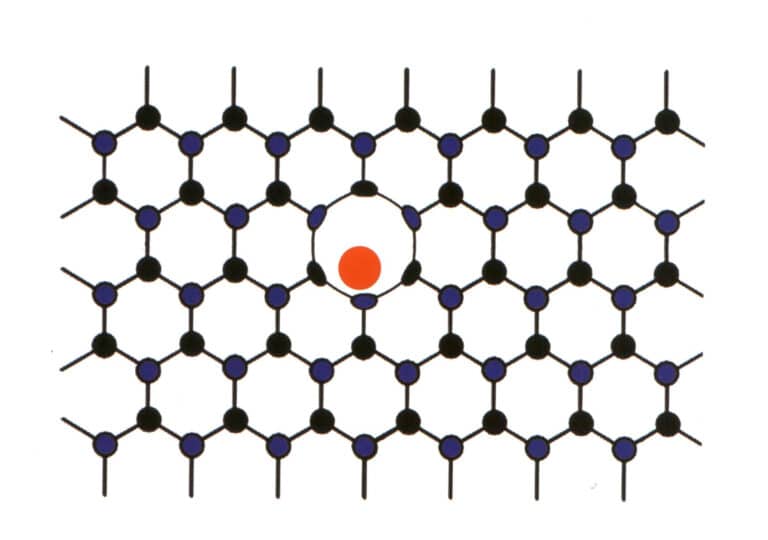
4. El agua en los minerales gema
Algunas piedras preciosas contienen agua, que es un componente importante de los minerales gema y está estrechamente relacionado con las propiedades de las gemas. En función de la forma de agua presente en los minerales gema y de su papel en la estructura cristalina, el agua de las piedras preciosas puede dividirse en dos categorías: una es el agua de absorción, que no está relacionada con la estructura cristalina, y la otra es el agua que participa en la estructura cristalina del mineral, incluyendo el agua de cristalización, el agua zeolítica, el agua entre capas y el agua de constitución. El agua estrechamente relacionada con las piedras preciosas incluye el agua de absorción, el agua de cristalización y el agua de constitución.
Uno es el agua de absorción, tales como ópalo (composición química es SiO₂ - nH₂O, n representa el número de H₂O, el contenido es variable) en la molécula de agua, que es una molécula de agua neutra adsorbido mecánicamente para partículas minerales o superficies de fractura. Cuando la temperatura alcanza 100 ~ 110 ° grados bajo presión normal, las moléculas de agua pueden escapar y no dañar la estructura de la red cristalina, por lo que para evitar el ópalo en el mostrador en un largo tiempo de fuerte exposición a la luz grieta seca, debe poner una taza de agua en el mostrador.
En segundo lugar está el agua de cristalización, como el agua de cristalización de la turquesa [la composición química es CuAl₆(PO₄)₄(OH)₈-4H₂O, donde el contenido de H₂O puede alcanzar 19,47% ]. Esta molécula de agua neutra existe en posiciones fijas dentro de la red y sirve como unidad estructural, formando parte de la composición química del mineral. La temperatura a la que escapa el agua de cristalización no suele superar los 600℃ y suele escapar a los 100 -200℃. Cuando una piedra preciosa pierde su agua de cristalización, su estructura cristalina se daña, formándose una nueva estructura.
En tercer lugar está el agua de constitución, también conocida como agua combinada, que participa en la red mineral en forma de OH-, H⁺, H₃O⁺ plasma, siendo el OH- el más común. El agua de constitución forma parte de la composición química del mineral, ocupando posiciones fijas en la estructura reticular con una proporción definida en su composición. El agua estructural requiere una temperatura más alta para escapar y dañar su estructura, normalmente alrededor de 600 -1000℃. Cuando una piedra preciosa pierde agua estructural, se destruye su estructura cristalina. Muchas piedras preciosas contienen agua de constitución, como la turmalina[composición química es ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), donde R incluye principalmente Mg , Fe , Cr, Li, Al, Mn, etc., y los elementos de R pueden sustituirse total o parcialmente entre sí], y el topacio [la composición química es Al₂SiO₄( F, OH) ₂ ].
5. La composición química de las piedras preciosas
Las gemas, como otras sustancias, están compuestas de elementos químicos. Cada tipo de gema tiene su composición química específica y un cierto rango de variación, que determina las diversas características y propiedades de la gema. Las gemas pertenecen a los minerales y las rocas, y la clasificación de la composición química de una gema puede remontarse a la composición química de los minerales.
En la actualidad, los principales métodos de clasificación de minerales incluyen la clasificación por composición química (sistema Dana), la clasificación geoquímica, la clasificación genética, la clasificación por aplicación y la clasificación cristalino-química. El método ampliamente adoptado es la clasificación química basada en la composición química y la estructura cristalina (sistema Hugo Strunz) (Tabla 5).
Cuadro 5: Sistema de clasificación química de los cristales minerales
| Secuencia de niveles | Base de la división | Ejemplo |
|---|---|---|
| Categoría principal | Tipo de compuesto | Sal que contiene oxígeno Categoría principal |
| Clase | Tipos de aniones o aniones complejos | Clase de silicato |
| (Subcategoría) | Estructura del complejo aniónico | Subclase de silicatos de estructura |
| Grupo | Tipos de estructuras cristalinas y propiedades iónicas | Grupo del corindón, grupo del berilo, grupo del granate |
| (Subgrupo) | Tipos de cationes | Subgrupo de feldespatos alcalinos |
| Especie | Determinada estructura cristalina y composición química | Ortoclasa KAlSi3O8 |
| (Subespecie) | Misma estructura cristalina, diferente composición o propiedades, morfología | Adularia KAlSi3O8 |