¿Por qué las piedras preciosas tienen varios colores?
Introducción a la teoría del campo cristalino, la teoría de los orbitales moleculares y la teoría de bandas de energía
Los colores de las piedras preciosas son ricos y variados, y poseen un encanto único que siempre ha gustado a la gente. La calidad de las piedras preciosas depende en gran medida de su color. El color de una gema es un indicador importante en la evaluación de las piedras preciosas, y la mayoría de los tratamientos de optimización para las piedras preciosas implican cambiar o mejorar su color. Por lo tanto, comprender las causas de la coloración de las piedras preciosas es un requisito previo crucial para su tratamiento de optimización. Sólo dominando cómo adquieren su color las piedras preciosas se puede determinar si una piedra preciosa puede ser optimizada, qué esquema de optimización adoptar y qué plan experimental establecer. Existen cinco teorías comunes sobre la coloración de las piedras preciosas: la teoría de la mineralogía clásica, la teoría del campo cristalino, la teoría de los orbitales moleculares, la teoría de las bandas de energía y los efectos ópticos físicos. Estas teorías constituyen las teorías de coloración de las piedras preciosas naturales comunes, y lo que sigue es una breve introducción a estas cinco teorías de coloración.
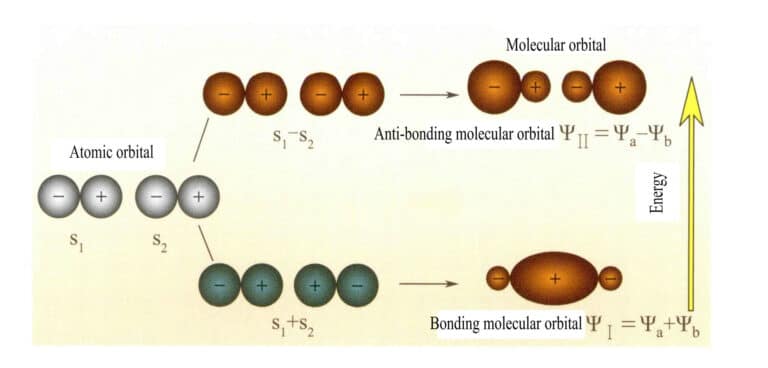
Orbitales moleculares formados por dos orbitales atómicos s
Índice
Sección I Teoría del campo cristalino
En la década de 1930, los científicos propusieron la teoría del campo cristalino para explicar las propiedades de los cristales. La teoría del campo cristalino es una teoría que estudia los enlaces químicos de los elementos de transición (complejos). Explica las propiedades físicas y químicas de los elementos de transición y los lantánidos combinando algunos puntos de vista de la teoría electrostática, la mecánica cuántica y la teoría de grupos (la teoría que estudia la simetría de la materia), centrándose en la influencia de los ligandos sobre los orbitales d y f de los iones centrales. En la década de 1950, se aplicó la teoría del campo cristalino a los complejos y se propuso la teoría del campo de ligandos. La teoría del campo del ligando es un avance de la teoría del campo cristalino; considera tanto la influencia del campo eléctrico del ligando sobre el ion central como el efecto de relleno de los electrones del ligando sobre el ion central, lo que la hace más completa que la teoría del campo cristalino. Sin embargo, no existe ninguna diferencia esencial entre ambas, y generalmente no se distinguen en el estudio de los minerales inorgánicos.
1. Conceptos básicos de la teoría de los campos de cristal
Los iones de los metales de transición se encuentran en el campo cristalino de los aniones o moléculas dipolares que los rodean. La teoría del campo cristalino es un modelo electrostático que considera el cristal como una interacción electrostática entre iones positivos y negativos, donde el catión cargado positivamente se denomina ion central y el anión cargado negativamente se denomina ligando.
La aplicación de la teoría del campo cristalino para explicar el color de los minerales gema afecta principalmente a los electrones d o a la energía de los electrones f de los iones de los elementos de transición. Por ejemplo, los orbitales d son de cinco tipos: dxy, dxz, dyzd y d . Estos cinco orbitales d tienen diferentes distribuciones espaciales en el estado libre del ion, pero tienen la misma energía. Sin embargo, sufren cambios significativos bajo la influencia del campo del ligando. Los cinco orbitales d de energía degenerada del átomo central se dividen bajo la influencia del campo eléctrico negativo formado por los ligandos circundantes. Algunos orbitales d aumentan su energía, mientras que otros la disminuyen. Debido a la división de los niveles de energía de los orbitales d, los electrones de los orbitales d del átomo central se reorganizarán, ocupando preferentemente los orbitales de menor energía, reduciendo así la energía total del sistema y haciendo que el complejo sea más estable.
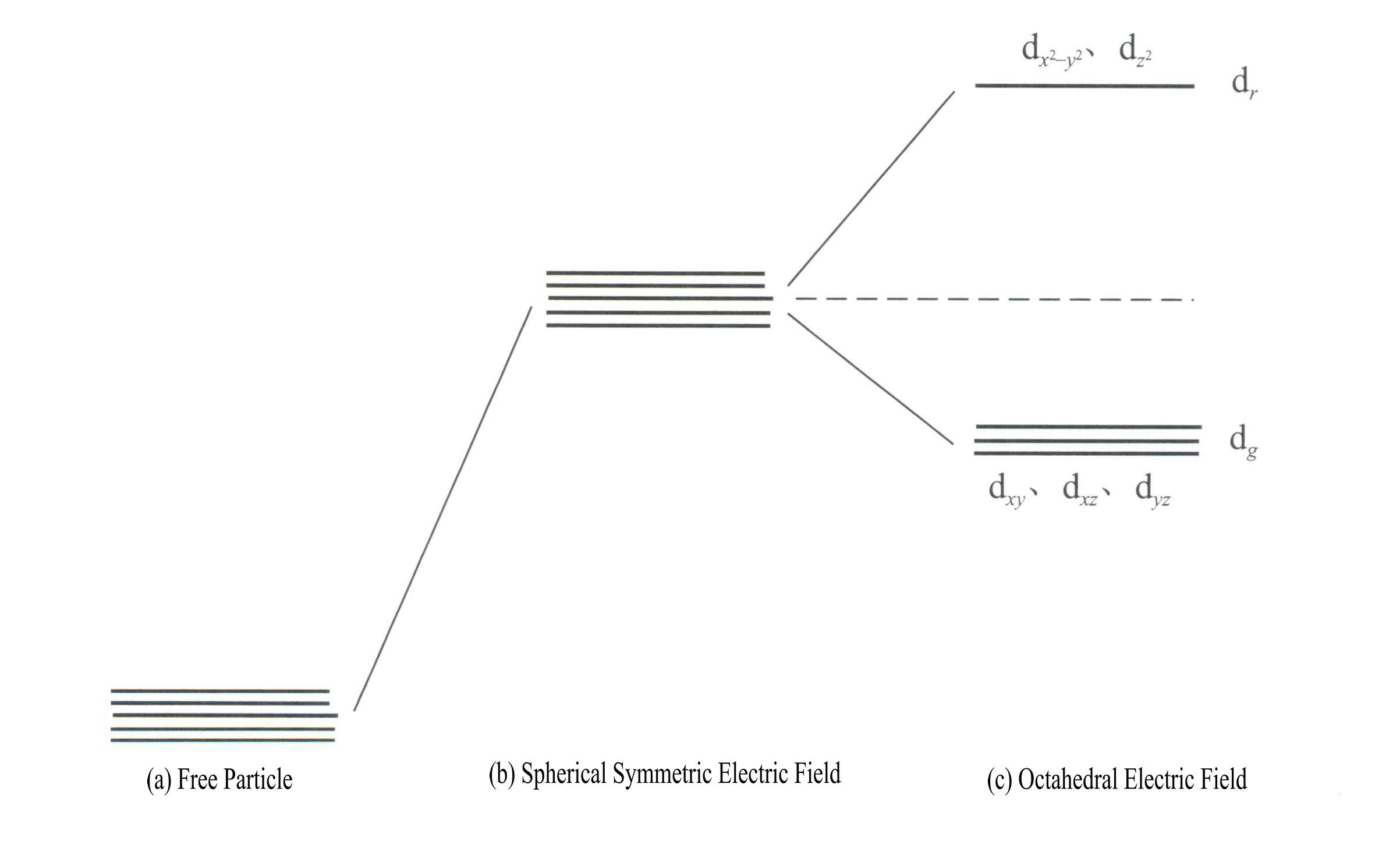
La energía de los orbitales d es la misma cuando no hay campo eléctrico [Figura 3-19 (a)]; bajo un campo electrostático esféricamente simétrico, los orbitales d tienen mayor energía pero no se dividen [Figura 3-19 (b)]; cuando el campo del ligando es octaédrico, se divide en dr y dg. De ellos, dr se componen de orbitales d y d , de mayor energía; los de menor energía dg se componen de orbitales dxy, dxz, dyz.
Los iones de los metales de transición se encuentran en el campo cristalino de los aniones o moléculas dipolares que los rodean. La teoría del campo cristalino es un modelo electrostático que considera el cristal como una interacción electrostática entre iones positivos y negativos, donde el catión cargado positivamente se denomina ion central y el anión cargado negativamente se denomina ligando.
La aplicación de la teoría del campo cristalino para explicar el color de los minerales gema afecta principalmente a los electrones d o a la energía de los electrones f de los iones de los elementos de transición. Por ejemplo, los orbitales d son de cinco tipos: dxy, dxz, dyzd y d . Estos cinco orbitales d tienen diferentes distribuciones espaciales en el estado libre del ion, pero tienen la misma energía. Sin embargo, sufren cambios significativos bajo la influencia del campo del ligando. Los cinco orbitales d de energía degenerada del átomo central se dividen bajo la influencia del campo eléctrico negativo formado por los ligandos circundantes. Algunos orbitales d aumentan su energía, mientras que otros la disminuyen. Debido a la división de los niveles de energía de los orbitales d, los electrones de los orbitales d del átomo central se reorganizarán, ocupando preferentemente los orbitales de menor energía, reduciendo así la energía total del sistema y haciendo que el complejo sea más estable.
La energía de los orbitales d es la misma cuando no hay campo eléctrico [Figura 3-19 (a)]; bajo un campo electrostático esféricamente simétrico, los orbitales d tienen mayor energía pero no se dividen [Figura 3-19 (b)]; cuando el campo del ligando es octaédrico, se divide en dr y dg. De ellos, dr se componen de orbitales dx2– y2 y dz2
con mayor energía; el dg se componen de orbitales dxy, dxz, dyz. [Figura 3-19 (c)]
La diferencia entre los niveles de energía más alto y más bajo después de la división del orbital d se denomina energía de separación △ . Las energías de separación producidas por diferentes configuraciones de campos de ligandos no son iguales (Figura 3-20). Su orden energético es:
Campo cuadrado > Campo octaédrico > Campo tetraédrico

Incluso para campos de la misma configuración, también pueden diferir debido a las diferencias en ligandos e iones centrales; cuanto mayor sea, más estable será el cristal. Los tres factores siguientes determinan principalmente el tamaño de la energía de separación del cristal:
(1) Cristales formados por el mismo elemento de transición; cuando los ligandos son iguales, cuanto mayor es la carga del ion central, mayor es la energía de separación △ . Cuanto mayor es la carga positiva del ion central, mayor es la atracción hacia los ligandos, lo que da lugar a una menor distancia entre el ion central y el núcleo del ligando, y cuanto mayor es la fuerza de repulsión del campo cristalino generada por los ligandos sobre los electrones, mayor es la energía de separación △ .
(2) Para cristales formados por diferentes iones con la misma carga positiva y los mismos ligandos, cuanto mayor sea el radio del ion central, más alejados estarán los orbitales d del núcleo y mayor será la energía de separación △ .
(3) Para cristales formados por el mismo ion central y diferentes ligandos, la energía de separación varía debido a las diferentes intensidades del campo cristalino del ligando. Diferentes ligandos tienen diferentes intensidades de campo, y la energía de separación △ varía con la intensidad de campo del ligando.
La energía de separación se utiliza para explicar cualitativamente la estabilidad de los cristales; no es necesario obtener el valor absoluto △ , ya que basta con conocer los valores relativos del cristal en diferentes condiciones.
Basándose en la energía relativa de los orbitales d escindidos, se puede calcular la energía total de los iones de metales de transición en los orbitales d. Esta energía es menor que antes del desdoblamiento, proporcionando así energía adicional al cristal, conocida como energía de estabilización del campo cristalino, representada por el símbolo CFSE. La Tabla 3-10 enumera las energías de estabilización de los iones que contienen orbitales dn electrones en diferentes condiciones.
Tabla 3-10 Energías de estabilización del campo cristalino bajo diferentes ligandos (Wu Ruihua, 1994)
| dn | Campo débil | Campo Fuerte | ||||
|---|---|---|---|---|---|---|
| dn | Cuadrado | Octaedro regular | Tetraedro regular | Cuadrado | Octaedro regular | Tetraedro regular |
| d0 | 0 | 0 | 0 | 0 | 0 | 0 |
| d1 | 5.14 | 4 | 2.67 | 5.14 | 4 | 2.67 |
| d2 | 10.28 | 8 | 5.34 | 10.28 | 8 | 5.34 |
| d3 | 14.56 | 12 | 3.56 | 14.56 | 12 | 8.01 |
| d4 | 12.28 | 6 | 1.78 | 19.70 | 16 | 10.68 |
| d5 | 0 | 0 | 0 | 24.84 | 20 | 8.90 |
| d6 | 5.14 | 4 | 2.67 | 29.12 | 24 | 6.12 |
| d7 | 10.28 | 8 | 5.34 | 26.84 | 18 | 5.34 |
| d8 | 14.56 | 12 | 3.56 | 24.56 | 12 | 3.56 |
| d9 | 12.28 | 6 | 1.70 | 12.28 | 6 | 1.78 |
| d10 | 0 | 0 | 0 | 0 | 0 | 0 |
2. Características cromáticas de los iones de metales de transición
En sus gemas coloreadas, el color de la mayoría de las gemas se debe a los iones de metales de transición, y el color de las gemas está relacionado con si los iones colorantes contienen electrones no apareados en los orbitales d o f. Las características de coloración de los iones de metales de transición incluyen principalmente los siguientes aspectos:
(1) La coloración de los iones de metales de transición está relacionada con los estados electrónicos del orbital d o del orbital f. Cuando los electrones del orbital d o del orbital f están llenos o vacíos, la piedra preciosa no mostrará color. Por ejemplo, el Cr6+, Ce4+y Cu+.
(2) Diferentes iones colorantes presentan diferentes colores en el mismo material de piedra preciosa. Debido a las diferentes energías de separación de los diferentes iones colorantes, pueden presentar diferentes colores incluso en el mismo material. Por ejemplo, el Fe2+ produce un color azul ligeramente grisáceo en la espinela, mientras que el Cr3+ produce rojo.
(3) Los iones colorantes de un mismo elemento en diferentes estados de valencia suelen presentar colores diferentes en el mismo material de gema. Dado que la energía necesaria para las transiciones de los electrones d del ion central es diferente, las longitudes de onda de la luz absorbida son distintas, lo que da lugar a colores diferentes. Por ejemplo, un castrum que contenga Mn2+ presenta un tono rosa suave, mientras que un berilo que contiene Mn2+ presenta un color rojo brillante, conocido como berilo rojo.
(4) Los iones coloreados del mismo elemento en el mismo estado de valencia a menudo presentan colores diferentes cuando se encuentran en configuraciones diferentes de ligandos. Por ejemplo, el Co2+ en la configuración tetraédrica de la espinela muestra un característico color "azul diamante", mientras que en la configuración octaédrica de la calcita aparece de color rosa. Fe2+ en la olivina de coordinación octaédrica muestra un verde oliva característico, mientras que en la almandina de coordinación cúbica distorsionada, aparece de color rojo intenso.
(5) El mismo tipo de iones coloreados tienen el mismo estado de valencia y geometría de coordinación, pero diferentes átomos de coordinación adyacentes presentan colores diferentes. Por ejemplo, en la coordinación tetraédrica del Co2+en la esfalerita, Co2+ está conectado al azufre, mostrándose verde, mientras que en la espinela, el Co2+ está conectado al oxígeno, mostrándose en azul.
(6) El mismo tipo de iones coloreados con el mismo estado de valencia, geometría de coordinación y átomos adyacentes presentan colores diferentes en distintas piedras preciosas. La distorsión de la geometría de coordinación causada por las diferentes composiciones químicas de las piedras preciosas cambia la naturaleza de los enlaces químicos entre el ion central y los ligandos de coordinación, alterando la energía de transición de los electrones d. Por ejemplo, el Cr3+ aparece rojo en el rubí, verde en la esmeralda y muestra colores variables en la alejandrita. La razón de estos cambios en el Cr3+ está relacionada con sus características y los ligandos de coordinación adyacentes, con el análisis de características específicas que se indica a continuación.
① Cr3+ Características:
Cr3+ tiene una estructura externa de 3s23p63d3, con 11 electrones en la capa exterior, perteneciente a una estructura de capa de electrones irregular (8-18).
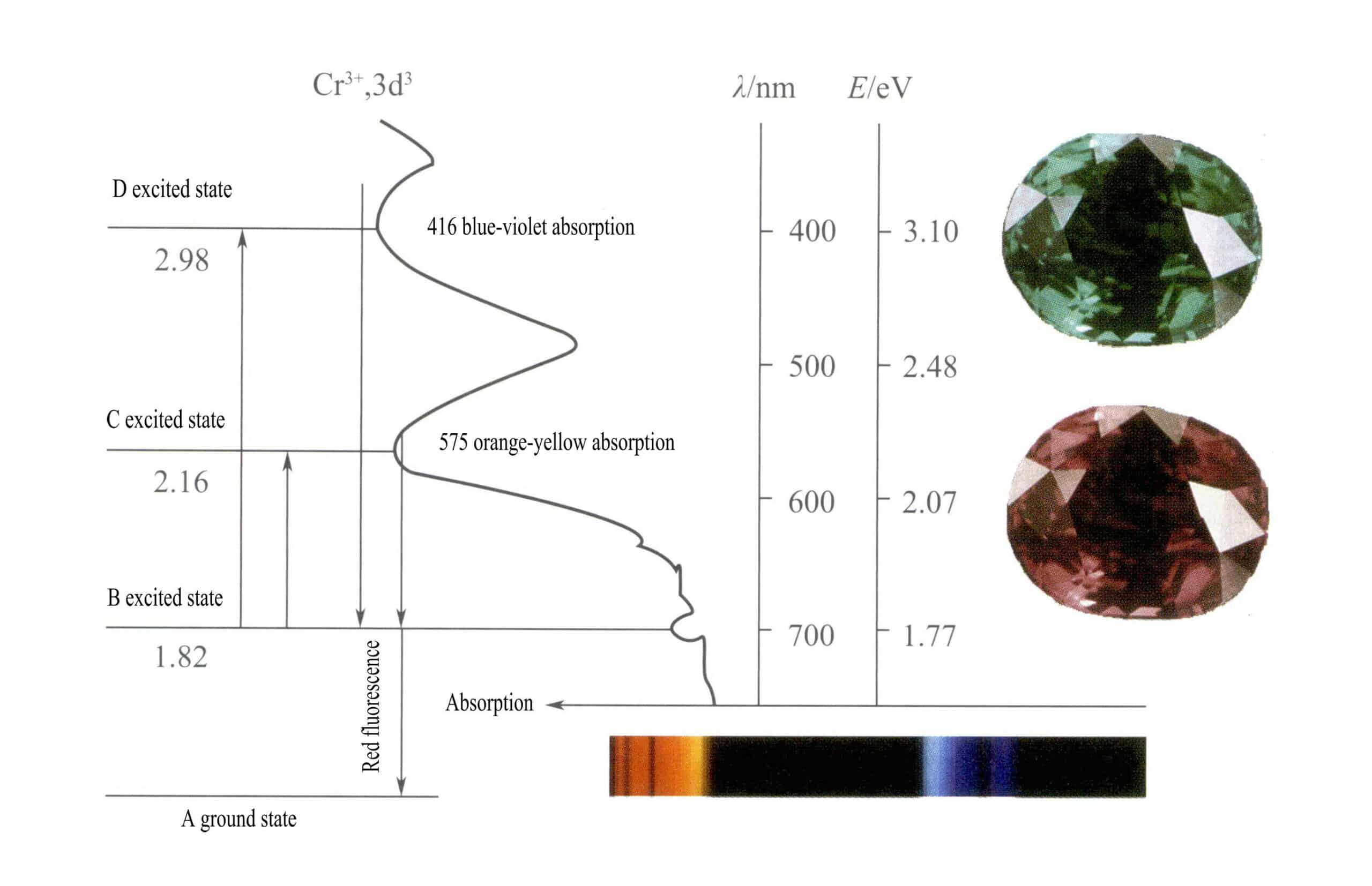
Esta estructura tiene un menor efecto de apantallamiento sobre el núcleo que la estructura de cáscara de 8 electrones, dando como resultado Cr3+ tiene una mayor carga positiva efectiva, mientras que su radio iónico es también menor, lo que constituye las características básicas del Cr3+un fuerte campo eléctrico positivo y orbitales d vacíos. Cr3+ puede proporcionar seis orbitales vacíos para alojar seis ligandos de coordinación, con una configuración espacial octaédrica, pertenecientes a d2sp3 hibridación (Figura 3-21).
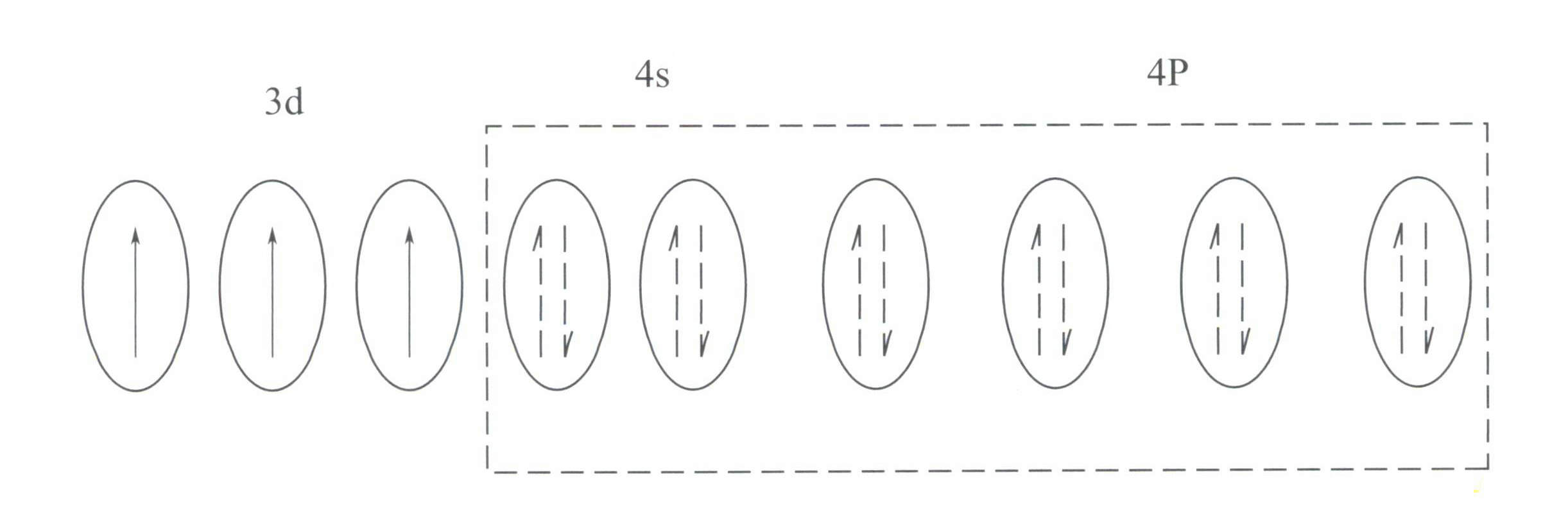
Según la teoría del campo cristalino, en un campo octaédrico, los orbitales d del Cr3+ puede dividirse en dƐ y la órbita dr órbita. Dado que los tres electrones d del Cr3+ están todos en el dƐ y son todos electrones individuales, las transiciones d-d pueden producirse bajo luz visible, provocando que las gemas que contienen Cr3+ exhibir color.
② El mecanismo de coloración del Cr3+:
En el rubí El principal componente químico del rubí es el Al2O3. Cuando un pequeño porcentaje de Cr3+ sustituye a Al3+produce un color rojo brillante. En la estructura del rubí, debido al mayor radio de Cr3+ en comparación con el radio de Al3+Cr3+ entra en la red de corindón, reduciendo la simetría en torno al óxido de aluminio.
Los orbitales d del Cr3+ y cuando los electrones en estado excitado vuelven de D o C al estado de reposo A, deben pasar primero por B, liberando calor. Regresan de B a A, acompañados de luminiscencia, emitiendo fluorescencia roja. En este proceso, los electrones absorben energía luminosa, haciendo que el rubí absorba el espectro visible violeta D (400 nm) y amarillo-verde C (555 nm) (Figura 3-22), formando una banda de absorción.

Cuando la luz blanca atraviesa un rubí, los fotones del espectro que va del púrpura al amarillo verdoso son absorbidos, mientras que casi toda la luz roja y parte de la azul pasan, lo que da al rubí un color rojo intenso con un toque de púrpura, conocido como rojo sangre de paloma.
Los rubíes presentan una breve absorción de nivel B, que se manifiesta como fluorescencia roja. Esta absorción de nivel B que produce fluorescencia roja hace que el color del rubí sea más vivo; cuanto mayor sea el contenido de iones de cromo, más intensa será la fluorescencia.
Los iones de hierro en la piedra preciosa pueden suprimir la fluorescencia de absorción del nivel B, lo que explica el fenómeno de que los rubíes parezcan más oscuros cuando contienen impurezas de hierro.
③ Cr3+ El mecanismo de coloración de las esmeraldas
El principal componente químico de la esmeralda es el Be3Al2Si6O18Cr3+que sustituye a Al3+ en la red esmeralda, y Cr3+ también está rodeado por un octaedro compuesto por seis iones de oxígeno, donde el Cr3+-O es también bastante similar a la de los rubíes. Sin embargo, en comparación con los rubíes, las esmeraldas tienen dos iones más, Be2+ y Si4+. En la estructura de las esmeraldas, aumenta la naturaleza de enlace covalente entre los óxidos metálicos, mientras que las características iónicas se debilitan.
Los cambios menores, como los enlaces químicos, provocan una ligera disminución del Cr3+nivel C y la energía del nivel D, lo que provoca un ligero desplazamiento de la banda de absorción (Figura 3-23), bloqueando significativamente la transmisión de la luz azul-púrpura (425nm) y naranja-amarilla (608nm) en el espectro, mientras que aumenta la transmisión de la luz azul-verde, formando así el característico verde esmeralda.

La absorción del nivel B de la dioptasa casi no se modifica. Cuando la impureza hierro no tiene efecto "inhibidor" en el componente esmeralda, la fuerte fluorescencia roja hace que el característico verde esmeralda brille aún más.
④ Cr3+ El mecanismo del color en la alejandrita:
El color de la alejandrita también se debe al Cr3+ sustituyendo a Al3+ en coordinación octaédrica distorsionada. Debido a que la composición química de la alejandrita es BeAL2O4La naturaleza de los enlaces químicos entre sus iones de metal-oxígeno se sitúa entre la del rubí y la de la esmeralda. Por lo tanto, sus bandas de absorción también se sitúan entre las del rubí y la esmeralda, siendo las probabilidades de transmisión de la luz azul-violeta y naranja-amarilla aproximadamente iguales, lo que hace imposible determinar si predomina la luz roja o la azul-verde (Figura 3-24).
Por lo tanto, el color de la alejandrita sólo puede depender de la distribución de la energía y de la gama cromática de la luz incidente, lo que da lugar al "efecto de cambio de color" de la alejandrita, es decir, que aparezca verde a la luz del día con un alto componente de luz azul y roja a la luz incandescente con un alto componente de luz roja. Por eso, la alejandrita suele llamarse "la esmeralda del día y el rubí de la noche".
El "efecto de cambio de color" aparece en muchos tipos de piedras preciosas, como el corindón de color cambiante y el granate de color cambiante. Actualmente, el corindón que cambia de color sintetizado artificialmente se produce utilizando el principio del cambio de color, empleando V3+ como ion colorante para la síntesis.
3. Colores de las gemas minerales
Los colores producidos por los componentes de los metales de transición pueden deducirse de la composición química de los minerales de las piedras preciosas. Por ejemplo, la turquesa que contiene Cu2+ debe ser azul, mientras que Cu+ es incoloro. La Tabla 3-11 enumera los colores producidos por los componentes comunes de los metales de transición en los minerales de las gemas naturales.
Tabla 3-11 Colores producidos por los componentes de los metales de transición en los minerales de piedras preciosas naturales
| Elemento | Color | Minerales comunes |
|---|---|---|
| Cerio (Ce) | Amarillo | Parisita |
| Cromo (Cr) | Rojo, Verde, Naranja, etc. | Crocoisita, Crocoisita roja, Uvarovita |
| Cobalto (Co) | Azul | Espinela sintética |
| Cobre (Cu) | Azul, Verde | Azurita, crisocola , Malaquita turquesa, Dioptasa |
| Hierro (Fe) | Rojo, verde, amarillo | Almandino, olivino, goethita |
| Manganeso (Mn) | Rosa, naranja | Rodonita, espesartina |
| Níquel (Ni) | Verde | Bunsenita, Calcedonia |
El color de la mayoría de las piedras preciosas se debe a las impurezas de los metales de transición que contienen. Por ejemplo, los rubíes son rojos debido a trazas de Cr3+. Varios factores influyen en el color causado por los iones de impureza en la piedra preciosa. Por lo tanto, las impurezas pueden producir diferentes colores en diferentes piedras preciosas. Por ejemplo, el Cr3+ aparece rojo en los rubíes y verde en las esmeraldas.
Las mismas impurezas pueden no causar necesariamente el mismo color de una piedra preciosa. Por ejemplo, el color verde de la mayoría de las esmeraldas está causado por el Cr, mientras que el color verde de algunas esmeraldas está parcial o totalmente causado por el vanadio (V).
La teoría del campo cristalino no sólo puede utilizarse para explicar los colores de las piedras preciosas producidos por componentes o impurezas de metales de transición, sino también los colores producidos por defectos estructurales (centros de color); el proceso específico de generación del color puede consultarse en el capítulo 3.3 de este libro.
También existen deficiencias en la explicación de los colores de los minerales gema mediante la teoría del campo cristalino, que se reflejan principalmente en los siguientes aspectos:
(1) Los electrones del ion central d no están completamente localizados en sus orbitales originales. También pueden aparecer alrededor de los átomos de coordinación, lo que indica una interacción covalente entre el átomo central y los ligandos.
(2) Sólo considera la interacción iónica electrostática entre el átomo central y los ligandos, ignorando por completo la interacción de enlace covalente entre el átomo central y los ligandos. En la investigación física, los resultados de los cálculos cuantitativos suelen diferir significativamente de las situaciones reales.
(3) Las razones del color de los minerales gema, además de la interacción entre el ion central y los ligandos, pueden deberse también a los efectos combinados de los defectos estructurales y el campo cristalino.
Sección II Teoría de los orbitales moleculares
Mulliken y Hund propusieron inicialmente la teoría de los orbitales moleculares (teoría MO). Gracias a la continua exploración de muchos científicos, se ha convertido en una teoría madura. Los orbitales moleculares (MO) pueden obtenerse mediante combinaciones lineales de orbitales atómicos, un método muy utilizado para construir orbitales moleculares. A partir de n orbitales atómicos, pueden obtenerse n orbitales moleculares, y los coeficientes de combinación lineal pueden determinarse mediante el método variacional u otros métodos. Los orbitales moleculares formados por dos orbitales atómicos, con niveles de energía inferiores a los de los orbitales atómicos, se denominan orbitales enlazantes; los que tienen niveles de energía superiores a los de los orbitales atómicos se denominan orbitales antienlazantes; los que tienen niveles de energía próximos a los de los orbitales atómicos suelen ser orbitales no enlazantes.
La teoría del orbital molecular es una teoría utilizada para explicar cuestiones como la formación, la estructura y las propiedades moleculares. También puede explicar algunas de las causas de los colores de las piedras preciosas, que se han desarrollado a partir de la teoría del campo cristalino y la teoría de los orbitales moleculares de los metales de transición. Los orbitales moleculares son una extensión natural de los orbitales atómicos. En una molécula, los electrones ya no pertenecen a un átomo concreto, sino que se mueven por todo el rango molecular; por tanto, el movimiento de los electrones en una molécula se describe mediante orbitales moleculares.
1. Conceptos básicos de la teoría de orbitales moleculares
La teoría de los orbitales moleculares postula que, después de que los átomos formen una molécula, los electrones ya no pertenecen a los orbitales atómicos originales, como propone la teoría del campo cristalino, sino que se mueven dentro de determinados orbitales moleculares. Los orbitales moleculares componen una molécula igual que los orbitales atómicos componen un átomo. Los electrones de valencia ya no se consideran localizados en átomos individuales, sino que se mueven por toda la molécula. La distribución de electrones en la molécula puede tratarse de acuerdo con los principios de distribución de electrones en los átomos (el principio de energía mínima y la regla de Hund).
La combinación lineal de orbitales atómicos en una molécula forma orbitales moleculares. El número de orbitales moleculares es igual al número de orbitales atómicos antes de la combinación. La combinación de orbitales atómicos en orbitales moleculares efectivos debe cumplir los tres principios siguientes:
(1) Principio de coincidencia de simetrías: Sólo los orbitales atómicos con la misma simetría pueden formar orbitales moleculares.
(2) Principio de proximidad energética: Sólo los orbitales atómicos con energías similares pueden combinarse para formar orbitales moleculares efectivos.
(3) Principio de solapamiento máximo: En el caso de coincidencia de simetría, cuanto mayor es el solapamiento de los orbitales atómicos, más disminuye la energía de los orbitales moleculares resultantes y más estable es el enlace químico resultante.
El orbital molecular ψ es la función de onda de un solo electrón. Puede representarse como una combinación lineal de orbitales atómicos, correspondiendo cada orbital a una energía específica, que es la suma de la energía cinética y potencial del electrón que se mueve en el campo eléctrico molecular. Dos orbitales atómicos, a y b, mediante combinaciones lineales superpuestas, producen dos orbitales moleculares ψI y ψII :
ψI=ψa + ψb (3-5)
ψII = ψa - ψb (3-6)
Cuando los orbitales moleculares con electrones se llenan primero, los orbitales de enlace ψI se llenan primero. Cuando los electrones llenan orbitales moleculares de igual energía, según la regla de Hund, también deben ocupar orbitales moleculares diferentes con el mismo sentido de espín en la medida de lo posible.
Los orbitales moleculares ψI obtenidos sumando dos funciones orbitales atómicas (Ecuación 3-5) se denominan orbitales moleculares de enlace. Los orbitales moleculares ψII obtenidos restando dos funciones orbitales atómicas (Ecuación 3-6) se denominan orbitales moleculares antienlazantes. La energía de los orbitales moleculares enlazantes es menor que la de los orbitales moleculares antienlazantes y menor que las energías de los dos orbitales atómicos originales. Por lo tanto, al igual que en el caso del llenado de orbitales atómicos, cuando se llenan orbitales moleculares, los electrones se colocan primero en orbitales de enlace, y un orbital molecular puede alojar dos electrones con espines opuestos. Cuando los electrones llenan orbitales moleculares de igual energía, según la regla de Hund, también deben ocupar, en la medida de lo posible, orbitales moleculares diferentes con la misma dirección de espín. Los orbitales moleculares formados por dos orbitales atómicos s se muestran en la Figura 3-25.

Los orbitales p y los orbitales d también pueden formar orbitales moleculares de diferentes niveles de energía; por ejemplo, la combinación de orbitales moleculares diatómicos en el O2 moléculas es relativamente complejo.
En los experimentos se midieron las propiedades magnéticas de estos dos electrones individuales, lo que proporcionó un sólido apoyo a la teoría de los orbitales moleculares. A diferencia de las moléculas compuestas por los mismos átomos, las compuestas por dos o más átomos diferentes tienen niveles de energía orbital molecular más complejos, pero el principio es el mismo.
2. Características de la coloración por transferencia de carga
Esta teoría de orbitales moleculares, en la que toda la molécula comparte electrones, también se considera la transición de electrones de un orbital atómico a otro, conocida como transferencia de carga. La transferencia de carga puede producirse en interacciones metal-metal (M-M), no metal-no metal (L-L) y no metal-metal (L-M). Entre ellas, L-L, M-L estos dos tipos de enlace suelen ser principalmente enlaces covalentes. O2 pertenece a la transferencia de carga L-L, que es un enlace covalente.
(1) Transferencia de Carga Metal-Metal ( Transferencia de Carga M - M)
Este tipo de transferencia de carga se produce generalmente entre iones comunes de metales de transición. La mayoría de las causas de coloración de las piedras preciosas coloreadas se producen por transferencia de carga metal-metal. La transferencia de carga M-M incluye principalmente los siguientes tipos: Fe2+ - Fe3+/Fe3+ - Fe2+Ti3+ - Ti4+ / Ti4+- T3+ ;Fe2+ - T4+/Fe3+ - T3+Mn2+ - Mn4+/Mn3+ - Mn3+ . La transferencia de carga entre metales se divide en dos tipos: transferencia de carga entre átomos homonucleares y transferencia de carga entre átomos heteronucleares.
① Transferencia de carga entre átomos isoelectrónicos.
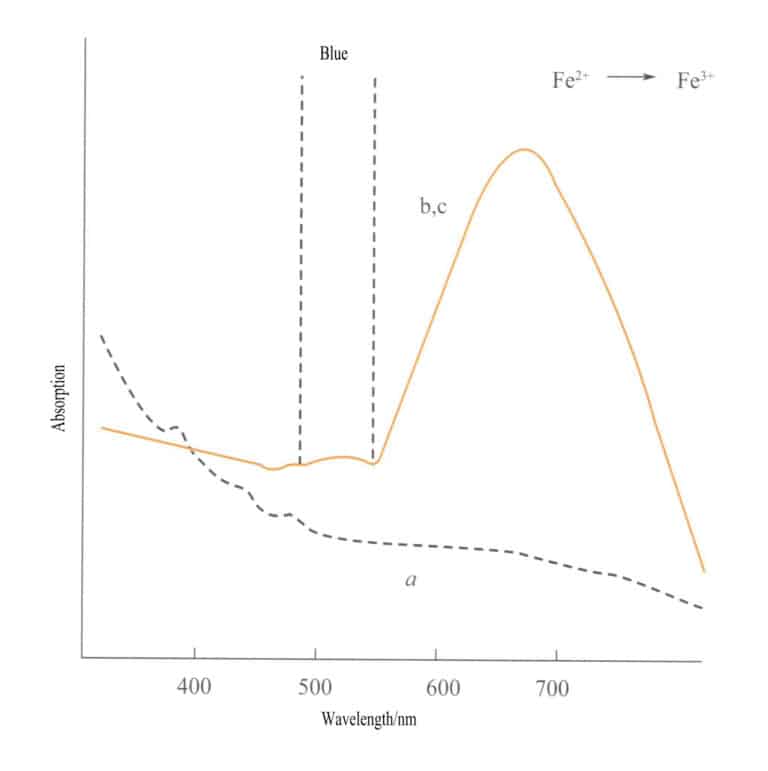
La transferencia de carga entre átomos isoelectrónicos se produce entre dos átomos del mismo elemento metálico de transición en diferentes estados de oxidación. Por ejemplo, Fe2+ y Fe3+ sufren transferencia de carga en diferentes condiciones redox, absorbiendo energía y produciendo color. El color azul púrpura de la iolita se produce por la transferencia de carga de iones de hierro en diferentes estados de oxidación. Fe3+ y Fe2+ están en posiciones tetraédrica y octaédrica, respectivamente, con dos ligandos conectados por bordes. Cuando la luz visible incide sobre la iolita, un electrón d del Fe2+ absorbe luz de cierta energía y transiciona a Fe3+absorbiendo la luz amarilla a 588 nm y produciendo un color azul púrpura. La aguamarina, la turmalina verde y otras también pueden mostrar color debido a la transferencia de carga entre iones de hierro.
② Transferencia de carga entre heteroátomos.
Los zafiros azules son el ejemplo más típico del color producido por la transferencia de carga entre dos tipos de iones de metales de transición. Los poliedros de coordinación de los iones de metales de transición están conectados por aristas o caras, lo que facilita la transferencia de carga entre metales.
Por ejemplo, en los zafiros, cuando los iones de hierro y los iones de titanio entran en los octaedros conectados, tanto el Fe como el Ti existen en dos estados de oxidación:
Fe2+ + Ti4+ baja energía (3-7)
Fe3+ + Ti3+ alta energía (3-8)
La transición de la ecuación (3-7) a la ecuación (3-8) requiere la absorción de cierta cantidad de energía luminosa, lo que da lugar a una amplia banda de absorción que va del amarillo al rojo. Por el contrario, la mayor parte de la luz azul atraviesa la piedra preciosa, dándole un aspecto azulado.
La transferencia de carga entre diferentes estados de valencia tiene una fuerte direccionalidad, y las piedras preciosas que exhiben color debido a este mecanismo a menudo muestran pleocroísmo. Por ejemplo, la aguamarina coloreada por Fe2+→ Fe3+ la transferencia de carga muestra el color estrictamente a lo largo de la dirección del eje óptico. La figura 3-26 muestra que la aguamarina aparece amarilla en los planos b y c. Al mismo tiempo, no hay tal transferencia a lo largo de la dirección del eje a, lo que resulta en ninguna absorción de luz y, por lo tanto, ningún color a lo largo de la dirección del eje a.
(2) Transferencia de carga de no metal a metal (L-M)
Este tipo de transferencia de carga L-M se produce a menudo entre el oxígeno y los iones metálicos, y algunas piedras preciosas que contienen oxígeno están coloreadas por transferencia de carga de no metal a metal, como el O2–→ Fe3+, O2- →Cr6+, O2-→Mn6+O →V5+.
En el espectro de absorción de los óxidos de hierro simples (Figura 3-27), aparecen dos bandas de absorción débiles en la región infrarroja de la ilmenita, la hematites y la lepidocrocita ( transiciones electrónicas d - d). Aparece una banda de absorción fuerte en el rango de onda corta, producida por O2-→Fe3+ transferencia de carga, y esta banda de absorción determina los colores característicos de estos compuestos: marrón rojizo, marrón y marrón amarillento.
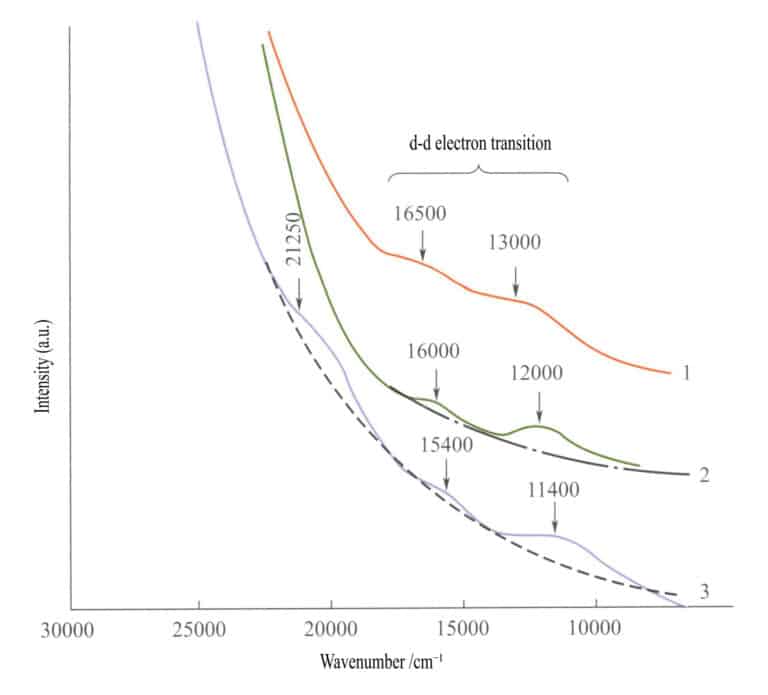
1 -Iilmenita; 2 - Hematites; 3 - Lepidocrocita
El berilo amarillo obtiene su color del O2–→ Fe3+ transferencia de carga. En la estructura del berilo amarillo, el O2–→ Fe3+ La fuerte absorción por transferencia de carga puede extenderse desde el extremo ultravioleta hasta el extremo azul del espectro visible, absorbiendo el púrpura y el azul, lo que da lugar a un color amarillo.
El zafiro, que tiene un entorno de coordinación completamente diferente al del berilo, también puede producir las mismas bandas de absorción espectral que éste, dando lugar al color amarillo, que también es resultado del O2–→ Fe3+ transferencia de carga.
Según la teoría del campo cristalino, algunos minerales gema no contienen electrones no apareados y no pueden producir color. Por ejemplo, las capas electrónicas de la crocoíta (PbCrO4), Pb2+Cr6+y O2– están llenos. Sin embargo, en el CrO42- son los "orbitales moleculares", que corresponden a los estados de excitación del O2-→Cr6+ transferencia, formando bandas de absorción y presentándose de color naranja.
L→M La transferencia de carga también incluye la transferencia de azufre a metal, como en la pirita común; este fenómeno óptico causado por la transferencia es más fácil de entender cuando se discute utilizando la teoría de bandas.
(3) Transferencia de carga de no metal a no metal (L-L)
La teoría de los orbitales moleculares sugiere que el color azul intenso del lapislázuli se debe a los niveles de energía de excitación del S3- grupo atómico.
En el grafito, los anillos de seis átomos de carbono están dispuestos en capas. A lo largo de esta capa, los electrones pueden moverse hasta cierto punto libremente, lo que da lugar a una fuerte absorción de la luz, anisotropía y conductividad.
Algunas piedras preciosas orgánicas, como el ámbar y las perlas, tienen electrones que se mueven y excitan a través de los grupos atómicos de los pigmentos orgánicos en orbitales moleculares compartidos, provocando la absorción de la luz visible y produciendo el color. Por ejemplo, el "amarillo miel" del ámbar, los colores del coral y algunas conchas y perlas de colores.
Los mecanismos de color de las piedras preciosas más comunes se muestran en la Tabla 3-12.
Tabla 3-12 Clasificación de los mecanismos de color de las piedras preciosas más comunes
| Transferencia de carga metal-metal | Fe2+ - Fe3+ /Fe3+ - Fe2+ : iolita (azul), berthierita (azul), magnetita (negra), etc. |
| Fe2+ -Ti4+/Fe3+ - Ti3+ : Cianita (azul), Zafiro (azul) | |
| Mn2+-Mn4+/Mn3+-Mn3+: Manganita (negra), Bixbyita (negra) | |
| Transferencia de carga de no metal a metal | O2- -Fe3+: Berilo amarillo dorado, zafiro amarillo dorado, ilmenita, hematites, lepidocrocita, etc. |
| O2- - Cr6+: Crocoita (naranja) | |
| O2- -V5+:Vanadinita (naranja) | |
| De azufre a metal: pirita, marcasita, etc. (véase semiconductor con hueco) | |
| Transferencia de carga no metálica - no metálica | S3-: Lapislázuli (azul) |
| Π electrónico: grafito (negro) | |
| Los colores de algunas gemas orgánicas como el ámbar y el coral. |
Copywrite @ Sobling.Jewelry - Fabricante de joyería personalizada, fábrica de joyería OEM y ODM
Sección III Teoría de bandas de energía
La teoría de bandas de energía es un modelo mecánico cuántico para estudiar los materiales de las piedras preciosas, que es una ampliación y expansión de la teoría de orbitales moleculares. El estudio de la teoría de bandas de energía puede explicar mejor el mecanismo del color de algunas piedras preciosas de color natural.
1. Conceptos básicos de la teoría de bandas de energía
La teoría de bandas de energía es una teoría aproximada utilizada para estudiar las leyes del movimiento de los electrones en los sólidos. Los sólidos están compuestos por átomos, que incluyen los núcleos atómicos y los electrones más externos, todos ellos en constante estado de movimiento. La teoría de bandas postula que los electrones de los sólidos no están ligados a un átomo concreto, sino que son compartidos por todo el cristal y se mueven dentro del campo de potencial periódico del espacio tridimensional del cristal. La amplitud del movimiento de los electrones se encuentra dentro del campo de potencial periódico de la red, lo que permite que la distribución espacial de las órbitas de los electrones supere a la de las moléculas, alcanzando un máximo. Los niveles de energía de los electrones individuales se amplían en bandas de energía.
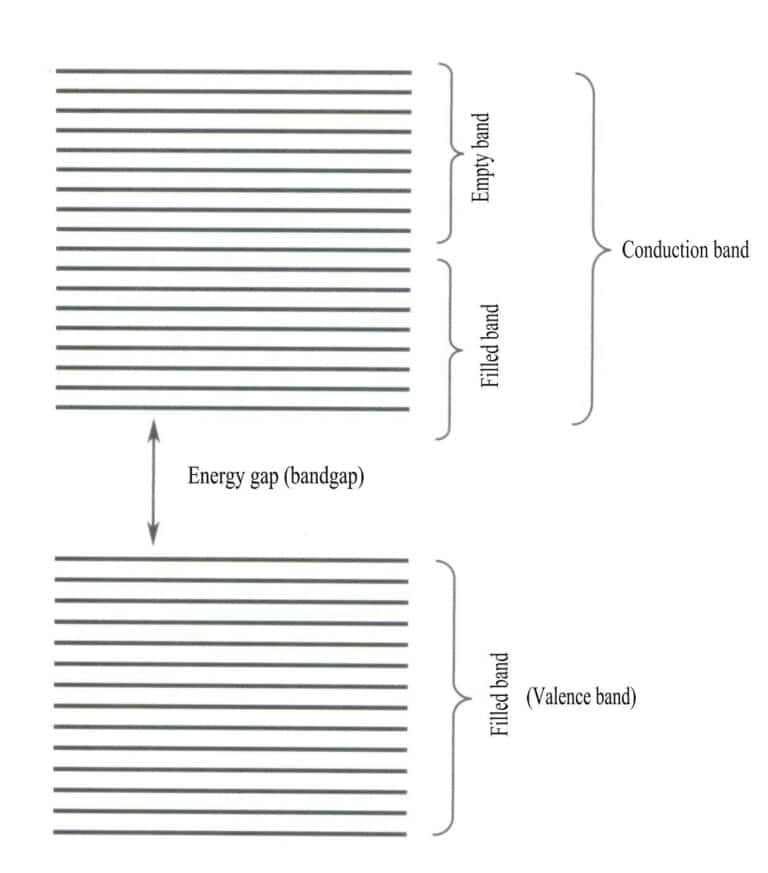
La teoría de bandas analiza principalmente las transiciones de electrones entre estados no locales, en los que todos los electrones de valencia deben pertenecer a toda la red sólida. Según la teoría de bandas, los materiales sólidos pueden dividirse en diferentes bandas de energía en función de si los orbitales atómicos están llenos: una banda llena está formada por los niveles de energía de los orbitales atómicos que están totalmente ocupados por electrones, lo que representa una banda de baja energía; una banda vacía está formada por niveles de energía que no están totalmente ocupados por electrones, lo que representa una banda de alta energía. La diferencia de energía entre estos dos tipos de bandas se denomina "brecha de banda" (Figura 3-28).
Cuando todas las bandas de energía de un material están llenas, es un no conductor; cuando está parcialmente lleno de electrones, es un conductor. Los defectos de la red introducen niveles de energía adicionales en el cristal, lo que permite que los electrones entren en estos niveles de energía, dando lugar a una conductividad condicional.
2. Características de las transiciones de banda prohibida
Algunos minerales de piedras preciosas contienen elementos del Grupo IV A de la tabla periódica, como el diamante y la moissanita, que se enlazan principalmente de forma covalente. También hay otros minerales, como el sulfuro de cadmio (CdS), cuyos colores pueden explicarse mediante la teoría de bandas.
Los electrones absorben la energía de la luz y se mueven entre las bandas de valencia y conducción, formando "transiciones de banda interna". La probabilidad de que se produzcan transiciones está estrechamente relacionada con la diferencia de energía entre las bandas de valencia y de conducción, conocida como energía de brecha de banda (Eg) (Figura 3-29).

La Figura 3-29 (a) es un diagrama de banda típico de un semiconductor. En función del tamaño de la energía de la banda prohibida del cristal, éste puede dividirse en tres tipos: banda prohibida ancha, banda prohibida estrecha y banda prohibida media. Una brecha de banda ancha tiene una energía de brecha de banda mayor que la energía de la luz visible; cuando la energía de brecha de banda supera la energía de la luz visible, ésta no se absorbe y pasa completamente, haciendo que el mineral sea incoloro. Por ejemplo, la energía de band gap del diamante Eg es de unos 5,5 eV, por lo que es incoloro.
La energía de bandgap de los materiales de bandgap estrecho es menor que la de la luz visible, lo que provoca que toda la luz visible sea absorbida, dando lugar a colores gris verdoso oscuro o negro. Por ejemplo, la energía de banda prohibida de la galena es Eg inferior a 0,4 eV, que parece ser gris plomo. Cuando este "semiconductor de banda prohibida estrecha" tiene una forma geométrica adecuada, presenta propiedades rectificadoras y amplificadoras.
La energía de los materiales de bandgap medio se encuentra exactamente dentro del rango de luz visible, y los minerales gema muestran varios colores. Su secuencia de colores se muestra en la Figura 3-29 (c), yendo del rojo-amarillo al verde-azul y al púrpura. Por ejemplo, la energía de bandgap (Eg) del sulfuro de cadmio (CdS) es de aproximadamente 2,5 eV, que absorbe la luz azul y violeta, apareciendo de color amarillo. La energía de banda prohibida del cinabrio es de unos 2 eV, por lo que sólo deja pasar la luz roja y parece rojo. La energía de bandgap del oropimente es de unos 2,5 eV, por lo que aparece amarillo.
Otra categoría de minerales gema naturales explicada por la teoría de bandas es el color de los materiales de banda prohibida ancha que contienen impurezas. Por ejemplo, en el caso de un diamante con impurezas, la energía de bandgap del diamante es Eg aproximadamente 5,5eV, y la luz visible no se absorbe al atravesar el diamante; el diamante puro es incoloro, pero la situación cambia cuando contiene impurezas.
(1) El mecanismo del color de los diamantes amarillos
Los átomos de nitrógeno sustituyen las posiciones de los átomos de carbono. Como los átomos de nitrógeno tienen un electrón más que los átomos de carbono, este electrón extra forma un nivel de energía de impureza en el bandgap, conocido como nivel de energía donante, actuando los átomos de nitrógeno como "donantes."
La existencia de este nivel de impureza reduce la energía de la banda prohibida a 4eV[ [Figura 3-30 (a)]. Puede ser incluso inferior, lo que le permite absorber luz ultravioleta y un poco de luz violeta de 3eV, haciendo que el diamante parezca amarillo.
Este efecto es fuerte; tener un átomo de nitrógeno por cada cien mil átomos de carbono puede hacer que el diamante adquiera un color amarillo intenso. Sin embargo, la reducción de la brecha de banda sigue siendo insuficiente para que el diamante sea conductor a temperatura ambiente.
(2) Mecanismo del color en los diamantes azules
Puesto que el boro tiene un electrón menos que el carbono, forma un "nivel aceptor" en el hueco de banda del diamante. No tiene electrones extra, pero puede aceptar electrones de la banda de valencia de un diamante, creando huecos en la banda de valencia [Figura 3-30 (b)] y formando una banda de energía de impureza alrededor de 0.4eV por encima de la banda de valencia conocida como nivel aceptor.

El nivel de energía del aceptor no es simple; se trata de una estructura compleja de bandas de energía de impurezas que puede producir el azul. El nivel de energía aceptor crea "agujeros" en la banda de valencia, lo que permite a este diamante azul tipo II b "agujero" conducir la electricidad.
Un átomo de boro entre cada millón de átomos de carbono puede formar el azul. Debido al mayor contenido de aluminio en este diamante azul y a que el aluminio tiene un electrón menos en la capa externa que el carbono, antes se pensaba que el aluminio desempeñaba el papel de aceptor. Sin embargo, los experimentos actuales han demostrado que es el boro y no el aluminio.
Los diamantes azules conductores de tipo II b son azules por naturaleza, y su conductividad es una de las diferencias con respecto a los diamantes azules irradiados (centros de color). Esta propiedad se utiliza a menudo para distinguir entre los dos tipos de diamantes. Sin embargo, los diamantes amarillos donantes de nitrógeno no conducen la electricidad, por lo que este método no puede utilizarse para diferenciarlos de los diamantes amarillos irradiados.
3. Minerales gema coloreados por transiciones de banda
La teoría de las bandas de energía puede explicar parte de la formación del color de las piedras preciosas naturales. Dado que la energía de banda es una propiedad inherente al cristal y no cambia debido a condiciones externas, el color de las piedras preciosas tiene una buena estabilidad. La conductividad del cristal puede determinarse en función de si las bandas de energía del cristal están llenas de electrones. La Tabla 3-13 enumera los tipos de colores de las piedras preciosas que pueden explicarse mediante la teoría de bandas y sus propiedades de conductividad.
Tabla 3-13 Tipos de colores de gemas explicados por la teoría de bandas y su conductividad
| Conductores (colores metálicos y brillo metálico) | Elemento | Cobre, oro, hierro, plata, mercurio, etc. |
| Aleación | Amalgama, Meteorito níquel hierro | |
| Semiconductor | Banda estrecha | Gris opaco a negro: altaita, galena |
| Color metálico opaco: cobaltina, marcasita, pirita, smaltita | ||
| Separación de banda moderada | Rojo: cinabrio, proustita, pirargirita | |
| Naranja: Realgar | ||
| Amarillo: Sulfuro de cadmio, realgar, azufre | ||
| Banda prohibida ancha | Incoloro: diamante, esfalerita | |
| Semiconductores de banda prohibida ancha con impurezas | Impureza donante: Diamante dopado con nitrógeno (amarillo) | |
| Impurezas en el huésped: diamante con boro (azul) |
El color de las piedras preciosas causado por las transiciones de bandas está relacionado con la estructura y el tipo de enlace en el momento de la formación de la piedra preciosa. Tiene poca relación con impurezas y defectos cristalinos posteriores. El tamaño de la energía de banda prohibida de las piedras preciosas es fijo. No cambia con las propiedades del material de la gema, por lo que los métodos convencionales de optimización no pueden mejorar el color de las gemas.
Sección IV Efectos físicos ópticos
La mayoría de las piedras preciosas naturales pueden causar una absorción selectiva de la luz, y diferentes piedras preciosas absorben la luz visible en diferentes longitudes de onda, lo que resulta en diferentes colores. Además de la absorción selectiva de la luz, la estructura interna de los cristales de las piedras preciosas también puede causar efectos ópticos físicos, lo que da lugar a diferentes colores en las piedras preciosas.
1. Minerales gema relacionados con efectos ópticos físicos
Los colores producidos por efectos ópticos físicos se forman debido a la dispersión, interferencia, difracción y otros motivos de la luz causados por la estructura o composición del cristal y las inclusiones. Se trata simplemente de un efecto óptico que puede explicarse mediante la teoría física óptica. Diferentes piedras preciosas pueden producir diferentes colores bajo los mismos efectos ópticos. Además de los oligoelementos comunes que causan el color, las razones de los colores producidos por efectos ópticos físicos están relacionadas principalmente con la estructura interna y las propiedades físicas de las piedras preciosas. En la Tabla 3-14 se enumeran los tipos de minerales de las piedras preciosas que producen colores debido a efectos ópticos físicos.
Tabla 3-14 Tipos de minerales gema causados por efectos ópticos físicos
| Función | Propiedades ópticas y color | Minerales gema |
|---|---|---|
| Dispersión Dispersión | Resplandeciente | "Fuego" en piedras preciosas de dispersión, como diamantes, circón, rutilo y titanato de estroncio. |
| Azul | Piedra de luna, cuarzo azul, ópalo | |
| Morado | Fluorita (dispersión de microcristales de calcio) | |
| Rojo | Cristal rubí, dispersión de microcristales de cobre u oro | |
| Blanco | Cuarzo lechoso | |
| Efecto ojo de gato | aguamarina ojo de gato, piroxeno ojo de gato, etc. | |
| Efecto luz de las estrellas | Diversos efectos estelares del corindón y el granate | |
| Lustre | Lustre de perlas, apofilita, etc. | |
| Destello | Destellos de aventurina, obsidiana, etc. | |
| Difracción de interferencias | Los colores espectrales puros de la película fina | El arco iris de la calcopirita, la película descolorida en una fisura de cuarzo iris |
| Efectos de interferencia | El cambio de color del ópalo, el efecto de la labradorita | |
| Inclusión | Azul | Dumortierita en cuarzo |
| Verde | Calcedonia verde y venas de níquel en calcedonia verde, fucsita en cuarzo estrellado | |
| Naranja | Óxido de hierro hidratado en ópalo de fuego y calcedonia color carne | |
| Rojo | Escamas de hematites en ortoclasa |
2. Efectos de interferencia y difracción
(1) Efectos de interferencia
Los fenómenos de interferencia se producen cuando dos haces de luz se propagan por el mismo camino óptico o en direcciones paralelas. Un fenómeno de interferencia común en las piedras preciosas es la iridiscencia. Por ejemplo, en el cuarzo iridiscente, los colores de interferencia dependen del grosor de la película, del índice de refracción de la misma y de la naturaleza de la luz incidente.
Los colores de interferencia de las perlas se forman por la superposición alterna de capas concéntricas de dos sustancias con diferentes índices de refracción (aragonito y nácar), donde la luz incidente se refleja en las superficies entre las capas alternas, y la luz reflejada interfiere con la luz incidente para producir hermosos colores de interferencia.
(2) Efectos de difracción
La difracción es el fenómeno físico por el que las ondas luminosas se desvían de su propagación original en línea recta al encontrar obstáculos. En física, las ondas luminosas sufren diversos grados de curvatura y dispersión al atravesar obstáculos como rendijas, pequeños orificios o discos. Si se interpone un obstáculo entre la fuente de luz y la pantalla de observación, aparecerán regiones claras y oscuras en la pantalla de observación, y los límites de estas regiones no son nítidos, formando un complejo patrón de claros y oscuros. Este fenómeno se denomina difracción. Este fenómeno puede producirse siempre que las ondas luminosas encuentren obstáculos a lo largo de su trayectoria de propagación. El factor más importante para que se produzca la difracción es la presencia de rejillas de difracción espaciadas periódicamente en los minerales de las piedras preciosas.
① Cambio de color del ópalo
En el ópalo, las esferas de sílice que contienen agua tienen diámetros iguales y están dispuestas en una estructura de capas alternas regulares, formando rejillas de difracción espaciadas periódicamente. Cuando la luz entra en el ópalo, se produce la difracción, cambiando el color (Figuras 3-31, 3-32). Los tipos de colores y el grado de cambio de color dependen principalmente del espaciado interplanar de las esferas de sílice apiladas.
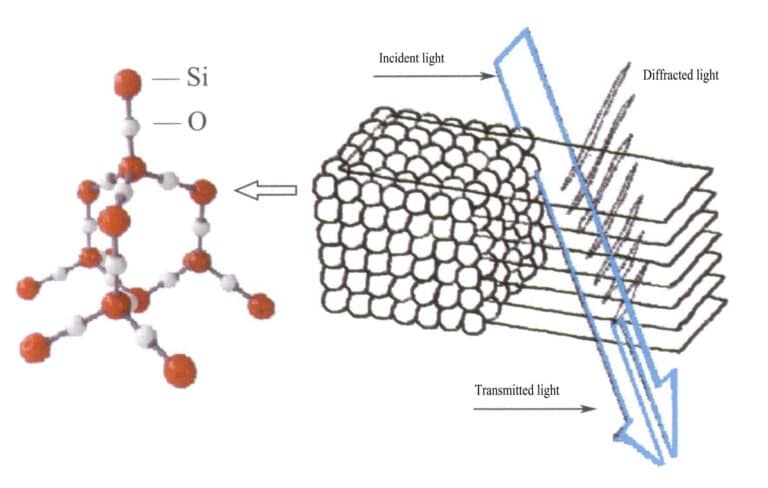

Por ejemplo, el ópalo con una estructura de placa plana cúbica centrada en la cara y una separación reticular de 3×10-10m muestra colores que van del verde al rojo; este tipo de ópalo con una separación reticular de 2,5×10-10m muestra colores que van del azul al amarillo.
② Efecto Labradorita
La labradorita también presenta efectos similares a los del ópalo (Figura 3-33). La labradorita también se conoce como espectrolita porque puede destellar con la colorida luz del sol. Varios tipos de labradorita de Finlandia pueden mostrar una gama de colores espectrales, un fenómeno conocido como "efecto labradorita." El efecto de cambio de color en la labradorita se debe a pequeñas fusiones entre capas de plagioclasa con diferentes composiciones. Las ligeras diferencias de índice de refracción entre los distintos feldespatos provocan interferencias y difracción de la luz, lo que da lugar a luminiscencia y cambio de color. Los colores producidos por esta estructura están relacionados con el grosor relativo de las capas y sus índices de refracción. Ocasionalmente, la andradita de México también presenta fenómenos de difracción.

3. Dispersión e inclusiones
(1) Dispersión
La dispersión suele producirse cuando la estructura interna de los materiales gema es irregular o cuando el tamaño de los componentes supera los límites de las condiciones de difracción. Los efectos cromáticos producidos por la dispersión están relacionados con el tamaño y la forma de las partículas del material gema. Cuando la luz incidente interactúa con partículas dispuestas de forma irregular y de tamaño inferior a la longitud de onda de la luz visible, las ondas de luz de alta energía transmitidas son más fuertes que las ondas de luz de baja energía, lo que significa que, en la mayoría de los casos, sólo pueden verse los colores púrpura y azul. Por ejemplo, el SiO2 Las pequeñas esferas del ópalo tienen diámetros inferiores a la longitud de onda de la luz visible, y cuando el tamaño de las partículas de dispersión se aproxima a la longitud de onda de la luz visible, también pueden producirse colores de dispersión.
Por ejemplo, la fluorita púrpura se debe a que la irradiación radiactiva expulsa átomos de flúor, lo que da lugar a átomos de calcio que se enlazan con átomos de flúor condensándose en placas hexagonales de un tamaño comparable a la longitud de onda de la luz visible. La interacción entre las placas de calcio y las ondas luminosas produce dispersión. Absorbe algunas ondas de luz, creando un fuerte pico de absorción en la región de luz verde-roja, permitiendo el paso de la luz púrpura y produciendo el color púrpura.
Dado que partículas del mismo tamaño de elementos metálicos pueden producir efectos de color similares, y partículas metálicas diferentes pueden producir colores diferentes, algunas gemas de imitación se fabrican utilizando esta propiedad.
Por ejemplo, el vidrio "rubí" se produce añadiendo partículas de cobre u oro al vidrio, lo que da lugar a un color rojo similar al de los rubíes. Cuando el material de la gema contiene inclusiones, microfisuras o burbujas mayores que la longitud de onda de la luz visible, las ondas luminosas interactúan con estas partículas dispersoras, haciendo que las ondas luminosas dispersas se recombinen, produciendo una luz lechosa translúcida. Por ejemplo, ciertas imitaciones de piedra lunar.
El efecto de luz de luna de la piedra lunar también se produce por la dispersión de la luz (figura 3-34). La piedra lunar es un feldespato alcalino, un compuesto formado por capas paralelas alternas de feldespato rico en potasio y rico en sodio. El espesor entre capas oscila normalmente entre 50~1000nm, con capas más finas capaces de producir dispersión. El mismo color de dispersión puede darse también en la plagioclasa, conocido como "efecto labradorita".
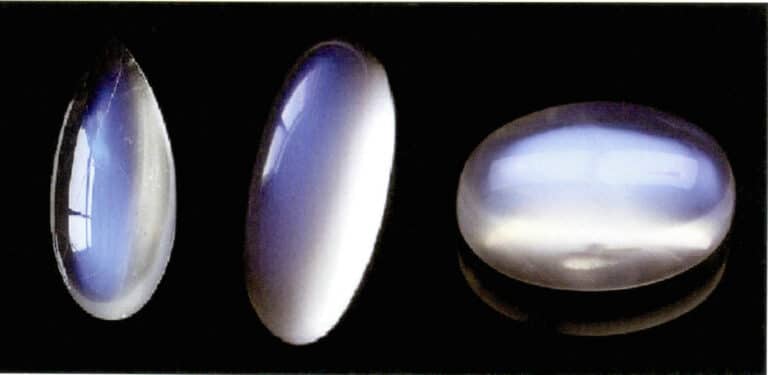
Una disposición especialmente orientada de las partículas dispersoras puede producir efectos ópticos característicos. Por ejemplo, cuando las partículas de dispersión están en forma fibrosa paralela, producen un efecto de ojo de gato o estrella, como los zafiros estrella y los ojos de gato de cuarzo. Cuando las partículas de dispersión son lo suficientemente grandes como para distinguirse a simple vista, pueden producir un "efecto de piedra dorada", como la piedra solar (figura 3-35) y el cristal de piedra dorada.

(2) Inclusiones
El color y los fenómenos ópticos producidos por las inclusiones son un tipo especial de dispersión. Las inclusiones con color incrustadas en cristales principales casi incoloros presentarán el color de las inclusiones, como la calcedonia bandeada que contiene níquel y el óxido de hierro(II) que contiene agua (FeO - H2O) calcedonia de color carne; el color de la ortoclasa de Madagascar y de algunas cordieritas está formado por inclusiones de hematites ligeramente más grandes, aunque microscópicas, que crean tonalidades rojas; inclusiones submicroscópicas de hidróxido férrico colorean a menudo el ópalo de fuego.
Los diamantes suelen presentar diferentes colores debido a la presencia de numerosas inclusiones. Los diamantes coloreados por inclusiones pueden ser negros, rojo anaranjado y rojo pardo. Cuando un diamante contiene innumerables inclusiones minerales oscuras y opacas, parece negro; cuando se examina con luz transmitida intensa, pueden observarse muchas inclusiones oscuras, y el diamante parece gris oscuro; otro tipo son las inclusiones secundarias que se producen en las grietas del diamante. Cuando las grietas se desarrollan y se rellenan con estas inclusiones coloreadas, el diamante aparece de color rojo pardo o rojo anaranjado, lo que también se conoce como diamante "oxidado".
4. Dispersión
El fenómeno de descomposición de la luz blanca en varios colores espectrales a través de un objeto se denomina dispersión. La dispersión de las piedras preciosas se refiere a la propiedad de la luz de dispersarse en distintas longitudes de onda de colores espectrales al atravesar los planos inclinados de las piedras preciosas transparentes. Debido a que las distintas longitudes de onda de la luz monocromática que componen la luz blanca se propagan a distintas velocidades e índices de refracción en distintos materiales, la luz blanca puede descomponerse en varios colores espectrales en determinadas condiciones. El tamaño del valor de dispersión de una piedra preciosa viene determinado por sus propiedades físicas; cada piedra preciosa tiene su valor de dispersión inherente, que no cambia con las propiedades de la piedra. El encanto único de los diamantes está estrechamente relacionado con su elevado valor de dispersión (0,044).
La mayoría de los simulantes de diamante tienen un valor de dispersión más elevado, como el valor de dispersión del circón de 0,039 y el valor de dispersión de la moissanita sintética de 0,104. En la Tabla 3-15 se comparan los valores de dispersión de los diamantes y sus simulantes más comunes.
Tabla 3-15 Comparación de los valores de dispersión de los diamantes y de sus piedras preciosas simulantes comunes
| Nombre de la gema | Valor de dispersión |
|---|---|
| Diamante | 0.044 |
| Zircón | 0.039 |
| Corindón | 0.018 |
| Espinela | 0.020 |
| Topacio | 0.014 |
| Beryl | 0.014 |
| Cristal | 0.014 |
| Rutilo sintético | 0.280 |
| Titanato de estroncio sintético | 0.190 |
| Moissanita sintética | 0.104 |
La dispersión se conoce comúnmente como el "fuego" de las piedras preciosas. Por ejemplo, los diamantes tienen un alto valor de dispersión, y su fuego es muy pronunciado, lo que realza el estatus ya de por sí real de los diamantes y pone de manifiesto su encanto único.
Hay muchos tipos de colores producidos por efectos físicos ópticos, todos los cuales pueden explicarse mediante la teoría física óptica. Excepto la dispersión, que es una propiedad inherente a la propia piedra preciosa, otros fenómenos se deben a cambios estructurales posteriores a la formación de la piedra preciosa y a las diferencias en las inclusiones mecánicas. Comprender las distintas causas de los colores de las piedras preciosas proporciona una base teórica para optimizar el tratamiento de las piedras preciosas naturales y sintéticas.