Einmal alles über Edelsteinkristallographie wissen
Ein umfassender Leitfaden über Formen, Arten, Klassifizierungen und Unterschiede der Kristallographie
Die Erde ist aus unzähligen Molekülen und Atomen zusammengesetzt. Die moderne wissenschaftliche Forschung hat festgestellt, dass feste Materialien in der Natur aus verschiedenen chemischen Elementen bestehen. Die Ergebnisse der Röntgenanalyse zeigen, dass die Atome in den Elementen bestimmter fester Materialien sauber und regelmäßig angeordnet sind. Diese Materialien werden als kristallin eingestuft oder als Kristalle bezeichnet, und ihr geordnetes Atomgitter wird als Kristallstruktur bezeichnet (Abbildung 2-1-1).
Die meisten Edelsteinmaterialien, die in der Natur und in Labors wachsen, sind kristallin. In diesem Kapitel werden das Konzept der Kristalle, ihre Klassifizierung und die Beziehung zwischen Kristallen und der grundlegenden Terminologie in der Gemmologie behandelt.

Inhaltsübersicht
Abschnitt ⅠDer Begriff und die Beschreibung von Kristallen
Wenn wir von Edelsteinen sprechen, denken wir oft an ihre funkelnden und durchscheinenden Eigenschaften (Abbildung 2-1-2). Aus der Sicht von Geologen und Gemmologen gehören die meisten beliebten Edelsteine zu einer geometrischen Form von Festkörpern - Kristallen. Das Wesen der Schönheit von Kristallen ist in der Tat die Schönheit der Geometrie.

1. Das Konzept der Kristalle
Kristalle sind die am leichtesten zu assoziierenden und am häufigsten in der Natur vorkommenden Elemente. Kristalle sind auf allen sieben Kontinenten der Erde zu finden, und wenn sie in der Natur vorkommen, haben sie oft die Form von geometrischen Polyedern (Abbildung 2-1-3). Sie werden im Allgemeinen als Kristalle bezeichnet. Später wurde dieser Begriff auf natürlich vorkommende feste Stoffe mit geometrischen polyedrischen Formen ausgeweitet, wie z. B. Diamanten und Aquamarinkristalle (Abbildung 2-1-4). Kristalle können auch feste Materialien mit unregelmäßiger, unebener, abgenutzter, zerbrochener oder künstlich bearbeiteter Oberfläche bezeichnen, deren atomare Anordnung jedoch immer noch einem regelmäßigen Muster folgt. Kristallographen gehen davon aus, dass alle Kristalle sechs grundlegende Eigenschaften besitzen: Selbstbegrenzung, Gleichförmigkeit, Anisotropie, Symmetrie, Stabilität und einen festen Schmelzpunkt.
① Selbstbegrenzung bezieht sich auf die Eigenschaft chemischer Elemente, spontan geometrische polyedrische Formen zu bilden. Diese Eigenschaft kann erklären, warum verschiedene Elemente unterschiedliche geometrische Kristallformen aufweisen.
② Gleichmäßigkeit bezeichnet die Eigenschaft, dass die physikalischen und chemischen Eigenschaften aller Kristallteile gleich sind. Diese Eigenschaft kann uns helfen, verschiedene Mineralkristalle zu unterscheiden und zu identifizieren.
Anisotropie bezieht sich auf die Eigenschaft, dass die Anordnung der Elemente in verschiedenen Richtungen variiert, was zu leichten Unterschieden in den physikalischen Eigenschaften je nach Richtung führt. Diese Eigenschaft kann erklären, warum sich Diamanten mit der höchsten Härte schneiden und polieren lassen.
Unter Symmetrie versteht man die Eigenschaft, dass sich identische Teile oder Eigenschaften in einem Kristall in einem regelmäßigen Muster wiederholen. Diese Eigenschaft ist äußerst wichtig und speziell für Kristalle und wird im zweiten Abschnitt dieses Kapitels näher erläutert.
⑤ Stabilität bezieht sich auf die Stabilität eines Kristalls, die sich aus seiner minimalen inneren Energie ergibt. Wenn die innere Energie eines Kristalls hoch und ungleichmäßig ist, neigt er dazu, von selbst zu zerbrechen. Diese Eigenschaft kann erklären, warum Rubinkristalle, die mit der Flammenfusionstechnik synthetisiert werden, immer eher halb als ganz zu sein scheinen.
⑥ Fixer Schmelzpunkt bezieht sich auf die Eigenschaft, dass ein Kristall einen festen Schmelzpunkt hat.

Abbildung 2-1-3 Granat (die linke Seite ist der Kristall, die rechte Seite ist der polierte Granat)

Abbildung 2-1-4 Aquamarin-Kristall
2. Die ideale Form von Kristallen
Bei den in der Kristallographie behandelten Kristallen handelt es sich hauptsächlich um ideale Einkristalle. Ein idealer Einkristall ist definiert als ein Kristall, dessen innere Struktur streng den Regeln des Raumgitters folgt und dessen Form eine regelmäßige geometrische Kombinationsform ist. Die Formen idealer Einkristalle werden in zwei Typen unterteilt: einfache Formen und kombinierte Formen.
(1) Einfache Form
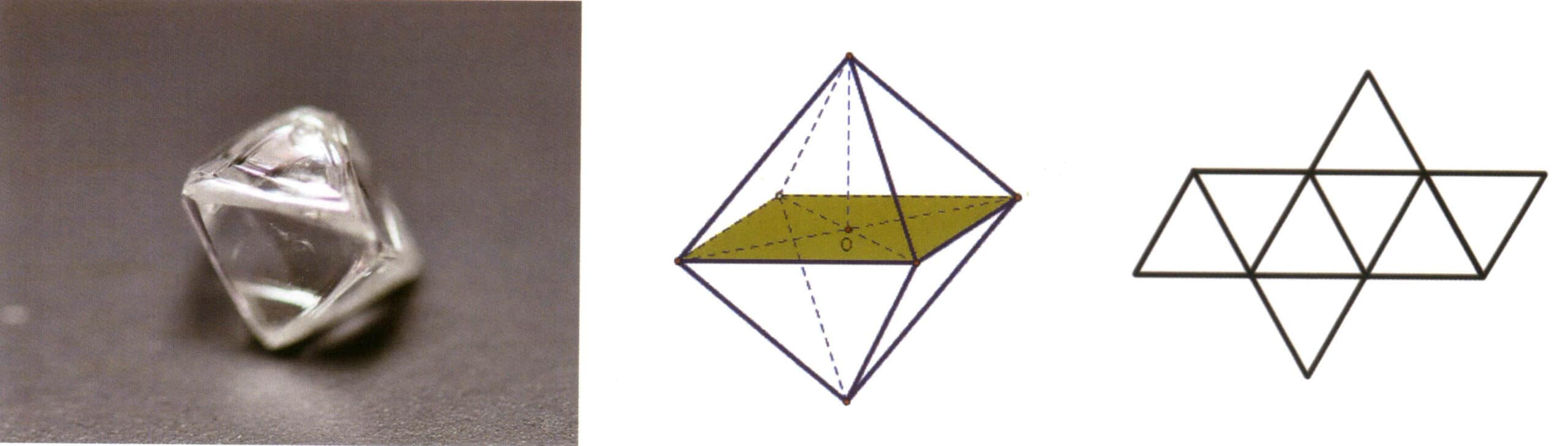
Eine einfache Form ist eine Kombination aus einer Gruppe von Kristallflächen, die durch Symmetrieelemente verbunden sind. Sie kann als geometrischer Körper verstanden werden, der aus Kristallflächen gleicher Form und Größe im Idealzustand besteht (Abbildung 2-1-5). Es gibt 47 Arten von Einfachformen in Kristallen.
Die wichtigsten Punkte zur Erkennung einfacher Formen sind: Alle Kristallflächen des Kristalls haben die gleiche Form und Größe, und die Kristallflächen können unterschiedlich ausgerichtet sein.
(2) Kombinieren Sie Formular
Die Aggregation von einfachen Formen wird als kombinierte Form bezeichnet, die aus zwei oder mehr verschiedenen einfachen Formen besteht. Nicht alle einfachen Formen können frei zu einer kombinierten Form kombiniert werden; nur einfache Formen mit der gleichen Punktgruppe können sich zusammenschließen (Abbildungen 2-1-6 bis 2-1-8).
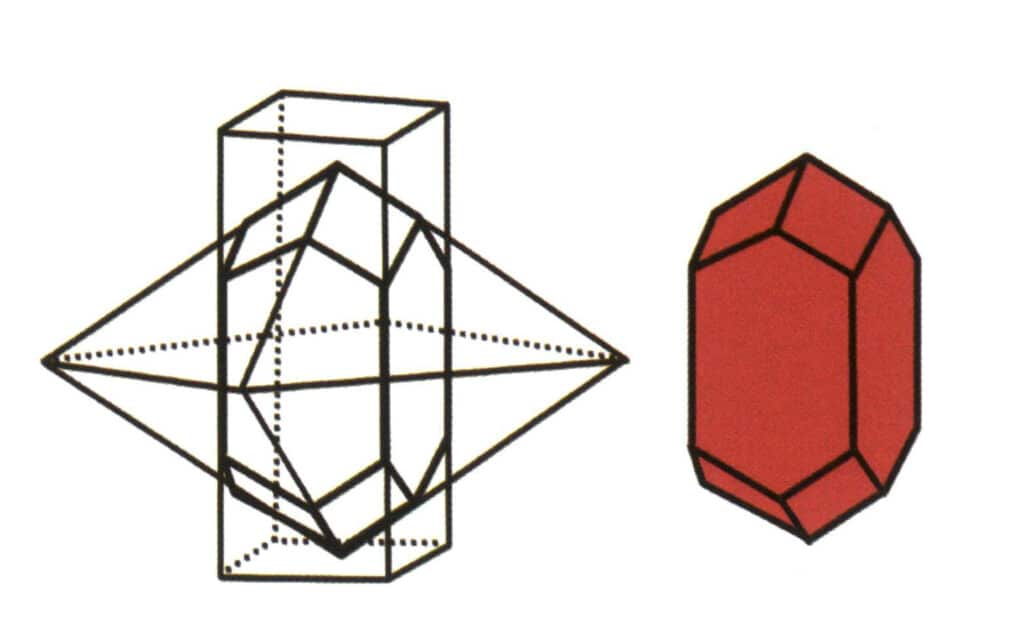
Abbildung 2-1-6 Kombinat aus tetragonalen Prismen und tetragonalen Dipyramiden
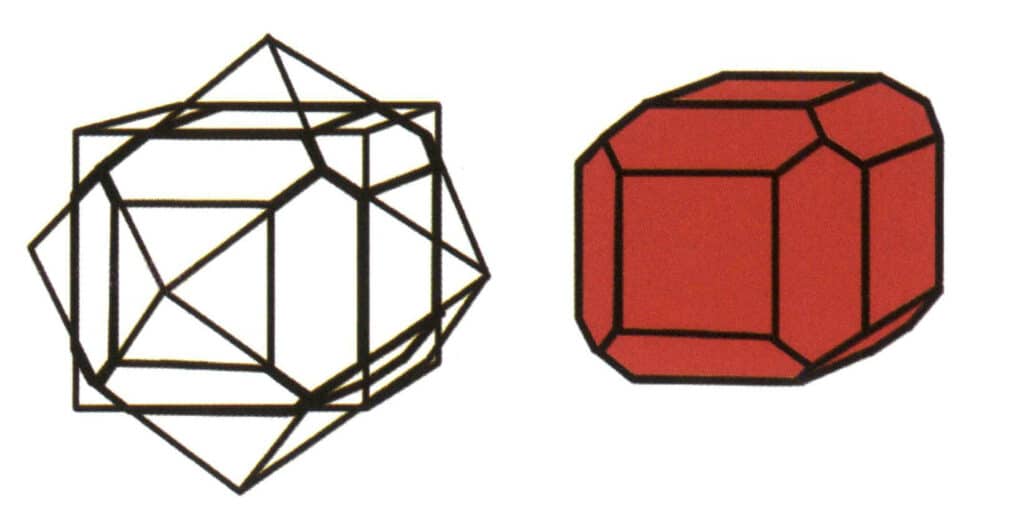
Abbildung 2-1-7 Kombinat aus Würfeln und Rhombendodekaedern
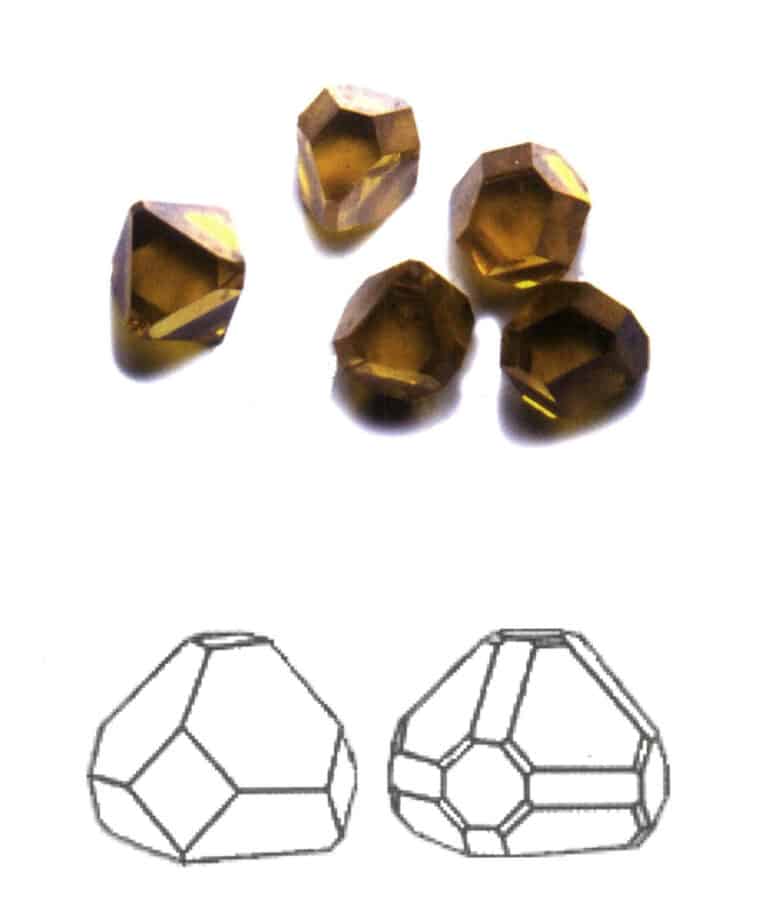
Der wichtigste Punkt bei der Identifizierung von Kombinationsformen ist das Vorhandensein von zwei oder mehr unterschiedlich geformten Kristallflächen im Kristall.
Wenn Einkristalle in der Natur vorkommen, weichen sie immer erheblich von der idealen Morphologie von Einkristallen ab (Abbildung 2-1-9), wie z. B. eine einzelne Fläche, die nicht unbedingt die gleiche Form und Größe hat, und das Verschwinden von Kristallflächen, was als verzerrte Kristalle bezeichnet wird.

Verzerrte Kristalle können auch als echte Kristalle bezeichnet werden, die in der Natur unter dem Einfluss der Wachstumsumgebung entstehen. Die mehrfachen Kristallflächen, die sich bei idealen Kristallen in festen Winkeln wiederholen, müssen nicht unbedingt die gleiche Form und Größe haben. Dennoch müssen die Kristallflächen desselben monomorphen Kristalls das gleiche Muster und die gleichen physikalischen Eigenschaften aufweisen. Die Winkel zwischen den entsprechenden Kristallflächen bleiben unverändert, was die inhärente Symmetrie des Kristalls selbst widerspiegelt. Die in der Realität vorkommenden Kristalle sind in unterschiedlichem Maße verzerrt.
Zwillingskristalle können auch als Kristalle bezeichnet werden, die in der Natur unter dem Einfluss der Wachstumsumgebung entstehen. Die mehrfachen Kristallflächen, die sich bei idealen Kristallen in festen Winkeln wiederholen, müssen nicht unbedingt die gleiche Form und Größe haben. Dennoch müssen bei der gleichen Art von Kristall die Flächen der gleichen Form die gleichen Muster und physikalischen Eigenschaften aufweisen. Die Winkel zwischen den entsprechenden Kristallflächen bleiben unverändert, was die inhärente Symmetrie des Kristalls selbst widerspiegelt. Die in der Realität vorkommenden Kristalle sind alle in unterschiedlichem Maße verzwillingt.
3. Die Kristallisationsgewohnheiten von Kristallen
In der Natur entstandene Kristalle können nie eine perfekte Form erreichen. Wenn sie in den Zwischenräumen von Gesteinsschichten wachsen und von Gestein umgeben sind, wird die natürliche Form des Kristalls verzerrt. Auch im Labor gezüchtete Kristalle werden durch den Einfluss der Schwerkraft deformiert. Nur unter den Bedingungen der Schwerelosigkeit auf der Internationalen Raumstation können die Wissenschaftler Kristalle in perfekter Form züchten.
Obwohl die Formen der Kristalle nicht perfekt sind, neigt jede Art von Mineralkristall dazu, auf unterschiedliche Art und Weise zu wachsen oder zusammenzuwachsen.
Jedes Mineral neigt dazu, sich unter bestimmten Bedingungen zu bilden, und seine Eigenschaften spiegeln die Bedingungen seiner Bildung wider. Einige Mineralien, wie z. B. Quarz, haben komplexe und variable Entstehungsbedingungen. Daher besitzt auch Quarz mehrere Habits.
Im Allgemeinen bezieht sich der Begriff Kristallgewohnheiten auf die Eigenschaften eines bestimmten Kristalls, der unter bestimmten äußeren Bedingungen dazu neigt, eine bestimmte Form anzunehmen. Manchmal bezieht sich der Begriff auch auf die allgemeinen Typen der einfachen Form dieses Kristalls.
Je nach dem Grad der Entwicklung der Kristalle im dreidimensionalen Raum werden die Kristallgewohnheiten in drei Grundtypen unterteilt.
(1) Uni-direktionale Erweiterung
Die Kristalle erstrecken sich in eine Richtung und treten in säulenförmigen, nadelförmigen, faserigen Formen usw. auf. Mineralien wie Beryll, Turmalin, Hornblende und Malachit weisen häufig diesen Habitus auf (Abbildungen 2-1-10 bis 2-1-11).

Abbildung 2-1-10 Säulenförmiger Aquamarin (oben) und sein Kristallhabitusdiagramm (unten)

Abbildung 2-1-11 Faseriger Malachit (oben) und sein Kristallhabitusdiagramm (unten)
(2) Bi-direktionale Erweiterung
Die Kristalle erstrecken sich in einer Ebene und treten in Form von Platten, Blättern, Schuppen usw. auf, da Minerale wie Wolframit, Glimmer, Plumbago und Tansanit häufig diesen Habitus aufweisen (Abbildung 2-1-12).
(3) Tri-Richtungsisometrisch
Die Kristalle entwickeln sich gleichmäßig in drei Richtungen und weisen isometrische, körnige Formen auf, wie Spinell, Granat, Diamant, Pyrit und Fluorit, die häufig diesen Habitus aufweisen (Abbildungen 2-1-13, 2-1-14).

Abbildung 2-1-12 Der plättchenförmige Kristallhabitus des Tansanits (oben) und sein Kristallhabitusdiagramm (unten)

Abbildung 2-1-13 Der oktaedrische Kristallhabitus des Edelsteins Spinell (oben) und sein Kristallhabitusdiagramm (unten)
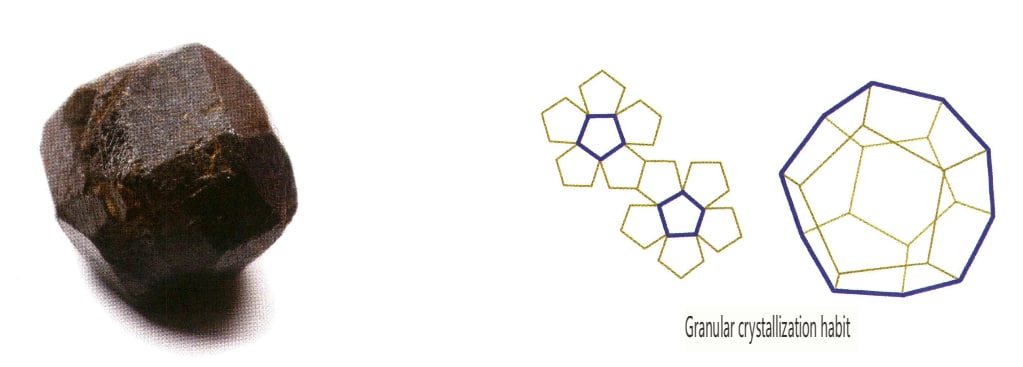
Darüber hinaus gibt es Übergangstypen wie kurze säulenförmige, plattenförmige, streifenförmige und dicke plattenförmige Formen.
Die chemische Zusammensetzung und Struktur des Kristalls bestimmen hauptsächlich die Kristallform. Sie steht auch in engem Zusammenhang mit den äußeren Bedingungen während der Kristallbildung (wie Temperatur, Druck, Konzentration, Viskosität und Verunreinigungen), wie z. B. die Unterschiede in der Kristallform zwischen Diamanten und synthetischen Diamantkristallen.
4. Regelmäßige Aggregation von Kristallen
In der Natur findet man einzelne Kristalle (Abbildung 2-1-15) und zwei oder mehr Einkristalle, die zu einem Ganzen zusammenwachsen. Dieses Phänomen des Zusammenwachsens mehrerer Kristalle wird als Kristallaggregation bezeichnet. Die Kristallaggregation kann in unregelmäßige und regelmäßige Formen unterteilt werden. Die unregelmäßige Kristallaggregation kann als Kollektiv verstanden werden, worauf in Kapitel drei näher eingegangen wird. Bei der regelmäßigen Kristallaggregation gibt es vier gängige Typen: parallele Aggregation, Zweikristallbildung, Überwachsen und Zwischenwachsen (Abbildungen 2-1-16 bis 2-1-18). In diesem Abschnitt wird hauptsächlich die als Bikristalle bekannte Art der regelmäßigen Aggregation behandelt.

Abbildung 2-1-15 Einkristall (Turmalin)
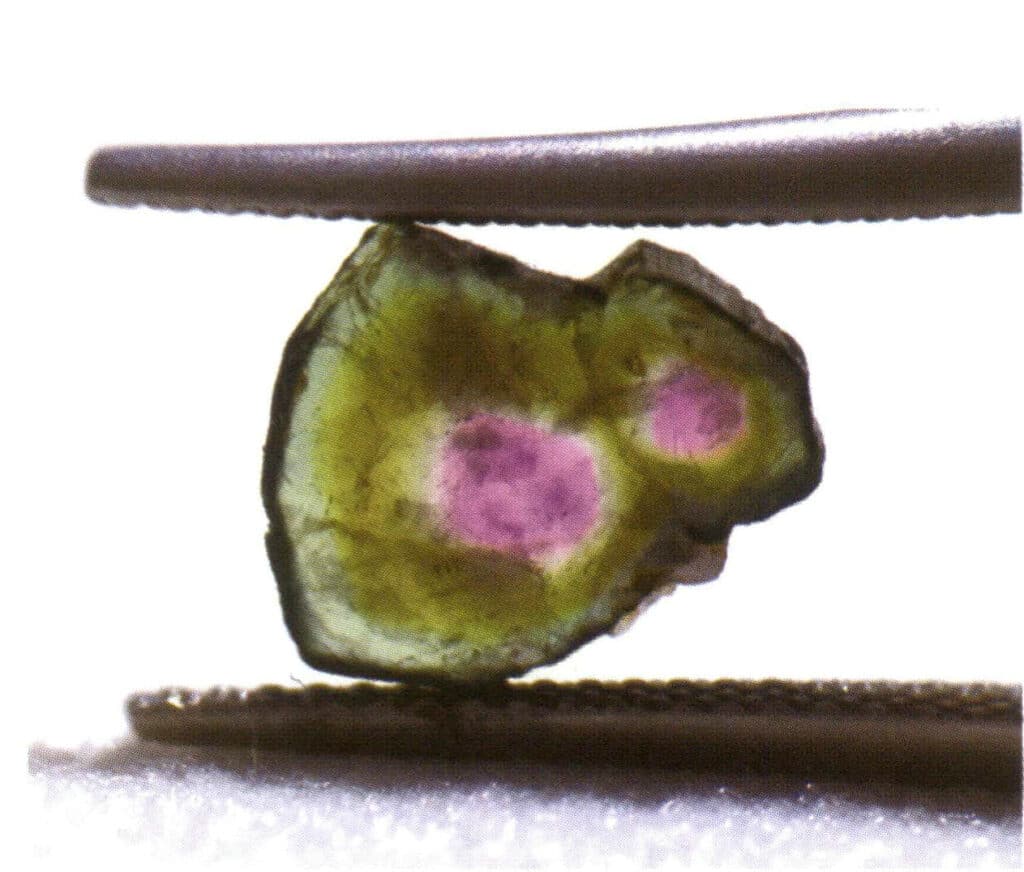
Abbildung 2-1-16 Parallelaggregation (Wenn mehrere Kristalle desselben Typs parallel im Raum wachsen, spricht man von Parallelaggregation. Zu diesem Zeitpunkt sind die entsprechenden Kristallflächen und Kanten der gewachsenen Kristalle alle parallel zueinander).

Abbildung 2-1-17 Zwillingskristall (Spinell)

Abbildung 2-1-18 Überwachsen (eine Art von Kristall wächst auf der Oberfläche eines anderen Kristalls in einer bestimmten kristallographischen Richtung, auch bekannt als epitaxiales Wachstum)
Bikristalle sind die regelmäßige Ansammlung von zwei oder mehr identischen Kristallen nach bestimmten symmetrischen Regeln. (Zwillingsachse, Zwillingsebene) Die entsprechenden Flächen, Kanten und Winkel der beiden benachbarten Individuen sind nicht vollständig parallel. Dennoch können sie sich durch symmetrische Operationen wie Rotation und Rotationsumkehrung gegenseitig spiegeln, so dass die beiden Individuen zusammenfallen oder sich ausrichten können.
4.1 Schlüsselpunkte für die Identifizierung von Zweikristallen
① Konkave Winkel sichtbar in verzwillingten Kristallen (Abbildung 2-1-19).
② Stylolith: Die Mikromorphologie und andere Merkmale der Kristallflächen auf beiden Seiten des Styloliths sind diskontinuierlich (Abbildung 2-1-20).
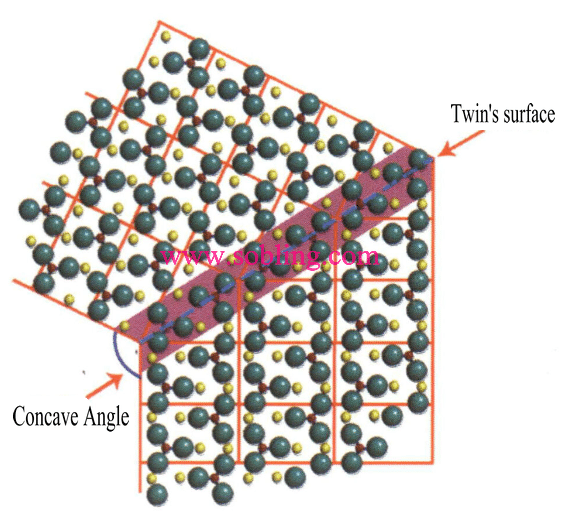
Abbildung 2 - 1-19 Konkaver Winkel des Zwillings
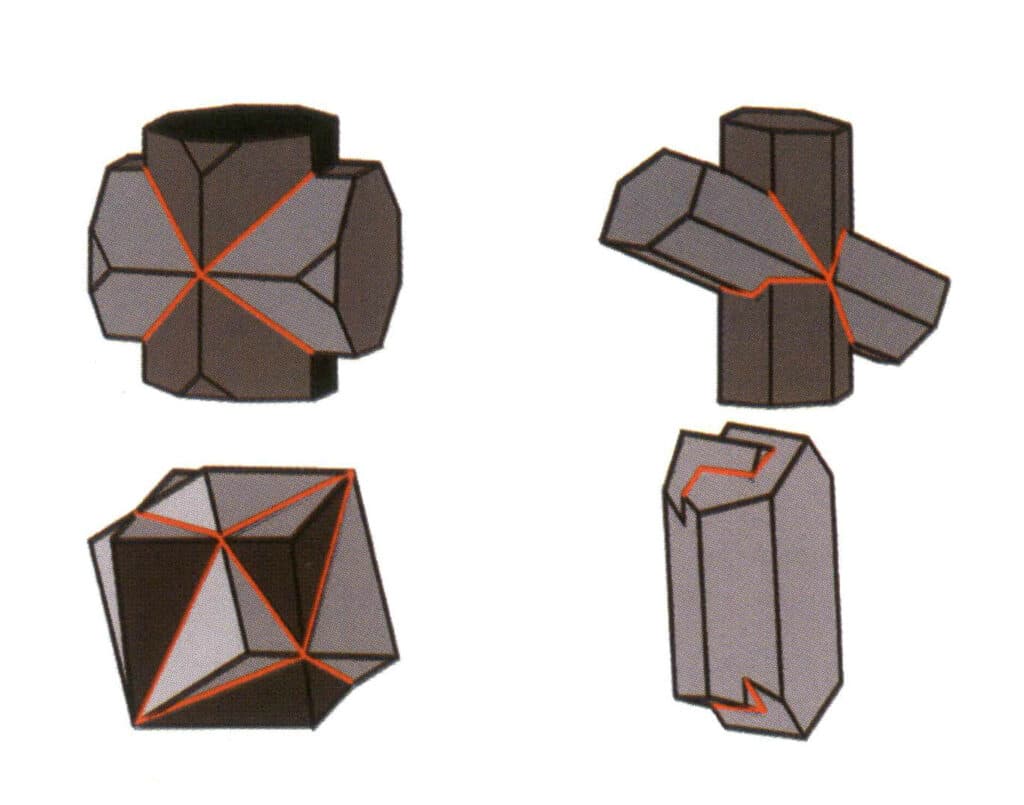
Abbildung 2-1-20 Stylolith (verschiedene Farben in der Abbildung stehen für verschiedene Kristalle; die roten Linien zeigen den Zwillingsstylolith an)
③ Zwillingsstreifung: Kristallflächen oder Spaltungsebenen zeigen feine Zwillingsstreifen (Abbildung 2-1-21)
④ Ätzfigur: Das Aussehen des Ätzbildes weist auf das Vorhandensein von Zwillingen hin (Abbildung 2-1-22)

Abbildung 2-1-21 Schematische Darstellung von polysynthetischen Zwillingen

Abbildung 2-1-22 Oberfläche von Spinell mit umgekehrten dreieckigen Vertiefungen.
⑤ Das Auftreten von Pseudosymmetrie: das Auftreten von Symmetriebeziehungen, die nicht mit der inhärenten Punktgruppe des Einkristalls übereinstimmen (Abbildung 2-1-23 bis Abbildung 2-1-24).

Abbildung 2-1-23 Einkristall von Chrysoberyll

Abbildung 2-1-24 Knieförmiger Zwilling des Chrysoberylls
Die Zwillingsbildung wird anhand ihrer Stapelungseigenschaften in fünf Typen unterteilt: Kontaktzwillinge (Abbildung 2-1-25 bis Abbildung 2-1-26), polysynthetische Zwillinge (Abbildung 2-1-27), interpenetrierende Zwillinge (Abbildung 2-1-28), Triplettkristalle (Abbildung 2-1-29) und komplexe Zwillinge, von denen die ersten vier Typen am häufigsten vorkommen.


Abbildung 2-1-26 Kontaktverzwillingung von Spinell (oben) und seine schematische Darstellung (unten)

Abbildung 2-1-27 Polysynthetischer Zwilling von Labradorit (oben) und seine schematische Darstellung (unten)
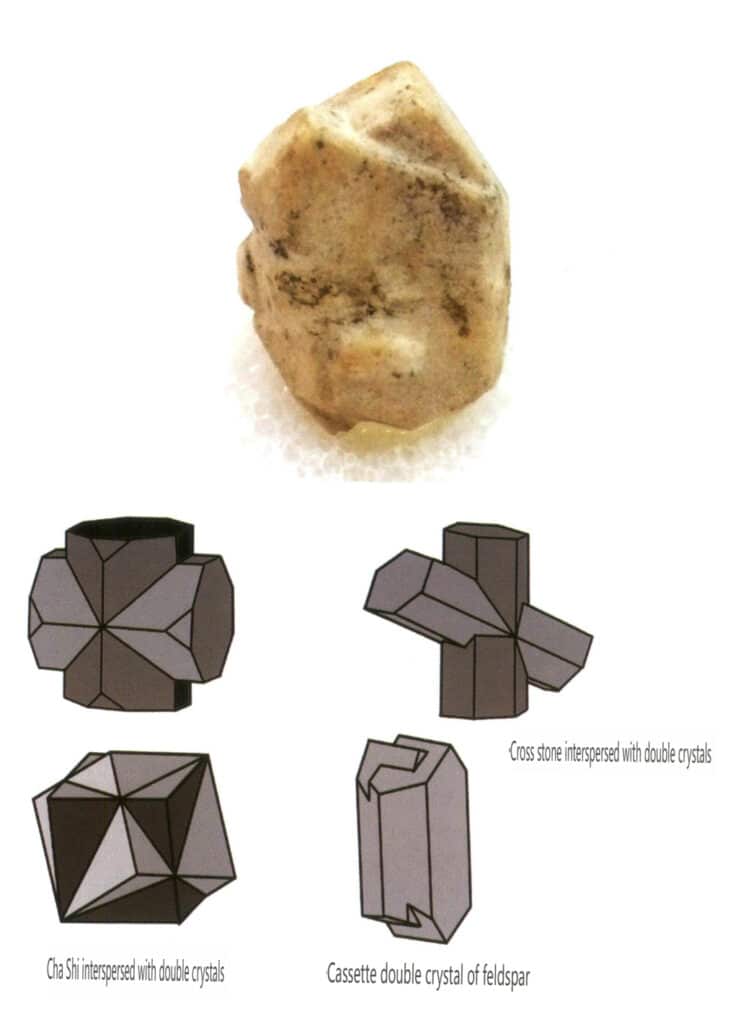
Abbildung 2-1-28 Feldspat-Zwillingskristalle (oben) und Schema der sich gegenseitig durchdringenden Zwillingskristalle anderer Typen (unten)

Abbildung 2-1-29 Trigonale Verzwillingung von Chrysoberyll (oben) und ihre schematische Darstellung (unten)
4.2 Die Bildung von Zweikristallen
① Entsteht während des Kristallwachstums und kann sich aus kristallinen Zwillingskeimen oder kleinen Kristallen entwickeln, die je nach Position des Zwillings wachsen.
② Entsteht bei der Umwandlung von Heteromorphismen, z. B. wenn sich α-Quarz in β-Quarz verwandelt und Zwillinge bildet.
③ Entsteht durch mechanische Einwirkung, wobei ein Teil des Kristalls entlang einer bestimmten Richtungsebene gleitet und Verformungszwillinge bildet, wie z. B. die Zwillinge von Calcit.
5.Crystal Face Patterns
Wenn Kristalle in der Natur entdeckt werden, weisen sie oft unvollständige Formen (Abbildung 2-1-30) und besondere Oberflächenmuster auf. Manchmal wachsen sie in Clustern zusammen (Abbildung 2-1-31), die oft erhebliche Unterschiede zu den uns bekannten geometrischen Standardpolyedern wie Würfel und sechseckige Prismen aufweisen. Dieses Phänomen wird als reale Form von Kristallen bezeichnet. Die reale Form von Kristallen wird in der Kristallographie detailliert klassifiziert, z. B. als verzerrte Kristalle, konvexe Kristalle, gekrümmte Kristalle, schwebende Kristalle, Kristallflächenstreifen, Ätzfiguren, Zwillingsstreifen usw.

Abbildung 2-1-30 Rubinkristall

Abbildung 2-1-31 Pyritkristalle (links: mehrere zusammengewachsene Pyritkristalle, rechts: ein einzelner Pyritkristall)
In diesem Abschnitt geht es hauptsächlich um die Kristallflächenmuster in der realen Form von Kristallen.
Theoretisch sind die Kristallebenen glatt und flach. Während des Wachstums oder der Auflösung von Kristallen hinterlässt die Oberfläche jedoch oft leicht ungleichmäßige, regelmäßige Muster, die gemeinhin als Kristallflächenmuster bezeichnet werden. Zu den Kristallflächenmustern gehören Wachstumsstreifen, Wachstumsschichten, spiralförmige Muster, Wachstumshügel und Ätzfiguren. Die in diesem Buch besprochenen Kristallflächenmuster beziehen sich hauptsächlich auf die Kristallflächenstreifen und Ätzfiguren, die mit bloßem Auge oder unter geringen Vergrößerungsbedingungen beobachtet werden können.
Bei den Kristallflächenstreifen handelt es sich um eine Reihe von parallelen geraden Linien auf der Kristalloberfläche, die durch das wiederholte Zusammentreffen und abwechselnde Wachstum verschiedener Einzelformen entstehen. Diese auch als "Kombinatstreifen" bezeichneten Streifen sind nur auf der Kristalloberfläche zu sehen und werden auch als Wachstumsstreifen bezeichnet. Zum Beispiel weist die hexagonal prismatische Kristallfläche von Quarz oft hexagonal prismatische und rhombisch dodekaedrische Feinkristallflächen auf, die sich abwechselnd zu Aggregat-Querstreifen entwickeln (Abbildung 2-1-32).

Als Ätzfiguren werden die spezifisch geformten Vertiefungen (d. h. Ätzgruben) bezeichnet, die nach der Kristallbildung aufgrund von Korrosion auf der Kristalloberfläche zurückbleiben. Die Ätzgrübchen werden durch die Anordnung der Elementarteilchen innerhalb der Kristallfläche gesteuert. Daher variieren die Formen und Ausrichtungen der Ätzfiguren zwischen verschiedenen Mineralen und einzelnen Formen desselben Kristalls. So variieren beispielsweise die Ätzfiguren auf verschiedenen Einheitsformen von Diamantkristallen; dreieckige Vertiefungen sind auf oktaedrischen Kristallen zu sehen (Abbildung 2-1-33), viereckige Vertiefungen auf kubischen Flächen, überlappende viereckige Vertiefungen bilden ein gitterartiges Muster, und Linienmuster oder mikroskopische scheibenartige Muster sind auf rhombischen Dodekaedern zu sehen (Abbildung 2-1-34).

Abbildung 2-1-33 Sichtbare umgekehrte dreieckige Vertiefungen auf dem oktaedrischen Diamantkristall

Abbildung 2-1-34 Geradlinig gemusterte Textur, sichtbar an rautenförmigen dodekaedrischen Kristallen
Nur die Ätzfiguren auf der gleichen Kristallfläche der gleichen Form können gleich sein. Daher werden Ätzfiguren oft zur Identifizierung von Mineralen und zur Feststellung verwendet, ob die Kristallflächen zur gleichen Einheitsform gehören (Abbildung 2-1-35 bis Abbildung 2-1-42).

Abbildung 2-1-35 Streifen aus Fluoritkristallen mit Intarsien im Holzbodenstil

Abbildung 2-1-36 Natürliche dreieckige Ätzfigur in Rubin (häufige horizontale Streifen in Rubinen, Wachstumslinien parallel zur rhomboedrischen Richtung, natürliche Ätzungen in dreieckiger oder sechseckiger Form)

Abbildung 2-1-37 Längsstreifen an der Oberfläche von Turmalin

Abbildung 2-1-38 Horizontale Streifen auf der Oberfläche des Kristalls

Abbildung 2-1-39 Ätzfiguren auf der Oberfläche des Kristalls

Abbildung 2-1-40 Oberflächenlängsstreifen von Topas

Abbildung 2-1-41 Topographisches Bild eines Topaskristalls

Abbildung 2-1-42 Ätzbilder von Spinell
Abschnitt II 47 Arten von Kristallformen
In der Kristallographie gibt es 146 verschiedene Einzelformen, die sich aufgrund ihrer geometrischen Form, wenn sie unabhängig voneinander existieren, in 47 geometrische Formen einteilen lassen. Diese geometrischen Formen werden auf folgende Weise benannt:
① Benannt nach den Merkmalen der Querschnittsform, wie trigonales Prisma, tetragonales Prisma, hexagonales Prisma, rhomboedrische Bipyramide usw.
② Benannt nach der Form der Einzelform, z. B. Zylinder, Doppelkegel, Würfel usw.
③ Benannt nach der Anzahl der geometrischen Flächen, z. B. Einflächner, Oktaeder usw.
④ Benannt nach der Form der geometrischen Flächen, z. B. Rhomboeder, Pentakontaeder, usw.
In der Kristallographie werden Einzelformen in vier Kategorien eingeteilt: allgemeine Formen und Sonderformen, geschlossene Formen und offene Formen, regelmäßige Formen und unregelmäßige Formen, linksdrehende Formen und rechtsdrehende Formen. In diesem Kapitel wird kurz auf geschlossene und offene Formen eingegangen.
Geschlossene Formen beziehen sich auf solche, deren Kristallflächen einen geschlossenen Raum einschließen können. Sie werden in drei Hauptkategorien unterteilt: polyedrische Klassen, schiefpolyedrische Klassen und bipyramidale Klassen, die insgesamt 30 Typen umfassen. Jede Kategorie hat detailliertere Klassifizierungen; die polyedrische Klasse ist beispielsweise in die tetraedrische Klasse, die oktaedrische Klasse, die kubische Klasse usw. unterteilt (Abbildungen 2-1-43 bis 2-1-48).

Abbildung 2-1-43 Tetraederklasse
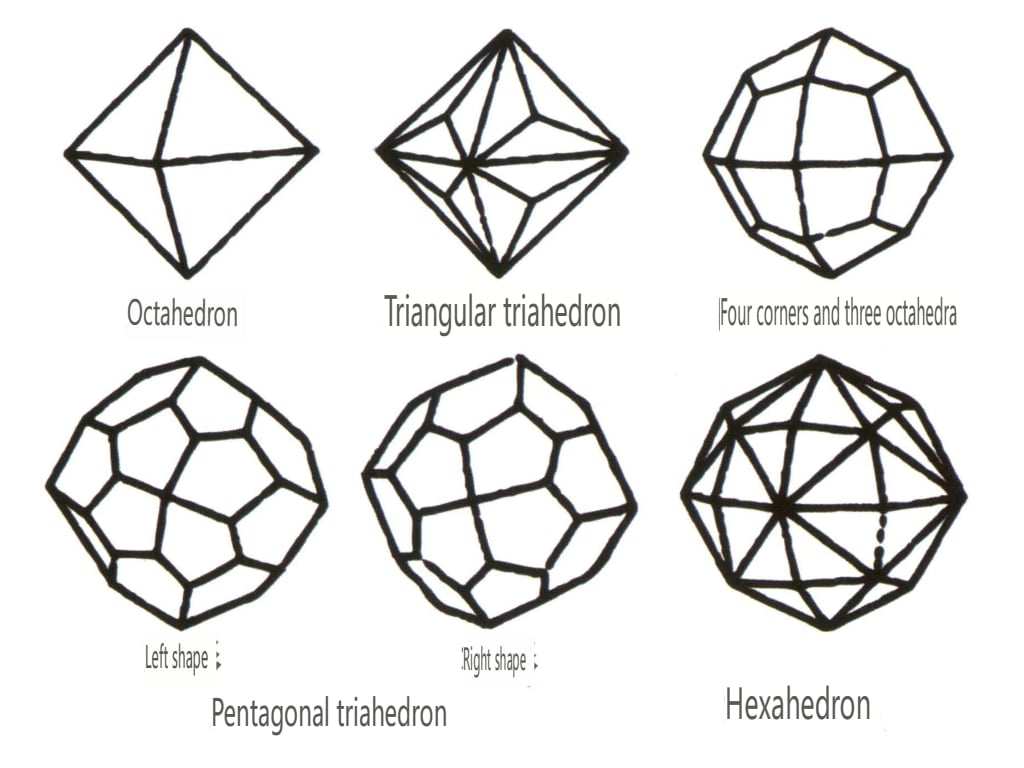
Abbildung 2-1-44 0ktaedrische Klasse
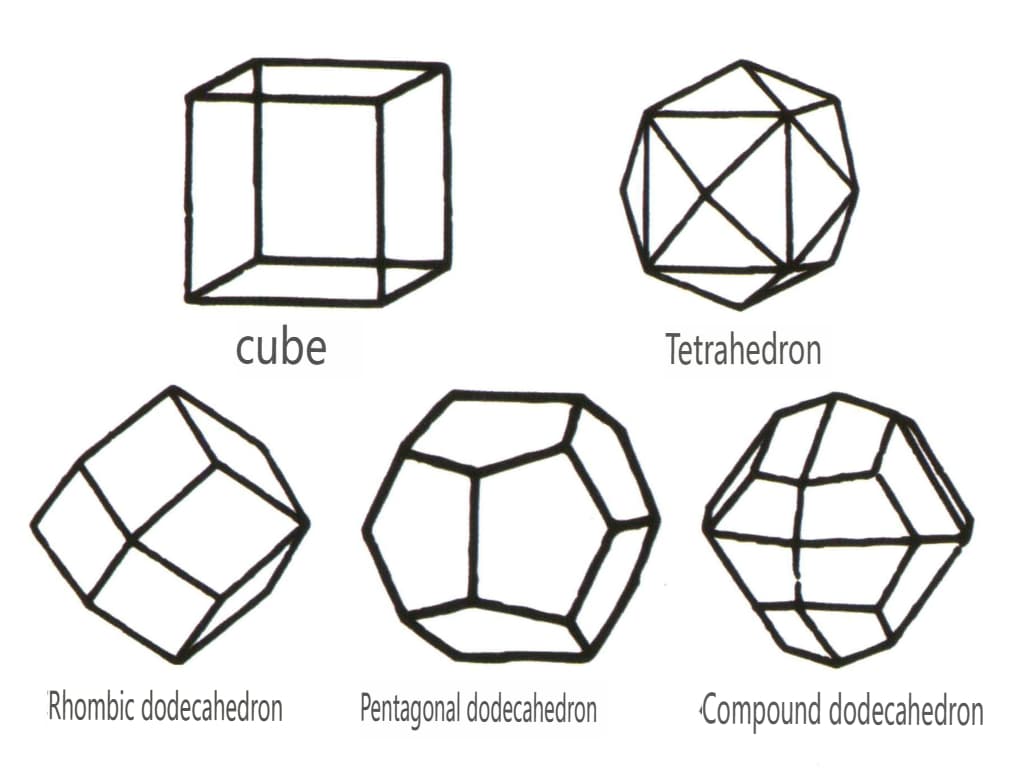
Abbildung 2-1-45 Kubische und dodekaedrische Klassen
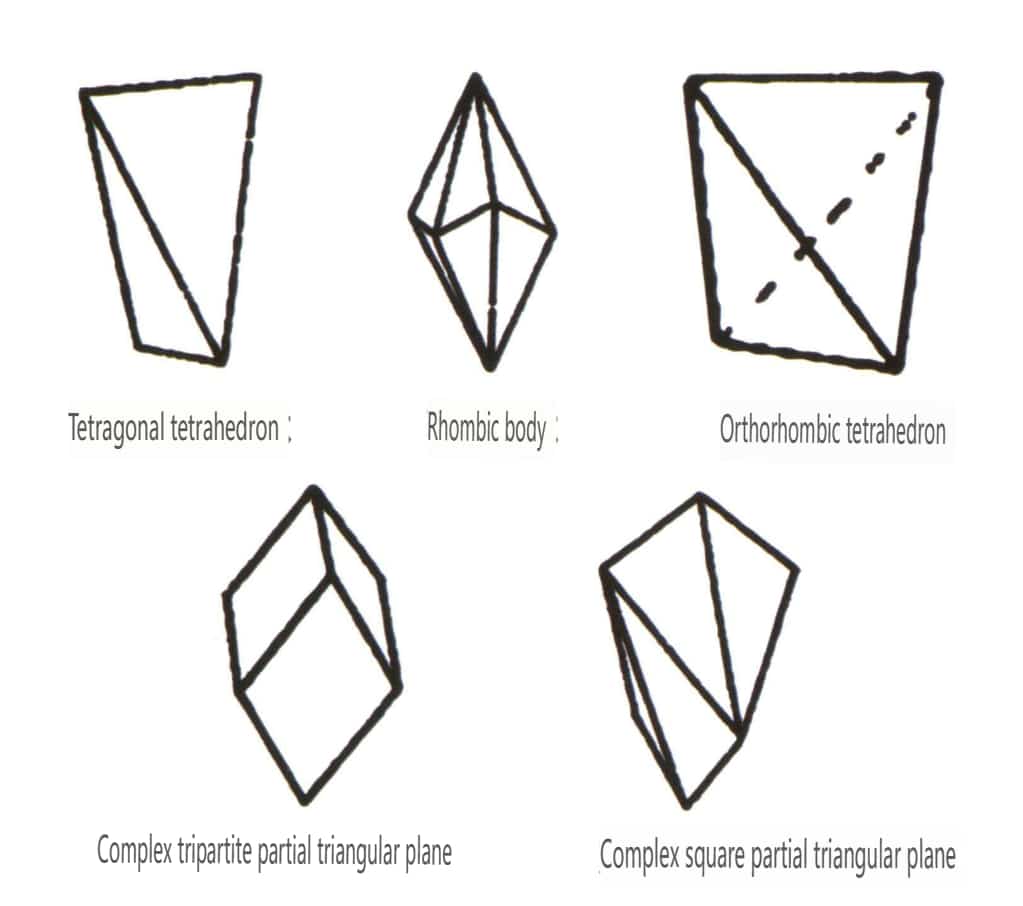
Abbildung 2-1-46 Andere polyedrische Typen
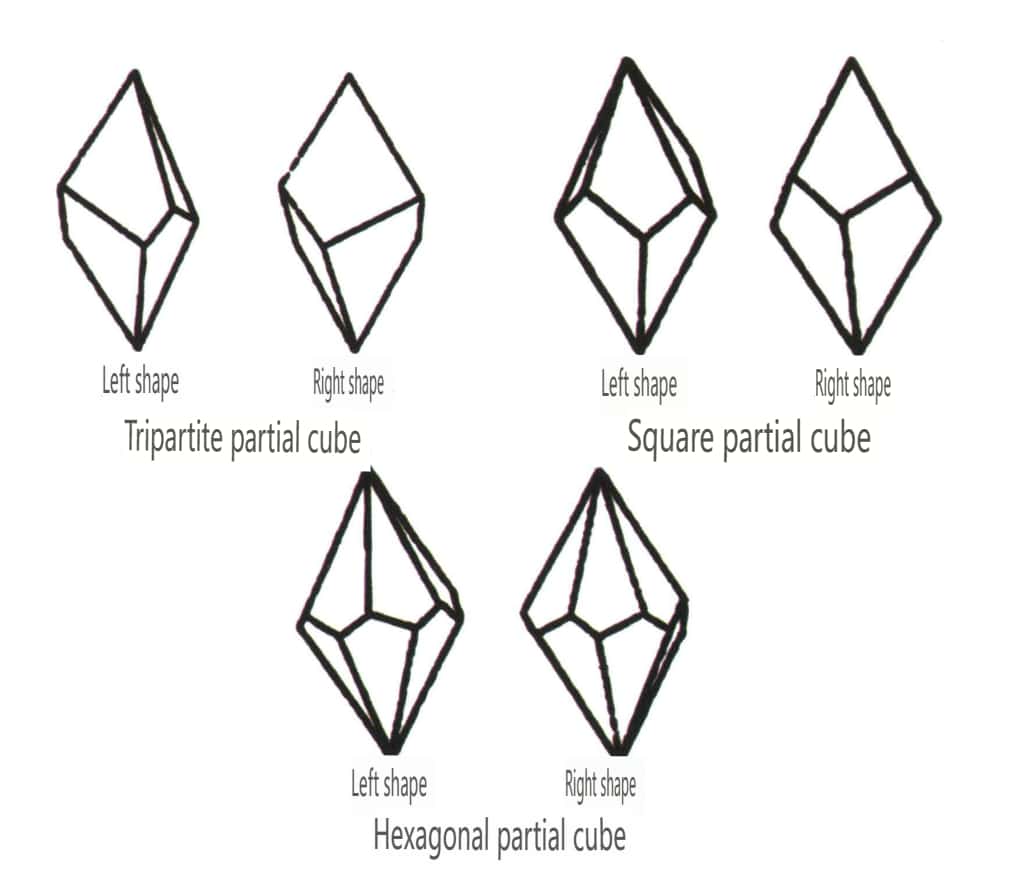
Abbildung 2-1-47 Schräge Kombinationsform Klasse
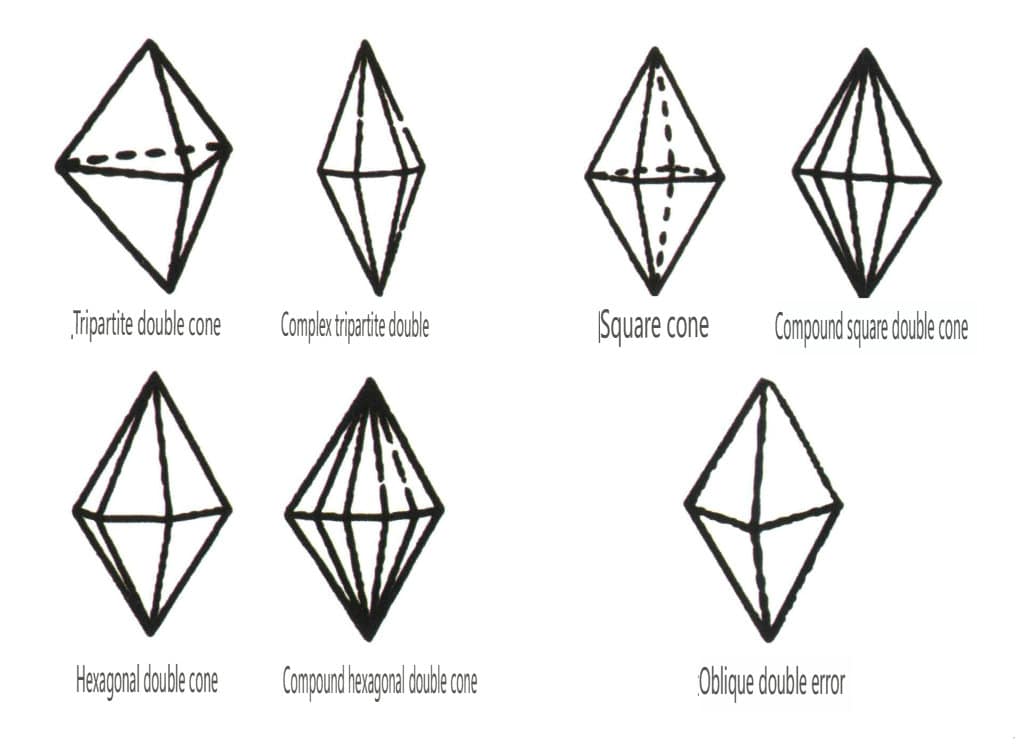
Abbildung 2-1-48 Doppelpyramidale Klasse
Offene Formen beziehen sich auf solche, deren Kristallflächen keinen geschlossenen Raum einschließen. Sie werden in vier Hauptkategorien unterteilt: einflächige, doppelflächige, säulenförmige und einpyramidale Klassen, die insgesamt 17 Typen umfassen (Abbildungen 2-1-49 und 2-1-51)
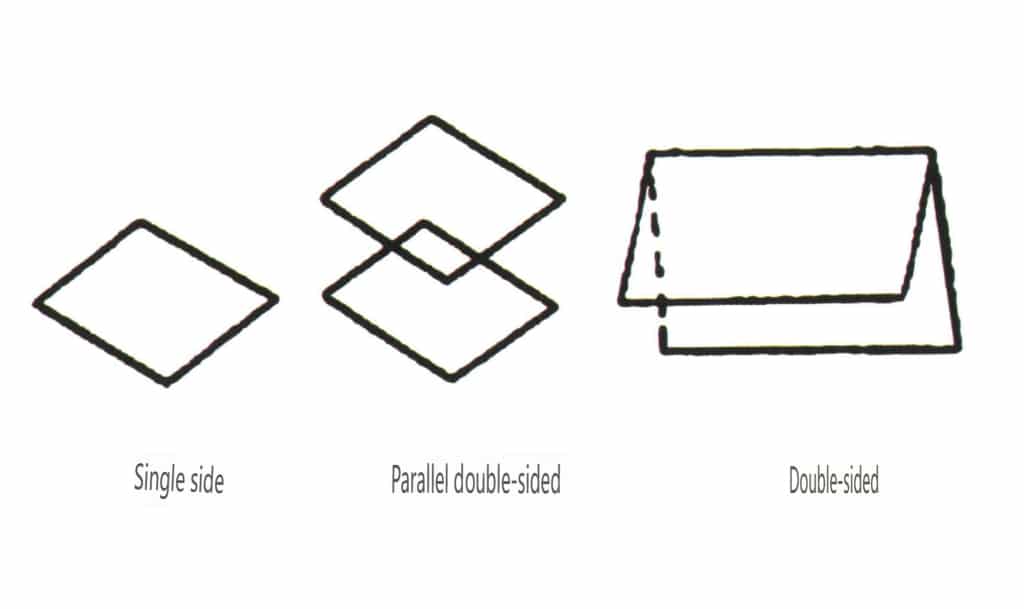
Abbildung 2-1-49 Einseitig und doppelseitig
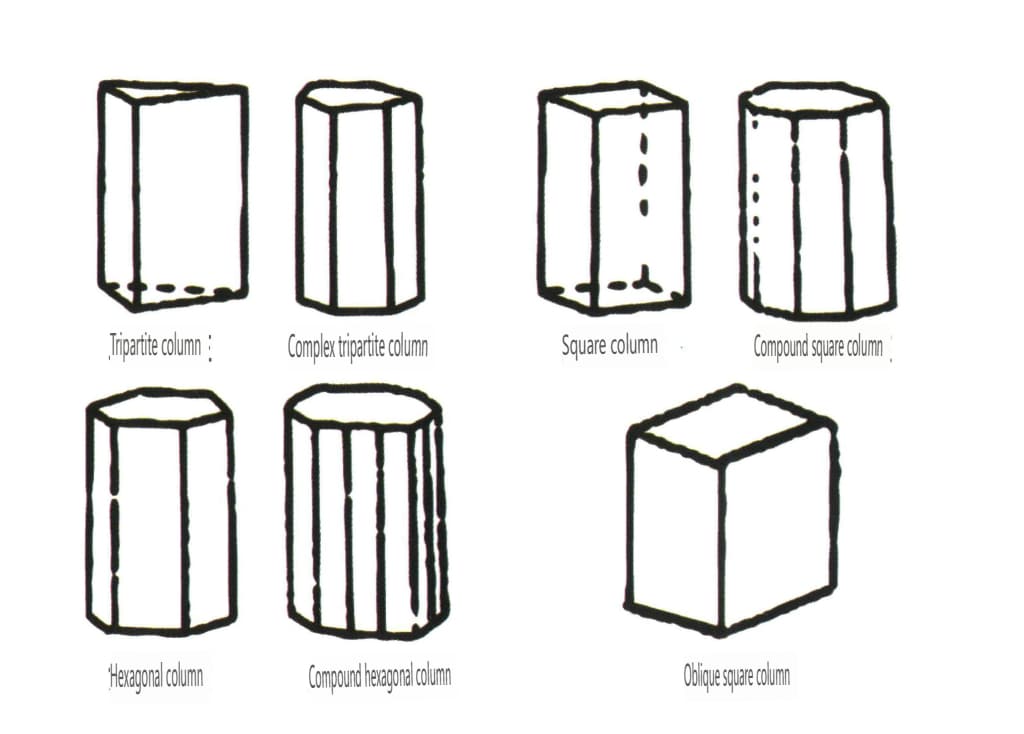
Abbildung 2-1-50 Spalten

Abschnitt III Klassifizierung von Kristallen
1. Symmetrie der Kristalle
Symmetrie ist ein abstraktes Konzept, das bei der Untersuchung echter Kristalle und unbearbeiteter Edelsteinmaterialien eine Rolle spielt. Es beschreibt die Wiederholung, die sich ergibt, wenn die Kristallstruktur durch eine Richtung oder Ebene, die durch sie verläuft, referenziert wird. Dies ist die Grundlage für die Klassifizierung von Kristallen.
Die Symmetrie eines Kristalls kann aus mikroskopischer Sicht als eine Methode zur Beschreibung der Wiederholbarkeit der Kristallstruktur und aus makroskopischer Sicht als die Wiederholung von zwei oder mehr geometrischen Flächen verstanden werden, die in Form und Größe gleich sind, sich aber in der Richtung nach bestimmten Regeln unterscheiden können. Dieses Wiederholungsmuster kann mit Hilfe von Symmetrieachsen und Symmetrieebenen beschrieben werden, wobei jede Symmetrieachse oder Symmetrieebene als Symmetrieelement bezeichnet wird. Wenn man die Symmetrie eines Objekts beobachtet oder daraus ableitet, bezeichnet man diesen Vorgang als Symmetrieoperationen.
2. Symmetrieelemente von Kristallen
In der Kristallographie gibt es vier Symmetrieelemente: die Symmetrieachse, die Symmetrieebene, die Rotoinversionssymmetrieachsen und das Symmetriezentrum. Hier geht es um die beiden Symmetrieelemente der Symmetrieachse und der Symmetrieebene.
2.1 Symmetrie-Achse
(1) Der Begriff der Symmetrieachse und ihre Schreibweise.
Die Symmetrieachse ist eine imaginäre gerade Linie, die angibt, wie oft die Basisebene (Abbildungen 2-2-1 bis 2-2-2) in derselben Position erscheint, wenn die Gitterstruktur um 360° um diese imaginäre Linie gedreht wird. Diese Zahl kann in 4 Fällen nur 2, 3, 4 oder 6 Mal sein. Sie kann auch als eine imaginäre Linie verstanden werden, die durch den Mittelpunkt des geometrischen Körpers verläuft, wobei der geometrische Körper entlang dieser Linie um 360° gedreht wird. Nehmen wir an, die Form des geometrischen Körpers nach der Drehung um einen bestimmten Winkel stimmt mit der Form des geometrischen Körpers im anfänglichen Null-Grad-Bereich überein. In diesem Fall wird diese imaginäre Linie als Symmetrieachse bezeichnet.
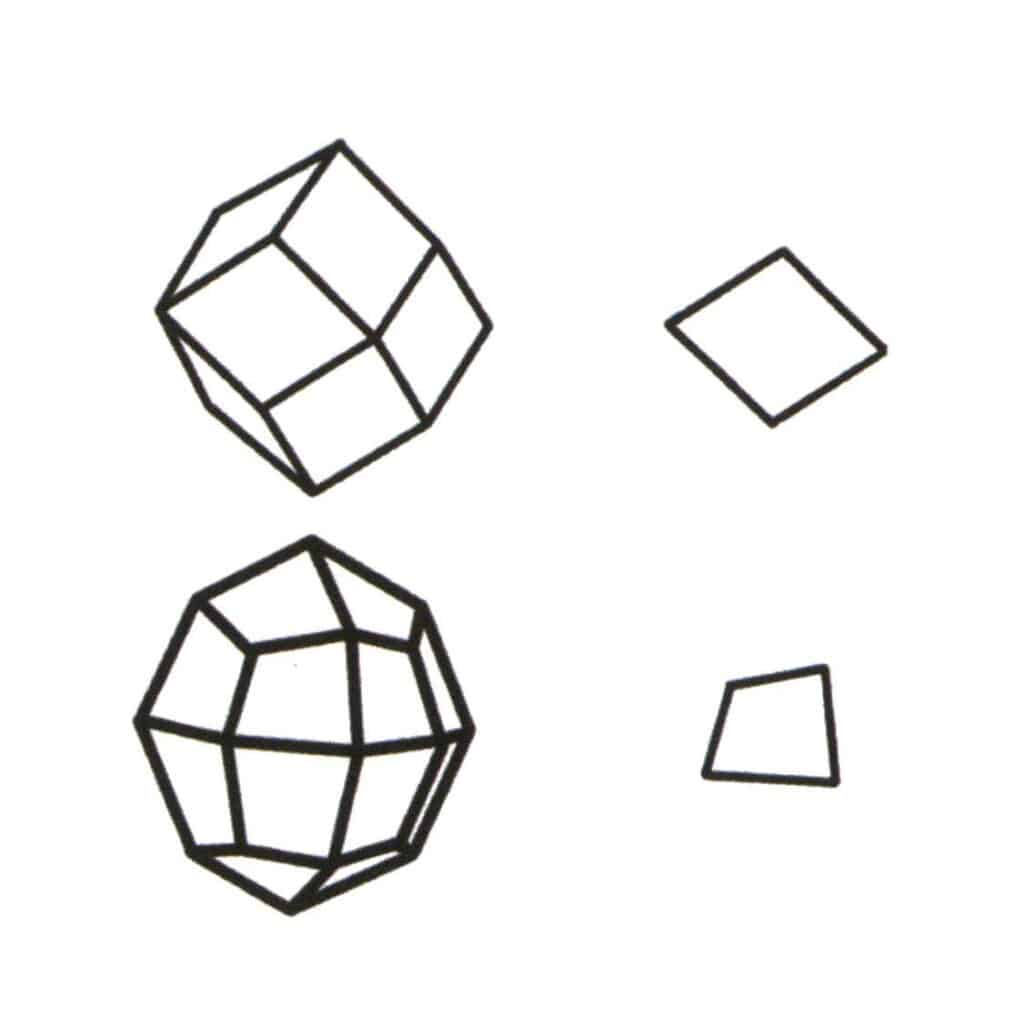
Abbildung 2-2-1 Auswahl der Basisebene für das Einzelformular.
Die Basisebene der Einzelform ist die kleinste sich wiederholende Ebene, die das Simplex bildet. Die obere linke Seite der Abbildung zeigt ein Rhombendodekaeder, eine geschlossene Form, die aus einer Art von Fläche besteht. Die kleinste sich wiederholende Ebene ist der oben rechts dargestellte Rhombus, so dass die Basisebene des Rhombendodekaeders der Rhombus ist. Unten links in der Abbildung ist ein vierseitiges Oktaeder zu sehen, das eine geschlossene Form ist, die aus einer Art von Fläche besteht. Die kleinste sich wiederholende Ebene ist das rechts unten dargestellte Viereck, so dass die Basisebene für das vierseitige Oktaeder das Viereck ist.
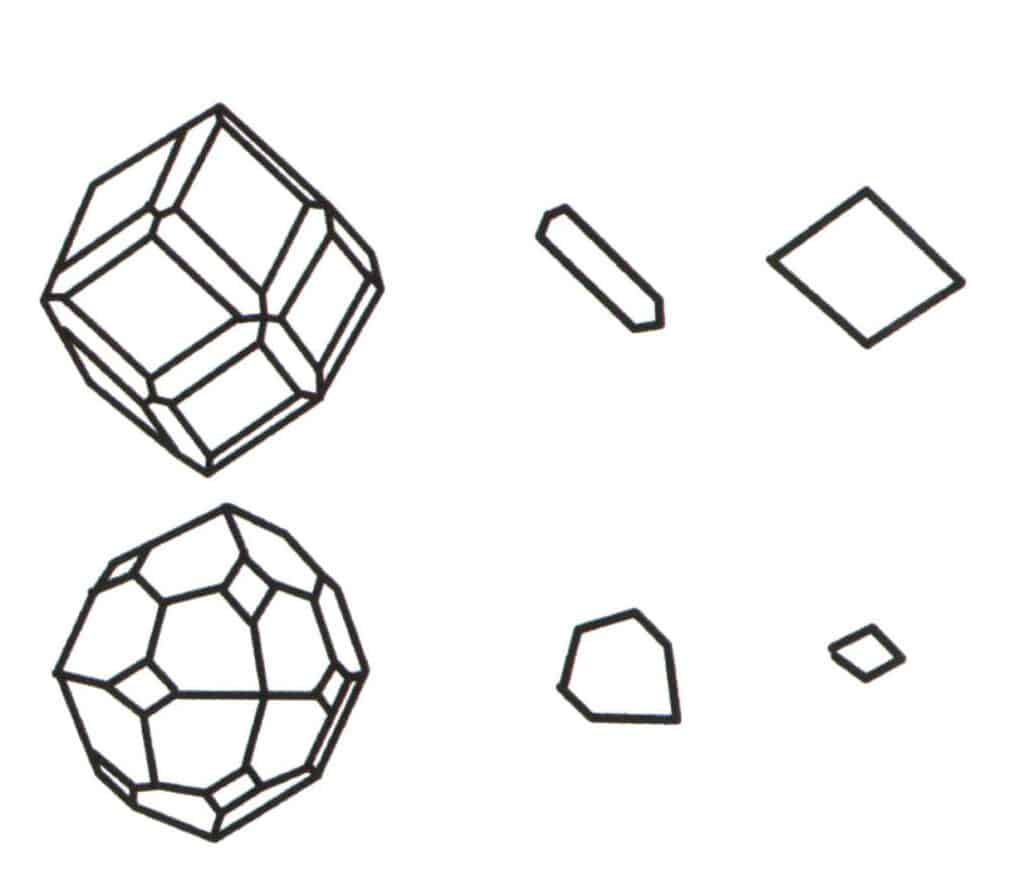
Abbildung 2-2-2 Auswahl der Basisebene für das Polytop.
Die Aggregation mehrerer einfacher Formen bildet eine kombinierte Form, und die Wahl der Basisebene für die kombinierte Form ist das Urteil über die Einzelformen, die sich zu der kombinierten Form zusammenschließen. Die erste Spalte von links in der Abbildung stellt eine kombinierte Form dar (gebildet durch die Aggregation der Einzelformen eines Dodekaeders und eines Tetraeders), und dieser geometrische Körper ist eine geschlossene Figur, die aus zwei Arten von Flächen besteht. Das Sechseck stellt die minimale Wiederholungsebene in der zweiten Spalte dar und die Raute rechts in der dritten Spalte. Die Basisebene für die Kombinationsform in der ersten Spalte ist also entweder das Sechseck oder die Raute. Bei der Berechnung der Symmetrieachse kann nur eine Form als Basisebene für die Symmetrieerfassung gewählt werden.
Die Symmetrieachse wird durch den Großbuchstaben L dargestellt, wobei die Reihenfolge der Achsen n in der oberen rechten Ecke von L geschrieben, geschrieben als Lⁿ. Zum Beispiel wird eine 2-fache Achse als L², eine 3-fache Achse als L³, eine 4-fache Achse als L⁴ und eine 6-fache Achse als L⁶ dargestellt. L⁶, L⁴, L³ werden üblicherweise als Achsen höherer Ordnung bezeichnet.
Kristalle können Symmetrieachsen in verschiedenen Richtungen haben, und die Anzahl dieser nicht zusammenfallenden Symmetrieachsen wird üblicherweise links von L geschrieben. Zum Beispiel werden sechs sekundäre Achsen als 6L² (Abbildung 2-2-3 bis Abbildung 2-2-9), drei tertiäre Achsen als 3L³ (Abbildung 2-2-10 bis Abbildung 2-2-14), vier tertiäre Achsen als 4L³ (Abbildung 2-2-15 bis Abbildung 2-2-18) und eine hexagonale Achse als L⁶ (Abbildung 2-2-19) dargestellt.
Wenn ein Kristall mehrere Symmetrieachsen hat, werden sie bei der aufgezeichneten Methode von links nach rechts in absteigender Reihenfolge angeordnet, wobei die Anzahl der Symmetrieachsen auf der linken Seite der entsprechenden Achse steht, z. B. L⁶6L², 3L⁴4L³6L².
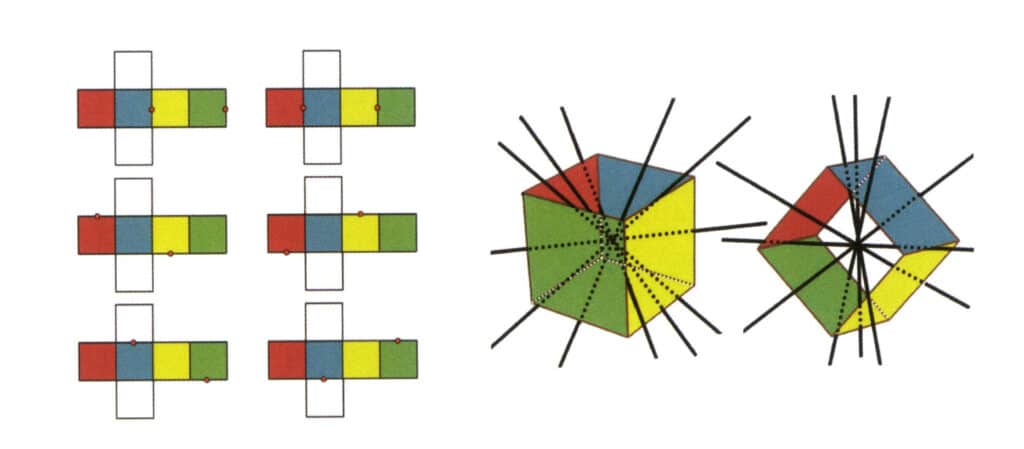
Abbildung 2-2-3 Sekundärachse des Würfels
Die linke Seite der Abbildung zeigt die aufgeklappte Ansicht eines Würfels, wobei die roten Punkte die Schnittpunkte der imaginären Linie und der Kanten anzeigen. Die rechte Seite der Abbildung zeigt einen geschlossenen Würfel, bei dem die sekundäre Achse im Mittelpunkt paralleler Kantenlinien, im Mittelpunkt paralleler rechteckiger Flächen oder in den Schnittpunkten dreier oder mehrerer paralleler Flächen, die einem Rechteck ähneln.
Copywrite @ Sobling.Jewelry - Hersteller von kundenspezifischem Schmuck, OEM- und ODM-Schmuckfabrik
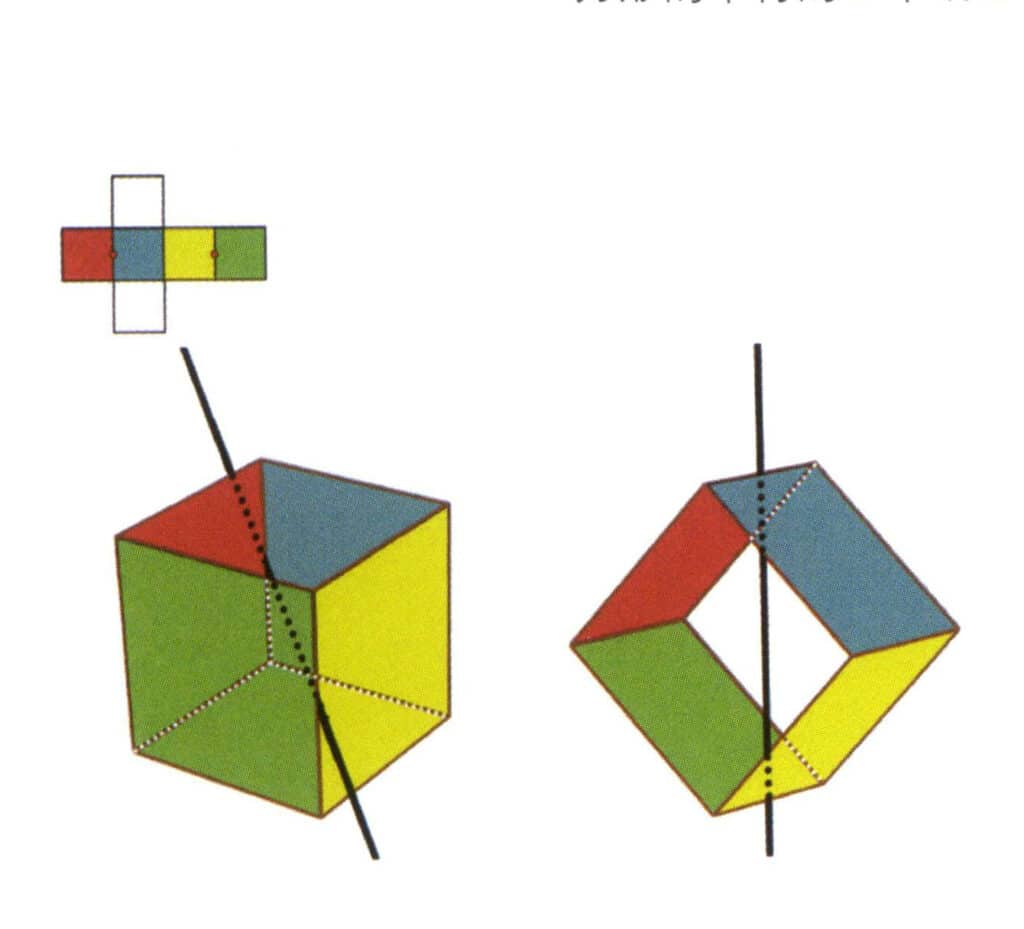
Abbildung 2-2-4 Die erste Nebenachse des Würfels
Wählen Sie den Mittelpunkt der parallelen Linien, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, und drehen Sie den Würfel um 360°. Die Basisebenen mit unterschiedlichen Farben, aber derselben Form, werden sich zweimal an derselben Stelle wiederholen (die rote und die blaue Fläche, die gelbe und die grüne Fläche, die beiden farblosen Flächen und drei Sätze von sich wiederholenden Flächen. Obwohl drei Sätze von wiederholten Flächen erscheinen, da die imaginäre Linie ihre Position und ihren Winkel nicht verändert hat, wird die sekundäre Achse nur einmal erfasst). Diese imaginäre Linie wird als Sekundärachse aufgezeichnet.
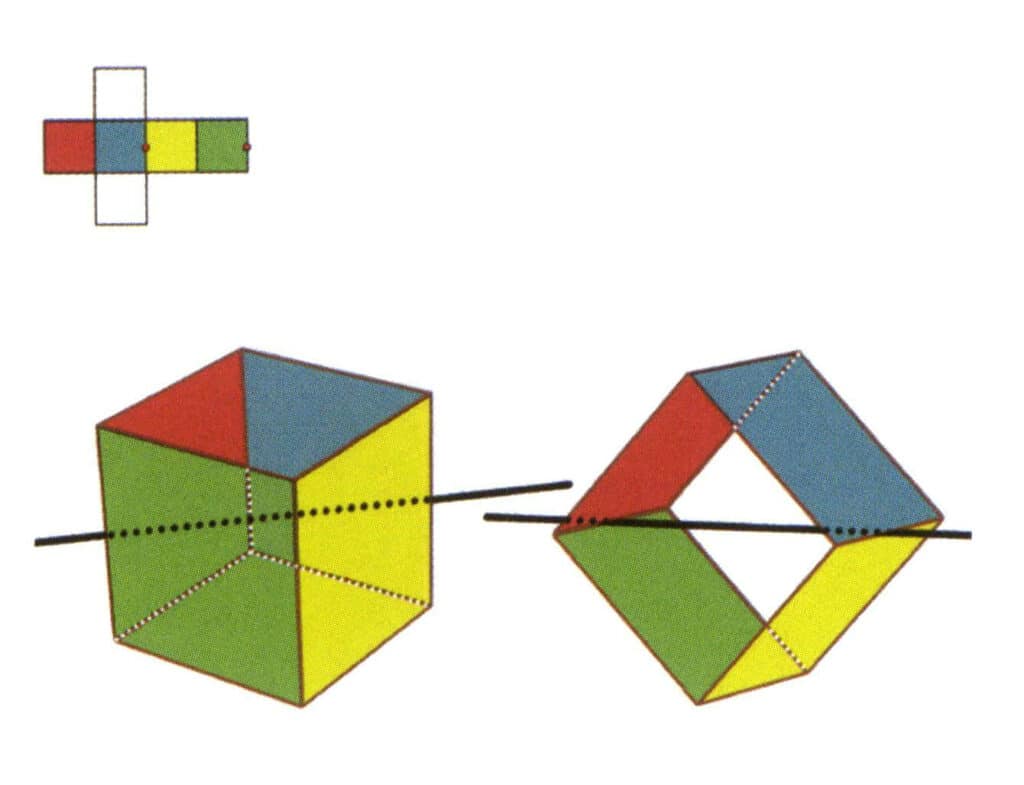
Abbildung 2-2-5 Die zweite Sekundärachse des Würfels
Wählen Sie den Mittelpunkt der parallelen Linien, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, und drehen Sie den Würfel um 360°. Die Basisebenen mit unterschiedlichen Farben, aber gleicher Form, werden sich zweimal an der gleichen Stelle wiederholen (die rote und die grüne Fläche, die gelbe und die blaue Fläche, die beiden farblosen Flächen und drei Sätze von wiederholten Flächen). Diese imaginäre Linie wird als zweite sekundäre Achse aufgezeichnet.
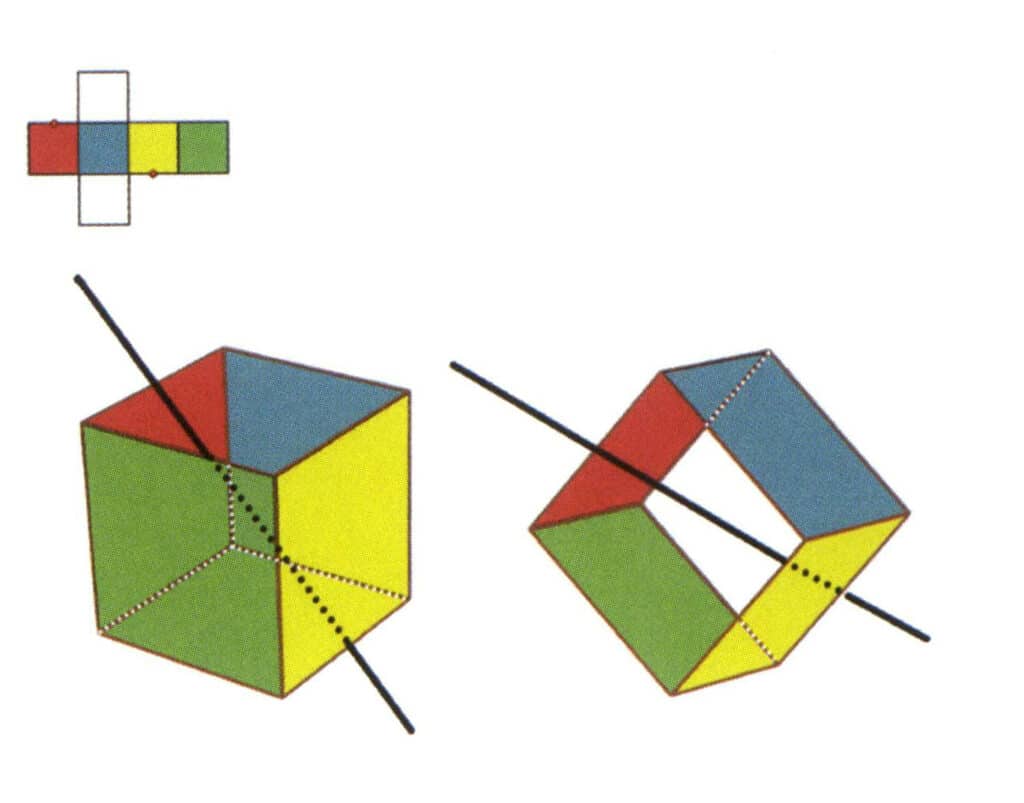
Abbildung 2-2-6 Die dritte Sekundärachse des Würfels.
Wählen Sie den Mittelpunkt der parallelen Linien, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft und den Würfel um 360° dreht. Die Basisebenen mit unterschiedlichen Farben, aber der gleichen Form werden sich zweimal an der gleichen Stelle wiederholen (die rote und die farblose Fläche, die grüne und die blaue Fläche, die farblose und die gelbe Fläche, drei Sätze sich wiederholender Flächen). Diese imaginäre Linie wird als dritte sekundäre Achse aufgezeichnet
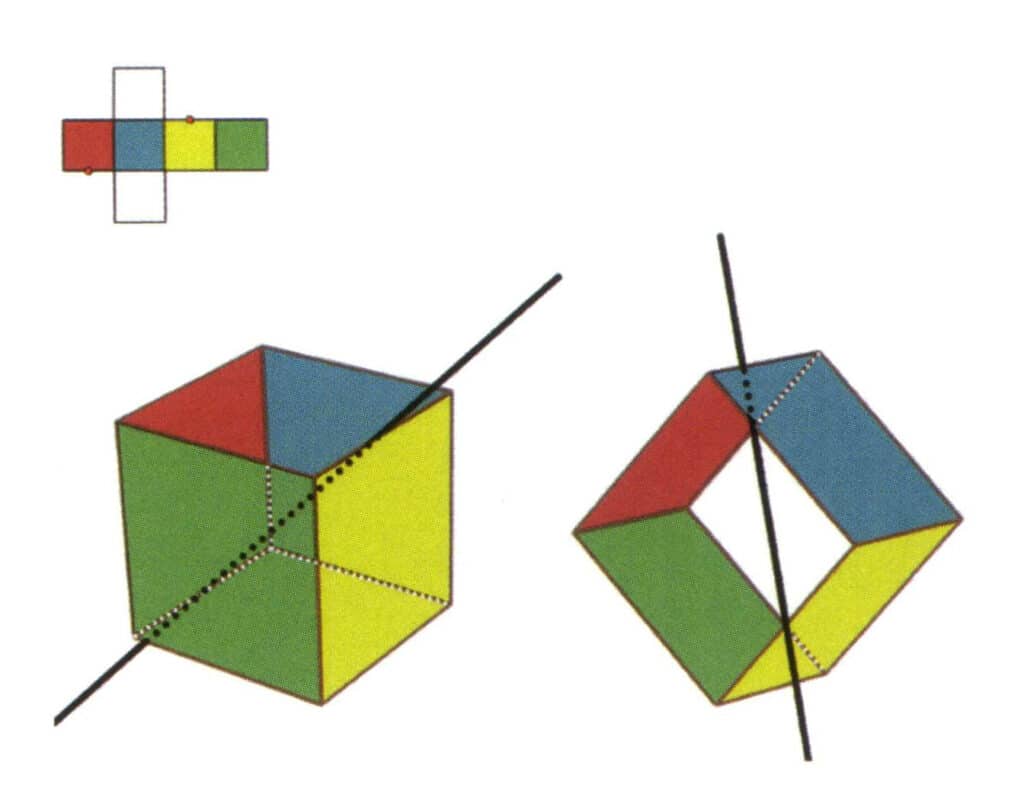
Abbildung 2-2-7 Die vierte Sekundärachse des Würfels
Wählen Sie den Mittelpunkt der parallelen Linien, wie in der Abbildung gezeigt, stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, und drehen Sie den Würfel um 360°; die verschiedenfarbigen, aber identisch geformten Bezugsebenen werden sich an derselben Stelle zweimal wiederholen (die rote und die farblose Fläche, die grüne und die blaue Fläche, die farblose und die gelbe Fläche, drei Sätze von sich wiederholenden Flächen), diese imaginäre gerade Linie wird als vierte sekundäre Achse aufgezeichnet.
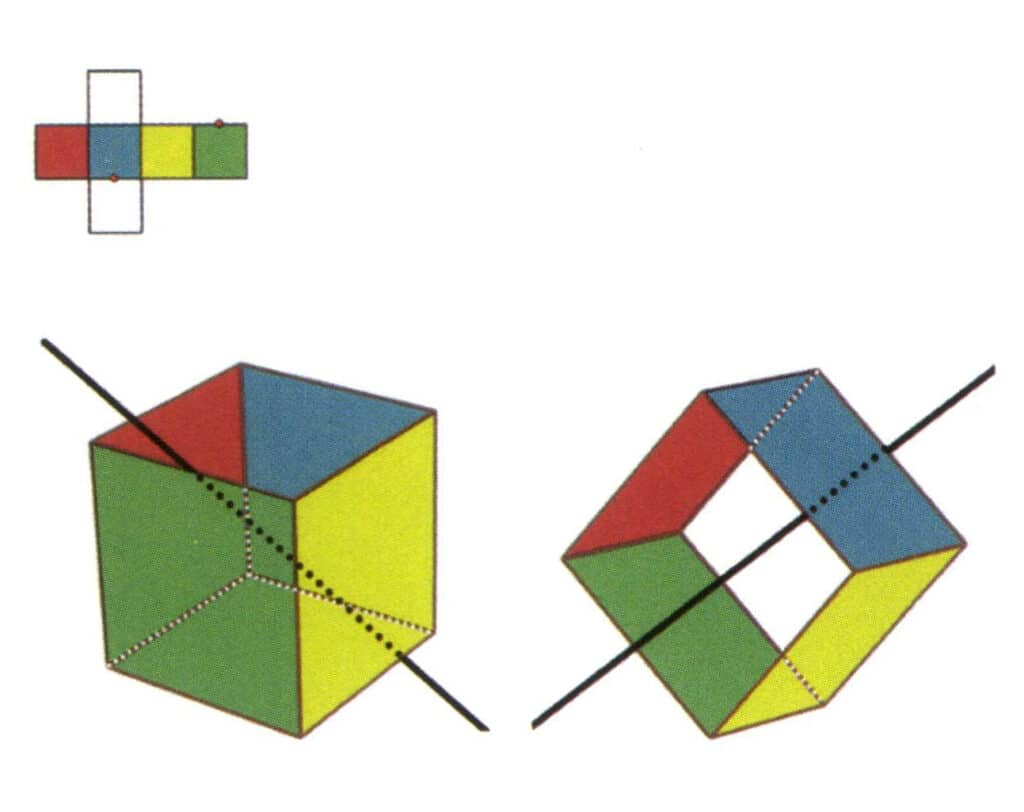
Abbildung 2-2-8 Die fünfte Sekundärachse des Würfels.
Wählen Sie die Mittelpunkte der parallelen Linien, wie in der Abbildung gezeigt, und stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft. Drehen Sie den Würfel um 360°, die verschiedenfarbigen, aber identisch geformten Bezugsebenen wiederholen sich zweimal an der gleichen Stelle (rote und farblose Flächen, grüne und blaue Flächen, farblose und gelbe Flächen, drei Sätze von sich wiederholenden Flächen), diese gedachte gerade Linie wird als fünfte sekundäre Achse aufgezeichnet.
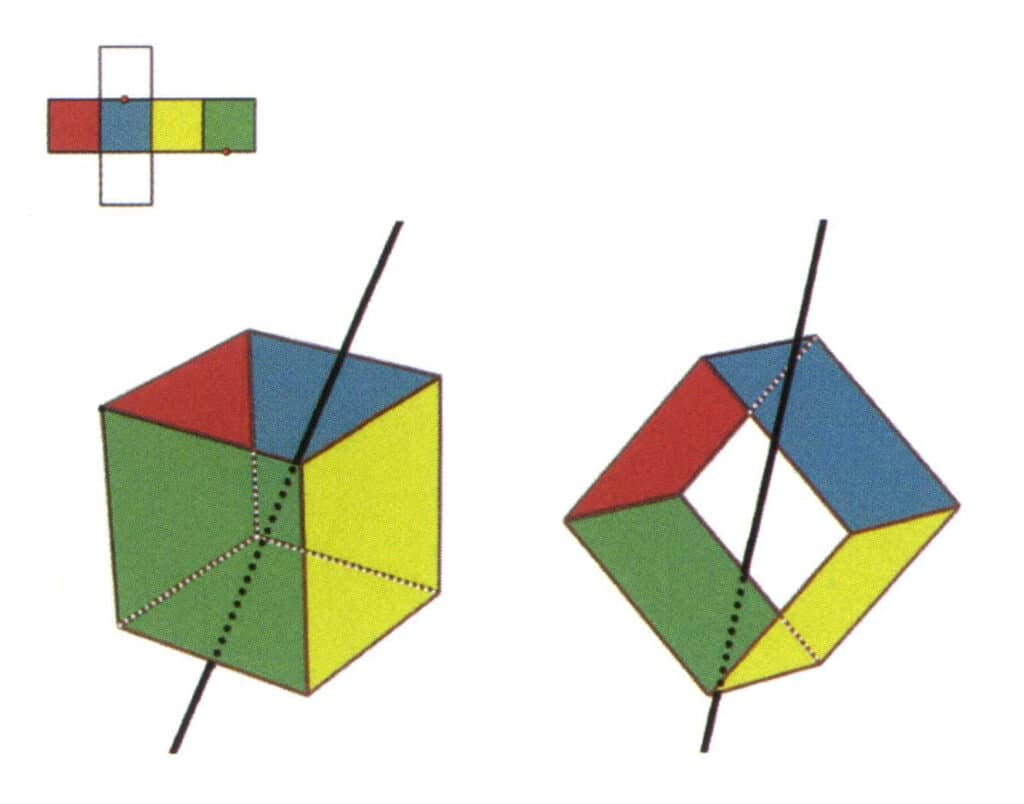
Abbildung 2-2-9 Die sechste Nebenachse des Würfels
Wählen Sie den Mittelpunkt der parallelen Linien, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft und den Würfel um 360° dreht. Die unterschiedlich gefärbten, aber identisch geformten Basisebenen wiederholen sich zweimal an der gleichen Stelle (grüne und farblose Flächen, rote und gelbe Flächen, farblose und blaue Flächen, drei Sätze von wiederholten Flächen). Diese imaginäre Linie wird als sechste Nebenachse aufgezeichnet.
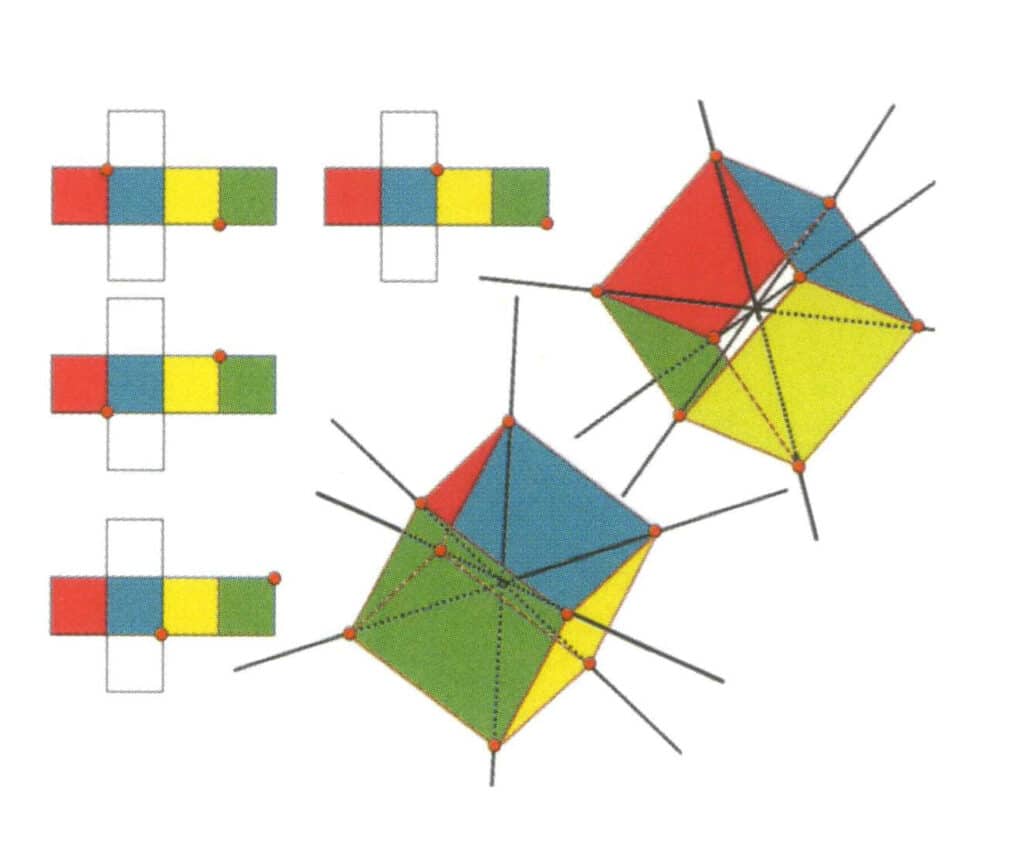
Abbildung 2-2-10 Die tertiäre Achse des Würfels
Die linke Seite der Abbildung zeigt die aufgeklappte Ansicht des Würfels, wobei der rote Punkt den Schnittpunkt der imaginären Geraden und der Kantenlinie anzeigt. Die rechte Seite der Abbildung zeigt den geschlossenen Würfel; die roten Punkte zeigen den Schnittpunkt der imaginären Geraden und der Kanten an. Die Tertiärachse kann in der Mitte der Flächen eines parallelen gleichseitigen Dreiecks oder im Schnittpunkt von drei oder mehr parallelen Flächen, die einem gleichseitigen Dreieck ähneln, liegen.
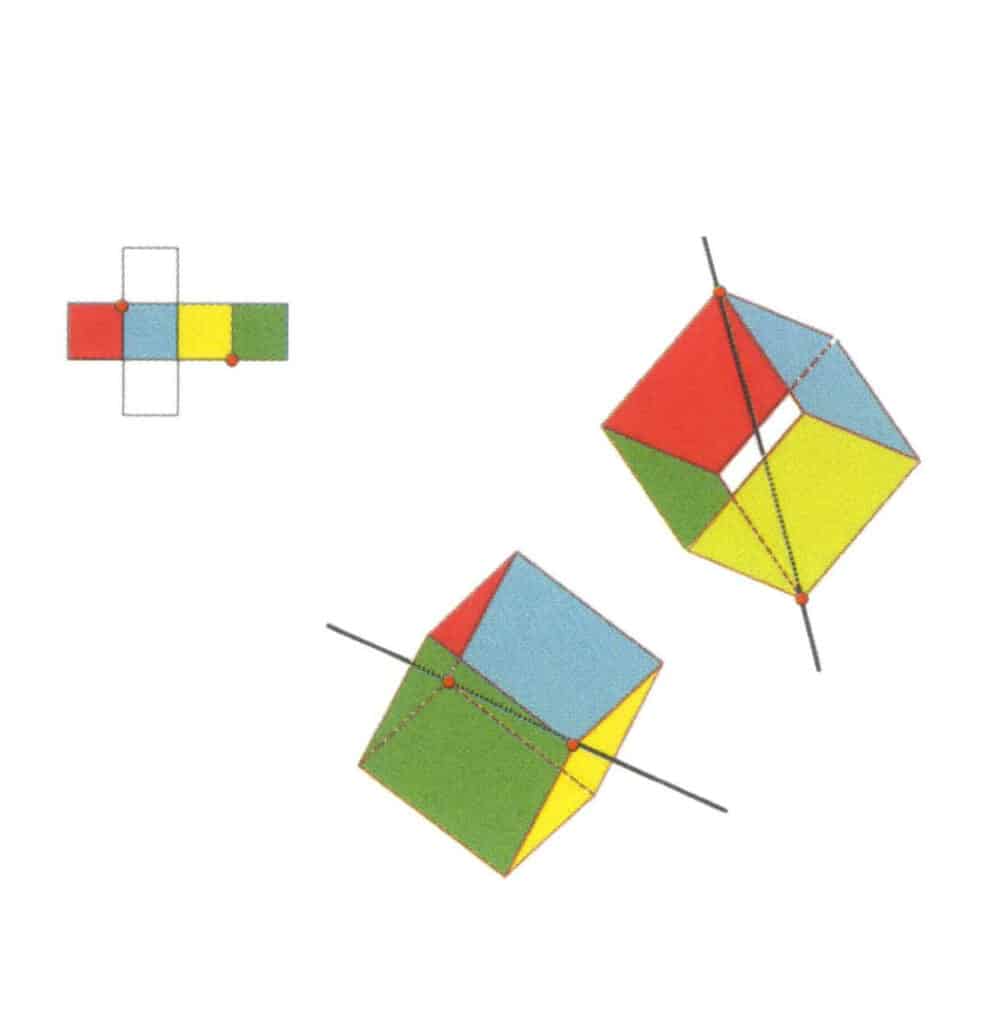
Abbildung 2-2-11 Die erste Tertiärachse des Würfels.
Wählen Sie die Schnittpunkte der drei Flächen wie in der Abbildung gezeigt, stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, drehen Sie den Würfel um 360°, die verschiedenfarbigen, aber identisch geformten Bezugsebenen wiederholen sich dreimal an der gleichen Stelle (rote, farblose und blaue Flächen, grüne, farblose und gelbe Flächen, zwei Sätze von wiederholten Flächen), diese gedachte gerade Linie wird als erste tertiäre Achse aufgezeichnet
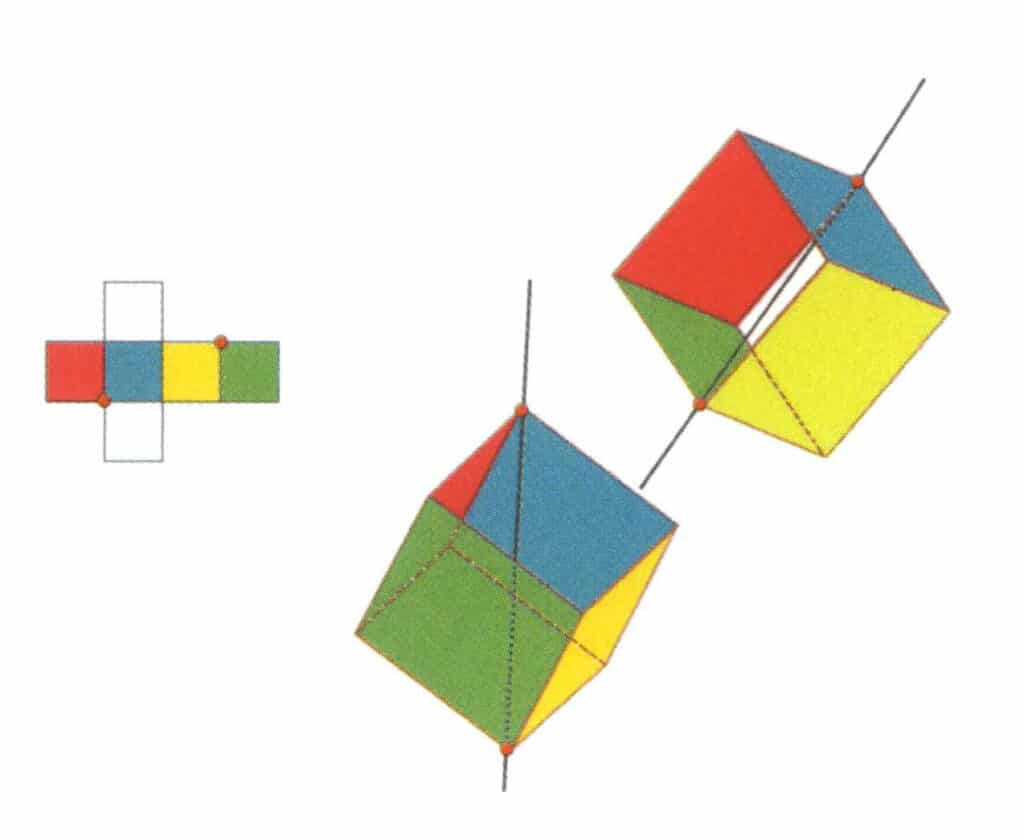
Abbildung 2-2-12 Die zweite Tertiärachse des Würfels.
Wählen Sie die Schnittpunkte der drei Flächen, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, und drehen Sie den Würfel um 360°. Die unterschiedlich gefärbten, aber identisch geformten Basisebenen wiederholen sich dreimal an der gleichen Stelle (rote, farblose und blaue Flächen; grüne, farblose und gelbe Flächen, zwei Sätze von wiederholten Flächen). Diese imaginäre Linie wird als zweite Tertiärachse aufgezeichnet.
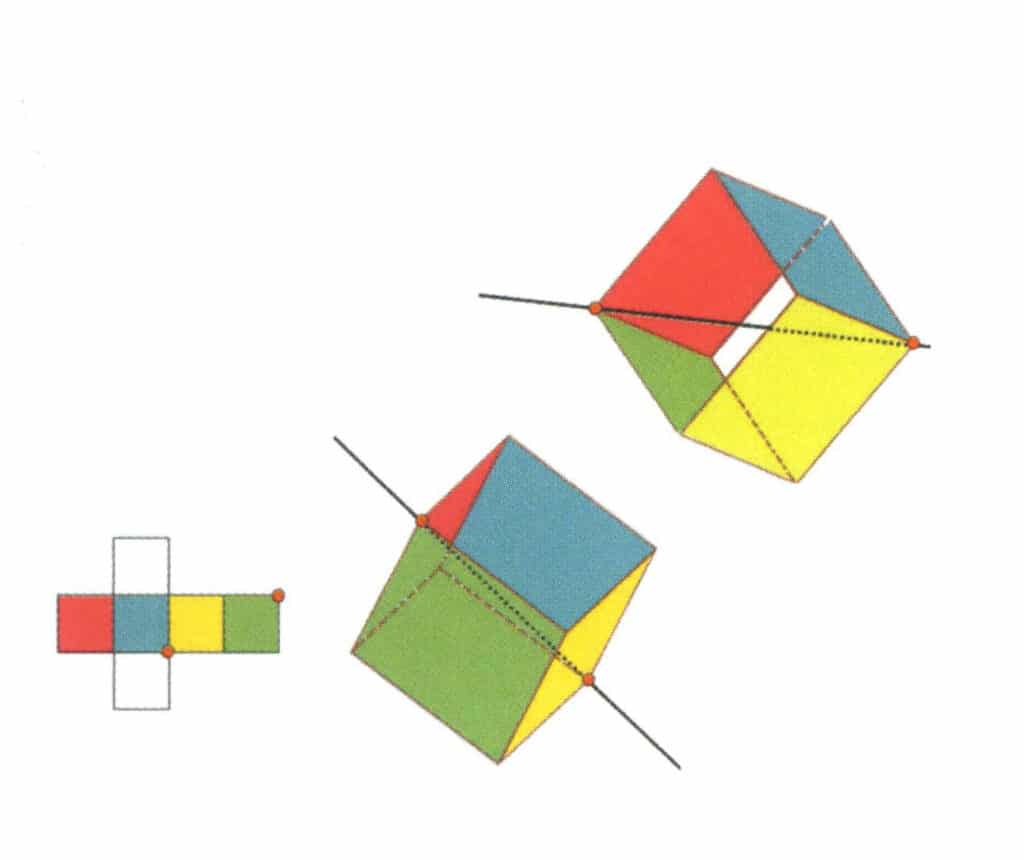
Abbildung 2-2-13 Die dritte Tertiärachse des Würfels
Wählen Sie die Schnittpunkte der drei Flächen, wie in der Abbildung gezeigt. Stellen Sie sich eine gerade Linie vor, die durch die Mittelpunkte dieser beiden Kanten verläuft, und drehen Sie den Würfel um 360°. Die unterschiedlich gefärbten, aber identisch geformten Basisebenen wiederholen sich dreimal an der gleichen Stelle (rote, farblose und grüne Flächen; blaue, farblose und gelbe Flächen, zwei Sätze von wiederholten Flächen). Diese imaginäre Linie wird als dritte Tertiärachse aufgezeichnet.
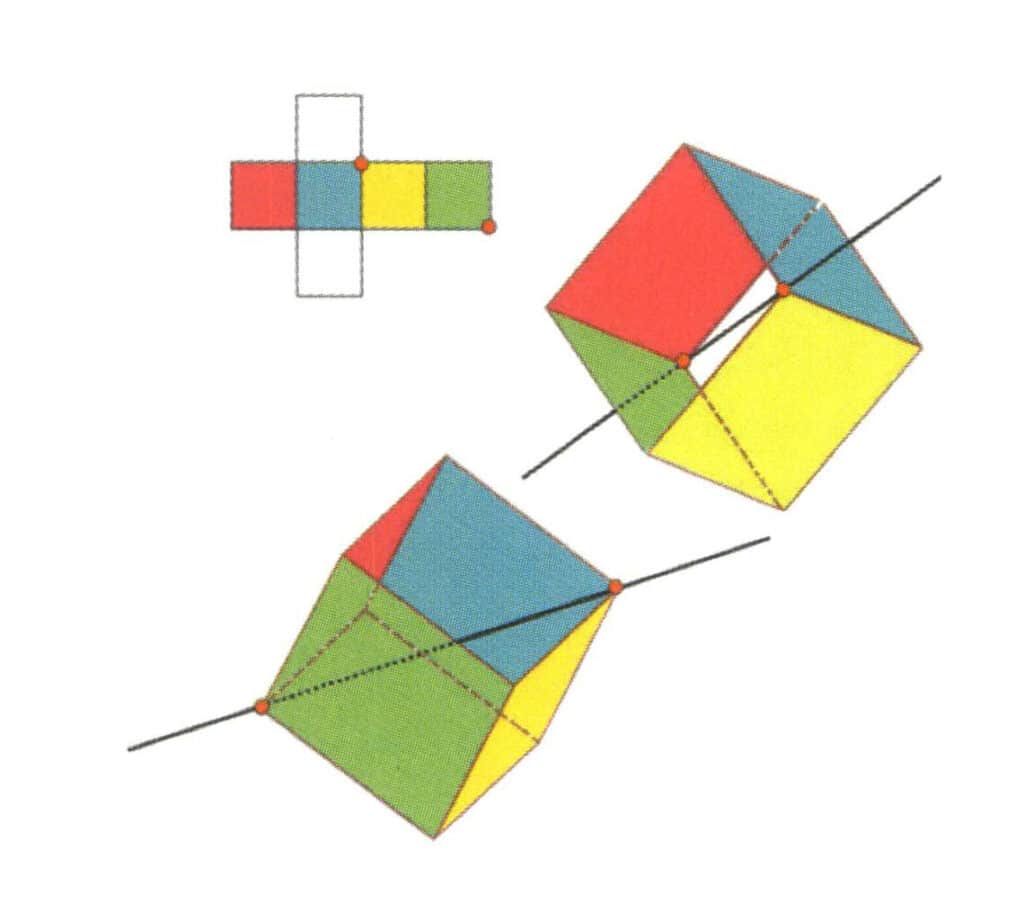
Abbildung 2-2-14 Vierte kubische Achse des Würfels.
Wählen Sie den Schnittpunkt der drei Flächen, wie in der Abbildung gezeigt, unter der Annahme, dass es eine gerade Linie durch den Mittelpunkt der beiden Kanten dreht den Würfel 360 °, unterschiedliche Farben, aber die gleiche Form Grundniveau wird die gleiche sein. Wiederholen Sie die Position dreimal (rote, farblose, grüne Fläche, blaue, farblose und gelbe Flächen, zwei Sätze von wiederholten Flächen). Diese imaginäre Linie wird als vierte Würfelachse aufgezeichnet.
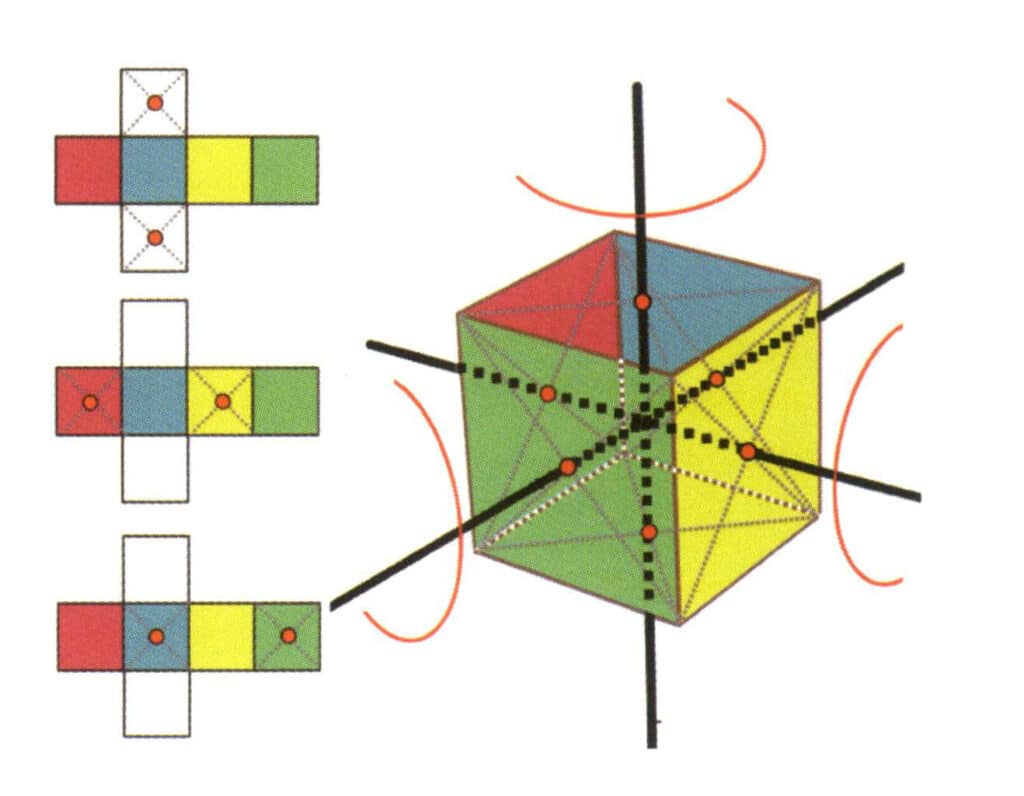
Abbildung 2-2-15 Vierte Achse des Würfels
Die linke Seite der Abbildung zeigt die aufgeklappte Ansicht des Würfels, wobei die roten Punkte die Schnittpunkte der imaginären Linie und der Kanten anzeigen. Die rechte Seite der Abbildung zeigt einen geschlossenen Würfel, wobei die roten Punkte die Schnittpunkte der imaginären Linie und der Ebene angeben. Die vierte Achse kann im Mittelpunkt von parallelen quadratischen Flächen erscheinen, im Schnittpunkt von drei oder mehr parallelen Flächen, die einem Quadrat ähneln.
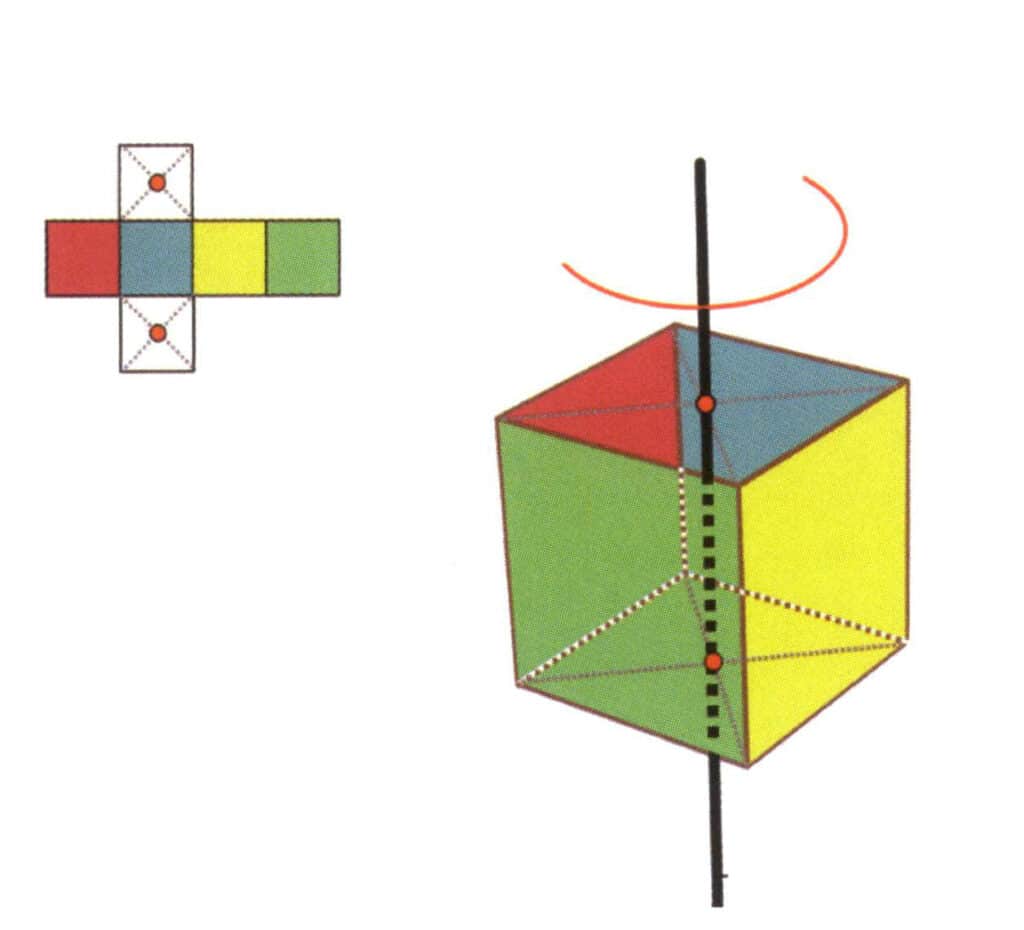
Abbildung 2-2-16 Die erste quartische Achse des Würfels
Wählen Sie die Mittelpunkte der in der Abbildung gezeigten Ebenen, nehmen Sie an, dass es eine gerade Linie durch die Mittelpunkte der beiden Ebenen gibt, und drehen Sie den Würfel um 360°. Die unterschiedlich gefärbten, aber gleich geformten Flächen der Basisebene wiederholen sich viermal an derselben Stelle (rote, blaue, grüne und gelbe Flächen), und diese hypothetische Gerade wird als vierfache Achse aufgezeichnet.
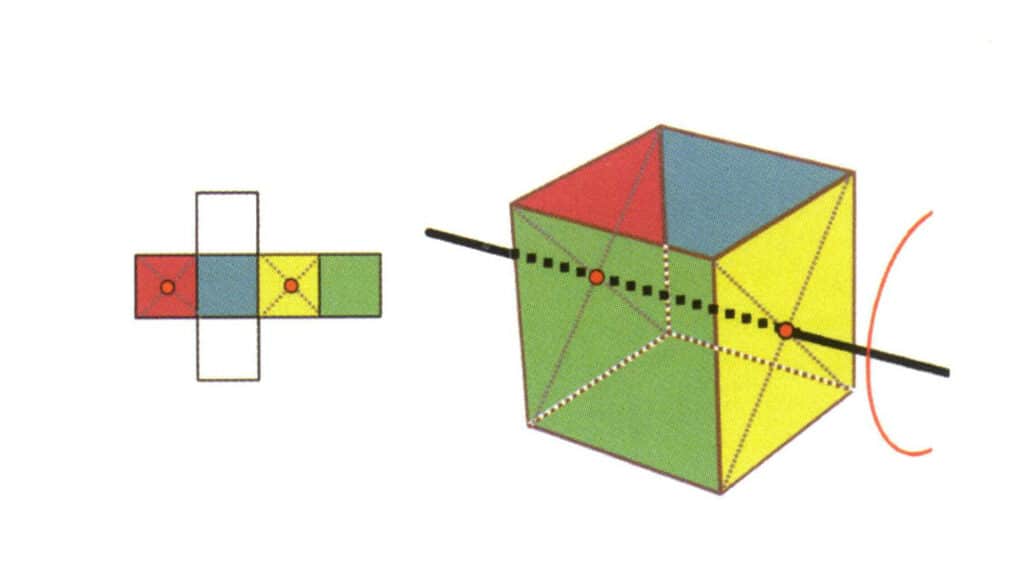
Abbildung 2-2-17 Die zweite quartische Achse des Würfels
Wählen Sie den Mittelpunkt der Ebene, wie in der Abbildung gezeigt, stellen Sie sich eine gerade Linie durch den Würfel vor und drehen Sie den Würfel um 360°; die Grundfläche mit unterschiedlichen Farben, aber gleicher Form wird viermal an der gleichen Stelle wiederholt (farblose, blaue Fläche oben, farblose, grüne Fläche unten), und diese imaginäre Linie wird als zweite quadratische Achse aufgezeichnet.
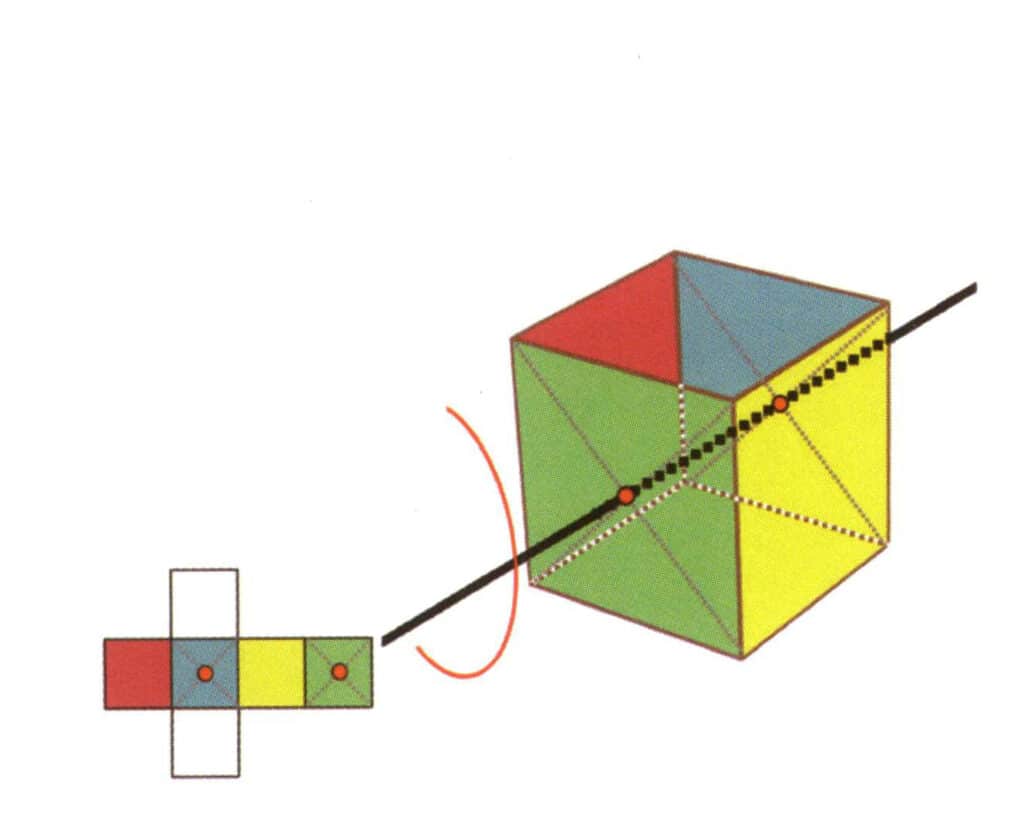
Abbildung 2-2-18 Dritte quartische Achse des Würfels
Wählen Sie den Mittelpunkt der Ebene wie in der Abbildung gezeigt, stellen Sie sich eine gerade Linie durch den Würfel vor und drehen Sie den Würfel um 360°. Die Basisebene mit unterschiedlichen Farben, aber gleicher Form, wird viermal an der gleichen Stelle wiederholt (farblose, rote Fläche oben, farblose, gelbe Fläche unten), und diese imaginäre Linie wird als dritte, vierte Achse aufgezeichnet
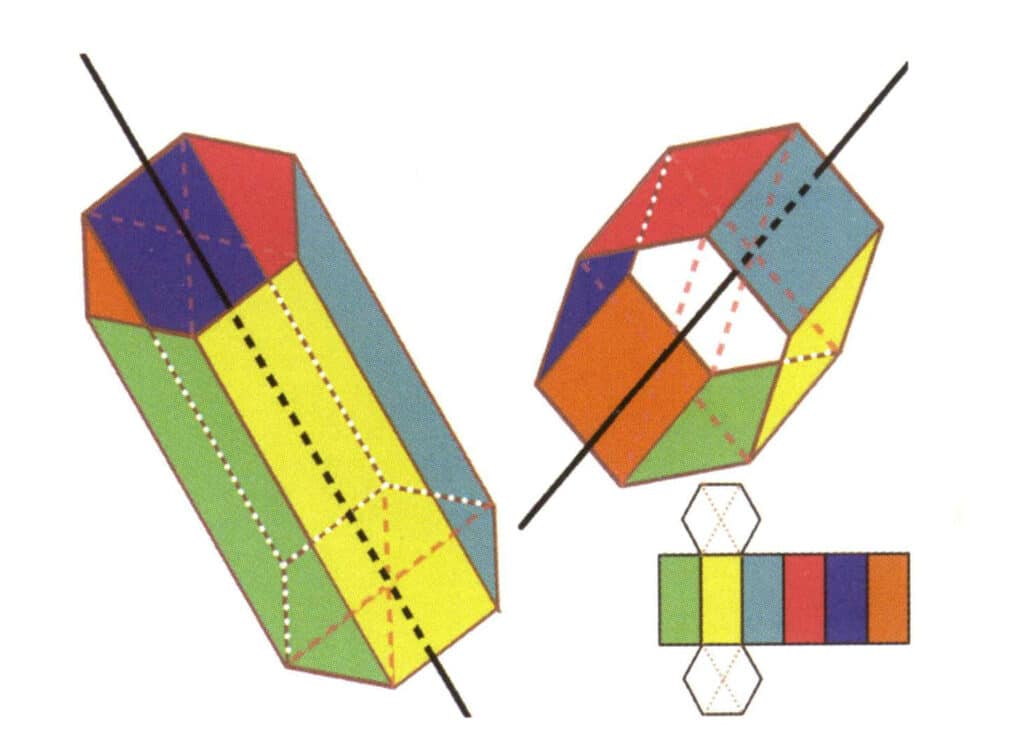
Abbildung 2-2-19 Sechs Achsen eines sechseckigen Prismas
Die schwarzen Linien links und rechts oben stellen die sechs Achsen des sechseckigen Prismas dar. Rechts unten ist eine Erweiterung des sechseckigen Prismas dargestellt Die Sextachse kann im Mittelpunkt der Flächen eines parallelen Sechsecks oder im Schnittpunkt der sechs Flächen eines Sechsecks liegen.
(2) Überlegungen zur Bestimmung der Symmetrieachse.
① Es gibt fünf Arten von Positionen für die Symmetrieachse.
Der Mittelpunkt zweier paralleler Kanten, z. B. die Position der Nebenachse eines Würfels.
Der Mittelpunkt zweier paralleler Ebenen, z. B. die Position der Quartachse eines Würfels.
Zwischen zwei Scheitelpunkten (den Schnittpunkten mehrerer Flächen), z. B. die Position der Tertiärachse eines Würfels.
Der Mittelpunkt zwischen einem Scheitelpunkt und einer parallelen Ebene, z. B. die Position der Tertiärachse eines Tetraeders.
Der Mittelpunkt der Kantenlinie und der Mittelpunkt der parallelen Ebene, z. B. die Position der Nebenachse eines dreieckigen Prismas.
② Die Auswahl der Symmetrieachse in derselben Richtung folgt dem Prinzip der niedrigsten Zahl. Wenn zum Beispiel in einer Richtung sechs Symmetrieachsen und drei Symmetrieachsen gefunden werden, wird sie nach dem Prinzip der niedrigsten Zahl als L³ erfasst. Die Symmetrieachsen in verschiedenen Richtungen sollten entsprechend der gefundenen Anzahl erfasst werden.
Mit Ausnahme der sechsfachen Symmetrieachse und der vierfachen Symmetrieachse, die nicht gleichzeitig auftreten können, und der sechsfachen Symmetrieachse, die nur einmal auftreten kann, können die anderen Symmetrieachsen in verschiedenen Formen oder in mehreren Ausprägungen nebeneinander bestehen.
③ Die Basisebene muss als kleinste Einheitsebene gewählt werden; zwei oder mehr sich schneidende Ebenen können nicht als Basisebene gewählt werden. Andernfalls wird die Genauigkeit der Beurteilung der Symmetrieachse beeinträchtigt.
④ Bei der Erfassung der Anzahl der Symmetrieachsen ist es wichtig, die Anzahl der Wiederholungen der gleichen Form und Größe der Ebene an derselben Stelle zu bestimmen.
⑤ Wenn es eine sekundäre Achse der vertikalen Symmetrie Lⁿ(n = 3, 4 oder 6) gibt, muss es n sekundäre Achsen senkrecht zu Lⁿ geben.
2.2 Ebene der Symmetrie
(1) Konzept und Aufzeichnungsmethode der Ebene der Symmetrie
Eine Symmetrieebene ist eine imaginäre Ebene, die, wenn der Kristall entlang dieser Ebene geschnitten wird, es ermöglicht, dass jede Hälfte des Kristalls ein Spiegelbild der anderen Hälfte ist (Abbildung 2-2-20). In ein und derselben Kristallstruktur kann eine solche Ebene maximal 9 Mal vorkommen (Abbildung 2-2-21), d. h. sie kann auf 9 verschiedene Arten halbiert werden, und die beiden Hälften können vollständig übereinstimmen. Natürlich haben nicht alle Kristallstrukturen Symmetrieebenen.
Der Großbuchstabe P steht für die Symmetrieebene. Einige Kristalle haben mehrere nicht zusammenfallende Symmetrieebenen, und die Anzahl dieser Symmetrieebenen wird üblicherweise links von P geschrieben; beispielsweise werden vier Symmetrieebenen als 4P und eine Symmetrieebene als P dargestellt.
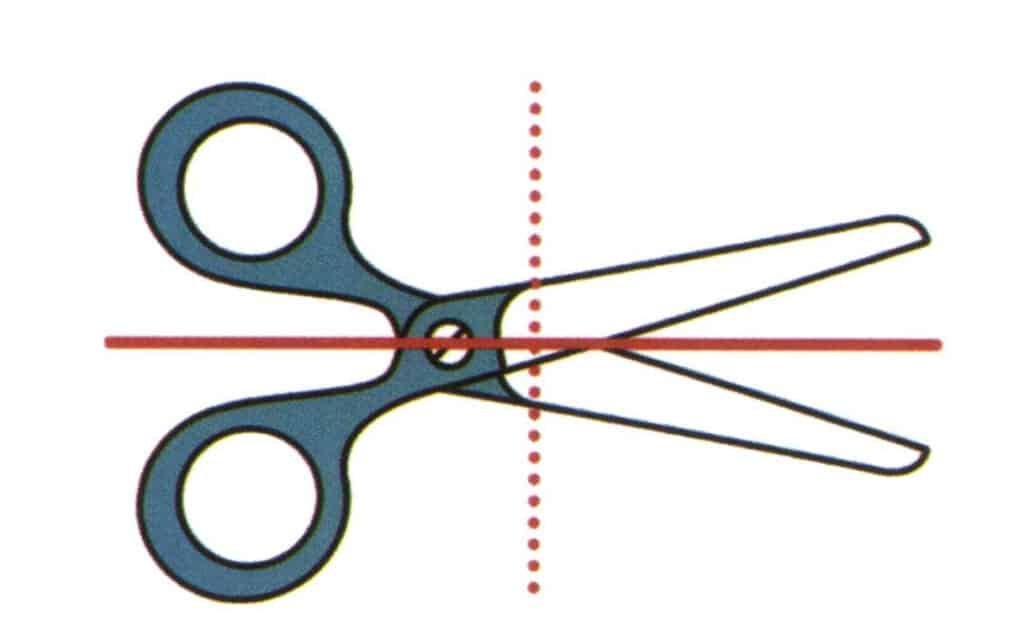
Abbildung 2-2-20 Man stelle sich eine senkrechte Papierebene und eine Ebene vor, die sich in Richtung der roten durchgezogenen Linie erstreckt, die die Schere in einen oberen und einen unteren Teil teilt, wobei der obere und der untere Teil spiegelsymmetrisch sind. Diese gedachte Ebene wird als Symmetrieebene bezeichnet. Stellen Sie sich eine weitere Ebene vor, die senkrecht zur Papieroberfläche liegt und sich in Richtung der rot gestrichelten Linie erstreckt, die die Schere in einen linken und einen rechten Teil unterteilt, aber die Formen der Schere auf der linken und der rechten Seite sind nicht symmetrisch.
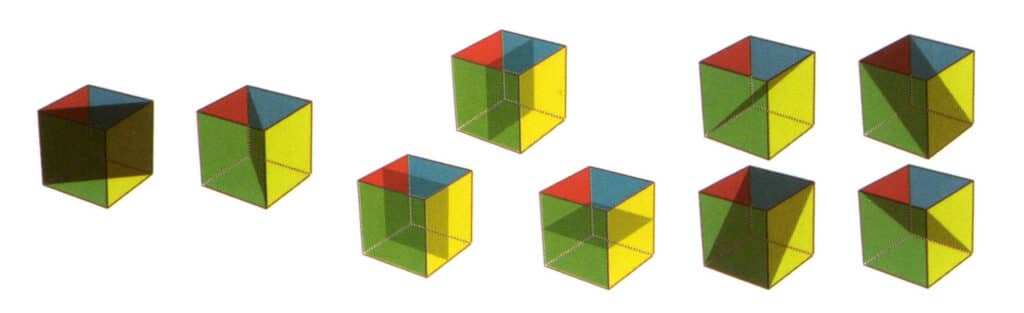
Abbildung 2-2-21 Neun Symmetrieebenen eines Würfels
(2) Tipps für die Suche nach Symmetrieebenen.
① Die Symmetrieebene ist oft parallel und fällt mit der Symmetrieachse zusammen.
② Die Symmetrieebene ist eine imaginäre Ebene, die die kristalline Geometrie teilt und sich von der parallelen Doppelebene in der Geometrie unterscheidet.
③ Wenn eine Symmetrieebene die Symmetrieachse Lⁿ enthält, dann muss es n Symmetrieebenen geben, die Lⁿ enthalten.
(3) Punkt Gruppe.
Die Punktgruppe ist die Summe aller Symmetrieelemente in einem Kristall. Die Reihenfolge der Aufzeichnung der Punktgruppe ist Symmetrieachse + Symmetrieebene, z. B. 3L²3P (Abbildung 2-2-22). Weist ein Kristall mehrere Symmetrieachsen auf, so ist es üblich, sie von links nach rechts, von der Achse der höheren Ordnung zur Achse der niedrigeren Ordnung, und die Reihenfolge der Symmetrieebenen anzugeben, z. B. L⁴4L²5P (Abbildung 2-2-23). Es gibt 32 Arten von Symmetrie in Kristallen.
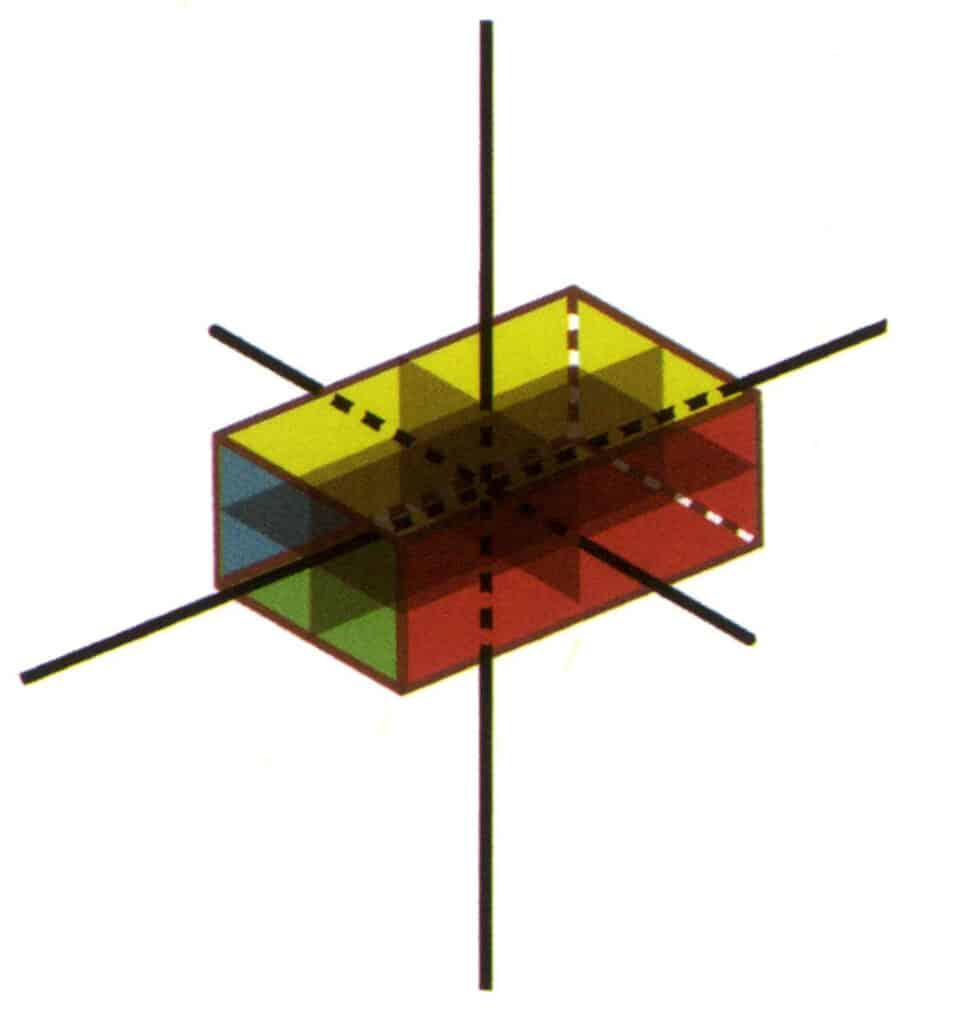
Abbildung 2-2-22 3L²3P Punktgruppe (rechteckiger Quader mit rechteckigem Querschnitt)
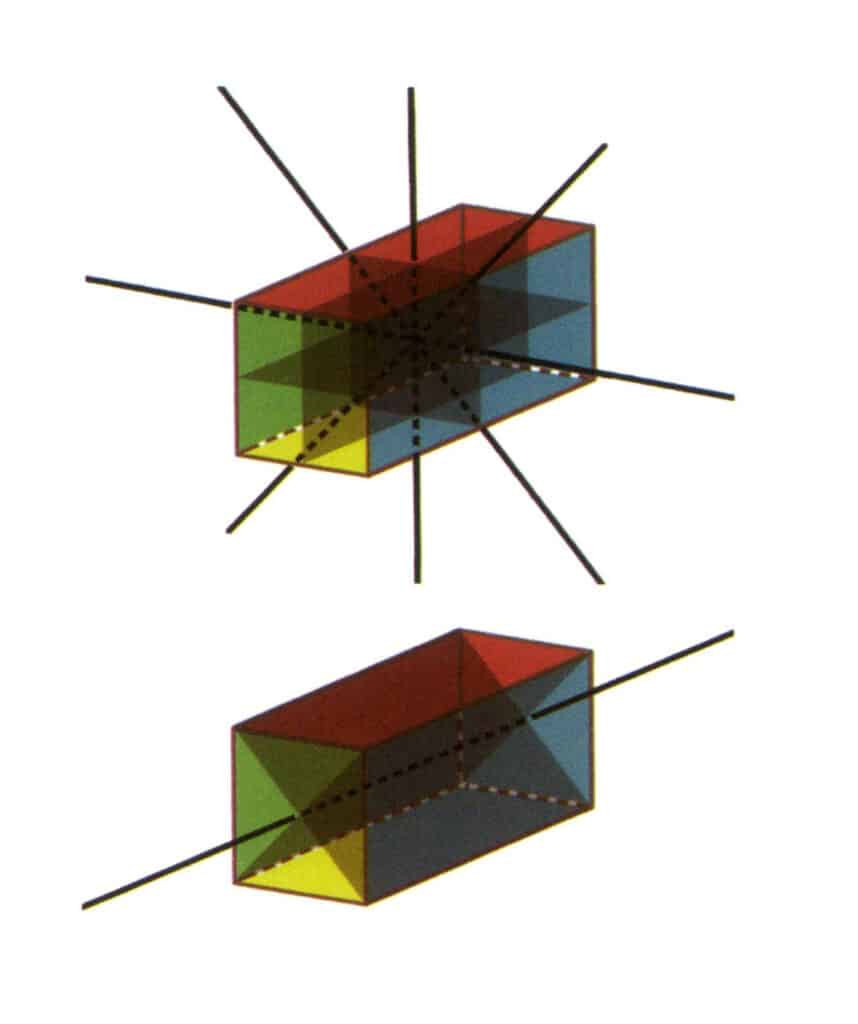
Abbildung 2-2-23 L⁴4L²5P-Punktgruppe (ein rechteckiges Prisma mit quadratischem Querschnitt), mit vier zweiten Achsen und drei symmetrischen Flächen auf der Oberseite und einer vierten Achse und zwei symmetrischen Flächen auf der Unterseite.
3. Klassifizierung von Kristallen
Die Symmetrie ist ein Teil der Kristallklassifikation. Ein weiteres Konzept - die Kristallachse - muss eingeführt werden, um die Kristallstruktur natürlicher und künstlicher Edelsteine in einem Kristallklassifizierungsschema zu beschreiben. Die Kristallachse ist eine imaginäre Linie durch die Kristallstruktur, die die Richtung angibt, in der sich die Gitterknoten wiederholen, sowie den relativen Abstand, in dem sich die Knoten entlang dieser Richtung wiederholen. Die Kristallachse fällt mit der Normalen der Symmetrieachse oder der Symmetrieebene zusammen. Gibt es keine Symmetrieachse oder Symmetrieebene, so kann die Kristallachse parallel zur Kristallkantenrichtung gewählt werden.
Auf der Grundlage von Symmetrieelementen und Kristallachsen unterteilt das akademische System Kristalle in drei Kristallfamilien und sieben Kristallsysteme (Tabelle 1).
Tabelle 1: Eckpunkte zur Bestimmung von Kristallfamilien und -systemen
| Familie Kristall | Kristall | Wichtige Punkte für die Bestimmung | Gebräuchliche Edelsteinsorten |
|---|---|---|---|
| Low-Level-Kristall-System | Triklines System | Keine zweite Achse oder Symmetrieebene | Amazonit, Rhodonit, Türkis |
| Monoklines Kristallsystem | Keine Achsen höherer Ordnung, nicht mehr als eine Nebenachse und Symmetrieebene | Jadeit, Diopsid, Spodumen, Epidot | |
| Orthorhombisches Kristallsystem | Keine Achsen höherer Ordnung, mehr als eine Nebenachse oder Symmetrieebene | Olivin, Topas, Saualpite (einschließlich Tansanit), Cordierit, Chrysoberyll, Enstatit | |
| Zwischenkristall-Familie | Tetragonales Kristallsystem | 1 vierfache Achse (kann dargestellt werden durch L4) | Diamant |
| Trigonales Kristallsystem | 1 trigonale Achsen (darstellbar durch L3) | Korund, Rubin, Saphir, Turmalin, Kristalle der Quarzfamilie (wie Kristall, Amethyst, Citrin usw.), Rhodochrosit | |
| Hexagonales Kristallsystem | 1 sechseckige Achse (kann durch L dargestellt werden6) | Aquamarin, Smaragd und andere Edelsteine der Beryllitfamilie, Apatit | |
| Erweiterte Kristallfamilie | Isometrisches Kristallsystem | 4 trigonale Achsen (kann durch 4L dargestellt werden)3) | Diamant, Granat, Spinell, Flussspat |
4. Gemeinsame Merkmale von Edelsteinkristallen
Zu den gängigen Edelsteinen gehören Diamant, Spinell, Flussspat, Granat, Beryllit, Zirkon, Korund, Turmalin, Kristall, Chrysoberyll, Topas usw. Jede Art von Edelstein hat ihre eigenen festen Kristalleigenschaften.
Edelsteine aus der Familie der Hochkristalle haben meist eine körnige Kristallform, und häufige Varietäten treten oft in festen Kristallformen auf (Tabelle 2).
Die Kristallform der mittleren und unteren Kristallfamilien ist kolumnar (Tabelle 3).
Tabelle 2: Gemeinsame Kristalleigenschaften von High-Level-Kristallfamilien
| Edelsteine Ton Name | Kristall-Klassifizierung | Wichtige Kristalleigenschaften | |||
|---|---|---|---|---|---|
| Edelsteine Ton Name | Kristall-Klassifizierung | Kristall Gewohnheit | Häufige Kristallformen | Gemeinsame Zwillingsformen | Gemeinsame Kristallflächenmuster |
| Diamant | Isometrisches Kristallsystem | Körnige Kristallform (Abbildung 2-2-24), häufig in oktaedrischen Körnern zu sehen | Das Oktaeder ist eine häufige Kristallform, aber auch komplexere Kristallformen, einschließlich rhombischer Dodekaeder, können vorkommen, oft mit abgerundeten Kristallflächen, die eine dreifache Symmetrie aufweisen können | Dreieckiger flacher Zwilling, manchmal ohne sichtbare konkave Winkel (Abbildung 2-2-25) | Die Oberfläche zeigt umgekehrte dreieckige Ätzgruben (Abbildungen 2-2-26, 2-2-27) und andere Kristallflächenmuster (Abbildungen 2-2-28, 2-2-29) |
| Spinell | Körnige kristalline Form (Abbildung 2-2-30), häufig in oktaedrischen Körnern | Oft in oktaedrischer Form hergestellt, können die Kristallflächen sehr flach sein und wie poliert erscheinen (Abbildung 2-2-31). | Die Zwillingskristalle sind sehr flach und ähneln einer dreieckigen Form mit abgeschnittenen Ecken (Abbildung 2¬2-32). | Auf der Oberfläche sichtbare Ätzgruben, von denen einige die Form von Rauten in einem umgekehrten Dreieck haben (Abbildung 2-2-33) | |
| Fluorit | Körnige Kristallform (Abbildung 2-2-34) | Oktaedrische und kubische Kristallformen (Abbildung 2-2-35) | Interpenetrierende Partnerschaften | Quadratische Stufenwuchsmarken, meist mit Spaltlücken, Farbbänder parallel zu den Richtungen der sechs Würfelflächen | |
| Granat | Körnige kristalline Form, häufig in rhombisch-dodekaedrischen Körnern (Abbildung 2-2-36) | Rhombendodekaeder oder Quadrat-Trapezoeder | Seltene | Konzentrische Ringbänder mit der gleichen Form wie die Kristallflächen sind sichtbar (Abbildung 2-2-37). | |
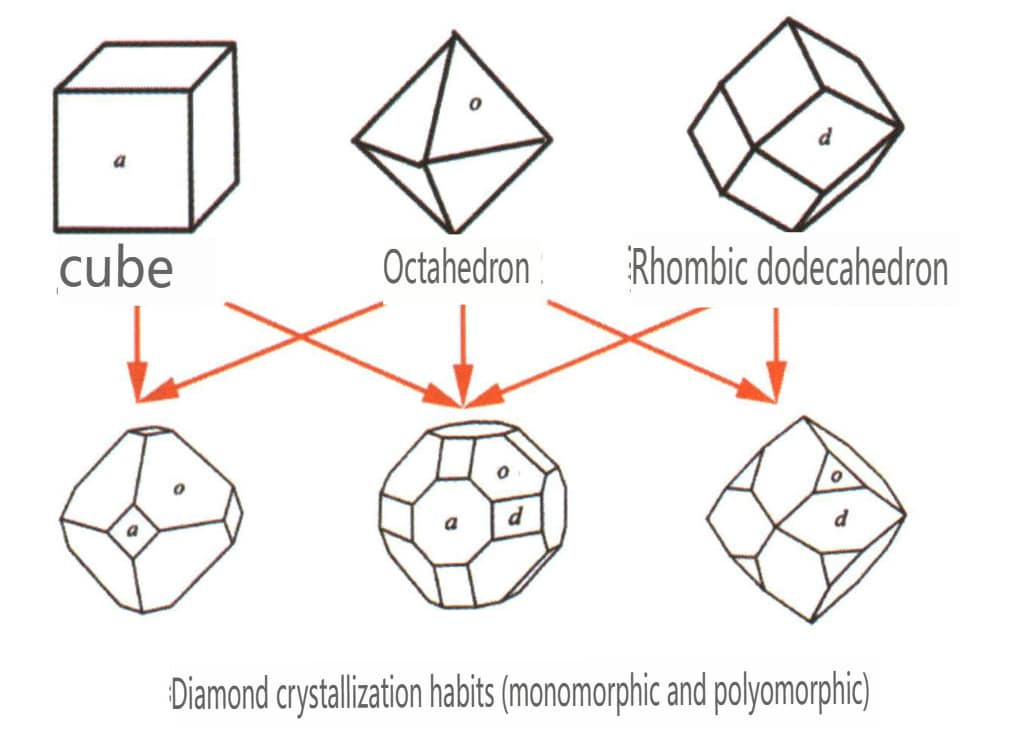
Abbildung 2-2-24 Kristallgewohnheiten von Diamanten
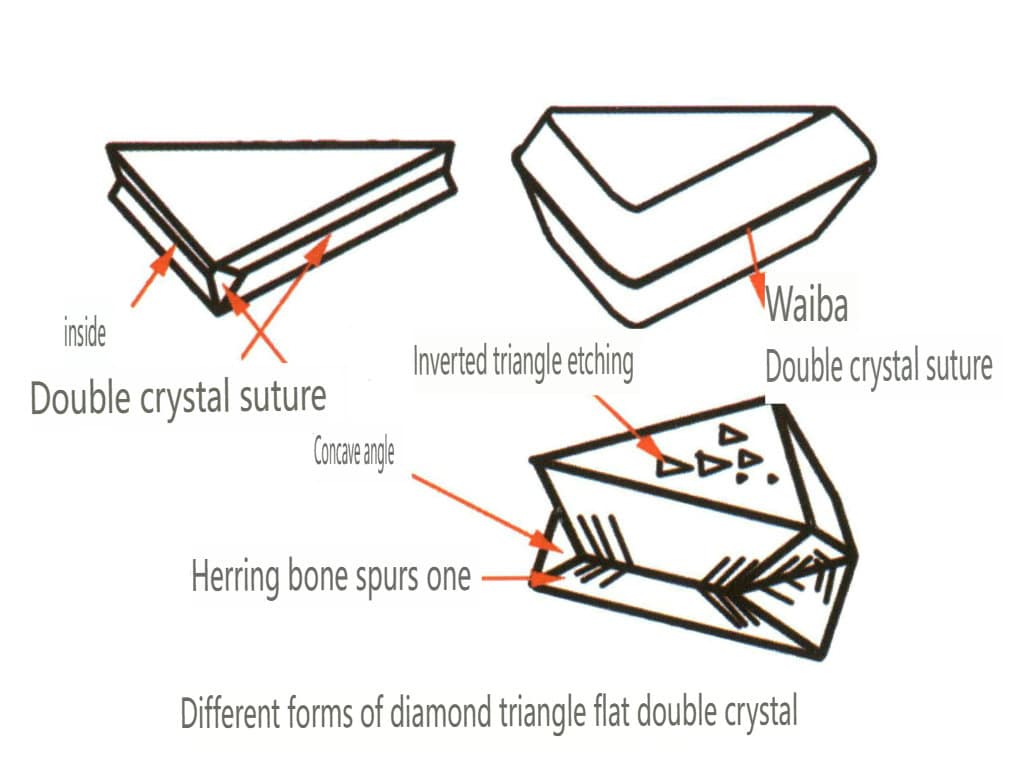
Abbildung 2-2-25 Diamant-Zwillingshabit
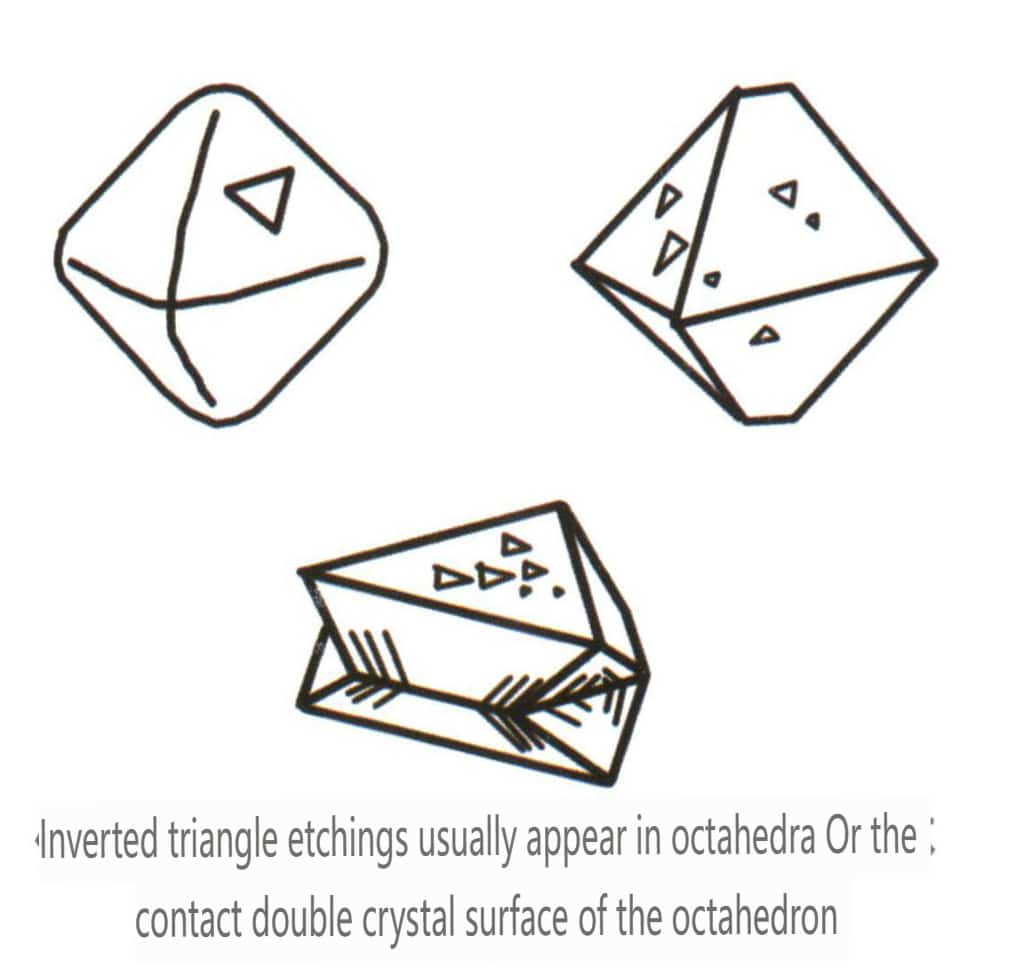
Abbildung 2-2-26 Umgekehrtes Dreiecksätzbild der oktaedrischen Kristallflächen von Diamant

Abbildung 2-2-27 Umgekehrte dreieckige Ätzfigur auf der Oberfläche eines oktaedrischen Diamantkristalls
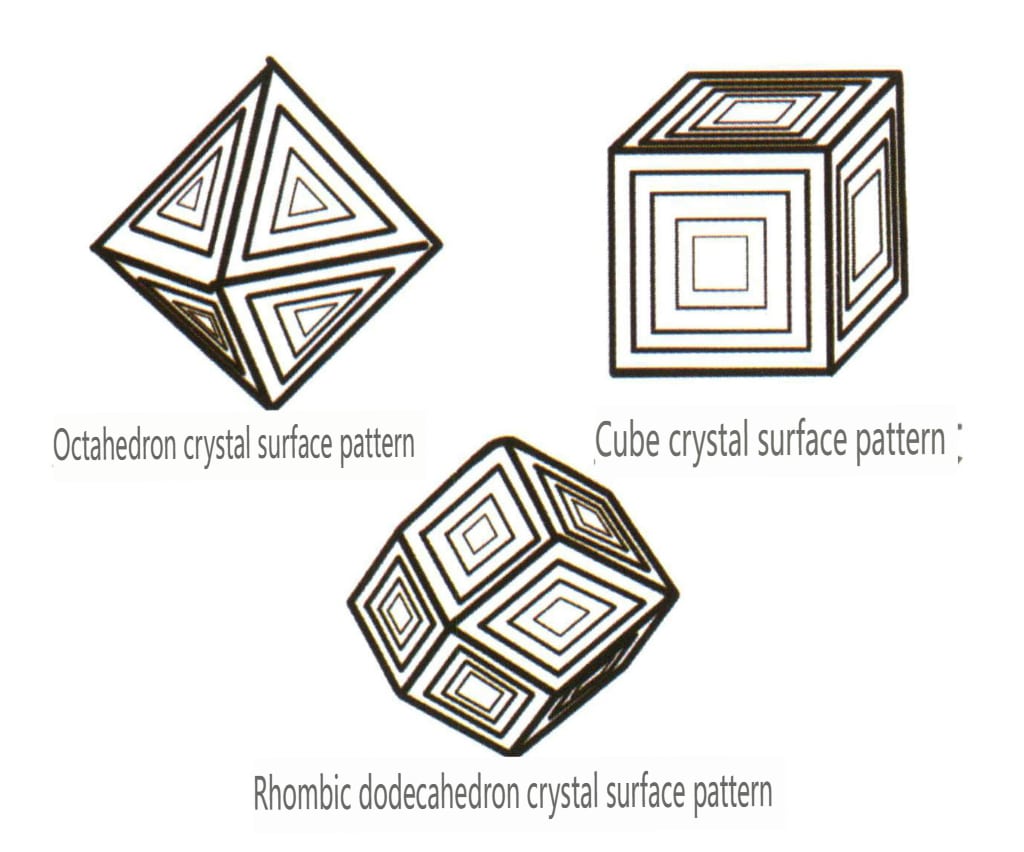
Abbildung 2-2-28 Umgekehrtes Dreiecksätzbild der oktaedrischen Kristallflächen von Diamant

Abbildung 2-2-29 Umgekehrte dreieckige Ätzfigur auf der Oberfläche eines oktaedrischen Diamantkristalls
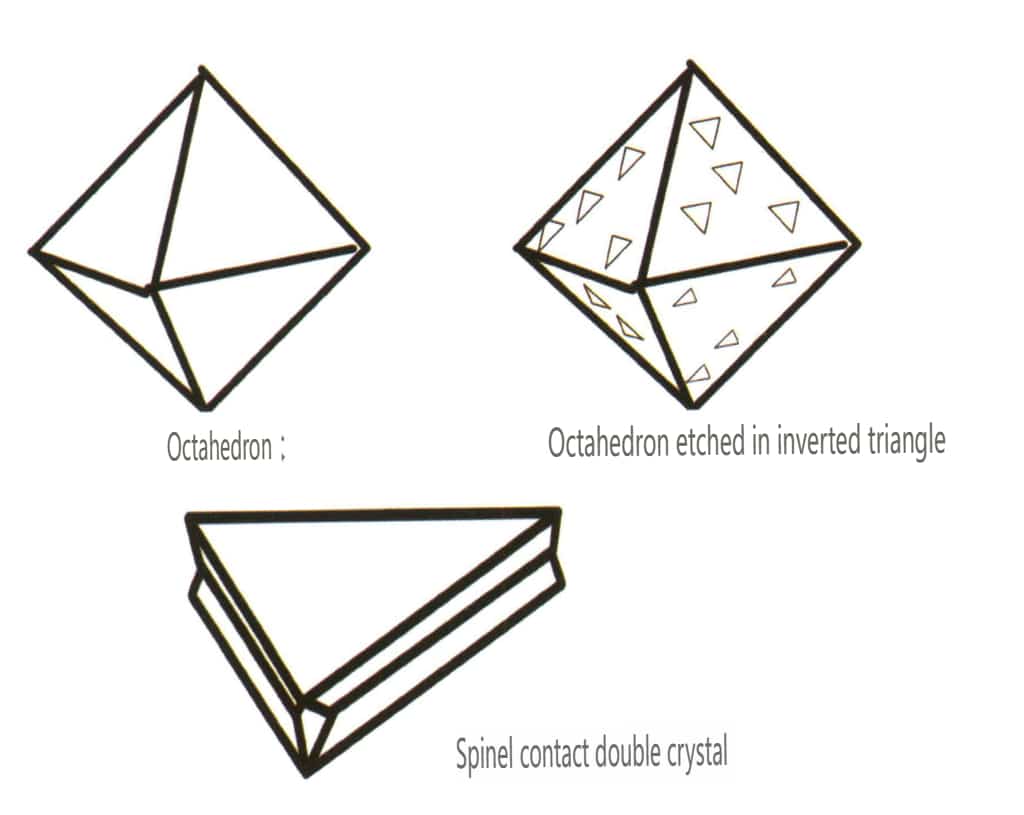
Abbildung 2-2-30 Kristallhabitus von Spinell

Abbildung 2-2-31 Häufige Formen von Spinellkristallen

Abbildung 2-2-32 Kontaktverzwillingung von Spinell
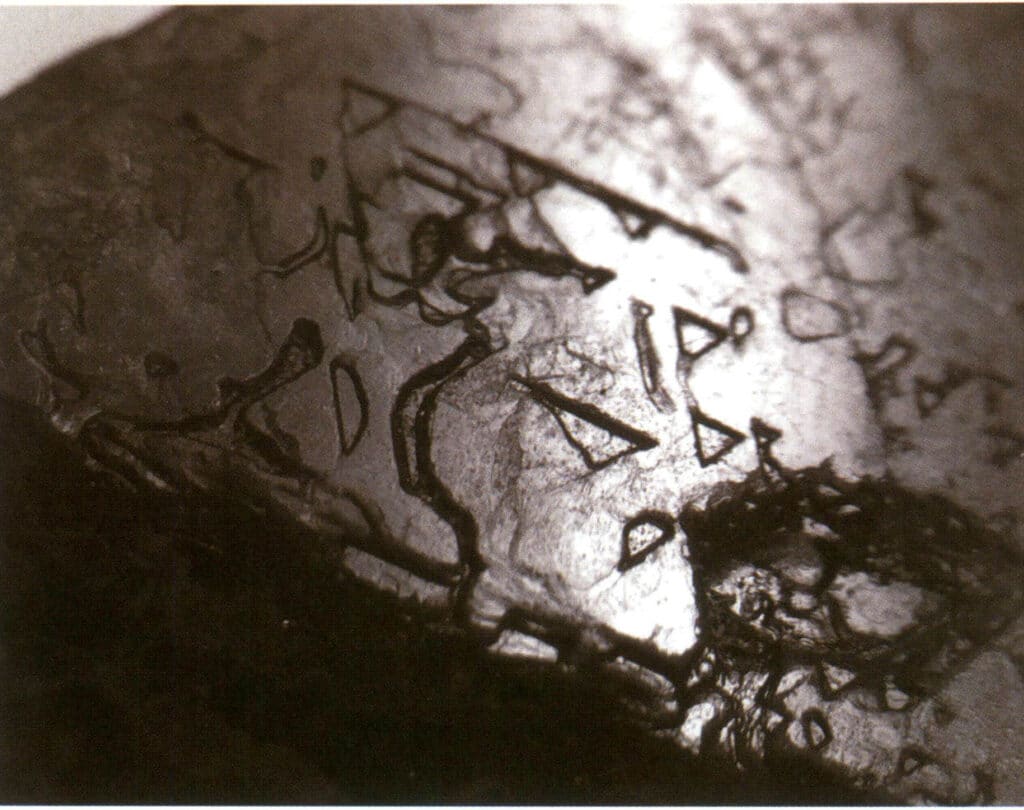
Abbildung 2-2-33 Umgekehrtes dreieckiges Ätzmuster auf der Oberfläche von Spinell
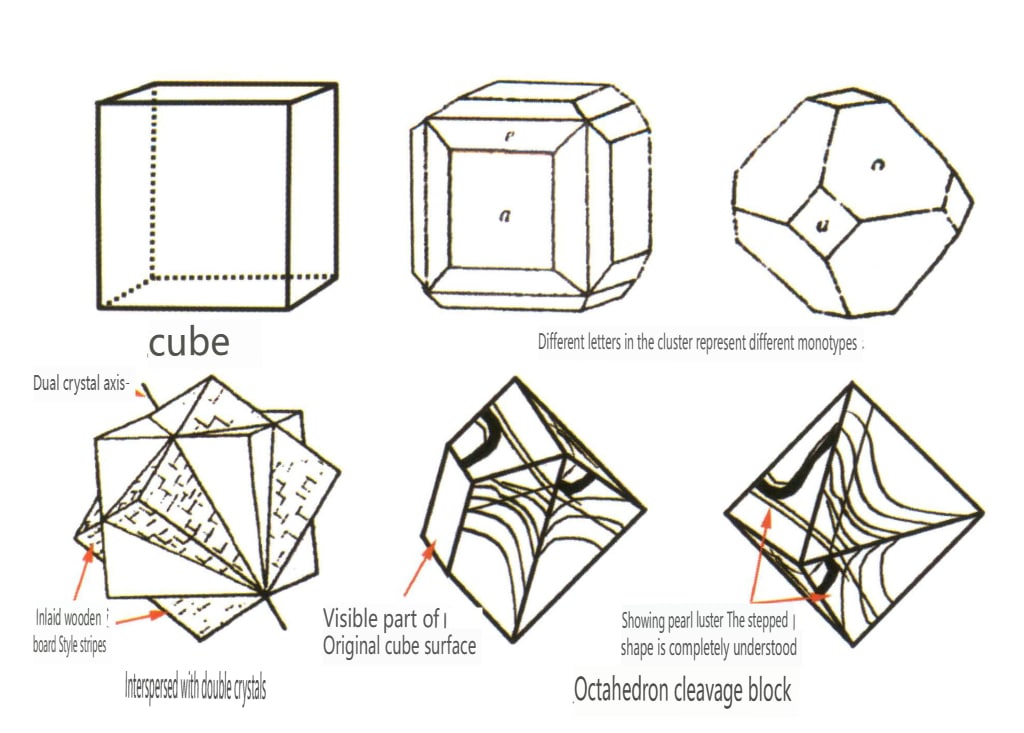
Abbildung 2-2-34 Kristallformen von Fluorit

Abbildung 2-2-35 Fluoritkristall
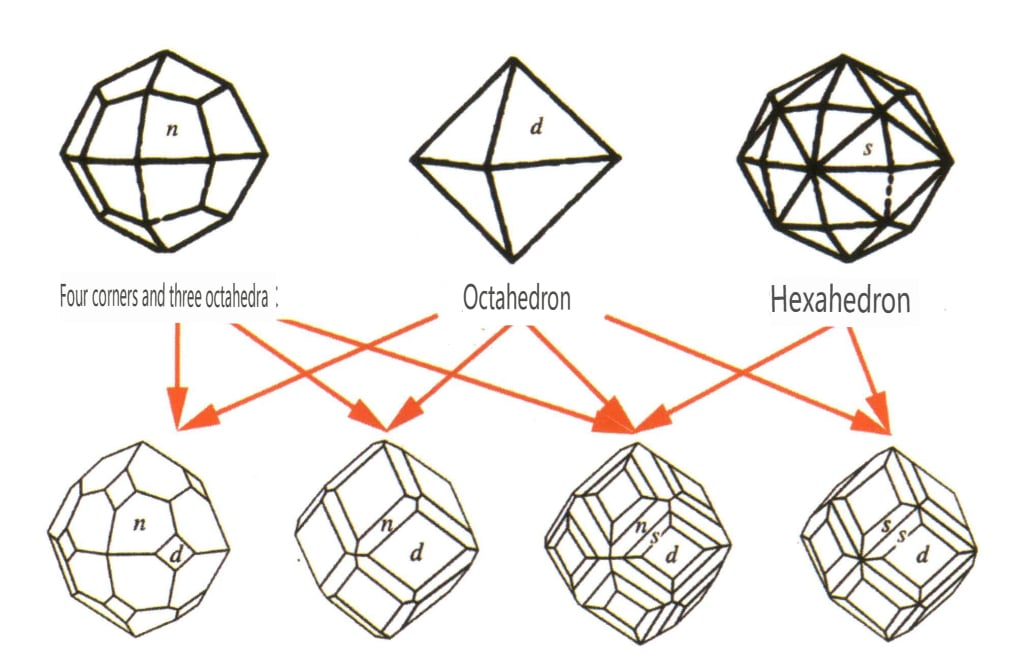
Abbildung 2-2-36 Granat-Kristallhabitus

Abbildung 2-2-37 Konzentrische Ringbänder auf der Oberfläche von Granatkristallen, die die gleiche Form wie die Kristallflächen haben
Tabelle 3: Gemeinsame Merkmale von Edelsteinkristallen der mittleren und niedrigen Kristallfamilien
| Edelsteine Ton Name | Kristall-Klassifizierung | Wichtige Kristalleigenschaften | |||
|---|---|---|---|---|---|
| Edelsteine Ton Name | Kristall-Klassifizierung | Kristall Gewohnheit | Häufige Kristallformen | Gemeinsame Zwillingsformen | Gemeinsame Kristallflächenmuster |
| Beryl | Hexagonales Kristallsystem | Säulenförmige Kristallform (Abbildung 2-2-38) | Hexagonale säulenförmige Kristallform (Abbildungen 2-2-39, 2-2-40) | Seltene | Sichtbare Längsstreifen |
| Bleistein | Tetragonales Kristallsystem | Säulenförmige Kristallform (Abbildung 2-2-41) | Eine quadratische Säule mit quadratischem Querschnitt, die zusammen mit einem quadratischen Doppelkegel auftritt (Abbildung 2-2-42) | Sichtbare knieförmige Zwillingskristalle | Keine besonderen Muster |
| Korund | Trigonales Kristallsystem | Plattenförmige Kristallform, säulenförmige Kristallform (Abbildung 2-2-43) | Rubine haben oft eine hexagonale Prismenform (Abbildung 2-2-44), während Saphire oft eine hexagonale bipyramidale tonnenförmige Kristallform aufweisen (Abbildung 2-2-45). | Häufig vorkommende Zweikristalle. | Sichtbare Rillen. |
| Turmalin . | Säulenförmige Kristallform (Abbildung 2-2-46) | Die Kristallflächen an beiden Enden sind unterschiedlich, und der Querschnitt ist ein kugelförmiges Dreieck (Abbildung 2-2-47). | Seltene | Sichtbare Längsstreifen (Abbildung 2-2-48) | |
| Quarz (Kristallquarz) | Säulenförmige Kristallform (Abbildung 2-2-49) | Der Querschnitt ist hexagonal, hexagonale Bipyramiden sind selten (Abbildungen 2-2-50, 2-2-51), hexagonale Monopyramiden sind häufig | Häufiger Kontakt mit Bi-Kristallen (auch bekannt als japanische Bikristalle) | Häufige horizontale Streifen auf Kristalloberflächen | |
| Chrysoberyll | Trigonales Kristallsystem | Säulenkristallisationsmerkmale (Abbildung 2-¬2-52) | Monokristallin ist selten | Dreikristallin ist üblich (Abbildung 2-2-53), hexagonale und konkave Winkel können als Identifikationskriterien verwendet werden | Die Streifen von Trikristallin können als Erkennungsmerkmal verwendet werden |
| Topas | Säulenförmige Kristallform (Abbildung 2-2-54) | Der Querschnitt ist rautenförmig, und die Spitze erscheint oft hüllenförmig (Abbildung 2-2-55). | Bi-Kristalle sind selten | Sichtbare Längsstreifen | |
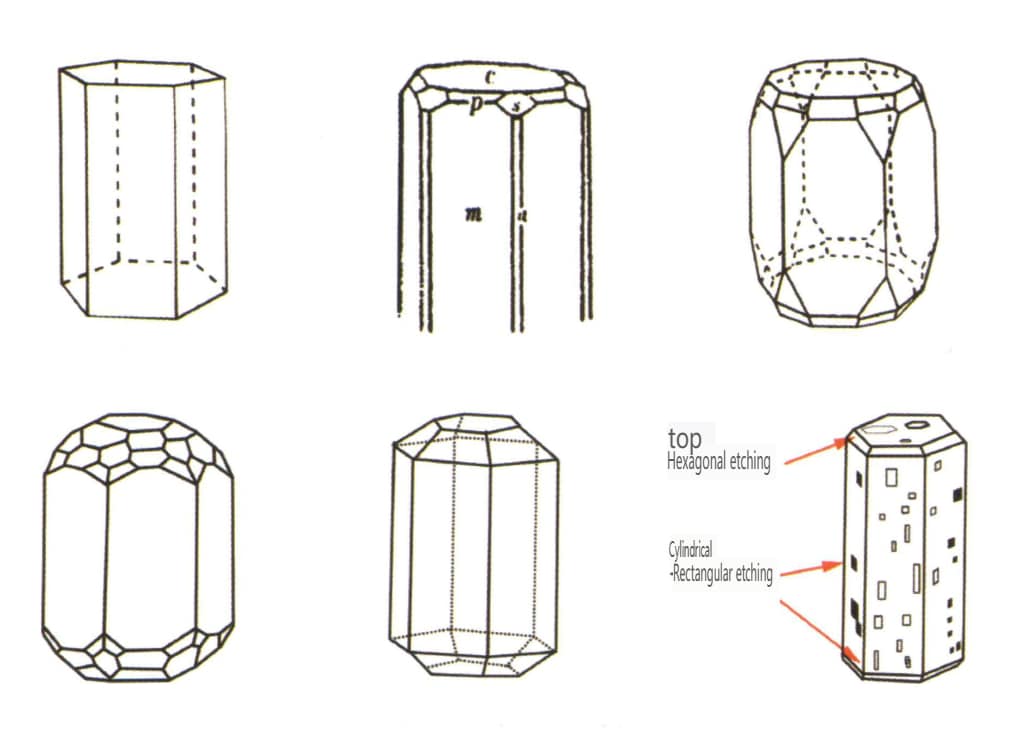
Abbildung 2-2-38 Kristallhabitus des Berylls

Abbildung 2-2-39 Häufige Formen von Smaragdkristallen

Abbildung 2-2-40 Häufige Formen von Aquamarin-Kristallen
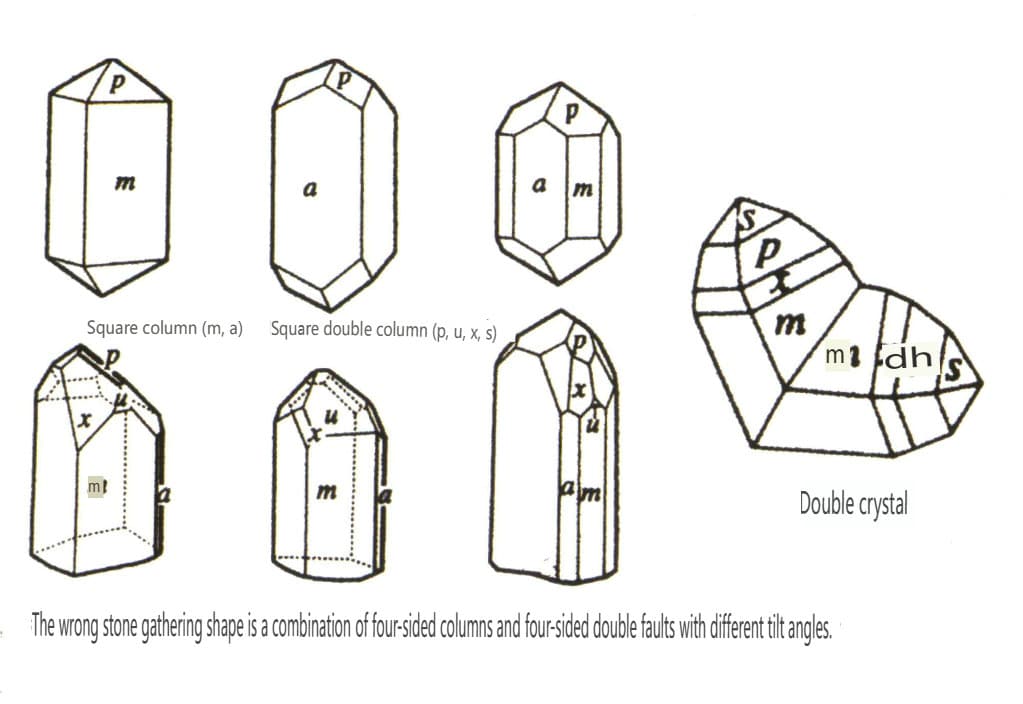
Abbildung 2-2-41 Zirkon-Kristallhabitus

Abbildung 2-2-42 Zirkonkristall
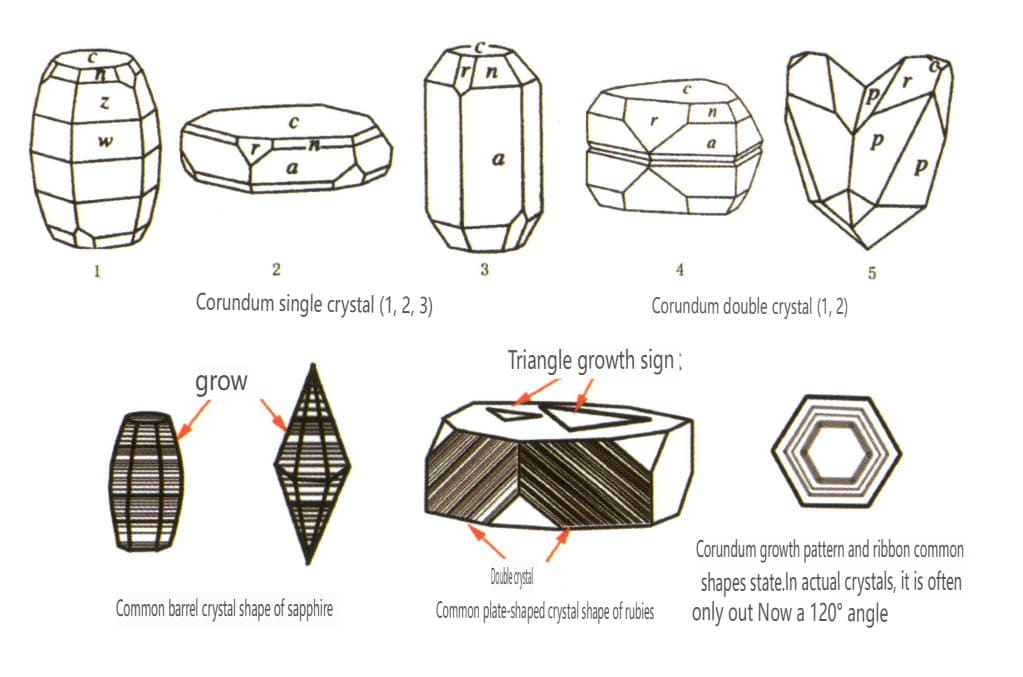
Abbildung 2-2-43 Korund-Kristallhabitus

Abbildung 2-2-44 Rubinkristall

Abbildung 2-2-45 Mechanischer Zwilling des Rubins
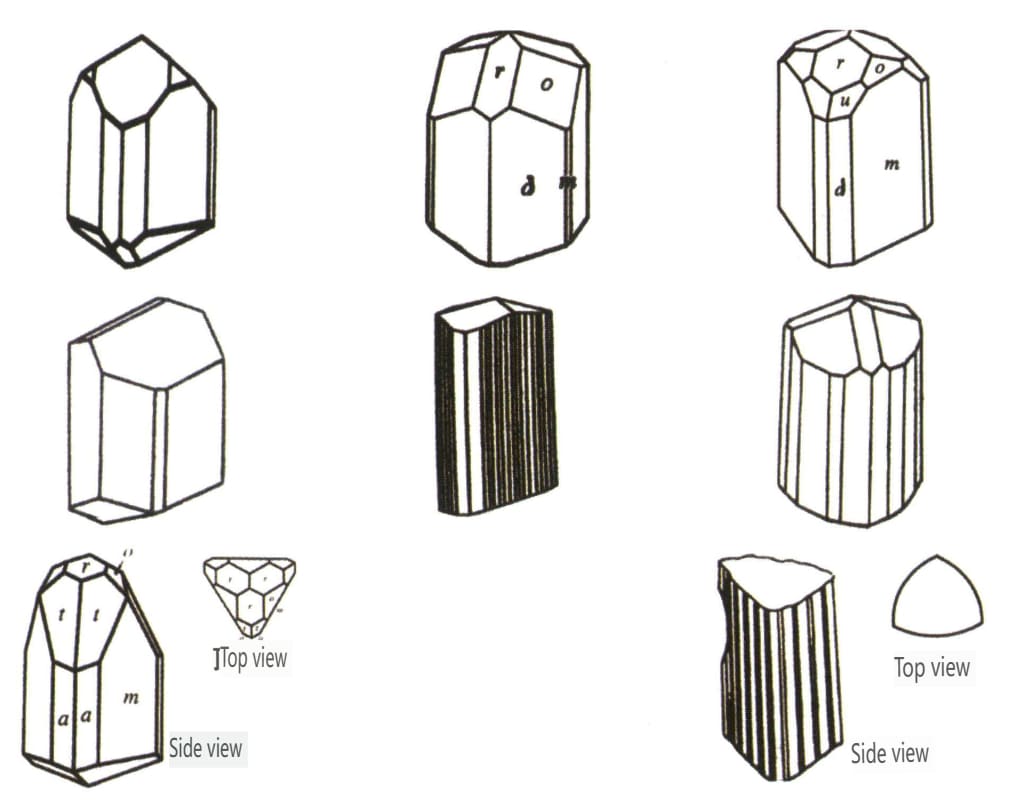
Abbildung 2-2-46 Turmalin-Kristallhabitus

Abbildung 2-2-47 Turmalinkristall

Abbildung 2-2-48 Längsstreifen an der Oberfläche eines Turmalinkristalls
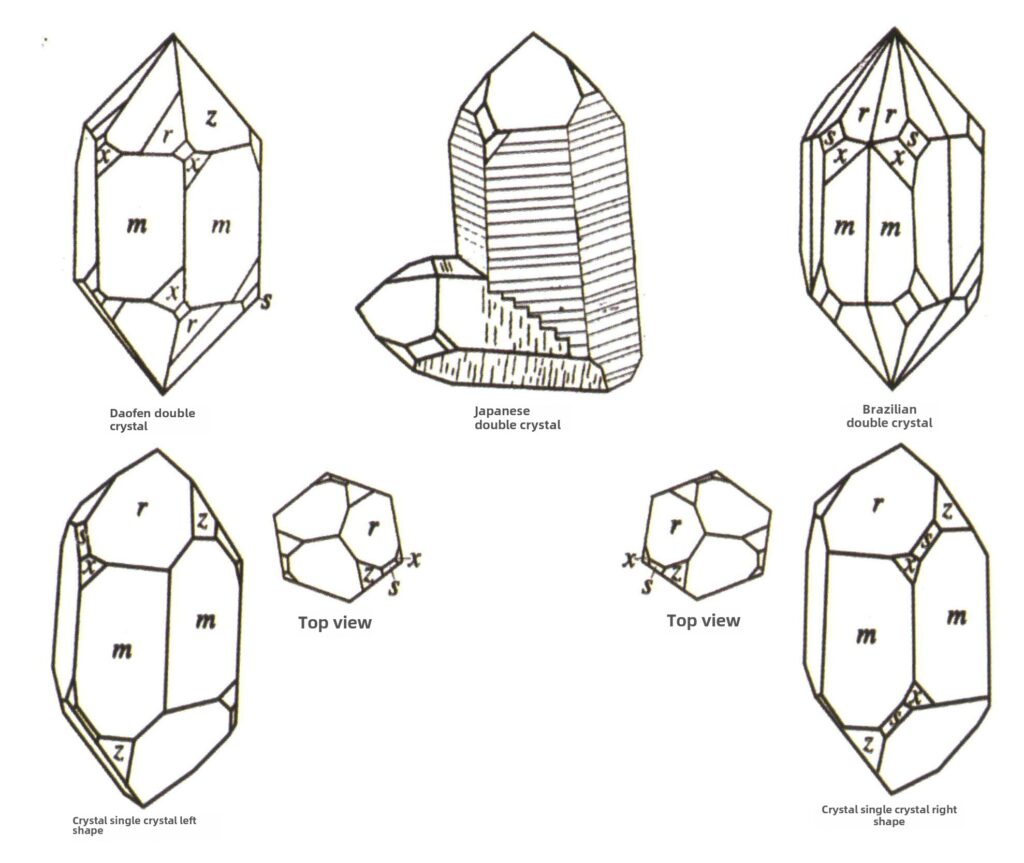
Abbildung 2-2-49 Kristall Kristallisationsgewohnheiten

Abbildung 2-2-50 Kristallkörper

Abbildung 2-2-51 Kristallkörper
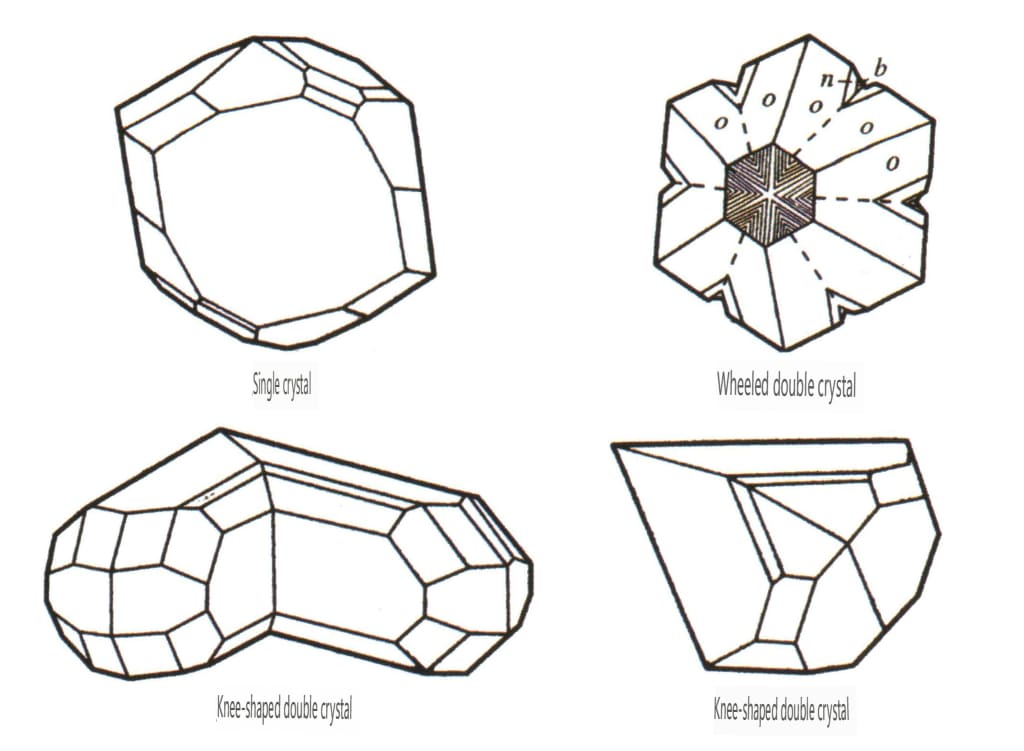
Abbildung 2-2-52 Kristallhabitus von Chrysoberyll

Abbildung 2-2-53 Kristall des Chrysoberylls
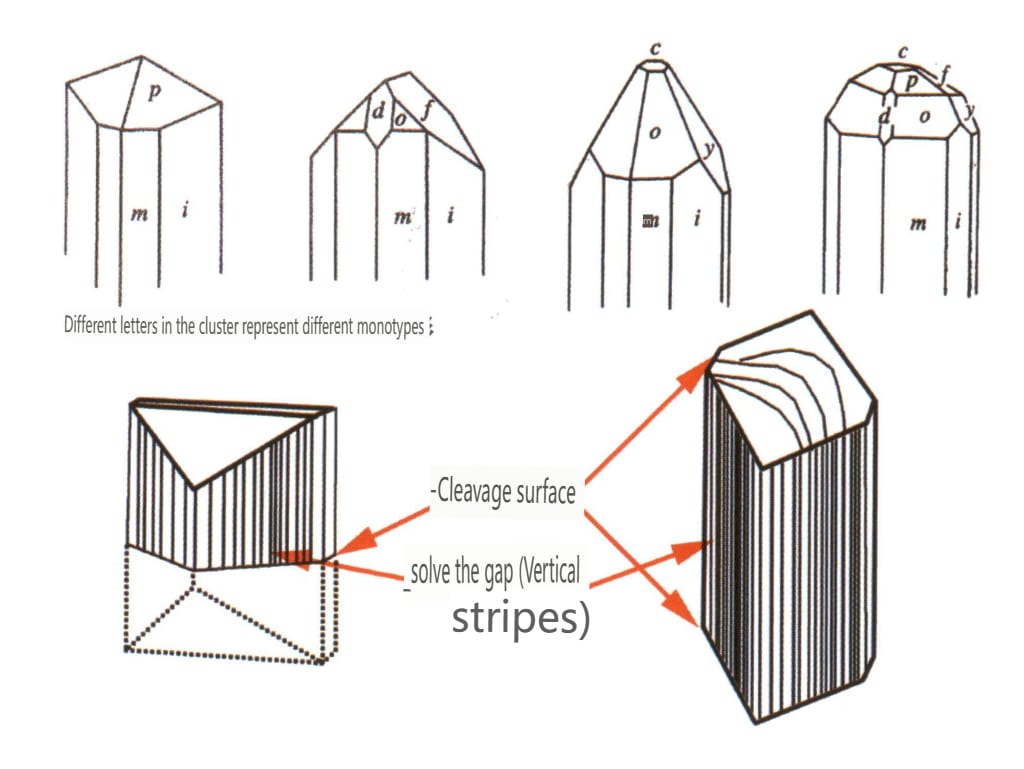
Abbildung 2-2-54 Kristallverhalten von Topas

Abbildung 2-2-55 Topas-Kristall
Abschnitt IV Warum wachsen Edelsteinkristalle unterschiedlich?
Aus mikroskopischer Sicht ist der Edelsteinkristall ein Festkörper, der aus Elementen unterschiedlicher Größe besteht, die nach unterschiedlichen Regeln angeordnet sind. Aus makroskopischer Sicht weisen viele Edelsteine aufgrund ihrer unterschiedlichen Zusammensetzung kristalline Formen auf. Es gibt jedoch einige Sonderfälle, wie z. B. heteromorphe Kristalle. Um besser zu verstehen, warum Edelsteinkristalle unterschiedlich aussehen, stellen wir hier fünf Aspekte vor: Heteromorphie, Isomorphie, molekularmechanische Durchmischung, Wasser in Edelsteinmineralien und chemische Zusammensetzung von Edelsteinen.
1. Heteromorphe
Obwohl einige Minerale die gleiche chemische Zusammensetzung aufweisen, haben sie sehr unterschiedliche Kristallstrukturen (die Anordnung der Elemente im dreidimensionalen Raum) und weisen erhebliche Unterschiede in den physikalischen und chemischen Eigenschaften auf (Tabelle 4). Wir bezeichnen dieses Phänomen als Heteromorphismus, z. B. bei Diamant und Graphit (Abbildung 2-2-56).
Bei gewöhnlichem Quarz tritt das Phänomen des Heteromorphismus auf. Sillimanit, Andalusit und Kyanit sind eine Gruppe von Heteromorphismusvarianten.
Die Umwandlung der Heteromorphie erfolgt unter Festkörperbedingungen. Während des strukturellen Umwandlungsprozesses kann sich innerhalb des Kristalls ein Druck entwickeln, der häufig zur Bildung von Zwillingen im Inneren des Kristalls führt.

Tabelle 4: Vergleich der Eigenschaften von Diamant und Graphit
| Mineral | Diamant | Graphit |
|---|---|---|
| Komponenten | Kohlenstoff (C) | Kohlenstoff (C) |
| Entstehungsbedingungen | Hohe Temperatur und hoher Druck | Hohe Temperatur |
| Kristallsystem, Gewohnheit | Isometrisches Kristallsystem, Oktaeder, rhombisches Dodekaeder | Hexagonales Kristallsystem, geschichtet |
| Farbe | Farblos, gelb, blau, rosa, grün, usw. | Schwarz |
| Lüster | Adamantine-Glanz | Metallischer Glanz |
| Transparenz | Transparent bis undurchsichtig | Undurchsichtig |
| Brechungsindex | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Mechanische Eigenschaften | Mäßige oktaedrische Spaltung, Härte 10, Dichte 3,52 | Ein Satz mit perfekter Spaltbarkeit, Härte 1, Dichte 2.10 |
| Andere Eigenschaften | Ausgezeichnete Wärmeleitfähigkeit; mit Ausnahme der blauen Naturdiamanten, die Halbleiter sind, sind Diamanten anderer Farben Isolatoren. | Mäßige Wärmeleitfähigkeit, gute elektrische Leitfähigkeit |
2. Isomorphismus
Isomorphismus bezeichnet das Phänomen, dass einige Teilchen in der Gitterstruktur durch andere Teilchen mit ähnlichen Eigenschaften ersetzt werden, was zu geringfügigen Änderungen der Gitterparameter und der physikalischen und chemischen Eigenschaften führt. Im Gegensatz dazu bleibt die Kristallstruktur im Wesentlichen unverändert. Dies kann so verstanden werden, dass die Elemente im Edelsteinkristall durch andere Elemente ersetzt werden. Das sich wiederholende Muster der Elemente des Edelsteinkristalls bleibt dagegen gleich, mit leichten Abweichungen bei den Abständen zwischen den Atomen. Dennoch verändern sich die physikalisch-chemischen Eigenschaften des Edelsteinkristalls geringfügig (Abbildung 2-2-57 bis Abbildung 2-2-58).
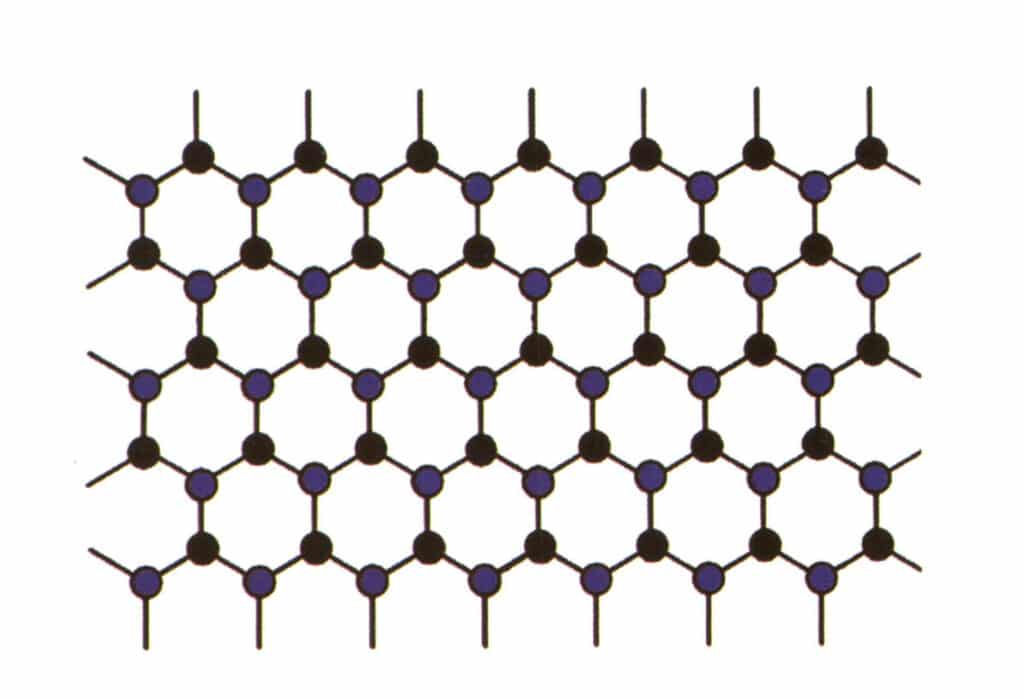
Abbildung 2-2-57 Kristallstruktursimulationsdiagramm (blau und schwarz kennzeichnen Elementteilchen)
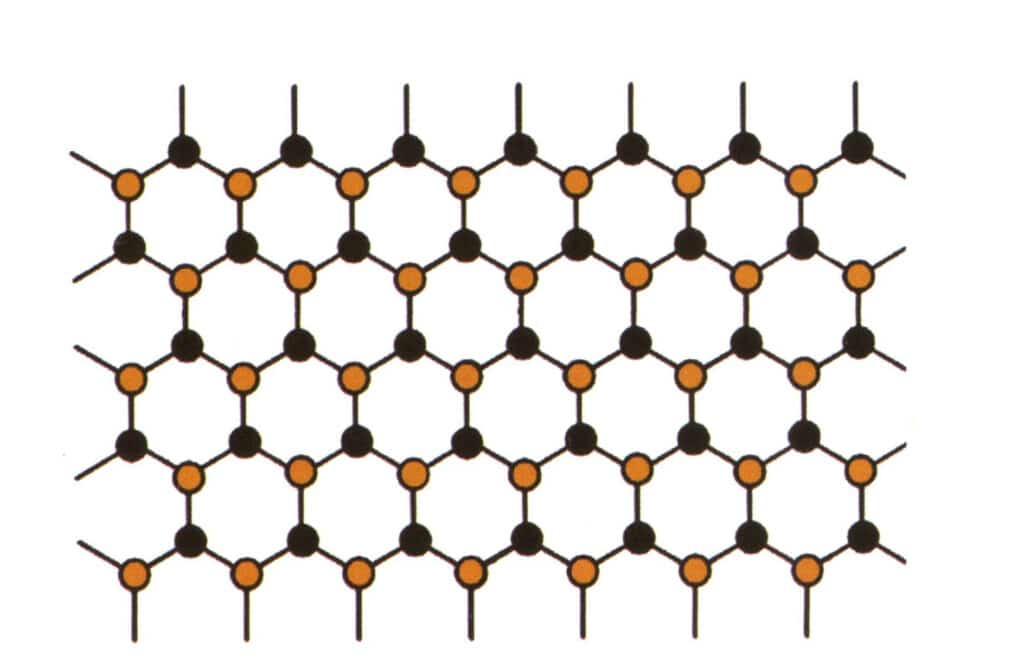
Abbildung 2-2-58 Kristallstruktursimulationsdiagramm (schwarz steht für Elementarteilchen, gelb für neue Elementarteilchen, die die blauen Elementarteilchen teilweise ersetzen, gelb kann nicht alle blauen Teilchen vollständig ersetzen)
Das Konzept der Isomorphie kann erklären, warum Edelsteine aus ein und derselben Familie so viele Farben haben können und warum es Unterschiede im Brechungsindex und in der Dichte zwischen Edelsteinen ein und derselben Familie gibt.
Eine Familie kann als eine Art von Edelstein verstanden werden, bei dem die sich wiederholenden Muster der Kristallelemente gleich sind, aber die physikalischen und chemischen Formen leicht unterschiedlich sind. Die Korundfamilie umfasst beispielsweise zwei Mitglieder, Rubin und Saphir, während die Beryllfamilie Smaragd-, Aquamarin- und Morganitvarianten umfasst.
(1) Olivin
Die chemische Zusammensetzung von Olivin ist (Mg,Fe)₂SiO₄. In seiner Zusammensetzung findet eine vollständige isomorphe Substitution der Elemente Fe und Mg statt. Mit steigendem Fe-Gehalt im Olivin wird die Farbe des Olivins dunkler, der Brechungsindex steigt und die Dichte nimmt ebenfalls zu.
(2) Korund
Reiner Korund ohne Verunreinigungen (Al₂O₃) ist farblos, und wenn Cr das Al ersetzt, hat der Edelstein einen rosaroten bis roten Farbton, der als Rubin bezeichnet wird. Die übrigen Farben werden als Saphir bezeichnet, z. B. orange-gelber Saphir oder farbloser Saphir. Der gemeinhin als Saphir bezeichnete blaue Saphir enthält Fe und Ti anstelle von Al. Je höher der Gehalt der färbenden Elemente im Ersatzstein ist, desto tiefer ist die Farbe des Edelsteins; umgekehrt ist die Farbe umso heller, je niedriger der Gehalt ist.
(3) Turmalin
Turmalin bezieht sich auf dieselbe Art von Edelstein wie Turmalin, wobei Turmalin der mineralogische Name und Turmalin der gemmologische Name ist. Die chemische Zusammensetzung des Berylls ist (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), wobei R hauptsächlich Mg , Fe , Cr , Li, Al , Mn ist und die Elemente in R sich vollständig oder teilweise gegenseitig ersetzen können, was zu einer extrem großen Farbvielfalt des Turmalins führt. Wenn R hauptsächlich Fe ist, hat Beryll beispielsweise eine tiefblaue oder sogar schwarze Farbe; wenn R hauptsächlich Mg ist, ist Beryll gelb bis braun; wenn R hauptsächlich Li oder Mn ist, ist der Beryll rosa oder hellblau; wenn R hauptsächlich Cr ist, ist der Turmalin tiefgrün.
Daraus ist ersichtlich, dass die Substitution von Elementen mit ähnlichen Eigenschaften zu schöneren und brillanteren Farben bei Edelsteinen führt.
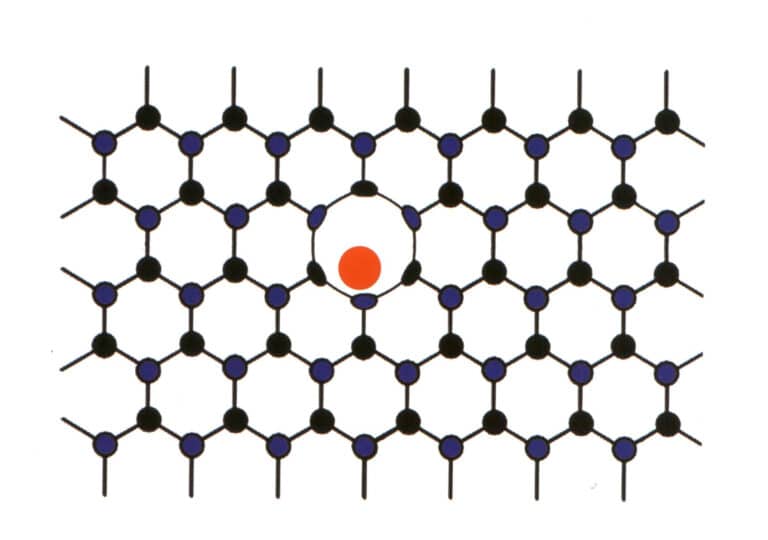
3. Molekularmechanische Durchmischung
Manchmal dringen bestimmte Elemente gewaltsam zwischen die Hauptelemente von regelmäßig angeordneten Edelsteinen ein. Der geringe Anteil der eingedrungenen Elemente stört jedoch nicht das sich wiederholende Muster der Hauptelemente des Edelsteins, sondern verursacht lediglich eine Verformung (Abbildung 2-2-59). Diese Situation wird als molekularmechanische Durchmischung bezeichnet, wie z. B. die molekularmechanische Durchmischung von Stickstoff und Bor in Diamanten, durch die blaue, rosa und gelbe Diamanten entstehen, die sehr wertvoll sind.
4. Wasser in Edelsteinmineralien
Einige Edelsteine enthalten Wasser, das ein wichtiger Bestandteil von Edelsteinmineralien ist und eng mit den Eigenschaften der Edelsteine zusammenhängt. Basierend auf der Form des Wassers in Edelsteinmineralien und seiner Rolle in der Kristallstruktur kann das Wasser in Edelsteinen in zwei Kategorien unterteilt werden: Absorptionswasser, das nichts mit der Kristallstruktur zu tun hat, und Wasser, das an der Kristallstruktur des Minerals beteiligt ist, einschließlich Kristallisationswasser, zeolithisches Wasser, Zwischenschichtwasser und Konstitutionswasser. Das Wasser, das eng mit Edelsteinen verbunden ist, umfasst Absorptionswasser, Kristallisationswasser und Konstitutionswasser.
Eine ist die Absorption von Wasser, wie Opal (chemische Zusammensetzung ist SiO₂ - nH₂O, n steht für die Anzahl der H₂O, der Inhalt ist variabel) in das Wassermolekül, das ein neutrales Wassermolekül mechanisch adsorbiert für mineralische Partikel oder Bruchflächen ist. Wenn die Temperatur 100 ~ 110°Grad unter normalem Druck erreicht, können die Wassermoleküle alle entkommen und beschädigen nicht die Kristallgitterstruktur, so dass der Opal in der Theke in einer langen Zeit der starken Lichteinwirkung trockenen Riss zu vermeiden, sollte eine Tasse Wasser in der Theke setzen.
Das zweite ist das Kristallwasser, wie z. B. das Kristallwasser in Türkis [chemische Zusammensetzung: CuAl₆(PO₄)₄(OH)₈-4H₂O, wobei der Gehalt an H₂O 19,47% erreichen kann]. Dieses neutrale Wassermolekül befindet sich an festen Positionen im Kristallgitter und dient als Struktureinheit, die Teil der chemischen Zusammensetzung des Minerals ist. Die Temperatur, bei der das Kristallwasser entweicht, beträgt im Allgemeinen nicht mehr als 600℃ und liegt in der Regel bei 100 -200℃. Wenn ein Edelstein sein Kristallwasser verliert, wird seine Kristallstruktur beschädigt und es bildet sich eine neue Struktur.
An dritter Stelle steht das Konstitutionswasser, auch kombiniertes Wasser genannt, das in Form von OH-, H⁺, H₃O⁺-Plasma am Mineralgitter beteiligt ist, wobei OH- am häufigsten vorkommt. Das Konstitutionswasser ist Teil der chemischen Zusammensetzung des Minerals und nimmt feste Positionen in der Gitterstruktur mit einem bestimmten Anteil an der Zusammensetzung ein. Strukturelles Wasser benötigt eine höhere Temperatur, um zu entweichen und seine Struktur zu beschädigen, in der Regel etwa 600-1000℃. Wenn ein Edelstein Strukturwasser verliert, wird seine Kristallstruktur zerstört. Viele Edelsteine enthalten Konstitutionswasser, wie z. B. Turmalin [die chemische Zusammensetzung ist ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), wobei R hauptsächlich Mg , Fe , Cr, Li, Al, Mn, etc. enthält, und die Elemente in R können sich ganz oder teilweise gegenseitig ersetzen], und Topas [chemische Zusammensetzung ist Al₂SiO₄( F, OH) ₂ ].
5. Die chemische Zusammensetzung von Edelsteinen
Edelsteine bestehen, wie andere Stoffe auch, aus chemischen Elementen. Jede Edelsteinart hat ihre spezifische chemische Zusammensetzung und eine gewisse Variationsbreite, die die verschiedenen Merkmale und Eigenschaften des Edelsteins bestimmt. Edelsteine gehören zu den Mineralien und Gesteinen, und die Klassifizierung der chemischen Zusammensetzung von Edelsteinen lässt sich auf die chemische Zusammensetzung von Mineralien zurückführen.
Zu den wichtigsten Klassifizierungsmethoden für Mineralien gehören derzeit die Klassifizierung nach der chemischen Zusammensetzung (Dana-System), die geochemische Klassifizierung, die genetische Klassifizierung, die Verwendungsklassifizierung und die kristallchemische Klassifizierung. Die am weitesten verbreitete Methode ist die chemische Klassifikation auf der Grundlage der chemischen Zusammensetzung und der Kristallstruktur (Hugo-Strunz-System) (Tabelle 5).
Tabelle 5: Chemisches Klassifizierungssystem für Mineralkristalle
| Reihenfolge der Ebenen | Grundlage für die Aufteilung | Beispiel |
|---|---|---|
| Hauptkategorie | Verbindungstyp | Sauerstoffhaltige Salze Hauptkategorie |
| Klasse | Anionen- oder Komplexe Anionenarten | Silikat-Klasse |
| (Unterkategorie) | Struktur eines anionischen Komplexes | Unterklasse Gerüstsilikat |
| Gruppe | Kristallstrukturtypen und ionische Eigenschaften | Korundgruppe, Beryllgruppe, Granatgruppe |
| (Untergruppe) | Kationen-Typen | Untergruppe der Alkalifeldspäte |
| Specie | Bestimmte Kristallstruktur und chemische Zusammensetzung | Orthoklas KAlSi3O8 |
| (Unterart) | Gleiche Kristallstruktur, unterschiedliche Zusammensetzung oder Eigenschaften, Morphologie | Adularia KAlSi3O8 |