Warum haben Edelsteine mehrere Farben?
Einführung in die Kristallfeldtheorie & Molekülorbitaltheorie & Energiebandtheorie
Die Farben der Edelsteine sind reich und vielfältig und besitzen einen einzigartigen Charme, den die Menschen seit jeher lieben. Die Qualität von Edelsteinen hängt weitgehend von ihrer Farbe ab. Die Farbe eines Edelsteins ist ein wichtiger Indikator für die Bewertung von Edelsteinen, und die meisten Optimierungsbehandlungen für Edelsteine beinhalten die Veränderung oder Verbesserung ihrer Farbe. Daher ist das Verständnis der Ursachen für die Färbung von Edelsteinen eine entscheidende Voraussetzung für die Optimierung von Edelsteinen. Nur wenn man weiß, wie Edelsteine ihre Farbe erhalten, kann man feststellen, ob ein Edelstein optimiert werden kann, welches Optimierungsschema man anwenden und welchen Versuchsplan man aufstellen sollte. Es gibt fünf gängige Theorien zur Färbung von Edelsteinen: die klassische Mineralogietheorie, die Kristallfeldtheorie, die Molekularorbitaltheorie, die Energiebandtheorie und die physikalisch-optischen Effekte. Diese Theorien bilden die Färbungstheorien der gängigen natürlichen Edelsteine, und im Folgenden wird eine kurze Einführung in diese fünf Färbungstheorien gegeben.
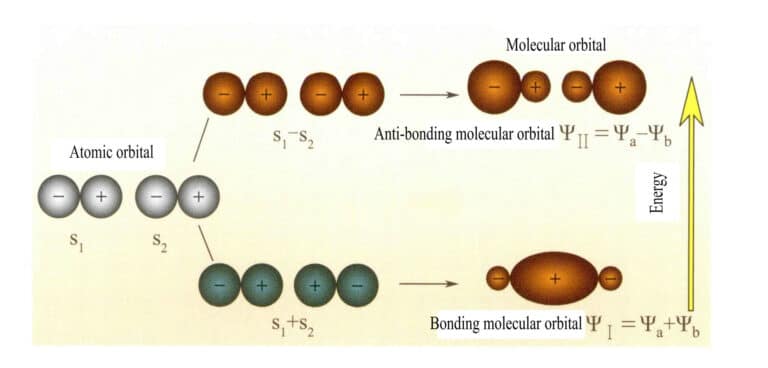
Molekülorbitale, die aus zwei s-Atomorbitalen gebildet werden
Inhaltsübersicht
Abschnitt I Kristallfeldtheorie
In den 1930er Jahren schlugen Wissenschaftler die Kristallfeldtheorie vor, um die Eigenschaften von Kristallen zu erklären. Die Kristallfeldtheorie ist eine Theorie, die die chemischen Bindungen von Übergangselementen (Komplexen) untersucht. Sie erklärt die physikalischen und chemischen Eigenschaften von Übergangselementen und Lanthaniden, indem sie einige Gesichtspunkte der elektrostatischen Theorie, der Quantenmechanik und der Gruppentheorie (der Theorie, die die Symmetrie der Materie untersucht) kombiniert und sich dabei auf den Einfluss der Liganden auf die d- und f-Orbitale der zentralen Ionen konzentriert. In den 1950er Jahren wandte man die Kristallfeldtheorie auf Komplexe an und schlug die Ligandenfeldtheorie vor. Die Ligandenfeldtheorie ist eine Weiterentwicklung der Kristallfeldtheorie; sie berücksichtigt sowohl den Einfluss des elektrischen Feldes des Liganden auf das Zentralion als auch die Füllwirkung der Elektronen des Liganden auf das Zentralion und ist damit vollständiger als die Kristallfeldtheorie. Es besteht jedoch kein wesentlicher Unterschied zwischen den beiden Theorien, und sie werden bei der Untersuchung anorganischer Mineralien im Allgemeinen nicht unterschieden.
1. Grundlegende Konzepte der Kristallfeldtheorie
Die Ionen der Übergangsmetalle befinden sich im Kristallfeld der sie umgebenden Anionen oder Dipolmoleküle. Die Kristallfeldtheorie ist ein elektrostatisches Modell, das den Kristall als eine elektrostatische Wechselwirkung zwischen positiven und negativen Ionen betrachtet, wobei das positiv geladene Kation als Zentralion und das negativ geladene Anion als Ligand bezeichnet wird.
Die Anwendung der Kristallfeldtheorie zur Erklärung der Farbe von Edelsteinmineralien bezieht sich hauptsächlich auf die d-Elektronen oder die f-Elektronenenergie von Übergangselement-Ionen. Die d-Orbitale haben zum Beispiel fünf Typen: dxy, dxz, dyz, d , und d . Diese fünf d-Orbitale haben im freien Ionenzustand unterschiedliche räumliche Verteilungen, aber die gleiche Energie. Unter dem Einfluss des Ligandenfeldes erfahren sie jedoch erhebliche Veränderungen. Die fünf energetisch entarteten d-Orbitale des Zentralatoms spalten sich unter dem Einfluss des negativen elektrischen Feldes, das von den umgebenden Liganden gebildet wird. Einige d-Orbitale haben eine höhere Energie, während andere eine niedrigere Energie aufweisen. Aufgrund der Aufspaltung der Energieniveaus der d-Orbitale ordnen sich die Elektronen in den d-Orbitalen des Zentralatoms neu an und besetzen bevorzugt die Orbitale mit niedrigerer Energie, wodurch die Gesamtenergie des Systems verringert und der Komplex stabiler wird.
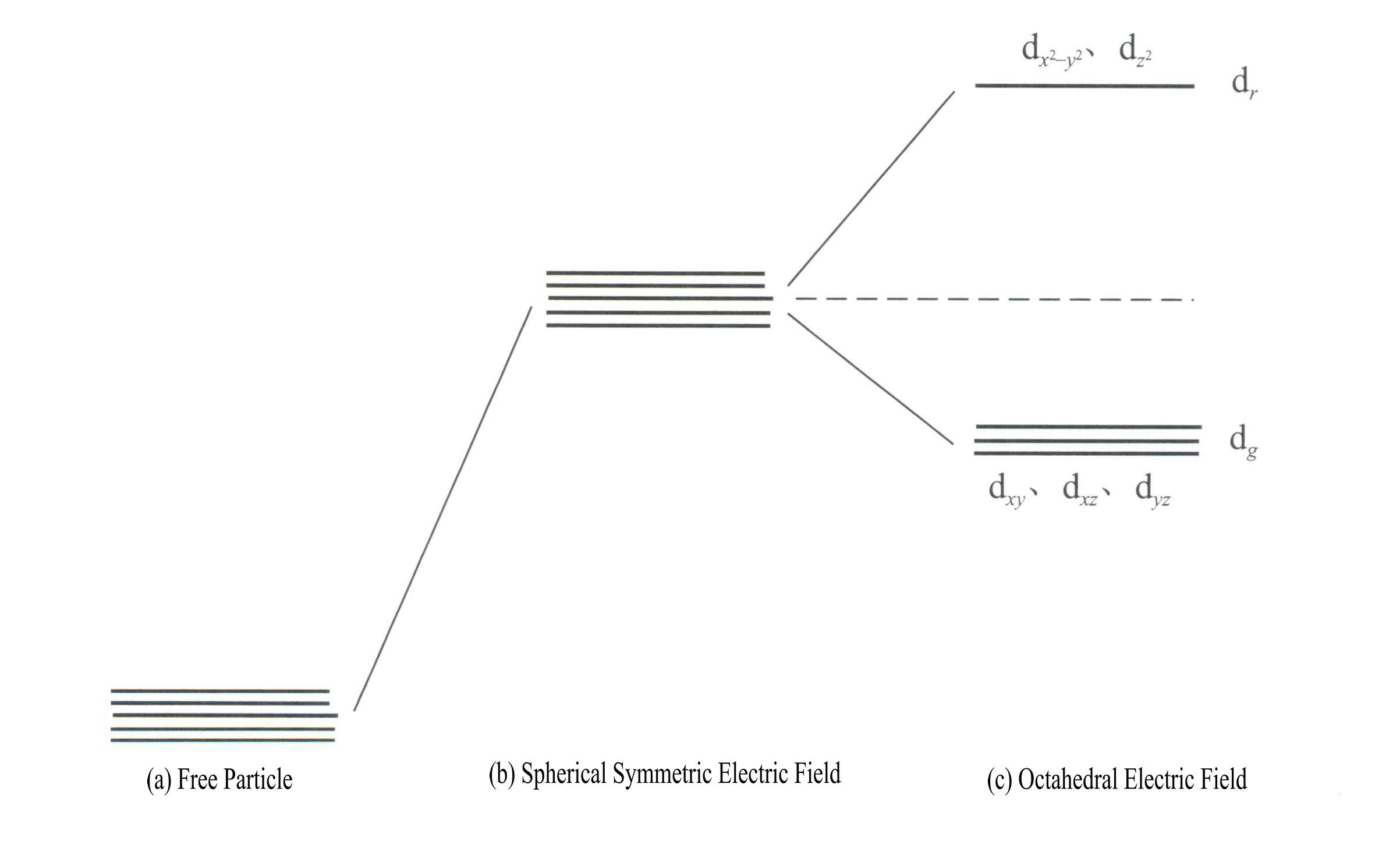
Die Energie der d-Orbitale ist gleich, wenn kein elektrisches Feld vorhanden ist [Abbildung 3-19 (a)]; unter einem sphärisch symmetrischen elektrostatischen Feld haben die d-Orbitale eine höhere Energie, spalten sich aber nicht auf [Abbildung 3-19 (b)]; wenn das Ligandenfeld oktaedrisch ist, spaltet es sich in dr und dg. Davon sind dr Orbitale bestehen aus d und d , mit höherer Energie; die energieärmeren dg Orbitale bestehen aus dxy, dxz, dyz.
Die Ionen der Übergangsmetalle befinden sich im Kristallfeld der sie umgebenden Anionen oder Dipolmoleküle. Die Kristallfeldtheorie ist ein elektrostatisches Modell, das den Kristall als eine elektrostatische Wechselwirkung zwischen positiven und negativen Ionen betrachtet, wobei das positiv geladene Kation als Zentralion und das negativ geladene Anion als Ligand bezeichnet wird.
Die Anwendung der Kristallfeldtheorie zur Erklärung der Farbe von Edelsteinmineralien bezieht sich hauptsächlich auf die d-Elektronen oder die f-Elektronenenergie von Übergangselement-Ionen. Die d-Orbitale haben zum Beispiel fünf Typen: dxy, dxz, dyz, d , und d . Diese fünf d-Orbitale haben im freien Ionenzustand unterschiedliche räumliche Verteilungen, aber die gleiche Energie. Unter dem Einfluss des Ligandenfeldes erfahren sie jedoch erhebliche Veränderungen. Die fünf energetisch entarteten d-Orbitale des Zentralatoms spalten sich unter dem Einfluss des negativen elektrischen Feldes, das von den umgebenden Liganden gebildet wird. Einige d-Orbitale haben eine höhere Energie, während andere eine niedrigere Energie aufweisen. Aufgrund der Aufspaltung der Energieniveaus der d-Orbitale ordnen sich die Elektronen in den d-Orbitalen des Zentralatoms neu an und besetzen bevorzugt die Orbitale mit niedrigerer Energie, wodurch die Gesamtenergie des Systems verringert und der Komplex stabiler wird.
Die Energie der d-Orbitale ist gleich, wenn kein elektrisches Feld vorhanden ist [Abbildung 3-19 (a)]; unter einem sphärisch symmetrischen elektrostatischen Feld haben die d-Orbitale eine höhere Energie, spalten sich aber nicht auf [Abbildung 3-19 (b)]; wenn das Ligandenfeld oktaedrisch ist, spaltet es sich in dr und dg. Davon sind dr Orbitale bestehen aus dx2– y2 und dz2
mit höherer Energie; das energieärmere dg Orbitale bestehen aus dxy, dxz, dyz. [Abbildung 3-19 (c)]
Die Differenz zwischen dem höchsten und dem niedrigsten Energieniveau nach der d-Orbitalaufspaltung wird als Trennungsenergie △ bezeichnet. Die Trennungsenergien, die durch verschiedene Konfigurationen von Ligandenfeldern erzeugt werden, sind nicht gleich (Abbildung 3-20). Ihre Energiereihenfolge ist:
Quadratisches Feld > Oktaedrisches Feld > Tetraedrisches Feld

Selbst bei Feldern gleicher Konfiguration können sie sich aufgrund der Unterschiede bei den Liganden und Zentralionen unterscheiden; je größer sie ist, desto stabiler ist der Kristall. Die folgenden drei Faktoren bestimmen hauptsächlich die Größe der Kristalltrennungsenergie:
(1) Kristalle, die von demselben Übergangselement gebildet werden; wenn die Liganden gleich sind, ist die Trennungsenergie △ umso größer, je höher die Ladung des Zentralions ist. Je höher die positive Ladung des Zentralions ist, desto größer ist die Anziehung zu den Liganden, was zu einem geringeren Abstand zwischen dem Zentralion und dem Ligandenkern führt, und je größer die Abstoßungskraft des von den Liganden erzeugten Kristallfeldes auf die Elektronen ist, desto größer ist die Trennungsenergie △.
(2) Für Kristalle, die aus verschiedenen Ionen mit derselben positiven Ladung und denselben Liganden gebildet werden, gilt: Je größer der Radius des Zentralions ist, desto weiter sind die d-Orbitale vom Kern entfernt, und desto größer ist die Trennungsenergie △.
(3) Bei Kristallen, die von demselben Zentralion und verschiedenen Liganden gebildet werden, variiert die Trennungsenergie aufgrund der unterschiedlichen Stärke des Kristallfeldes des Liganden. Verschiedene Liganden haben unterschiedliche Feldstärken, und die Trennungsenergie △ variiert mit der Feldstärke des Liganden.
Die Trennungsenergie wird verwendet, um die Stabilität von Kristallen qualitativ zu erklären; es ist nicht notwendig, den absoluten Wert △ zu erhalten, da es ausreicht, die relativen Werte des Kristalls unter verschiedenen Bedingungen zu kennen.
Anhand der relativen Energie der aufgespaltenen d-Orbitale lässt sich die Gesamtenergie der Übergangsmetallionen in den d-Orbitalen berechnen. Diese Energie ist niedriger als vor der Aufspaltung, wodurch dem Kristall zusätzliche Energie zugeführt wird, die als Kristallfeldstabilisierungsenergie bezeichnet wird und durch das Symbol CFSE dargestellt wird. In Tabelle 3-10 sind die Stabilisierungsenergien von Ionen mit dn Elektronen unter verschiedenen Bedingungen.
Tabelle 3-10 Kristallfeld-Stabilisierungsenergien unter verschiedenen Liganden (Wu Ruihua, 1994)
| dn | Schwaches Feld | Starkes Feld | ||||
|---|---|---|---|---|---|---|
| dn | Quadratisch | Regelmäßiges Oktaeder | Regelmäßiges Tetraeder | Quadratisch | Regelmäßiges Oktaeder | Regelmäßiges Tetraeder |
| d0 | 0 | 0 | 0 | 0 | 0 | 0 |
| d1 | 5.14 | 4 | 2.67 | 5.14 | 4 | 2.67 |
| d2 | 10.28 | 8 | 5.34 | 10.28 | 8 | 5.34 |
| d3 | 14.56 | 12 | 3.56 | 14.56 | 12 | 8.01 |
| d4 | 12.28 | 6 | 1.78 | 19.70 | 16 | 10.68 |
| d5 | 0 | 0 | 0 | 24.84 | 20 | 8.90 |
| d6 | 5.14 | 4 | 2.67 | 29.12 | 24 | 6.12 |
| d7 | 10.28 | 8 | 5.34 | 26.84 | 18 | 5.34 |
| d8 | 14.56 | 12 | 3.56 | 24.56 | 12 | 3.56 |
| d9 | 12.28 | 6 | 1.70 | 12.28 | 6 | 1.78 |
| d10 | 0 | 0 | 0 | 0 | 0 | 0 |
2. Farbmerkmale von Übergangsmetall-Ionen
In seinen Farbedelsteinen ist die Farbe der meisten Edelsteine auf Übergangsmetallionen zurückzuführen, und die Farbe der Edelsteine hängt davon ab, ob die farbgebenden Ionen ungepaarte Elektronen in den d- oder f-Orbitalen enthalten. Zu den farbgebenden Eigenschaften von Übergangsmetallionen gehören hauptsächlich die folgenden Aspekte:
(1) Die Färbung von Übergangsmetallionen hängt mit den elektronischen Zuständen des d-Orbitals oder des f-Orbitals zusammen. Wenn die Elektronen des d-Orbitals oder des f-Orbitals gefüllt oder leer sind, weist der Edelstein keine Farbe auf. Zum Beispiel: Cr6+, Ce4+und Cu+.
(2) Verschiedene farbgebende Ionen weisen in ein und demselben Edelsteinmaterial unterschiedliche Farben auf. Aufgrund der unterschiedlichen Trennungsenergien der verschiedenen Farbionen können sie selbst in ein und demselben Material unterschiedliche Farben aufweisen. Zum Beispiel: Fe2+ erzeugt in Spinell eine leicht graublaue Farbe, während Cr3+ produziert Rot.
(3) Färbende Ionen desselben Elements in verschiedenen Wertigkeitsstufen weisen in ein und demselben Edelsteinmaterial oft unterschiedliche Farben auf. Da die für die d-Elektronenübergänge des Zentralions erforderliche Energie unterschiedlich ist, sind die absorbierten Wellenlängen des Lichts unterschiedlich, was zu unterschiedlichen Farben führt. Zum Beispiel enthält ein Castrum mit Mn2+ hat einen zartrosa Farbton, während ein Beryll mit Mn2+ präsentiert leuchtend rot, bekannt als roter Beryll.
(4) Färbende Ionen desselben Elements in derselben Wertigkeitsstufe weisen oft unterschiedliche Farben auf, wenn sie in verschiedenen Ligandenkonfigurationen vorliegen. Zum Beispiel: Co2+ in der tetraedrischen Konfiguration von Spinell zeigt eine charakteristische "diamantblaue" Farbe, während es in der oktaedrischen Konfiguration von Calcit rosa erscheint. Fe2+ im oktaedrisch koordinierten Olivin zeigt ein charakteristisches Olivgrün, während es im verzerrt kubisch koordinierten Almandin tiefrot erscheint.
(5) Farbige Ionen desselben Typs haben denselben Valenzzustand und dieselbe Koordinationsgeometrie, aber verschiedene benachbarte koordinierende Atome weisen unterschiedliche Farben auf. Zum Beispiel ist die tetraedrische Koordination von Co2+in Sphalerit, Co2+ mit Schwefel verbunden ist und grün erscheint, während in Spinell Co2+ ist mit Sauerstoff verbunden und zeigt blau.
(6) Dieselbe Art von farbigen Ionen mit derselben Valenzstufe, Koordinationsgeometrie und benachbarten Atomen weist in verschiedenen Edelsteinen unterschiedliche Farben auf. Die durch die unterschiedlichen chemischen Zusammensetzungen der Edelsteine verursachte Verzerrung der Koordinationsgeometrie verändert die Art der chemischen Bindungen zwischen dem Zentralion und den koordinierenden Liganden, wodurch sich die Übergangsenergie der d-Elektronen ändert. Zum Beispiel: Cr3+ erscheint in Rubinen rot, in Smaragden grün und zeigt in Alexandriten unterschiedliche Farben. Der Grund für diese Veränderungen in Cr3+ steht im Zusammenhang mit seinen Eigenschaften und den benachbarten koordinierenden Liganden, wobei die spezifischen Merkmale wie folgt analysiert werden.
① Cr3+ Merkmale:
Cr3+ hat eine Außenelektronenschalenstruktur von 3s23p63d3mit 11 Elektronen in der äußeren Schale, die zu einer unregelmäßigen (8-18) Elektronenschalenstruktur gehören.
Diese Struktur hat eine geringere abschirmende Wirkung auf den Kern als die 8-Elektronen-Schalenstruktur, was zu Cr3+ mit einer höheren effektiven positiven Ladung, während sein Ionenradius ebenfalls kleiner ist, was die grundlegenden Merkmale von Cr3+: ein starkes positives elektrisches Feld und leere d-Orbitale. Cr3+ kann sechs leere Orbitale zur Aufnahme von sechs koordinierenden Liganden mit oktaedrischer Raumkonfiguration bereitstellen, die zu d2sp3 Hybridisierung (Abbildung 3-21).
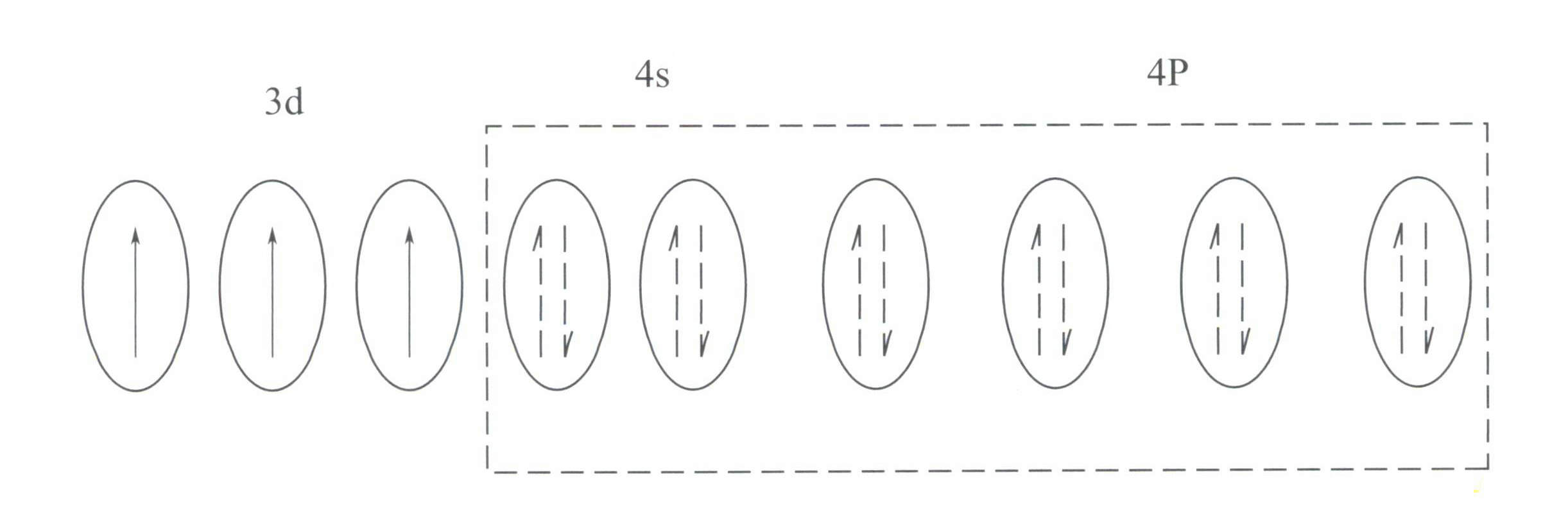
Nach der Kristallfeldtheorie sind in einem oktaedrischen Feld die d-Orbitale von Cr3+ kann sich in energieärmere dƐ Umlaufbahn und höherer Energie dr Umlaufbahn. Da die drei d-Elektronen von Cr3+ sind alle in der dƐ Orbital und sind allesamt Einzelelektronen, können d-d-Übergänge unter sichtbarem Licht auftreten, wodurch Edelsteine, die Cr3+ um Farbe zu zeigen.
② Der Färbungsmechanismus von Cr3+:
In Rubin Der chemische Hauptbestandteil von Rubin ist Al2O3. Wenn ein paar Prozent der Cr3+ ersetzt Al3+erzeugt er eine leuchtend rote Farbe. In der Struktur des Rubins, aufgrund der größeren Radius von Cr3+ im Vergleich zum Radius von Al3+, Cr3+ tritt in das Korundgitter ein und verringert die Symmetrie um das Aluminiumoxid.
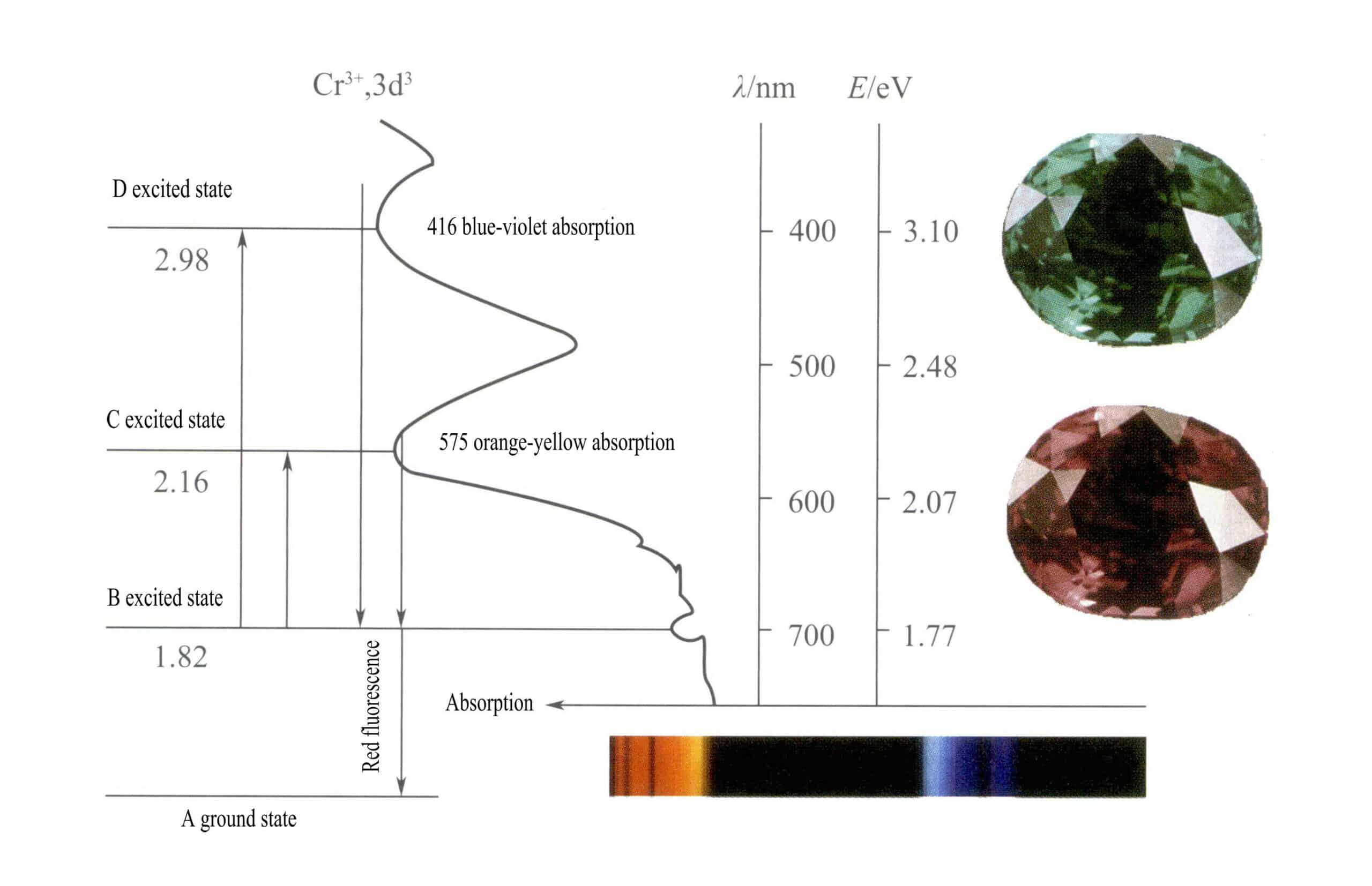
Die d-Orbitale von Cr3+ gespalten, und wenn die Elektronen im angeregten Zustand von D oder C in den Grundzustand A zurückkehren, müssen sie zunächst B durchqueren, wobei Wärme freigesetzt wird. Sie kehren von B nach A zurück, begleitet von Lumineszenz, und emittieren rote Fluoreszenz. Bei diesem Prozess absorbieren die Elektronen Lichtenergie, wodurch der Rubin im sichtbaren Spektrum D violett (400 nm) und C gelb-grün (555 nm) absorbiert (Abbildung 3-22) und eine Absorptionsbande bildet.

Wenn weißes Licht durch einen Rubin fällt, werden Photonen im Spektrum von Violett bis Gelbgrün absorbiert, während fast das gesamte rote Licht und etwas blaues Licht durchgelassen wird, was dem Rubin eine tiefrote Farbe mit einem Hauch von Violett verleiht, die als Taubenblutrot bekannt ist.
Rubine weisen eine kurze B-Absorption auf, die sich als rote Fluoreszenz äußert. Diese B-Absorption, die eine rote Fluoreszenz hervorruft, macht die Farbe des Rubins lebendiger; je höher der Chromionengehalt, desto stärker die Fluoreszenz.
Eisenionen im Edelstein können die Fluoreszenz der B-Absorption unterdrücken, was das Phänomen erklärt, dass Rubine, die Eisenverunreinigungen enthalten, dunkler erscheinen.
③ Cr3+ Der Färbemechanismus in Smaragden
Der chemische Hauptbestandteil von Smaragd ist Be3Al2Si6O18, Cr3+das Al ersetzt3+ im Smaragd-Gitter und Cr3+ ist ebenfalls von einem Oktaeder aus sechs Sauerstoffionen umgeben, wobei das Cr3+-O-Bindung ist der von Rubinen ebenfalls recht ähnlich. Im Vergleich zu Rubinen haben Smaragde jedoch zwei weitere Ionen, Be2+ und Si4+. In der Struktur der Smaragde nimmt die kovalente Bindung zwischen den Metalloxiden zu, während die ionischen Eigenschaften schwächer werden.
Geringfügige Veränderungen wie chemische Bindungen führen zu einer leichten Abnahme von Cr3+C-Niveau und D-Niveau-Energie, was zu einer leichten Verschiebung der Absorptionsbande führt (Abbildung 3-23), wodurch die Durchlässigkeit für blau-violettes (425 nm) und orange-gelbes (608 nm) Licht im Spektrum erheblich eingeschränkt wird, während die Durchlässigkeit für blau-grünes Licht erhöht wird, wodurch das charakteristische Smaragdgrün entsteht.

Die B-Absorption der Dioptase ist nahezu unverändert. Wenn die Verunreinigung Eisen keine "hemmende" Wirkung auf die Smaragdkomponente hat, lässt die starke rote Fluoreszenz das charakteristische Smaragdgrün noch heller leuchten.
④ Cr3+ Der Farbmechanismus in Alexandrit:
Die Farbe von Alexandrit wird auch durch Cr3+ als Ersatz für Al3+ in verzerrter oktaedrischer Koordination. Aufgrund der chemischen Zusammensetzung von Alexandrit als BeAL2O4Die Art der chemischen Bindungen zwischen seinen Metall-Sauerstoff-Ionen liegt zwischen der von Rubin und Smaragd. Daher liegen auch seine Absorptionsbanden zwischen denen des Rubins und des Smaragds, wobei die Transmissionswahrscheinlichkeiten für blau-violettes und orange-gelbes Licht ungefähr gleich sind, so dass nicht festgestellt werden kann, ob rotes oder blau-grünes Licht dominiert (Abbildung 3-24).
Daher kann die Farbe des Alexandrits nur von der Energieverteilung und dem Farbspektrum des einfallenden Lichts abhängen. Daraus ergibt sich der "Farbwechseleffekt" des Alexandrits, d. h. er erscheint bei Tageslicht mit einem hohen Blauanteil grün und bei Glühlampenlicht mit einem hohen Rotanteil rot. Daher wird Alexandrit oft als "der Smaragd des Tages und der Rubin der Nacht" bezeichnet.
Der "Farbwechseleffekt" tritt bei vielen Arten von Edelsteinen auf, z. B. bei farbwechselndem Korund und farbwechselndem Granat. Derzeit wird künstlich hergestellter farbwechselnder Korund nach dem Prinzip des Farbwechsels unter Verwendung von V3+ als färbendes Ion für die Synthese.
3. Farben von Edelsteinmineralien
Die Farben, die von Übergangsmetallkomponenten erzeugt werden, lassen sich aus der chemischen Zusammensetzung von Edelsteinmineralien ableiten. Zum Beispiel enthält Türkis Cu2+ muss blau sein, während Cu+ ist farblos. In Tabelle 3-11 sind die Farben aufgelistet, die durch häufige Übergangsmetallkomponenten in natürlichen Edelsteinmineralien entstehen.
Tabelle 3-11 Farben, die durch Übergangsmetallkomponenten in natürlichen Edelsteinmineralien erzeugt werden
| Element | Farbe | Gewöhnliche Mineralien |
|---|---|---|
| Cerium (Ce) | Gelb | Parisit |
| Chrom (Cr) | Rot, Grün, Orange, usw. | Krokoisit, Roter Krokoisit, Uvarovit |
| Kobalt (Co) | Blau | Synthetischer Spinell |
| Kupfer (Cu) | Blau, Grün | Azurit, Chrysokoll, Türkis, Malachit, Dioptas |
| Eisen (Fe) | Rot, grün, gelb | Almandin, Olivin, Goethit |
| Mangan (Mn) | Rosa, orange | Rhodonit, Spessartin |
| Nickel (Ni) | Grün | Bunsenit, Chalcedon |
Die Farbe der meisten Edelsteine wird durch die in ihnen enthaltenen Übergangsmetallverunreinigungen verursacht. Rubine zum Beispiel erscheinen rot aufgrund von Spuren von Cr3+. Verschiedene Faktoren beeinflussen die Farbe, die durch Verunreinigungsionen im Edelstein verursacht wird. Daher können Verunreinigungen bei verschiedenen Edelsteinen unterschiedliche Farben hervorrufen. Zum Beispiel, Cr3+ erscheint rot in Rubinen und grün in Smaragden.
Dieselben Verunreinigungen sind nicht unbedingt für dieselbe Farbe eines Edelsteins verantwortlich. So wird beispielsweise die grüne Farbe der meisten Smaragde durch Cr verursacht, während die grüne Farbe einiger Smaragde teilweise oder vollständig durch Vanadium (V) verursacht wird.
Mit Hilfe der Kristallfeldtheorie lassen sich nicht nur die durch Übergangsmetallbestandteile oder Verunreinigungen erzeugten Edelsteinfarben erklären, sondern auch die durch Strukturdefekte (Farbzentren) erzeugten Farben; der spezifische Prozess der Farbentstehung kann in Kapitel 3.3 dieses Buches nachgelesen werden.
Auch bei der Erklärung der Farben von Edelsteinmineralien durch die Kristallfeldtheorie gibt es Unzulänglichkeiten, die sich vor allem in den folgenden Aspekten zeigen:
(1) Die Elektronen des Zentralions d sind nicht vollständig in ihren ursprünglichen Orbitalen lokalisiert. Sie können auch um die koordinierenden Atome herum auftreten, was auf eine kovalente Wechselwirkung zwischen dem Zentralatom und den Liganden hinweist.
(2) Sie berücksichtigt nur die elektrostatische ionische Wechselwirkung zwischen dem Zentralatom und den Liganden und lässt die kovalente Bindungswechselwirkung zwischen dem Zentralatom und den Liganden völlig außer Acht. In der physikalischen Forschung weichen die Ergebnisse quantitativer Berechnungen oft erheblich von den tatsächlichen Gegebenheiten ab.
(3) Die Gründe für die Farbe von Edelsteinmineralien können neben der Wechselwirkung zwischen dem Zentralion und den Liganden auch auf die kombinierte Wirkung von Strukturdefekten und dem Kristallfeld zurückzuführen sein.
Abschnitt II Molekülorbitaltheorie
Mulliken und Hund schlugen ursprünglich die Molekularorbitaltheorie (MO-Theorie) vor. Durch die kontinuierliche Erforschung durch viele Wissenschaftler hat sie sich zu einer ausgereiften Theorie entwickelt. Molekülorbitale (MOs) können durch lineare Kombinationen von Atomorbitalen erhalten werden, eine häufig verwendete Methode zur Konstruktion von Molekülorbitalen. Aus n Atomorbitalen lassen sich n Molekülorbitale gewinnen, und die Koeffizienten der Linearkombination können mit Hilfe der Variationsmethode oder anderer Methoden bestimmt werden. Molekülorbitale, die aus zwei Atomorbitalen gebildet werden und deren Energieniveaus niedriger sind als die der Atomorbitale, werden als bindende Orbitale bezeichnet; solche mit höheren Energieniveaus als die Atomorbitale werden als antibindende Orbitale bezeichnet; solche mit Energieniveaus nahe den Atomorbitalen sind im Allgemeinen nichtbindende Orbitale.
Die Molekülorbitaltheorie ist eine Theorie, die zur Erklärung von Themen wie Molekülbildung, -struktur und -eigenschaften verwendet wird. Sie kann auch einige der Ursachen für die Farben von Edelsteinen erklären, die auf der Grundlage der Kristallfeldtheorie und der Molekularorbitaltheorie für Übergangsmetalle entwickelt wurden. Molekulare Orbitale sind eine natürliche Erweiterung der atomaren Orbitale. In einem Molekül gehören die Elektronen nicht mehr zu einem bestimmten Atom, sondern bewegen sich über den gesamten Molekülbereich; daher wird die Bewegung der Elektronen in einem Molekül mit Hilfe von Molekülorbitalen beschrieben.
1. Grundlegende Konzepte der Molekülorbitaltheorie
Die Molekülorbitaltheorie besagt, dass die Elektronen, nachdem die Atome ein Molekül gebildet haben, nicht mehr zu den ursprünglichen Atomorbitalen gehören, wie es die Kristallfeldtheorie vorschlägt, sondern sich in bestimmten Molekülorbitalen bewegen. Molekulare Orbitale bilden ein Molekül genauso wie atomare Orbitale ein Atom bilden. Die Valenzelektronen werden nicht mehr als in einzelnen Atomen lokalisiert betrachtet, sondern bewegen sich im gesamten Molekül. Die Elektronenverteilung im Molekül kann nach den Grundsätzen der Elektronenverteilung in Atomen behandelt werden (Prinzip der minimalen Energie und Hundsche Regel).
Die lineare Kombination von Atomorbitalen in einem Molekül bildet Molekülorbitale. Die Anzahl der Molekülorbitale ist gleich der Anzahl der Atomorbitale vor der Kombination. Bei der Kombination von Atomorbitalen zu effektiven Molekülorbitalen müssen die folgenden drei Grundsätze beachtet werden:
(1) Prinzip der Symmetrieübereinstimmung: Nur Atomorbitale mit der gleichen Symmetrie können Molekülorbitale bilden.
(2) Prinzip der energetischen Annäherung: Nur Atomorbitale mit ähnlichen Energien können sich zu effektiven Molekülorbitalen verbinden.
(3) Prinzip der maximalen Überlappung: Bei Symmetrieanpassung nimmt die Energie der resultierenden Molekülorbitale um so mehr ab, je größer die Überlappung der Atomorbitale ist, und die resultierende chemische Bindung ist umso stabiler.
Das Molekülorbital ψ ist die Wellenfunktion eines einzelnen Elektrons. Es kann als Linearkombination von Atomorbitalen dargestellt werden, wobei jedes Orbital einer bestimmten Energie entspricht, die sich aus der Summe der kinetischen und potentiellen Energie des sich im molekularen elektrischen Feld bewegenden Elektrons ergibt. Zwei Atomorbitale, a und b, ergeben durch überlappende Linearkombinationen zwei Molekülorbitale ψI und ψII :
ψI=ψa + ψb (3-5)
ψII = ψa - ψb (3-6)
Wenn Molekülorbitale mit Elektronen zuerst gefüllt werden, werden die Bindungsorbitale ψI werden zuerst besetzt. Wenn Elektronen Molekülorbitale gleicher Energie besetzen, sollten sie nach der Hund'schen Regel möglichst auch unterschiedliche Molekülorbitale mit gleicher Spinrichtung besetzen.
Die Molekülorbitale ψI die durch Addition von zwei Atomorbitalfunktionen (Gleichung 3-5) erhalten werden, werden als bindende Molekülorbitale bezeichnet. Die Molekülorbitale ψII die durch Subtraktion zweier Atomorbitalfunktionen (Gleichung 3-6) erhalten werden, werden als antibindende Molekülorbitale bezeichnet. Die Energie von bindenden Molekülorbitalen ist niedriger als die von antibindenden Molekülorbitalen und niedriger als die Energie der beiden ursprünglichen Atomorbitalen. Wie beim Auffüllen von Atomorbitalen werden also auch beim Auffüllen von Molekülorbitalen die Elektronen zunächst in Bindungsorbitalen untergebracht, und ein Molekülorbital kann zwei Elektronen mit entgegengesetztem Spin aufnehmen. Wenn Elektronen Molekülorbitale mit gleicher Energie besetzen, sollten sie nach der Hund'schen Regel möglichst auch verschiedene Molekülorbitale mit gleicher Spinrichtung besetzen. Die Molekülorbitale, die von zwei s-Atomorbitalen gebildet werden, sind in Abbildung 3-25 dargestellt.

p-Orbitale und d-Orbitale können auch Molekülorbitale unterschiedlicher Energieniveaus bilden; so ist beispielsweise die Kombination von zweiatomigen Molekülorbitalen in O2 Molekülen ist relativ komplex.
In Experimenten wurden die magnetischen Eigenschaften dieser beiden Einzelelektronen gemessen, was die Molekülorbitaltheorie stark unterstützt. Im Gegensatz zu Molekülen, die aus denselben Atomen bestehen, haben Moleküle, die aus zwei oder mehr verschiedenen Atomen zusammengesetzt sind, komplexere Molekülorbitalenergieniveaus, aber das Prinzip ist dasselbe.
2. Färbungsmerkmale durch Ladungsübertragung
Diese Theorie der Molekülorbitale, bei der sich das gesamte Molekül die Elektronen teilt, wird auch als Übergang von Elektronen von einem Atomorbital in ein anderes betrachtet, der als Ladungstransfer bezeichnet wird. Der Ladungstransfer kann bei Metall-Metall- (M-M), Nicht-Metall-Nicht-Metall- (L-L) und Nicht-Metall-Metall- (L-M) Wechselwirkungen auftreten. Bei diesen beiden Bindungsarten L-L und M-L handelt es sich in erster Linie um kovalente Bindungen. O2 gehört zur L-L-Ladungsübertragung, die eine kovalente Bindung ist.
(1) Metall-Metall-Ladungsübertragung (M - M Ladungsübertragung)
Diese Art der Ladungsübertragung findet im Allgemeinen zwischen gewöhnlichen Übergangsmetallionen statt. Die meisten Färbungen von Farbedelsteinen werden durch Metall-Metall-Ladungstransfer verursacht. Der M-M-Ladungstransfer umfasst hauptsächlich die folgenden Arten: Fe2+ - Fe3+/Fe3+ - Fe2+; Ti3+ - Ti4+ / Ti4+- T3+ ;Fe2+ - T4+/Fe3+ - T3+Mn2+ - Mn4+/Mn3+ - Mn3+ . Der Ladungstransfer zwischen Metallen wird in zwei Arten unterteilt: Ladungstransfer zwischen homonuklearen Atomen und Ladungstransfer zwischen heteronuklearen Atomen.
① Ladungsübertragung zwischen isoelektronischen Atomen
Der Ladungstransfer zwischen isoelektronischen Atomen findet zwischen zwei Atomen desselben Übergangsmetallelements in unterschiedlichen Oxidationsstufen statt. Zum Beispiel, Fe2+ und Fe3+ unter verschiedenen Redoxbedingungen einen Ladungstransfer durchlaufen, Energie absorbieren und Farbe erzeugen. Die blau-violette Farbe von Iolith entsteht durch den Ladungstransfer von Eisenionen in verschiedenen Oxidationsstufen. Fe3+ und Fe2+ befinden sich in tetraedrischer bzw. oktaedrischer Position, wobei zwei Liganden durch Kanten verbunden sind. Wenn sichtbares Licht auf Iolith fällt, wird ein d-Elektron von Fe2+ absorbiert Licht einer bestimmten Energie und wandelt sich in Fe3+Er absorbiert gelbes Licht bei 588nm und erzeugt eine blau-violette Farbe. Aquamarin, grüner Turmalin und andere können ebenfalls eine Farbe aufweisen, die auf den Ladungstransfer zwischen Eisen-Ionen zurückzuführen ist.
② Ladungsübertragung zwischen Heteroatomen
Blaue Saphire sind ein typisches Beispiel für die Farbe, die durch Ladungsübertragung zwischen zwei Arten von Übergangsmetall-Ionen entsteht. Die Koordinationspolyeder der Übergangsmetallionen sind durch Kanten oder Flächen miteinander verbunden, was den Ladungstransfer zwischen den Metallen erleichtert.
Wenn zum Beispiel in Saphiren Eisen- und Titanionen in die verbundenen Oktaeder eindringen, liegen sowohl Fe als auch Ti in zwei Oxidationsstufen vor:
Fe2+ + Ti4+ geringe Energie (3-7)
Fe3+ + Ti3+ hohe Energie (3-8)
Der Übergang von Gleichung (3-7) zu Gleichung (3-8) erfordert die Absorption einer bestimmten Menge an Lichtenergie, was zu einer breiten Absorptionsbande führt, die von gelb bis rot reicht. Im Gegensatz dazu wird das meiste blaue Licht durch den Edelstein hindurchgelassen, was ihm ein blaues Aussehen verleiht.
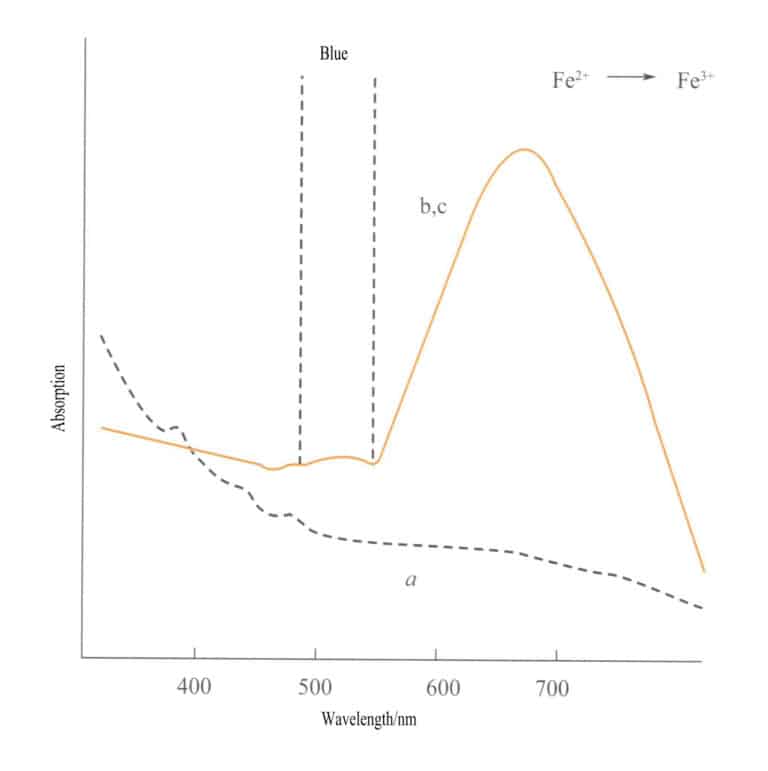
Der Ladungstransfer zwischen verschiedenen Valenzzuständen hat eine starke Richtungsabhängigkeit, und Edelsteine, deren Farbe auf diesen Mechanismus zurückzuführen ist, weisen häufig Pleochroismus auf. Zum Beispiel ist Aquamarin durch Fe2+→ Fe3+ Der Ladungstransfer zeigt die Farbe strikt in Richtung der optischen Achse. Abbildung 3-26 zeigt, dass Aquamarin in der b- und c-Ebene gelb erscheint. Gleichzeitig findet kein solcher Transfer entlang der a-Achse statt, was zu keiner Lichtabsorption und somit auch zu keiner Farbe entlang der a-Achse führt.
(2) Ladungsübertragung von Nicht-Metall auf Metall (L-M)
Diese Art des L-M-Ladungstransfers findet häufig zwischen Sauerstoff- und Metallionen statt, und einige sauerstoffhaltige Edelsteine sind durch einen Ladungstransfer von Nicht-Metall zu Metall gefärbt, wie z. B. O2–→ Fe3+, O2- →Cr6+, O2-→Mn6+, O →V5+.
Im Absorptionsspektrum einfacher Eisenoxide (Abbildung 3-27) erscheinen zwei schwache Absorptionsbanden im Infrarotbereich von Ilmenit, Hämatit und Lepidokrokit ( d - d elektronische Übergänge). Im kurzwelligen Bereich erscheint eine starke Absorptionsbande, die von O2-→Fe3+ Diese Absorptionsbande bestimmt die charakteristischen Farben dieser Verbindungen: rötlich-braun, braun und gelb-braun.
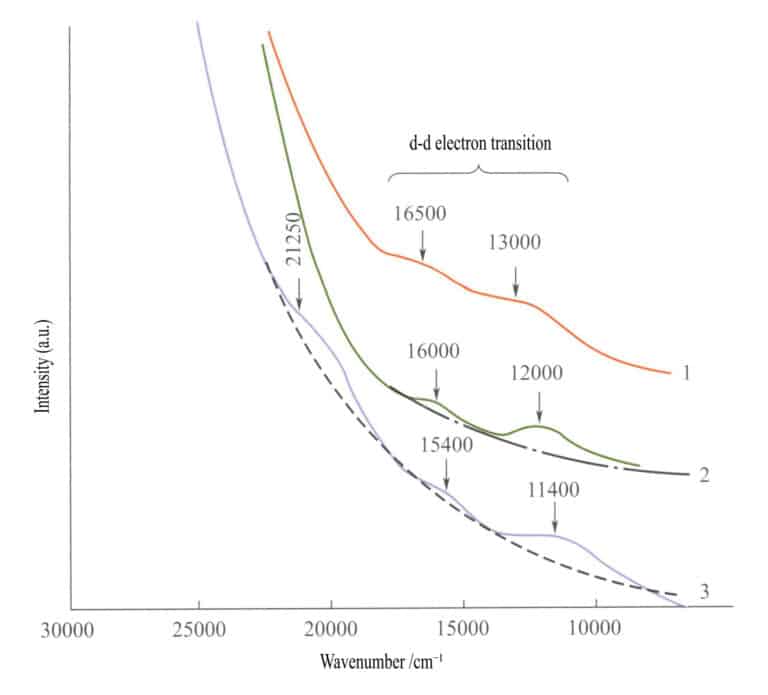
1 -Iilmenit; 2 - Hämatit; 3 - Lepidokrokit
Der gelbe Beryll erhält seine Farbe durch O2–→ Fe3+ Ladungsübertragung. In der Struktur des gelben Berylls ist O2–→ Fe3+ Die starke Absorption des Ladungstransfers kann sich vom ultravioletten Ende bis zum blauen Ende des sichtbaren Spektrums erstrecken, wobei Violett und Blau absorbiert werden, was zu einer gelben Farbe führt.
Saphir, der eine völlig andere Koordinationsumgebung als Beryll hat, kann ebenfalls die gleichen spektralen Absorptionsbanden wie Beryll erzeugen, was zu einer gelben Farbe führt, die ebenfalls eine Folge von O2–→ Fe3+ Ladungsübertragung.
Nach der Kristallfeldtheorie enthalten einige Edelsteinminerale keine ungepaarten Elektronen und können keine Farbe erzeugen. Zum Beispiel enthalten die elektronischen Schichten von Krokoit (PbCrO4), Pb2+, Cr6+und O2– voll sind. Dennoch, in der CrO42- Atomcluster sind "molekulare Orbitale", die den angeregten Zuständen bei O2-→Cr6+ übertragen, Absorptionsbanden bilden und orangefarben erscheinen.
L→M Der Ladungstransfer umfasst auch die Übertragung von Schwefel auf Metall, wie z. B. bei Pyrit; dieses durch den Transfer verursachte optische Phänomen ist leichter zu verstehen, wenn man die Bändertheorie verwendet.
(3) Ladungsübertragung von Nicht-Metall zu Nicht-Metall (L-L)
Die Molekülorbitaltheorie legt nahe, dass die tiefblaue Farbe von Lapislazuli auf die Anregungsenergieniveaus der S3- Atomgruppe.
In Graphit sind die Ringe aus sechs Kohlenstoffatomen in Schichten angeordnet. Entlang dieser Schicht können sich die Elektronen bis zu einem gewissen Grad frei bewegen, was zu einer starken Lichtabsorption, Anisotropie und Leitfähigkeit führt.
Einige organische Edelsteine, wie Bernstein und Perlen, haben Elektronen, die sich durch die Atomgruppen der organischen Pigmente in gemeinsamen Molekülorbitalen bewegen und anregen, was die Absorption von sichtbarem Licht und die Erzeugung von Farbe bewirkt. So zum Beispiel das "Honiggelb" des Bernsteins, die Farben der Koralle und einiger Muscheln und farbiger Perlen.
Die Farbmechanismen gängiger Edelsteine sind in Tabelle 3-12 dargestellt.
Tabelle 3-12 Klassifizierung der Farbmechanismen gängiger Edelsteine
| Metall-Metall-Ladungsübertragung | Fe2+ - Fe3+ /Fe3+ - Fe2+ Iolith (blau), Berthierit (blau), Magnetit (schwarz), usw. |
| Fe2+ -Ti4+/Fe3+ - Ti3+ : Kyanit (blau), Saphir (blau) | |
| Mn2+-Mn4+/Mn3+-Mn3+: Manganit (schwarz), Bixbyit (schwarz) | |
| Ladungsübertragung von Nicht-Metall zu Metall | O2- -Fe3+: Goldgelber Beryll, goldgelber Saphir, Ilmenit, Hämatit, Lepidokrokit, usw. |
| O2- - Cr6+: Krokoit (orange) | |
| O2- -V5+:Vanadinit (orange) | |
| Schwefel zu Metall: Pyrit, Markasit, usw. (siehe Halbleiter mit Lücke) | |
| Nicht-Metall - Nicht-Metall-Ladungsübertragung | S3-: Lapislazuli (blau) |
| Π elektronisch: Graphit (schwarz) | |
| Die Farben einiger organischer Edelsteine wie Bernstein und Koralle. |
Copywrite @ Sobling.Jewelry - Hersteller von kundenspezifischem Schmuck, OEM- und ODM-Schmuckfabrik
Abschnitt III Energiebandtheorie
Die Energiebandtheorie ist ein quantenmechanisches Modell zur Untersuchung von Edelsteinmaterialien, das eine Erweiterung und Ergänzung der Molekularorbitaltheorie darstellt. Die Untersuchung der Energiebandtheorie kann den Farbmechanismus einiger natürlich gefärbter Edelsteine besser erklären.
1. Grundlegende Konzepte der Energiebandtheorie
Die Energiebandtheorie ist eine Näherungstheorie, die zur Untersuchung der Gesetze der Elektronenbewegung in Festkörpern verwendet wird. Festkörper bestehen aus Atomen, zu denen Atomkerne und die äußersten Elektronen gehören, die sich alle in ständiger Bewegung befinden. Die Bandentheorie besagt, dass die Elektronen in Festkörpern nicht an ein bestimmtes Atom gebunden sind, sondern vom gesamten Kristall geteilt werden und sich innerhalb des periodischen Potenzialfelds des dreidimensionalen Raums des Kristalls bewegen. Der Bereich der Elektronenbewegung liegt innerhalb des periodischen Potenzialfelds des Gitters, so dass die räumliche Verteilung der Elektronenbahnen diejenige von Molekülen übersteigt und ein Maximum erreicht. Die Energieniveaus der einzelnen Elektronen sind zu Energiebändern verbreitert.
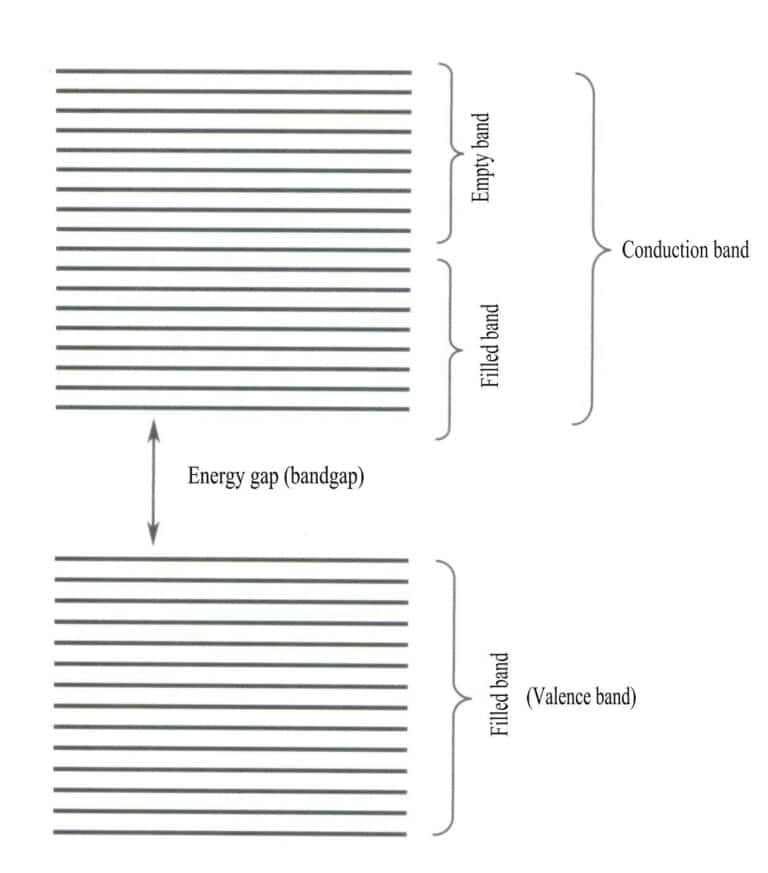
Die Bandtheorie befasst sich hauptsächlich mit Elektronenübergängen zwischen nichtlokalen Zuständen, bei denen alle Valenzelektronen dem gesamten Festkörpergitter angehören sollten. Nach der Bandentheorie können feste Materialien in verschiedene Energiebänder unterteilt werden, je nachdem, ob die Atomorbitale gefüllt sind oder nicht: Ein gefülltes Band wird durch die Energieniveaus von Atomorbitalen gebildet, die vollständig von Elektronen besetzt sind, was ein Niedrigenergieband darstellt; ein leeres Band wird durch Energieniveaus gebildet, die nicht vollständig von Elektronen besetzt sind, was ein Hochenergieband darstellt. Der Energieunterschied zwischen diesen beiden Arten von Bändern wird als "Bandlücke" bezeichnet (Abbildung 3-28).
Wenn alle Energiebänder eines Materials gefüllt sind, ist es ein Nichtleiter; wenn es teilweise mit Elektronen gefüllt ist, ist es ein Leiter. Gitterdefekte führen zusätzliche Energieniveaus in den Kristall ein und ermöglichen den Eintritt von Elektronen in diese Energieniveaus, was zu bedingter Leitfähigkeit führt.
2. Merkmale von Bandlückenübergängen
Einige Edelsteinminerale enthalten Elemente der Gruppe IV A des Periodensystems, wie Diamant und Moissanit, die hauptsächlich kovalent gebunden sind. Es gibt auch andere Mineralien wie Cadmiumsulfid (CdS), deren Farben sich durch die Bandentheorie erklären lassen.
Elektronen absorbieren Lichtenergie und bewegen sich zwischen den Valenz- und Leitungsbändern, wobei sie "interne Bandübergänge" bilden. Die Wahrscheinlichkeit von Übergängen steht in engem Zusammenhang mit dem Energieunterschied zwischen Valenz- und Leitungsband, der so genannten Bandlückenenergie (Eg) (Abbildung 3-29).

Abbildung 3-29 (a) ist ein typisches Halbleiter-Banddiagramm. Basierend auf der Größe der Bandlückenenergie des Kristalls kann dieser in drei Typen unterteilt werden: breite Bandlücke, schmale Bandlücke und mittlere Bandlücke. Eine breite Bandlücke hat eine Bandlückenenergie, die größer ist als die Energie des sichtbaren Lichts; wenn die Bandlückenenergie die Energie des sichtbaren Lichts übersteigt, wird das sichtbare Licht nicht absorbiert und geht vollständig hindurch, wodurch das Mineral farblos wird. Zum Beispiel ist die Bandlückenenergie von Diamant Eg beträgt etwa 5,5 eV und ist damit farblos.
Die Energie der Bandlücke von Materialien mit geringer Bandlücke ist geringer als die des sichtbaren Lichts, so dass das gesamte sichtbare Licht absorbiert wird, was zu dunklen grau-grünen oder schwarzen Farben führt. Die Bandlückenenergie von Bleiglanz beträgt beispielsweise Eg von weniger als 0,4 eV, der bleigrau zu sein scheint. Wenn dieser "Halbleiter mit enger Bandlücke" eine geeignete geometrische Form hat, weist er gleichrichtende und verstärkende Eigenschaften auf.
Die Energie von Materialien mit mittlerer Bandlücke liegt genau im Bereich des sichtbaren Lichts, und Edelsteinminerale weisen verschiedene Farben auf. Ihre Farbreihenfolge ist in Abbildung 3-29 (c) dargestellt und reicht von rot-gelb über grün-blau bis violett. Zum Beispiel liegt die Energie der Bandlücke (Eg) von Cadmiumsulfid (CdS) beträgt etwa 2,5 eV, das blaues und violettes Licht absorbiert und gelb erscheint. Die Bandlückenenergie von Zinnober liegt bei etwa 2 eV und lässt nur rotes Licht durch, so dass es rot erscheint. Die Bandlückenenergie von Orpiment liegt bei etwa 2,5 eV und erscheint gelb.
Eine weitere Kategorie natürlicher Edelsteinmineralien, die sich mit der Bandentheorie erklären lässt, ist die Farbe von Materialien mit großer Bandlücke und Verunreinigungen. Bei einem Diamanten mit Verunreinigungen beispielsweise beträgt die Bandlückenenergie des Diamanten Eg etwa 5,5 eV, und sichtbares Licht wird beim Durchgang durch den Diamanten nicht absorbiert; reiner Diamant ist farblos, aber die Situation ändert sich, wenn er Verunreinigungen enthält.
(1) Der Farbmechanismus von gelben Diamanten
Stickstoffatome ersetzen die Positionen der Kohlenstoffatome. Da Stickstoffatome ein Elektron mehr haben als Kohlenstoffatome, bildet dieses zusätzliche Elektron ein Verunreinigungsenergieniveau in der Bandlücke, das so genannte Donator-Energieniveau, wobei die Stickstoffatome als "Donatoren" fungieren.
Das Vorhandensein dieses Verunreinigungsniveaus reduziert die Energie der Bandlücke auf 4eV[ [Abbildung 3-30 (a)]. Sie kann sogar noch niedriger sein, so dass er ultraviolettes Licht und ein wenig violettes Licht von 3eV absorbiert, was den Diamanten gelb erscheinen lässt.
Dieser Effekt ist stark; ein Stickstoffatom auf hunderttausend Kohlenstoffatome kann den Diamanten tiefgelb machen. Die Verringerung der Bandlücke reicht jedoch noch nicht aus, um den Diamanten bei Raumtemperatur leitfähig zu machen.
(2) Mechanismus der Farbe in blauen Diamanten
Da Bor ein Elektron weniger hat als Kohlenstoff, bildet es ein "Akzeptorniveau" in der Bandlücke von Diamant. Es hat keine zusätzlichen Elektronen, kann aber Elektronen aus dem Valenzband eines Diamanten aufnehmen, wodurch Löcher im Valenzband entstehen [Abbildung 3-30 (b)] und ein Verunreinigungs-Energieband etwa 0,4 eV oberhalb des Valenzbandes gebildet wird, das als Akzeptorniveau bekannt ist.

Das Akzeptorenergieniveau ist nicht einfach; es ist eine komplexe Struktur von Verunreinigungsenergiebändern, die Blau erzeugen können. Das Akzeptor-Energieniveau erzeugt "Löcher" im Valenzband, wodurch dieser "löchrige" blaue Diamant vom Typ II b Elektrizität leiten kann.
Ein Boratom auf eine Million Kohlenstoffatome kann blau sein. Aufgrund des höheren Aluminiumgehalts in diesem blauen Diamanten und der Tatsache, dass Aluminium ein Elektron weniger in der Außenschicht hat als Kohlenstoff, wurde früher angenommen, dass Aluminium die Rolle des Akzeptors spielt. Aktuelle Experimente haben jedoch bewiesen, dass es Bor und nicht Aluminium ist.
Leitfähige blaue Diamanten vom Typ II b sind von Natur aus blau, und ihre Leitfähigkeit ist einer der Unterschiede zu bestrahlten blauen Diamanten (Farbzentren). Diese Eigenschaft wird häufig zur Unterscheidung zwischen den beiden Diamanttypen verwendet. Gelbe Stickstoffdonor-Diamanten leiten jedoch keinen Strom, so dass diese Methode nicht zur Unterscheidung von bestrahlten gelben Diamanten verwendet werden kann.
3. Durch Bandübergänge gefärbte Edelsteinminerale
Die Energiebandtheorie kann einen Teil der Farbbildung von natürlichen Edelsteinen erklären. Da die Energie der Bandlücke eine inhärente Eigenschaft des Kristalls ist und sich durch äußere Bedingungen nicht verändert, ist die Farbe von Edelsteinen sehr stabil. Die Leitfähigkeit des Kristalls kann anhand der Tatsache bestimmt werden, ob die Energiebänder im Kristall mit Elektronen gefüllt sind. In Tabelle 3-13 sind die Arten von Edelsteinfarben, die sich durch die Bandentheorie erklären lassen, und ihre Leitfähigkeitseigenschaften aufgeführt.
Tabelle 3-13 Arten von Edelsteinfarben, die durch die Bandentheorie erklärt werden, und ihre Leitfähigkeit
| Leitern (Metallfarben und Metallglanz) | Element | Kupfer, Gold, Eisen, Silber, Quecksilber, usw. |
| Legierung | Amalgam, Meteoriten-Nickel-Eisen | |
| Halbleiter | Schmalbandlücke | Undurchsichtiges Grau bis Schwarz: Altait, Bleiglanz |
| Undurchsichtige Metallfarbe: Kobalt, Markasit, Pyrit, Smaltit | ||
| Mäßige Bandlücke | Rot: Zinnober, Proustit, Pyrargyrit | |
| Orange: Realgar | ||
| Gelb: Kadmiumsulfid, Realgar, Schwefel | ||
| Breite Bandlücke | Farblos: Diamant, Sphalerit | |
| Verunreinigungen enthaltende Halbleiter mit breiter Bandlücke | Donor-Verunreinigung: Stickstoffdotierter Diamant (gelb) | |
| Verunreinigungen im Wirt: Borhaltiger Diamant (blau) |
Die Farbe von Edelsteinen, die durch Bandübergänge verursacht wird, hängt mit der Struktur und der Art der Bindung zum Zeitpunkt der Entstehung des Edelsteins zusammen. Sie hat wenig Bezug zu späteren Verunreinigungen und Kristalldefekten. Die Größe der Bandlückenenergie von Edelsteinen ist fest. Sie ändert sich nicht mit den Eigenschaften des Edelsteinmaterials, so dass herkömmliche Optimierungsmethoden die Farbe von Edelsteinen im Allgemeinen nicht verbessern können.
Abschnitt IV Physikalisch-optische Effekte
Die meisten natürlichen Edelsteine können Licht selektiv absorbieren, und verschiedene Edelsteine absorbieren sichtbares Licht in unterschiedlichen Wellenlängen, was zu unterschiedlichen Farben führt. Neben der selektiven Lichtabsorption kann die innere Struktur von Edelsteinkristallen auch physikalische optische Effekte verursachen, die zu unterschiedlichen Farben bei Edelsteinen führen.
1. Edelsteinmineralien im Zusammenhang mit physikalisch-optischen Effekten
Die durch physikalisch-optische Effekte erzeugten Farben entstehen durch Dispersion, Interferenz, Beugung und andere Ursachen des Lichts, die durch die Kristallstruktur oder -zusammensetzung und Einschlüsse verursacht werden. Dies ist lediglich ein optischer Effekt, der durch die physikalische optische Theorie erklärt werden kann. Verschiedene Edelsteine können bei gleichen optischen Effekten unterschiedliche Farben erzeugen. Neben den üblichen Spurenelementen, die Farben verursachen, hängen die Gründe für Farben, die durch physikalische optische Effekte entstehen, hauptsächlich mit der inneren Struktur und den physikalischen Eigenschaften der Edelsteine zusammen. Die Arten von Edelsteinmineralen, die aufgrund physikalisch-optischer Effekte Farben hervorrufen, sind in Tabelle 3-14 aufgeführt.
Tabelle 3-14 Arten von Edelsteinmineralien, die durch physikalische optische Effekte verursacht werden
| Funktion | Optische Eigenschaften und Farbe | Edelstein-Mineralien |
|---|---|---|
| Streuung Streuung | Schimmernde | "Feuer" in Dispersionsedelsteinen wie Diamanten, Zirkon, Rutil und Strontiumtitanat |
| Blau | Mondstein, blauer Quarz, Opal | |
| Lila | Fluorit (Streuung von Mikrokristallen aus Calcium) | |
| Rot | Rubinglas, Streuung von Mikrokristallen aus Kupfer oder Gold | |
| Weiß | Milchquarz | |
| Katzenaugen-Effekt | Katzenaugen-Aquamarin, Katzenaugen-Pyroxen, usw. | |
| Sternenlicht-Effekt | Verschiedene Sterneffekte von Korund und Granat | |
| Lüster | Lüster von Perlen, Apophyllit usw. | |
| Funkeln | Glitzern von Aventurin, Obsidian, etc. | |
| Interferenzbeugung | Die reinen Spektralfarben der Dünnschicht | Der Regenbogen des Chalkopyrits, der verfärbte Film in einer Irisquarzspalte |
| Störeffekte | Farbveränderung von Opal, die Wirkung von Labradorit | |
| Eingliederung | Blau | Dumortierit in Quarz |
| Grün | Grüner Chalzedon und Nickeladern in grünem Chalzedon, Fuchsit in Sternquarz | |
| Orange | Hydratisiertes Eisenoxid in Feueropal und fleischfarbenem Chalzedon | |
| Rot | Hämatitflocken in Orthoklas |
2. Interferenz- und Beugungseffekte
(1) Störeffekte
Interferenzerscheinungen treten auf, wenn sich zwei Lichtstrahlen auf demselben optischen Weg oder in parallelen Richtungen ausbreiten. Ein häufiges Interferenzphänomen bei Edelsteinen ist das Schillern. Bei irisierendem Quarz zum Beispiel hängen die Interferenzfarben von der Dicke der Schicht, dem Brechungsindex der Schicht und der Art des einfallenden Lichts ab.
Die Interferenzfarben von Perlen entstehen durch die konzentrische, abwechselnde Überlagerung von zwei Substanzen mit unterschiedlichem Brechungsindex (Aragonit und Nacrum), wobei das einfallende Licht von den Oberflächen zwischen den abwechselnden Schichten reflektiert wird und das reflektierte Licht mit dem einfallenden Licht interferiert, wodurch wunderschöne Interferenzfarben entstehen.
(2) Beugungseffekte
Unter Beugung versteht man das physikalische Phänomen, dass Lichtwellen von ihrer ursprünglichen geradlinigen Ausbreitung abweichen, wenn sie auf Hindernisse treffen. In der Physik werden Lichtwellen unterschiedlich stark gebeugt und gestreut, wenn sie durch Hindernisse wie Schlitze, kleine Löcher oder Scheiben laufen. Befindet sich ein Hindernis zwischen der Lichtquelle und dem Beobachtungsschirm, erscheinen auf dem Beobachtungsschirm helle und dunkle Bereiche, die nicht scharf voneinander abgegrenzt sind und ein komplexes Muster aus Hell und Dunkel bilden. Dieses Phänomen wird als Beugung bezeichnet. Solche Phänomene können immer dann auftreten, wenn Lichtwellen auf ihrem Ausbreitungsweg auf Hindernisse treffen. Der wichtigste Faktor bei der Erzeugung von Beugung ist das Vorhandensein von periodisch angeordneten Beugungsgittern in Edelsteinmineralien.
① Opal Farbwechsel
Im Opal haben die wasserhaltigen Siliziumdioxidkugeln gleiche Durchmesser und sind in einer regelmäßigen, abwechselnden Schichtstruktur angeordnet, die periodisch angeordnete Beugungsgitter bildet. Wenn Licht in den Opal eintritt, kommt es zu einer Beugung, die die Farbe verändert (Abbildungen 3-31 und 3-32). Die Art der Farben und der Grad der Farbveränderung hängen hauptsächlich von den Abständen zwischen den Ebenen der gestapelten Quarzkugeln ab.
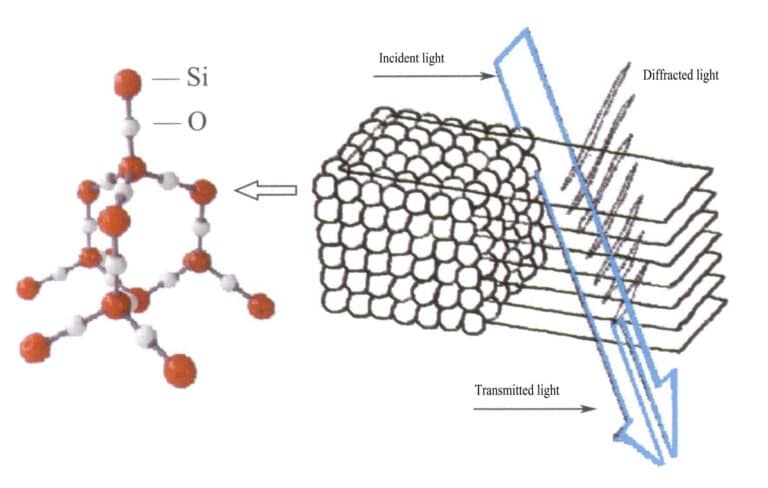

Zum Beispiel Opal mit einer flächenzentrierten kubischen Plattenstruktur und einem Gitterabstand von 3×10-10m zeigt Farben von grün bis rot; diese Art von Opal mit einem Gitterabstand von 2,5×10-10m zeigt Farben von blau bis gelb.
② Labradorit-Effekt
Labradorit weist auch ähnliche Effekte wie Opal auf (Abbildung 3-33). Labradorit ist auch als Spektrolith bekannt, da er im farbigen Licht der Sonne aufblitzen kann. Verschiedene Arten von Labradorit aus Finnland können eine Reihe von Spektralfarben aufweisen, ein Phänomen, das als "Labradorit-Effekt" bekannt ist. Der Farbwechseleffekt bei Labradorit ist auf kleine Zwischenschichtschmelzen von Plagioklas mit unterschiedlicher Zusammensetzung zurückzuführen. Die geringfügigen Unterschiede im Brechungsindex zwischen den verschiedenen Feldspäten führen zu Interferenz und Beugung des Lichts, was zu Lumineszenz und Farbwechsel führt. Die durch diese Struktur erzeugten Farben hängen von der relativen Dicke der Schichten und ihren Brechungsindizes ab. Gelegentlich weist auch Andradit aus Mexiko Beugungserscheinungen auf.

3. Streuung und Einschlüsse
(1) Streuung
Streuung tritt im Allgemeinen auf, wenn die innere Struktur von Edelsteinmaterialien unregelmäßig ist oder wenn die Größe der Bestandteile die Grenzen der Beugungsbedingungen überschreitet. Die durch Streuung erzeugten Farbeffekte hängen mit der Partikelgröße und -form des Edelsteinmaterials zusammen. Wenn einfallendes Licht mit unregelmäßig angeordneten Teilchen, die kleiner als die Wellenlänge des sichtbaren Lichts sind, in Wechselwirkung tritt, sind die übertragenen hochenergetischen Lichtwellen stärker als die niederenergetischen Lichtwellen, so dass in den meisten Fällen nur Violett und Blau zu sehen sind. Zum Beispiel ist das SiO2 Die kleinen Kugeln im Opal haben einen Durchmesser, der kleiner ist als die Wellenlänge des sichtbaren Lichts, und wenn die Größe der streuenden Teilchen in der Nähe der Wellenlänge des sichtbaren Lichts liegt, können auch streuende Farben auftreten.
Violetter Fluorit beispielsweise entsteht durch radioaktive Bestrahlung, bei der Fluoratome freigesetzt werden, wodurch Kalziumatome, die sich mit Fluoratomen verbinden, zu hexagonalen Plättchen kondensieren, deren Größe mit der Wellenlänge des sichtbaren Lichts vergleichbar ist. Die Wechselwirkung zwischen den Kalziumplättchen und den Lichtwellen führt zur Streuung. Es absorbiert einige Lichtwellen, wodurch ein starker Absorptionspeak im grün-roten Lichtbereich entsteht, der violettes Licht durchlässt und die violette Farbe erzeugt.
Da Partikel der gleichen Größe von Metallelementen ähnliche Farbeffekte erzeugen können und verschiedene Metallpartikel unterschiedliche Farben hervorbringen können, werden einige Edelsteinimitate unter Ausnutzung dieser Eigenschaft hergestellt.
Rubinglas" wird beispielsweise durch die Zugabe von Kupfer- oder Goldpartikeln zu Glas hergestellt, wodurch eine rote Farbe ähnlich der von Rubinen entsteht. Wenn das Edelsteinmaterial Einschlüsse, Mikrorisse oder Blasen enthält, die größer sind als die Wellenlänge des sichtbaren Lichts, interagieren die Lichtwellen mit diesen Streuteilchen, wodurch sich die gestreuten Lichtwellen rekombinieren und ein durchscheinendes, milchiges Licht erzeugen. Zum Beispiel bestimmte Mondstein-Imitationen.
Der Mondlichteffekt des Mondsteins entsteht ebenfalls durch die Streuung des Lichts (Abbildung 3-34). Mondstein ist ein alkalischer Feldspat, ein Verbundwerkstoff, der aus abwechselnden parallelen Schichten aus kaliumreichem und natriumreichem Feldspat besteht. Die Dicke der Zwischenschichten liegt in der Regel zwischen 50 und 1000 nm, wobei auch dünnere Schichten eine Streuung bewirken können. Die gleiche streuende Farbe kann auch bei Plagioklas auftreten, was als "Labradorit-Effekt" bekannt ist.
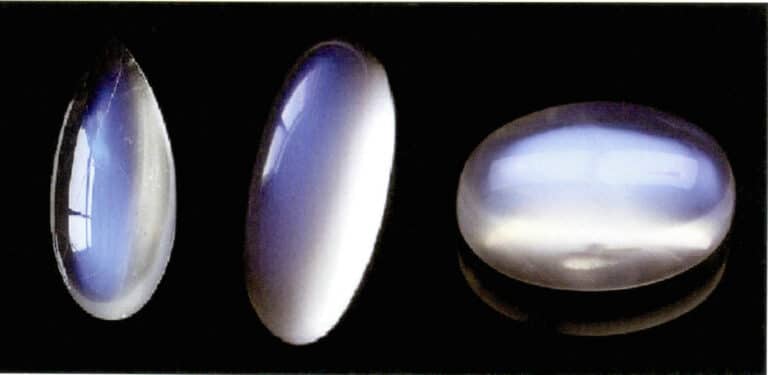
Eine speziell ausgerichtete Anordnung von Streupartikeln kann charakteristische optische Effekte erzeugen. Wenn die Streuteilchen beispielsweise in paralleler faseriger Form vorliegen, erzeugen sie einen Katzenaugen- oder Sterneffekt, wie z. B. Sternsaphire und Quarzkatzenaugen. Wenn die streuenden Teilchen groß genug sind, um mit bloßem Auge unterschieden werden zu können, können sie einen "Goldsteineffekt" erzeugen, wie z. B. Sonnenstein (Abbildung 3-35) und Goldsteinglas.

(2) Einschlüsse
Die durch Einschlüsse hervorgerufenen farblichen und optischen Phänomene sind eine besondere Art der Streuung. Einschlüsse mit Farbe, die in nahezu farblose Hauptkristalle eingebettet sind, zeigen die Farbe der Einschlüsse, wie z. B. nickelhaltiger gebänderter Chalcedon und wasserhaltiges Eisen(II)-oxid (FeO - H2O) fleischfarbener Chalcedon; die Farbe von Orthoklas aus Madagaskar und einigen Cordieriten entsteht durch etwas größere, aber immer noch mikroskopisch kleine Einschlüsse von Hämatit, die Rottöne erzeugen; submikroskopische Einschlüsse von Eisenhydroxid färben oft Feueropal.
Diamanten weisen aufgrund zahlreicher Einschlüsse oft unterschiedliche Farben auf. Die durch Einschlüsse gefärbten Diamanten können schwarz, orange-rot und braun-rot sein. Wenn ein Diamant zahllose dunkle, undurchsichtige Mineraleinschlüsse enthält, erscheint er schwarz; wenn er mit starkem Durchlicht untersucht wird, sind viele dunkle Einschlüsse zu sehen, und der Diamant erscheint dunkelgrau; eine andere Art sind sekundäre Einschlüsse, die in den Rissen des Diamanten auftreten. Wenn sich die Risse entwickeln und mit diesen farbigen Einschlüssen gefüllt sind, erscheint der Diamant braunrot oder orangerot, was auch als "oxidierter" Diamant bezeichnet wird.
4. Streuung
Das Phänomen der Zerlegung von weißem Licht in verschiedene Spektralfarben durch ein Objekt wird als Dispersion bezeichnet. Die Dispersion von Edelsteinen bezieht sich auf die Eigenschaft des Lichts, sich in verschiedene Wellenlängen von Spektralfarben aufzuteilen, wenn es die schrägen Ebenen von transparenten Edelsteinen durchläuft. Aufgrund der unterschiedlichen Wellenlängen des monochromatischen Lichts, aus dem weißes Licht besteht, das sich mit unterschiedlichen Geschwindigkeiten und Brechungsindizes in verschiedenen Materialien ausbreitet, kann weißes Licht unter bestimmten Bedingungen in verschiedene Spektralfarben zerlegt werden. Die Größe des Dispersionswertes eines Edelsteins wird durch seine physikalischen Eigenschaften bestimmt; jeder Edelstein hat seinen eigenen Dispersionswert, der sich nicht mit den Eigenschaften des Edelsteins ändert. Der einzigartige Charme von Diamanten ist eng mit ihrem hohen Dispersionswert (0,044) verbunden.
Die meisten Diamantsimulanzien haben einen höheren Dispersionswert, wie z. B. Zirkon mit einem Dispersionswert von 0,039 und synthetischer Moissanit mit einem Dispersionswert von 0,104. Der Vergleich der Dispersionswerte von Diamanten und ihren gängigen Edelsteinsimulanzien ist in Tabelle 3-15 dargestellt.
Tabelle 3-15 Vergleich der Dispersionswerte von Diamanten und ihren gemeinsamen Simulanz-Edelsteinen
| Edelstein Name | Dispersionswert |
|---|---|
| Diamant | 0.044 |
| Zirkon | 0.039 |
| Korund | 0.018 |
| Spinell | 0.020 |
| Topas | 0.014 |
| Beryl | 0.014 |
| Kristall | 0.014 |
| Synthetisches Rutil | 0.280 |
| Synthetisches Strontiumtitanat | 0.190 |
| Synthetischer Moissanit | 0.104 |
Die Dispersion wird gemeinhin als das "Feuer" von Edelsteinen bezeichnet. Diamanten zum Beispiel haben einen hohen Dispersionswert, und ihr Feuer ist sehr ausgeprägt, was den ohnehin schon königlichen Status von Diamanten noch verstärkt und ihren einzigartigen Charme unterstreicht.
Es gibt viele Arten von Farben, die durch physikalische optische Effekte hervorgerufen werden und die sich alle durch die physikalische optische Theorie erklären lassen. Abgesehen von der Dispersion, die eine inhärente Eigenschaft des Edelsteins selbst ist, werden andere Phänomene durch strukturelle Veränderungen nach der Entstehung des Edelsteins und die Unterschiede bei mechanischen Einschlüssen verursacht. Das Verständnis der verschiedenen Ursachen der Edelsteinfarben bietet eine theoretische Grundlage für die Optimierung der Behandlung von natürlichen und synthetischen Edelsteinen.