O singură dată pentru a afla totul despre cristalografia pietrelor prețioase
Un ghid cuprinzător despre formele, tipurile, clasificările și diferențele cristalografice
Pământul este compus din nenumărate molecule și atomi. Cercetările științifice moderne au descoperit că materialele solide din natură sunt alcătuite din diferite elemente chimice. Rezultatele analizelor cu raze X arată că atomii din elementele anumitor materiale solide sunt aranjați ordonat și regulat între ei. Aceste materiale sunt clasificate ca fiind cristaline sau denumite cristale, iar rețeaua lor atomică ordonată se numește structură cristalină (figura 2-1-1).
Majoritatea materialelor prețioase care cresc în natură și în laborator sunt cristaline. Acest capitol va discuta conceptul de cristale, clasificarea lor și relația dintre cristale și terminologia de bază în gemologie.

Tabla de conținut
Secțiunea Ⅰ Conceptul și descrierea cristalelor
Când vorbim de pietre prețioase, ne gândim adesea la caracteristicile lor strălucitoare și translucide (figura 2-1-2). Din perspectiva geologilor și gemologilor, cele mai iubite pietre prețioase aparțin unei forme geometrice de solid - cristalele. Esența frumuseții cristalelor este, de fapt, frumusețea geometriei.

1. Conceptul de cristale
Cristalele sunt cele mai ușor de asociat și cele mai des întâlnite în natură. Cristalele se găsesc pe toate cele șapte continente ale Pământului și, atunci când se găsesc în natură, ele iau adesea forma unor poliedre geometrice (figura 2-1-3). Ele sunt denumite în mod obișnuit cristale. Ulterior, acest termen a fost extins pentru a se referi la substanțele solide naturale cu forme geometrice poliedrice, cum ar fi cristalele de diamant și acvamarin (figura 2-1-4). Cristalele pot descrie, de asemenea, materiale solide cu suprafețe neregulate, inegale, uzate, sparte sau prelucrate artificial, dar cu un aranjament atomic care urmează încă un model regulat. Cristalografiștii consideră că toate cristalele posedă șase caracteristici de bază: autolimitare, uniformitate, anizotropie, simetrie, stabilitate și punct de topire fix.
① Auto-limitarea se referă la proprietatea elementelor chimice de a forma spontan forme geometrice poliedrice. Această proprietate poate explica de ce elemente diferite au forme geometrice cristaline diferite.
② Uniformitatea se referă la proprietatea conform căreia proprietățile fizice și chimice ale tuturor părților cristalului sunt aceleași. Această proprietate ne poate ajuta să distingem și să identificăm diferite cristale minerale.
③ Anizotropia se referă la proprietatea în care dispunerea elementelor variază în direcții diferite, ceea ce duce la ușoare diferențe în proprietățile fizice în funcție de direcție. Această proprietate poate explica de ce diamantele cu cea mai mare duritate pot fi tăiate și lustruite.
④ Simetria se referă la proprietatea prin care părțile sau proprietățile identice dintr-un cristal se repetă într-un model regulat. Această proprietate este extrem de importantă și specială pentru cristale și va fi detaliată în a doua secțiune a acestui capitol.
⑤ Stabilitatea se referă la stabilitatea unui cristal care rezultă din energia sa internă minimă. Dacă energia internă a unui cristal este ridicată și neuniformă, acesta este predispus să se fisureze singur. Această proprietate poate explica de ce cristalele de rubin sintetizate prin tehnica flamefusion par întotdeauna a fi mai degrabă pe jumătate decât complete.
⑥ Punctul de topire fix se referă la proprietatea unui cristal de a avea un punct de topire fix.

Figura 2-1-3 Granat (partea stângă este cristalul, partea dreaptă este granatul lustruit)

Figura 2-1-4 Cristal de acvamarin
2. Forma ideală a cristalelor
Cristalele discutate în cristalografie sunt în principal monocristale ideale. Un monocristal ideal este definit ca unul a cărui structură internă respectă cu strictețe regulile rețelelor spațiale și a cărui formă este o formă geometrică combinată regulată. Formele monocristalelor ideale sunt împărțite în două tipuri: forme simple și forme combinate.
(1) Formular simplu
O formă simplă se referă la o combinație a unui grup de fețe cristaline conectate prin elemente de simetrie, care poate fi înțeleasă ca un corp geometric compus din fețe cristaline de aceeași formă și dimensiune într-o stare ideală (figura 2-1-5). Există 47 de tipuri de forme simple în cristale.
Punctele cheie pentru identificarea formelor simple sunt: toate fețele cristaline din cristal au aceeași formă și dimensiune, iar fețele cristaline pot fi orientate diferit.
(2) Combinați Forma
Agregarea formelor simple se numește formă combinată, compusă din două sau mai multe forme simple diferite. Nu toate formele simple pot fi combinate liber în forme combinate; numai formele simple cu același grup de puncte pot fi agregate (figurile 2-1-6-218).
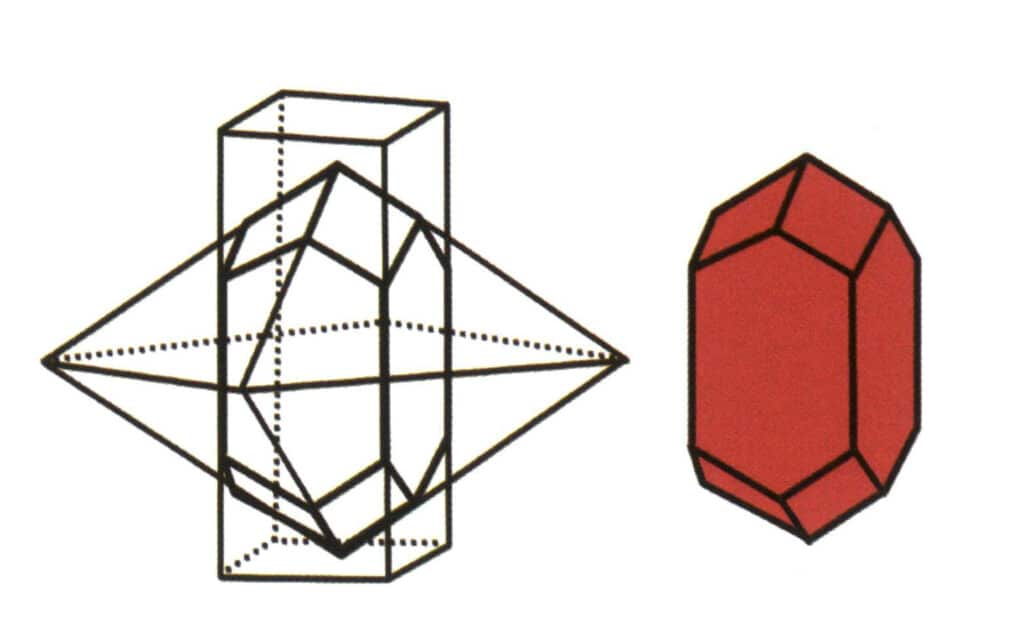
Figura 2-1-6 Combinație de prisme tetragonale și dipiramidale tetragonale
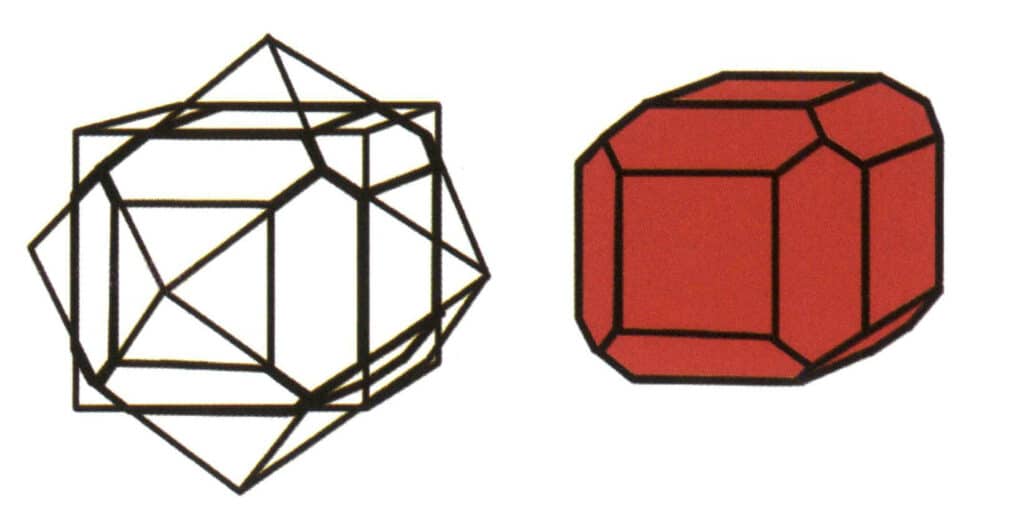
Figura 2-1-7 Combinație de cuburi și dodecaedre rombice
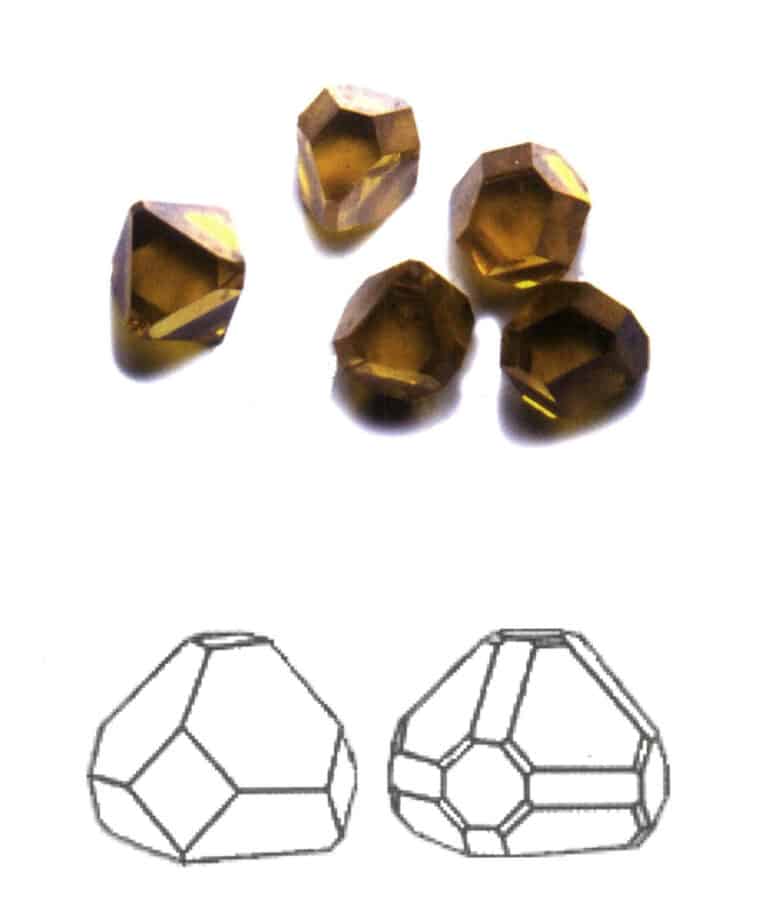
Punctul cheie al identificării formei combinate este prezența a două sau mai multe fețe cristaline de formă diferită în cristal.
Atunci când se găsesc cristale unice în natură, acestea prezintă întotdeauna o diferență semnificativă față de morfologia ideală a cristalelor unice (figura 2-1-9), cum ar fi o față unică care nu are neapărat aceeași formă și dimensiune și dispariția fețelor cristaline, care este descrisă drept cristale distorsionate.

Cristalele distorsionate pot fi descrise și ca cristale reale produse în natură, influențate de mediul de creștere. Multiplele fețe cristaline care se repetă la unghiuri fixe în cristalele ideale pot să nu aibă neapărat aceeași formă și dimensiune. Totuși, pentru același tip de cristal, fețele cristaline ale aceluiași monomorf trebuie să aibă același model și aceleași proprietăți fizice. Unghiurile dintre fețele corespunzătoare ale cristalului rămân neschimbate, reflectând simetria inerentă a cristalului însuși. Cristalele găsite în realitate sunt distorsionate în diferite grade.
Cristalele geminate pot fi descrise și ca cristale reale produse în natură, influențate de mediul de creștere. Multiplele fețe cristaline care se repetă la unghiuri fixe în cristalele ideale nu au neapărat aceeași formă și dimensiune. Totuși, pentru același tip de cristal, fețele de aceeași formă trebuie să aibă aceleași modele și proprietăți fizice. Unghiurile dintre fețele corespunzătoare ale cristalului rămân neschimbate, reflectând simetria inerentă a cristalului însuși. Cristalele întâlnite în realitate sunt toate, în diferite grade, geminate.
3. Obiceiurile de cristalizare ale cristalelor
Cristalele formate în natură nu pot atinge niciodată o formă perfectă. Dacă acestea cresc în golurile dintre straturile de rocă, înconjurate de rocă, forma naturală a cristalului va fi distorsionată. Chiar și cristalele cultivate în laborator vor fi deformate din cauza influenței gravitației. Numai în condițiile de gravitație zero de pe Stația Spațială Internațională oamenii de știință pot cultiva cristalele de formă perfectă pe care le caută.
Deși formele cristalelor sunt imperfecte, fiecare tip de cristal mineral tinde să crească sau să se grupeze în moduri sau obiceiuri diferite.
Fiecare mineral tinde să se formeze în condiții specifice, iar obiceiurile sale reflectă condițiile de formare. Unele minerale, cum ar fi cuarțul, au condiții de formare complexe și variabile. Astfel, cuarțul posedă, de asemenea, obiceiuri multiple.
În general, obiceiurile cristalelor se referă la caracteristicile unui anumit cristal care tinde să formeze o anumită formă în anumite condiții externe. Uneori, se referă la tipurile comune ale formei simple a acelui cristal.
Pe baza gradului de dezvoltare a cristalelor în spațiul tridimensional, obiceiurile cristalelor sunt împărțite în trei tipuri de bază.
(1) Uni-extindere direcțională
Cristalele se extind într-o singură direcție, apărând în forme columnare, aciculare, fibroase etc. Minerale precum beriliul, turmalina, hornblenda și malachitul prezintă adesea acest obicei (figurile 2-1-10 și 2-1-11).

Figura 2-1-10 Acvamarin columnar (sus) și diagrama sa de obiceiuri cristaline (jos)

Figura 2-1-11 Malachit fibros (sus) și diagrama sa de obiceiuri cristaline (jos)
(2) Bi-extindere direcțională
Cristalele se extind într-un plan, apărând sub formă de plăci, foițe, solzi etc., deoarece minerale precum wolframitul, mica, plumbagul și tanzanitul prezintă adesea acest obicei (figura 2-1-12).
(3) Tri-izometric direcțional
Cristalele se dezvoltă uniform în trei direcții, prezentând forme izometrice, granulare, cum ar fi spinelul, granatul, diamantul, pirita și fluoritul, care prezintă adesea acest obicei (figurile 2-1-13, 2-1-14).

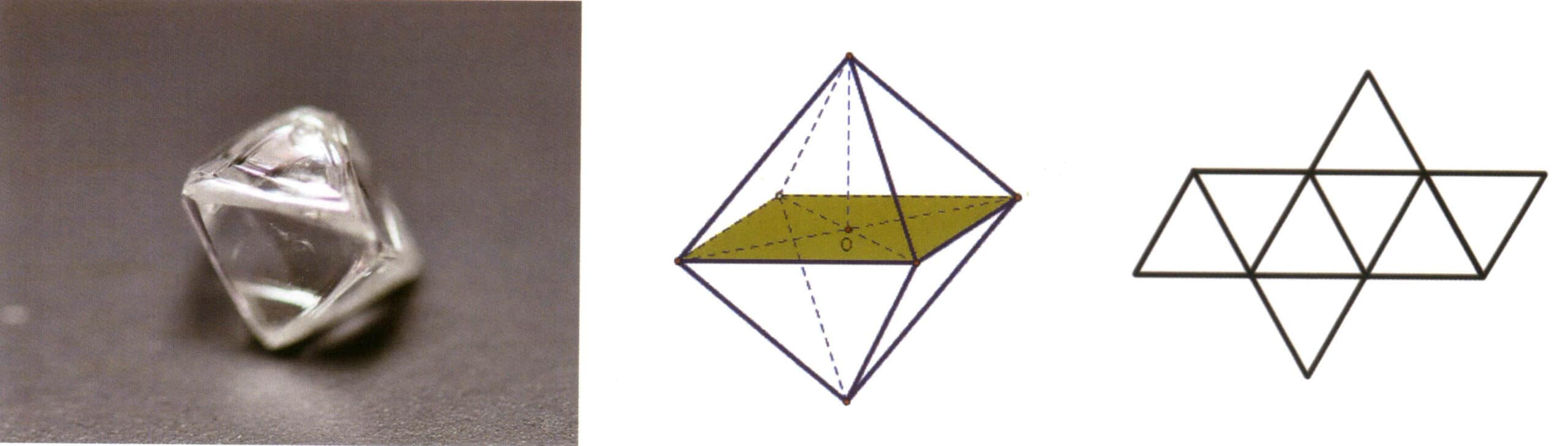
Figura 2-1-12 Obiceiul cristalin în formă de placă al tanzanitei (sus) și diagrama obiceiului său cristalin (jos)

Figura 2-1-13 Structura cristalină octaedrică a pietrei prețioase spinel (sus) și diagrama structurii sale cristaline (jos)
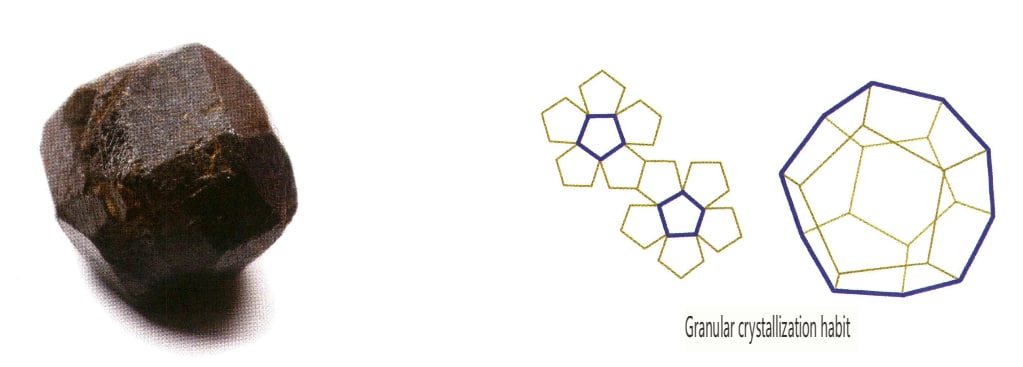
În plus, există tipuri de tranziție, cum ar fi formele columnare scurte, columnare în plăci, în benzi și în plăci groase.
Compoziția chimică și structura cristalului determină în principal aspectul cristalului. De asemenea, este strâns legată de condițiile externe din timpul formării cristalului (cum ar fi temperatura, presiunea, concentrația, vâscozitatea și impuritățile), cum ar fi diferențele de formă ale cristalului între diamante și cristalele de diamant sintetic.
4. Agregarea regulată a cristalelor
În natură, putem găsi cristale individuale (figura 2-1-15) și două sau mai multe cristale individuale care cresc împreună pentru a forma un întreg. Acest fenomen de creștere împreună a mai multor cristale se numește agregare cristalină. Agregarea cristalelor poate fi clasificată în tipuri neregulate și regulate. Agregarea neregulată a cristalelor poate fi înțeleasă ca o colectivitate, pe care capitolul trei o va detalia. În cazul agregării cristaline regulate, există patru tipuri comune: agregare paralelă, bicristale, supracreștere și intergreștere (figurile 2-1-16 - 2-1-18). Această secțiune abordează în principal tipul de agregare regulată cunoscut sub numele de bicristale.

Figura 2-1-15 Monocristal (turmalină)
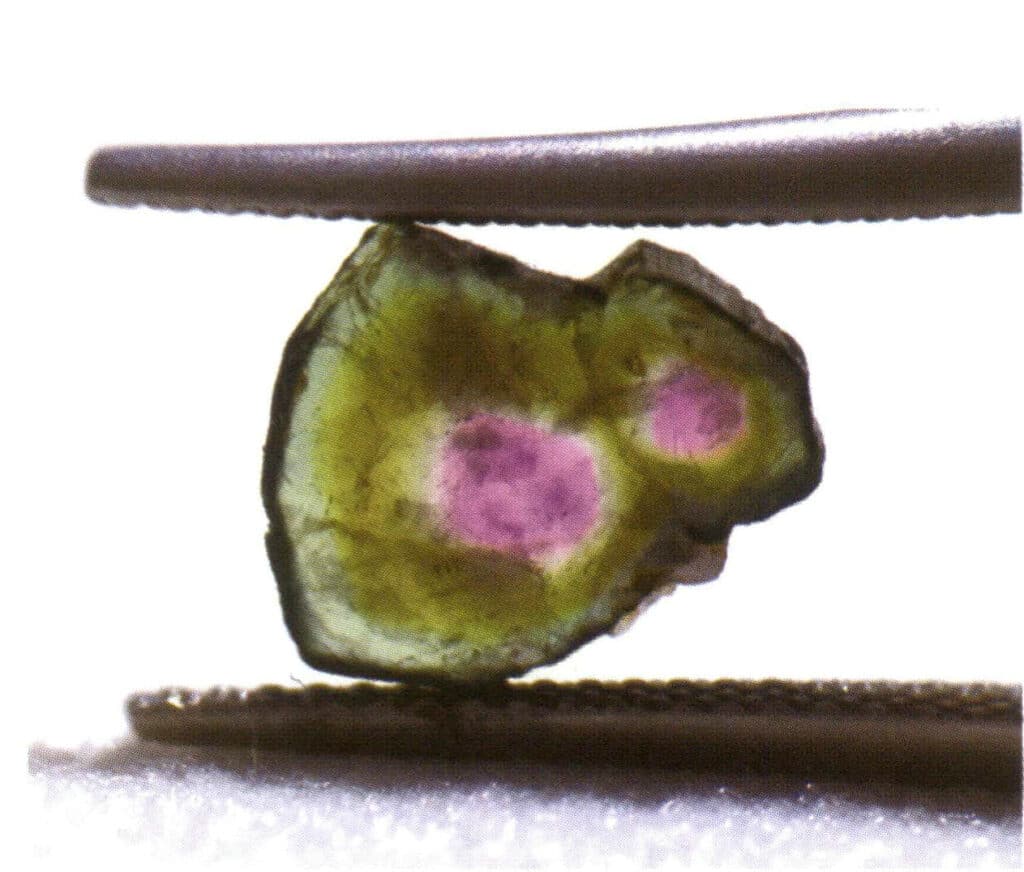
Figura 2-1-16 Agregare paralelă (Când mai multe cristale de același tip cresc paralel în spațiu, se numește agregare paralelă. În acest moment, fețele și marginile cristaline corespunzătoare ale cristalelor crescute sunt toate paralele între ele).

Figura 2-1-17 Cristal geamăn (Spinel)

Figura 2-1-18 Supracreștere (un tip de cristal crește pe suprafața altui cristal într-o direcție cristalografică specifică, cunoscută și sub denumirea de creștere epitaxială)
Bicristalele reprezintă agregarea regulată a două sau mai multe cristale identice în conformitate cu anumite reguli de simetrie. (Twin axis, twin plane) Fețele, marginile și unghiurile corespunzătoare ale celor doi indivizi adiacenți nu sunt complet paralele. Cu toate acestea, ele se pot reflecta reciproc prin operații simetrice precum rotația și inversarea rotației, permițând celor doi indivizi să coincidă sau să se alinieze.
4.1 Puncte cheie pentru identificarea bicristalelor
① Unghiuri concave vizibile în cristalele geminate (Figura 2-1-19).
② Stilolit: Micromorfologia și alte caracteristici ale suprafețelor cristaline de pe ambele părți ale stilolitului sunt discontinue (figura 2-1-20).
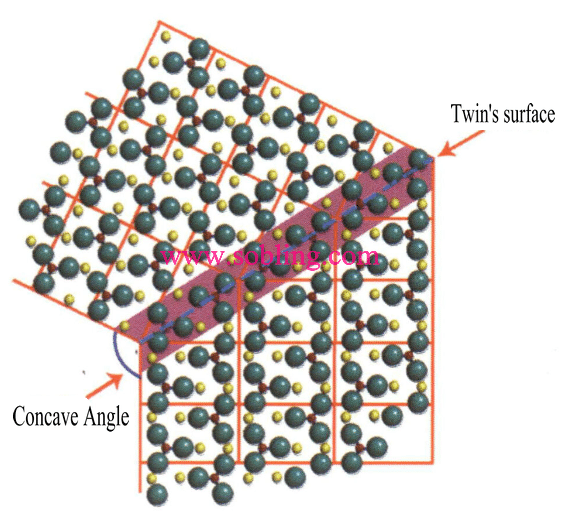
Figura 2 - 1-19 Unghiul concav al geamănului
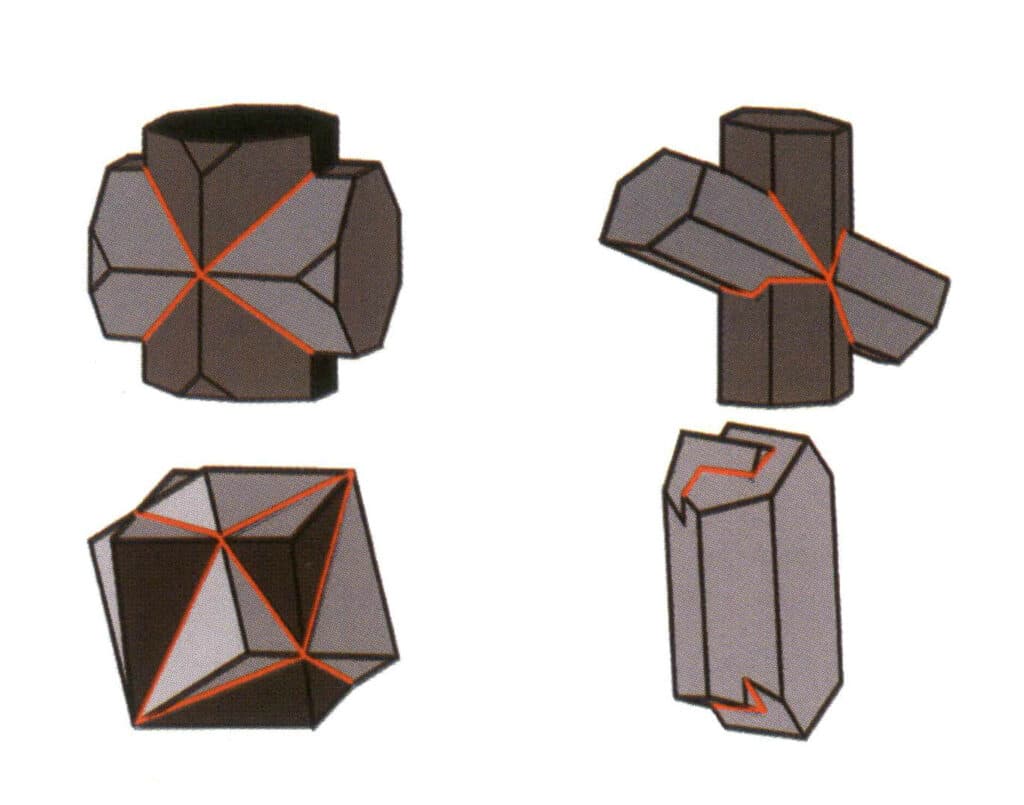
Figura 2-1-20 Stilolit (diferitele culori din figură reprezintă diferite cristale; liniile roșii indică stilolitul geamăn)
③ Striație de înfrățire: Fețele cristaline sau planurile de clivaj prezintă striații fine de înfrățire (figura 2-1-21)
④ Figura de gravură: Aspectul figurii de gravură indică prezența geamănării (figura 2-1-22)

Figura 2-1-21 Diagrama schematică a gemenilor polisintetici

Figura 2-1-22 Suprafață de spinel cu gropi triunghiulare inversate.
⑤ Apariția pseudo-simetriei: apariția unor relații de simetrie incompatibile cu grupul de puncte inerent al cristalului unic (Figura 2-1-23 la Figura 2-1-24).

Figura 2-1-23 Cristal unic de crioberil

Figura 2-1-24 Geamăn în formă de genunchi de crioberil
Gemenii sunt împărțiți în cinci tipuri, pe baza caracteristicilor lor de stivuire: gemeni de contact (Figura 2-1-25 - Figura 2-1-26), gemeni polisintetici (Figura 2-1-27), gemeni interpenetranți (Figura 2-1-28), cristal triplet (Figura 2-1-29) și gemeni complecși, dintre care primele patru tipuri sunt comune.


Figura 2-1-26 Îngemănarea de contact a spinelului (sus) și schema sa (jos)

Figura 2-1-27 Geamăn polisintetic de labradorit (sus) și schema sa (jos)
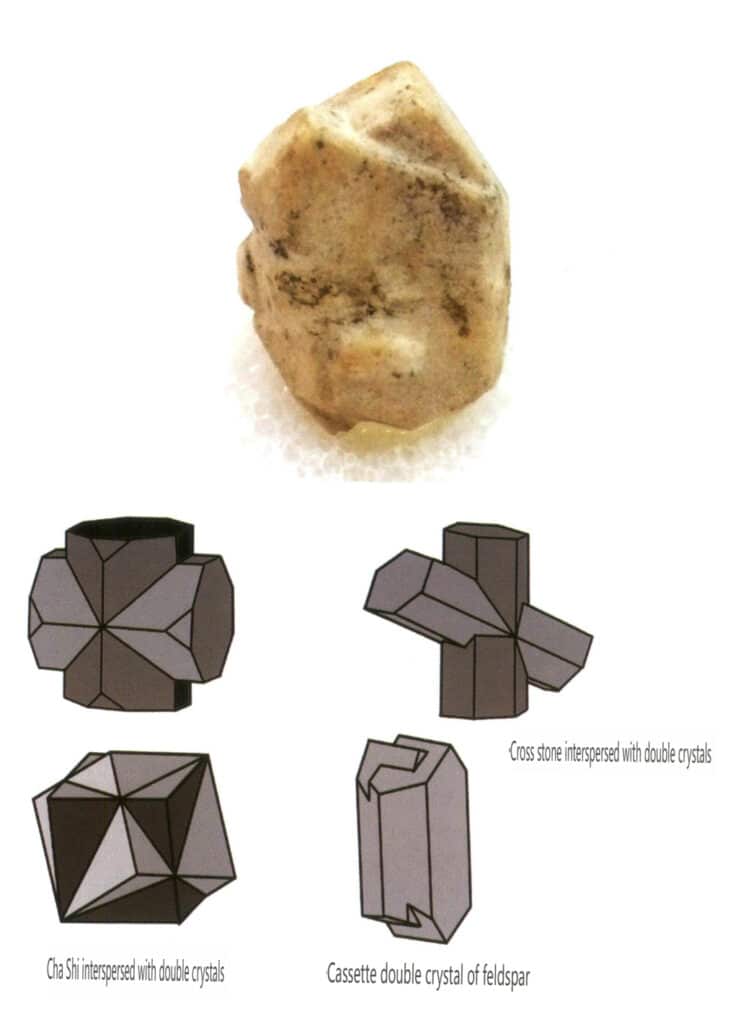
Figura 2-1-28 Cristale gemene de feldspat (sus) și schemă de cristale gemene întrepătrunse de alte tipuri (jos)

Figura 2-1-29 Îngemănarea trigonală a crisoberilului (sus) și schema sa (jos)
4.2 Formarea bicristalelor
① Formată în timpul creșterii cristalului, se poate dezvolta din germeni cristalini gemeni sau din cristale mici care cresc în mod dependent în funcție de poziția gemenilor.
② Formată în timpul procesului de transformare a heteromorfismului, cum ar fi atunci când cuarțul α se transformă în cuarț β, formând gemeni.
③ Formată prin acțiune mecanică, în care o parte a cristalului alunecă de-a lungul unui anumit plan direcțional pentru a forma gemeni de deformare, cum ar fi gemenii de calcit.
5.Crystal Modele de față
Atunci când cristalele sunt descoperite în natură, ele au adesea forme incomplete (Figura 2-1-30) și modele de suprafață speciale. Uneori, ele cresc împreună în grupuri (Figura 2-1-31), care prezintă adesea diferențe semnificative față de poliedrele geometrice standard cu care suntem familiarizați, cum ar fi cuburile și prismele hexagonale. Acest fenomen este denumit forma reală a cristalelor. Forma reală a cristalelor are o clasificare detaliată în cristalografie, cum ar fi cristalele distorsionate, cristalele convexe, cristalele curbate, cristalele plutitoare, dungile feței cristalului, figurile de gravură, dungile de înfrățire etc.

Figura 2-1-30 Cristal rubin

Figura 2-1-31 Cristale de pirită (în stânga se văd mai multe cristale de pirită care cresc împreună, iar în dreapta se vede un singur cristal de pirită)
Această secțiune abordează în principal modelele de fețe de cristal în forma reală a cristalelor.
Teoretic, planele cristalelor sunt netede și plate. Cu toate acestea, în timpul creșterii sau dizolvării reale a cristalelor, suprafața lasă adesea în urmă modele regulate ușor inegale, denumite în mod obișnuit modele ale feței cristalului. Modelele suprafețelor cristaline includ striații de creștere, straturi de creștere, modele spiralate, coline de creștere și figuri de gravură. Modelele feței cristaline discutate în această carte se referă în principal la striațiile feței cristaline și la figurile de gravură care pot fi observate cu ochiul liber sau în condiții de mărire redusă.
Dungile de pe fața cristalului se referă la o serie de linii drepte paralele pe suprafața cristalului, datorate convergenței repetate și creșterii alternante a diferitelor forme simple. Cunoscute și sub denumirea de "dungi combinate", acestea sunt observate doar pe suprafețele cristalelor, numite și dungi de creștere. De exemplu, fața cristalină prismatică hexagonală a cuarțului are adesea fețe cristaline fine prismatice hexagonale și dodecaedrice rombice dezvoltate alternativ în dungi transversale agregate (figura 2-1-32).

Figurile de gravură se referă la gropile de formă specifică (de exemplu, gropile de gravură) lăsate pe fața cristalului din cauza coroziunii după formarea cristalului. Figurile de gravură sunt controlate de dispunerea particulelor elementare în fața cristalului. Astfel, formele și orientările figurilor de gravură variază între diferite minerale și forme unice ale aceluiași cristal. De exemplu, figurile de gravură de pe diferite forme simple de cristale de diamant variază; pot fi observate gropi triunghiulare pe cristalele octaedrice (figura 2-1-33), gropi cvadrilaterale pe fețele cubice, gropi cvadrilaterale suprapuse care formează un model tip grilă, iar modele de linii sau modele microscopice tip disc pot fi observate pe dodecaedrele rombice (figura 2-1-34).

Figura 2-1-33 Gropi triunghiulare inversate vizibile pe cristalul octaedral de diamant

Figura 2-1-34 Textura cu model liniar vizibilă pe cristalele dodecaedrice în formă de diamant
Numai figurile gravate de pe aceeași față cristalină a aceleiași forme pot fi identice, astfel încât figurile gravate sunt adesea utilizate pentru a identifica mineralele și pentru a determina dacă fețele cristaline aparțin aceleiași forme unice (Figura 2-1-35 până la Figura 2-1-42).

Figura 2-1-35 Cristale de fluorit încrustate în dungi stil podea de lemn

Figura 2-1-36 Figură naturală de gravură triunghiulară în rubin (dungi orizontale comune în rubine, linii de creștere paralele cu direcția romboedrică, gravuri naturale în forme triunghiulare sau hexagonale)

Figura 2-1-37 Dungi longitudinale de suprafață ale turmalinei

Figura 2-1-38 dungi orizontale pe suprafața cristalului

Figura 2-1-39 Figuri gravate pe suprafața cristalului

Figura 2-1-40 Striații longitudinale de suprafață ale topazului

Figura 2-1-41 Imagine topografică a unui cristal de topaz

Figura 2-1-42 Figuri de gravură ale Spinelului
Secțiunea II 47 Tipuri de forme cristaline
Există 146 de forme unice diferite în cristalografie, care pot fi clasificate în 47 de forme geometrice pe baza formelor lor geometrice atunci când există independent. Aceste forme geometrice sunt denumite în felul următor:
① Numite în funcție de caracteristicile formei secțiunii transversale, cum ar fi prismă trigonală, prismă tetragonală, prismă hexagonală, bipiramidă romboedrică etc.
② Numite în funcție de forma formei unice, cum ar fi cilindru, con dublu, cub etc.
③ Numite în funcție de numărul de fețe geometrice, cum ar fi față unică, octaedru etc.
④ Numite în funcție de forma fețelor geometrice, cum ar fi romboedru, pentacontaedru etc.
În cristalografie, formele simple sunt împărțite în patru categorii: forme generale și forme speciale, forme închise și forme deschise, forme regulate și forme neregulate, forme stângace și forme drepte. Acest capitol va discuta pe scurt formele închise și formele deschise.
Formele închise se referă la cele ale căror fețe cristaline pot cuprinde un spațiu închis, împărțite în trei categorii principale: clase poliedrice, clase poliedrice oblice și clase bipiramidale, totalizând 30 de tipuri. Fiecare categorie are clasificări mai detaliate; de exemplu, clasa poliedrică este subîmpărțită în clasa tetraedrică, clasa octaedrică, clasa cubică etc. (figurile 2-1-43 - 2-1-48)

Figura 2-1-43 Clasa tetraedru
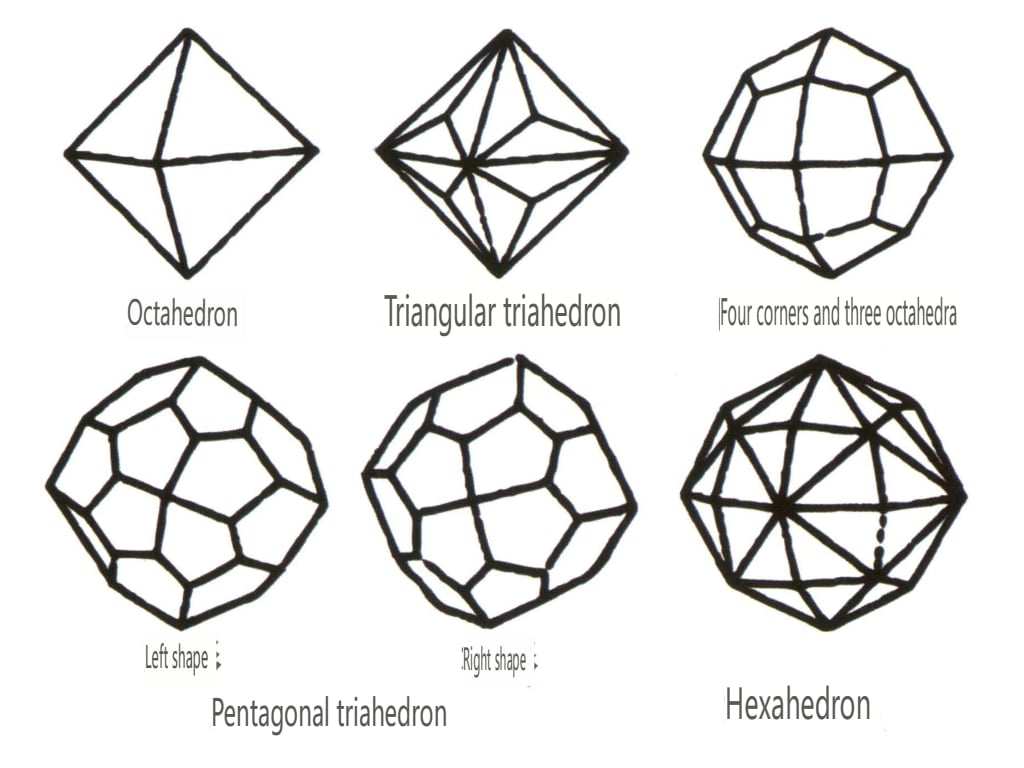
Figura 2-1-44 Clasa 0ctaedrică
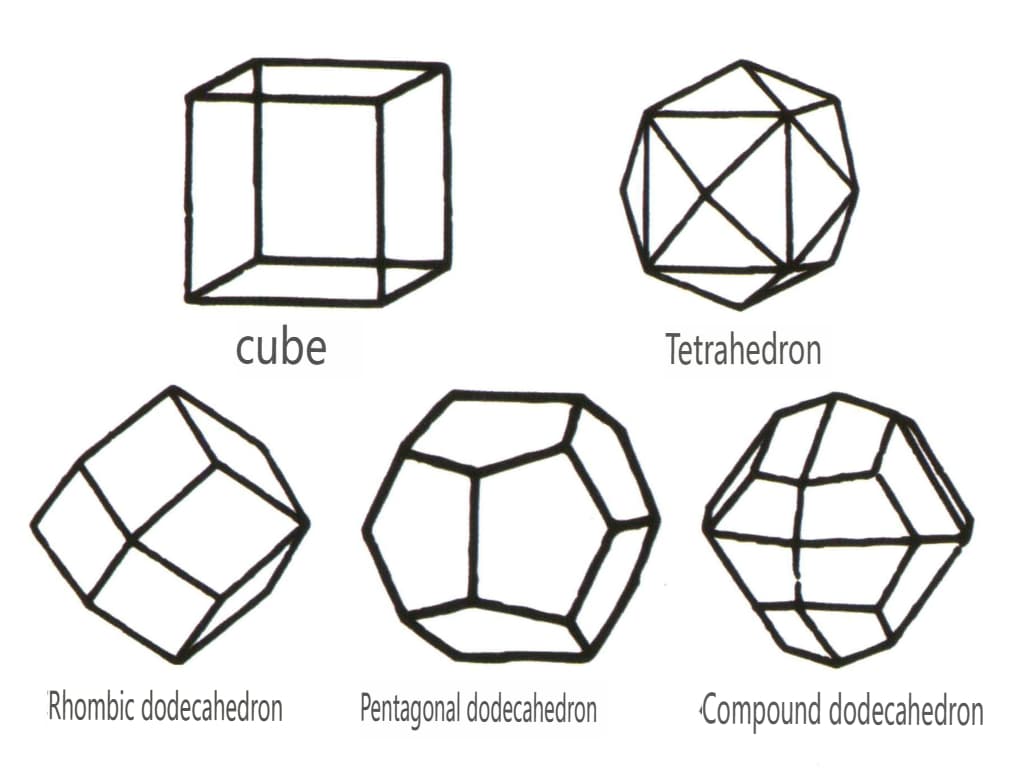
Figura 2-1-45 Clase cubice și dodecaedrice
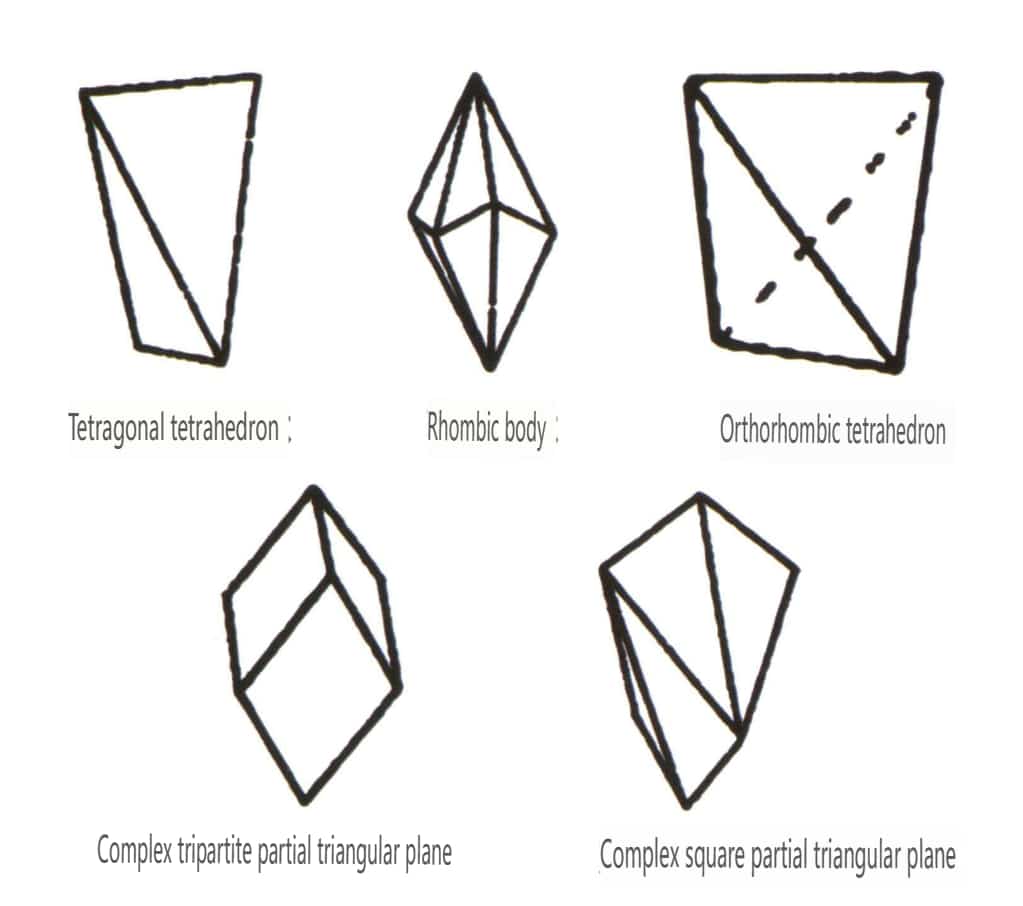
Figura 2-1-46 Alte tipuri de poliedre
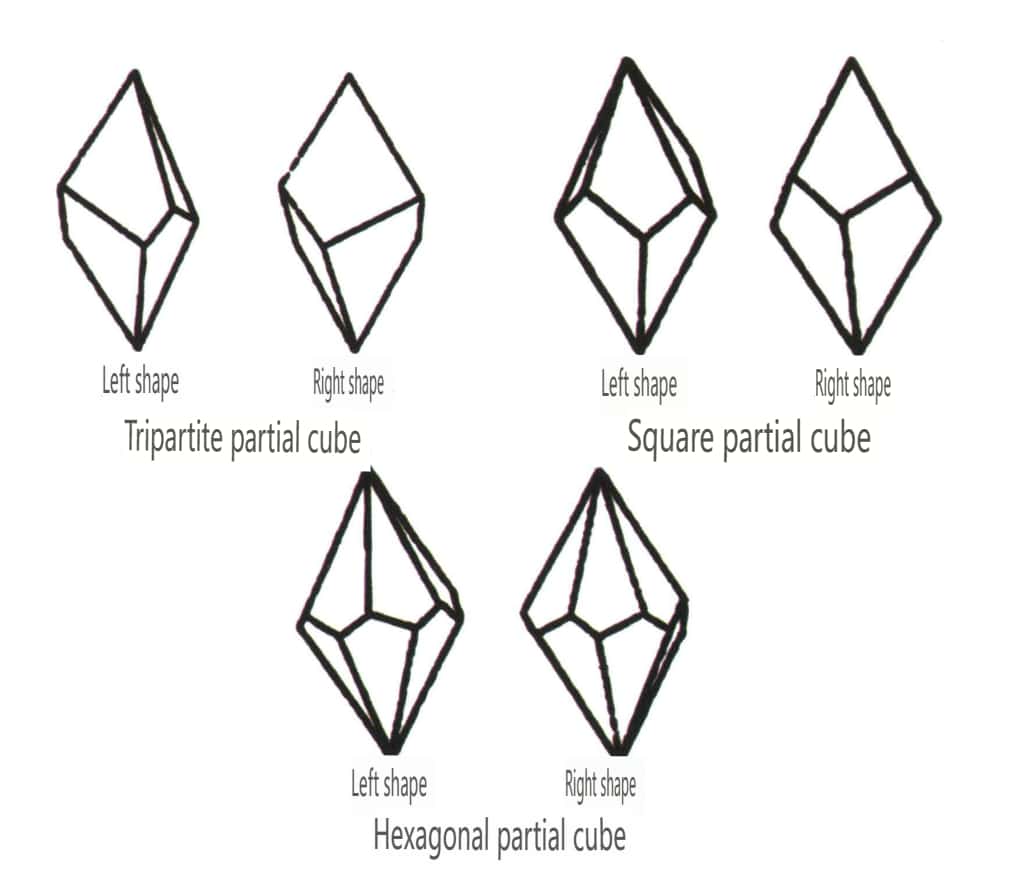
Figura 2-1-47 Forma combinată oblică Clasa
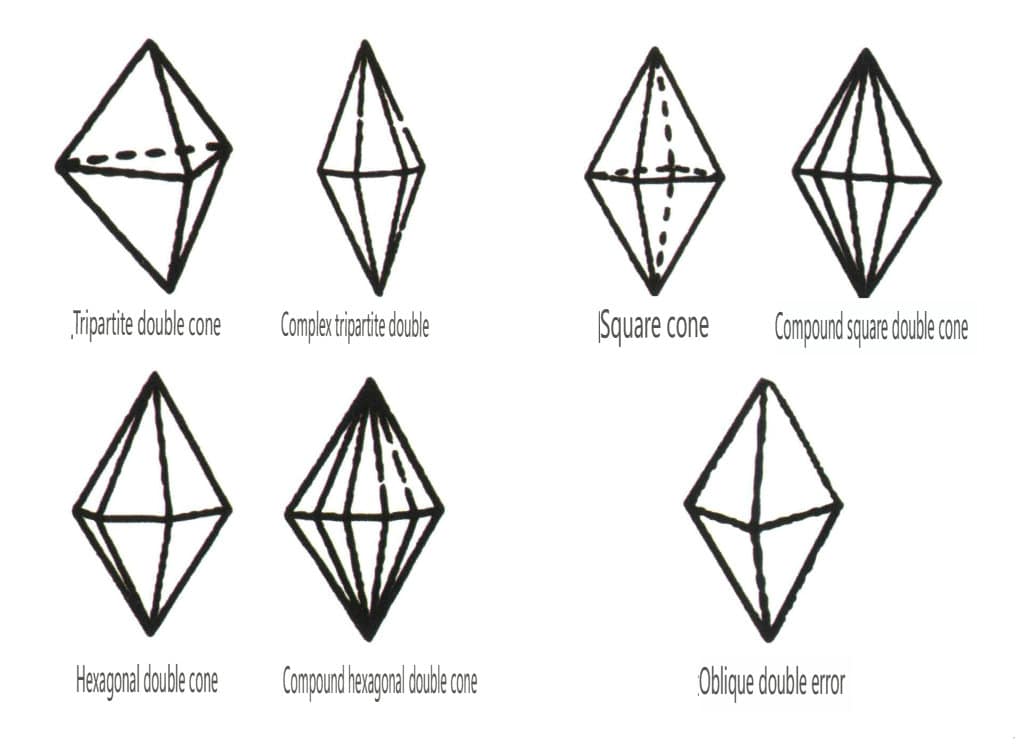
Figura 2-1-48 Clasă piramidală dublă
Formele deschise se referă la cele ale căror fețe cristaline nu pot cuprinde un spațiu închis, împărțite în patru categorii principale: cu o singură față, cu două fețe, clase columnare și clase piramidale simple, totalizând 17 tipuri (figurile 2-1-49 și 2-1-51)
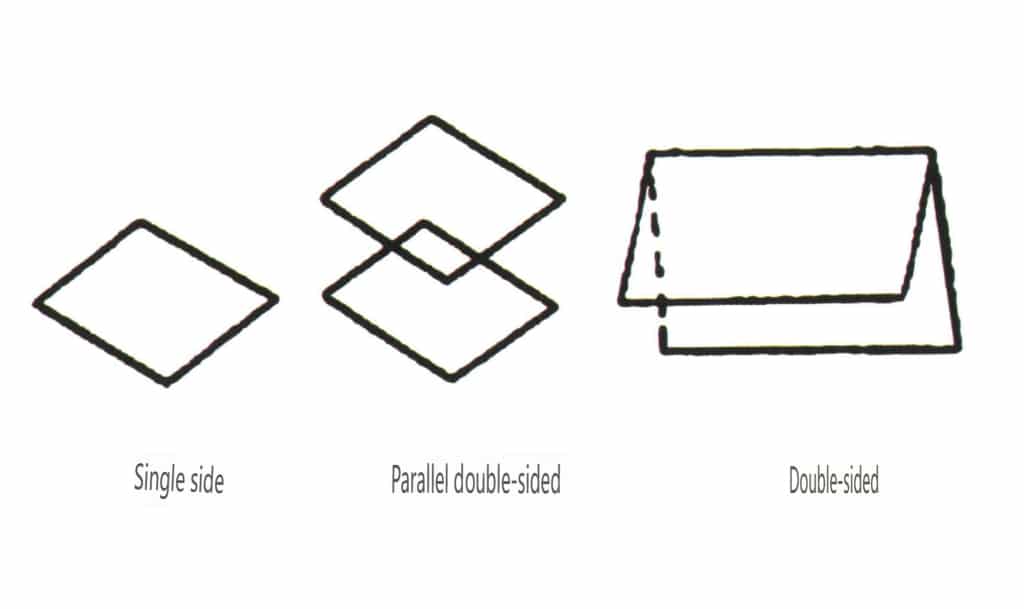
Figura 2-1-49 Față simplă și față dublă
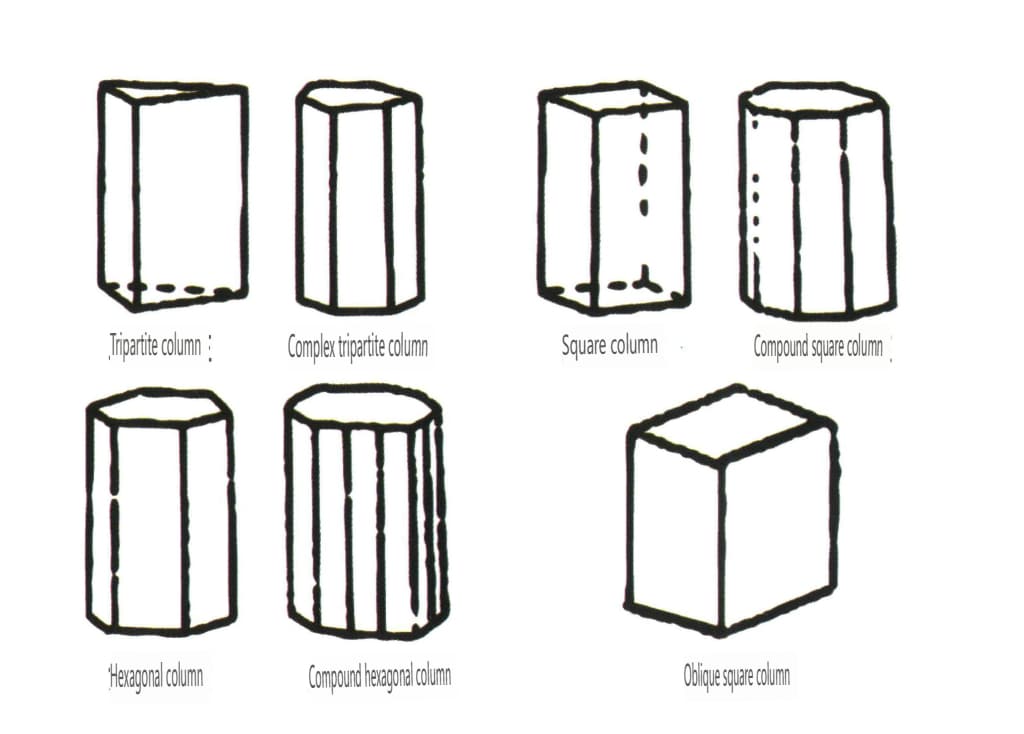
Figura 2-1-50 Coloane

Secțiunea III Clasificarea cristalelor
1. Simetria cristalelor
Simetria este un concept abstract implicat în studiul cristalelor reale și al pietrelor prețioase neprocesate. Acesta descrie repetiția prezentă atunci când structura cristalină se raportează la o direcție sau la un plan care trece prin ea. Aceasta este baza pentru clasificarea cristalelor.
Simetria unui cristal poate fi înțeleasă dintr-o perspectivă microscopică ca o metodă de descriere a repetitivității structurii cristaline și dintr-o perspectivă macroscopică ca repetarea a două sau mai multe fețe geometrice care sunt identice ca formă și dimensiune, dar pot diferi ca direcție, în conformitate cu anumite reguli. Acest model de repetiție poate fi descris folosind axe de simetrie și planuri de simetrie, fiecare axă de simetrie sau plan de simetrie fiind denumit element de simetrie. Atunci când se observă sau se deduce simetria unui obiect, această acțiune este descrisă ca efectuarea de operații asupra simetriei.
2. Elemente de simetrie ale cristalelor
În cristalografie, există patru elemente de simetrie: axa de simetrie, planul de simetrie, axele de simetrie rotoinversoare și centrul simetric. Acest lucru va implica cele două elemente de simetrie: axa de simetrie și planul de simetrie.
2.1 Axa de simetrie
(1) Conceptul de axă de simetrie și notarea acestora.
Axa de simetrie este o linie dreaptă imaginară care indică numărul de ori în care nivelul de bază (figurile 2-2-1 și 2-2-2) apare în aceeași poziție atunci când structura rețelei este rotită cu 360° în jurul acestei linii imaginare. Acest număr nu poate fi decât de 2, 3, 4 sau 6 ori în 4 cazuri. De asemenea, poate fi înțeles ca o linie imaginară care trece prin centrul corpului geometric, rotirea corpului geometric de-a lungul acestei linii la 360°. Să presupunem că forma corpului geometric după rotirea unui anumit unghi este consecventă cu forma corpului geometric la zero grade inițial. În acest caz, această linie imaginară se numește axă de simetrie.
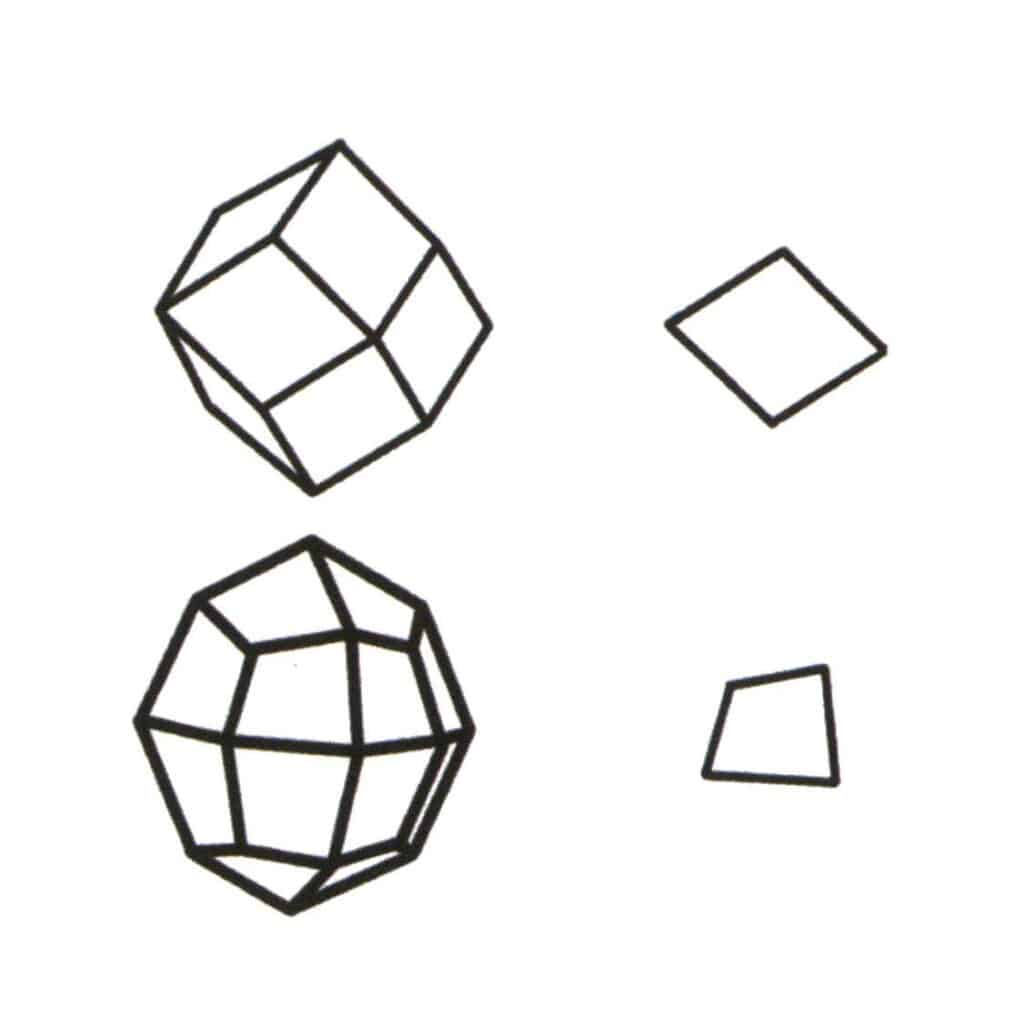
Figura 2-2-1 Selectarea nivelului de bază pentru formularul unic.
Nivelul de bază al formei simple este cel mai mic plan repetitiv care alcătuiește simplexul. Partea din stânga sus a figurii prezintă un dodecaedru rombic, care este o formă închisă compusă dintr-un singur tip de față. Cel mai mic plan care se repetă este rombul prezentat în dreapta sus, astfel încât nivelul de bază pentru dodecaedrul rombic este rombul. Figura din stânga jos arată un octaedru cvadrilateral, care este o formă închisă compusă dintr-un singur tip de față. Cel mai mic plan care se repetă este cvadrilaterul prezentat în dreapta jos, astfel încât nivelul de bază pentru octaedrul cvadrilateral este cvadrilaterul.
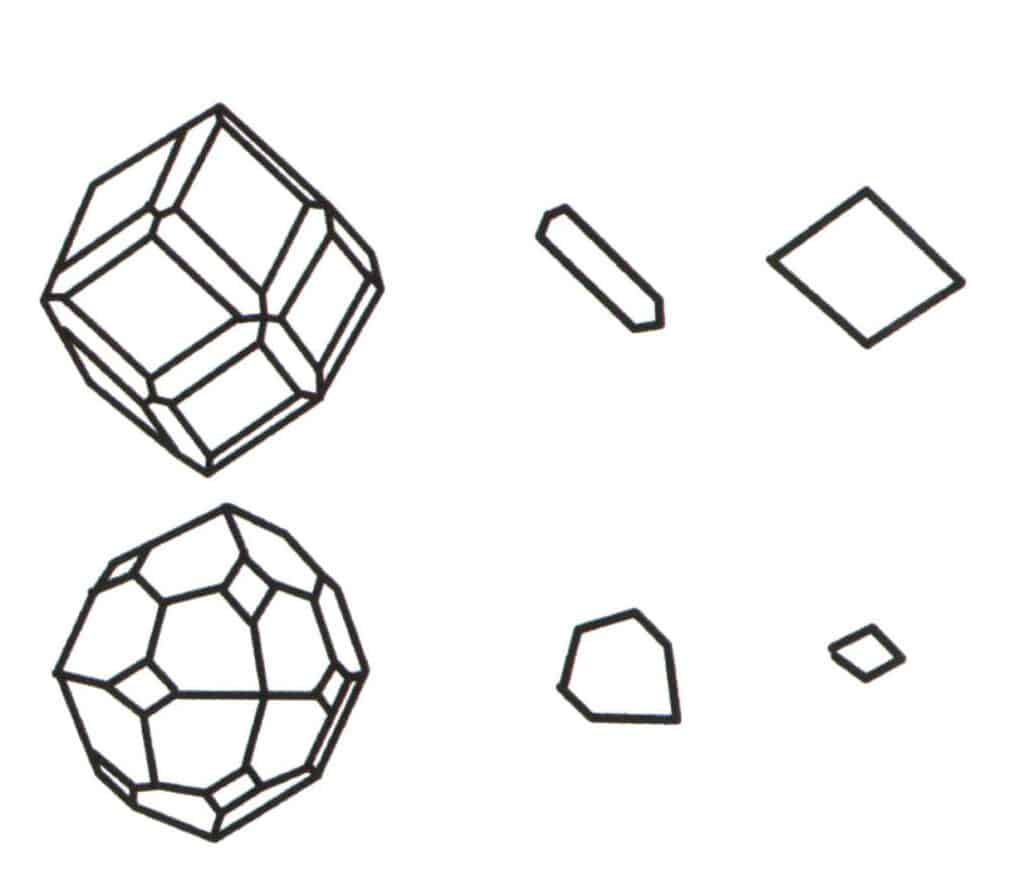
Figura 2-2-2 Selectarea nivelului de bază pentru politop.
Agregarea mai multor forme simple formează o formă combinată, iar alegerea nivelului de bază pentru forma combinată este judecata formei simple care se combină pentru a forma forma combinată. Prima coloană din stânga în figură reprezintă o formă combinată (formată prin agregarea formelor simple ale unui dodecaedru și ale unui tetraedru), iar acest corp geometric este o figură închisă compusă din două tipuri de fețe. Hexagonul reprezintă planul minim de repetare în coloana a doua, iar rombul din dreapta în coloana a treia. Prin urmare, planul de bază pentru forma combinată din prima coloană este fie hexagonul, fie rombul. La calcularea axei de simetrie, o singură formă poate fi selectată ca nivel de bază pentru înregistrarea simetriei.
Axa de simetrie este reprezentată de litera L majusculă, cu ordinea axei n scrisă în colțul din dreapta sus al lui L, scrisă ca Lⁿ. De exemplu, o axă de 2 ori este reprezentată ca L², o axă de 3 ori ca L³, o axă de 4 ori ca L⁴, iar o axă de 6 ori ca L⁶. L⁶, L⁴, L³ este denumită în mod obișnuit o axă de ordin superior.
Cristalele pot avea axe de simetrie în direcții diferite, iar numărul acestor axe de simetrie necoincidente se scrie convențional în stânga lui L. De exemplu, șase axe secundare sunt reprezentate prin 6L² (figura 2-2-3 la figura 2-2-9), trei axe terțiare sunt reprezentate prin 3L³ (figura 2-2-10 la figura 2-2-14), patru axe terțiare sunt reprezentate prin 4L³ (figura 2-2-15 la figura 2-2-18), iar o axă hexagonală este reprezentată prin L⁶ (figura 2-2-19).
Atunci când un cristal are mai multe axe de simetrie, metoda înregistrată le ordonează de la stânga la dreapta în ordine descrescătoare, cu numărul de axe de simetrie scris în partea stângă a axei corespunzătoare, de exemplu, L⁶6L², 3L⁴4L³6L².
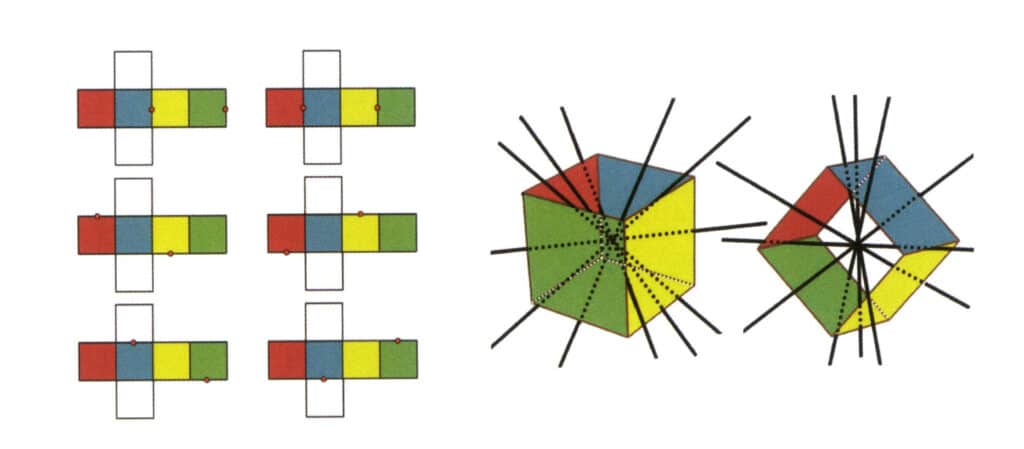
Figura 2-2-3 Axa secundară a cubului
Partea stângă a figurii prezintă o vedere desfășurată a unui cub, cu puncte roșii care indică punctele de intersecție ale liniei imaginare și ale marginilor. Partea dreaptă a figurii arată un cub închis, în care axa secundară poate apărea la mijlocul liniilor paralele ale marginilor, la mijlocul fețelor dreptunghiulare paralele sau la punctele de intersecție a trei sau mai multe fețe paralele care seamănă cu un dreptunghi.
Copywrite @ Sobling.Jewelry - Producător de bijuterii personalizate, fabrică de bijuterii OEM și ODM
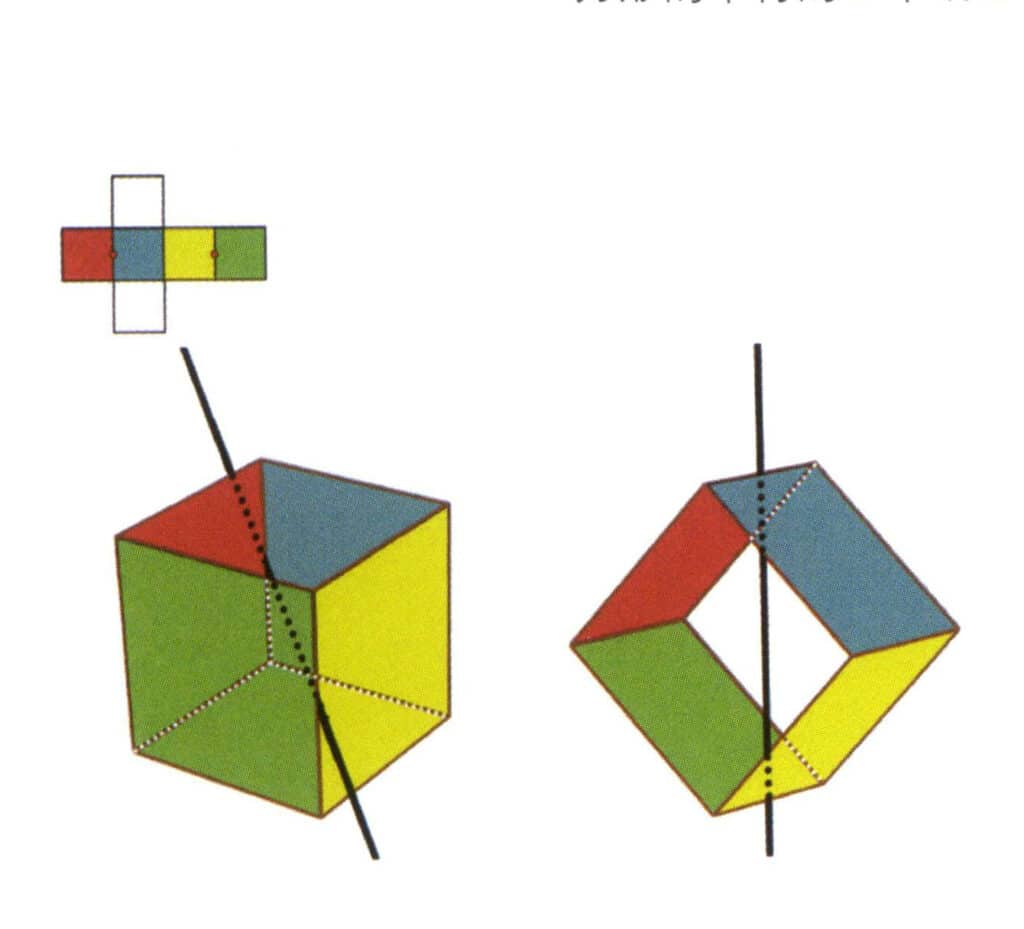
Figura 2-2-4 Prima axă secundară a cubului
Selectați punctul median al liniilor paralele, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele mediane ale acestor două muchii, rotind cubul cu 360°. Nivelele de bază cu culori diferite, dar cu aceeași formă, se vor repeta de două ori în aceeași poziție (fețele roșii și albastre, fețele galbene și verzi, cele două fețe incolore și trei seturi de fețe repetate. Deși vor apărea trei seturi de fețe repetate, deoarece linia imaginară nu și-a schimbat poziția și unghiul, axa secundară este înregistrată o singură dată). Această linie imaginară este înregistrată ca axă secundară.
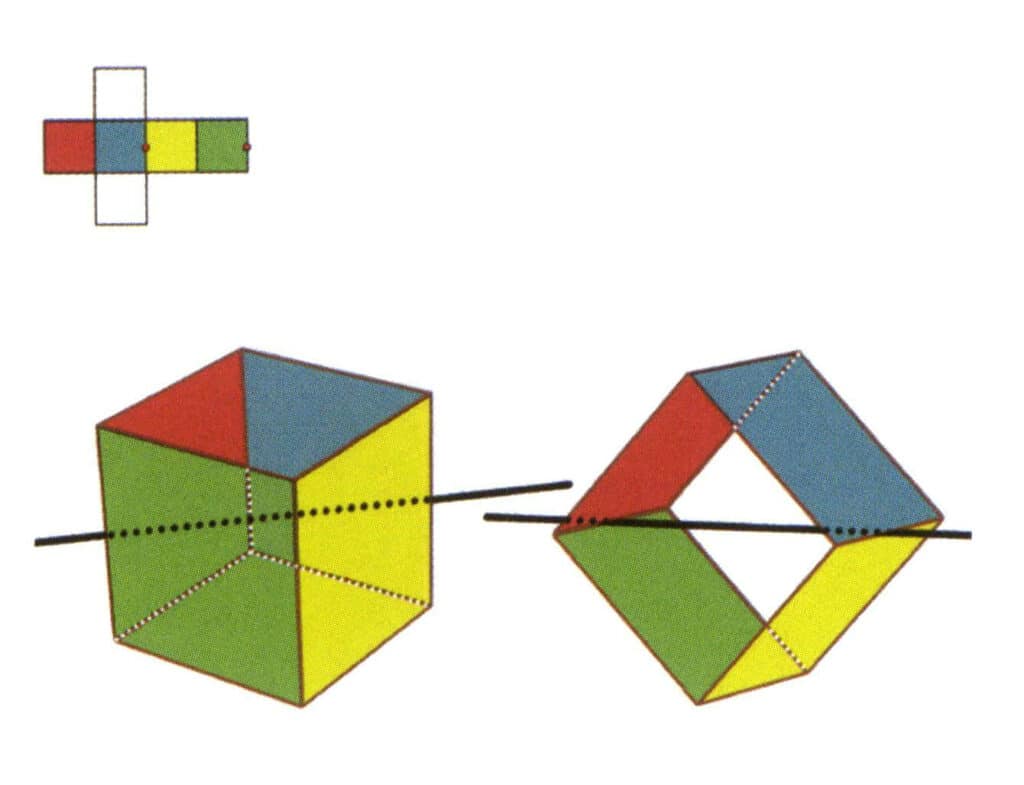
Figura 2-2-5 A doua axă secundară a cubului
Selectați punctul median al liniilor paralele, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele mediane ale acestor două muchii, rotind cubul cu 360°. Nivelele de bază cu culori diferite, dar cu aceeași formă, se vor repeta de două ori în aceeași poziție (fețele roșii și verzi, fețele galbene și albastre, cele două fețe incolore și trei seturi de fețe repetate). Această linie imaginară este înregistrată ca a doua axă secundară.
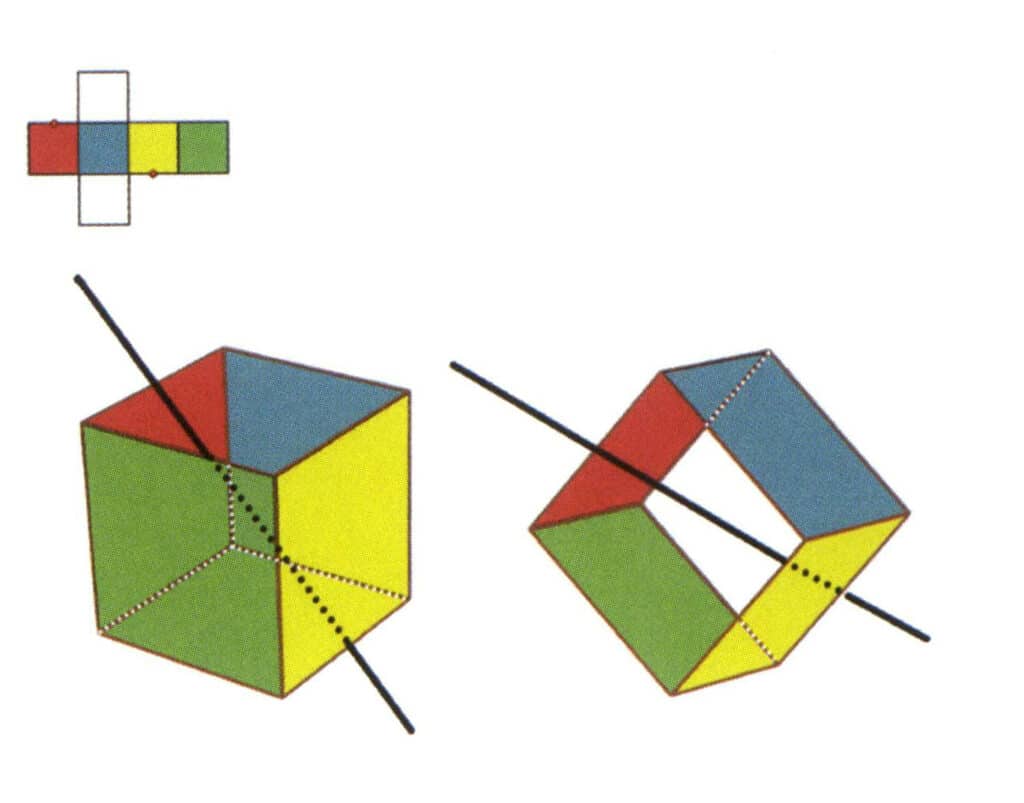
Figura 2-2-6 A treia axă secundară a cubului.
Selectați punctul median al liniilor paralele, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele de mijloc ale acestor două muchii, rotindu-se cubul cu 360°. Nivelele de bază cu culori diferite, dar aceeași formă se va repeta de două ori în aceeași poziție (fețele roșii și incolore, fețele verzi și albastre, fețele incolore și galbene, trei seturi de fețe repetate). Această linie imaginară este înregistrată ca a treia axă secundară
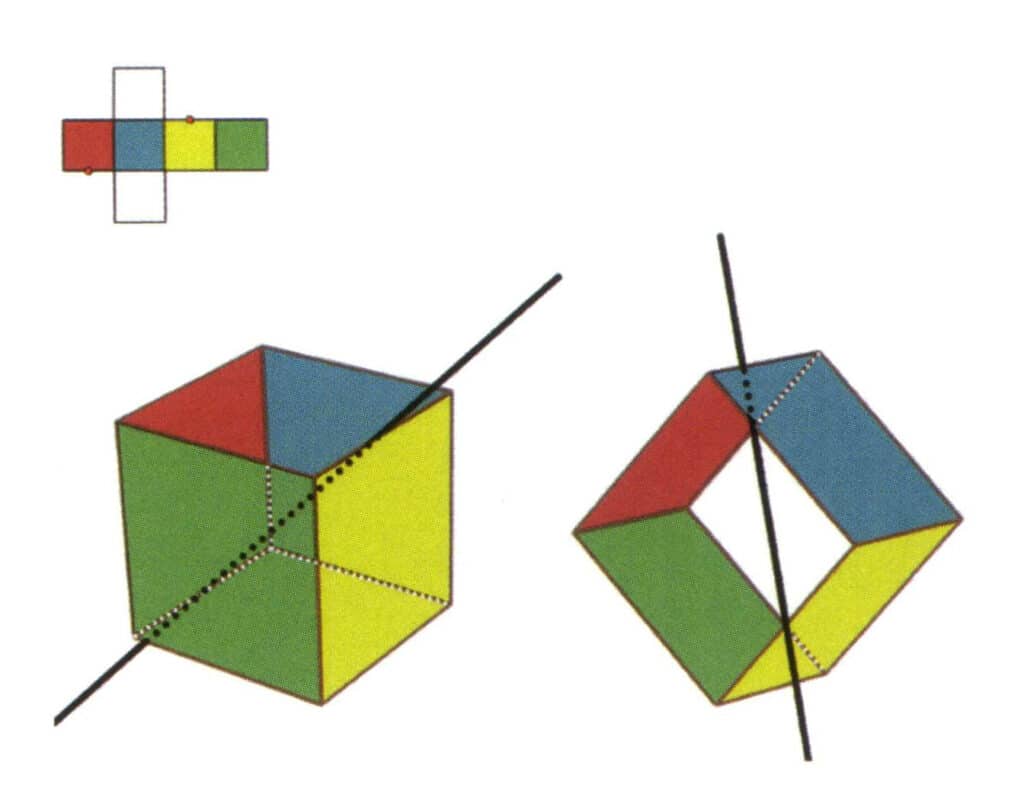
Figura 2-2-7 A patra axă secundară a cubului
Selectați punctul central al liniilor paralele, așa cum se arată în figură, imaginați-vă o linie dreaptă care trece prin punctele centrale ale acestor două muchii și rotiți cubul cu 360°; planurile de referință de culori diferite, dar de formă identică, se vor repeta în aceeași poziție de două ori (fețele roșii și incolore, fețele verzi și albastre, fețele incolore și galbene, trei seturi de fețe repetate); această linie dreaptă imaginară este înregistrată ca a patra axă secundară.
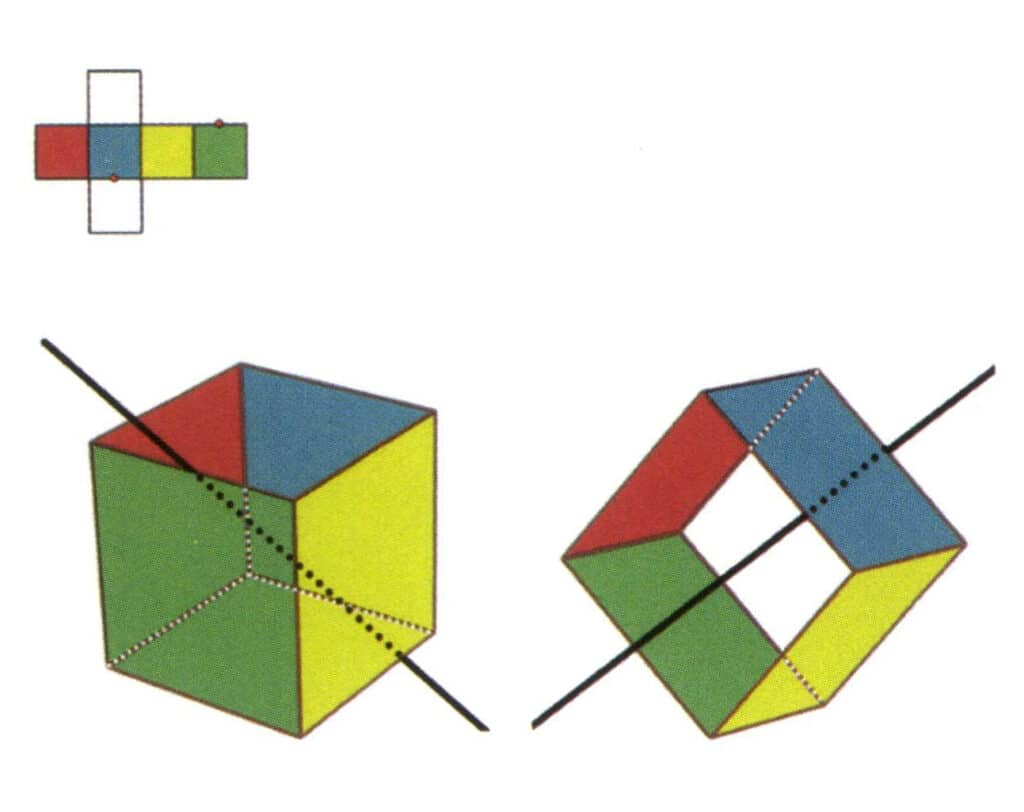
Figura 2-2-8 A cincea axă secundară a cubului.
Selectați punctele mediane ale liniilor paralele, așa cum se arată în figură, imaginați-vă o linie dreaptă care trece prin punctele mediane ale acestor două muchii, rotiți cubul la 360°, planurile de referință colorate diferit, dar de formă identică, se vor repeta în aceeași poziție de două ori (fețe roșii și incolore, fețe verzi și albastre, fețe incolore și galbene, trei seturi de fețe repetate), această linie dreaptă imaginată este înregistrată ca a cincea axă secundară.
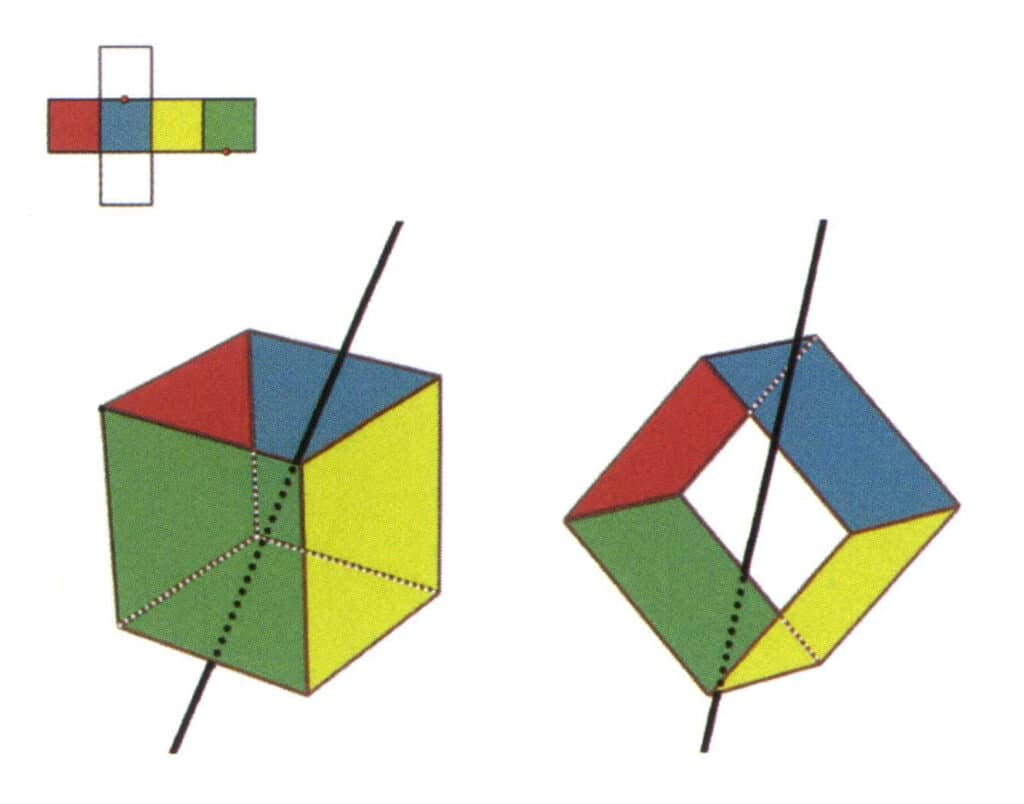
Figura 2-2-9 A șasea axă secundară a cubului
Selectați punctul median al liniilor paralele, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele de mijloc ale acestor două muchii, rotindu-se cubul cu 360°. Nivelele de bază colorate diferit, dar de formă identicăse vor repeta în aceeași poziție de două ori (fețe verzi și incolore, fețe roșii și galbene, fețe incolore și albastre, trei seturi de fețe repetate). Această linie imaginară este înregistrată ca a șasea axă secundară.
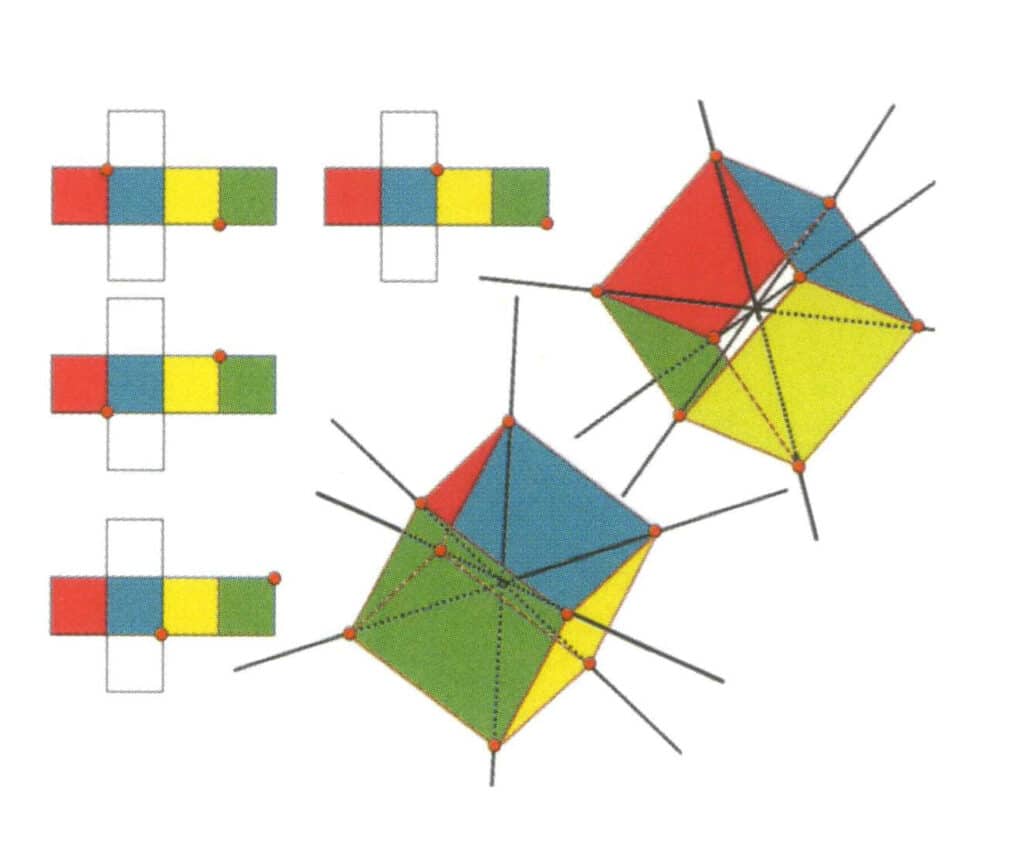
Figura 2-2-10 Axa terțiară a cubului
Partea stângă a figurii arată vederea desfășurată a cubului, punctul roșu indicând punctul de intersecție al liniei imaginare și al liniei marginilor. Partea dreaptă a figurii arată cubul închis; punctele roșii indică intersecția liniei drepte imaginare și a marginilor. Axa terțiară poate apărea în punctul median al fețelor unui triunghi echilateral paralel, la intersecția a trei sau mai multe fețe paralele care seamănă cu un triunghi echilateral.
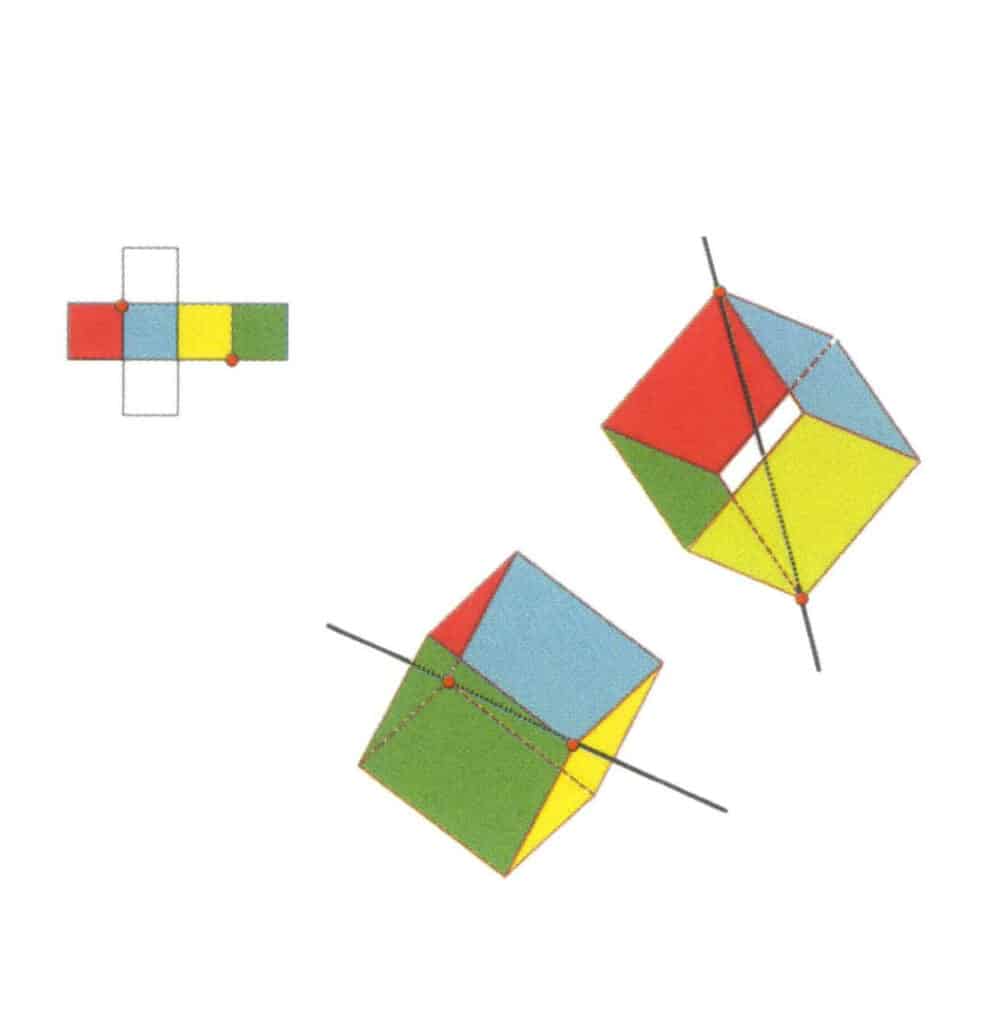
Figura 2-2-11 Prima axă terțiară a cubului.
Selectați punctele de intersecție ale celor trei fețe, așa cum se arată în figură, imaginați-vă o linie dreaptă care trece prin punctele mediane ale acestor două muchii, rotiți cubul la 360°, planurile de referință colorate diferit, dar de formă identică, se vor repeta în aceeași poziție de trei ori (fețe roșii, incolore și albastre, fețe verzi, incolore și galbene, două seturi de fețe repetate), această linie dreaptă imaginată este înregistrată ca prima axă terțiară
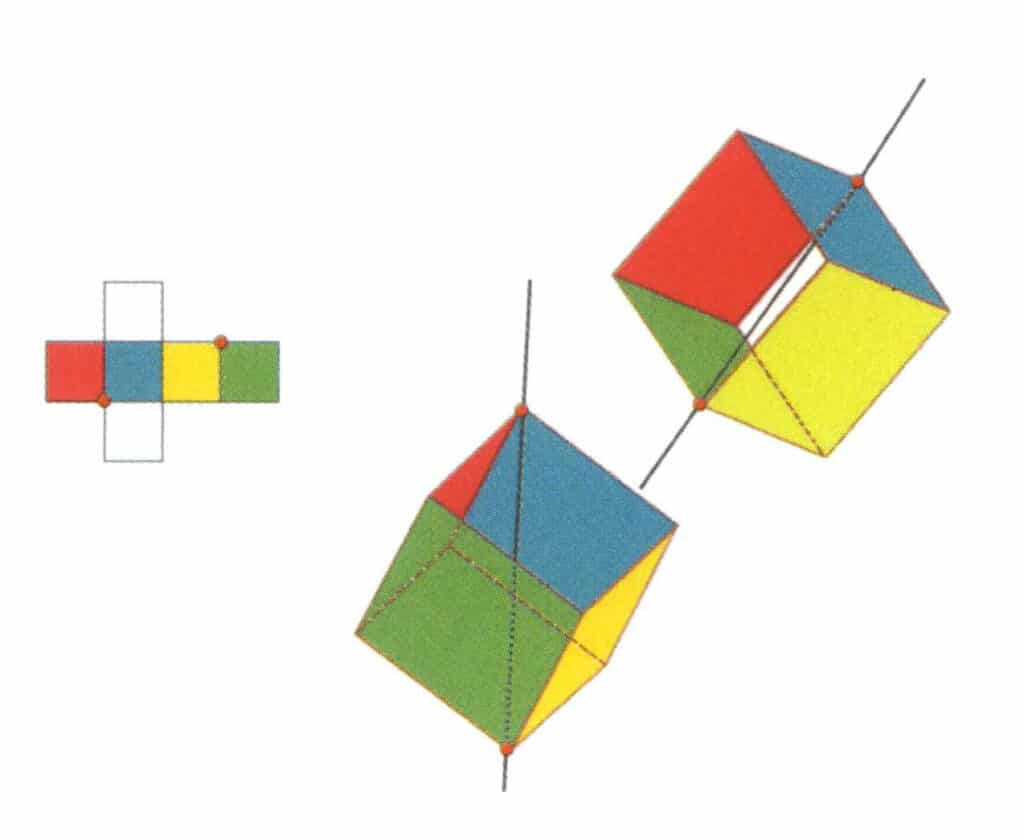
Figura 2-2-12 A doua axă terțiară a cubului.
Selectați punctele de intersecție ale celor trei fețe, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele de mijloc ale acestor două muchii, rotind cubul cu 360°. Nivelele de bază colorate diferit, dar de formă identică, se vor repeta în aceeași poziție de trei ori (fețe roșii, incolore și albastre; fețe verzi, incolore și galbene, două seturi de fețe repetate). Această linie imaginară este înregistrată ca a doua axă terțiară.
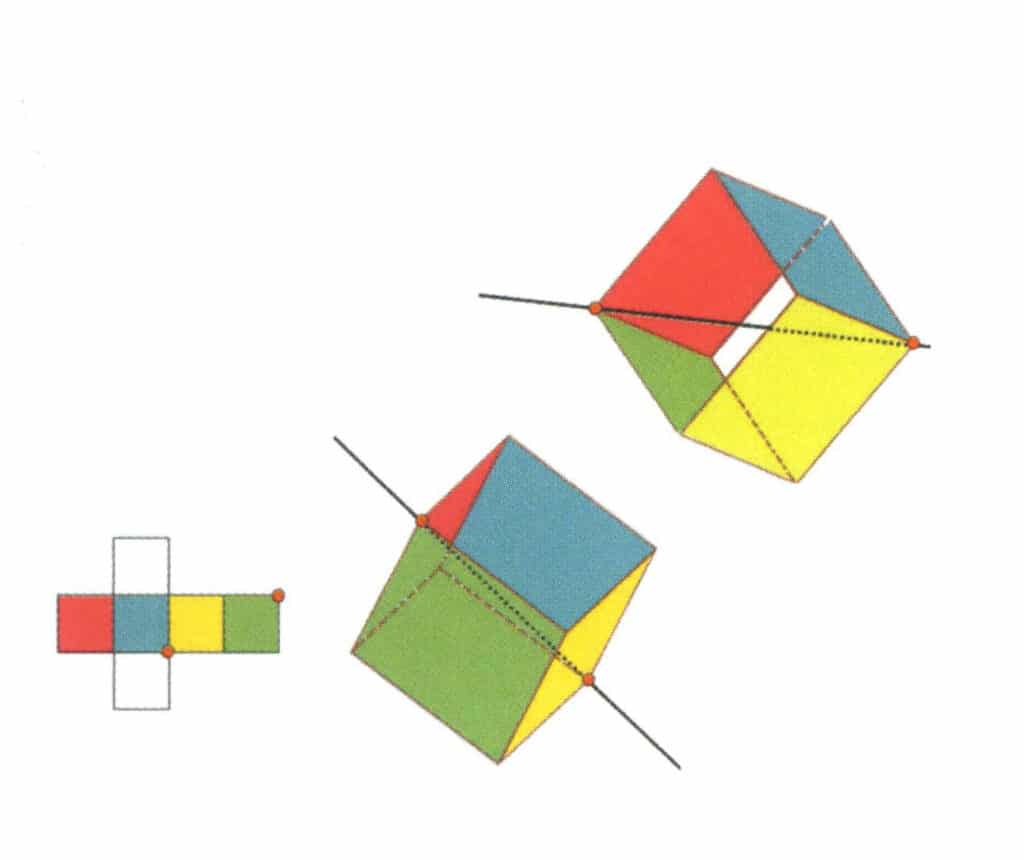
Figura 2-2-13 A treia axă terțiară a cubului
Selectați punctele de intersecție ale celor trei fețe, așa cum se arată în figură. Imaginați-vă o linie dreaptă care trece prin punctele de mijloc ale acestor două muchii, rotind cubul cu 360°. Nivelele de bază colorate diferit, dar de formă identică, se vor repeta în aceeași poziție de trei ori (fețe roșii, incolore și verzi; fețe albastre, incolore și galbene, două seturi de fețe repetate). Această linie imaginară este înregistrată ca a treia axă terțiară.
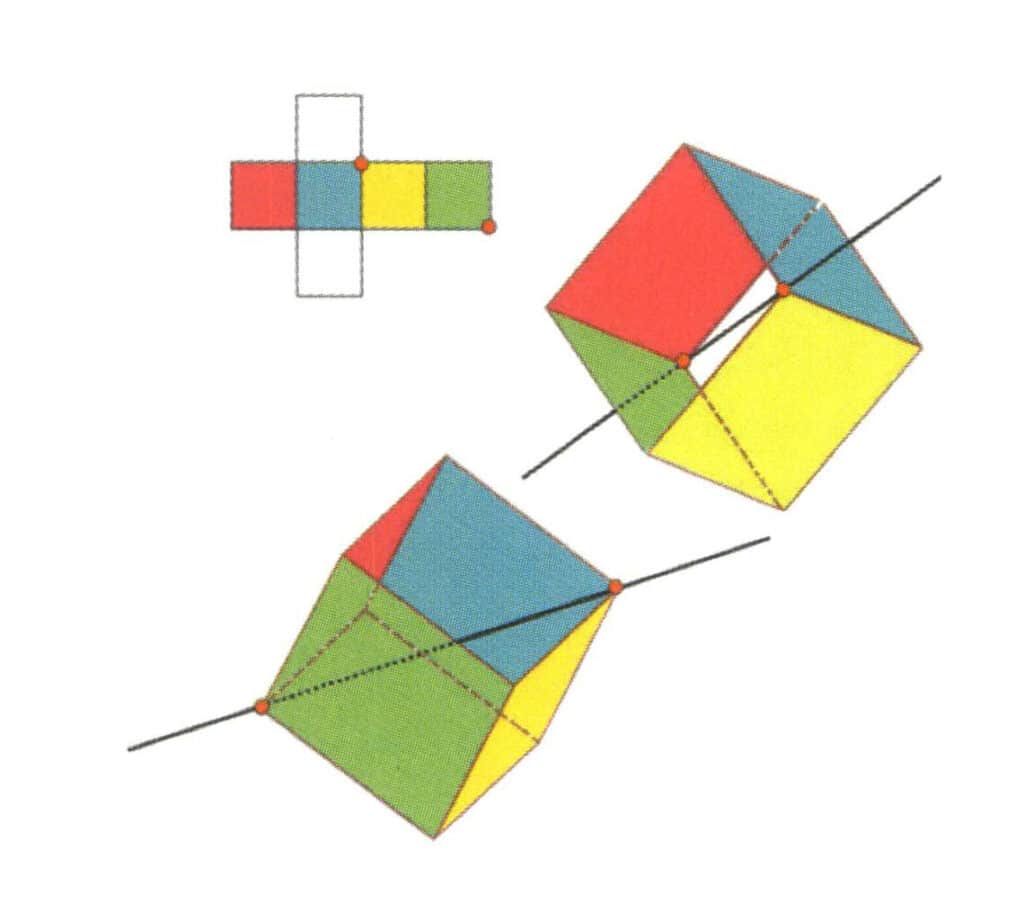
Figura 2-2-14 A patra axă cubică a cubului.
Selectați intersecția celor trei fețe așa cum se arată în figură, presupunând că există o linie dreaptă prin punctul median al celor două muchii rotește cubul cu 360°, culori diferite dar aceeași formă nivelul de bază va fi același. Se repetă poziția de trei ori (fața roșie, incoloră, verde, fețele albastră, incoloră și galbenă, două seturi de fețe repetate). Această linie imaginară este înregistrată ca a patra axă cubică.
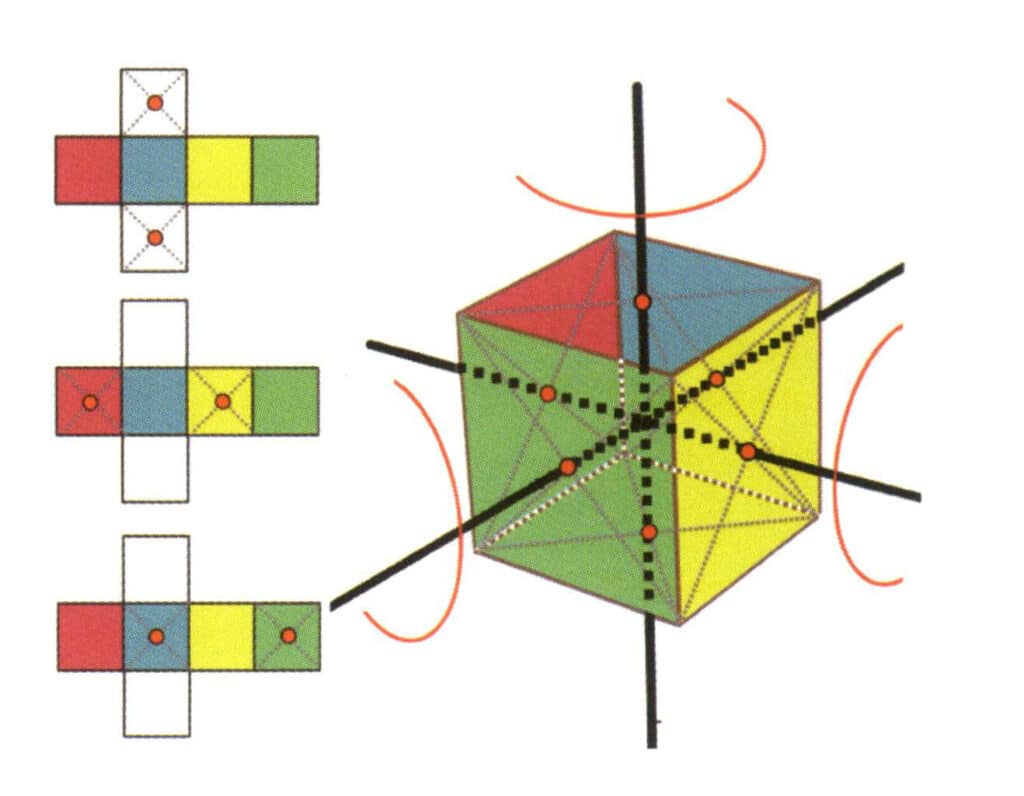
Figura 2-2-15 A patra axă a cubului
Partea stângă a figurii prezintă o vedere desfășurată a cubului, punctele roșii indicând punctele de intersecție ale liniei imaginare și ale marginilor. Partea dreaptă a figurii arată un cub închis, punctele roșii indicând punctele de intersecție ale liniei imaginare și ale planului. A patra axă poate apărea în punctul median al fețelor pătrate paralele, la intersecția a trei sau mai multe fețe paralele care seamănă cu un pătrat.
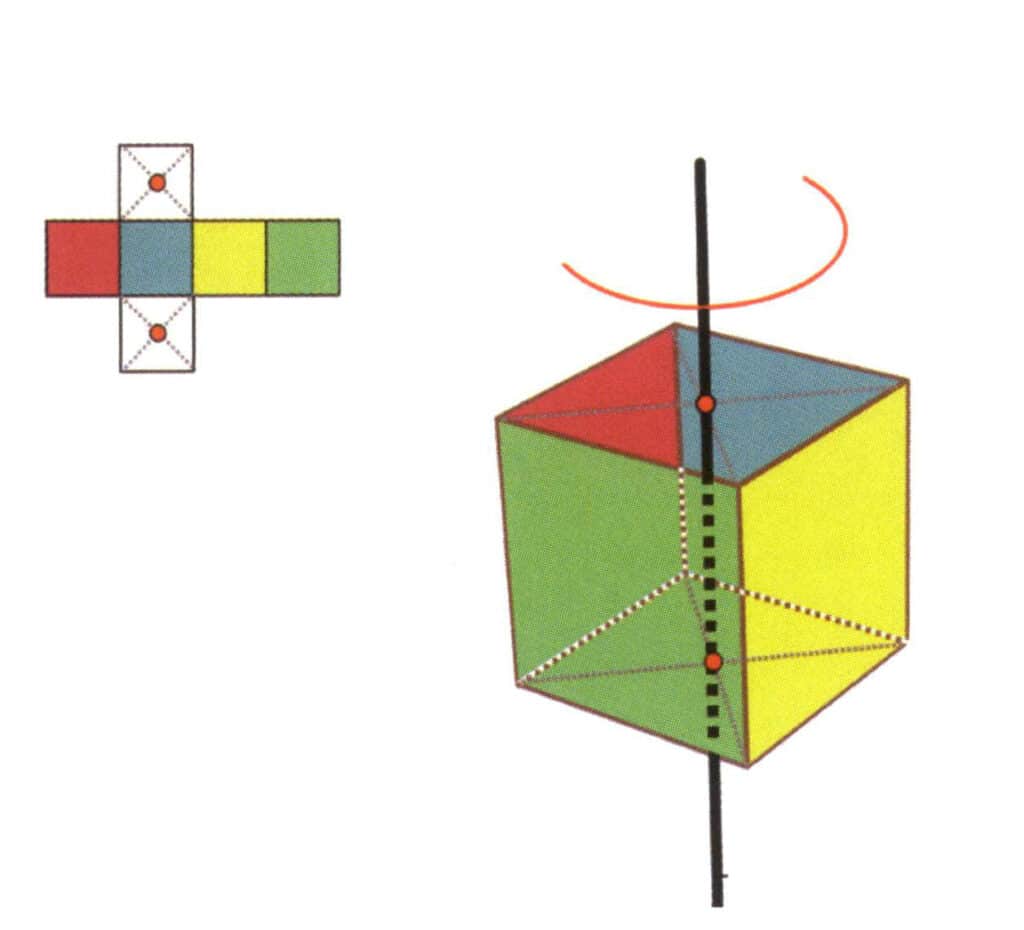
Figura 2-2-16 Prima axă quartică a cubului
Alegeți punctele medii ale planurilor prezentate în figură, presupuneți că există o linie dreaptă care trece prin punctele medii ale celor două planuri și rotiți cubul cu 360°. Fețele nivelului de bază de culori diferite, dar de aceeași formă, se vor repeta în aceeași poziție de patru ori (fețele roșie, albastră, verde și galbenă), iar această linie dreaptă ipotetică este înregistrată ca o axială cvadruplă.
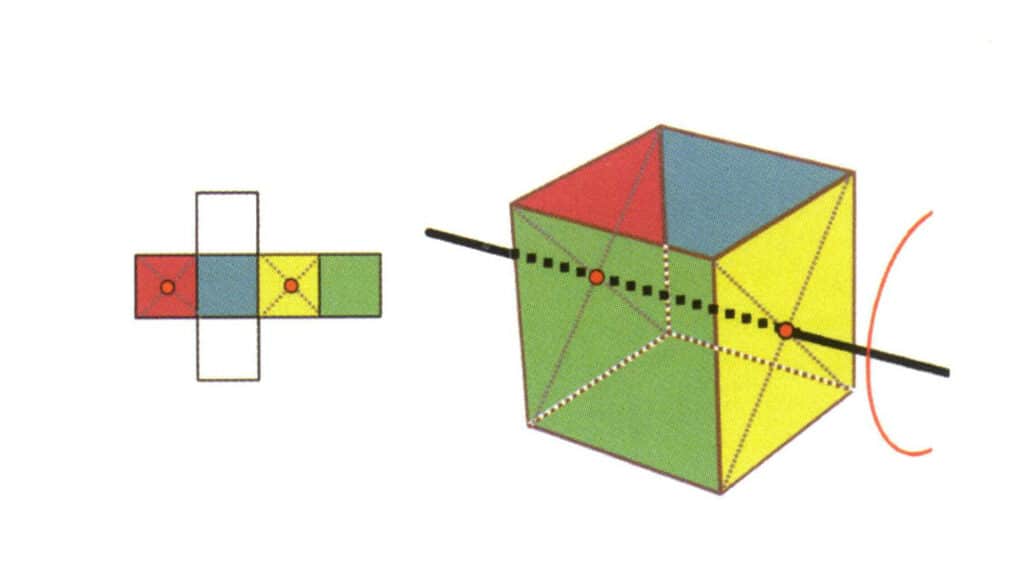
Figura 2-2-17 A doua axă quartică a cubului
Selectați punctul median al planului, după cum se arată în figură, imaginați-vă o linie dreaptă care să treacă prin cub și rotiți cubul cu 360 °; suprafața nivelului de bază de culori diferite, dar de aceeași formă, se va repeta de patru ori în aceeași poziție (incoloră, fața albastră în partea de sus, incoloră, fața verde în partea de jos), iar această linie imaginară va fi înregistrată ca a doua axă cvadrică.
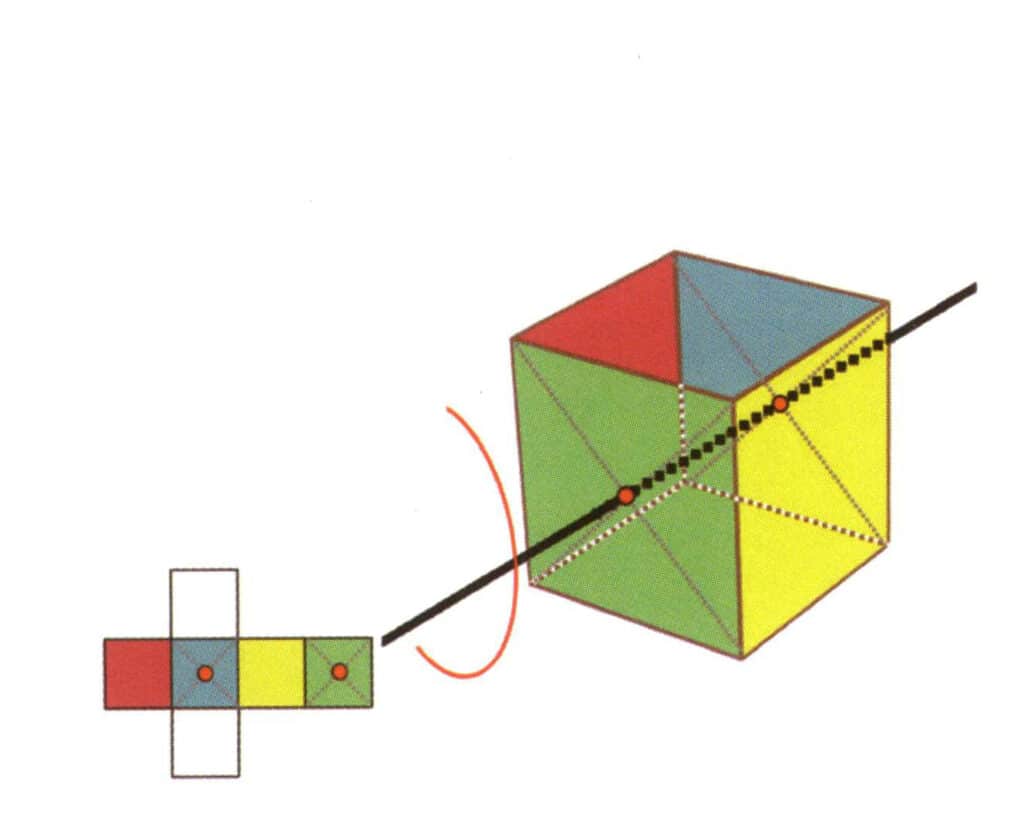
Figura 2-2-18 A treia axă quartică a cubului
Selectați punctul median al planului, așa cum se arată în figură, imaginați-vă o linie dreaptă care să treacă prin cub și rotiți cubul cu 360°. Nivelul de bază de culori diferite, dar de aceeași formă, va fi repetat de patru ori în aceeași poziție (incolor, fața roșie în partea de sus, incolor, fața galbenă în partea de jos), iar această linie imaginară va fi înregistrată ca a treia, a patra axă
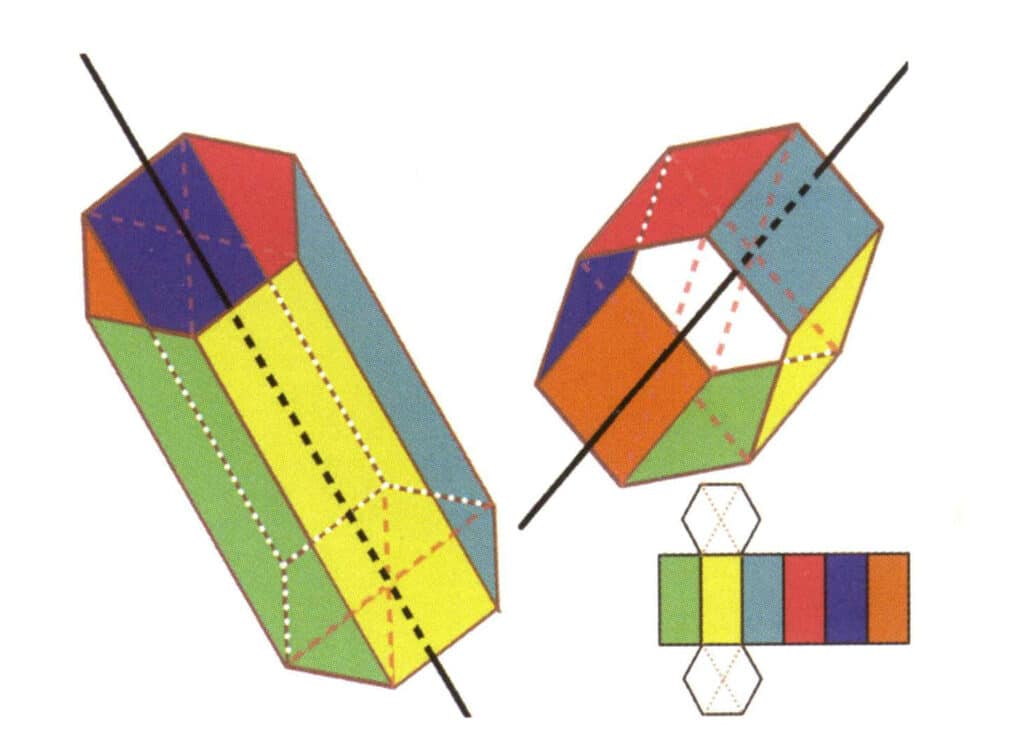
Figura 2-2-19 Șase axe ale unei prisme hexagonale
Liniile negre din stânga și din dreapta sus reprezintă cele șase axe ale prismei hexagonale. Partea din dreapta jos este o expansiune a prismei hexagonale Axa sextică poate apărea în punctul median al fețelor unui hexagon paralel sau la intersecția celor șase fețe ale unui hexagon.
(2) Considerații pentru găsirea axei de simetrie.
① Există cinci tipuri de poziții pentru axa de simetrie.
Punctul median a două muchii paralele, cum ar fi poziția axei secundare a unui cub.
Punctul median a două planuri paralele, cum ar fi poziția axei quartice a unui cub.
Între două vârfuri (punctele de intersecție ale mai multor fețe), cum ar fi poziția axei terțiare a unui cub.
Punctul median dintre un vârf și un plan paralel, cum ar fi poziția axei terțiare a unui tetraedru.
Punctul median al liniei de margine și punctul median al planului paralel, cum ar fi poziția axei secundare a unei prisme triunghiulare.
② Selectarea axei de simetrie în aceeași direcție urmează principiul numărului cel mai mic. De exemplu, în conformitate cu principiul celui mai mic număr, dacă într-o direcție se găsesc șase axe de simetrie și trei axe de simetrie, aceasta va fi înregistrată în cele din urmă ca L³. Axele de simetrie în direcții diferite trebuie înregistrate în funcție de numărul găsit.
Trebuie remarcat faptul că, cu excepția axei de simetrie de șase ori și a axei de simetrie de patru ori, care nu pot apărea simultan și poate apărea o singură axă de șase ori, alte axe de simetrie pot coexista în diferite forme sau în mai multe cazuri.
③ Nivelul de bază trebuie să fie selectat ca cel mai mic plan unitar; două sau mai multe planuri care se intersectează nu pot fi selectate ca nivel de bază. În caz contrar, aceasta va afecta precizia judecării axei de simetrie.
④ La înregistrarea numărului de axe de simetrie, este esențial să se determine de câte ori aceeași formă și dimensiune a planului se repetă în aceeași poziție.
⑤ Dacă există o axă secundară de simetrie verticală Lⁿ(n = 3, 4 sau 6), trebuie să existe n axe secundare verticale față de Lⁿ.
2.2 Avion de simetrie
(1) Conceptul și metoda de înregistrare a planului de simetrie
Un plan de simetrie este un plan imaginar care, atunci când cristalul este tăiat de-a lungul acestui plan, permite ca fiecare jumătate a cristalului să fie o imagine în oglindă a celeilalte jumătăți (figura 2-2-20). În aceeași structură cristalină, un astfel de plan poate apărea de maximum 9 ori (figura 2-2-21), ceea ce înseamnă că poate fi secționat în 9 moduri diferite, iar cele două jumătăți pot coincide complet. Desigur, nu toate structurile cristaline au planuri de simetrie.
Litera majusculă P reprezintă planul de simetrie. Unele cristale au mai multe planuri de simetrie care nu coincid, iar numărul acestor planuri de simetrie se scrie convențional la stânga lui P; de exemplu, patru planuri de simetrie sunt reprezentate prin 4P, iar un plan de simetrie este reprezentat prin P.
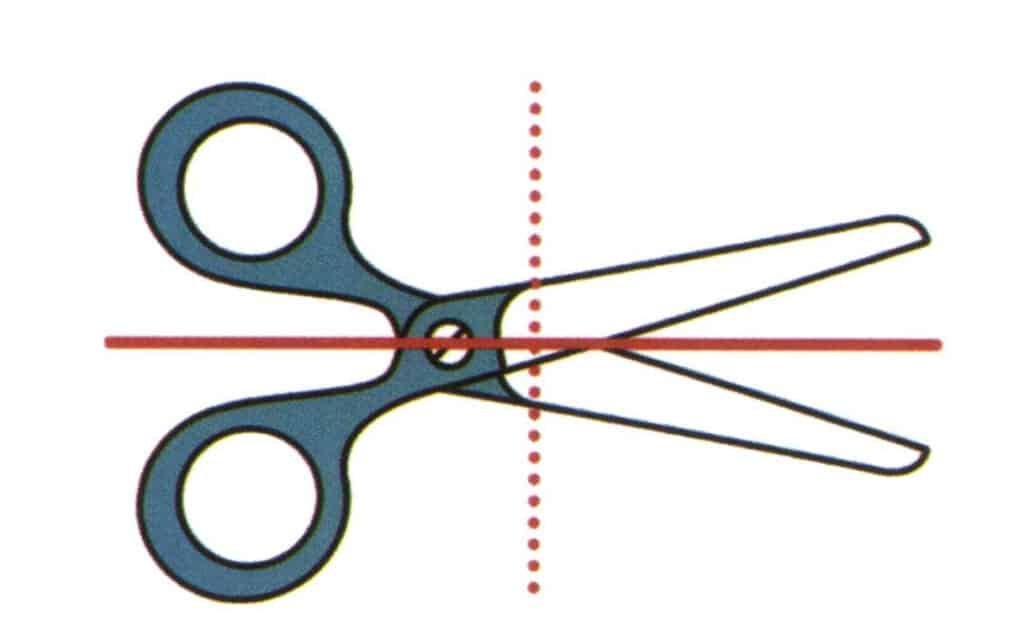
Figura 2-2-20 Imaginați-vă un plan vertical de hârtie și un plan care se întinde de-a lungul direcției liniei roșii continue, care împarte foarfeca în părțile superioară și inferioară, iar părțile superioară și inferioară sunt simetrice în oglindă. Acest plan imaginat se numește planul de simetrie. Imaginați-vă un alt plan perpendicular pe suprafața hârtiei și care se întinde de-a lungul direcției liniei roșii punctate, care împarte foarfecele în părțile stângă și dreaptă, dar formele foarfecelor de pe părțile stângă și dreaptă nu sunt simetrice.
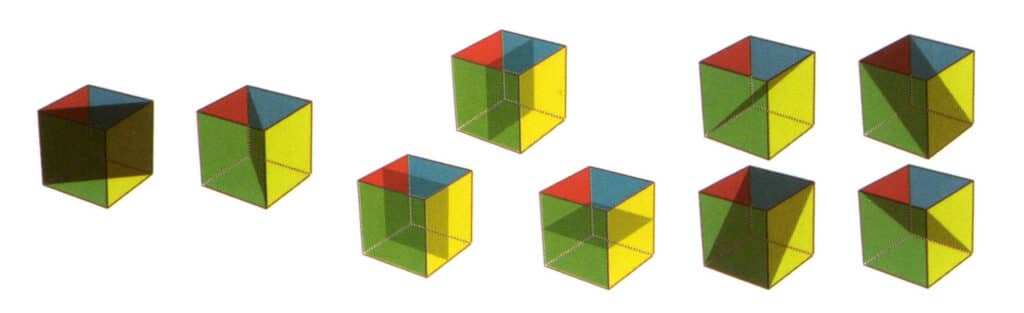
Figura 2-2-21 Nouă planuri de simetrie ale unui cub
(2) Sfaturi pentru găsirea Planuri de simetrie.
① Planul de simetrie este adesea paralel și coincide cu axa de simetrie.
② Planul de simetrie este un plan imaginar care împarte geometria cristalină, care este diferit de planul dublu paralel în geometrie.
③ Dacă un plan de simetrie conține axa de simetrie Lⁿ, atunci trebuie să existe n planuri de simetrie care conțin Lⁿ.
(3) Punct Grup.
Grupul de puncte este suma tuturor elementelor de simetrie dintr-un cristal. Ordinea de scriere a grupului de puncte este axă de simetrie + plan de simetrie, de exemplu, 3L²3P (figura 2-2-22). Dacă un cristal are mai multe axe de simetrie, se obișnuiește să le înregistreze de la stânga la dreapta, de la axa de ordin superior la axa de ordin inferior, și ordinea planurilor de simetrie, de exemplu, L⁴4L²5P (figura 2-2-23). Există 32 de tipuri de simetrie în cristale.
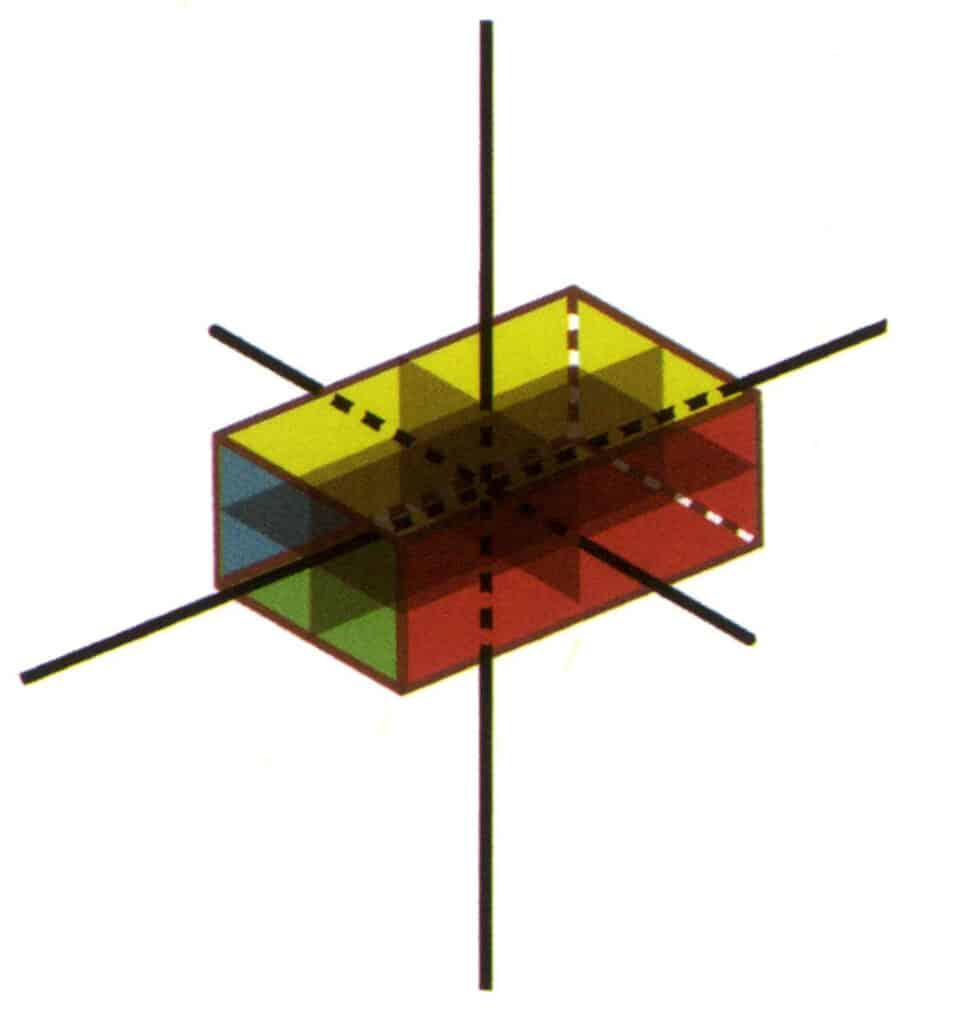
Figura 2-2-22 Grup de puncte 3L²3P (cuboid dreptunghiular cu secțiune dreptunghiulară)
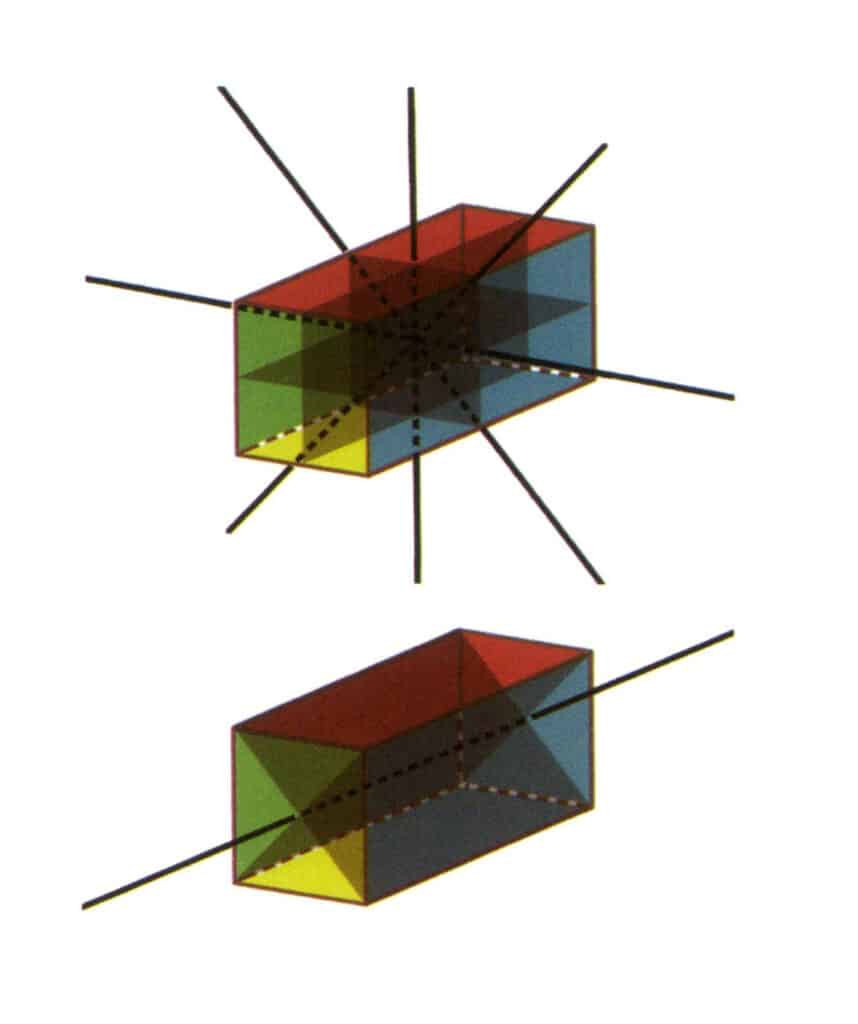
Figura 2-2-23 Grupul de puncte L⁴4L²5P (o prismă dreptunghiulară cu secțiune pătrată), cu patru a doua axe și trei fețe simetrice în partea superioară și o a patra axă și două fețe simetrice în partea inferioară.
3. Clasificarea cristalelor
Simetria este o parte a clasificării cristalelor. Un alt concept - axa cristalină - trebuie introdus pentru a descrie structura cristalină a pietrelor prețioase cristaline naturale și artificiale într-o schemă de clasificare a cristalelor. Axa cristalină este o linie imaginară care trece prin structura cristalină, indicând direcția în care se repetă nodurile rețelei și distanța relativă la care se repetă nodurile de-a lungul acestei direcții. Axa cristalină coincide cu norma axei de simetrie sau cu planul de simetrie. Dacă nu există axă de simetrie sau plan de simetrie, axa cristalului poate fi selectată paralel cu direcția muchiei cristalului.
Pe baza elementelor de simetrie și a axelor cristaline, sistemul academic clasifică cristalele în trei familii cristaline și șapte sisteme cristaline (tabelul 1).
Tabelul 1: Puncte cheie pentru determinarea familiilor și sistemelor de cristal
| Familia Crystal | Cristal | Puncte-cheie pentru determinare | Varietăți comune de pietre prețioase |
|---|---|---|---|
| Sistem de cristal de nivel scăzut | Sistem triclinic | Fără a doua axă sau plan de simetrie | Amazonită, Rodonită, Turcoaz |
| Sistem cristalin monoclinic | Nu există axe de ordin superior, nu mai mult de o axă secundară și un plan de simetrie | Jadeit, diopside, spodumene, epidot | |
| Sistem cristalin ortorhombic | Nu există axe de ordin superior, mai mult de o axă secundară sau plan de simetrie | Olivină, topaz, saualpite (inclusiv tanzanit), cordierit, crioberil, enstatită | |
| Familie de cristale intermediare | Sistem cristalin tetragonal | 1 axă cvadruplă (poate fi reprezentată prin L4) | Diamant |
| Sistem cristalin trigonal | 1 axe trigonale (pot fi reprezentate prin L3) | Corindon, rubin, safir, turmalină , cristale din familia cuarțului (cum ar fi cristal, ametist, citrin etc.), rodocrosit | |
| Sistem cristalin hexagonal | 1 axă hexagonală (poate fi reprezentată prin L6) | Acvamarin, smarald și alte pietre prețioase din familia beriliților, apatită | |
| Familie avansată de cristale | Sistem de cristal izometric | 4 axe trigonale (pot fi reprezentate prin 4L3) | Diamant, granat, spinel, fluorospar |
4. Caracteristicile cristalelor comune ale pietrelor prețioase
Pietrele prețioase comune includ diamantul, spinelul, fluorura, granatul, beriliul, zirconul, corindonul, turmalina, cristalul, crisoberilul, topazul etc. Fiecare tip de piatră prețioasă are propriile sale caracteristici cristaline fixe.
Pietrele prețioase din familia cristalelor de nivel înalt au în cea mai mare parte un obicei cristalin granular, iar varietățile comune apar adesea în forme cristaline fixe (tabelul 2).
Obiceiul cristalin al familiilor de cristale de nivel intermediar și scăzut este columnar (tabelul 3).
Tabelul 2: Caracteristici comune ale cristalelor din familiile de cristale de nivel înalt
| Nume ton Gems | Clasificarea cristalelor | Caracteristici importante ale cristalului | |||
|---|---|---|---|---|---|
| Nume ton Gems | Clasificarea cristalelor | Obiceiul de cristal | Forme comune de cristal | Forme comune de gemeni | Modele comune de fețe de cristal |
| Diamant | Sistem de cristal izometric | Structură cristalină granulară (figura 2-2-24), frecvent întâlnită în granule octaedrice | Octaedrul este o formă cristalină obișnuită, dar pot apărea și forme cristaline mai complexe, inclusiv dodecaedrele rombice, adesea cu fețe cristaline rotunjite, care pot prezenta simetrie triplă | Gemene plate triunghiulare, uneori fără unghiuri concave vizibile (figura 2-2-25) | Suprafața prezintă gropi de gravură triunghiulare inversate (figurile 2-2-26, 2-2-27) și alte modele de fețe cristaline (figurile 2-2-28, 2-2-29) |
| Spinel | Structură cristalină granulară (figura 2-2-30), frecvent întâlnită în granule octaedrice | Adesea produse în formă octaedrică, fețele cristalului pot fi foarte plate, părând ca și cum ar fi lustruite (Figura 2-2-31) | Cristalele gemene sunt foarte plate, semănând cu o formă triunghiulară cu colțurile tăiate (Figura 2¬2-32) | Gropi de gravură vizibile la suprafață, unele semănând cu diamante în formă de triunghi inversat (figura 2-2-33) | |
| Fluorit | Structură cristalină granulară (figura 2-2-34) | Forme cristaline octaedrice și cubice (figura 2-2-35) | Îngemănare interpenetrantă | Urme de creștere în trepte pătrate, majoritatea cu goluri de clivaj, benzi de culoare paralele cu direcțiile celor șase fețe ale cubului | |
| Granat | Obicei cristalin granular, frecvent întâlnit în granule rombice dodecaedrice (figura 2-2-36) | Dodecaedru rombic sau trapezoedru pătrat | Rare | Benzile inelare concentrice vizibile au aceeași formă ca și fețele cristalului (figura 2-2-37) | |
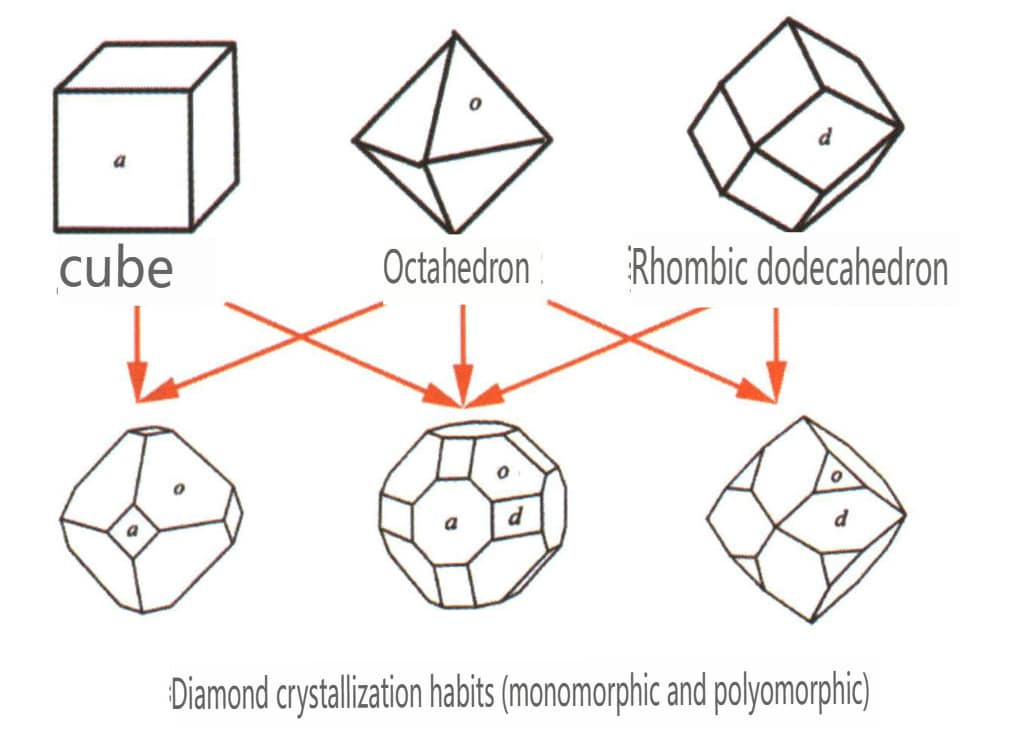
Figura 2-2-24 Obiceiuri ale cristalului de diamant
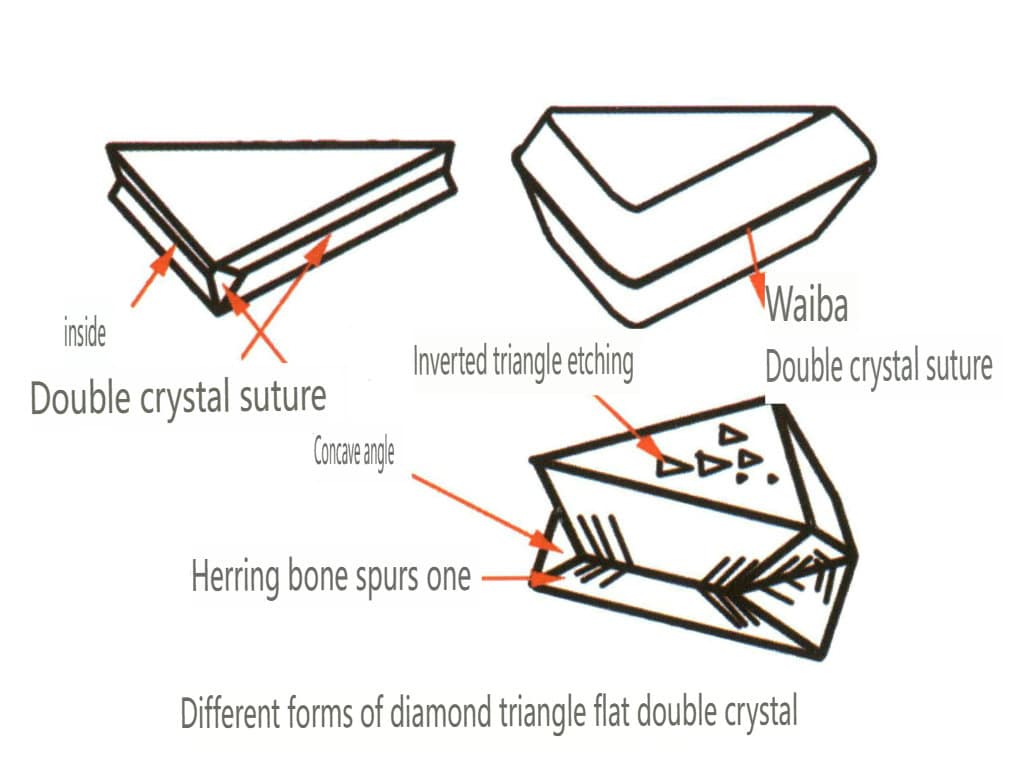
Figura 2-2-25 Diamant Twin Habit
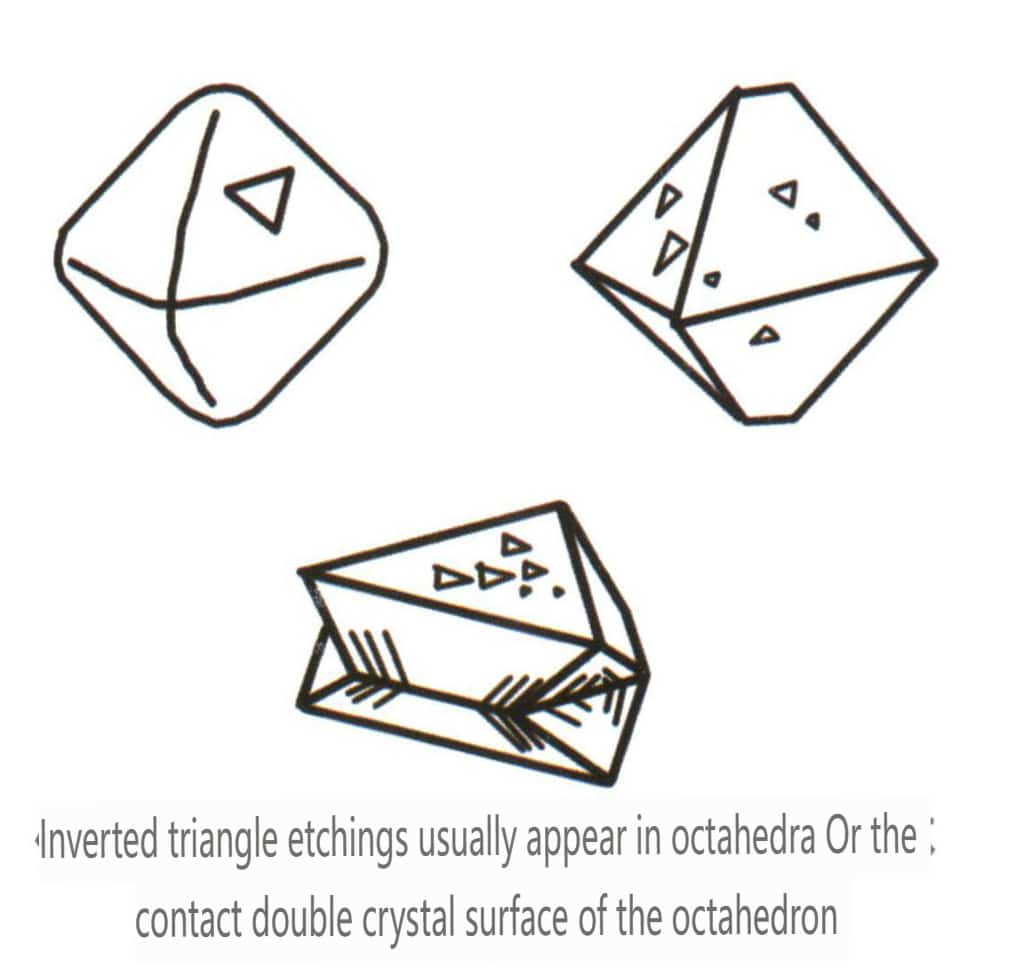
Figura 2-2-26 Figura de gravură în triunghi inversat a fețelor cristalului octaedric de diamant

Figura 2-2-27 Figură de gravură triunghiulară inversată pe suprafața unui cristal octaedral de diamant
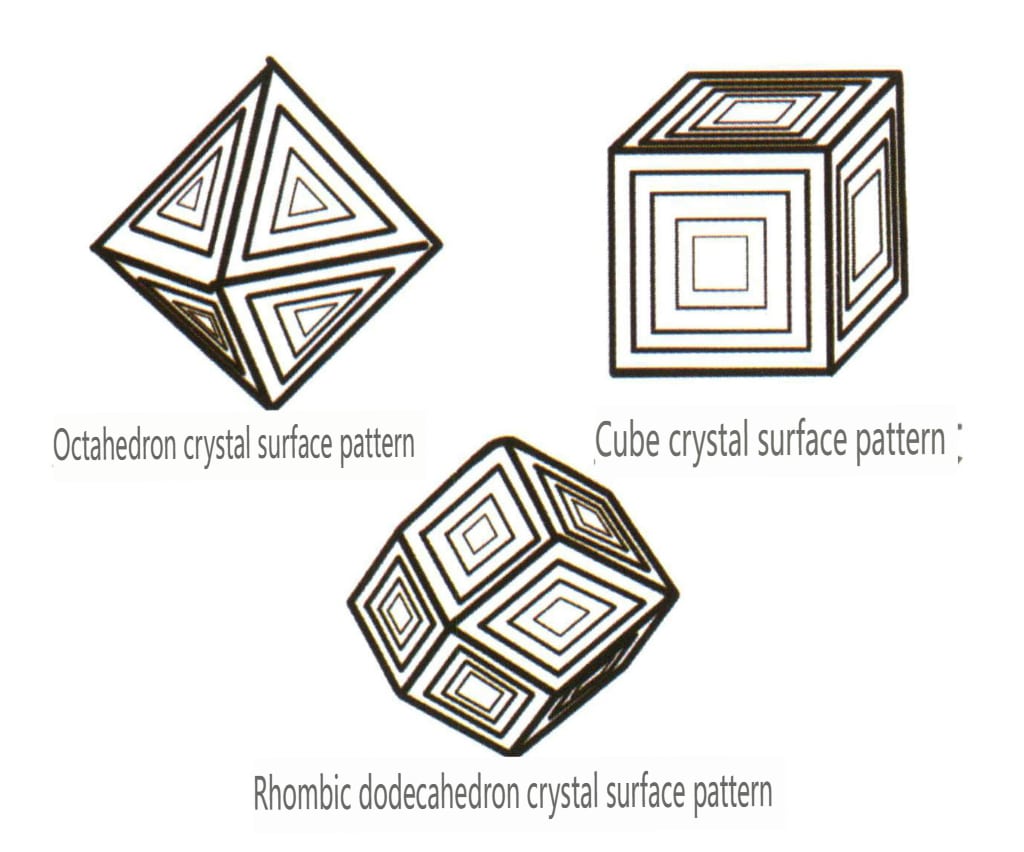
Figura 2-2-28 Figura de gravură în triunghi inversat a fețelor cristalului octaedric de diamant

Figura 2-2-29 Figură de gravură triunghiulară inversată pe suprafața unui cristal octaedral de diamant
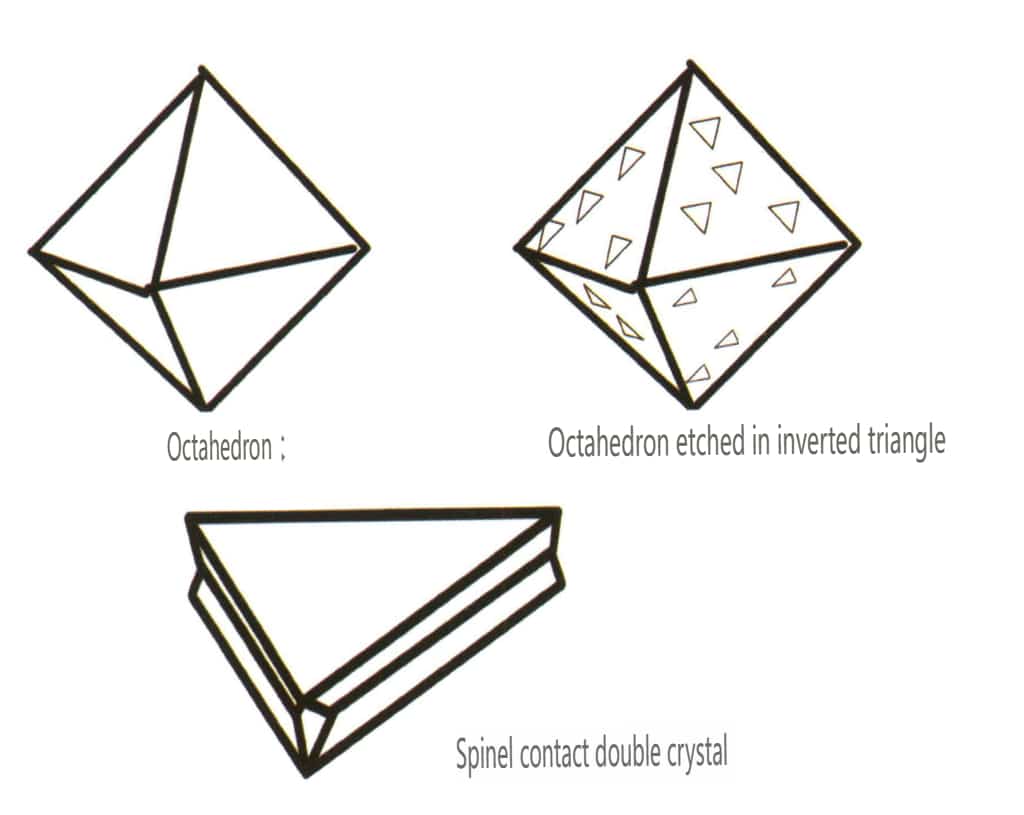
Figura 2-2-30 Structura cristalină a spinelului

Figura 2-2-31 Forme comune de cristale de spinel

Figura 2-2-32 Îngemănarea de contact a spinelului
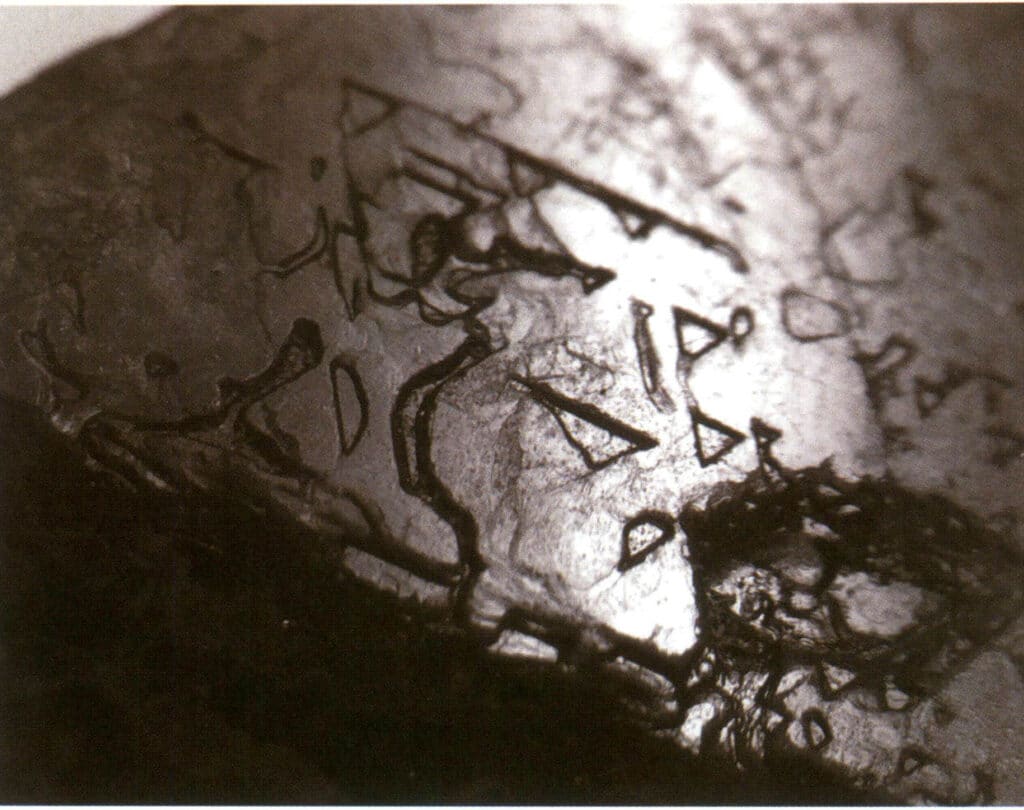
Figura 2-2-33 Figura de gravură triunghiulară inversată pe suprafața spinelului
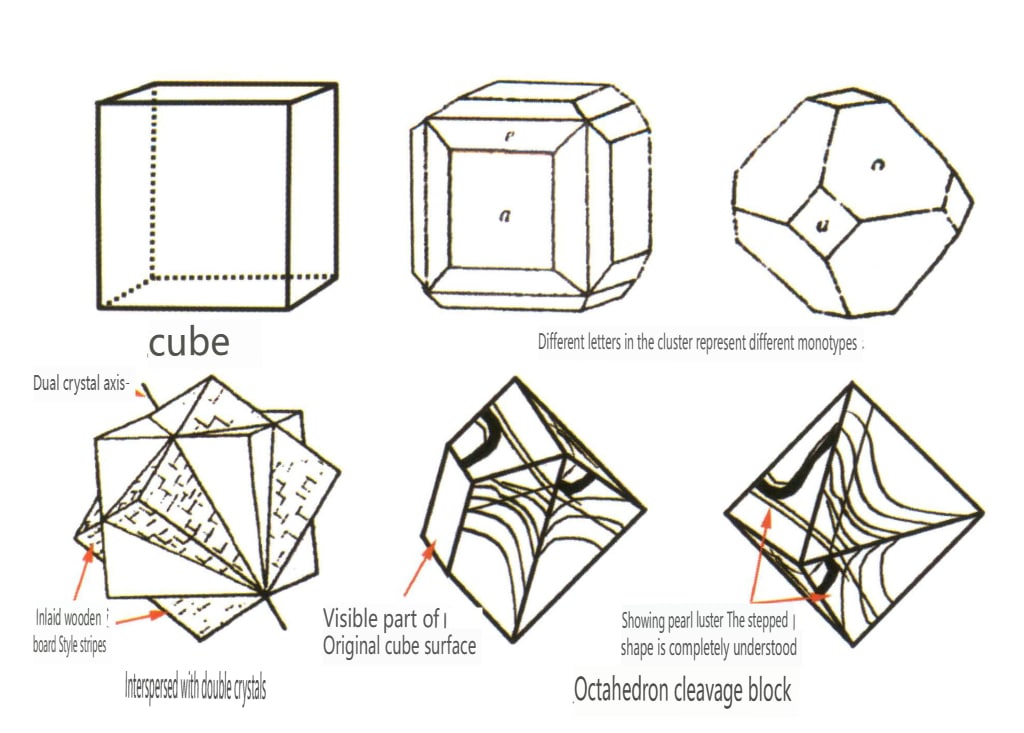
Figura 2-2-34 Obiceiurile cristalelor de fluorit

Figura 2-2-35 Fluorit cristal
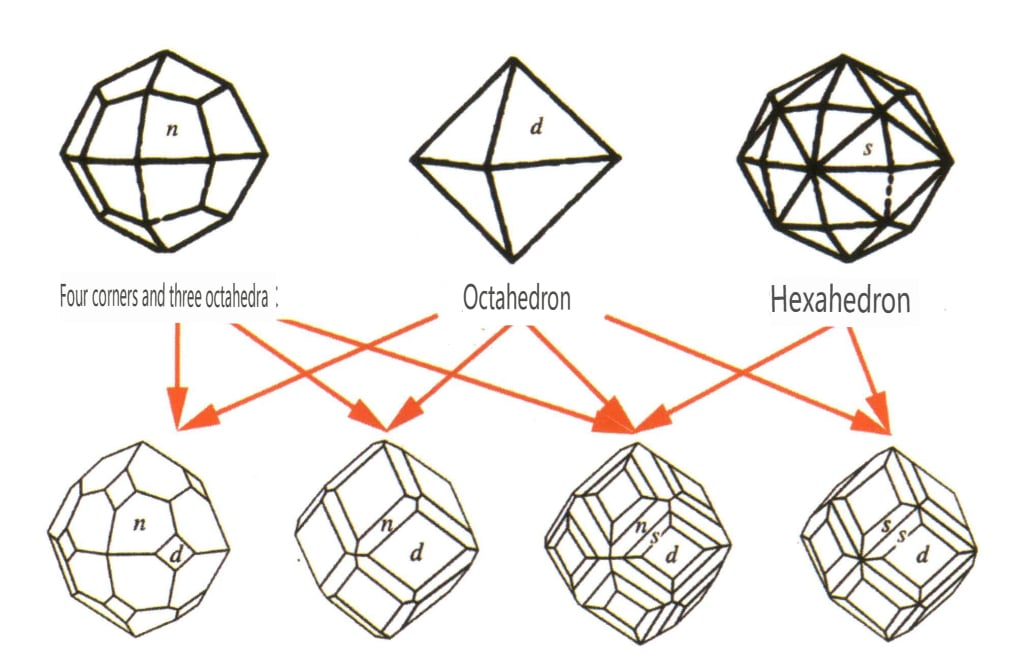
Figura 2-2-36 Obiceiul cristalului de granat

Figura 2-2-37 Benzile inelare concentrice de pe suprafața cristalelor de granat care au aceeași formă ca și fețele cristalului
Tabelul 3: Caracteristici comune ale cristalelor Gem din familiile de cristale intermediare și joase
| Nume ton Gems | Clasificarea cristalelor | Caracteristici importante ale cristalului | |||
|---|---|---|---|---|---|
| Nume ton Gems | Clasificarea cristalelor | Obiceiul de cristal | Forme comune de cristal | Forme comune de gemeni | Modele comune de fețe de cristal |
| Beryl | Sistem cristalin hexagonal | Structură cristalină columnară (figura 2-2-38) | Forma cristalină hexagonală columnară (figurile 2-2-39, 2-2-40) | Rare | Dungi longitudinale vizibile |
| Piatră de plumb | Sistem cristalin tetragonal | Structură cristalină columnară (Figura 2-2-41) | O coloană pătrată cu secțiune pătrată, care apare împreună cu un con dublu pătrat (figura 2-2-42) | Cristale gemene vizibile în formă de genunchi | Nu există modele speciale |
| Corindon | Sistem cristalin trigonal | Structură cristalină tip placă, structură cristalină columnară (figura 2-2-43) | Rubinele prezintă adesea o formă de prismă hexagonală (figura 2-2-44), în timp ce safirele prezintă adesea o formă de cristal hexagonal bipiramidal în formă de butoi (figura 2-2-45) | Bi-cristale des întâlnite. | Striații vizibile. |
| Turmalină . | Structură cristalină columnară (Figura 2-2-46) | Fețele cristalului de la ambele capete sunt diferite, iar secțiunea transversală este un triunghi sferic (figura 2-2-47) | Rare | dungi longitudinale vizibile (figura 2-2-48) | |
| Cuarț (cristal de cuarț) | Structură cristalină columnară (Figura 2-2-49) | Secțiunea transversală este hexagonală, bipiramidele hexagonale sunt rare (figurile 2-2-50, 2-2-51), monopiramidele hexagonale sunt comune | Contact obișnuit cu bicristalele (cunoscute și ca bicristale japoneze) | Dungi orizontale comune pe suprafețele cristalelor | |
| Chrysoberyl | Sistem cristalin trigonal | Caracteristici de cristalizare columnară (figura 2-¬2-52) | Monocristalinul este rar | Tri-cristalina este comună (figura 2-2-53), unghiurile hexagonale și concave pot fi utilizate ca criterii de identificare | Dungile tricristaline pot fi utilizate ca criterii de identificare |
| Topaz | Structură cristalină columnară (Figura 2-2-54) | Secțiunea transversală este în formă de diamant, iar partea superioară are adesea aspectul unui plic (Figura2-2-55) | Bi-cristalele sunt rare | Dungi longitudinale vizibile | |
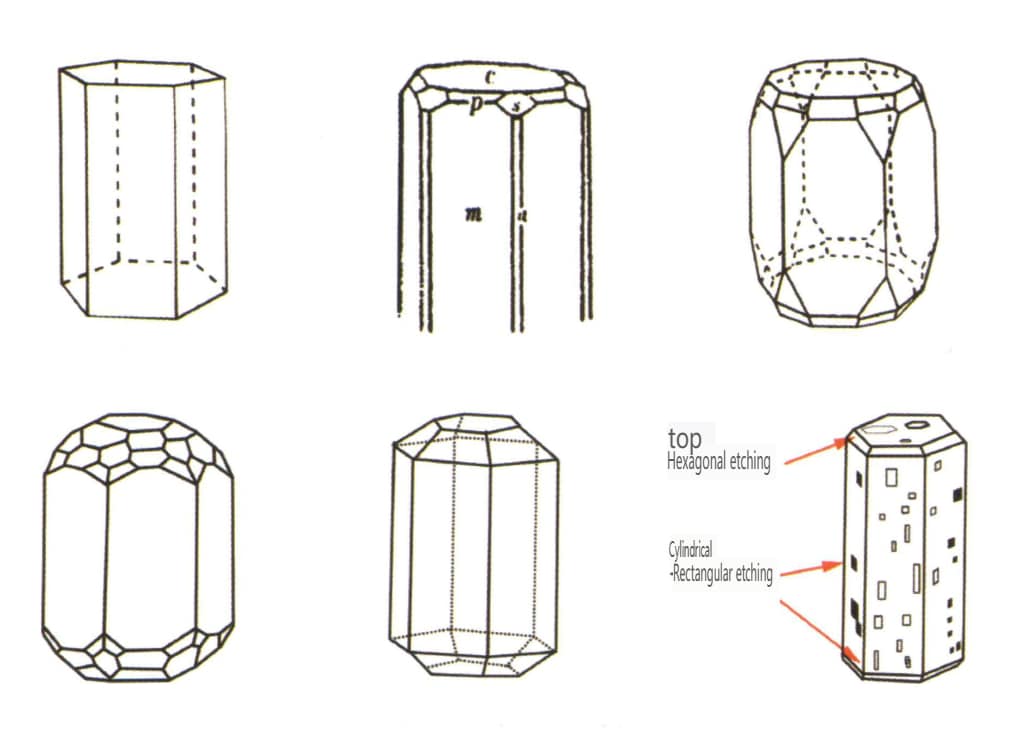
Figura 2-2-38 Obiceiul cristalin al beriliului

Figura 2-2-39 Forme comune de cristale de smarald

Figura 2-2-40 Forme comune de cristale de acvamarin
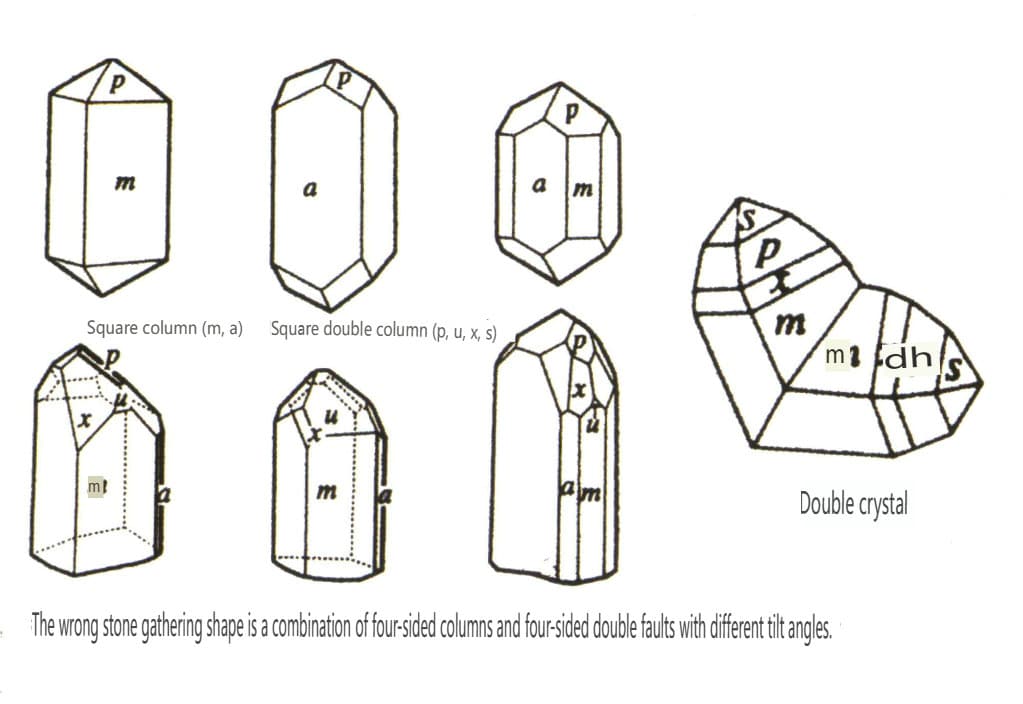
Figura 2-2-41 Obiceiurile cristaline ale zirconului

Figura 2-2-42 Zircon cristal
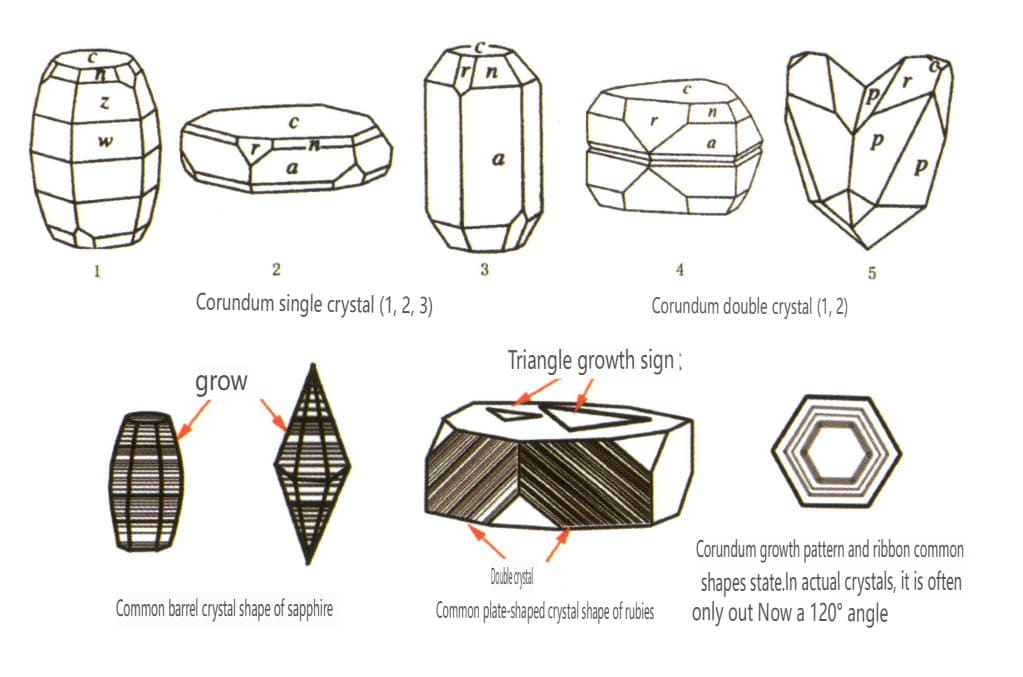
Figura 2-2-43 Obiceiul cristalului Corundum

Figura 2-2-44 Cristal rubin

Figura 2-2-45 Geamăn mecanic al ruby
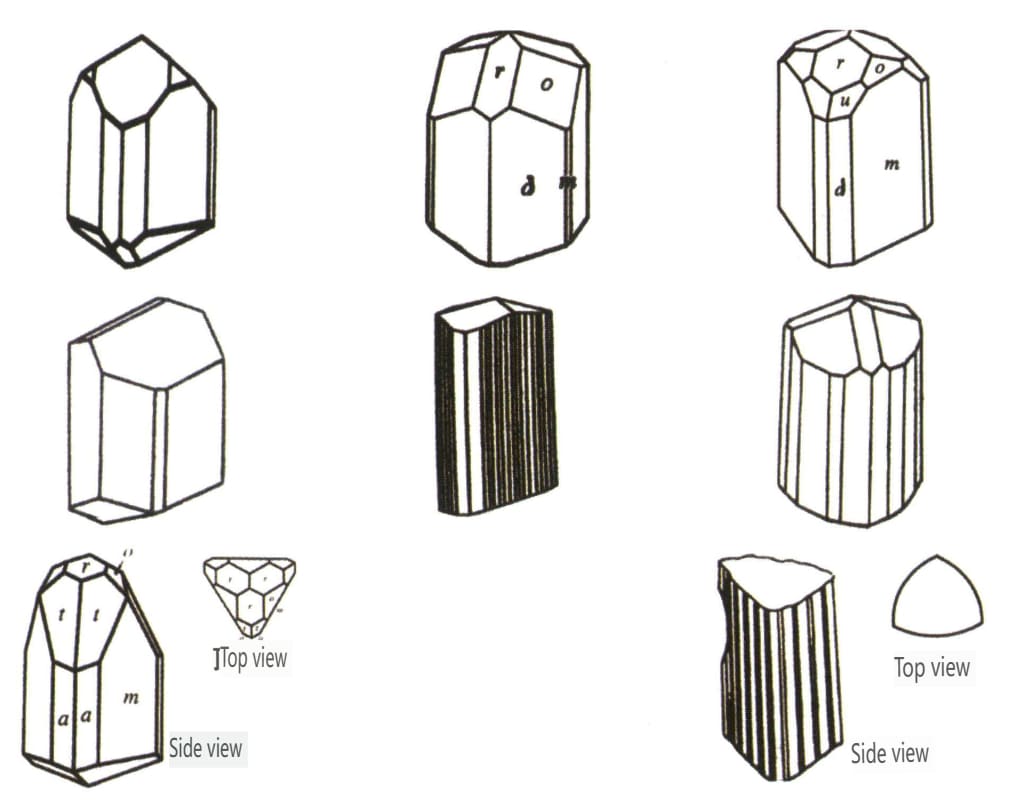
Figura 2-2-46 Obiceiurile cristalelor de turmalină

Figura 2-2-47 Cristal de turmalină

Figura 2-2-48 Dungi longitudinale de suprafață ale cristalului de turmalină
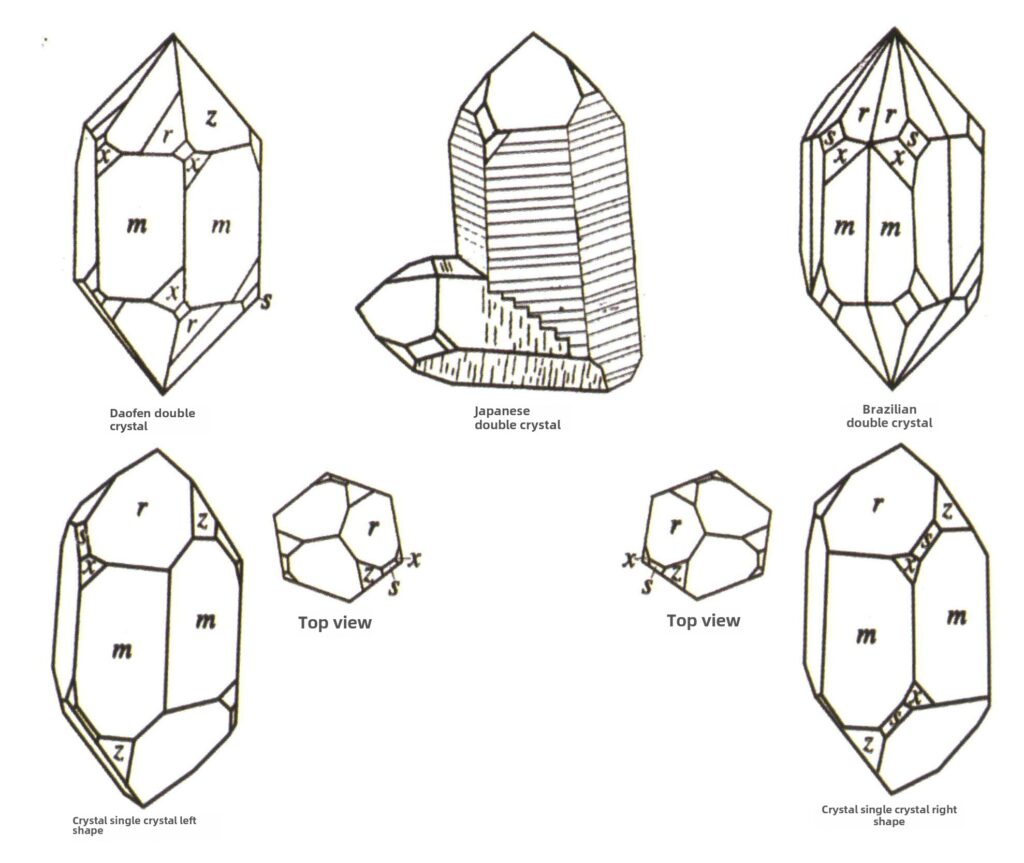
Figura 2-2-49 Obiceiuri de cristalizare a cristalelor

Figura 2-2-50 Corpul cristalului

Figura 2-2-51 Corpul cristalului
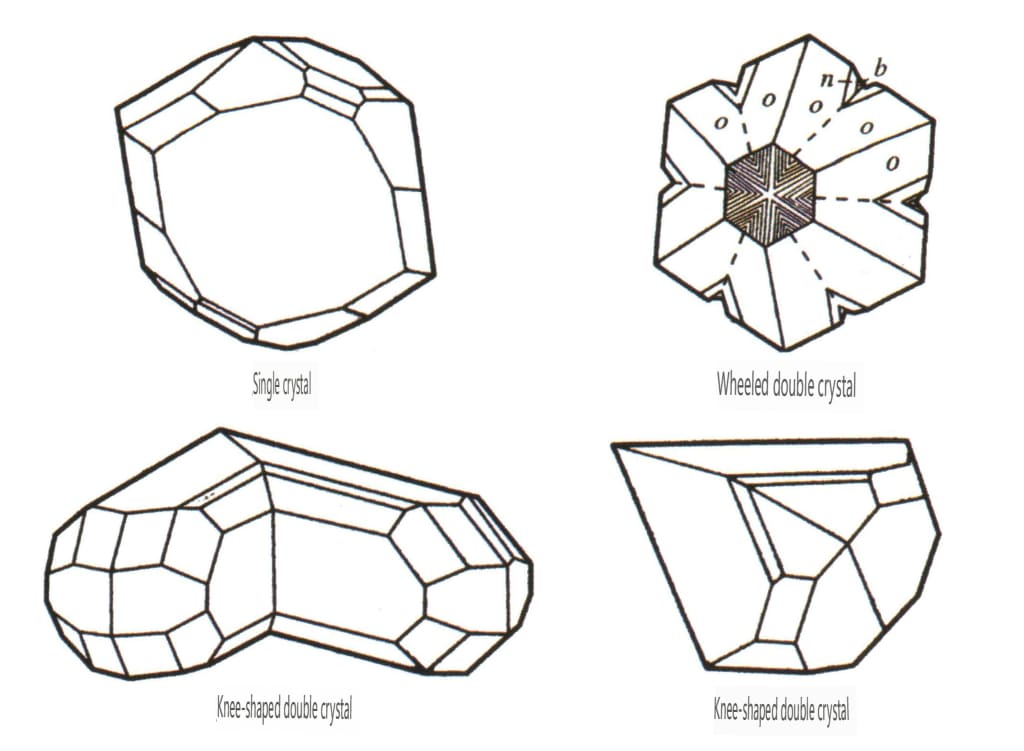
Figura 2-2-52 Habit cristalin al crisoberilului

Figura 2-2-53 Cristal de crisoberil
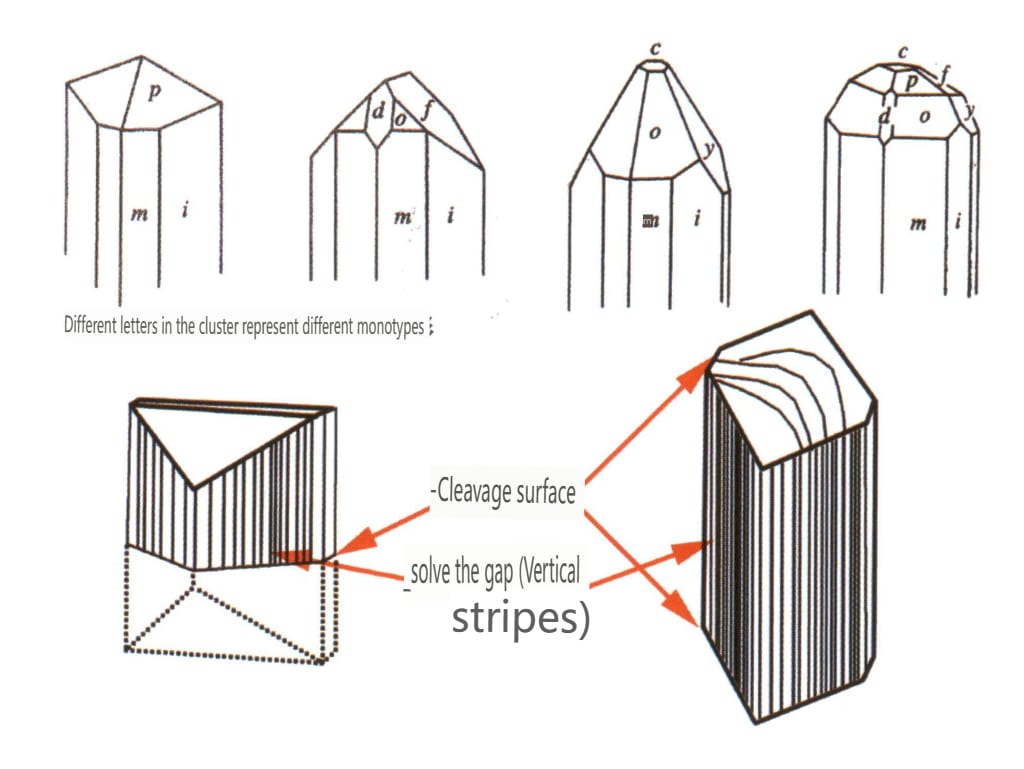
Figura 2-2-54 Obiceiuri cristaline ale topazului

Figura 2-2-55 Cristal topaz
Secțiunea IV De ce cresc diferit cristalele de pietre prețioase
Din punct de vedere microscopic, cristalul gemei este un solid compus din elemente de dimensiuni diferite, dispuse după reguli diferite. Din punct de vedere macroscopic, multe pietre prețioase au caracteristici de formă cristalină din cauza compozițiilor lor diferite. Cu toate acestea, există unele cazuri speciale, cum ar fi heteromorfele. Pentru a înțelege mai bine de ce cristalele prețioase arată diferit, vom prezenta aici cinci aspecte: heteromorfismul, izomorfismul, amestecul mecanic molecular, apa din mineralele prețioase și compoziția chimică a pietrelor prețioase.
1. Heteromorfă
Deși unele minerale au aceeași compoziție chimică, ele au structuri cristaline foarte diferite (dispunerea elementelor în spațiul tridimensional) și prezintă diferențe semnificative în ceea ce privește proprietățile fizice și chimice (tabelul 4). Acest fenomen se numește heteromorfism, de exemplu, diamantul și grafitul (figura 2-2-56).
Cuarțul comun are fenomenul de heteromorfism. Sillimanita, andalusita și kyanita sunt un grup de variante de heteromorfism.
Transformarea heteromorfismului are loc în condiții de stare solidă. În timpul procesului de transformare structurală, se poate dezvolta presiune în interiorul cristalului, ceea ce duce adesea la formarea de înfrățiri în interiorul cristalului.

Tabelul 4: Compararea proprietăților diamantului și grafitului
| Minerale | Diamant | Grafit |
|---|---|---|
| Componente | Carbon (C) | Carbon (C) |
| Condiții de formare | Temperatură ridicată și presiune ridicată | Temperatură ridicată |
| Sistem de cristal, obicei | Sistem cristalin izometric, octaedru, dodecaedru rombic | Sistem cristalin hexagonal, stratificat |
| Culoare | Incolor, galben, albastru, roz, verde, etc. | Negru |
| Lustru | Lustru adamantin | Lustru metalic |
| Transparență | Transparent până la opac | Opace |
| Indice de refracție | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Proprietăți mecanice | Clivaj octaedric moderat, duritate 10, densitate 3,52 | Un set de cleavage perfect, duritate 1, densitate 2.10 |
| Alte proprietăți | Conductivitate termică excelentă; cu excepția diamantelor naturale albastre care sunt semiconductoare, diamantele de alte culori sunt izolatoare. | Conductivitate termică moderată, conductivitate electrică bună |
2. Isomorfism
Isomorfismul se referă la fenomenul în care unele particule din structura rețelei sunt înlocuite cu alte particule cu proprietăți similare, ceea ce duce la ușoare modificări ale parametrilor rețelei și ale proprietăților fizice și chimice. În schimb, structura cristalină rămâne fundamental neschimbată. Aceasta poate fi înțeleasă ca fiind înlocuirea elementelor din cristalul pietrei prețioase cu alte elemente. În schimb, modelul repetitiv al elementelor cristalului de piatră prețioasă rămâne același, cu mici abateri în ceea ce privește distanțele dintre atomi. Totuși, proprietățile fizico-chimice ale cristalului de piatră prețioasă suferă mici modificări (figura 2-2-57 - figura 2-2-58).
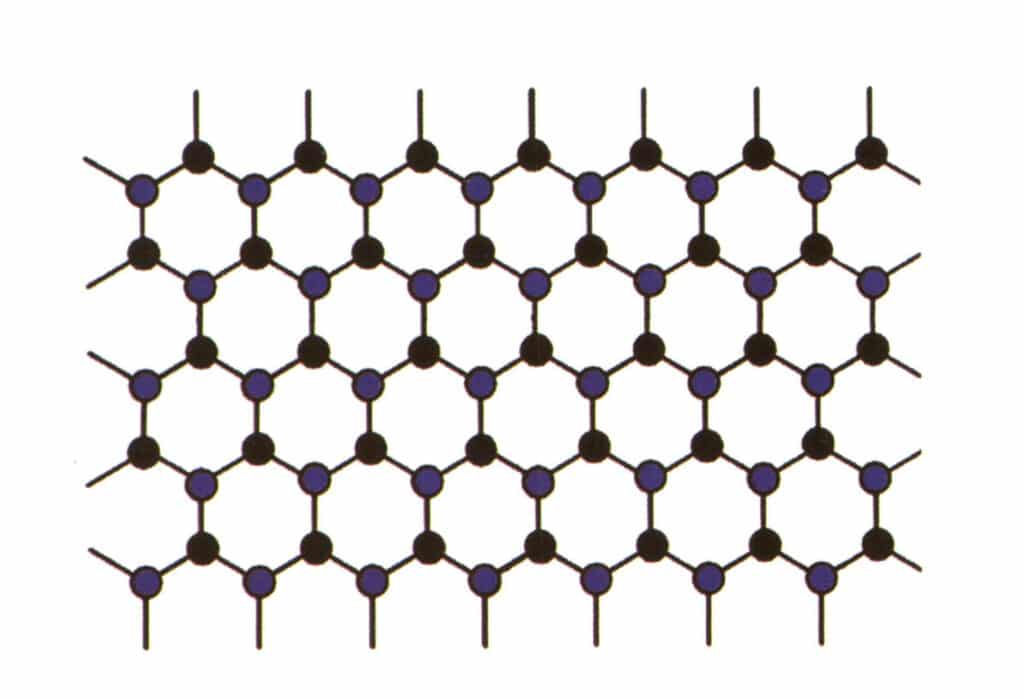
Figura 2-2-57 Diagrama de simulare a structurii cristaline (albastru și negru indică particulele elementelor)
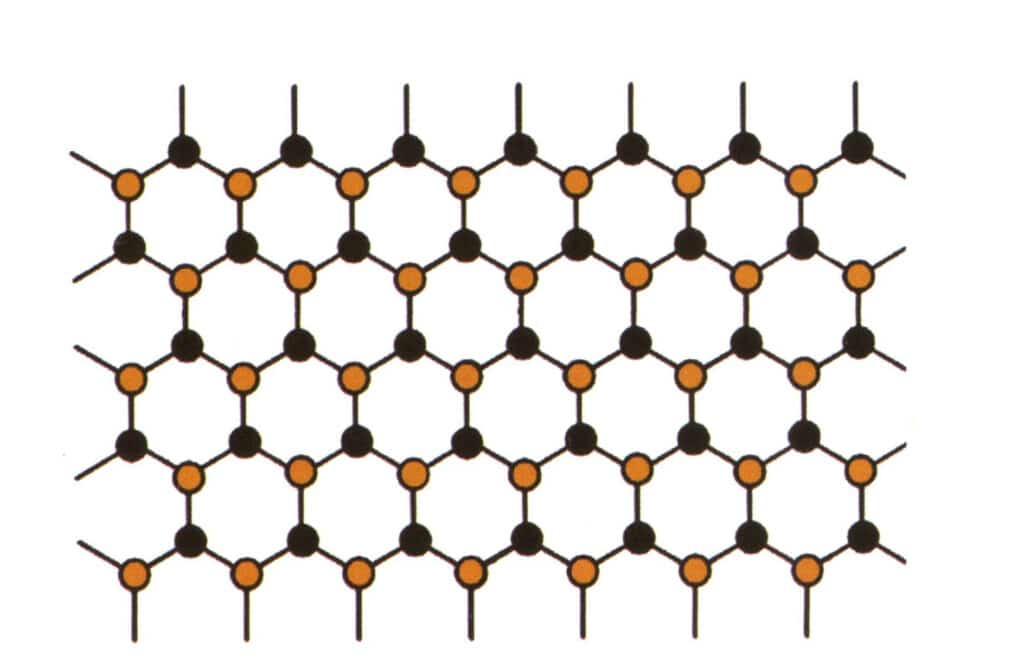
Figura 2-2-58 Diagrama de simulare a structurii cristalului (negrul reprezintă particule elementare, galbenul reprezintă particule elementare noi care înlocuiesc parțial particulele elementare albastre, galbenul poate să nu înlocuiască complet toate particulele albastre)
Conceptul de izomorfism poate explica de ce pietrele prețioase din aceeași familie pot avea atât de multe culori și de ce există variații în indicele de refracție și densitate între pietrele prețioase din aceeași familie.
O familie poate fi înțeleasă ca un tip de piatră prețioasă în care modelele repetitive ale elementelor cristaline sunt aceleași, dar formele fizice și chimice sunt ușor diferite. De exemplu, familia corindonului include doi membri, rubinul și safirul, în timp ce familia berilului include soiurile smarald, acvamarin și morganit.
(1) Olivină
Compoziția chimică a olivinei este (Mg,Fe)₂SiO₄. În compoziția sa are loc substituția izomorfă completă a elementelor Fe și Mg. Pe măsură ce conținutul de Fe din olivină crește, culoarea olivinei devine mai închisă, indicele de refracție crește, iar densitatea crește, de asemenea.
(2) Corindon
Corindonul pur fără impurități (Al₂O₃) este incolor, iar atunci când Cr înlocuiește Al, piatra prețioasă prezintă o nuanță de la roșu trandafirie la roșu, cunoscută sub numele de rubin. Celelalte culori sunt denumite safir, cum ar fi safirul galben-portocaliu sau safirul incolor. Safirul denumit în mod obișnuit este în special safirul albastru, unde Fe și Ti înlocuiesc Al. Cu cât este mai mare conținutul de elemente colorante în piatra prețioasă înlocuitoare, cu atât culoarea pietrei este mai profundă; invers, cu cât conținutul este mai mic, cu atât culoarea este mai deschisă.
(3) Turmalină
Turmalina se referă la același tip de gemă ca și turmalina, unde turmalina este denumirea sa mineralogică, iar turmalina este denumirea sa gemologică. Compoziția chimică a beriliului este (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), unde R este în principal Mg , Fe , Cr , Li, Al , Mn, iar elementele din R se pot înlocui complet sau parțial între ele, rezultând o varietate extrem de mare de culori pentru turmalină. De exemplu, atunci când R este în principal Fe, beriliul prezintă o culoare albastru intens sau chiar negru; atunci când R este în principal Mg, beriliul prezintă o culoare galbenă până la maro; atunci când R este în principal Li sau Mn, beriliul prezintă o culoare roz sau albastru deschis; atunci când R este în principal Cr, turmalina prezintă un verde intens.
Din cele de mai sus, se poate observa că înlocuirea elementelor cu proprietăți similare duce la obținerea unor culori mai frumoase și mai strălucitoare în pietre prețioase.
3. Intermixarea mecanică moleculară
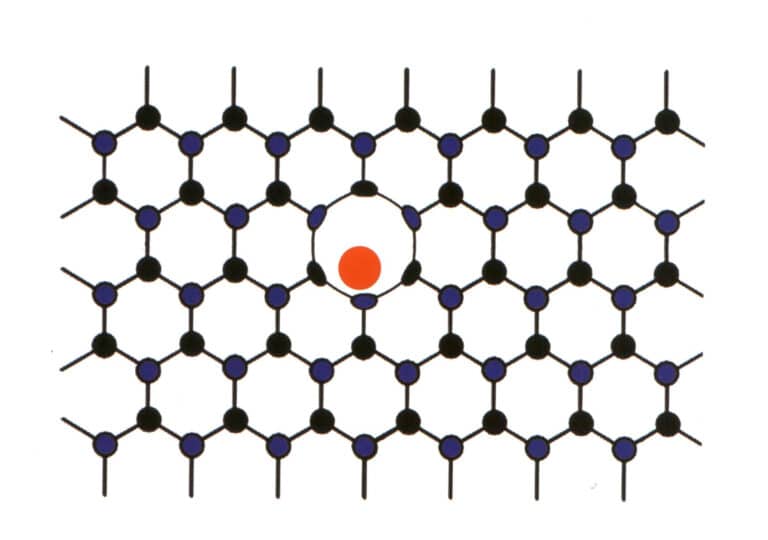
Uneori, anumite elemente pătrund forțat între elementele principale ale pietrelor prețioase dispuse în mod regulat. Cu toate acestea, proporția redusă a elementelor care intră nu perturbă modelul repetitiv al elementelor principale ale pietrelor prețioase, ci doar provoacă deformări (figura 2-2-59). Această situație este denumită amestec mecanic molecular, cum ar fi amestecul mecanic molecular al azotului și borului în diamante, care produce diamante albastre, roz și galbene, care sunt foarte valoroase.
4. Apa în mineralele prețioase
Unele pietre prețioase conțin apă, care este o componentă importantă a mineralelor prețioase și este strâns legată de proprietățile pietrelor prețioase. În funcție de forma apei prezente în mineralele prețioase și de rolul acesteia în structura cristalină, apa din pietrele prețioase poate fi împărțită în două categorii: una este apa de absorbție, care nu are legătură cu structura cristalină, iar cealaltă este apa care participă la structura cristalină a mineralului, inclusiv apa de cristalizare, apa zeolitică, apa interstrat și apa de constituție. Apa strâns legată de pietrele prețioase include apa de absorbție, apa de cristalizare și apa de constituție.
Una este absorbția apei, cum ar fi Opal (compoziția chimică este SiO₂ - nH₂O, n reprezintă numărul de H₂O, conținutul este variabil) în molecula de apă, care este o moleculă de apă neutră adsorbită mecanic pentru particule minerale sau suprafețe de fractură. Atunci când temperatura atinge 100 ~ 110°degrees sub presiune normală, moleculele de apă pot scăpa toate și nu deteriorează structura rețelei cristaline, astfel încât pentru a evita Opal în tejghea într-un timp îndelungat de expunere la lumină puternică crack uscat, ar trebui să pună o ceașcă de apă în tejghea.
A doua este apa de cristalizare, cum ar fi apa de cristalizare din turcoaz [compoziția chimică este CuAl₆(PO₄)₄(OH)₈-4H₂O, unde conținutul de H₂O poate ajunge la 19,47% ]. Această moleculă de apă neutră există în poziții fixe în cadrul rețelei și servește ca unitate structurală, făcând parte din compoziția chimică a mineralului. Temperatura la care apa de cristalizare scapă nu depășește în general 600 ℃ și, de obicei, scapă la 100 -200 ℃. Atunci când o piatră prețioasă își pierde apa de cristalizare, structura sa cristalină este deteriorată, formând o nouă structură.
A treia este apa de constituție, cunoscută și sub denumirea de apă combinată, care participă la rețeaua minerală sub formă de plasmă OH-, H⁺, H₃O⁺, OH- fiind cea mai comună. Apa de constituție face parte din compoziția chimică a mineralului, ocupând poziții fixe în structura rețelei cu o proporție definită în compoziția sa. Apa structurală are nevoie de o temperatură mai ridicată pentru a scăpa și a-și deteriora structura, de obicei în jur de 600 -1000 ℃. Atunci când o piatră prețioasă pierde apa structurală, structura sa cristalină este distrusă. Multe pietre prețioase conțin apă de constituție, cum ar fi turmalina[compoziția chimică este ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), unde R include în principal Mg , Fe , Cr, Li, Al, Mn, etc., iar elementele din R se pot înlocui complet sau parțial între ele], și topaz [compoziția chimică este Al₂SiO₄( F, OH) ₂ ].
5. Compoziția chimică a pietrelor prețioase
Pietrele prețioase, ca și alte substanțe, sunt compuse din elemente chimice. Fiecare tip de gemă are o compoziție chimică specifică și o anumită gamă de variații, care determină diferitele caracteristici și proprietăți ale gemei. Pietrele prețioase aparțin mineralelor și rocilor, iar clasificarea compoziției chimice a unei pietre prețioase poate fi trasată înapoi la compoziția chimică a mineralelor.
În prezent, principalele metode de clasificare a mineralelor includ clasificarea după compoziția chimică (sistemul Dana), clasificarea geochimică, clasificarea genetică, clasificarea aplicațiilor și clasificarea chimico-cristalină. Metoda adoptată pe scară largă este clasificarea chimică bazată pe compoziția chimică și structura cristalină (sistemul Hugo Strunz) (tabelul 5).
Tabelul 5: Sistemul de clasificare chimică a cristalelor minerale
| Secvența de nivel | Baza pentru divizare | Exemplu |
|---|---|---|
| Categoria majoră | Tip compus | Sare cu conținut de oxigen Categoria majoră |
| Clasa | Tipuri de anioni sau anioni complecși | Clasa silicaților |
| (Subcategorie) | Structura complexului anionic | Subclasa silicaților-cadru |
| Grup | Tipuri de structuri cristaline și proprietăți ionice | Grupa corindonului, grupa beriliului, grupa granatului |
| (Subgrup) | Tipuri de cationi | Subgrupul feldspat alcalin |
| Specie | O anumită structură cristalină și compoziție chimică | Orthoclase KAlSi3O8 |
| (Subspecie) | Aceeași structură cristalină, compoziție sau proprietăți diferite, morfologie | Adularia KAlSi3O8 |
















