Jednou se dozvědět vše o drahých kamenech krystalografie
Komplexní průvodce o formách, typech, klasifikacích a rozdílech v krystalografii
Země se skládá z bezpočtu molekul a atomů. Moderní vědecký výzkum zjistil, že pevné materiály v přírodě se skládají z různých chemických prvků. Výsledky rentgenové analýzy ukazují, že atomy v prvcích některých pevných materiálů jsou uspořádány úhledně a pravidelně vedle sebe. Tyto materiály jsou klasifikovány jako krystalické nebo označovány jako krystaly a jejich uspořádaná atomová mřížka se nazývá krystalová struktura (obrázek 2-1-1).
Většina drahých kamenů, které rostou v přírodě i v laboratořích, je krystalická. V této kapitole se budeme zabývat pojmem krystaly, jejich klasifikací, vztahem mezi krystaly a základní terminologií v gemologii.

Obsah
Oddíl ⅠPojmy a popis krystalů
Když se zmíníme o drahokamech, často si vybavíme jejich třpytivé a průsvitné vlastnosti (obrázek 2-1-2). Z pohledu geologů a gemologů patří většina oblíbených drahokamů ke geometrické formě pevných krystalů. Podstatou krásy krystalů je ve skutečnosti krása geometrie.

1. Pojem krystaly
Krystaly jsou nejsnáze asociovatelné a nejčastěji se vyskytují v přírodě. Krystaly se vyskytují na všech sedmi kontinentech Země, a pokud je v přírodě najdeme, mají často podobu geometrických mnohostěnů (obrázek 2-1-3). Běžně se označují jako krystaly. Později byl tento termín rozšířen na označení v přírodě se vyskytujících pevných látek s geometrickými mnohostěny, jako jsou krystaly diamantu a akvamarínu (obrázek 2-1-4). Krystaly lze také označit pevné materiály s nepravidelným, nerovným, opotřebovaným, porušeným nebo uměle opracovaným povrchem, ale s uspořádáním atomů, které stále dodržuje pravidelný vzorec. Krystalografové se domnívají, že všechny krystaly mají šest základních charakteristik: sebeomezení, stejnoměrnost, anizotropii, symetrii, stabilitu a pevný bod tání.
① Samoomezující se odkazuje na vlastnost chemických prvků spontánně vytvářet geometrické mnohostěny. Touto vlastností lze vysvětlit, proč mají různé prvky různé geometrické tvary krystalů.
② Uniformita znamená vlastnost, že fyzikální a chemické vlastnosti všech částí krystalu jsou stejné. Tato vlastnost nám může pomoci rozlišit a identifikovat různé krystaly minerálů.
③ Anizotropie označuje vlastnost, kdy se uspořádání prvků mění v různých směrech, což vede k mírným rozdílům ve fyzikálních vlastnostech v závislosti na směru. Touto vlastností lze vysvětlit, proč lze diamanty s nejvyšší tvrdostí brousit a leštit.
④ Symetrie označuje vlastnost, kdy se shodné části nebo vlastnosti krystalu opakují v pravidelném vzoru. Tato vlastnost je pro krystaly nesmírně důležitá a zvláštní a bude podrobněji popsána ve druhé části této kapitoly.
⑤ Stabilitou se rozumí stabilita krystalu vyplývající z jeho minimální vnitřní energie. Pokud je vnitřní energie krystalu vysoká a nerovnoměrná, je náchylný k samovolnému praskání. Tato vlastnost může vysvětlovat, proč se krystaly rubínu syntetizované technikou plamenné syntézy jeví vždy spíše jako poloviční než úplné.
⑥ Pevný bod tání označuje vlastnost, že krystal má pevný bod tání.

Obrázek 2-1-3 Granát (vlevo je krystal, vpravo leštěný granát)

Obrázek 2-1-4 Akvamarínový krystal
2. Ideální forma krystalů
Krystaly, o kterých se v krystalografii mluví, jsou většinou ideální monokrystaly. Ideální monokrystal je definován jako krystal, jehož vnitřní struktura se striktně řídí pravidly prostorových mřížek a jehož tvar je pravidelnou geometrickou kombinovanou formou. Tvary ideálních monokrystalů se dělí na dva typy: jednoduché tvary a kombinované tvary.
(1) Jednoduchý formulář
Jednoduchou formou se rozumí kombinace skupiny krystalových ploch spojených prvky symetrie, kterou lze chápat jako geometrické těleso složené z krystalových ploch stejného tvaru a velikosti v ideálním stavu (obrázek 2-1-5). V krystalech existuje 47 typů jednoduchých forem.
Klíčové body pro identifikaci jednoduchých forem jsou: všechny krystalové plochy v krystalu mají stejný tvar a velikost a krystalové plochy mohou být různě orientovány.
(2) Kombinace Formulář
Souhrn jednoduchých forem se nazývá kombinovaná forma, složená ze dvou nebo více různých jednoduchých forem. Ne všechny jednoduché formy lze volně kombinovat do kombinované formy; agregovat lze pouze jednoduché formy se stejnou skupinou bodů (obrázky 2-1-6 až 2-1-8).
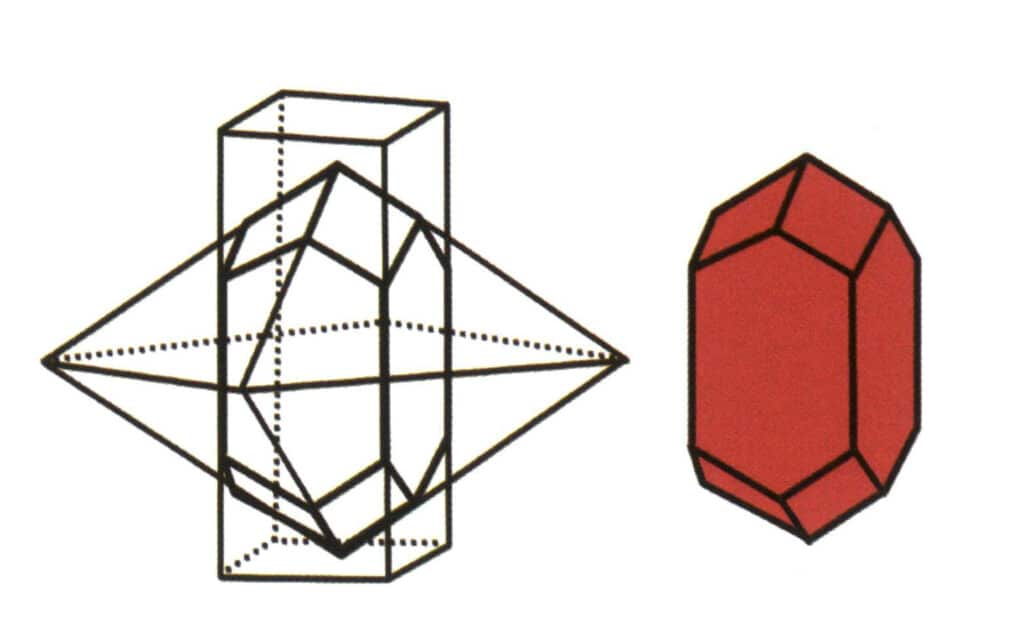
Obrázek 2-1-6 Kombinace tetragonálních hranolů a tetragonálních dipyramidálů
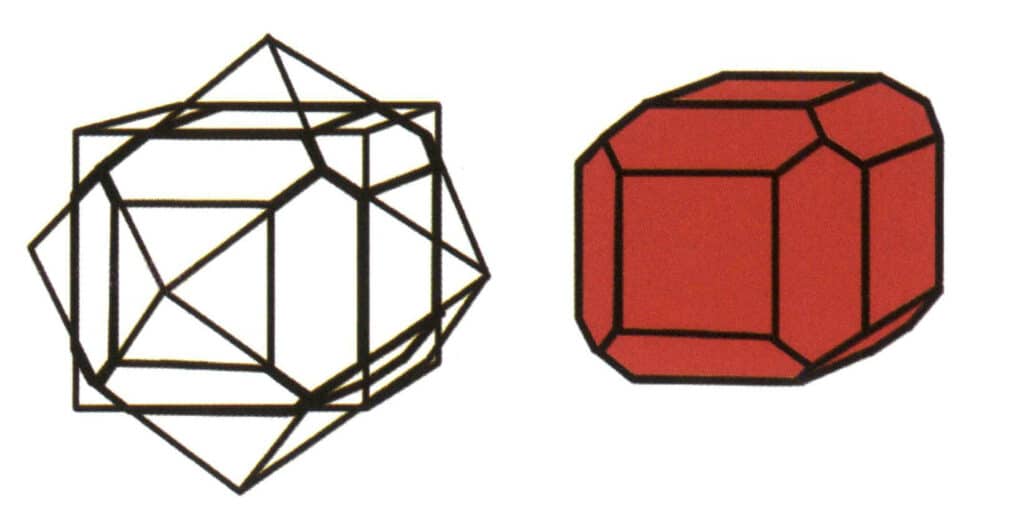
Obrázek 2-1-7 Kombinace z krychle a kosočtverečného dvanáctistěnu
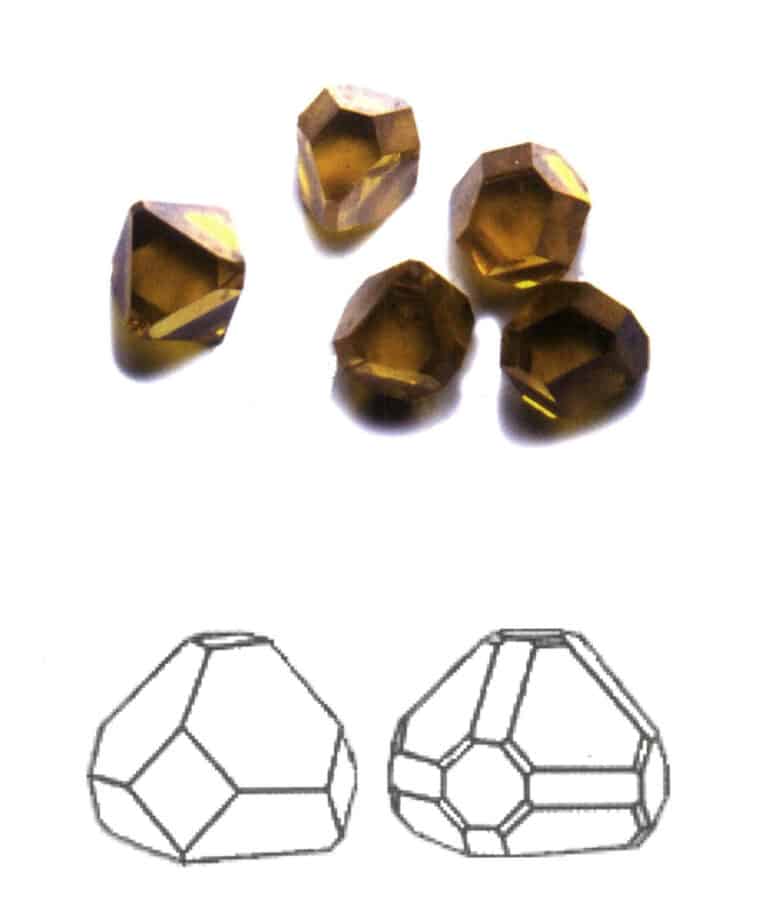
Klíčovým bodem identifikace kombinované formy je přítomnost dvou nebo více různě tvarovaných krystalových ploch v krystalu.
Pokud se v přírodě vyskytují monokrystaly, vždy se výrazně liší od ideální morfologie monokrystalů (obrázek 2-1-9), například jedna stěna nemusí mít stejný tvar a velikost a dochází k zániku krystalových stěn, což se popisuje jako deformované krystaly.

Deformované krystaly lze také popsat jako skutečné krystaly vznikající v přírodě, ovlivněné růstovým prostředím. Více krystalových ploch, které se v ideálních krystalech opakují pod pevnými úhly, nemusí mít nutně stejný tvar a velikost. Přesto však u stejného typu krystalu musí mít krystalové plochy stejného monomorfního tvaru stejný vzor a fyzikální vlastnosti. Úhly mezi odpovídajícími krystalovými plochami zůstávají nezměněny, což odráží vrozenou symetrii samotného krystalu. Krystaly vyskytující se ve skutečnosti jsou v různé míře deformované.
Dvojité krystaly lze také popsat jako skutečné krystaly vznikající v přírodě pod vlivem růstového prostředí. Vícenásobné krystalové plochy, které se v ideálních krystalech opakují pod pevnými úhly, nemusí mít nutně stejný tvar a velikost. Přesto však u stejného typu krystalu musí mít plochy stejného tvaru stejné vzory a fyzikální vlastnosti. Úhly mezi odpovídajícími krystalovými plochami zůstávají nezměněny, což odráží vrozenou symetrii samotného krystalu. Všechny krystaly, které se vyskytují ve skutečnosti, jsou v různé míře dvojčatové.
3. Krystalizační zvyklosti krystalů
Krystaly vzniklé v přírodě nemohou nikdy dosáhnout dokonalého tvaru. Pokud rostou v mezerách horninových vrstev, obklopených horninou, přirozený tvar krystalu se zkreslí. Dokonce i krystaly vypěstované v laboratoři se vlivem gravitace deformují. Pouze v podmínkách nulové gravitace na Mezinárodní vesmírné stanici mohou vědci kultivovat krystaly dokonalého tvaru, které hledají.
Přestože tvary krystalů jsou nedokonalé, každý typ krystalu minerálu má tendenci růst nebo se shlukovat různými způsoby nebo zvyky.
Každý minerál má tendenci vznikat za specifických podmínek a jeho zvyklosti odrážejí podmínky jeho vzniku. Některé minerály, například křemen, mají složité a proměnlivé podmínky vzniku. Proto má křemen také více habitusů.
Obecně se krystalové habity vztahují k vlastnostem určitého krystalu, který má za určitých vnějších podmínek tendenci vytvářet určitý tvar. Někdy odkazuje na běžné typy jednoduchého tvaru daného krystalu.
Podle stupně vývoje krystalů v trojrozměrném prostoru se krystalové habity dělí na tři základní typy.
(1) Uni-směrové rozšíření
Krystaly se rozšiřují v jednom směru a vyskytují se ve sloupcovitých, jehlicovitých, vláknitých formách atd. Tento habitus často vykazují minerály jako beryl, turmalín, rohovec a malachit (obr. 2-1-10 až obr. 2-1-11).

Obrázek 2-1-10 Sloupcovitý akvamarín (nahoře) a jeho krystalový habitus (dole)

Obrázek 2-1-11 Vláknitý malachit (nahoře) a jeho krystalový habitus (dole)
(2) Bi-směrové rozšíření
Krystaly se rozprostírají v rovině, objevují se v deskovitých, listovitých, šupinovitých apod. formách, neboť tento habitus často vykazují minerály jako wolframit, slída, plumbago a tanzanit (obr. 2-1-12).
(3) Tri-směrová izometrie
Krystaly se vyvíjejí rovnoměrně ve třech směrech a představují izometrické, zrnité formy, jako je spinel, granát, diamant, pyrit a fluorit, které často vykazují tento habitus (obrázky 2-1-13, 2-1-14).

Obrázek 2-1-12 Deskovitý krystalový habitus tanzanitu (nahoře) a jeho krystalový habitusový diagram (dole).

Obrázek 2-1-13 Oktaedrický krystalový habitus drahokamu spinel (nahoře) a jeho krystalový habitusový diagram (dole)
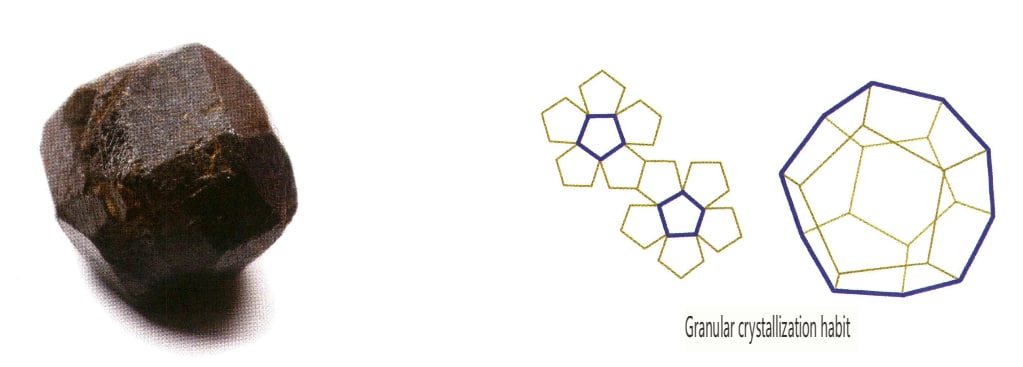
Kromě toho existují přechodné typy, jako jsou krátké sloupcovité, deskovité sloupcovité, pásovité a tlusté deskovité formy.
Chemické složení a struktura krystalu určují především krystalový habitus. Úzce souvisí také s vnějšími podmínkami při vzniku krystalu (jako je teplota, tlak, koncentrace, viskozita a nečistoty), například s rozdíly ve tvaru krystalů mezi diamanty a syntetickými krystaly diamantů.
4. Pravidelná agregace krystalů
V přírodě se můžeme setkat s jednotlivými krystaly (obrázek 2-1-15) a se dvěma nebo více jednotlivými krystaly, které spolu tvoří celek. Tento jev, kdy více krystalů roste dohromady, se nazývá agregace krystalů. Agregaci krystalů lze rozdělit na nepravidelné a pravidelné typy. Nepravidelnou agregaci krystalů lze chápat jako kolektivní, což bude podrobněji popsáno ve třetí kapitole. U pravidelné agregace krystalů se vyskytují čtyři běžné typy: paralelní agregace, bikrystaly, přerůstání a prorůstání (obrázky 2-1-16 až 2-1-18). Tato kapitola pojednává především o typu pravidelné agregace známé jako bikrystaly.

Obrázek 2-1-15 Monokrystal (turmalín)
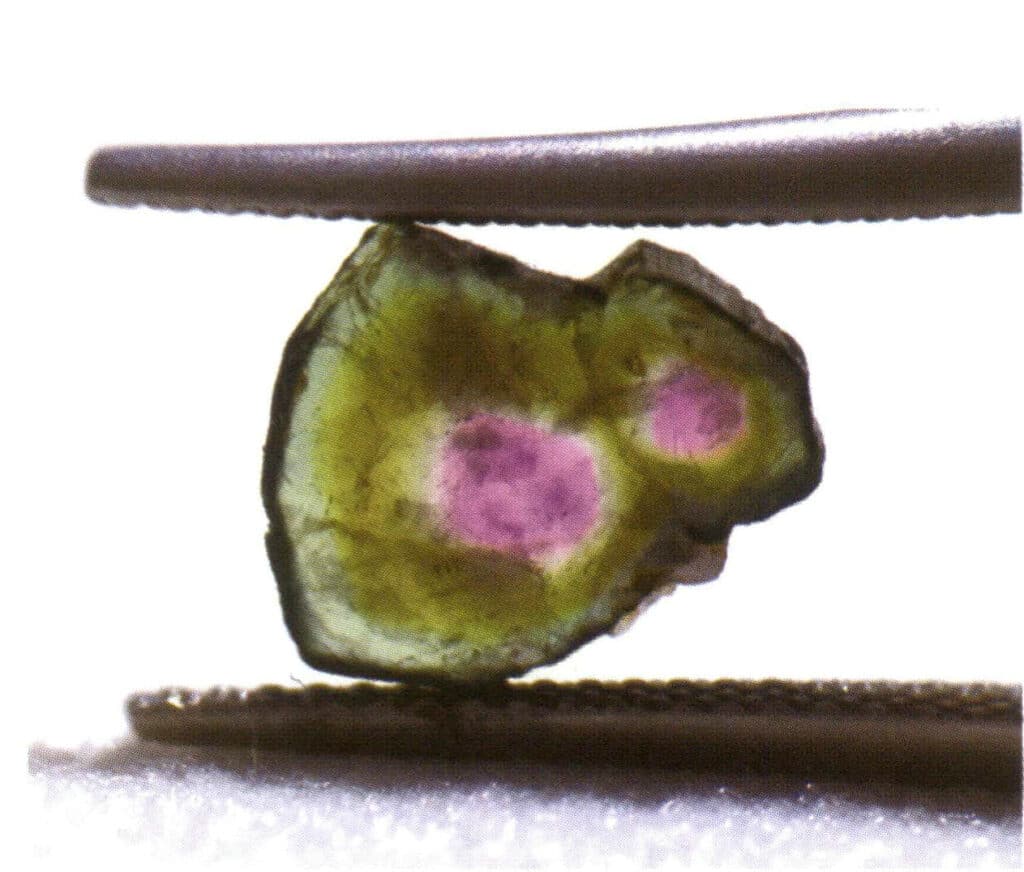
Obrázek 2-1-16 Paralelní agregace (Když více krystalů stejného typu roste paralelně v prostoru, nazývá se paralelní agregace. V tomto okamžiku jsou všechny odpovídající krystalové plochy a hrany vyrostlých krystalů navzájem rovnoběžné.)

Obrázek 2-1-17 Dvojitý krystal (spinel)

Obrázek 2-1-18 Přerůstání (určitý typ krystalu roste na povrchu jiného krystalu v určitém krystalografickém směru, známé také jako epitaxní růst)
Bikrystaly jsou pravidelné seskupení dvou nebo více stejných krystalů podle určitých symetrických pravidel. (Dvojitá osa, dvojitá rovina) Příslušné stěny, hrany a úhly dvou sousedních jedinců nejsou zcela rovnoběžné. Přesto se mohou vzájemně odrážet prostřednictvím symetrických operací, jako je rotace a inverze rotace, což umožňuje, aby se obě individua shodovala nebo vyrovnávala.
4.1 Klíčové body pro identifikaci bikrystalů
① Konkávní úhly viditelné u dvojčatných krystalů (obrázek 2-1-19).
② Stylolit: Mikromorfologie a další charakteristiky krystalových ploch na obou stranách stylolitu jsou nespojité (obrázek 2-1-20).
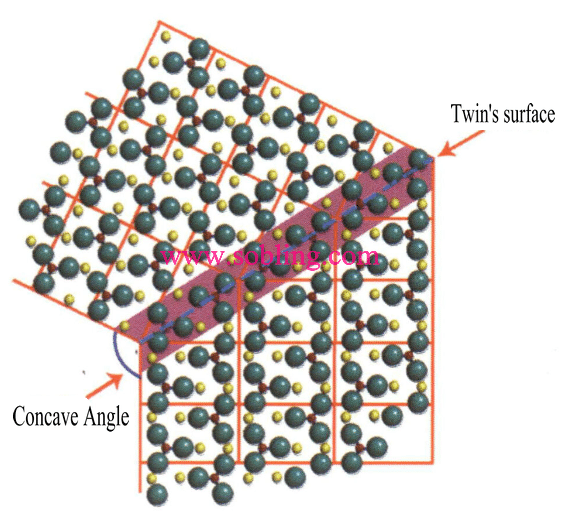
Obrázek 2 - 1-19 Konkávní úhel dvojčete
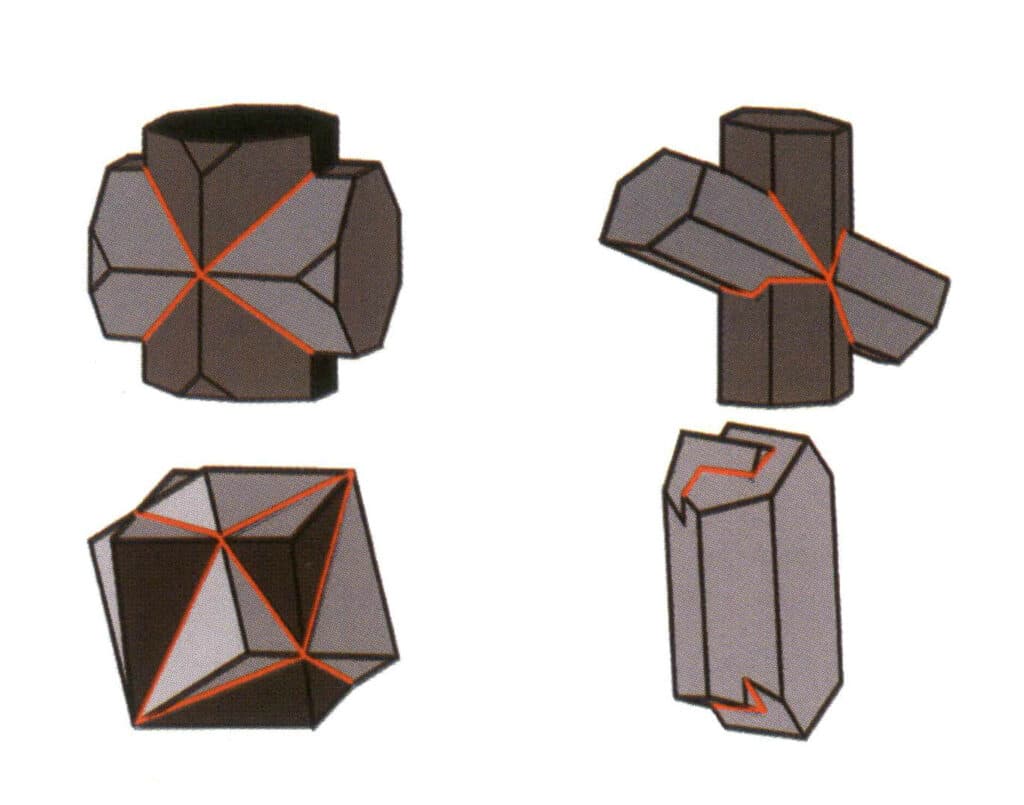
Obrázek 2-1-20 Stylolit (různé barvy na obrázku představují různé krystaly; červené čáry označují dvojčata stylolitu)
③ Dvojité pruhování: Krystalové plochy nebo štěpné roviny vykazují jemné dvojčatné proužky (obrázek 2-1-21).
④ Leptaná figurka: Vzhled leptacího obrázku indikuje přítomnost dvojčat (obrázek 2-1-22).

Obrázek 2-1-21 Schéma polysyntetických dvojčat

Obrázek 2-1-22 Povrch spinelu s obrácenými trojúhelníkovými jamkami.
⑤ Vznik pseudosymetrie: vznik symetrických vztahů, které neodpovídají vlastní bodové skupině krystalového monokrystalu (obr. 2-1-23 až obr. 2-1-24).

Obrázek 2-1-23 Monokrystal chryzoberylu

Obrázek 2-1-24 Kolenovité dvojče chryzoberylu
Dvojčata se dělí na pět typů podle jejich stohovacích vlastností: kontaktní dvojčata (obrázky 2-1-25 až 2-1-26), polysyntetická dvojčata (obrázek 2-1-27), prolínající se dvojčata (obrázek 2-1-28), tripletové krystaly (obrázek 2-1-29) a komplexní dvojčata, mezi nimiž jsou první čtyři typy běžné.


Obrázek 2-1-26 Kontaktní dvojčata spinelu (nahoře) a jejich schéma (dole)

Obrázek 2-1-27 Polysyntetické dvojče labradoritu (nahoře) a jeho schéma (dole)
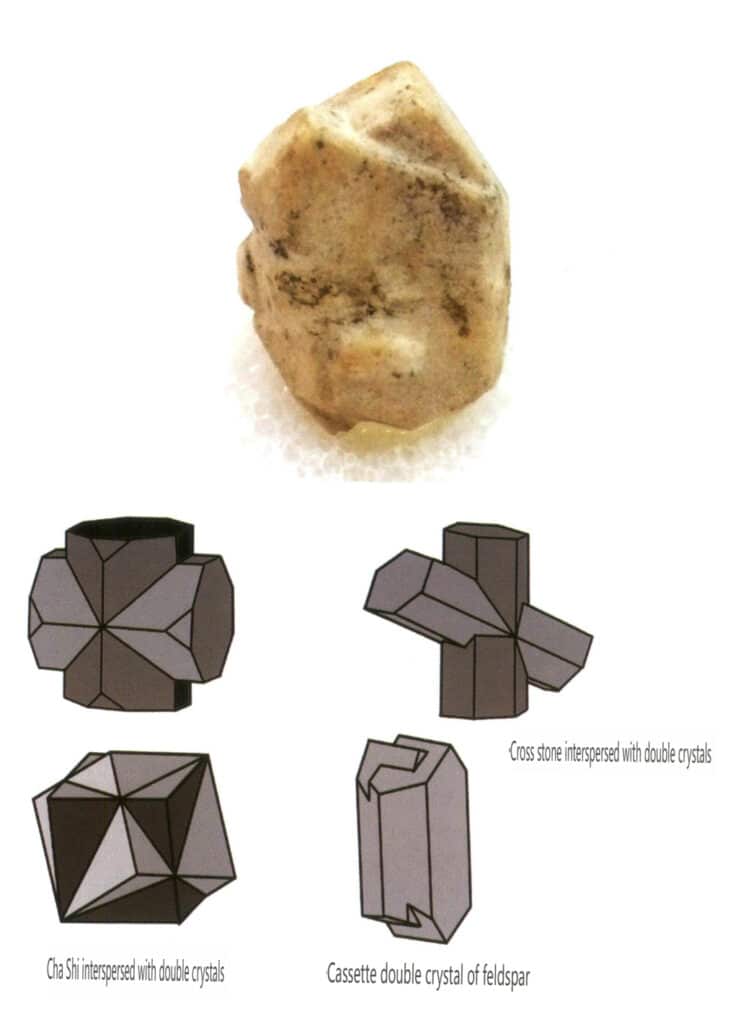
Obrázek 2-1-28 Dvojité krystaly živce (nahoře) a schéma prolínajících se dvojkrystalů jiných typů (dole)

Obrázek 2-1-29 Trigonální dvojčata chryzoberylu (nahoře) a jejich schéma (dole)
4.2 Vznik bikrystalů
① Vzniká během růstu krystalu, může se vyvinout z dvojčat krystalových zárodků nebo malých krystalů rostoucích v závislosti na poloze dvojčat.
② Vzniká během procesu heteromorfní přeměny, například když se α křemen přemění na β křemen a vytvoří dvojčata.
③ Vzniká mechanickým působením, kdy část krystalu klouže podél určité směrové roviny a vytváří deformační dvojčata, jako jsou dvojčata kalcitu.
5.Vzory křišťálových tváří
Pokud jsou krystaly objeveny v přírodě, mají často neúplné tvary (obrázek 2-1-30) a zvláštní povrchové vzory. Někdy rostou pohromadě ve shlucích (obrázek 2-1-31), které se často výrazně liší od standardních geometrických mnohostěnů, které známe, jako jsou krychle a šestiboké hranoly. Tento jev se nazývá skutečná forma krystalů. Reálná forma krystalů má v krystalografii podrobnou klasifikaci, např. deformované krystaly, konvexní krystaly, zakřivené krystaly, plovoucí krystaly, pruhy na krystalových plochách, leptané figury, dvojčatné pruhy atd.

Obrázek 2-1-30 Rubínový krystal

Obrázek 2-1-31 Krystaly pyritu (vlevo je znázorněno několik krystalů pyritu rostoucích společně, vpravo je znázorněn jediný krystal pyritu)
Tato část se zabývá především vzory krystalových ploch v reálné podobě krystalů.
Teoreticky jsou krystalové roviny hladké a ploché. Přesto se při skutečném růstu nebo rozpouštění krystalů na jejich povrchu často objevují mírně nerovnoměrné pravidelné obrazce, kterým se běžně říká obrazce krystalových ploch. Mezi vzory krystalových ploch patří růstové pruhy, růstové vrstvy, spirálové vzory, růstové pahorky a leptané obrazce. Vzory krystalových stěn, o nichž pojednává tato kniha, se týkají především pruhů krystalových stěn a leptaných figur, které lze pozorovat pouhým okem nebo za podmínek malého zvětšení.
Pruhy na krystalové ploše označují řadu rovnoběžných přímek na povrchu krystalu, které jsou důsledkem opakovaného sbližování a střídavého růstu různých jednoduchých forem. Jsou také známé jako "kombinované pruhy" a vyskytují se pouze na povrchu krystalů, nazývaných také růstové pruhy. Například hexagonální prizmatická krystalová plocha křemene má často střídavě vyvinuté hexagonální prizmatické a rombické dodekaedrické jemné krystalové plochy do agregátních příčných pruhů (obrázek 2-1-32).

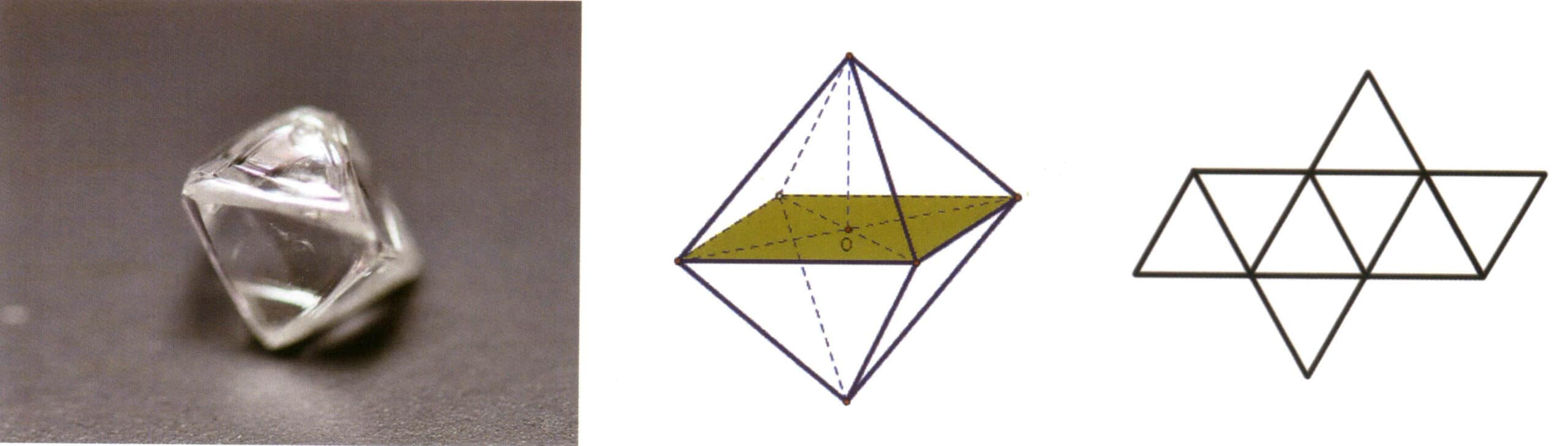
Leptací figury označují specifické tvarové důlky (tj. leptací jamky), které zůstaly na povrchu krystalu v důsledku koroze po vytvoření krystalu. Leptací figury jsou řízeny uspořádáním elementárních částic v ploše krystalu. Proto se tvary a orientace leptaných figur liší mezi různými minerály a jednotlivými formami téhož krystalu. Například leptací obrazce na různých jednoduchých formách krystalů diamantu se liší; trojúhelníkové důlky lze pozorovat na osmistěnných krystalech (obrázek 2-1-33), čtyřúhelníkové důlky na krychlových stěnách, překrývající se čtyřúhelníkové důlky vytvářejí mřížkovitý vzor a na kosočtvercových dvanáctistěnech lze pozorovat čárové vzory nebo mikroskopické diskovité vzory (obrázek 2-1-34).

Obrázek 2-1-33 Viditelné obrácené trojúhelníkové důlky na osmistěnném krystalu diamantu

Obrázek 2-1-34 Lineárně vzorovaná textura viditelná na kosočtverečných dodekaedrických krystalech
Pouze leptové figury na stejné krystalové ploše téže formy mohou být stejné, proto se leptové figury často používají k identifikaci minerálů a k určení, zda krystalové plochy patří k téže jediné formě (obr. 2-1-35 až obr. 2-1-42).

Obrázek 2-1-35 Pruhy ve stylu dřevěné podlahy vykládané krystaly fluoritu

Obrázek 2-1-36 Přirozený trojúhelníkový lept v rubínu (běžné vodorovné pruhy v rubínech, růstové linie rovnoběžné s kosočtverečným směrem, přirozené leptání ve tvaru trojúhelníku nebo šestiúhelníku)

Obrázek 2-1-37 Povrchové podélné proužky turmalínu

Obrázek 2-1-38 vodorovné pruhy na povrchu krystalu

Obrázek 2-1-39 Leptané obrazce na povrchu krystalu

Obrázek 2-1-40 Povrchové podélné proužky topazu

Obrázek 2-1-41 Topografický snímek krystalu topazu

Obrázek 2-1-42 Leptací figury spinelu
Oddíl II 47 Typy krystalových forem
V krystalografii existuje 146 různých jednoduchých forem, které lze na základě jejich samostatně existujících geometrických tvarů rozdělit do 47 geometrických forem. Tyto geometrické formy jsou pojmenovány následujícími způsoby:
① Pojmenování podle charakteristiky tvaru průřezu, např. trigonální hranol, tetragonální hranol, hexagonální hranol, kosočtvercový bipyramid atd.
② Pojmenování podle tvaru jednoduché formy, jako je válec, dvojitý kužel, krychle atd.
③ Pojmenování podle počtu geometrických stěn, např. jednoduchá stěna, osmistěn atd.
④ Pojmenování podle tvaru geometrických stěn, například kosočtverec, pětistěn atd.
V krystalografii se jednotlivé formy dělí do čtyř kategorií: obecné formy a speciální formy, uzavřené formy a otevřené formy, pravidelné formy a nepravidelné formy, levotočivé formy a pravotočivé formy. V této kapitole se budeme stručně zabývat uzavřenými formami a otevřenými formami.
Uzavřené formy se vztahují k těm, jejichž krystalové stěny mohou uzavřít uzavřený prostor, a dělí se do tří hlavních kategorií: polyedrické třídy, šikmé polyedrické třídy a bipyramidální třídy, celkem 30 typů. Každá kategorie má podrobnější klasifikaci; například polyedrická třída se dělí na tetraedrickou třídu, oktaedrickou třídu, kubickou třídu atd. (obrázky 2-1-43 až 2-1-48).

Obrázek 2-1-43 Třída tetraedrů
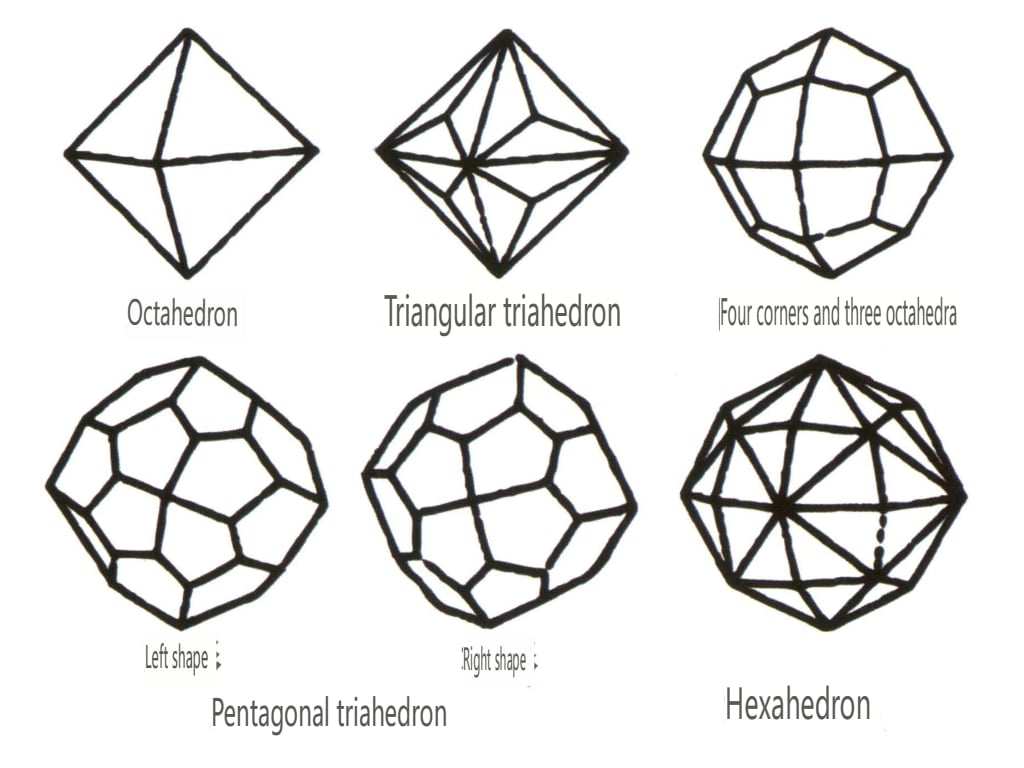
Obrázek 2-1-44 Třída 0ctahedral
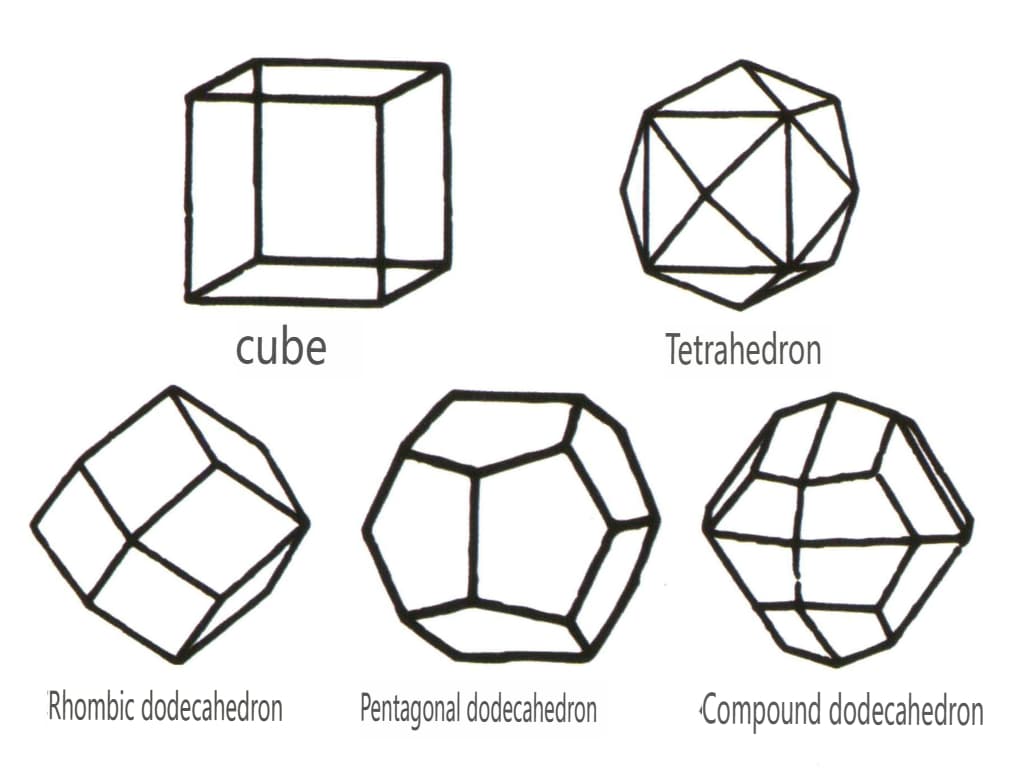
Obrázek 2-1-45 Krychlové a dodekaedrické třídy
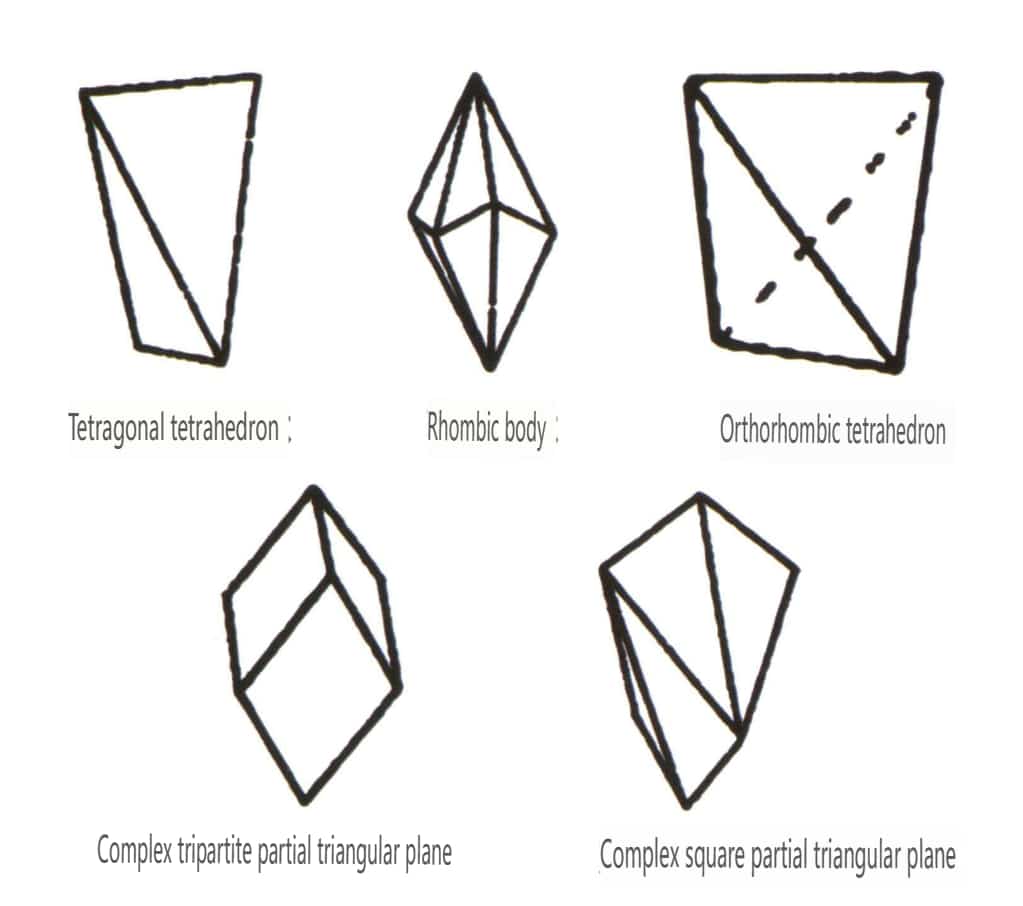
Obrázek 2-1-46 Další polyedrické typy
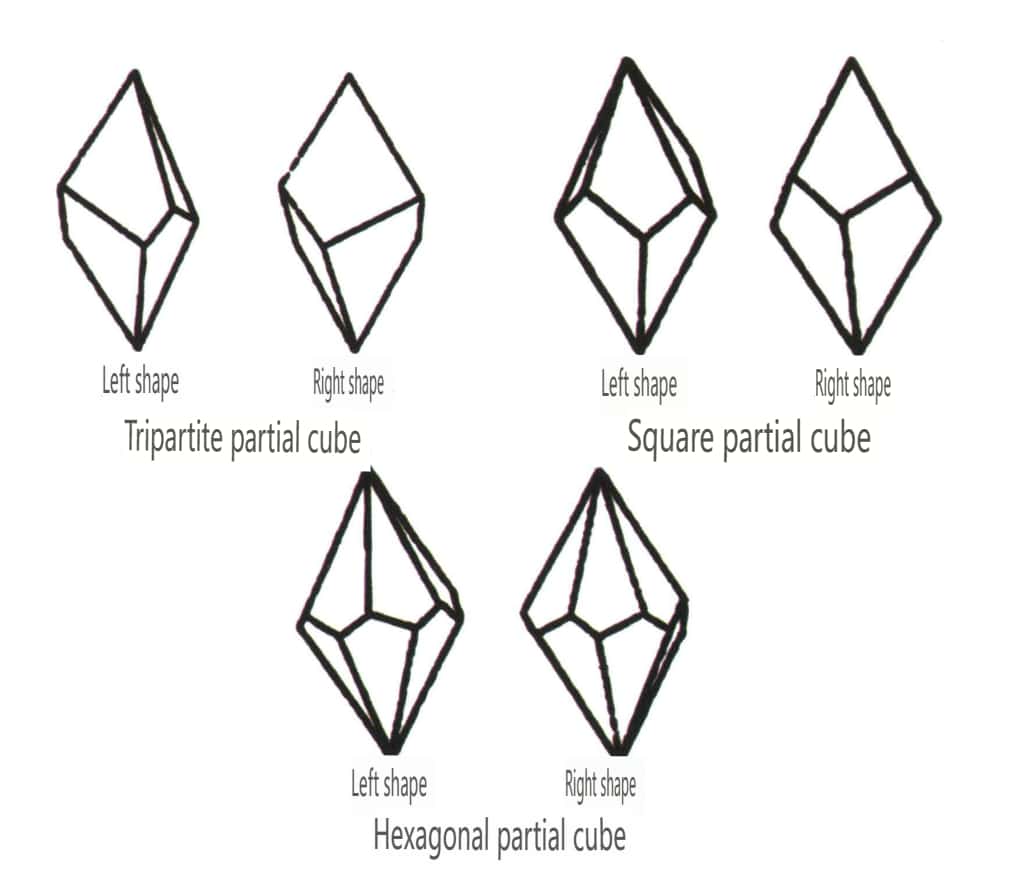
Obrázek 2-1-47 Šikmá kombinovaná forma Třída
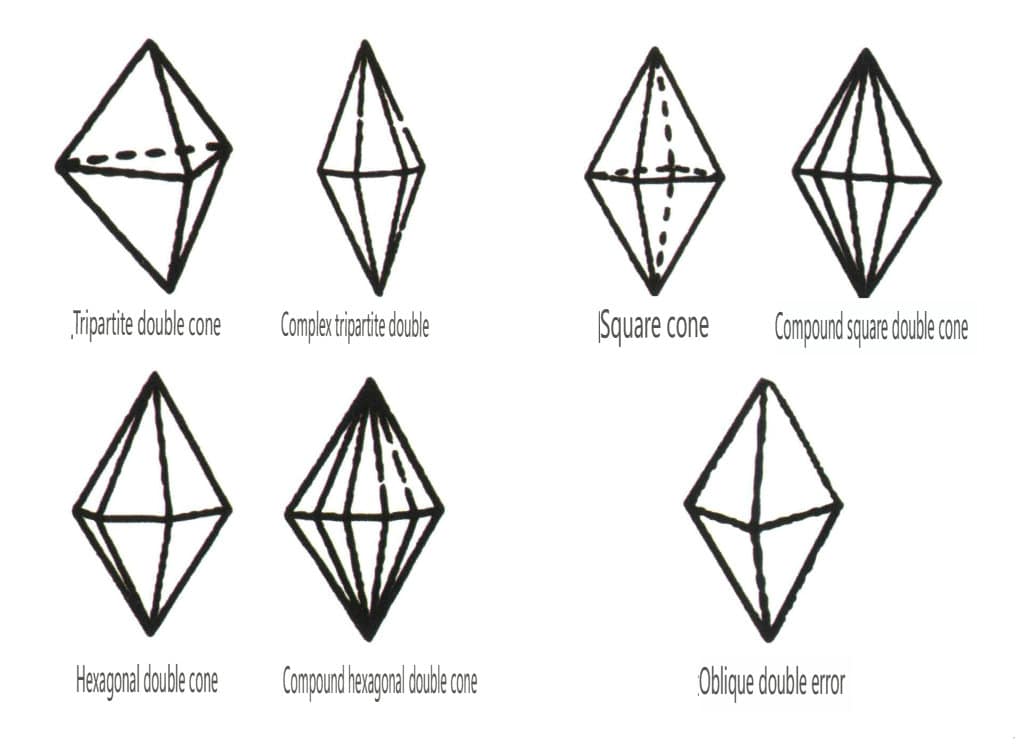
Obrázek 2-1-48 Dvojitá pyramidová třída
Otevřené formy se vztahují k těm, jejichž krystalové stěny nemohou uzavřít uzavřený prostor, a dělí se do čtyř hlavních kategorií: jednolité, dvojité, sloupcovité a jednoduché pyramidální třídy, celkem 17 typů (obrázky 2-1-49 a 2-1-51).
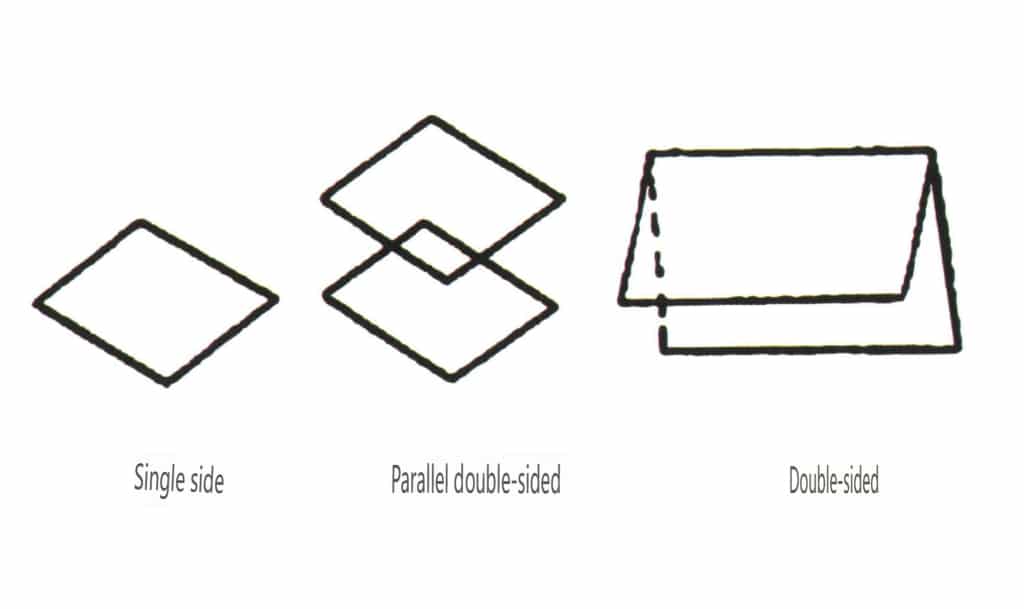
Obrázek 2-1-49 Jednostranný a oboustranný tisk
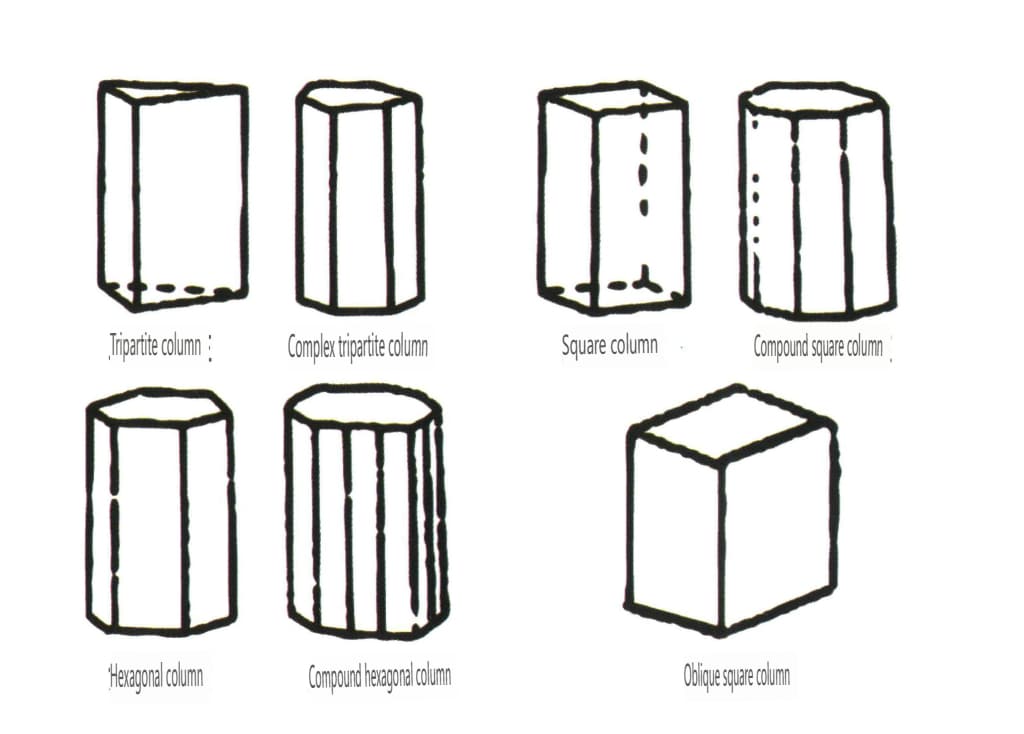
Obrázek 2-1-50 Sloupce

Oddíl III Klasifikace krystalů
1. Symetrie krystalů
Symetrie je abstraktní pojem při studiu skutečných krystalů a nezpracovaných drahých kamenů. Popisuje opakování, které se projevuje, když je krystalová struktura vztažena ke směru nebo rovině, která jí prochází. Je to základ pro klasifikaci krystalů.
Symetrii krystalu lze z mikroskopického hlediska chápat jako metodu popisu opakovatelnosti krystalové struktury a z makroskopického hlediska jako opakování dvou nebo více geometrických ploch, které mají stejný tvar a velikost, ale mohou se lišit ve směru podle určitých pravidel. Tento vzorec opakování lze popsat pomocí os symetrie a rovin symetrie, přičemž každá osa symetrie nebo rovina symetrie se označuje jako prvek symetrie. Při pozorování nebo odvozování symetrie objektu se tato činnost popisuje jako provádění operací se symetrií.
2. Symetrické prvky krystalů
V krystalografii existují čtyři prvky symetrie: osa symetrie, rovina symetrie, osy rotoinverzní symetrie a symetrický střed. Toto se bude týkat dvou prvků symetrie: osy symetrie a roviny symetrie.
2.1 Osa symetrie
(1) Pojem osy souměrnosti a jejich zápis.
Osa symetrie je pomyslná přímka, která udává, kolikrát se základní úroveň (obrázky 2-2-1 až 2-2-2) objeví ve stejné poloze, když se mřížová struktura otočí o 360° kolem této pomyslné přímky. Tento počet může být ve čtyřech případech pouze 2, 3, 4 nebo 6krát. Lze jej také chápat jako pomyslnou přímku procházející středem geometrického tělesa, přičemž geometrické těleso se podél této přímky otáčí o 360°. Předpokládejme, že tvar geometrického tělesa po otočení o určitý úhel je shodný s tvarem geometrického tělesa při počátečních nulových stupních. V takovém případě se tato pomyslná přímka nazývá osa souměrnosti.
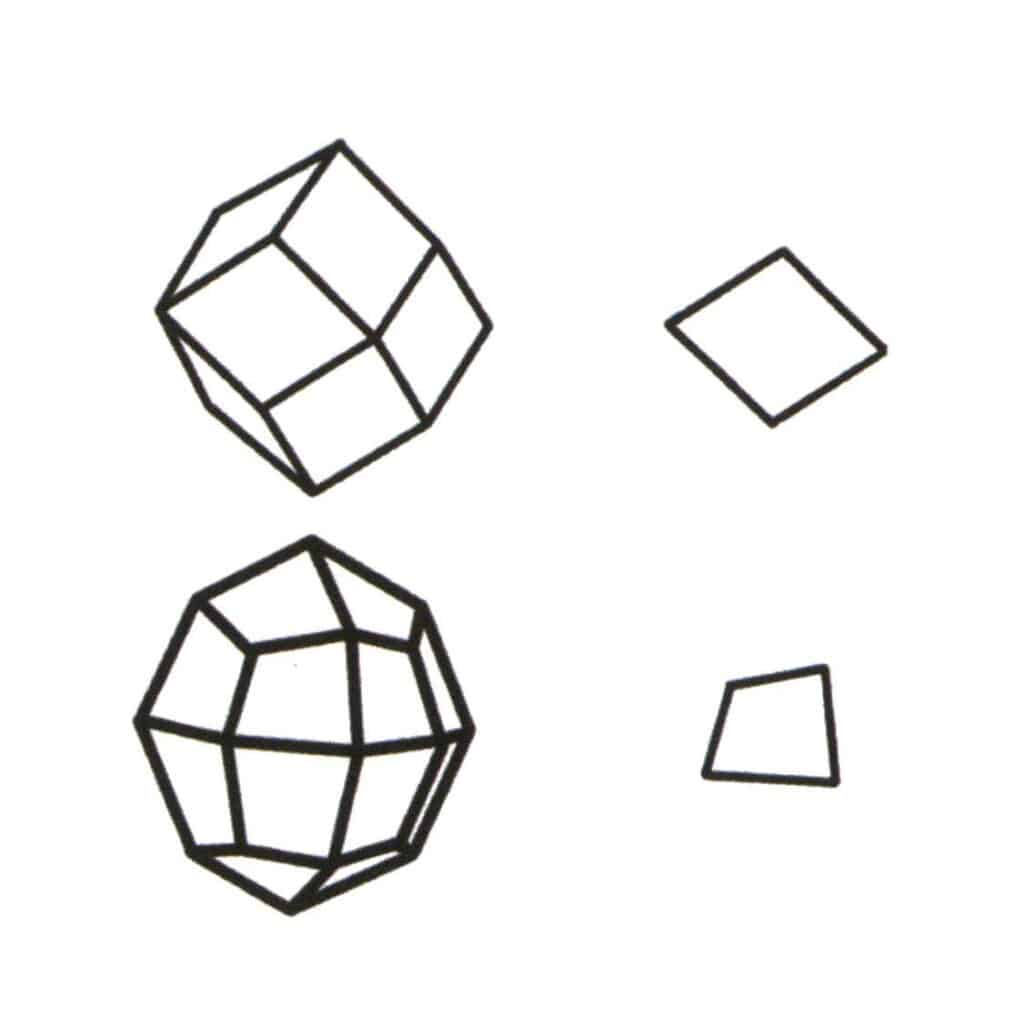
Obrázek 2-2-1 Výběr základní úrovně pro jednotný formulář.
Základní úroveň jednoduchého tvaru je nejmenší opakující se rovina, která tvoří simplex. Na obrázku vlevo nahoře je zobrazen kosočtvercový dvanáctistěn, což je uzavřený útvar složený z jednoho typu stěn. Nejmenší opakující se rovinou je kosočtverec zobrazený vpravo nahoře, takže základní úrovní pro kosočtvercový dodekaedr je kosočtverec. Vlevo dole na obrázku je zobrazen čtyřboký osmistěn, což je uzavřený útvar složený z jednoho typu stěny. Nejmenší opakující se rovinou je čtyřúhelník zobrazený vpravo dole, takže základní rovinou pro čtyřboký osmistěn je čtyřúhelník.
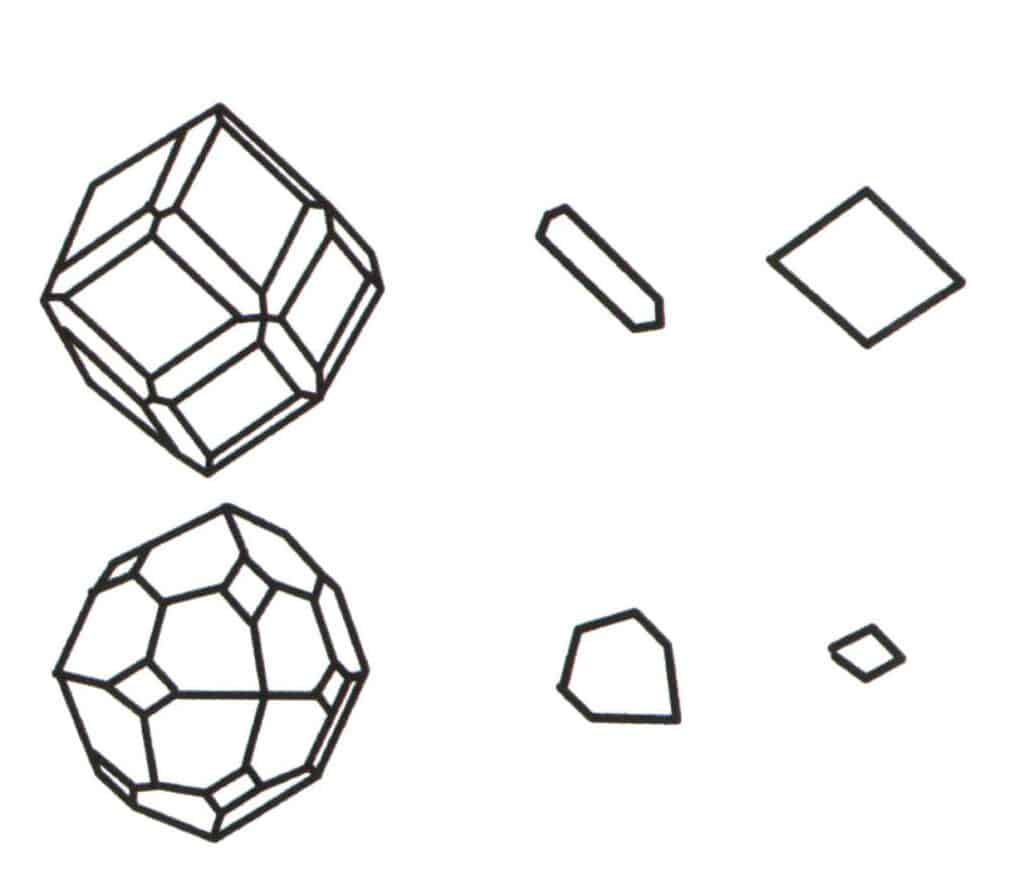
Obrázek 2-2-2 Výběr základní úrovně pro polytop.
Sdružením více jednoduchých forem vzniká kombinovaná forma a volba základní úrovně pro kombinovanou formu je úsudkem o jednoduché formě, která kombinovanou formu tvoří. První sloupec zleva na obrázku představuje kombinovanou formu (vzniklou agregací jednoduchých forem dodekaedru a tetraedru) a toto geometrické těleso je uzavřený útvar složený ze dvou typů stěn. Šestiúhelník představuje minimální opakující se rovinu ve druhém sloupci a kosočtverec vpravo ve třetím sloupci. Základní rovinou pro kombinovaný útvar v prvním sloupci je tedy buď šestiúhelník, nebo kosočtverec. Při výpočtu osy symetrie lze jako základní hladinu pro záznam symetrie zvolit pouze jeden tvar.
Osa symetrie se označuje velkým písmenem L, přičemž pořadí osy je následující n napsané v pravém horním rohu L, zapsané jako Lⁿ. Například 2násobná osa se označuje jako L², 3násobná osa jako L³, 4násobná osa jako L⁴ a 6násobná osa jako L⁶. L⁶, L⁴, L³ se obvykle označuje jako osa vyššího řádu.
Krystaly mohou mít osy symetrie v různých směrech a počet těchto neshodných os symetrie se obvykle zapisuje vlevo od L. Například šest sekundárních os se označuje jako 6L² (obrázek 2-2-3 až obrázek 2-2-9), tři terciární osy jako 3L³ (obrázek 2-2-10 až obrázek 2-2-14), čtyři terciární osy jako 4L³ (obrázek 2-2-15 až obrázek 2-2-18) a jedna hexagonální osa jako L⁶ (obrázek 2-2-19).
Pokud má krystal více os symetrie, zaznamenaná metoda je seřadí zleva doprava v sestupném pořadí, přičemž počet os symetrie je zapsán na levé straně příslušné osy, například L⁶6L², 3L⁴4L³6L².
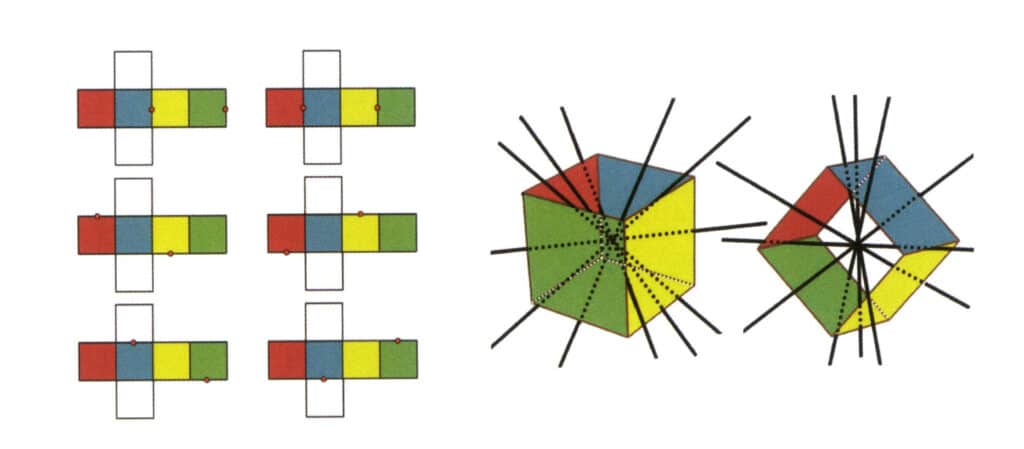
Obrázek 2-2-3 Sekundární osa krychle
Na levé straně obrázku je zobrazen rozložený pohled na krychli, červené tečky označují průsečíky pomyslné přímky a hran. Pravá strana obrázku znázorňuje uzavřenou krychli, kde se sekundární osa může objevit ve středu rovnoběžných hranových přímek, ve středu rovnoběžných pravoúhlých stěn nebo v průsečících tří nebo více rovnoběžných stěn připomínajících obdélník.
Kopírování @ Sobling.Jewelry - Výrobce šperků na zakázku, továrna na šperky OEM a ODM
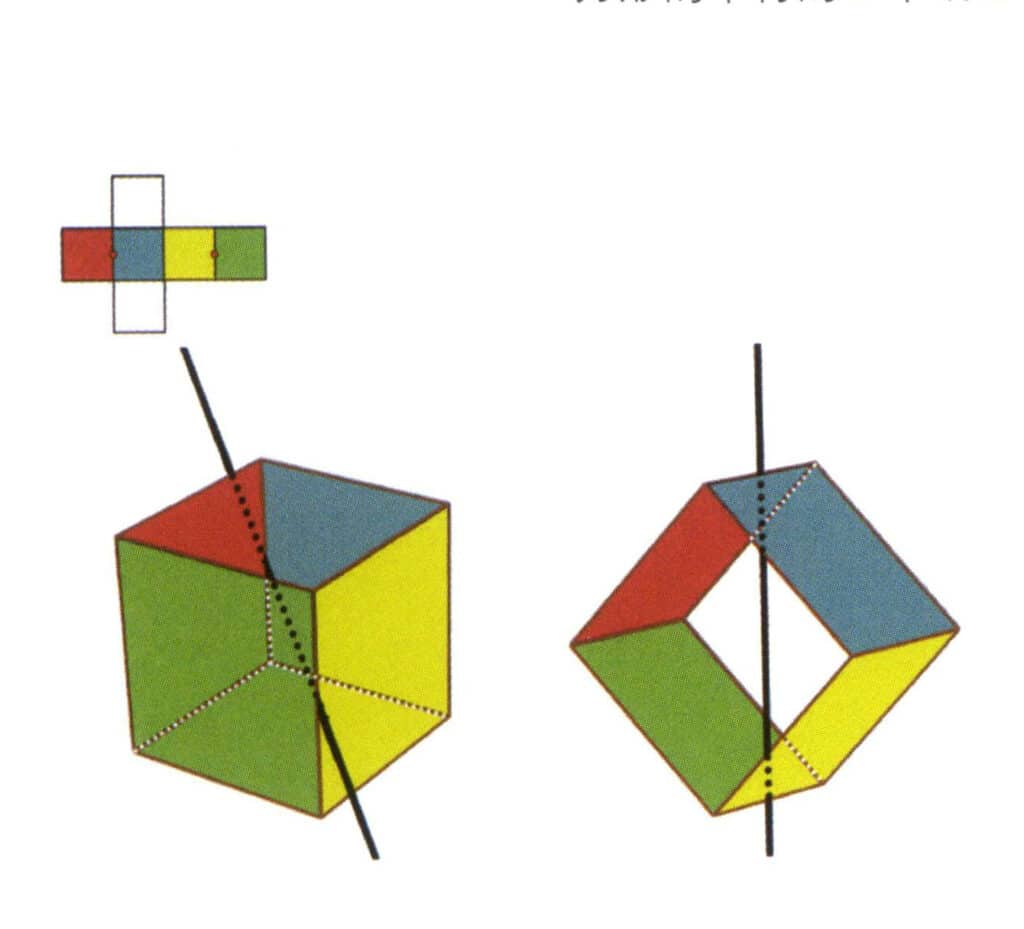
Obrázek 2-2-4 První sekundární osa krychle
Vyberte střed rovnoběžek, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Základní úrovně s různými barvami, ale stejným tvarem se budou opakovat dvakrát ve stejné poloze (červená a modrá stěna, žlutá a zelená stěna, dvě bezbarvé stěny a tři sady opakujících se stěn. Ačkoli se objeví tři sady opakujících se ploch, protože pomyslná čára nezměnila polohu ani úhel, sekundární osa je zaznamenána pouze jednou). Tato pomyslná čára je zaznamenána jako sekundární osa.
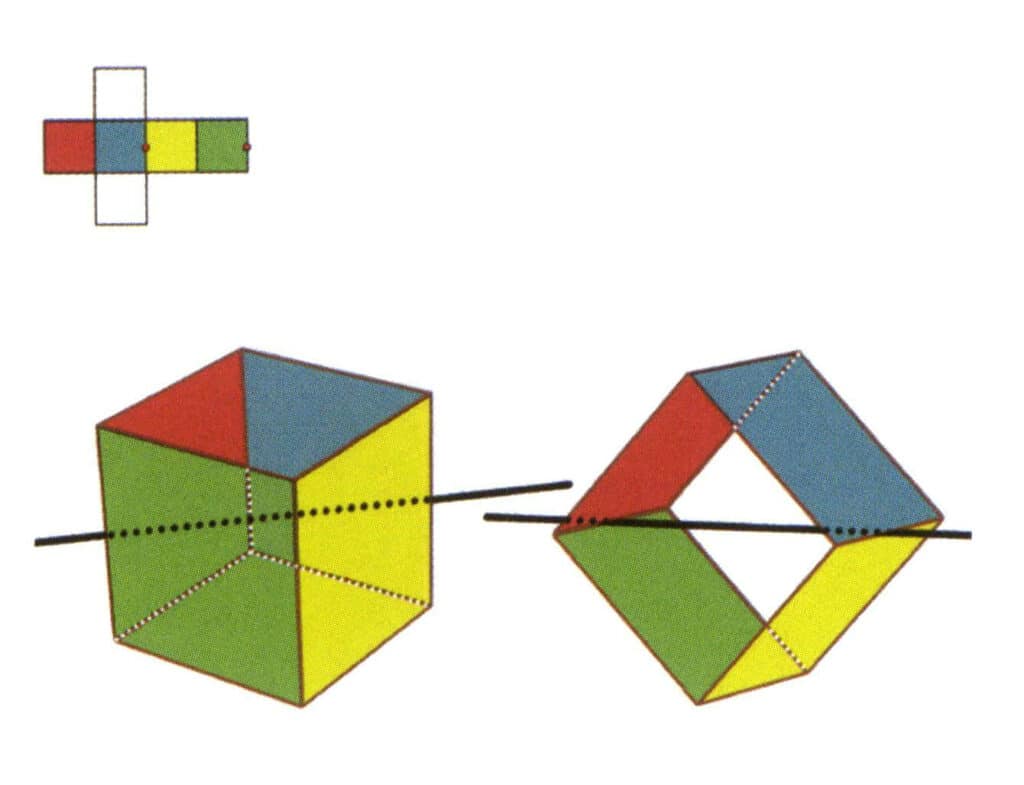
Obrázek 2-2-5 Druhá sekundární osa krychle
Vyberte střed rovnoběžek, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Základní úrovně s různými barvami, ale stejným tvarem se budou opakovat dvakrát ve stejné poloze (červená a zelená stěna, žlutá a modrá stěna, dvě bezbarvé stěny a tři sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako druhá sekundární osa.
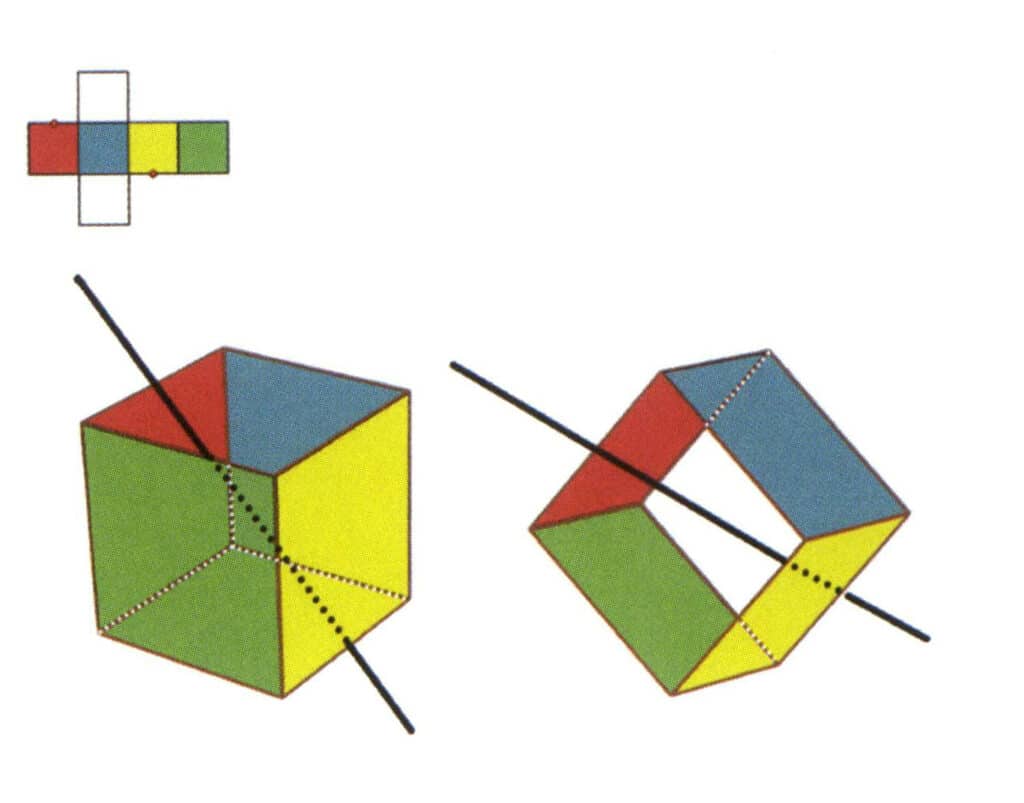
Obrázek 2-2-6 Třetí sekundární osa krychle.
Vyberte střed rovnoběžek, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Základní úrovně s různými barvami, ale stejným tvarem se budou opakovat dvakrát na stejném místě (červené a bezbarvé stěny, zelené a modré stěny, bezbarvé a žluté stěny, tři sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako třetí sekundární osa
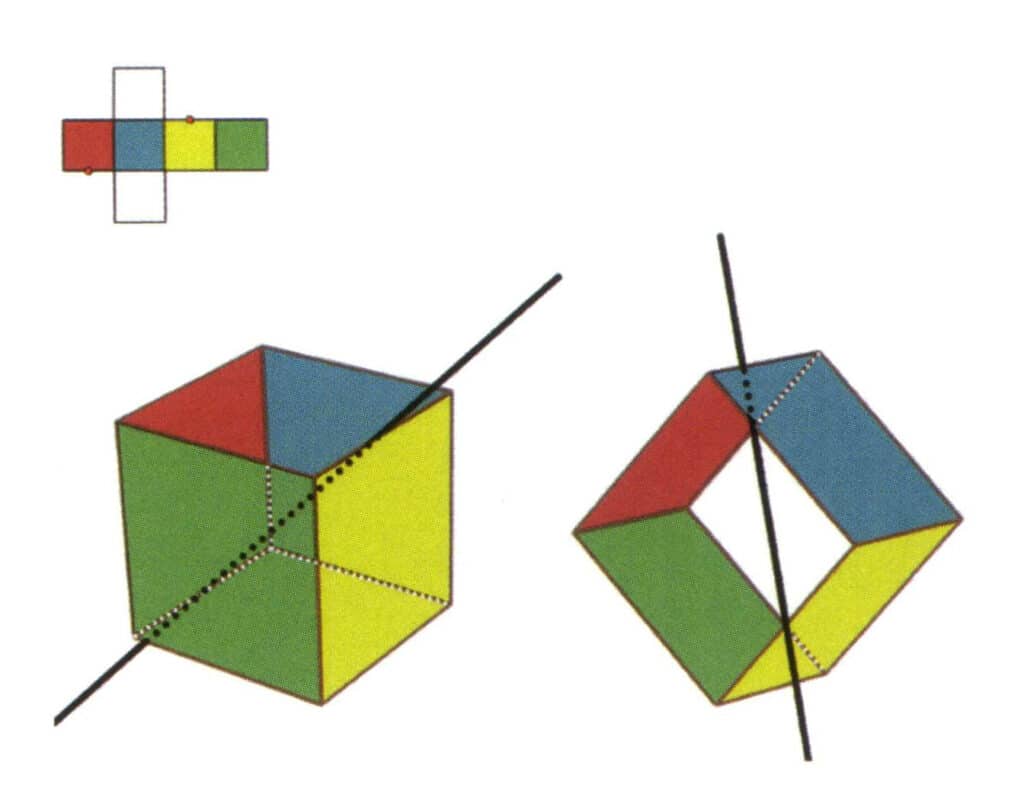
Obrázek 2-2-7 Čtvrtá sekundární osa krychle
Zvolte střed rovnoběžek, jak je znázorněno na obrázku, představte si přímku procházející středy těchto dvou hran a otočte krychli o 360°; různobarevné, ale stejně tvarované referenční roviny se budou opakovat ve stejné poloze dvakrát (červená a bezbarvá plocha, zelená a modrá plocha, bezbarvá a žlutá plocha, tři sady opakujících se ploch), tato pomyslná přímka je zaznamenána jako čtvrtá sekundární osa.
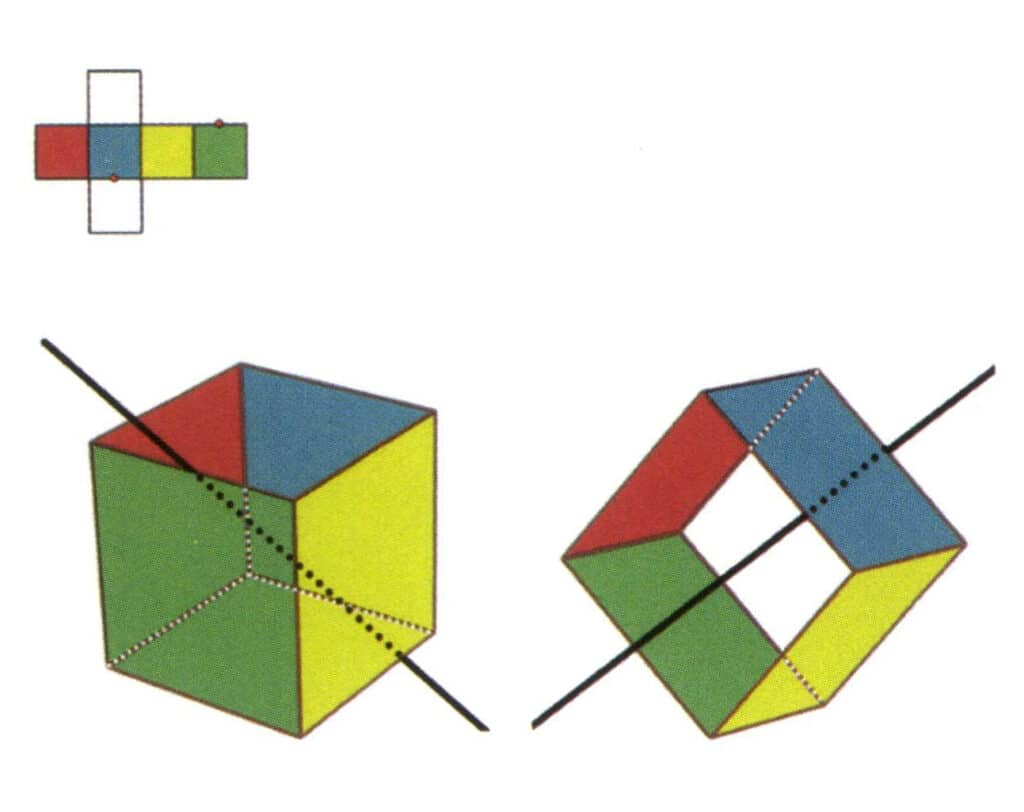
Obrázek 2-2-8 Pátá sekundární osa krychle.
Vyberte středy rovnoběžek, jak je znázorněno na obrázku, představte si přímku procházející středy těchto dvou hran, otočte krychli o 360°, různobarevné, ale stejně tvarované referenční roviny se budou opakovat ve stejné poloze dvakrát (červené a bezbarvé plochy, zelené a modré plochy, bezbarvé a žluté plochy, tři sady opakujících se ploch), tato představovaná přímka je zaznamenána jako pátá sekundární osa.
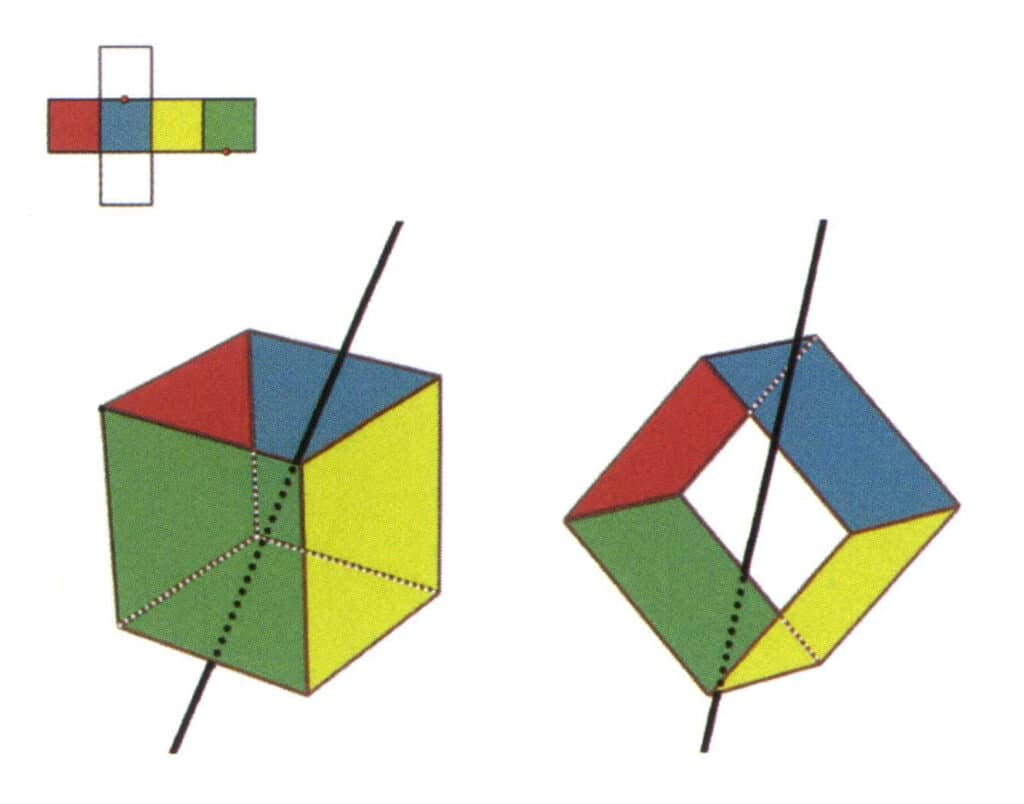
Obrázek 2-2-9 Šestá sekundární osa krychle
Vyberte střed rovnoběžek, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Různě zbarvené, ale stejně tvarované základní úrovněse budou opakovat ve stejné poloze dvakrát (zelené a bezbarvé stěny, červené a žluté stěny, bezbarvé a modré stěny, tři sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako šestá sekundární osa.
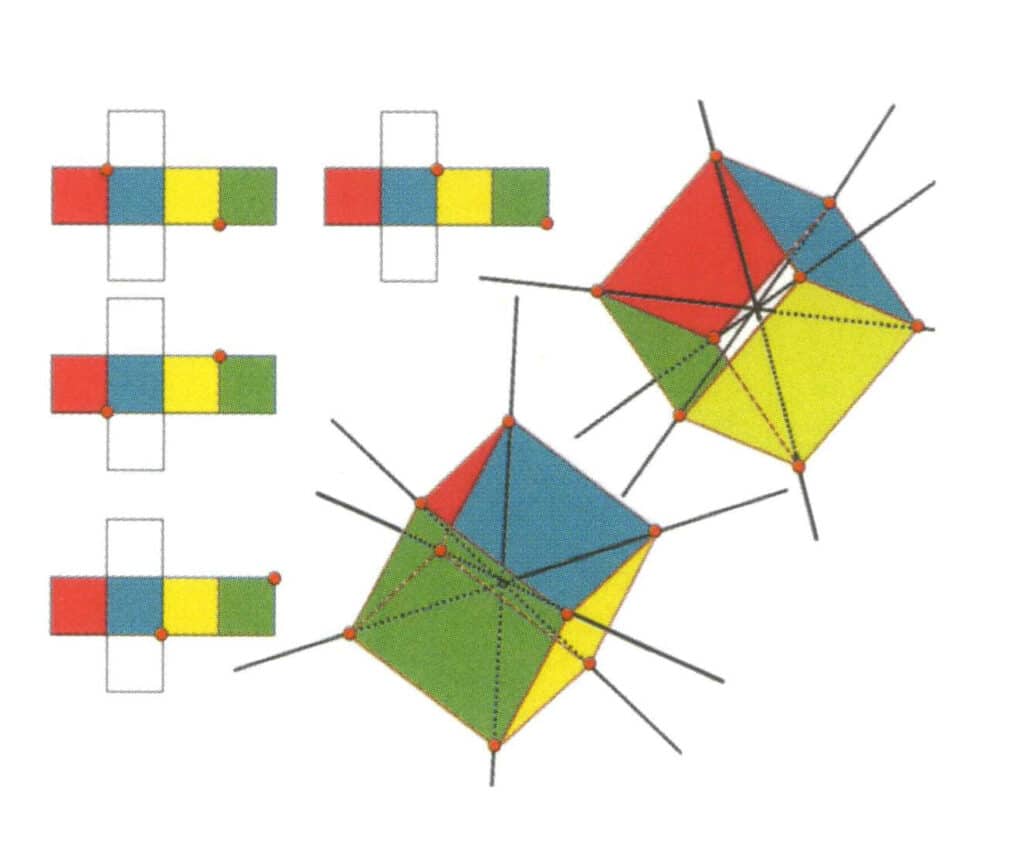
Obrázek 2-2-10 Terciární osa krychle
Na levé straně obrázku je zobrazen rozložený pohled na krychli, přičemž červená tečka označuje průsečík pomyslné přímky s hranovou čárou. Pravá strana obrázku ukazuje uzavřenou krychli; červené body označují průsečík pomyslné přímky a hrany. Třetinová osa se může objevit ve středu stěn rovnoběžného rovnostranného trojúhelníku, v průsečíku tří nebo více rovnoběžných stěn připomínajících rovnostranný trojúhelník.
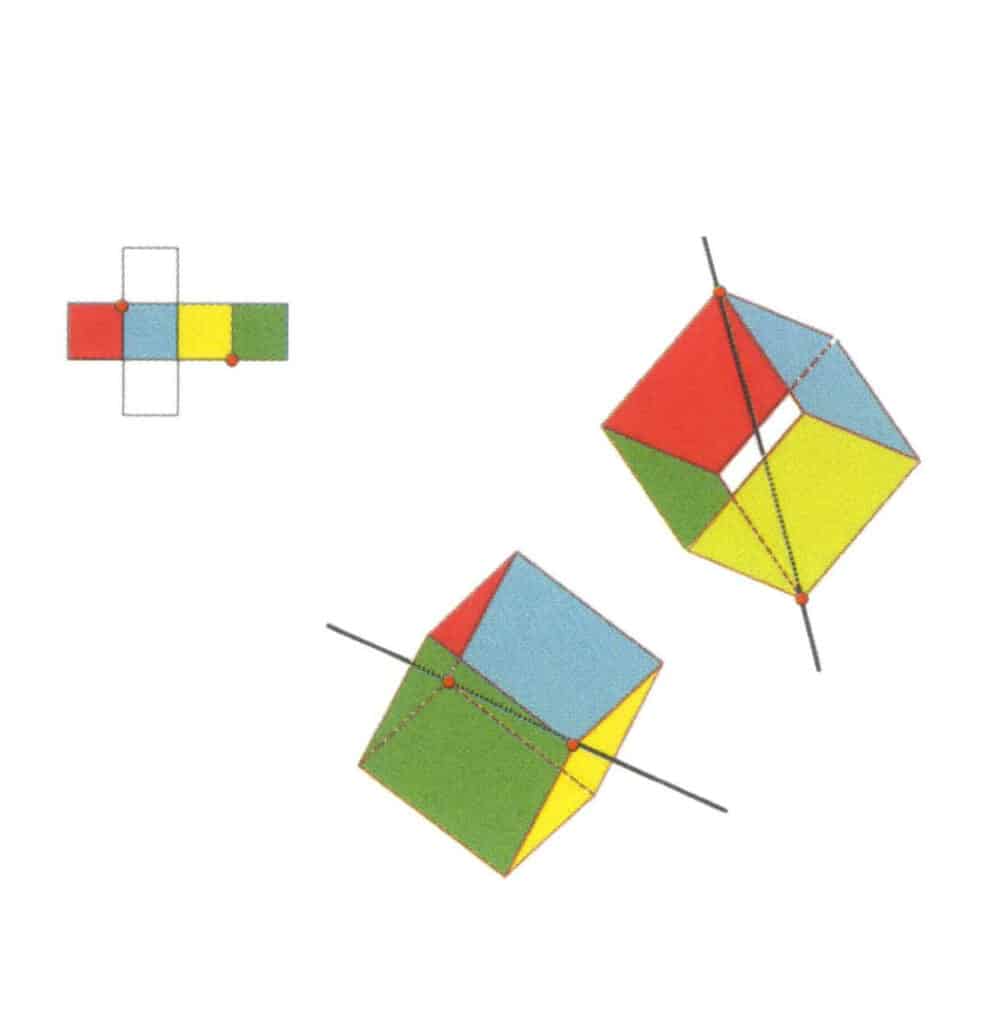
Obrázek 2-2-11 První terciární osa krychle.
Vyberte průsečíky tří stěn podle obrázku, představte si přímku procházející středy těchto dvou hran, otočte krychli o 360°, různobarevné, ale stejně tvarované referenční roviny se budou opakovat ve stejné poloze třikrát (červená, bezbarvá a modrá stěna, zelená, bezbarvá a žlutá stěna, dvě sady opakujících se stěn), tato představovaná přímka je zaznamenána jako první terciární osa.
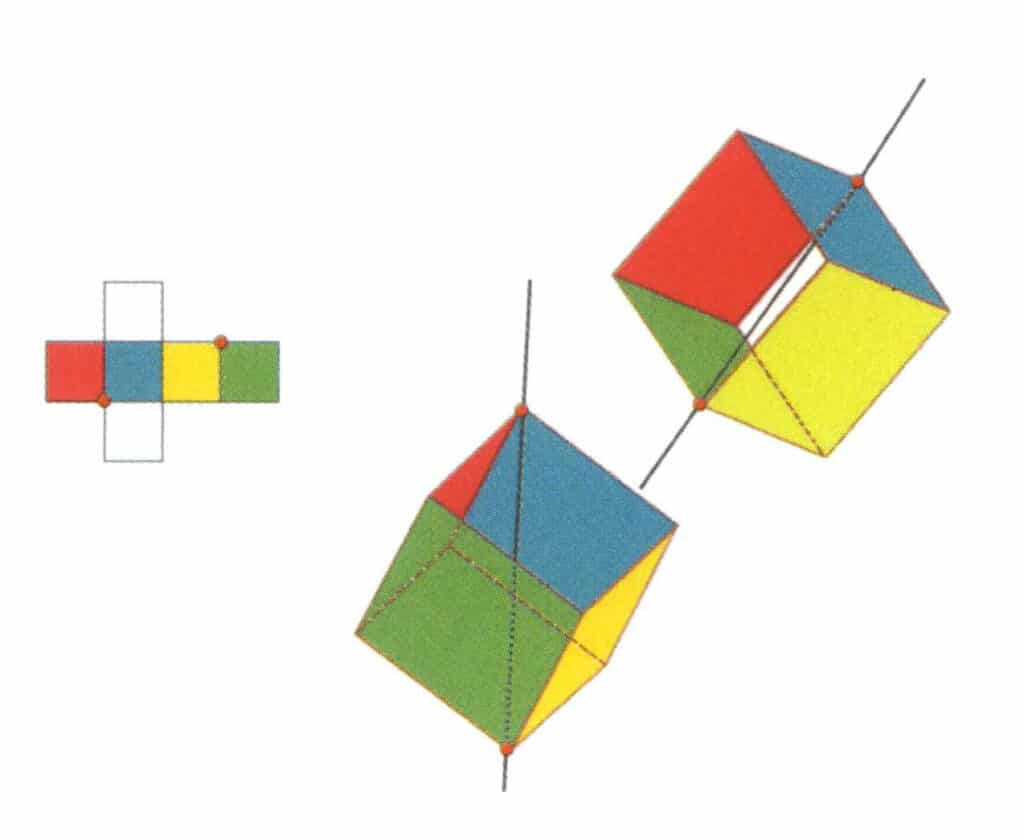
Obrázek 2-2-12 Druhá terciární osa krychle.
Vyberte průsečíky tří ploch, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Různě barevné, ale stejně tvarované základní roviny se budou opakovat ve stejné poloze třikrát (červené, bezbarvé a modré stěny; zelené, bezbarvé a žluté stěny, dvě sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako druhá terciární osa.
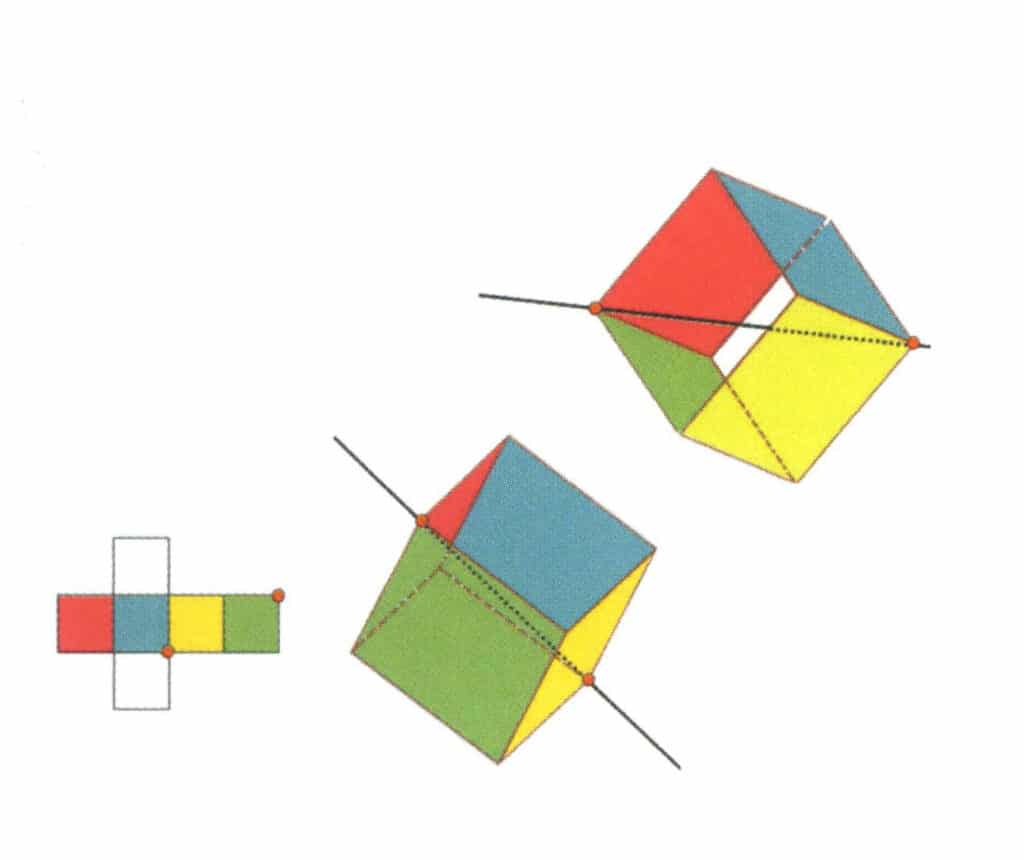
Obrázek 2-2-13 Třetí terciární osa krychle
Vyberte průsečíky tří ploch, jak je znázorněno na obrázku. Představte si přímku procházející středy těchto dvou hran a otáčející krychli o 360°. Různě barevné, ale stejně tvarované základní roviny se budou opakovat ve stejné poloze třikrát (červené, bezbarvé a zelené stěny; modré, bezbarvé a žluté stěny, dvě sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako třetí terciární osa.
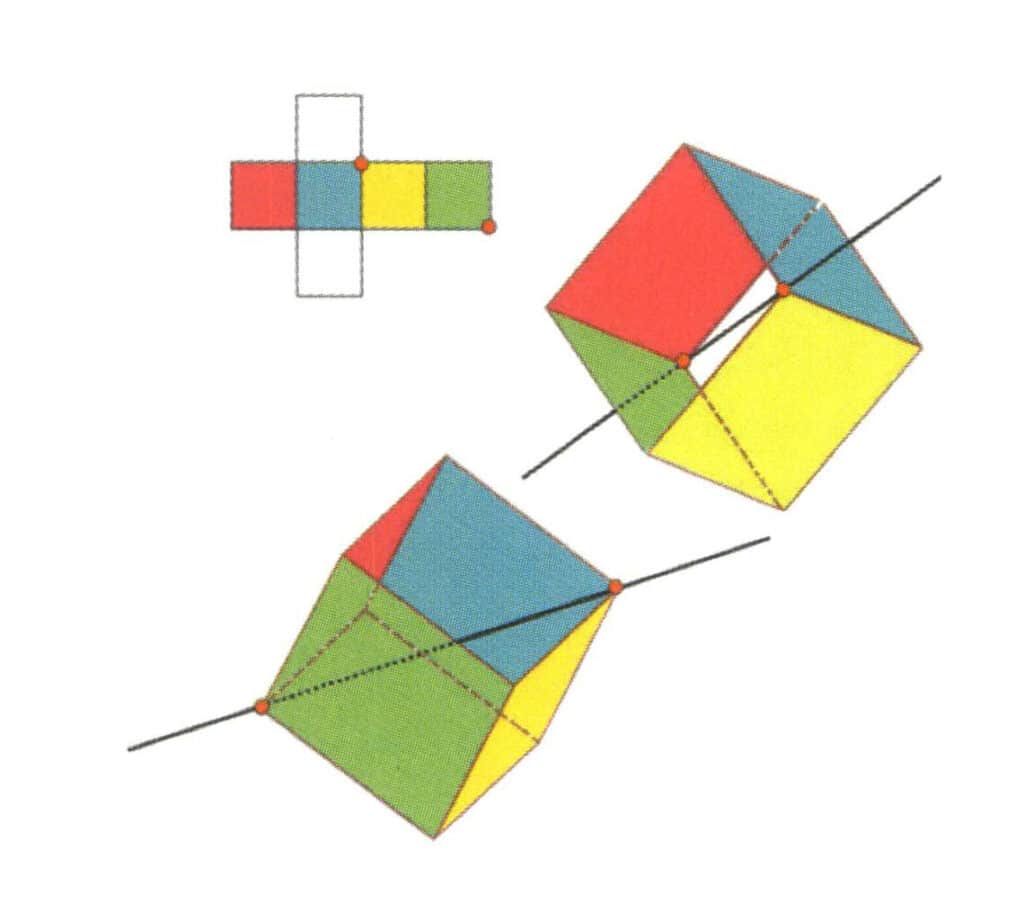
Obrázek 2-2-14 Čtvrtá krychlová osa krychle.
Vyberte průsečík tří stěn, jak je znázorněno na obrázku, za předpokladu, že středem obou hran prochází jedna přímka, otočte krychli o 360°, různé barvy, ale stejný tvar základní úrovně bude stejný. Polohu zopakujte třikrát (červená, bezbarvá, zelená stěna, modrá, bezbarvá a žlutá stěna, dvě sady opakujících se stěn). Tato pomyslná čára je zaznamenána jako čtvrtá osa krychle.
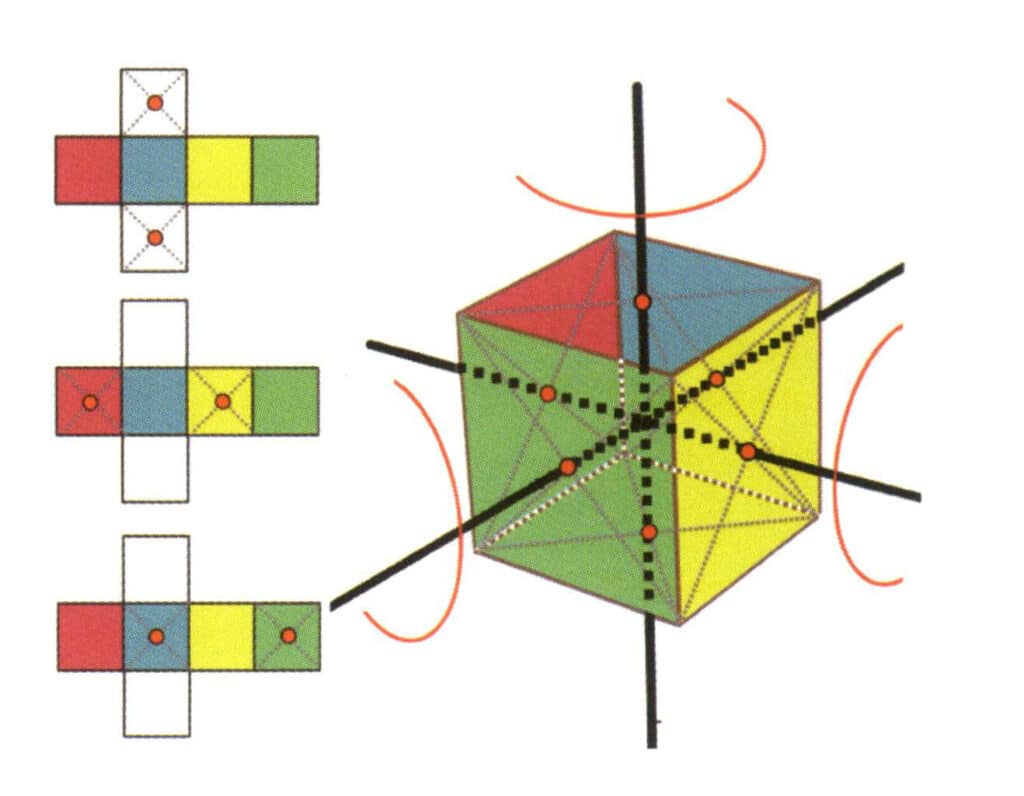
Obrázek 2-2-15 Čtvrtá osa kostky
Na levé straně obrázku je zobrazen rozložený pohled na krychli, přičemž červené tečky označují průsečíky pomyslné čáry a hran. Pravá strana obrázku ukazuje uzavřenou krychli, přičemž červené tečky označují průsečíky pomyslné přímky a roviny. Čtvrtá osa se může objevit ve středu rovnoběžných čtvercových ploch, v průsečíku tří nebo více rovnoběžných ploch, které připomínají čtverec.
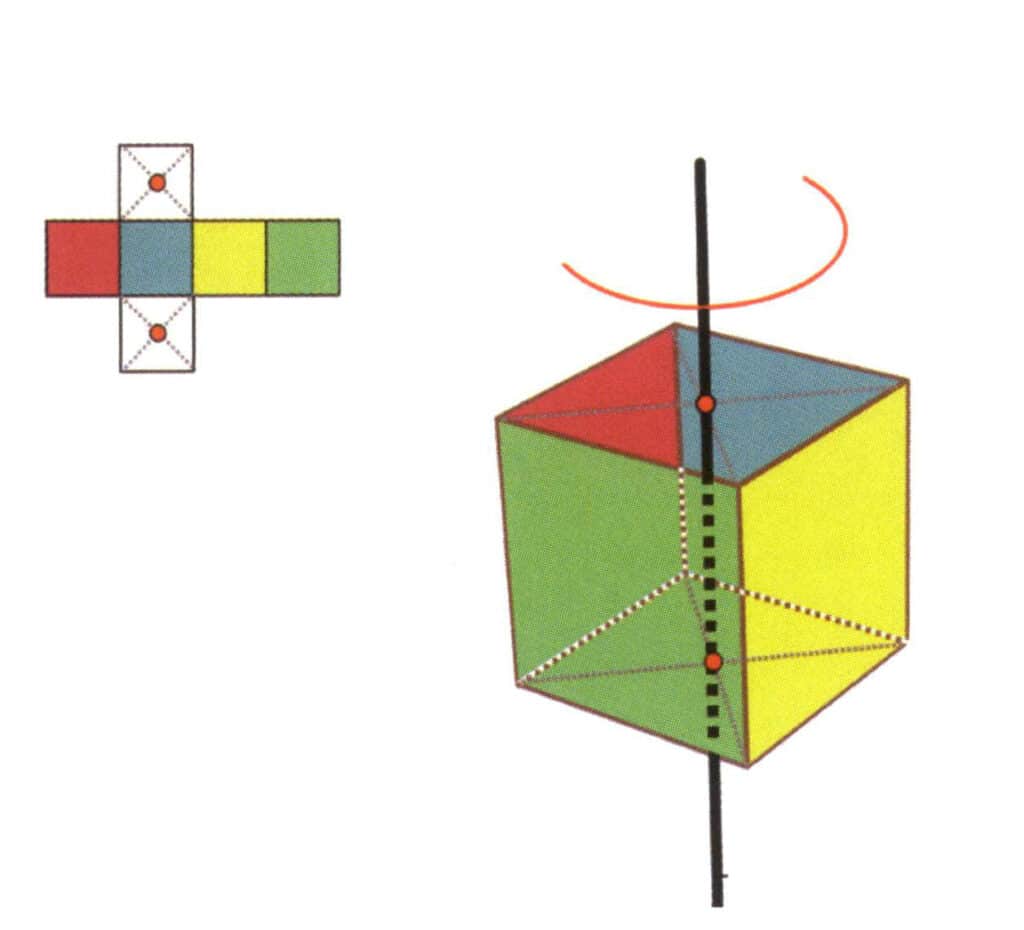
Obrázek 2-2-16 První kvartická osa krychle
Zvolte středy rovin znázorněných na obrázku, předpokládejte, že středy obou rovin prochází přímka, a otočte krychli o 360°. Různě barevné, ale stejně tvarované plochy základní roviny se budou opakovat ve stejné poloze čtyřikrát (červená, modrá, zelená a žlutá plocha) a tato hypotetická přímka je zaznamenána jako čtyřnásobná osová.
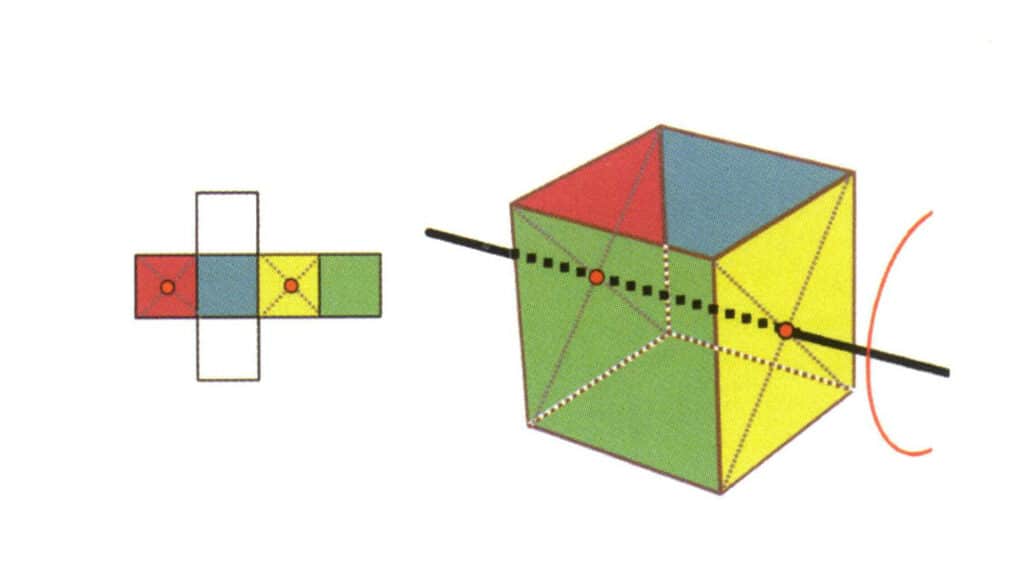
Obrázek 2-2-17 Druhá kvartická osa krychle
Vyberte střed roviny podle obrázku, představte si přímku procházející krychlí a otočte krychlí o 360°; základní rovinná plocha různých barev, ale stejného tvaru se bude čtyřikrát opakovat ve stejné poloze (bezbarvá, modrá plocha nahoře, bezbarvá, zelená plocha dole) a tato pomyslná přímka bude zaznamenána jako druhá čtyřúhelníková osa.
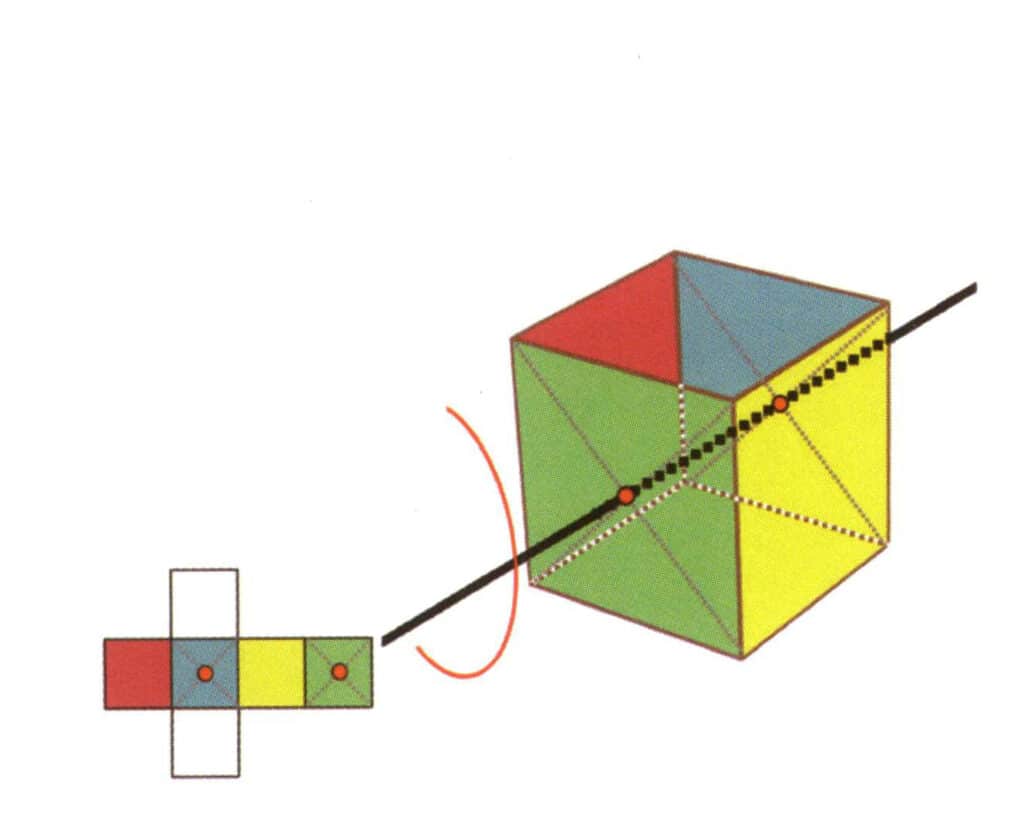
Obrázek 2-2-18 Třetí kvartická osa krychle
Vyberte střed roviny podle obrázku, představte si přímku procházející krychlí a otočte krychli o 360°. Základní rovina různých barev, ale stejného tvaru se bude čtyřikrát opakovat ve stejné poloze (bezbarvá, červená plocha nahoře, bezbarvá, žlutá plocha dole) a tato pomyslná přímka bude zaznamenána jako třetí, čtvrtá osa
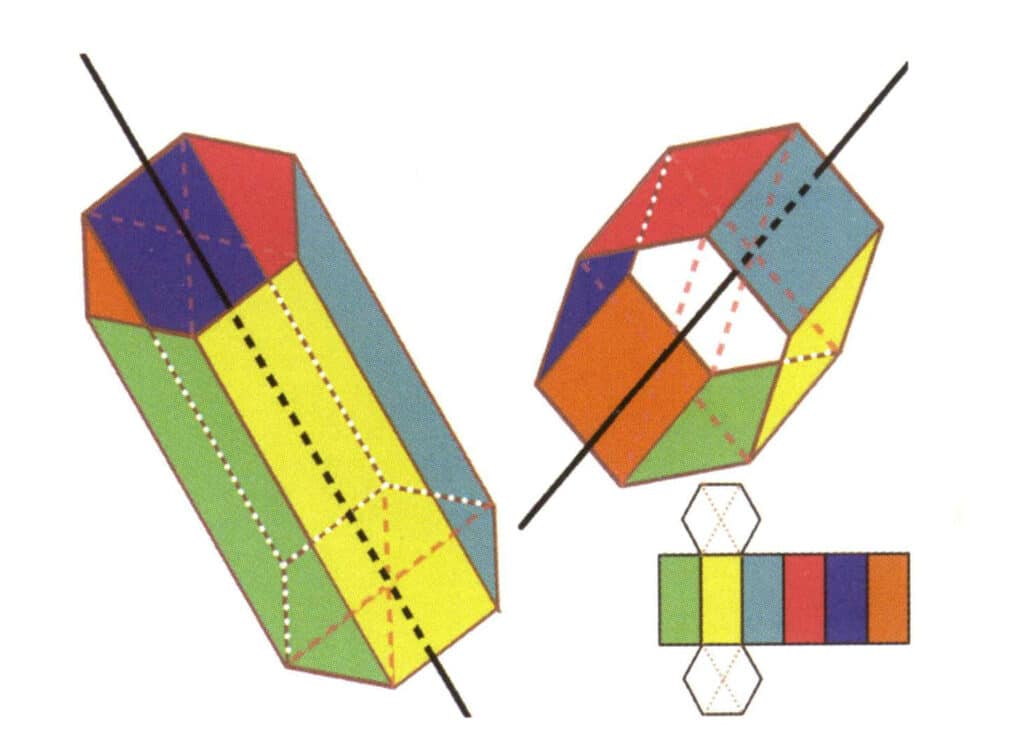
Obrázek 2-2-19 Šest os šestibokého hranolu
Černé čáry vlevo a vpravo nahoře představují šest os šestibokého hranolu. Vpravo dole je roztažení šestiúhelníkového hranolu. Šestihranná osa se může objevit ve středu stěn rovnoběžného šestiúhelníku nebo v průsečíku šesti stěn šestiúhelníku.
(2) Úvahy o nalezení osy symetrie.
① Existuje pět typů poloh osy symetrie.
Střed dvou rovnoběžných hran, například poloha sekundární osy krychle.
Střed dvou rovnoběžných rovin, například poloha osy krychle.
Mezi dvěma vrcholy (průsečíky více stěn), například poloha terciální osy krychle.
Střední bod mezi vrcholem a rovnoběžnou rovinou, například poloha terciální osy čtyřstěnu.
Střed hranové čáry a střed rovnoběžné roviny, například poloha vedlejší osy trojbokého hranolu.
② Výběr osy symetrie ve stejném směru se řídí principem nejmenšího čísla. Například podle principu nejnižšího čísla, pokud v jednom směru najdeme šest os souměrnosti a tři osy souměrnosti, bude nakonec zapsán jako L³. Osy souměrnosti v různých směrech by měly být zaznamenány podle nalezeného počtu.
Je třeba poznamenat, že kromě šestinásobné osy symetrie a čtyřnásobné osy symetrie, které se nemohou vyskytovat současně a může se vyskytovat pouze jedna šestinásobná osa, mohou ostatní osy symetrie existovat současně v různých formách nebo ve více případech.
③ Základní úroveň musí být vybrána jako nejmenší jednotková rovina; jako základní úroveň nelze vybrat dvě nebo více protínajících se rovin. V opačném případě to ovlivní přesnost posouzení osy symetrie.
④ Při zaznamenávání počtu os souměrnosti je nezbytné určit, kolikrát se stejný tvar a velikost roviny opakuje ve stejné poloze.
⑤ Pokud existuje vedlejší osa svislé symetrie Lⁿ(n = 3, 4 nebo 6), musí existovat n vedlejších os svislých na Lⁿ.
2.2 Rovina symetrie
(1) Koncepce a způsob záznamu roviny symetrie
Rovina symetrie je pomyslná rovina, která při řezání krystalu podél této roviny umožňuje, aby každá polovina krystalu byla zrcadlovým obrazem druhé poloviny (obrázek 2-2-20). Ve stejné krystalové struktuře se taková rovina může objevit maximálně devětkrát (obrázek 2-2-21), což znamená, že ji lze rozetnout devíti různými způsoby a obě poloviny se mohou zcela shodovat. Samozřejmě ne všechny krystalové struktury mají roviny symetrie.
Velké písmeno P představuje rovinu symetrie. Některé krystaly mají více neshodných rovin symetrie a počet těchto rovin symetrie se konvenčně píše vlevo od P; například čtyři roviny symetrie se označují jako 4P a jedna rovina symetrie se označuje jako P.
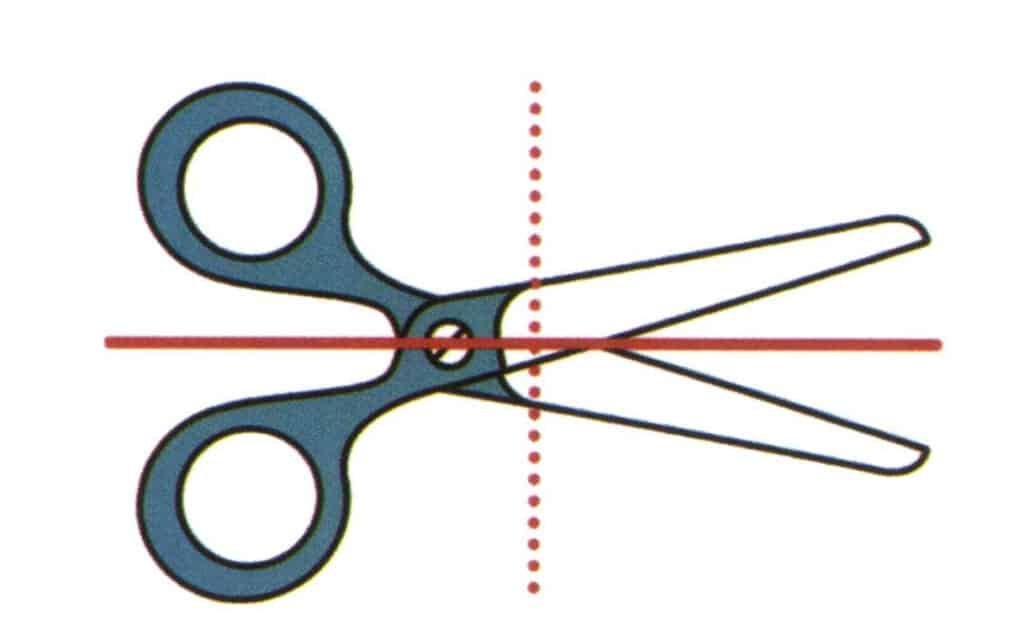
Obrázek 2-2-20 Představte si svislou rovinu papíru a rovinu táhnoucí se ve směru červené plné čáry, která dělí nůžky na horní a dolní část, přičemž horní a dolní část jsou zrcadlově souměrné. Tato představovaná rovina se nazývá rovina souměrnosti. Představte si další rovinu kolmou k povrchu papíru a táhnoucí se ve směru červené přerušované čáry, která dělí nůžky na levou a pravou část, ale tvary nůžek na levé a pravé straně nejsou souměrné.
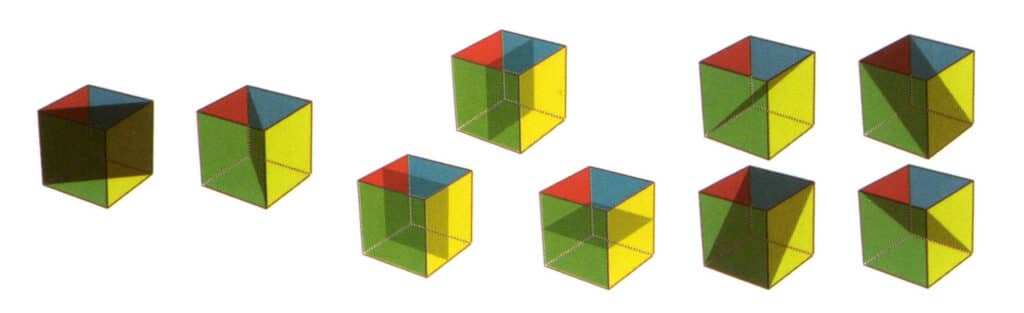
Obrázek 2-2-21 Devět rovin souměrnosti krychle
(2) Tipy pro vyhledávání Roviny symetrie.
① Rovina symetrie je často rovnoběžná a shodná s osou symetrie.
② Rovina symetrie je pomyslná rovina, která rozděluje krystalickou geometrii a která se liší od rovnoběžné dvojroviny v geometrii.
③ Pokud rovina symetrie obsahuje osu symetrie Lⁿ, pak musí existovat n rovin symetrie, které obsahují Lⁿ.
(3) Bod Skupina.
Bodová skupina je součet všech prvků symetrie v krystalu. Pořadí zápisu bodové skupiny je osa symetrie + rovina symetrie, například 3L²3P (obrázek 2-2-22). Pokud má krystal více os symetrie, je zvykem zapisovat je zleva doprava, od osy vyššího řádu k ose nižšího řádu, a pořadí rovin symetrie, například L⁴4L²5P (obrázek 2-2-23). V krystalech existuje 32 typů symetrie.
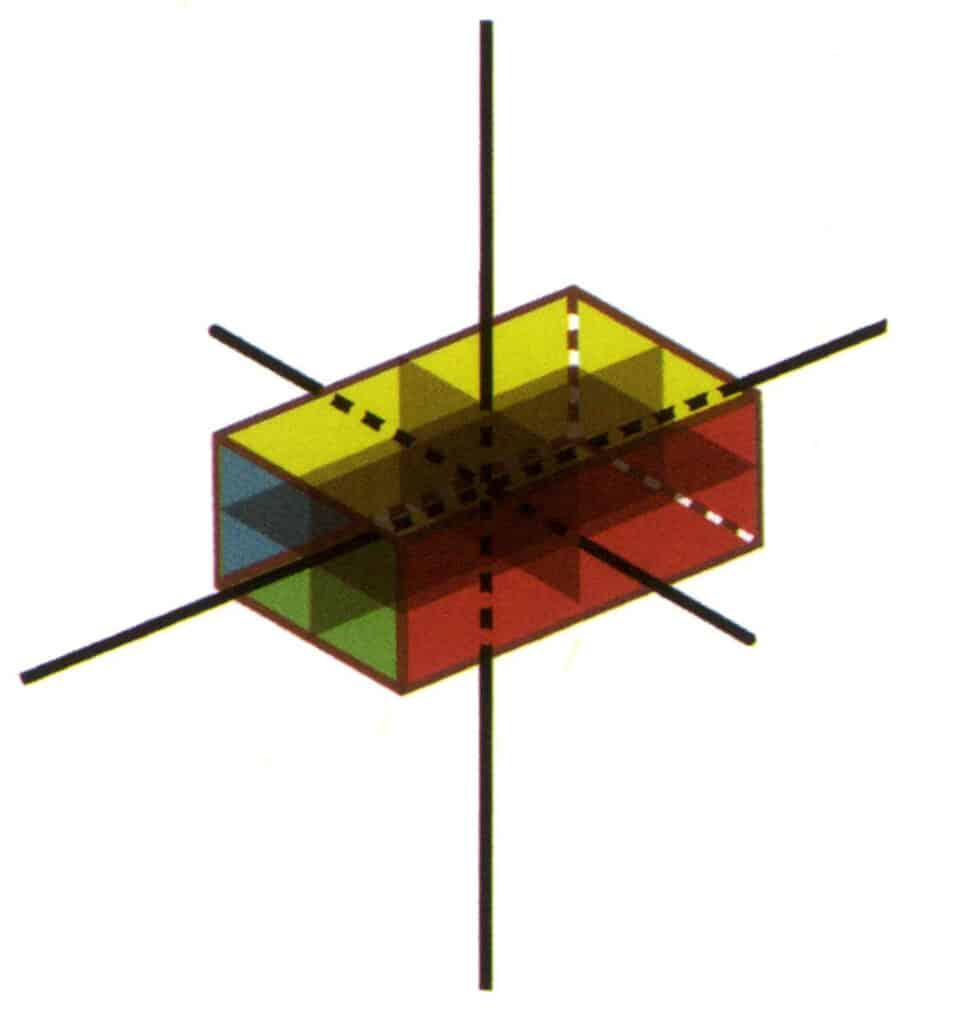
Obrázek 2-2-22 Skupina bodů 3L²3P (obdélníkový krychle s obdélníkovým průřezem)
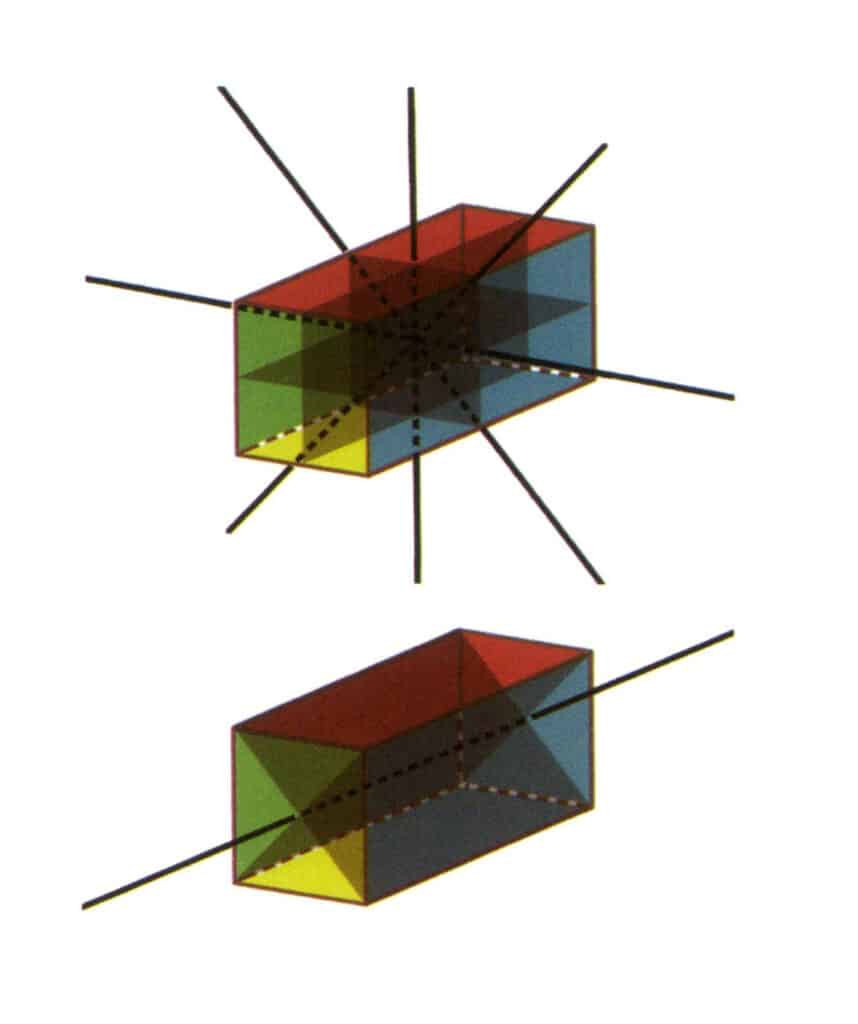
Obrázek 2-2-23 Skupina bodů L⁴4L²5P (pravoúhlý hranol se čtvercovým průřezem) se čtyřmi druhými osami a třemi souměrnými stěnami nahoře a jednou čtvrtou osou a dvěma souměrnými stěnami dole.
3. Klasifikace krystalů
Symetrie je součástí klasifikace krystalů. Pro popis krystalové struktury přírodních a umělých krystalů drahých kamenů v rámci klasifikace krystalů je třeba zavést další pojem - krystalovou osu. Krystalová osa je pomyslná čára procházející krystalovou strukturou, která udává směr, v němž se opakují uzly mřížky, a relativní vzdálenost, v níž se uzly podél tohoto směru opakují. Krystalová osa se shoduje s normálou osy symetrie nebo roviny symetrie. Pokud osa symetrie nebo rovina symetrie neexistuje, lze zvolit krystalovou osu rovnoběžnou se směrem hrany krystalu.
Na základě prvků symetrie a krystalových os rozděluje akademický systém krystaly do tří krystalových rodin a sedmi krystalových soustav (tabulka 1).
Tabulka 1: Klíčové body pro určení krystalových rodin a systémů
| Rodina Crystal | Crystal | Klíčové body pro určení | Běžné odrůdy drahých kamenů |
|---|---|---|---|
| Nízkoúrovňový krystalový systém | Triklinický systém | Žádná druhá osa nebo rovina symetrie | Amazonit, rodonit, tyrkys |
| Monoklinická krystalová soustava | Žádné osy vyššího řádu, maximálně jedna vedlejší osa a rovina symetrie. | Jadeit, diopsid, spodumen, epidot | |
| Orthorombická krystalová soustava | Žádné osy vyššího řádu, více než jedna sekundární osa nebo rovina symetrie | olivín, topaz, saualpit (včetně tanzanitu), cordierit, chryzoberyl, enstatit | |
| Rodina středně pokročilých krystalů | Tetragonální krystalová soustava | 1 čtyřnásobná osa (lze ji znázornit pomocí L4) | Diamond |
| Trigonální krystalová soustava | 1 trigonální osy (lze znázornit pomocí L3) | Korund, rubín, safír, turmalín , krystaly z rodiny křemene (např. křišťál, ametyst, citrín atd.), rodochrozit. | |
| Šestiboká krystalová soustava | 1 šestiúhelníková osa (lze znázornit pomocí L6) | Akvamarín, smaragd a další drahé kameny z rodiny berylitu, apatit | |
| Pokročilá rodina krystalů | Izometrický krystalový systém | 4 trigonální osy (lze znázornit pomocí 4L3) | Diamant, granát, spinel, fluorit |
4. Běžné vlastnosti drahých kamenů
Mezi běžné drahé kameny patří diamant, spinel, fluorit, granát, berylit, zirkon, korund, turmalín, křišťál, chryzoberyl, topaz atd. Každý typ drahého kamene má své pevné krystalové vlastnosti.
Drahé kameny z rodiny vysokých krystalů mají většinou zrnitý krystalový habitus a běžné odrůdy se často vyskytují v pevných krystalových formách (tabulka 2).
Krystalový habitus středních a nízkých krystalových rodin je sloupcovitý (tabulka 3).
Tabulka 2: Společné charakteristiky krystalů rodin krystalů vysoké úrovně
| Drahokamy tón Jméno | Klasifikace krystalů | Důležité vlastnosti krystalů | |||
|---|---|---|---|---|---|
| Drahokamy tón Jméno | Klasifikace krystalů | Křišťálový návyk | Běžné krystalové formy | Běžné formy dvojčat | Běžné vzory krystalových ploch |
| Diamond | Izometrický krystalový systém | zrnitý krystalový habitus (obrázek 2-2-24), běžně se vyskytuje v oktaedrických zrnech | Běžným krystalovým tvarem je osmistěn a mohou se objevit i složitější krystalové tvary, včetně kosočtverečných dvanáctistěnů, často se zaoblenými krystalovými stěnami, které mohou vykazovat trojnásobnou symetrii. | Trojúhelníková plochá dvojčata, někdy bez viditelných konkávních úhlů (obrázek 2-2-25) | Na povrchu jsou patrné obrácené trojúhelníkové leptací důlky (obrázky 2-2-26, 2-2-27) a další vzory krystalových ploch (obrázky 2-2-28, 2-2-29). |
| Spinel | zrnitý krystalický habit (obrázek 2-2-30), běžně se vyskytuje v oktaedrických granulích | Často se vyrábí v osmistěnné formě, krystalové plochy mohou být velmi ploché a vypadat jako vyleštěné (obrázek 2-2-31). | Dvojité krystaly jsou velmi ploché, připomínají trojúhelníkový tvar s uříznutými rohy (obrázek 2¬2-32). | Povrchově viditelné leptací důlky, některé připomínající diamanty ve tvaru obráceného trojúhelníku (obrázek 2-2-33). | |
| Fluorit | Zrnitý krystalový habitus (obrázek 2-2-34) | Oktaedrické a kubické krystaly (obrázek 2-2-35) | Vzájemně se prolínající dvojčata | Čtvercové stupňovité růstové značky, většinou s mezerami po štěpení, barevné pásy rovnoběžné se směry šesti stěn krychle. | |
| Garnet | Zrnitý krystalický habitus, běžně se vyskytuje v kosočtverečných dodekaedrických zrnech (obrázek 2-2-36). | Rhombický dodekaedr nebo čtvercový trapezoedr | Vzácné | Viditelné koncentrické prstencové pásy stejného tvaru jako krystalové plochy (obrázek2-2-37). | |
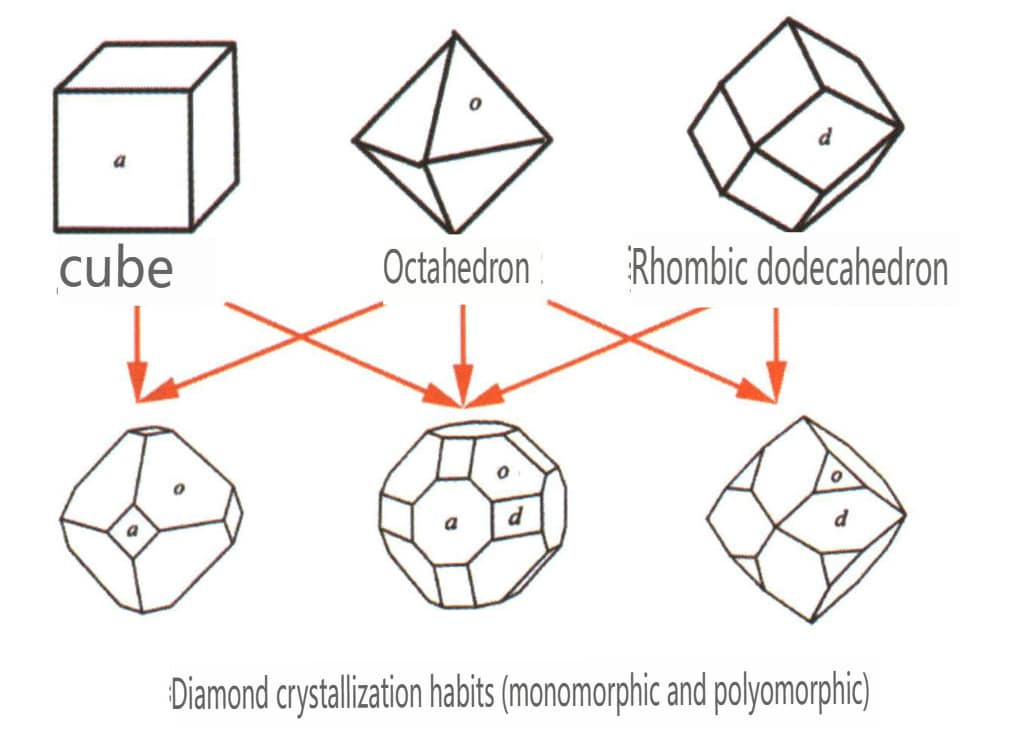
Obrázek 2-2-24 Krystalové zvyklosti diamantu
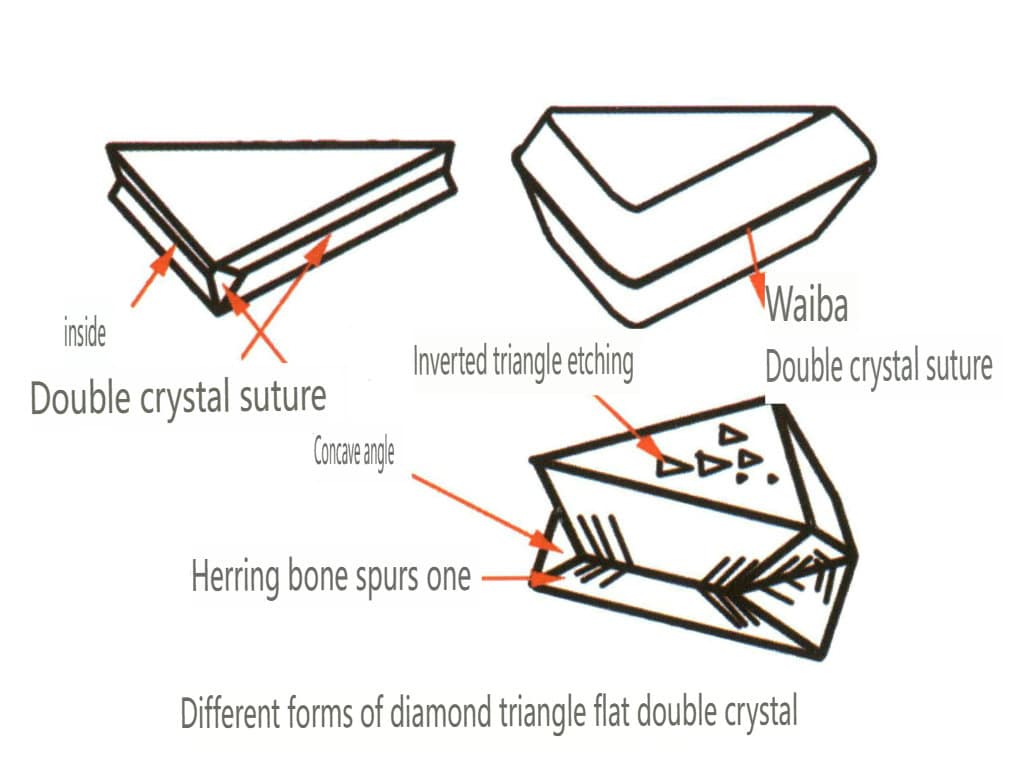
Obrázek 2-2-25 Dvojitý kosočtvercový habitus
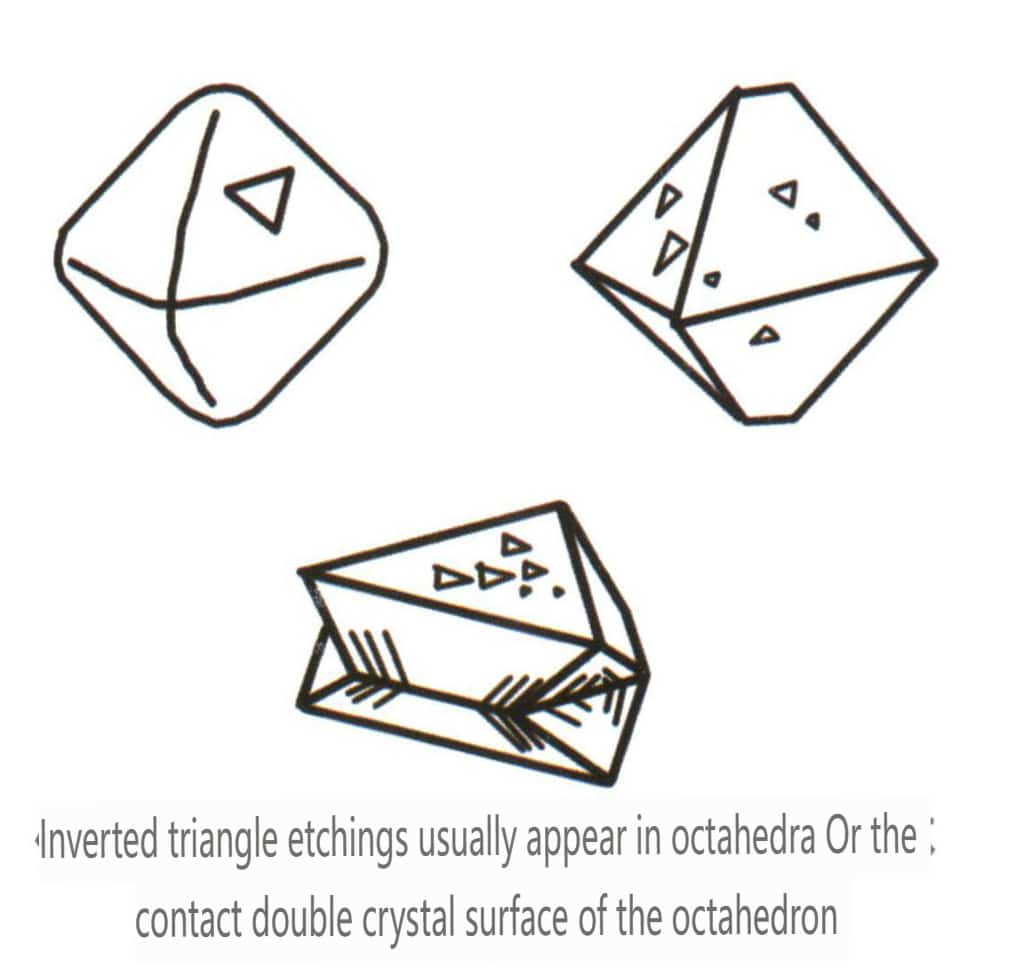
Obrázek 2-2-26 Obrázek leptaného obráceného trojúhelníku osmistěnných krystalových ploch diamantu

Obrázek 2-2-27 Obrácený trojúhelníkový lept na povrchu osmistěnného krystalu diamantu
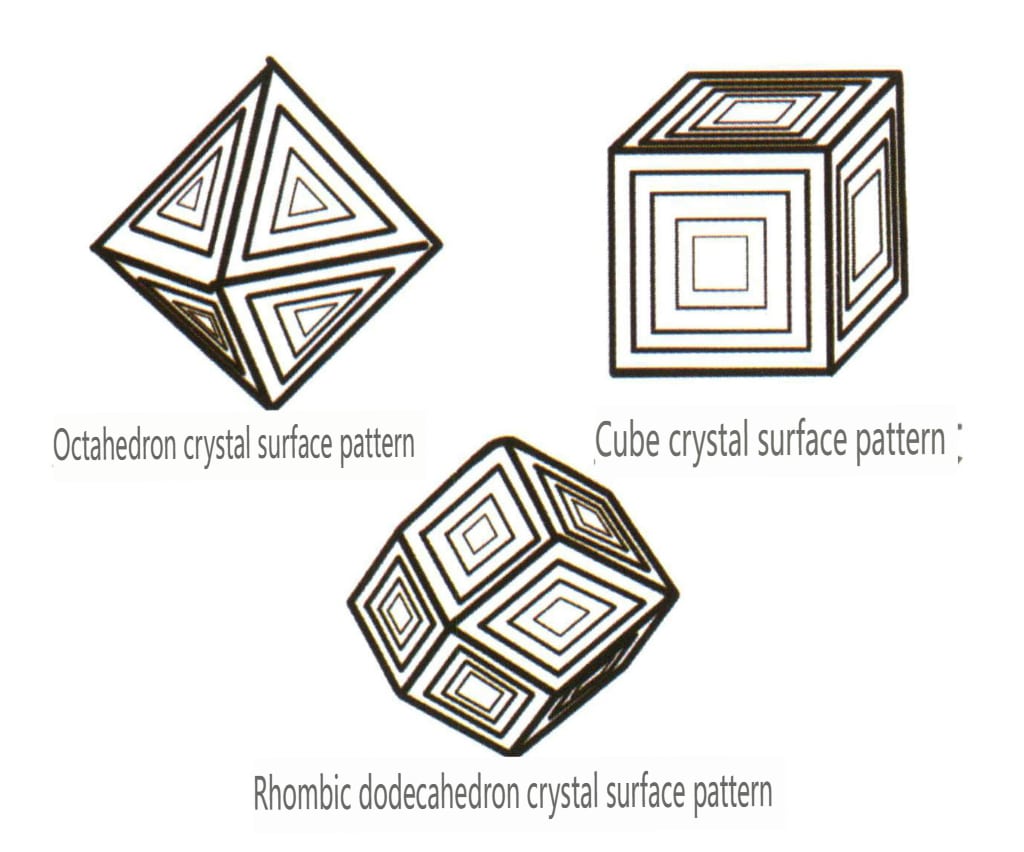
Obrázek 2-2-28 Obrázek leptaného obráceného trojúhelníku osmistěnných krystalových ploch diamantu

Obrázek 2-2-29 Obrácený trojúhelníkový lept na povrchu osmistěnného krystalu diamantu
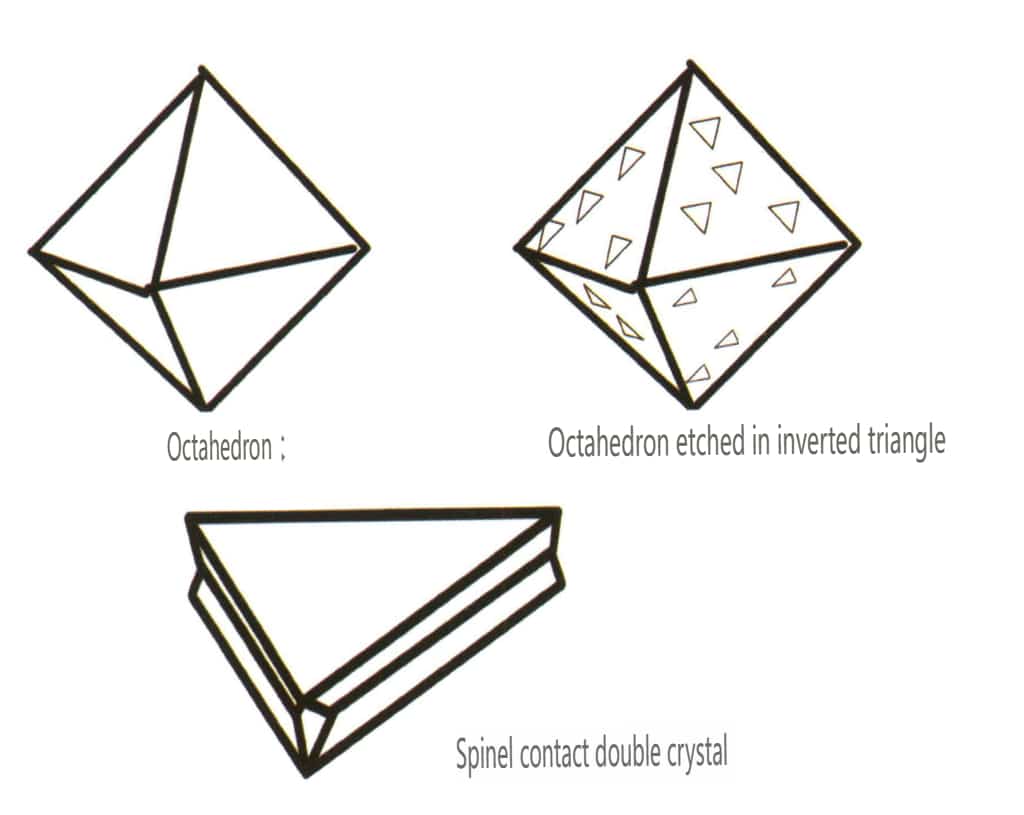
Obrázek 2-2-30 Krystalový habitus spinelu

Obrázek 2-2-31 Běžné formy krystalů spinelu

Obrázek 2-2-32 Kontaktní dvojčata spinelu
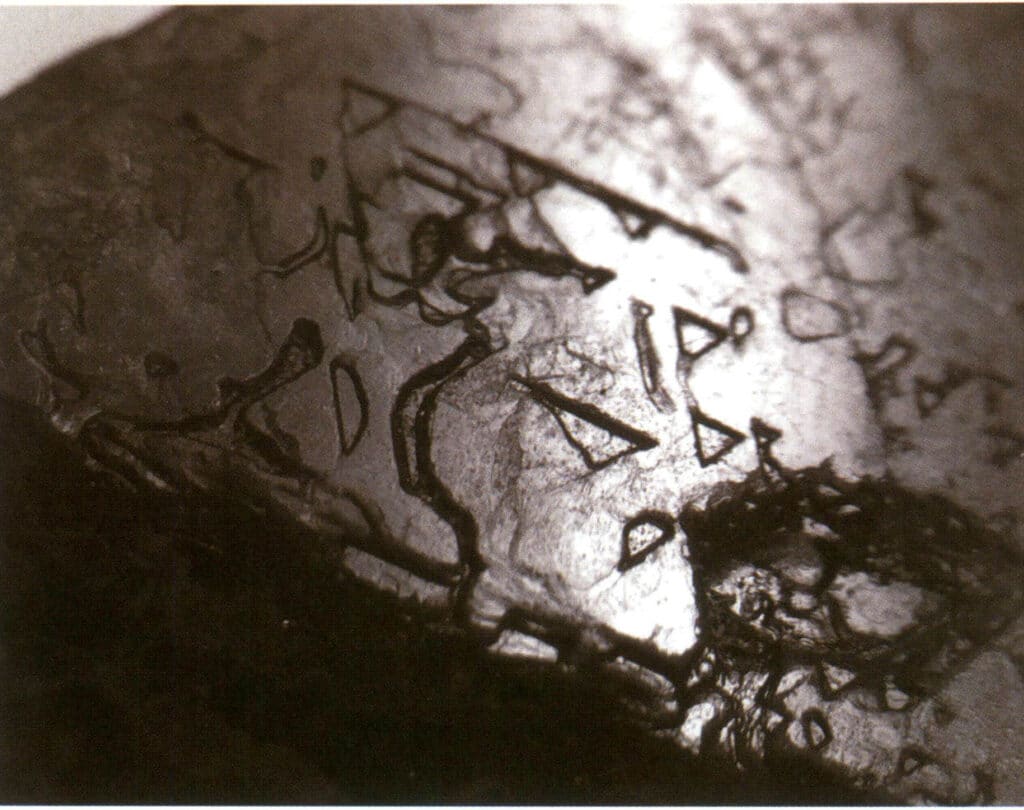
Obrázek 2-2-33 Obrácený trojúhelníkový leptaný obrazec na povrchu spinelu
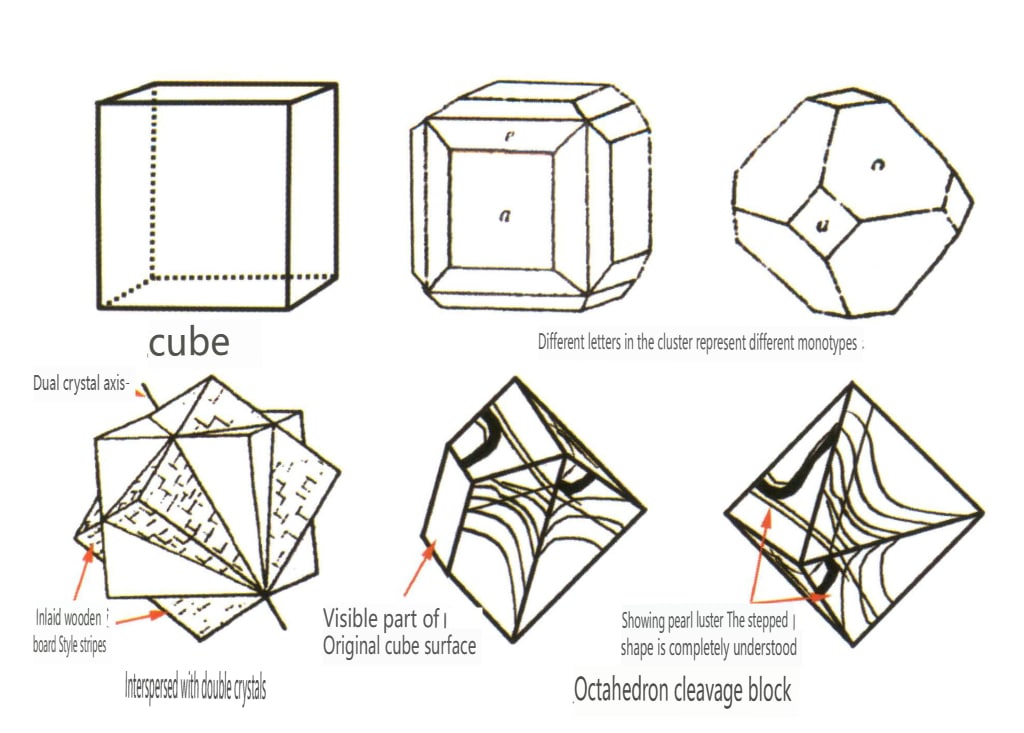
Obrázek 2-2-34 Krystalové zvyklosti fluoritu

Obrázek 2-2-35 Krystal fluoritu
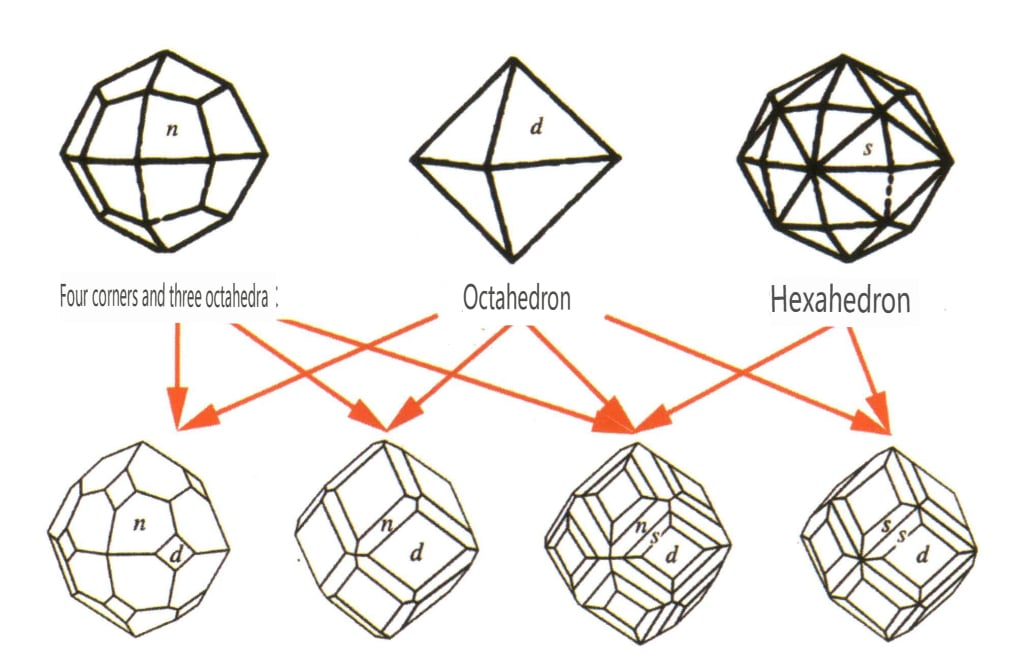
Obrázek 2-2-36 Krystalový habitus granátu

Obrázek 2-2-37 Soustředné prstencové pásy na povrchu krystalů granátu, které mají stejný tvar jako krystalové plochy
Tabulka 3: Společné charakteristiky drahokamových krystalů středních a nízkých krystalů
| Drahokamy tón Jméno | Klasifikace krystalů | Důležité vlastnosti krystalů | |||
|---|---|---|---|---|---|
| Drahokamy tón Jméno | Klasifikace krystalů | Křišťálový návyk | Běžné krystalové formy | Běžné formy dvojčat | Běžné vzory krystalových ploch |
| Beryl | Šestiboká krystalová soustava | Sloupcovitý krystalový habitus (obrázek 2-2-38) | Šestiboká sloupcovitá krystalová forma (obrázky 2-2-39, 2-2-40) | Vzácné | Viditelné podélné pruhy |
| Olověný kámen | Tetragonální krystalová soustava | Sloupcovitý krystalový habitus (obrázek 2-2-41) | Čtvercový sloup se čtvercovým průřezem, který se objevuje společně se čtvercovým dvojitým kuželem (obrázek 2-2-42). | Viditelné dvojkrystaly ve tvaru kolena | Žádné speciální vzory |
| Korund | Trigonální krystalová soustava | Deskovitý krystalový habitus, sloupcovitý krystalový habitus (obrázek 2-2-43) | Rubíny mají často tvar šestibokého hranolu (obrázek 2-2-44), zatímco safíry často vykazují šestiboký bipyramidální soudkovitý krystal (obrázek 2-2-45). | Běžně pozorované bikrystaly. | Viditelné pruhy. |
| Turmalín . | Sloupcovitý krystalový habitus (obrázek 2-2-46) | Krystalové plochy na obou koncích jsou různé a průřez je sférický trojúhelník (obrázek 2-2-47). | Vzácné | Viditelné podélné pruhy (obrázek 2-2-48) | |
| Křemen (křišťálový křemen) | Sloupcovitý krystalový habitus (obrázek 2-2-49) | Průřez je šestiboký, šestiboké bipyramidy jsou vzácné (obrázky 2-2-50, 2-2-51), šestiboké monopyramidy jsou běžné. | Běžný kontakt s bikrystaly (známými také jako japonské bikrystaly) | Běžné vodorovné pruhy na povrchu krystalů | |
| Chrysoberyl | Trigonální krystalová soustava | Charakteristiky sloupcové krystalizace (obrázek 2-¬2-52) | Monokrystalický je vzácný | Běžná je trikrystalická (obrázek 2-2-53), jako identifikační kritérium lze použít hexagonální a konkávní úhly. | Jako identifikační kritérium lze použít pruhy trikrystalu. |
| Topaz | Sloupcovitý krystalový habitus (obrázek 2-2-54) | Průřez je kosočtvercový a vrchol se často jeví jako obálka (obrázek2-2-55). | Bi-krystaly jsou vzácné | Viditelné podélné pruhy | |
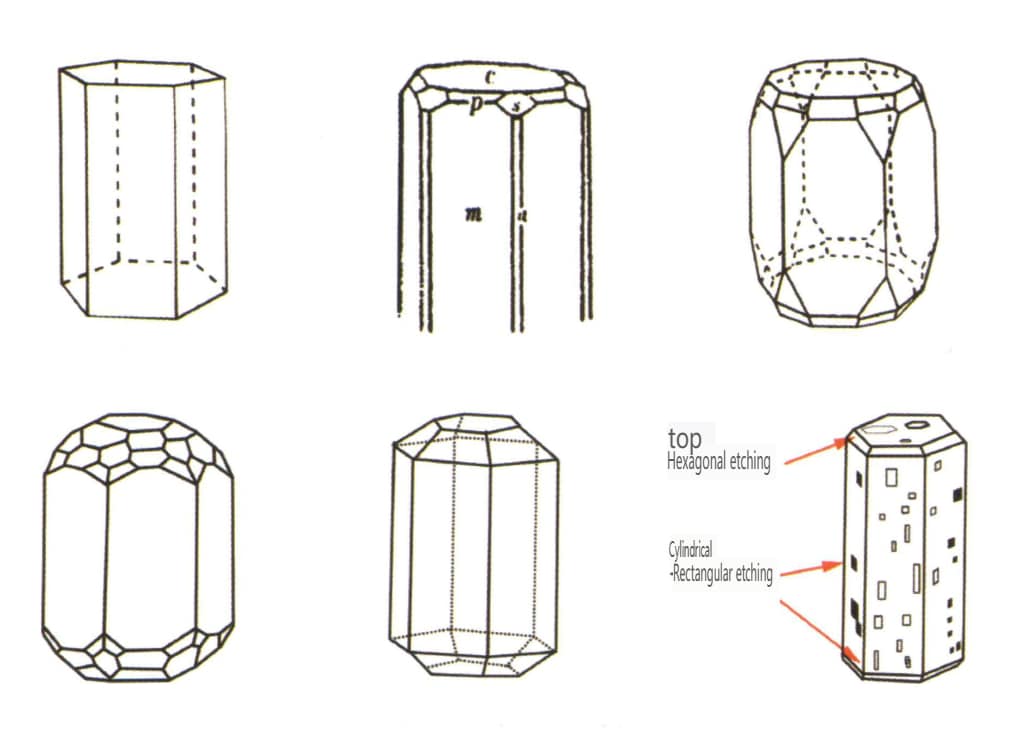
Obrázek 2-2-38 Krystalový habitus berylu

Obrázek 2-2-39 Běžné formy krystalů smaragdu

Obrázek 2-2-40 Běžné formy krystalů akvamarínu
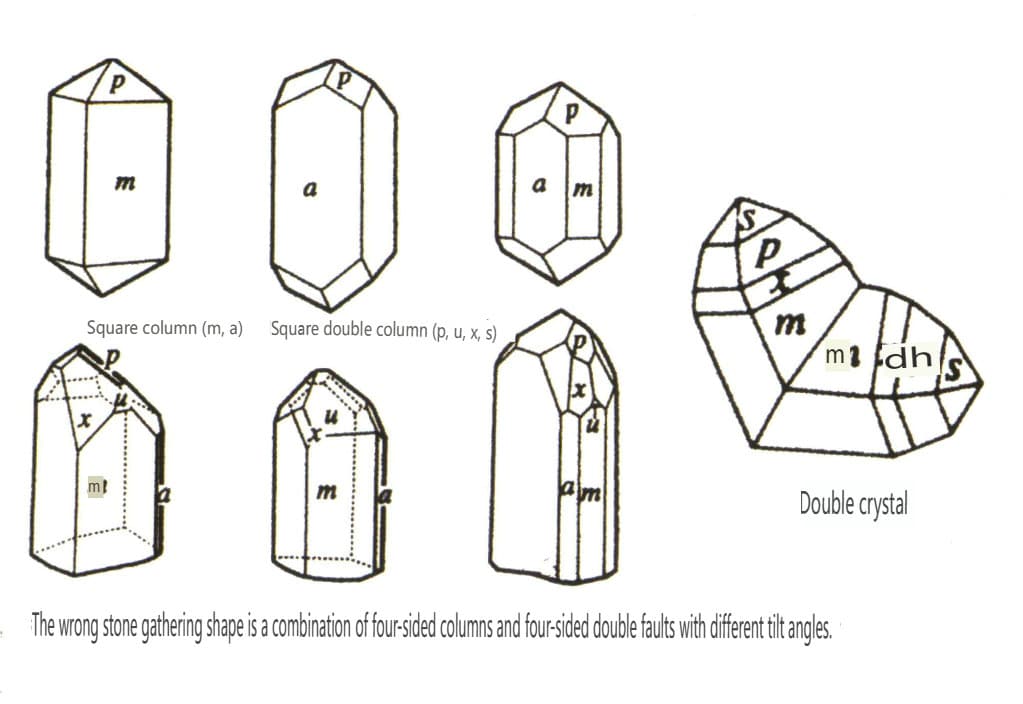
Obrázek 2-2-41 Krystalové habity zirkonu

Obrázek 2-2-42 Krystal zirkonu
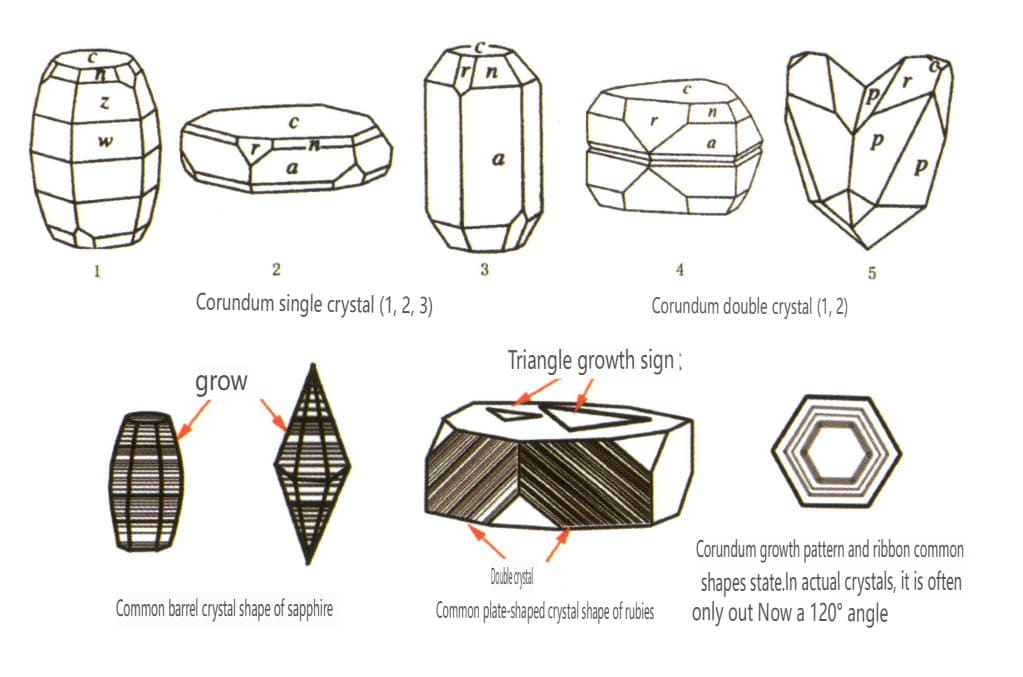
Obrázek 2-2-43 Krystalový habitus korundu

Obrázek 2-2-44 Rubínový krystal

Obrázek 2-2-45 Mechanické dvojče rubínu
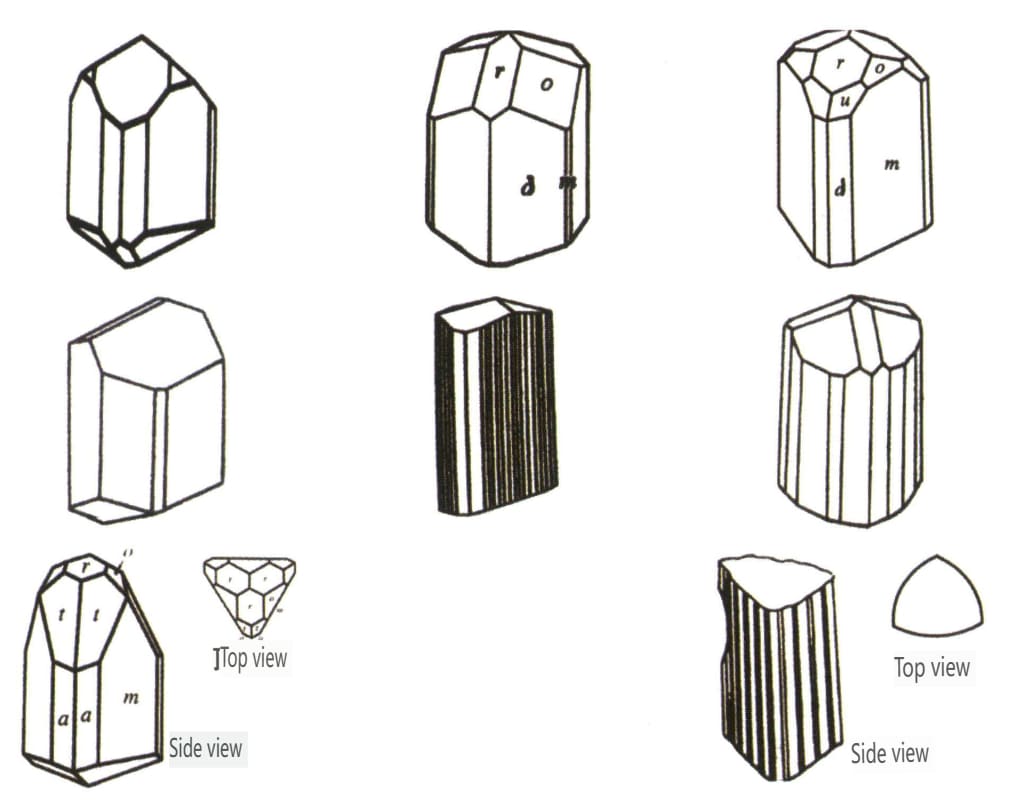
Obrázek 2-2-46 Krystalové habity turmalínu

Obrázek 2-2-47 Krystal turmalínu

Obrázek 2-2-48 Povrchové podélné proužky krystalu turmalínu
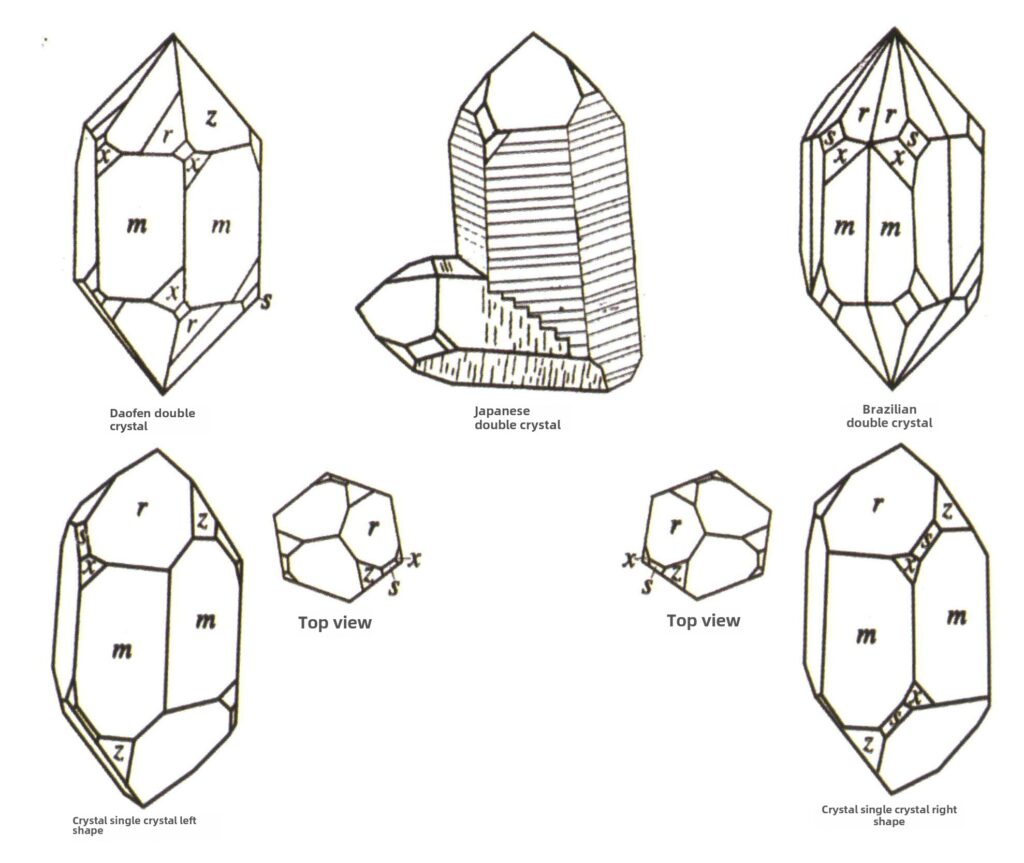
Obrázek 2-2-49 Krystalizační zvyklosti krystalů

Obrázek 2-2-50 krystalové těleso

Obrázek 2-2-51 Krystalové těleso
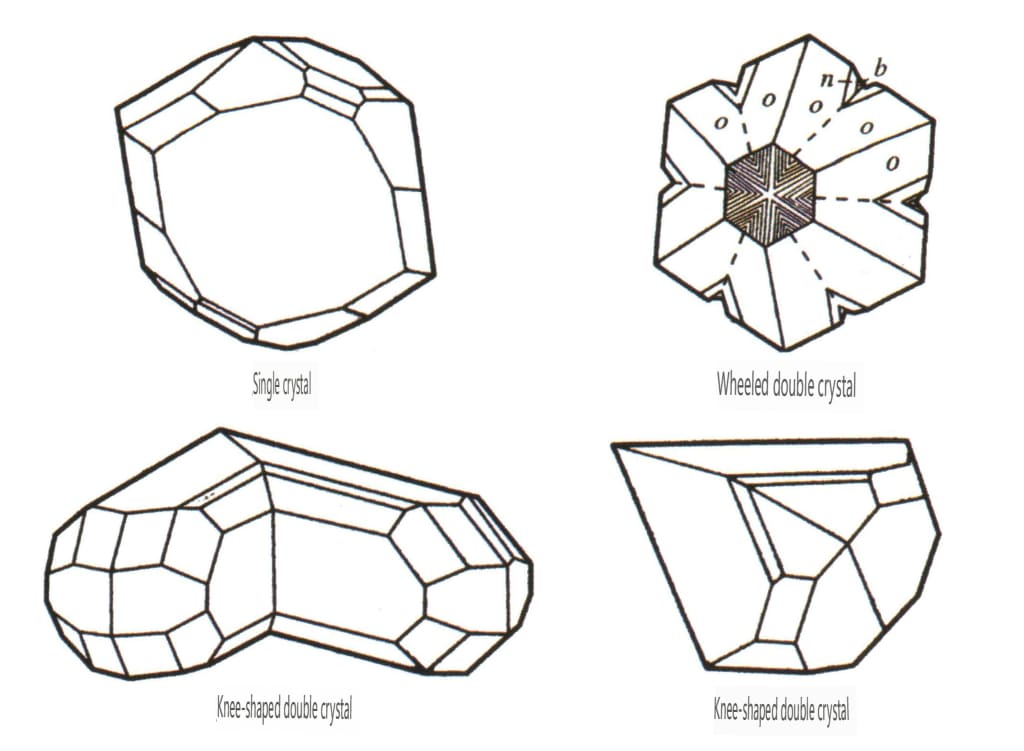
Obrázek 2-2-52 Krystalový habitus chryzoberylu

Obrázek 2-2-53 Krystal chryzoberylu
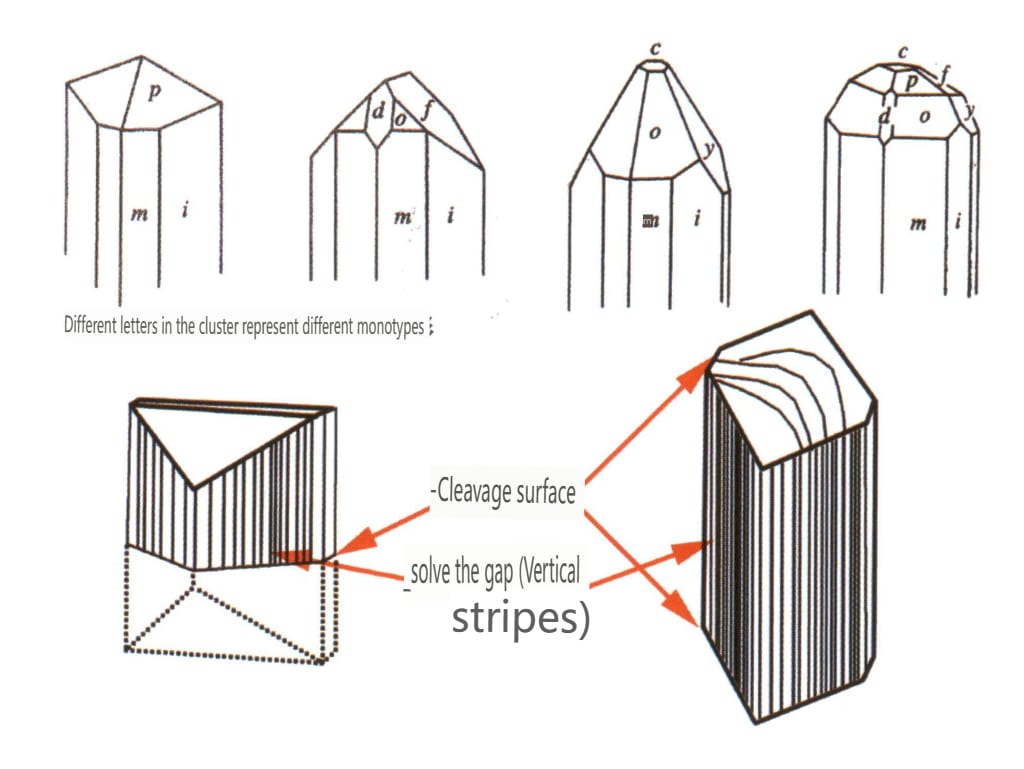
Obrázek 2-2-54 Krystalové zvyklosti topazu

Obrázek 2-2-55 Topazový krystal
Oddíl IV Proč krystaly drahých kamenů rostou různě
Z mikroskopického hlediska je drahokamový krystal těleso složené z prvků různých velikostí uspořádaných podle různých pravidel. Z makroskopického hlediska má mnoho drahých kamenů díky svému různému složení vlastnosti krystalu. Existují však i některé zvláštní případy, například heteromorfní. Abychom lépe pochopili, proč drahokamové krystaly vypadají jinak, představíme si zde pět aspektů: heteromorfnost, izomorfismus, molekulárně mechanické promíchávání, voda v drahokamových minerálech a chemické složení drahokamů.
1. Heteromorfní
Přestože některé minerály mají stejné chemické složení, mají velmi odlišnou krystalovou strukturu (uspořádání prvků v trojrozměrném prostoru) a vykazují značné rozdíly ve fyzikálních a chemických vlastnostech (tabulka 4). Tento jev označujeme jako heteromorfismus, například diamant a grafit (obrázek 2-2-56).
Běžný křemen má fenomén heteromorfismu. Sillimanit, andalusit a kyanit jsou skupinou variant heteromorfismu.
K přeměně heteromorfismu dochází za podmínek pevného stavu. Během procesu strukturní transformace může uvnitř krystalu vznikat tlak, který často vede ke vzniku dvojčat uvnitř krystalu.

Tabulka 4: Srovnání vlastností diamantu a grafitu
| Minerální | Diamond | Grafit |
|---|---|---|
| Komponenty | Uhlík (C) | Uhlík (C) |
| Podmínky tvorby | Vysoká teplota a vysoký tlak | Vysoká teplota |
| Krystalový systém, zvyk | Izometrická krystalová soustava, osmistěn, kosočtverečný dvanáctistěn | Šestiboká krystalová soustava, vrstevnatá |
| Barva | Bezbarvý, žlutý, modrý, růžový, zelený atd. | Černá |
| Luster | Adamantinový lesk | Kovový lesk |
| Transparentnost | Průhledné až neprůhledné | Neprůhledné |
| Index lomu | 2.40 ~ 2.48 | 1.93 ~ -2.07 |
| Mechanické vlastnosti | Mírná oktaedrická štěpnost, tvrdost 10, hustota 3,52 | Sada s dokonalým štěpením, tvrdost 1, hustota 2,10 |
| Ostatní vlastnosti | Vynikající tepelná vodivost; kromě přírodních modrých diamantů, které jsou polovodiče, jsou diamanty ostatních barev izolanty. | Mírná tepelná vodivost, dobrá elektrická vodivost |
2. Izomorfismus
Izomorfismus označuje jev, kdy jsou některé částice v mřížkové struktuře nahrazeny jinými částicemi s podobnými vlastnostmi, což vede k nepatrným změnám parametrů mřížky a fyzikálních a chemických vlastností. Naproti tomu krystalová struktura zůstává v zásadě nezměněna. Lze ji chápat tak, že prvky v krystalu drahého kamene jsou nahrazeny jinými prvky. Opakující se struktura prvků krystalu drahého kamene naopak zůstává stejná, s mírnými odchylkami ve vzdálenostech mezi atomy. Přesto fyzikálně-chemické vlastnosti krystalu drahého kamene procházejí mírnými změnami (obrázek 2-2-57 až obrázek 2-2-58).
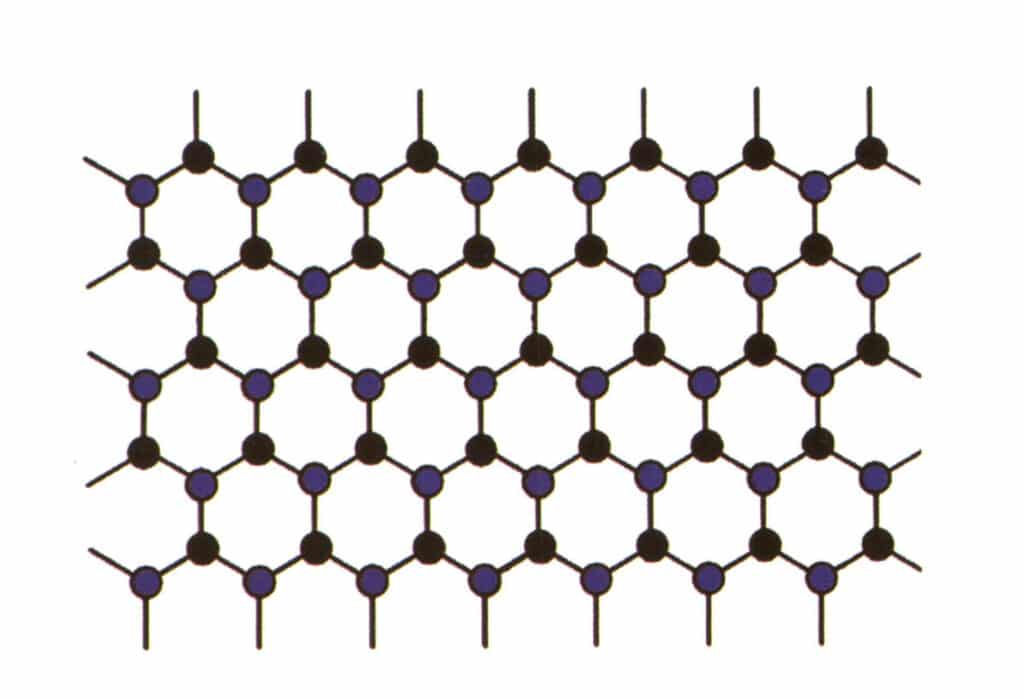
Obrázek 2-2-57 Schéma simulace krystalové struktury (modrá a černá barva označují částice prvků)
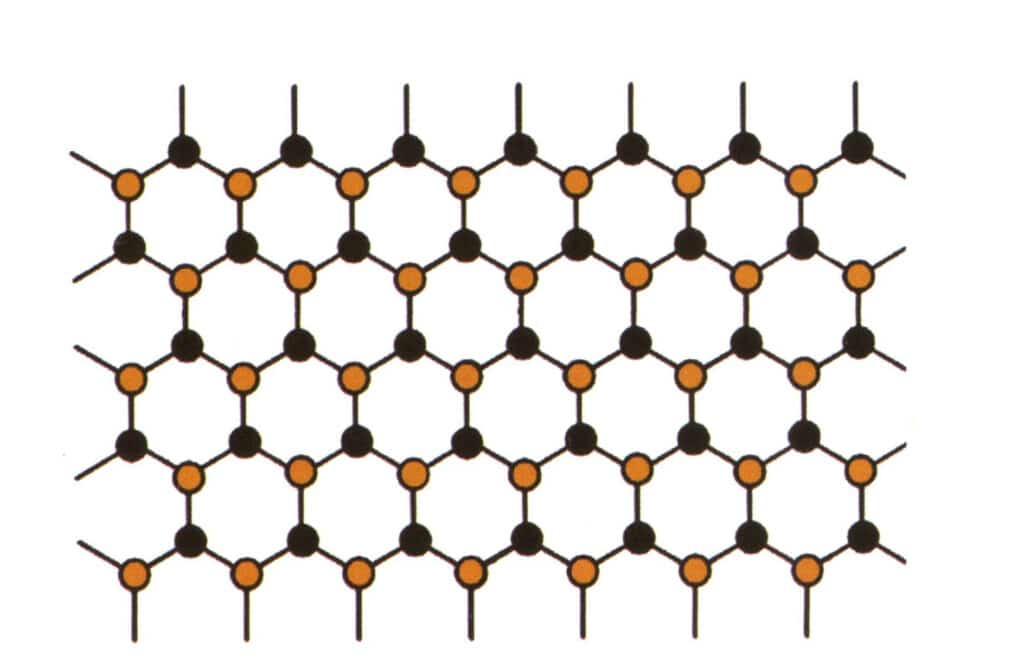
Obrázek 2-2-58 Schéma simulace krystalové struktury (černá představuje elementární částice, žlutá představuje nové elementární částice, které částečně nahrazují modré elementární částice, žlutá nemusí zcela nahradit všechny modré částice)
Koncept izomorfismu vysvětluje, proč mohou mít drahé kameny ze stejné rodiny tolik barev a proč existují rozdíly v indexu lomu a hustotě mezi drahými kameny ze stejné rodiny.
Rodinu lze chápat jako typ drahého kamene, u něhož jsou opakující se vzory krystalových prvků stejné, ale fyzikální a chemické formy se mírně liší. Například rodina korundů zahrnuje dva členy, rubín a safír, zatímco rodina berylů zahrnuje odrůdy smaragdu, akvamarínu a morganitu.
(1) olivín
Chemické složení olivínu je (Mg,Fe)₂SiO₄. V jeho složení dochází k úplné izomorfní substituci prvků Fe a Mg. Se zvyšujícím se obsahem Fe v olivínu se barva olivínu stává tmavší, zvyšuje se index lomu a také hustota.
(2) Korund
Čistý korund bez příměsí (Al₂O₃) je bezbarvý, a když Cr nahradí Al, získá drahokam růžově červený až červený odstín, známý jako rubín. Zbývající barvy se nazývají safír, například oranžovožlutý safír nebo bezbarvý safír. Běžně označovaný safír je konkrétně modrý safír, kde Fe a Ti nahrazují Al. Čím vyšší je obsah barvicích prvků v náhradním drahokamu, tím sytější je barva drahokamu; naopak čím nižší je obsah, tím světlejší je barva.
(3) Turmalín
Turmalín označuje stejný typ drahokamu jako turmalín, přičemž turmalín je jeho mineralogický název a turmalín je jeho gemologický název. Chemické složení berylu je (Na, Ca)R₃Al₃Si₆O₁₈(O, OH, F), kde R je především Mg , Fe , Cr , Li, Al , Mn, přičemž prvky v R se mohou navzájem zcela nebo částečně nahrazovat, což má za následek mimořádně širokou škálu barev turmalínu. Například když je R převážně Fe, beryl představuje tmavě modrou nebo dokonce černou barvu; když je R převážně Mg, beryl představuje žlutou až hnědou barvu; když R je převážně Li nebo Mn, je beryl růžový nebo světle modrý; je-li R převážně Cr, je turmalín sytě zelený.
Z výše uvedeného je patrné, že záměna prvků s podobnými vlastnostmi vede ke krásnějším a zářivějším barvám drahokamů.
3. Molekulárně mechanické mísení
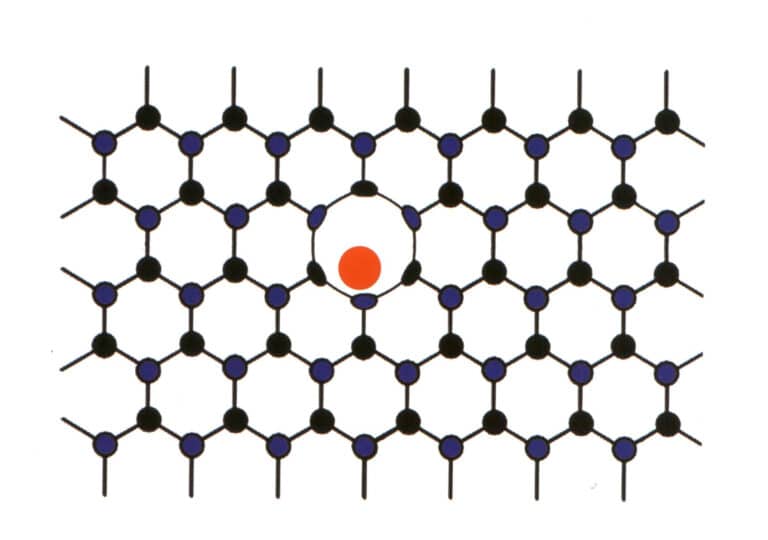
Mezi hlavní prvky pravidelně uspořádaných drahých kamenů někdy násilně vstupují určité prvky. Nízký podíl vstupujících prvků však nenarušuje opakující se vzor hlavních prvků drahokamu, pouze způsobuje deformaci (obrázek 2-2-59). Tato situace se označuje jako molekulárně mechanické mísení, například molekulárně mechanické mísení dusíku a boru v diamantech, při kterém vznikají modré, růžové a žluté diamanty, které jsou velmi cenné.
4. Voda v drahých minerálech
Některé drahé kameny obsahují vodu, která je důležitou složkou drahých minerálů a úzce souvisí s vlastnostmi drahých kamenů. Na základě formy vody přítomné v drahých kamenech a její úlohy v krystalové struktuře lze vodu v drahých kamenech rozdělit do dvou kategorií: jednou je absorpční voda, která s krystalovou strukturou nesouvisí, a druhou je voda, která se podílí na krystalové struktuře minerálu, včetně krystalizační vody, zeolitické vody, mezivrstvy a konstituční vody. Voda úzce související s drahými kameny zahrnuje absorpční vodu, krystalizační vodu a konstituční vodu.
Jedním z nich je absorpce vody, například opálu (chemické složení je SiO₂ - nH₂O, n představuje počet H₂O, obsah je proměnlivý) v molekule vody, což je neutrální molekula vody mechanicky adsorbovaná na částice minerálů nebo na lomové plochy. Když teplota dosáhne 100 ~ 110°stupňů za normálního tlaku, mohou všechny molekuly vody uniknout a nepoškodí strukturu krystalové mřížky, takže aby Opál v počítadle při dlouhodobém působení silného světla nepraskl za sucha, měl by se do počítadla vložit hrnek s vodou.
Druhou je krystalizační voda, například krystalizační voda v tyrkysu [chemické složení je CuAl₆(PO₄)₄(OH)₈-4H₂O, kde obsah H₂O může dosáhnout 19,47% ]. Tato neutrální molekula vody existuje v pevných pozicích v mřížce a slouží jako strukturní jednotka, je součástí chemického složení minerálu. Teplota, při které krystalizační voda uniká, obvykle nepřesahuje 600 ℃ a obvykle uniká při 100 -200 ℃. Když drahokam ztratí krystalizační vodu, jeho krystalová struktura se poškodí a vytvoří se nová struktura.
Třetí je konstituční voda, známá také jako kombinovaná voda, která se účastní minerální mřížky ve formě OH-, H⁺, H₃O⁺ plazmy, přičemž OH- je nejčastější. Konstituční voda je součástí chemického složení minerálu, zaujímá pevné pozice v mřížkové struktuře s definovaným podílem na jejím složení. Strukturní voda vyžaduje vyšší teplotu, aby se mohla uvolnit a poškodit svou strukturu, obvykle kolem 600 -1000 ℃. Když drahokam ztratí strukturní vodu, jeho krystalová struktura se zničí. Mnoho drahých kamenů obsahuje konstituční vodu, například turmalín[chemické složení je ( Na, Ca )R₃Al₃Si₆O₁₈(O, OH, F), kde R zahrnuje především Mg , Fe , Cr, Li, Al, Mn atd, a prvky v R se mohou navzájem zcela nebo částečně nahradit] a topaz [chemické složení je Al₂SiO₄( F, OH) ₂ ].
5. Chemické složení drahých kamenů
Drahokamy se stejně jako jiné látky skládají z chemických prvků. Každý typ drahokamu má své specifické chemické složení a určitý rozsah variací, který určuje různé charakteristiky a vlastnosti drahokamu. Drahé kameny patří mezi minerály a horniny a klasifikaci chemického složení drahých kamenů lze vysledovat podle chemického složení minerálů.
V současné době se mezi hlavní metody klasifikace minerálů řadí klasifikace podle chemického složení (systém Dana), geochemická klasifikace, genetická klasifikace, aplikační klasifikace a krystalově-chemická klasifikace. Nejrozšířenější metodou je chemická klasifikace založená na chemickém složení a krystalové struktuře (systém Hugo Strunze) (tabulka 5).
Tabulka 5: Systém chemické klasifikace minerálních krystalů
| Pořadí úrovní | Základ pro rozdělení | Příklad |
|---|---|---|
| Hlavní kategorie | Typ směsi | Hlavní kategorie soli obsahující kyslík |
| Třída | Typy aniontů nebo komplexních aniontů | Třída silikátů |
| (Podkategorie) | Struktura aniontového komplexu | Rámcová podtřída křemičitanů |
| Skupina | Typy krystalové struktury a iontové vlastnosti | Skupina korundu, skupina berylu, skupina granátu |
| (podskupina) | Typy kationtů | Podskupina alkalických živců |
| Specie | Určitá krystalová struktura a chemické složení | Ortoklas KAlSi3O8 |
| (poddruh) | Stejná krystalová struktura, odlišné složení nebo vlastnosti, morfologie | Adularia KAlSi3O8 |
















